Regularization Designs for Uniform Spatial Resolution and Noise Properties in Statistical Image Reconstruction for 3D X-ray CT

Abstract

Statistical image reconstruction methods for X-ray computed tomography (CT) provide improved spatial resolution and noise properties over conventional filtered back-projection (FBP) reconstruction, along with other potential advantages such as reduced patient dose and artifacts. Conventional regularized image reconstruction leads to spatially variant spatial resolution and noise characteristics because of interactions between the system models and the regularization. Previous regularization design methods aiming to solve such issues mostly rely on circulant approximations of the Fisher information matrix that are very inaccurate for undersampled geometries like short-scan cone-beam CT. This paper extends the regularization method proposed in [1] to 3D cone-beam CT by introducing a hypothetical scanning geometry that helps address the sampling properties. The proposed regularization designs were compared with the original method in [1] with both phantom simulation and clinical reconstruction in 3D axial X-ray CT. The proposed regularization methods yield improved spatial resolution or noise uniformity in statistical image reconstruction for short-scan axial cone-beam CT.

I. Introduction

Statistical image reconstruction methods for X-ray computed tomography (CT) use realistic models that incorporate the statistical properties of the noise and the physics of the data acquisition system [2]. Compared to conventional filtered back-projection (FBP) reconstruction, statistical methods are more accurate and are more flexible for modeling different kinds of physical constraints. Potential advantages of statistical image reconstruction methods over FBP reconstruction have been demonstrated in terms of noise, resolution, and artifacts [3]–[5]. Such improvements in image quality become more apparent in low-dose scans where FBP reconstruction suffers from increased streak artifacts [6]. However, many factors need to be addressed to ensure the success of statistical methods in clinical applications. Diagnostic readability of the reconstructed images depends on various characteristics such as texture, resolution, noise, and artifacts. In particular, uniformity of the resolution or noise characteristics throughout the reconstructed image is desirable. This paper proposes new space-variant regularization designs that yield reconstructed images with improved uniformity of resolution or noise.

Regularization is necessary to control noise since unregularized image reconstruction leads to excessively noisy images. By integrating a penalty term into the objective function, regularized image reconstruction methods, such as penalized-likelihood (PL) methods or penalized weighted least squares (PWLS) methods, provide controlled noise and resolution properties in the reconstructed image. However, interactions between the regularization, system models, and statistical weighting cause the reconstructed images to have object-dependent nonuniform and anisotropic spatial resolution and noise properties, even for idealized shift-invariant imaging systems [1]. Nonuniformity becomes severe for short-scans in cone-beam CT (CBCT), having angular spans of π + 2γ where γ is the fan angle of the detector, compared to full scans, and also for undersampled voxels¹ in 3D axial or helical scanning geometries. In [1], a regularizer based on the aggregated certainty was developed for 2D PET to yield images with approximately uniform spatial resolution, and that regularizer has been used for other geometries and modalities [9]–[13]. However, the aggregated certainty regularizer does not provide uniform resolution when applied to modalities such as 2D short-scan fan-beam CT or 3D cone beam CT because of asymmetric scan geometries caused by short-scan orbits or cone-angle effects or both. In [10] and [12], the original aggregated certainty regularizer was modified with a diagonal scaling factor for 3D PET. Recently, it was also extended to both static and multi-frame reconstruction in 3D PET by considering spatially variant and frame-dependent sensitivity [14]. Since the term “aggregated certainty” is less apt for some imaging modalities such as CT, instead, we use the more general term “pre-tuned spatial strength”, which represents that the purpose of the function is to control the regularization strength at each voxel, before the reconstruction process, so that the reconstructed image is guided to have desired characteristics, i.e., uniform resolution.

Many previous regularization design methods focussed on choosing directional coefficients in the regularizer by matching local characteristics, such as impulse response or correlation function, of the estimator to target characteristics to achieve uniform and isotropic resolution [15]–[17] or noise characteristics [18], [19]. Since both the global regulation parameters) and the pre-tuned spatial strengths can be incorporated into directional regularizer coefficients, those regulation design methods are more general and flexible than simply adjusting the regulation strength at each voxel. However, such design methods require additional computations to design the coefficients for every voxel, and it is challenging to obtain both uniformity and isotropy at the same time for either spatial resolution or noise characteristics. Especially for the undersampled voxels in cone-beam CT, locally circulant approximations of the Fisher information matrix are very inaccurate, leading to imperfect coefficient designs at such locations. Furthermore, the memory requirement to store all directional coefficients for every voxel can be burdensome.

This paper extends [1] by proposing a modified pre-tuned spatial strength function for 3D CT that yields improved resolution uniformity throughout the reconstructed image including undersampled voxel locations. We also propose a shift-variant regularizer that provides approximately uniform noise characteristics in the reconstructed image. Section II reviews the system models for statistical image reconstruction and some fundamental concepts such as estimator local impulse response (LIR) and covariance. Section III proposes new regularizes by generalizing the system matrix using a hypothetical geometry concept. Two different regularizers are presented that yield improved uniform resolution or noise characteristics in the reconstructed image, respectively. Section IV presents results using both simulated and real clinical X-ray CT data. Section V concludes by summarizing the contributions of this study and suggesting potential future work.

II. Spatial Resolution and Noise Properties of Statistical Image Reconstruction

This section first reviews statistical image reconstruction in terms of the system models for a penalized weighted least squares (PWLS) formulation. The concept of local impulse response and estimator covariance is also reviewed, and metrics for analyzing spatial resolution and noise properties in the reconstructed image are discussed.

A. Statistical Image Reconstruction

Noisy CT sinogram measurements can be expressed as a discrete vector, y = (y₁ …, y_nd), where y_i represents the ith line integral through the object for a given scanning geometry. These sinogram measurements are related to recorded detector measurements, I = (I₁, …, I_nd), by the Beer-Lambert law [20]. For simplicity, we use the following statistical model for the detector measurements under the mono-energetic assumption

$$E[I_i]={\overline{I}}_i=b_{i}exp(-{[\mathit{A}\mathit{x}]}_i)+r_i,$$

where A is the system matrix, x = (x₁, …, x_np) is the discrete vector of the imaged object, ${[\mathit{A}\mathit{x}]}_i={\sum }_{j=1}^{n_{\mathrm{p}}}{a}_{ij}{x}_j$, b_i is the X-ray source intensity for ith ray, and r_i denotes the background contributions from factors such as scatter and crosstalk.

The measurement noise statistics can be modeled using a probability density function by relating the measurements y_i to their mean values E[y_i], and are mainly affected by physical processes in the data acquisition system. For integrating detectors, the statistics of X-ray measurements is a complicated mixture of compound Poisson photon distribution and Gaussian electronic noise [21], [22]. In practice, the following simple models have been used successfully. A Poisson model for pre-log data I_i can be written as [23]

$$I_i~\text{Poisson}\{b_{i}exp(-{[\mathit{A}\mathit{x}]}_i)+r_i\}.$$ (1)

A quadratic approximation of the negative log-likelihood of (1) implies that the post-log data y_i is a approximately Gaussian random variable [24], [25]

$$y_i~N({[\mathit{A}\mathit{x}]}_i,\frac{{\overline{I}}_i}{{({\overline{I}}_i-r_i)}^2}).$$ (2)

CT image reconstruction often is formulated as a minimization problem with a PWLS cost function of the form

$$\mathrm{\Psi }(\mathit{x})=\mathrm{L}(\mathit{x})+\mathrm{R}(\mathit{x}),\mathrm{L}(\mathit{x})=\frac{1}{2}{\Vert \mathit{y}-\mathit{A}\mathit{x}\Vert }_{\mathit{W}}^2$$ (3)

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{arg\; min}\mathrm{\Psi }(\mathit{x}),$$ (4)

where R(x) is a regularizer that controls the spatial resolution and noise characteristics in the reconstructed image typically by penalizing local differences between voxels, and W = D[w_i] ≜ diag{w_i} is a statistical weighting matrix. (We assume the measurements are independent so the data covariance is diagonal.) The coefficients {w_i} of the statistical weighting matrix should be the reciprocal of the variances of the measurements by the Gauss-Markov theorem [26]:

$$w_i\triangleq \frac{1}{{\sigma }^2(E[y_i])}=\frac{{({\overline{I}}_i-r_i)}^2}{{\overline{I}}_i}.$$

In practice, the means of the measurements are unknown so typically the weights are estimated by a plug-in approach, i.e., w_i ≈ 1/σ²(y_i) for transmission tomography. The ideas in this paper generalize readily to other penalized-likelihood formulations [27].

We consider regularizers having the following form:

$$\mathrm{R}(\mathit{x})=\sum _{j=1}^{n_{\mathrm{p}}}{\kappa }_j\sum _{l=1}^{N_1}{\kappa }_{j-j_l}{\beta }_l{\psi }_l((c_l\ast \ast \ast x)[n,m,z]),$$ (5)

where N₁, is the size of the neighborhood, j_l denotes the offset of the lth neighbor in lexicographical order, β_l is a regulation parameter that balances between the data-fitting term and the regularizer [28], κ_j is a user-defined value that controls local spatial resolution and noise in the reconstructed image [1, eqn. (35)], ψ_l is a potential function, * * * denotes 3-D convolution. We define a first-order differencing function that penalizes lth neighbor as

$$c_l[n,m,z]=\frac{\delta [n,m,z]-\delta [n-n_l,m-m_l,z-z_l]}{\sqrt{n_l^2+m_l^2+z_l^2}},$$

where δ[n, m, z] is the Kronecker impulse at location [0, 0, 0], and n_l, m_l, z_l denote the offset of the lth neighbor. The regulation parameter β_l is usually determined based on data-independent factors like voxel sizes, and a typical choice is β_l = 1, ∀l. The parameter also can be selected more systematically as in [28].

The goal of this paper is to refine the regularizer R(x) by designing {κ_j} so that the reconstructed image has more uniform resolution or noise properties. We want to improve upon the design proposed in [1] which was

$${\kappa }_j=\sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{w}_i}{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2}}.$$ (6)

B. CRC and Ensemble Variance

The local impulse response describes the local spatial resolution properties. We used the following definition of local impulse response at the jth voxel [16]:

$$l_j\triangleq \underset{\varepsilon \to 0}{lim}\frac{\widehat{\mathit{x}}\left(\overline{\mathit{y}}\right({\mathit{x}}^{\text{true}}+\varepsilon {\mathit{\delta }}_j\left)\right)-\widehat{\mathit{x}}\left(\overline{\mathit{y}}\right({\mathit{x}}^{\text{true}}\left)\right)}{\varepsilon }$$ (7)

$$={\nabla }_{\mathit{y}}\widehat{\mathit{x}}(\mathit{y}){|}_{\mathit{y}=\overline{\mathit{y}}\left({\mathit{x}}^{\text{true}}\right)}{\nabla }_{\mathit{x}}\overline{\mathit{y}}(\mathit{x}){|}_{\mathit{x}={\mathit{x}}^{\text{true}}}{\mathit{\delta }}_j,$$ (8)

where δ_j is a Kronecker impulse at the jth voxel, and the gradient operations are matrices with the following elements:

$${[{\nabla }_{\mathit{y}}\widehat{\mathit{x}}(\mathit{y})]}_{ji}=\frac{\partial }{\partial y_i}{\widehat{x}}_j(\mathit{y}),{[{\nabla }_{\mathit{x}}\overline{\mathit{y}}(\mathit{x})]}_{ij}=\frac{\partial }{\partial x_j}{\overline{y}}_i(\mathit{x}).$$

For simplicity we focus on quadratic regularization, for which, from (8), the local impulse response of the PWLS estimator (4) is expressed as

$${\mathit{l}}_j={[{\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R}]}^{-1}{\mathit{A}}^{\prime }\mathit{W}\mathit{A}{\mathit{\delta }}_j,$$ (9)

where R is the Hessian of the regularizer R(x) [1].

One common metric for measuring the local resolution is the width of the local impulse response at the jth voxel, such as the full width half maximum (FWHM) [1]. Alternatively, the peak amplitude of the local impulse response, called the contrast recovery coefficient (CRC) [9], can be used to quantify resolution

$$\text{CRC}({\mathit{l}}_j)\triangleq {\mathit{\delta }}_j^T{\mathit{l}}_j={\mathit{\delta }}_j^T{[{\mathit{A}}^{\prime }\mathit{W}\mathbf{A}+\mathit{R}]}^{-1}{\mathit{A}}^{\prime }\mathit{W}\mathit{A}{\mathit{\delta }}_j.$$ (10)

To measure isotropy of an impulse response, the width measure is more effective. On the other hand, uniformity of the impulse responses is easier to assess with the CRC. In this paper, we use the CRC of the local impulse response to quantify spatial resolution.

With a quadratic regularizer, the closed-form solution of (4) is given by

$$\widehat{\mathit{x}}={({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\mathit{W}\mathit{y}.$$ (11)

The covariance of the reconstructed image x̂ [26] is

$$\text{cov}(\widehat{\mathit{x}})={({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\mathit{W}\text{cov}(\mathit{y})\mathit{W}\mathit{A}{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}.$$ (12)

If the weighting is chosen such that cov(y) = W⁻¹, then the reconstructed image covariance simplifies to

$$\text{cov}(\widehat{\mathit{x}})={({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\mathit{W}\mathit{A}{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}.$$ (13)

However, in some cases, additional factors are applied to W. For instance, Parker weighting [29] is applied to sinogram measurements for short-scan FBP reconstruction. It may also be used in iterative reconstructions so that the temporal resolution of such reconstructions matches that of FBP reconstruction. Such modifications change the statistical characteristics of W and it no longer satisfies cov(y) = W⁻¹ We can express the statistical weighting more generally as

$$\mathit{W}=\widehat{\mathit{W}}\mathit{V}=\mathit{D}[{\widehat{W}}_i{v}_i],$$ (14)

where the weighting Ŵ is the conventional choice that satisfies ŵ_i = 1/Var{y_i}, and {v_i} denotes additional weighting elements. The reconstructed image covariance (12) with such statistical weighting can be expressed as follows

$$\text{cov}(\widehat{\mathit{x}})={({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\stackrel{⌣}{\mathit{W}}\mathit{A}{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1},$$ (15)

where $\stackrel{⌣}{\mathit{W}}=\mathit{V}\widehat{\mathit{W}}\mathit{V}=\mathit{D}[{\widehat{W}}_i{v}_i^2]$.

The noise property of the estimator can be quantified with the ensemble variance at each voxel:

$$\text{var}({\widehat{\mathit{x}}}_j)={\mathit{\delta }}_j^T{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\stackrel{⌣}{\mathit{W}}{\mathit{A}}^{\prime }{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{\delta }}_j.$$ (16)

The entire jth column of the covariance matrix (15) represents the noise correlation of the jth voxel in the reconstructed image with all other voxels

$$\text{corr}({\widehat{\mathit{x}}}_j)\triangleq {({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{A}}^{\prime }\stackrel{⌣}{\mathit{W}}\mathit{A}{({\mathit{A}}^{\prime }\mathit{W}\mathit{A}+\mathit{R})}^{-1}{\mathit{\delta }}_j.$$ (17)

Our goal is to design regularizes for which l_j or corr(x̂_j) are approximately uniform over the 3D object.

III. New Regularization Designs

This section reviews the aggregated certainty regularizer developed in [1], and then develops new regularization designs that provide approximately uniform resolution or noise properties by using an “ideal” system matrix factorization.

A. System matrix augmentation using a hypothetical geometry

The aggregated certainty regularizer in [1] was developed for shift-invariant systems like 2D PET. For shift-variant systems like CBCT, the formulation in [1] must be modified.

The Fisher information matrix A′W A is shift-variant for both emission and transmission tomography, causing nonuniform properties of the reconstructed image. Statistical weighting is only partially responsible for the nonuniformity; even in the unweighted case, the Fisher information matrix A′ A is also shift-variant for 3D PET and CT. In [1], the system matrix A was factored into three elements as follows

$$a_{ij}=c_i{g}_{ij}{s}_j,$$ (18)

where {c_i} denote ray-dependent factors, {s_j} denote voxel-dependent factors, and G = [g_ij] represents the object-independent geometric portion of the tomographic system response. Ideally we would like to choose {c_i} and {s_j} and G such that G′G is shift-invariant. So it can be accurately approximated with a circulant matrix (implemented via a fast Fourier transform (FFT)), leading to improved regularizer designs. The matrix representation of (18) is

$$\mathit{A}=\mathit{D}[c_i]\mathit{G}\mathit{D}[s_j].$$ (19)

Since this representation is not unique, we can try to design each of the factors to make G′G “very shift-invariant”. The original design presented in [1] for PET assumed uniform voxel-dependent factors, i.e., s_j = 1, ∀j, and the ray-dependent part included only non-geometric aspects such as detector efficiency and dead time. In 2D PET, this leads to geometric factors {g_ij} for which G′G is nearly shift-invariant. However, this conventional choice of G leads to G′G that is highly shift-variant for 3D cone beam CT and even for 2D fan-beam CT for short-scan geometries.

Here, we present a new generalization of (18) that works in various geometries including 3D cone beam CT. First, we consider the geometric sampling properties of A and consider what rays are “missing” that cause A′ A to be shift-variant. For example, in a short-scan fan-beam geometry we are missing some of the views that would have been acquired with a full 360° scan. As another example, for a CBCT axial scan, we are missing the data that would have been acquired with a “step and shoot” set of axial scans. For axial CBCT with a full 360° scan, A′ A is approximately shift-invariant over the fully-sampled, so-called “football region”, so it is natural to define G to be a hypothetical system matrix having extra detector rows such that the entire reconstruction volume is contained in its corresponding football region². In general, we define G to be some N_g × n_p system matrix corresponding to an “ideal”, fully sampled geometry, for which G′G is approximately shift-invariant. The matrix G has the same number of columns as A but has more rows (N_g > n_d); the rows of A are a subset of the rows of G.

Second, we replace the usual diagonal matrix D[c_i] in (19) with D[c_i]P where P is a n_d × N_g matrix that selects the rows of the hypothetical geometry G corresponding to those of the actual geometry A. Each row of P is entirely zero except for a single element that is unity. By ordering the rows of G appropriately, we can use P = [I_nd 0_{nd ×(Ng −nd)}]. An important property of the row selection matrix P is that P′WP is a N_g × N_g diagonal matrix where each diagonal element corresponds to a w_i value for actual rays and is zero for the hypothetical rays.

With this generalization, we can rewrite the Fisher information matrix of the data fitting term as follows:

$${\mathit{A}}^{\prime }\mathit{W}\mathit{A}=\mathit{D}[s_j]{\mathit{G}}^{\prime }{\mathit{P}}^{\prime }\mathit{D}[c_i]\mathit{W}\mathit{D}[c_i]\mathit{P}\mathit{G}\mathit{D}[s_j]=\mathit{D}[s_j]{\mathit{G}}^{\prime }{\mathit{P}}^{\prime }\mathit{D}[W_i{c}_i^2]\mathit{P}\mathit{G}\mathit{D}[s_j].$$ (20)

Since the Fisher information matrix is fairly concentrated near its diagonal elements [1, Fig. 2], we approximate (20) as

Fig. 2.

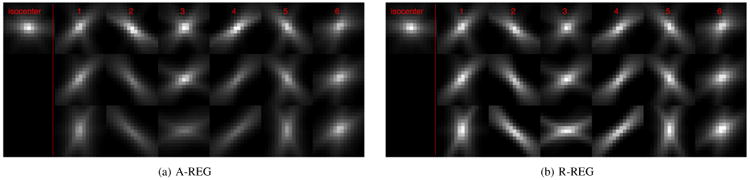
Comparison of xy plane through the center of each local impulse response at selected location (see Fig. 1 for the index of locations). Quadratic potential function was used. Top row is from a center slice (blue line in Fig. 1), middle row is from 1st slice of ROI (red line in Fig. 1), and bottom row is from outside ROI (green line in Fig. 1). (a) Regularization with original aggregated certainty (6) (A-REG) (b) Regularization with proposed pre-tuned spatial strength (38) (R-REG).

$${\mathit{A}}^{\prime }\mathit{W}\mathit{A}\approx \mathit{D}[s_j]\mathit{D}[{\eta }_j]{\mathit{G}}^{\prime }\mathit{G}\mathit{D}[{\eta }_j]\mathit{D}[s_j]=\mathit{D}[{\lambda }_j]{\mathit{G}}^{\prime }\mathit{G}\mathit{D}[{\lambda }_j]=\mathbf{\Lambda }{\mathit{G}}^{\prime }\mathit{G}\mathbf{\Lambda },$$ (21)

where the following factors match the diagonals of (21):

$${\eta }_j=\sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{g}_{ij}^2{c}_i^2{w}_i}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2}},$$ (22)

$${\lambda }_j=s_j{\eta }_j=\sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{w}_i}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2}},$$ (23)

$$\mathbf{\Lambda }\triangleq \mathit{D}[{\lambda }_j].$$ (24)

Different choices of c_i and s_j will lead to various designs for G = {g_ij}. As an example, for axial cone-beam CT, assuming c_i = 1, ∀i, and s_j = 1, ∀j, will lead to G that corresponds to another axial cone-beam CT geometry with extended detector rows and full 360 degree orbit. For some other choices, we may not have a physical interpretation for the system represented by G.

Both the ray- and voxel-dependent factors need to be designed based on the modality, i.e., for SPECT, s_j should be designed to properly model the nonuniform spatial sensitivity and, for PET, c_i should represent detector characteristics.

B. Regularization with Uniform Resolution Property

Substituting (21) into (9) yields the following approximation for the local impulse response at the jth voxel:

$${\mathit{l}}_j\approx {(\mathbf{\Lambda }{\mathit{G}}^{\prime }\mathit{G}\mathbf{\Lambda }+\mathit{R})}^{-1}\mathbf{\Lambda }{\mathit{G}}^{\prime }\mathit{G}\mathbf{\Lambda }{\mathit{\delta }}_j={\mathbf{\Lambda }}^{-1}{({\mathit{G}}^{\prime }\mathit{G}+{\mathbf{\Lambda }}^{-1}\mathit{R}{\mathbf{\Lambda }}^{-1})}^{-1}{\mathit{G}}^{\prime }\mathit{G}\mathbf{\Lambda }{\mathit{\delta }}_j.$$ (25)

Typically, the local impulse response l_j is concentrated about voxel j and clearly Λδ_j = λ_jδ_j. Following [1, eqn. (34)], we approximate (25) as the following final expression for the local impulse response:

$${\mathit{l}}_j\approx {({\mathit{G}}^{\prime }\mathit{G}+{\lambda }_j^{-2}\mathit{R})}^{-1}{\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j.$$ (26)

Having analyzed the local impulse response, we focus on designing the coefficients {κ_j} in the regularizer (5); these coefficients affect the Hessian R in (26) and thus control the spatial resolution. Our goal here is to choose {κ_j} to provide approximately uniform spatial resolution by matching the local impulse response at the jth voxel, l_j, to a target local impulse response, l_ref, i.e., l_j ≈ l_ref. Using (26), we write the target local impulse response at a reference point, such as the isocenter, as follows:

$${\mathit{l}}_{\text{ref}}\triangleq {({\mathit{G}}^{\prime }\mathit{G}+{\mathit{R}}_0)}^{-1}{\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}},$$ (27)

where R₀ is the Hessian of a regularizer R₀(x) that provides desirable spatial resolution properties at the reference point. R₀(x) has the same form as (5) but possibly with a different set of {κ_j} values, e.g., κ_j = 1, ∀j.

Our design for G leads to G′Gδ_j being approximately locally shift invariant, and we assume Rδ_j is also approximately locally shift-invariant [10, eqn. (15)]. Taking the Fourier transform of (26) yields the following expression for the local frequency response

$$L^j\approx \frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)}{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)+{\lambda }_j^{-2}F(\mathit{R}{\mathit{\delta }}_j)},$$ (28)

where F(·) denotes 3-D DFT centered at voxel j. We want to match the local frequency response of jth voxel to the target frequency response, i.e.,

$$L^j\approx \frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)}{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)+{\lambda }_j^{-2}F(\mathit{R}{\mathit{\delta }}_j)}\approx \frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})}{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})+F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}})}\approx L^{\text{ref}}.$$ (29)

Cross multiplying and simplifying yields

$$F(\mathit{R}{\mathit{\delta }}_j)F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})\approx {\lambda }_j^{2}F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}})F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j).$$ (30)

We design {κ_j} by minimizing the least squares difference between both sides of (30)

$${\widehat{\kappa }}_j=\underset{{\kappa }_j\in {ℝ}_{+}}{argmin}{\Vert F(\mathit{R}{\mathit{\delta }}_j)F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})-{\lambda }_j^{2}F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}})F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)\Vert }^2,$$

where ℝ₊ denotes nonnegative reals. For the quadratic potential function, the local frequency response of the regularizer Hessian is [16, eqn. (16)]

$$F(\mathit{R}{\mathit{\delta }}_j)={\kappa }_j^2{R}_{\omega },$$ (32)

$$R_{\omega }\triangleq \sum _{l=1}^{N_l}{\beta }_l{|C_l({\omega }_1,{\omega }_2,{\omega }_3)|}^2,$$ (33)

using the usual approximation κ_j ≈ κ_l for l within the neighborhood of j, where C_l denotes the discrete-space Fourier transform of C_l[n, m, z] and ω denotes the digital frequency. Without loss of generality, we choose R₀(x) such that

$$F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}})=\sum _{l=1}^{N_l}{\beta }_l{|C_l({\omega }_1,{\omega }_2,{\omega }_3)|}^2=R_{\omega }.$$ (34)

Substituting (32) and (34) into (31) yields the following simplified expression:

$${\widehat{\kappa }}_j=\underset{{\kappa }_j\in {ℝ}_{+}}{argmin}{\Vert {\kappa }_j^2{R}_{\omega }F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})-{\lambda }_j^2{R}_{\omega }F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)\Vert }^2.$$ (35)

Solving (35), we obtain

$${\widehat{\kappa }}_j={\lambda }_j\frac{\sqrt{{\Re }_{+}(\langle R_{\omega }F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}}),R_{\omega }F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)\rangle )}}{\Vert R_{\omega }F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})\Vert },$$ (36)

where 〈·, ·〉 denotes the inner product for 3D DFT space, and ℜ₊(·) denotes the nonnegative real part.

When G′G is approximately shift-invariant, we have

$$F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)\approx F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}}),$$ (37)

and the ratio in (36) becomes unity and (36) simplifies to κ̂_j = λ_j.

The presented design process can address more general purposes besides obtaining resolution uniformity. For instance, one may want to match a spatially varying target response that depends on certain characteristics, such as the sampling at each voxel, so that each voxel would have different resolution properties for specific purposes.

Our new regularizer for uniform resolution properties in the reconstructed image (hereafter R-REG) is given by (5) with

$${\widehat{\kappa }}_j={\lambda }_j=\sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{w}_i}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2}}.$$ (38)

This new pre-tuned spatial strength function (38) has a very similar form to that of the original certainty (6) proposed in [1], but with a different denominator. This new denominator takes effect when voxel j is at an undersampled location. When it is fully-sampled, the new pre-tuned spatial strength is exactly the same as the original certainty since ${\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2={\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2$ for such locations. For undersampled region, this new denominator decreases the regularization strength, leading to sharper and possibly noisier reconstructed images compared to using the original aggregated certainty (6).

To simplify implementation, we approximate (38) as follows

$${\widehat{\kappa }}_j\approx \sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}{w}_i}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}}}.$$ (39)

Unlike the back-projection of the statistical weighting, ${\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}{w}_i$, calculating the sum of rows of the Hessian A′W A, ${\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{w}_i$, is sometimes not available or easily implementable. Empirical results in the supplement verify that (39) closely approximates (38).

Even though the new regularizer design was derived for quadratic regularization, it can be also applied to regularizes with non-quadratic potential functions, following the spirit of [31]. Of course edge-preserving regularization always leads to non-uniform spatial resolution near image edges, and this important characteristic will be retained.

The proposed regularizer (38) attempts to address non-uniformities caused by both shift-variant scanning geometries and by interactions between the regularization and the statistical weights. The derivation assumed that κ_j changes very slowly within its neighborhood. However, this assumption may fail for certain regions such as near the edges of a structure. Furthermore, since we are only adjusting the “overall strength” of the regularization at each voxel and not its “directional strength” for each neighboring voxel, the proposed regulariza tion cannot correct for asymmetry in local impulse responses. The proposed regularization is designed to generate uniform spatial resolution in terms of CRC. To obtain isotropic local impulse response, one would need to design the directional coefficients, β_l, at each location [17].

C. Regularization with Uniform Noise Property

Using the Fisher information matrix approximation (21), we approximate the local noise correlation corr(x̂) as follows

$$\text{corr}({\widehat{\mathit{x}}}_j)\approx {(\overline{\mathbf{\Lambda }}{\mathit{G}}^{\prime }\mathit{G}\overline{\mathbf{\Lambda }}+\mathit{R})}^{-1}\widehat{\mathbf{\Lambda }}{\mathit{G}}^{\prime }\mathit{G}\widehat{\mathbf{\Lambda }}{(\overline{\mathbf{\Lambda }}{\mathit{G}}^{\prime }\mathit{G}\overline{\mathbf{\Lambda }}+\mathit{R})}^{-1}{\mathit{\delta }}_j,$$ (40)

where, using v_i and ŵ_i from (14):

$${\overline{\lambda }}_j\triangleq \sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{\widehat{w}}_i{v}_i}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2}},\overline{\mathbf{\Lambda }}\triangleq \mathit{D}[{\overline{\lambda }}_j],$$ (41)

$${\widehat{\lambda }}_j\triangleq \sqrt{\frac{{\sum }_{i=1}^{n_{\mathrm{d}}}{a}_{ij}^2{\widehat{w}}_i{v}_i^2}{{\sum }_{i=1}^{N_{\mathrm{g}}}{g}_{ij}^2}},\widehat{\mathbf{\Lambda }}\triangleq \mathit{D}[{\widehat{\lambda }}_j].$$ (42)

We further approximate (40) as

$$\text{corr}({\widehat{\mathit{x}}}_j)\approx {\overline{\mathbf{\Lambda }}}^{-1}{({\mathit{G}}^{\prime }\mathit{G}+{\overline{\mathbf{\Lambda }}}^{-1}\mathit{R}{\overline{\mathbf{\Lambda }}}^{-1})}^{-1-}{\overline{\mathbf{\Lambda }}}^{-1}\widehat{\mathbf{\Lambda }}{\mathit{G}}^{\prime }\mathit{G}\widehat{\mathbf{\Lambda }}{\overline{\mathbf{\Lambda }}}^{-1}{({\mathit{G}}^{\prime }\mathit{G}+{\overline{\mathbf{\Lambda }}}^{-1}\mathit{R}{\overline{\mathbf{\Lambda }}}^{-1})}^{-1}{\overline{\mathbf{\Lambda }}}^{-1}{\mathit{\delta }}_j\approx \frac{{\widehat{\lambda }}_j^2}{{\overline{\lambda }}_j^4}{({\mathit{G}}^{\prime }\mathit{G}+{\overline{\lambda }}_j^{-2}\mathit{R})}^{-1}{\mathit{G}}^{\prime }\mathit{G}{({\mathit{G}}^{\prime }\mathit{G}+{\overline{\lambda }}_j^{-2}\mathit{R})}^{-1}{\mathit{\delta }}_j,$$ (43)

using the usual assumption that the local noise correlation corr(x̂) is concentrated about voxel j. From (43), the local noise power spectrum (NPS) of voxel j is approximately

$$S^j\approx \frac{{\widehat{\lambda }}_j^2}{{\overline{\lambda }}_j^4}\frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)}{{(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)+{\overline{\lambda }}_j^{-2}F(\mathit{R}{\mathit{\delta }}_j))}^2}.$$ (44)

To obtain uniform noise properties, we want to match the local NPS at the jth voxel to a target NPS, i.e., S^j ≈ S^ref. For the target, we use the local NPS at a reference point and assume that the regularizer R₀(x) was chosen to provide a suitable NPS at that location. Our design goal becomes:

$$\frac{{\widehat{\lambda }}_j^2}{{\overline{\lambda }}_j^4}\frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)}{{(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)+{\overline{\lambda }}_j^{-2}F(\mathit{R}{\mathit{\delta }}_j))}^2}\approx \frac{{\widehat{\lambda }}_{\text{ref}}^2}{{\overline{\lambda }}_{\text{ref}}^4}\frac{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})}{{(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})+F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}}))}^2}.$$ (45)

Cross multiplying leads to

$${\widehat{\lambda }}_j^2{\overline{\lambda }}_{\text{ref}}^{4}F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j){(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})+F({\mathit{R}}_0{\mathit{\delta }}_{\text{ref}}))}^2\approx {\widehat{\lambda }}_{\text{ref}}^2{\overline{\lambda }}_j^{4}F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}}){(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)+{\overline{\lambda }}_j^{-2}F(\mathit{R}{\mathit{\delta }}_j))}^2.$$ (46)

Using (32) and (34), we simplify (46) to

$${\kappa }_j^2\sqrt{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})}{R}_{\omega }\approx \left(\frac{{\widehat{\lambda }}_j{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}\right)\sqrt{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)}(F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})+R_{\omega })-{\overline{\lambda }}_j^2\sqrt{F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})}F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j).$$ (47)

By defining $B_{\omega }^{\text{ref}}\triangleq F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_{\text{ref}})$ and $B_{\omega }^j\triangleq F({\mathit{G}}^{\prime }\mathit{G}{\mathit{\delta }}_j)$, can be rewritten as follows:

$${\kappa }_j^2\sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega }\approx \left(\frac{{\widehat{\lambda }}_j{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}\right)\sqrt{B_{\omega }^j}(B_{\omega }^{\text{ref}}+{\mathit{R}}_{\omega })-{\overline{\lambda }}_j^2\sqrt{B_{\omega }^{\text{ref}}}{B}_{\omega }^j.$$ (48)

We design {κ_j} by solving the following least squares problem

$${\widehat{\kappa }}_j=\underset{{\kappa }_j\in {ℝ}_{+}}{argmin}{\Vert {\kappa }_j^2\sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega }-\left[\right(\frac{{\widehat{\lambda }}_j{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}})\sqrt{B_{\omega }^j}(B_{\omega }^{\text{ref}}+R_{\omega })-{\overline{\lambda }}_j^2\sqrt{B_{\omega }^{\text{ref}}}{B}_{\omega }^j]\Vert }^2.$$ (49)

The solution to (49) is given by

$${\widehat{\kappa }}_j=\frac{1}{\Vert \sqrt{B_{\omega }^{\text{ref}}{R}_{\omega }}\Vert }{\left[{\Re }_{+}\right(\left(\frac{{\widehat{\lambda }}_j{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}\right)\langle \sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega },\sqrt{B_{\omega }^j}{R}_{\omega }\rangle +\left(\frac{{\widehat{\lambda }}_j{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}\right)\langle \sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega },\sqrt{B_{\omega }^j}{B}_{\omega }^{\text{ref}}\rangle -{\overline{\lambda }}_j^2\langle \sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega },\sqrt{B_{\omega }^{\text{ref}}}{B}_{\omega }^j\rangle \left)\right]}^{\frac{1}{2}}.$$ (50)

Using (37), we simplify (50) as follows

$${\widehat{\kappa }}_j=\sqrt{\left(\frac{{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}\right){\widehat{\lambda }}_j+E_{\omega }\left[\right(\frac{{\overline{\lambda }}_{\text{ref}}^2}{{\widehat{\lambda }}_{\text{ref}}}){\widehat{\lambda }}_j-{\overline{\lambda }}_j^2]},$$ (51)

Where $E_{\omega }={\Re }_{+}(\langle \sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega },\sqrt{B_{\omega }^{\text{ref}}}{B}_{\omega }^{\text{ref}}\rangle )/{\Vert \sqrt{B_{\omega }^{\text{ref}}}{R}_{\omega }\Vert }^2$.

Regularizer (5) with (51) (hereafter N-REG) provides approximately uniform noise properties in the reconstructed image. The new {κ_j} factors (51) consist of two terms within a square root. If we ignore the second term, then (51) is approximately the square root of the modified pre-tuned spatial strength (38) of R-REG. This suggests that N-REG has decreased regularization strength at undersampled region compared to A-REG, but with less spatial variation than R-REG. The second term of (51) is an “adjustment” that is usually smaller than the first term.

IV. Results

This section investigates the effect of the proposed regularizers (see Table I for acronyms) for PWLS image reconstruction of 3D short-scan axial CT using both phantom and clinical data. For the hypothetical geometry G, we assumed c_i = 1, ∀i, and s_j = 1, ∀j, in (20) and used a full 360° scan with increased number of detector rows, $N_{\mathrm{t}}^{\text{ext}}$ (see the supplement for a different choice of G).

Table I. Acronyms for regularizers.

Acronym	Description
A-REG	aggregated certainty (AC) regularizer (6)
R-REG	regularizer for spatial resolution uniformity (38)
N-REG	regularizer for noise uniformity (51)

A. Resolution Uniformity

1) Phantom Simulation

An anthropomorphic phantom simulation was used to demonstrate the improved spatial resolution uniformity induced by the regularizer with the modified pre-tuned spatial strength (38). We used 512 × 512 × 122 XCAT phantom [32] with voxel size Δ_x = Δ_y = 0.9766 mm and Δ_z = 0.625 mm as our true image, x^true (Fig. 1).

Fig. 1.

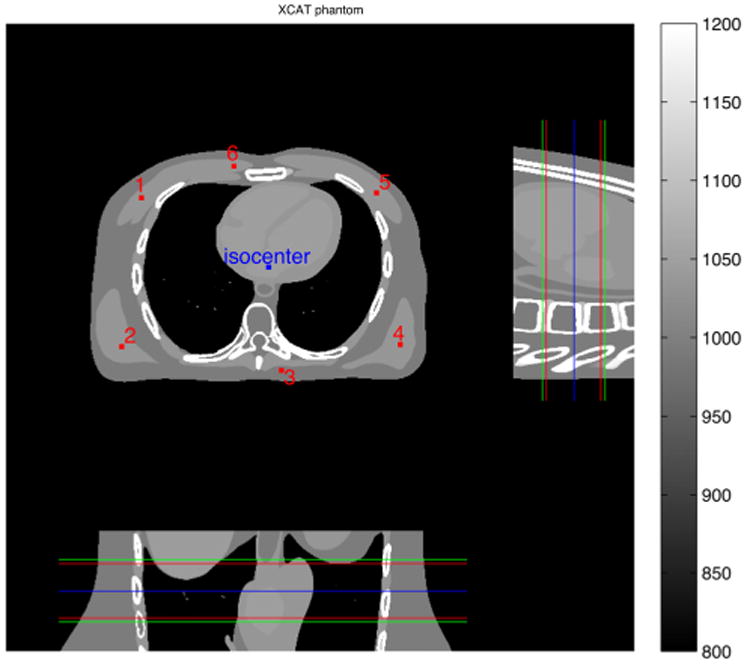
XCAT phantom used in the simulation. Middle 3 planes (xy, xz, and yz planes through the isocenter) are shown. Red and blue dots indicate locations of the added impulses and the isocenter, respectively. Red lines indicate our axial ROI, which is from 5th to 60th slices (out of 64). Blue line displays the location of the center slice. Finally, green lines show the detector coverage.

We used the separable footprint projector [33] to simulate a monoenergetic, noiseless sinogram for a 3rd-generation axial cone-beam CT system having N_s = 888 channels and N_t = 64 detector rows with spacings Δ_s = 1.0239 mm and Δ_t = 1.09878 mm. We assumed a short-scan protocol that covers an angular range of 227.6° with N_a = 622 evenly spaced views. We selected the hypothetical geometry G to have both extended views, $N_{\mathrm{a}}^{\text{ext}}=984$ over 360°, and detector rows, $N_{\mathrm{t}}^{\text{ext}}=168$. The statistical weights were w_i = b₀ exp(−[Ax]_i) where the X-ray intensity was b₀ = 10⁶.

To obtain local impulse responses at various locations, we added impulses with amplitude ε = 2.5 × 10⁻⁴ mm⁻¹, corresponding to approximately 14 HU, to 6 different locations in each of the selected 9 slices (see Fig. 1 for impulse locations in xy plane). Selected slices were evenly spaced through z-dimension including isoplane, end slices of region-of-interest (ROI), and slices outside ROI. Axial ROI was selected as 5th to 60th slices (out of 64) to focus on slices with less short-scan artifacts due to insufficient sampling [34]. We used (8) to evaluate the local impulse response at each location for regularizer designs with both the original aggregated certainty (6) (hereafter A-REG) and the modified pre-tuned spatial strength function (38) (R-REG). Both quadratic and edge-preserving regularizations were investigated to show that the proposed regularizer design R-REG is applicable to both cases. Image reconstruction was done on the same grid as the true image. For this experiment, we set the regularization parameter A β_l as β_l = β, ∀l, where β was selected based on the full-width at half-maximum (FWHM) of the local impulse response at the isocenter. To visualize the shape of the local impulse response more clearly, we selected a somewhat large β value for which the FWHM was approximately 3 times the voxel size. Image reconstruction used the ordered-subsets with double surrogates (OSDS) method [35]. The number of iterations was 20 with 41 subsets.

First, we present the results for regularization with a quadratic potential function. Fig. 2 illustrates that the proposed regularizer (38) leads to local impulse response functions having more uniform CRC values than the “conventional” aggregated certainty design (6), particularly for off-center slices. CRC values of local impulse responses at different locations become nonuniform when using A-REG (6). This nonuniformity becomes severe as we move away from center slices. Using the proposed regularizer R-REG (38), the CRC values become much more uniform regardless of the location or the amount of sampling. R-REG (38) corrects only the nonuniformity of peak values of local impulse responses. Anisotropy in the shape of the impulse response could be improved by designing directional coefficients [17].

Fig. 3 shows x profiles through the center of all local impulse responses to compare CRC values more closely. Using A-REG (6) leads to resolution nonuniformity even in the center slice, primarily due to short-scan geometry. Nonuniformity in resolution becomes most severe for locations 2 to 4 that have much worse sampling compared to the isocenter due to the axial cone-beam geometry and the short-scan orbit.

Fig. 3.

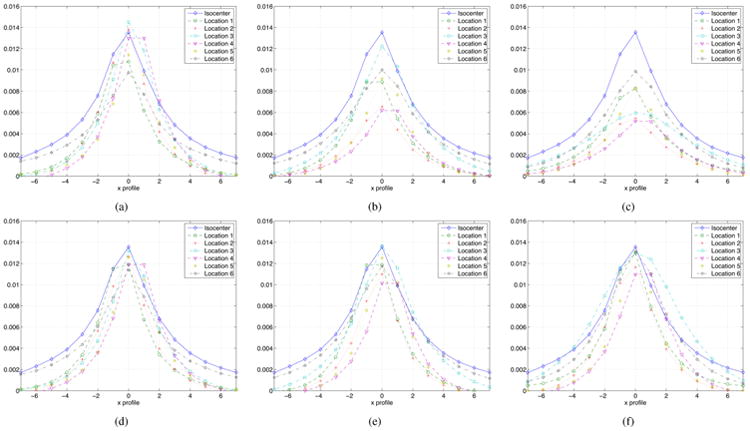
Comparison of x profiles through the center of each impulse response in Fig. 2. Left column is from a center slice, middle column is from 1st slice of ROI, and right column is from outside of ROI. Top and bottom rows represent the regularizers A-REG (6) and the proposed R-REG (38), respectively. (a) A-REG, center slice (b) A-REG, 1st slice of ROI (c) A-REG, outside ROI (d) R-REG, center slice (e) R-REG, 1st slice of ROI (f) R-REG, outside ROI.

Table II compares the average “mismatch” of the CRC values for the given 6 locations across slices and within each slice. We used the following definition of CRC mismatch

Table II.

Average CRC mismatch (52) for selected 6 locations across slices and within each slice, respectively (Units: %). See Fig.1 for the index of impulse locations.

	Locations						Averages
	1	2	3	4	5	6	Overall	Center Slice	1st slice of ROI	Outside ROI
A-REG (Fig. 3)	32.6	45.3	24.8	47.2	31.9	25.0	34.5	(a) 12.3	(b) 33.7	(c) 46.8
R-REG (Fig. 3)	7.5	14.9	3.9	20.0	5.9	7.2	9.9	(d) 8.7	(e) 11.6	(f) 7.4

$${\rho }_j\triangleq |\text{CRC}({\mathit{l}}_j)-\text{CRC}({\mathit{l}}_{\text{ref}})|/|\text{CRC}({\mathit{l}}_{\text{ref}})|.$$ (52)

The proposed regularizer R-REG improved the uniformity of CRC values throughout the reconstruction volume. The average CRC mismatch was significantly improved for all locations and slices, and undersampled voxels were most improved by the proposed regularizer, as designed. The overall improvement of CRC mismatch was from 34.5% to 9.9%.

We obtained similar results for edge-preserving regularization with a hyperbola potential function [36] given by

$$\varphi (t)={\delta }^2[\sqrt{1+{|t/\delta |}^2}-1].$$ (53)

Shape of the local impulse responses does not change much compared to the quadratic regularization, but CRC values become slightly higher. As in the quadratic case, the original certainty function (6) yields non-uniform CRC values across multiple voxel locations, and proposed regularization (38) leads to more uniform CRC values. Due to their similarity to the quadratic case, results for edge-preserving regularization are presented in the supplementary material.

Even though proposed designs were based on approximations, such as (26), the local impulse response calculated by (8) yields CRC values that closely match the target CRC. For both quadratic and edge-preserving regularizers, the proposed designs provide improved CRC uniformity (see also Table II).

2) Real Clinical Data

We reconstructed a clinical cardiac CT scan as a 1024 × 1024 × 122 image with 70 cm field-of-view (FOV). Measurements were obtained from a 64 row axial CT scanner with a short-scan protocol and 480 mAs tube current. The sinogram dimension was [N_s, N_t, N_a] = [888, 64, 642]. We selected the hypothetical geometry G to have both extended views, $N_{\mathrm{a}}^{\text{ext}}=984$ and detector rows, $N_{\mathrm{t}}^{\text{ext}}=148$. For this experiment, we set β_l in (5) using [28]. We used ICD with spatially non-homogeneous updates [37] for reconstruction. We show results from both quadratic and edge-preserving regularization using the q-generalized Gaussian potential function with p = 2, q = 1.2, and c = 10, [3]

$$\varphi (t)=\frac{{|t|}^p}{1+{|t/c|}^{p-q}}.$$ (54)

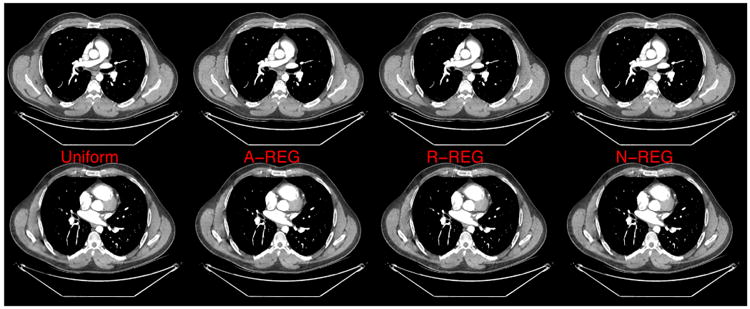
Fig. 4 compares the reconstructed images with a quadratic potential function and the following different regularizers: Uniform, A-REG, and R-REG When uniform regularization is used, i.e., κ_j = 1, ∀_j, the reconstructed image becomes over-smoothed even for some locations in the center slice, illustrating the importance of the pre-tuned spatial strength function in the regularization. Reconstructed image using A-REG (6) shows less blurring and sharper spatial resolution compared to that of the uniform regularizer. However, even in the center slice, both left and right sides of the reconstructed image have different resolution. This is consistent with the result in Fig. 3 (a) where the CRC values were nonuniform even in the center slice due to short-scan orbit. The proposed regularizer R-REG (38) improved resolution uniformity in the center slice. In the end slices of the ROI, the resolution nonuniformity becomes more apparent. A-REG (6) fails to provide resolution uniformity at under-sampled locations, leading to visible differences in smoothness between left and right side of the reconstructed images. On the other hand, the reconstucted image using R-REG (38) has more uniform resolution properties even in these undersampled region, causing the structures in the region to have sharper boundaries.

Fig. 4.

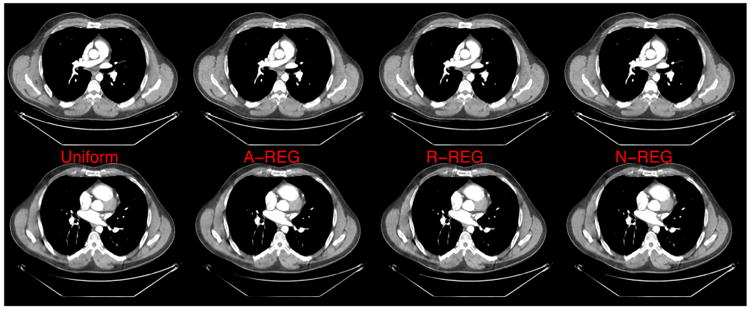
Reconstructed images using uniform regularizer (1st column), A-REG (2nd column), R-REG (3rd column), and N-REG (last column). Quadratic potential function was used. Top row: center slice; bottom row: the last slice of ROI. Display range is [800 1200] (HU).

Fig. 6 and Fig. 7 show reconstructed images for edge-preserving regularization. Clearly, the edge-preserving regularization preserves fine structures, leading to better image quality in terms of spatial resolution compared to the quadratic regularization. However, the choice of {κ_j} still affects the resolution uniformity in the reconstructed image. The results show similar tendencies as in the quadratic case: non-uniform resolution and over-regularization in the undersampled region for uniform regularizer and A-REG. On the other hand, the proposed R-REG achieves sharper and more uniform spatial resolution. This suggests that even though the proposed regularizer was derived for a quadratic regularization, it is also suitable for non-quadratic regularization.

Fig. 6.

Reconstructed images using uniform regularizer (1st column), A-REG (2nd column), R-REG (3rd column), and N-REG (last column). Edge-preserving potential function (54) was used. Top row: center slice; bottom row: the last slice of ROI. Display range is [800 1200] (HU).

Fig. 7.

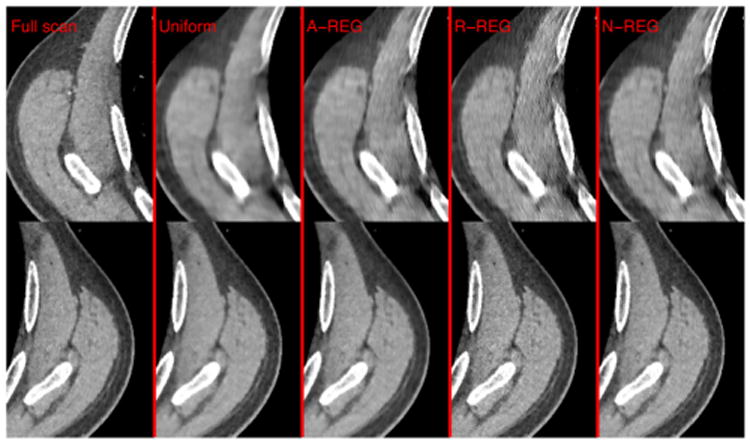
Comparison of reconstructed images in Fig. 6 at the last slice of ROI. From left to right, the images are from full scan measurements with A-REG, uniform regularizer, A-REG, R-REG, and N-REG, respectively. Top row is from a region on the left side where sampling is lower than a region on the right side (bottom row). Display range is [800 1200] (HU).

B. Noise Uniformity

Reconstructed images using R-REG (38) have better resolution uniformity throughout the entire volume, however, this improvement comes at the expense of the noise properties. As shown in Fig. 7, the proposed R-REG slightly increases the noise level in the reconstructed image when edge-preserving regularization is used. This trade-off is inevitable; thus we also investigated a regularizer that focuses on noise uniformity (N-REG, (51)).

1) Phantom Experiment

To compare the regularizes quantitativly, we used the GE performance phantom (GEPP) [20]. The phantom consists of a Plexiglas™ insert with resolution bars, and tungsten wires in water. The phantom was scanned with a 64 row axial CT scanner in short-scan mode and 70 mAs tube current, corresponding to a very low dose scan, and reconstructed to a grid of 1024 × 1024 × 90 with the following voxel size: Δ_x = Δ_y = 0.2246 mm and Δ_z = 0.625. We selected the hypothetical geometry G to have both extended views, $N_{\mathrm{a}}^{\text{ext}}=984$, and detector rows, $N_{\mathrm{t}}^{\text{ext}}=200$. Edge-preserving regularization with q-generalized Gaussian potential function (54) was used.

Fig. 8 shows the reconstructed image of the GEPP with A-REG. Due to small FOV (= 23 cm), the end slices of the ROI did not suffer much from under-sampling. However, the choice of regularization still leads to different image qualities in the reconstructed images even in the center slice. To compare different regularizations fairly, we chose the regularization parameter β such that the noise standard deviation near the isocenter is similar for all reconstructed images (≈ 13.7 HU). We selected 7 different homogeneous regions in the center slice to compare the noise standard deviation (see Fig. 8 for their locations). Table III illustrates that the proposed N-REG shows the best noise uniformity, i.e., the average standard deviation of the noise is reasonably close to that of the region near the isocenter. Since the FOV is small, the noise standard deviation does not vary much within the Plexiglas™ insert. However, the standard deviation in the wall depends significantly on the regularization method. Due to the symmetrical shape of the GEPP and thickness of its wall, the statistical weighting varies mostly only in the channel dimension (except for the views affected by an additional weighting such as Parker weighting) and is “U” shaped. As a result, the uniform regularizer generally increased noise in the reconstructed image, and both A-REG and R-REG over-regularized the region far away from the isocenter, i.e., the walls in this case. Both A-REG and R-REG showed similar performance as expected, and N-REG improved noise uniformity in the reconstructed image.

Fig. 8.

The GEPP used for quantitative comparison of regularizations. Red boxes indicate the regions selected for noise variance comparison.

Table III.

Comparison of the noise standard deviation for different regularizers method. All values are in Hounsfield units (HU).

	Uniform	A-REG	R-REG (38)	N-REG (51)
Plexiglas™ Insert (center)	14.0	13.7	13.7	13.6
Plexiglas™ Insert (right)	18.8	16.0	16.2	16.4
Plexiglas™ Insert (left)	15.1	14.4	14.5	14.9
Phantom Wall (left)	15.4	9.3	9.5	11.8
Phantom Wall (right)	16.9	8.8	6.8	10.1
Phantom Wall (top)	17.4	8.7	8.8	10.7
Phantom Wall (bottom)	16.1	7.7	8.8	10.9
Average	16.2±1.6	11.2±3.4	11.2 ±3.6	12.6 ±2.4

2) Real Clinical Data

Fig. 4 to Fig. 7 compare the reconstructed images obtained using various regularizers. For both quadratic and edge-preserving regularizers, the proposed N-REG provides improved noise uniformity in the reconstructed image. The uniform regularizer tends to over-smooth the reconstructed image, and A-REG shows nonuniform noise properties even in the center slice. Both proposed R-REG and N-REG show improved image qualities in terms of resolution and noise, respectively. R-REG shows somewhat sharper reconstructed image compared to N-REG on end slices for both regularizers, but has slightly higher and nonuniform noise variance.

Fig. 5 and Fig. 7 zoom into the reconstructed images at the last slice of ROI, which has nonuniform sampling over the slice. A reconstructed image from full scan measurements with A-REG was used as a reference with desirable image quality. Since the image quality of the reference image is also affected by the choice of regularization, it may not be the optimal image for clinical diagnosis. However, the under-sampling from short-scan measurements is a more dominant factor for the image quality in the displayed region, so the chosen reference image shows better image characteristics compared to the other reconstructed images from short-scan measurements. For each case, the region on the right side of the reconstructed image (bottom row) was compared to the left side of the image that has less sampling (top row). Uniform regularization clearly leads to over-regularization in the undersampled region, causing severe noise nonuniformity within the slice. Even though less severe, A-REG also suffers from the same issue. Proposed regularization N-REG generated a reconstructed image with better noise uniformity, improving visibility of structures in the undersampled region.

Fig. 5.

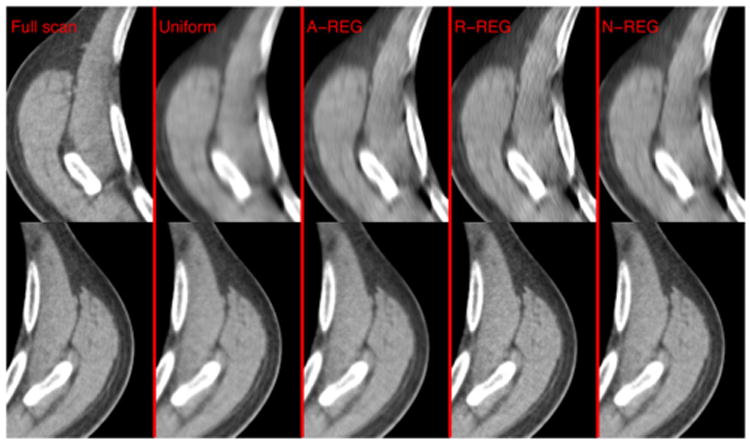
Comparison of reconstructed images in Fig. 4 at the last slice of ROI. From left to right, the images are from full scan measurements with A-REG, uniform regularizer, A-REG, R-REG, and N-REG, respectively. Top row is from a region on the left side where sampling is lower than a region on the right side (bottom row). Display range is [800 1200] (HU).

For both examples, the proposed N-REG (51) provides more uniform noise characteristics in the reconstructed image compared to other regularization methods.

V. Discussion

We proposed new regularization methods by modifying the aggregated certainty presented in [1] using the hypothetical geometry concept. Proposed regularizer R-REG in (38) improved the spatial resolution uniformity in the reconstructed images, and N-REG in (51) provided more uniform noise characteristics compared to the uniform and aggregated certainty regularizers.

The proposed methods, R-REG and N-REG, showed improved spatial resolution or noise uniformity compared to the conventional uniform regularizer and A-REG in both quadratic and edge-preserving regularizations and for both simulated and clinical scans. Even though the proposed regularizers were targeted to improve the uniformity of either the spatial resolution or noise, they yielded reconstructed images with qualitatively improved image quality in terms of resolution or noise compared to that from the uniform and the aggregated certainty regularizers. For quadratic regularization, the noise characteristics have less effect on the visual image quality than the spatial resolution, suggesting the use of R-REG to improve spatial resolution uniformity. On the other hand, since edge-preserving regularization provides improved resolution near edges, the noise uniformity primarily affects the readability of the reconstructed image. Thus, N-REG may be preferable for edge-preserving regularization. However, there are tradeoffs between spatial resolution and noise characteristics. Using either regularizer may not provide an optimal reconstructed image in terms of both resolution and noise. Furthermore, it is unknown which feature is more desirable for diagnosis. Diagnostic readability for the reconstructed images obtained from both methods needs to be investigated to determine the best regularizer, and possibly some combination of methods may be desirable. A compromise approach that balances spatial resolution and noise characteristics is explored in the supplement as a starting point for further research.

For experiments in this paper, we used the hypothetical scanning geometry obtained intuitively by extending both rows and views from given axial cone-beam CT geometry. Another option would be to use a step-and-shoot set of axial scans. For some other geometries, determining the appropriate hypothetical geometry may be harder. For example, in helical CT, simply extending views would not suffice, and since the actual scanning geometry must be a subset of the hypothetical geometry, we cannot use a very small pitch for G. Multiple intertwined helical geometries is a possible choice. Careful consideration is required to properly extend the proposed regularization designs to other scanning geometries.

One minor drawback of using the generalized geometry is the increased computation for (23). For a geometry having extended views or rows, since (23) is calculated only once prior to iterating, the increased computation is insignificant compared to the computation required for the actual reconstruction. However, using a step-and-shoot set of axial scans or intertwined multiple helical scans may require considerable computations. Fortunately, since calculating (23) only requires the hypothetical geometry, one could tabulate the denominator of (23).

The proposed regularizers improve the uniformity of spatial resolution or noise by controlling a scaling factor at each voxel. Even though the design process attempts to match the entire local impulse responses or NPS functions, they are primarily matching CRC values and variances at each location due to approximations (26) and (43). Thus, the proposed regularizers do not correct anisotropy of these characteristics. Designing directional coefficients in the regularizer may correct for such anisotropy, and has shown promising results for the well-sampled regions [16], [18]. However, the anisotropy of the image characteristics in the under-sampled region is hard to correct, especially since these methods use locally circulant approximations of the Fisher information matrix. One possible future work is to extend the methods in this paper to directional coefficient design.

Supplementary Material

Fig. 9. Middle 3 planes of the pre-tuned spatial strength (6) (xy, xz, and yz planes through the image center).

Fig. 10. Comparison of the pre-tuned spatial strengths for A-REG, R-REG, and N-REG at a center slice (left column) and an end slice (right column). Display range is [0 250].

Fig. 11. Comparison of the pre-tuned spatial strengths for R-REG and its approximation given in (38) at a center slice (left column) and an end slice (right column). Display range is [0 250].

Fig. 12. Comparison of x profiles through the center of the pre-tuned spatial strengths for A-REG, R-REG, and N-REG. From center slice (left) and end slice (right).

Fig. 13. Comparison of x profiles through the center of the pre-tuned spatial strength (38) and its approximation (39). From center slice (left) and end slice (right).

Fig. 14. Plot of (55) along the positive x axis at y = 0 (mm) and z = 1.25, 11.25, 21.25 (mm), with the hypothetical geometry G used in [1] (left) and with the system matrix A replacing G in (55) (right).

Fig. 15. The GEPP phantom used for quantitative comparison of regularizers. Red arrow indicate tungsten wire used for spatial resolution comparison.

Fig. 16. Comparison of the peak value of the tungsten wire in GEPP for the following regularizers: Uniform, A-REG, R-REG-1, R-REG-2, and N-REG-2.

Fig. 17. Comparison of the noise standard deviation in a homogeneous region of the GEPP, which corresponds to the left phantom wall in Table. III, for the following regularizers: A-REG, R-REG-1, N-REG-1, and N-REG-2.

Fig. 18. Comparison of reconstructed images obtained from A-REG (top), R-REG-1 (middle) and R-REG-2 (bottom) at 3 selected locations (separated by blue dash lines) on the last slice of ROI. Display window is [800 1200] (HU).

Fig. 19. Comparison of reconstructed images obtained from both uniform noise regularizers, N-REG-1 (top) and N-REG-2 (bottom), at 3 selected locations (separated by blue dash lines) on the 1st slice of ROI. Display window is [800 1200] (HU).

Fig. 20. Comparison of reconstructed images obtained using R-REG-1 (top), N-REG-1 (middle) and compromise regularizer (bottom) at 3 selected locations (separated by blue dash lines) on the last slice of ROI. Display window is [800 1200] (HU).

Fig. 21. Comparison of xy plane through the center of each local impulse response at selected location (see Fig.1 for the index of locations). Edge-preserving potential function was used. Top row is from a center slice, middle row is from 1st slice of ROI, and bottom row is from outside ROI. (a) Regularization with original aggregated certainty (6) (A-REG) (b) Regularization with proposed pre-tuned spatial strength (38) (R-REG-1).

Fig. 22. Comparison of x profiles through the center of each impulse response in Fig. 21. Left column is from a center slice, middle column is from 1st slice of ROI, and right column is from outside of ROI. Top and bottom rows represent the regularizers A-REG (6) and the proposed R-REG-1 (38), respectively. (a) A-REG, center slice (b) A-REG, 1st slice of ROI (c) A-REG, outside ROI (d) R-REG-1, center slice (e) R-REG-1, 1st slice of ROI (f) R-REG-1, outside ROI.

Fig. 23. Comparison of xy plane through the center of each local impulses responses at selected location (see Fig. 1 in [1] for the index of locations). Quadratic penalty function was used. Top row is from a center slice (blue line in Fig. 1 in [1]), middle row is from 1st slice of ROI (red line), and bottom row is from outside ROI (green line). (a) Regularization with original aggregated certainty (6) (A-REG) (b) Regularization with proposed pre-tuned spatial strength (62) (R-REG-2).

Fig. 24. Comparison of x profiles through the center of each local impulse response in Fig. 23. Left column is from a center slice, middle column is from 1st slice of ROI, and right column is from outside of ROI. Top and bottom rows represent the regularizers A-REG (6) and the proposed R-REG-2 (62), respectively. (a) A-REG, center slice (b) A-REG, 1st slice of ROI (c) A-REG, outside ROI (d) R-REG-2, center slice (e) R-REG-2, 1st slice of ROI (f) R-REG-2, outside ROI.

Fig. 25. Comparison of xy plane through the center of each local impulses responses at selected location (see Fig. 1 in [1] for the index of locations). Edge-preserving penalty function was used. Top row is from a center slice (blue line in Fig. 1 in [1]), middle row is from 1st slice of ROI (red line), and bottom row is from outside ROI (green line). (a) Regularization with original aggregated certainty (6)] (A-REG) (b) Regularization with proposed pre-tuned spatial strength (62) (R-REG-2).

Fig. 26. Comparison of x profiles through the center of each local impulse response in Fig. 25. Left column is from a center slice, middle column is from 1st slice of ROI, and right column is from outside of ROI. Top and bottom rows represent the regularizers A-REG (6) and the proposed R-REG-2 (62), respectively. (a) A-REG, center slice (b) A-REG, 1st slice of ROI (c) A-REG, outside ROI (d) R-REG-2, center slice (e) R-REG-2, 1st slice of ROI (f) R-REG-2, outside ROI.

Table IV Acronym suffixes for regularizers

Table V Average CRC mismatch (52) for selected 6 locations across slices and within each slice, respectively (Units: %). See Fig. 1 in [1] for the index of impulse locations.

Table VI Comparison of the noise standard deviation for different regularizers method. All values are in Hounsfield units (HU).