Variable-Domain Functional Regression for Modeling ICU Data

Abstract

We introduce a class of scalar-on-function regression models with subject-specific functional predictor domains. The fundamental idea is to consider a bivariate functional parameter that depends both on the functional argument and on the width of the functional predictor domain. Both parametric and nonparametric models are introduced to fit the functional coefficient. The nonparametric model is theoretically and practically invariant to functional support transformation, or support registration. Methods were motivated by and applied to a study of association between daily measures of the Intensive Care Unit (ICU) Sequential Organ Failure Assessment (SOFA) score and two outcomes: in-hospital mortality, and physical impairment at hospital discharge among survivors. Methods are generally applicable to a large number of new studies that record a continuous variables over unequal domains.

1 Introduction

We study the relationship between a scalar response and a functional predictor, when the functional predictor falls on a fine grid with a different length for each subject. Such data are most commonly encountered when the domain variable is time, and each subject is followed for a different length of time. We refer to this type of data as variable-domain functional data. In particular, we were motivated by covariates collected in an inpatient hospital setting, where measurements are recorded daily (or at another fixed interval) for as long as the subject remains in the hospital. Examples of such measurements include measures of patient status, nutritional intake, and medication dosing. We are interested in understanding how the functional covariate affects an outcome collected at the end of hospitalization, or afterward.

The feature of subject-specific functional domains is not limited to the inpatient hospital setting. In sleep studies, subjects are connected to an electroencephalography (EEG) machine, which records electric activity for as long as the patient is asleep. Each subject sleeps for a different length of time, and one goal may be to relate these electrical signals of varying lengths to a subject-specific outcome or condition. In studies on aging, each subject lives for a different length of time, so the amount of available data varies by subject.

Traditional approaches to analyzing variable-domain functional data fall into two categories. The first consists of collapsing the trajectory of values into a summary statistic that can be used in a regression model. Common statistics include the mean, median, or maximum value, or the sum of available data. Alternatively, the slope from a linear regression, or other ad hoc statistics may be used (Sakr et al., 2012; Dinglas et al., 2011). These approaches ignore the functional nature of the data, and are inefficient as they throw away much of the available information. Additionally, the choice of summary statistic is often arbitrary, and not driven by the data.

The second common approach to modeling variable-domain functional data is to register each function to a common domain, and then apply existing functional regression techniques (Goldsmith et al., 2011). In certain contexts this is a perfectly reasonable approach. However, it might be less appropriate for data in which the between-subject variability in the width of the domain is extreme, or when the original time domain is informative. For example, in the ICU data described above, the subject-specific lengths of stay range from a single day to over 100 days. It does not seem natural to align functions to a common domain when they differ in width by orders of magnitude. Similar problems occur in sleep data, where registering shorter and longer sleep intervals to the same domain would fundamentally affect the observed sleep architecture.

In response to these problems we introduce a class of statistical models that incorporate the functional covariate and account explicitly for varying domains across subjects. We assume that the primary analysis goal is to retrospectively explore the association between a functional covariate with subject-specific domain and a scalar outcome. The novel aspect of our modeling approach is to allow the functional coefficient to vary, smoothly, according to the domain width. We refer to this type of regression as variable-domain functional regression (VDFR). Our approach is fast, flexible, and easy to interpret.

The remainder of this paper is organized as follows. In the next section, we describe our data in more detail and provide the necessary scientific context. Section 3 introduces the VDFR model, and describes one approach to estimating the associated parameters. In Section 4, we present a number of re-parametrizations of the VDFR to create a useful expanded class of models. Section 5 presents the results of a detailed simulation study, and we apply our model to the ICU data in Section 6. We conclude with a discussion of what we have learned about regression on functions with variable domains.

2 Motivating Example

2.1 Data Description

The primary data for this analysis was taken from the Improving Care of Acute Lung Injury Patients (ICAP) study (Needham et al., 2006). Acute lung injury (ALI), also known as acute respiratory distress syndrome (ARDS), is a severe lung condition characterized by inflammation of the lung tissue (primary causes: pneumonia or sepsis). Patients with ALI/ARDS require mechanical ventilation in the intensive care unit (ICU), and experience high rates of mortality (Ware and Matthay, 2000). ICAP is a multi-site, prospective cohort study that enrolled 520 subjects with ALI/ARDS, 283 (54%) of which survived their hospitalization. Data for each patient are collected at baseline (enrollment into the study), daily while in the ICU, at hospital discharge or death, and among survivors, at seven follow-up points over five years.

Organ failure is measured by the Sequential Organ Failure Assessment (SOFA) score. The SOFA score is divided into six physiological components (respiratory, coagulation, liver, cardiovascular, central nervous system, and renal). Each component is assessed on a scale of 0–4 based on a set of physiological criteria, with larger values indicating poorer function. In cases where a physiological measurement is recorded repeatedly during the day, the worst 24-hour score is used. The component scores are then summed for a total SOFA score ranging from 0–24. Although it can only take integer values, we treat it as a continuous measure. The SOFA score is meant to be an overall measure of organ function, and is commonly used to track the physiological status of patients while in the ICU.

Thus, the observed data consist of {Y_i, Z_i, X_i(t_ij): 0 ≤ t_ij ≤ T_i}, where i is the index for subject and j is the index for observation time, j = 0, 1, …, J_i and {t_ij} are (not necessarily consecutive) integers with t_iJi = T_i for all i. In this notation, X_i(t_ij) are the SOFA scores, recorded daily in the ICU, T_i is the length of stay in the ICU, Z_i are non-functional covariates, and Y_i is an outcome, recorded at the end of hospitalization, or afterwards. We assume that {X_i(t_ij)} are sampled from an underlying stochastic process {X_i(t): t ∈ }, where is an interval on the real line.

Our analysis will focus on two binary outcomes: in-hospital mortality, and physical impairment at hospital discharge among ICU survivors. For the mortality outcome, one possible approach would be to model the time-to-event process for the two competing events, death and hospital discharge, and treat SOFA as a time-varying covariate in a proportional cause-specific hazards model (Cox, 1972; Holt, 1978). This approach could be extended to treat the SOFA scores as a longitudinal outcome in a joint model for the longitudinal and survival processes. Indeed, joint models for longitudinal and survival data have been the focus of intense research over the past two decades (Tsiatis et al., 1995; Wang and Taylor, 2001; Ibrahim et al., 2001; Brown and Ibrahim, 2003; Tsiatis and Davidian, 2004; Yu et al., 2004; Hanson et al., 2011; Ibrahim et al., 2010; Rizopoulos, 2012). An advantage of this modeling strategy is that it would allow for dynamic prediction of mortality, i.e., the ability to estimate whether or not a person will survive their ICU stay while they are still in the hospital (Yu et al., 2008; Garre et al., 2008; Proust-Lima and Taylor, 2009; Rizopoulos, 2011).

While this would certainly be a clinically important goal, it is not the focus of our analysis. Instead, our scientific problem is different: given a group of patients who died in the ICU and a group who survived, each with a different length of stay, how can we compare their within-ICU health trajectories? To accomplish this objective, we treat the outcome as a binary indicator of mortality, and we condition on each subject’s entire SOFA curve (including its domain length, T_i). Since we need to wait until the end of one’s hospitalization in order for T_i to be known, our methods will not be useful for dynamic prediction of mortality. Instead, our analysis is a retrospective analysis that aims to identify the precise features of one’s SOFA curve that differ between survivors and non-survivors. This allows us to better understand how patterns of dynamic organ failure differ between these two groups, and provides a way to quantify these differences.

Our second outcome is physical function at hospital discharge, measured using the Activities of Daily Living (ADL) scale (Katz et al., 1963). This questionnaire consists of six tasks, and for each one the subject indicates whether they can accomplish the activity independently, or that they require assistance. ADL information is available at both baseline and at hospital discharge, and at both time points the number of dependencies (i.e., total activities for which the subject requires assistance) are calculated. In order to isolate the effect of one’s hospital experience on physical function, the baseline number of dependencies is subtracted from the number of dependencies at discharge, and this number is dichotomized at ≥ 3. Thus, the outcome of interest will be whether or not the subject required assistance with three or more tasks than they did at baseline, a condition we refer to as “physical impairment.” The subjects who had 4 or more dependencies at baseline were removed from this analysis, as they were not eligible to experience the outcome. Of the 283 hospital survivors, 34 did not consent to followup, 1 was missing baseline ADL data, and 17 were ineligible for the outcome, resulting in a sample size of 231. Since this outcome is not available until hospital discharge, which typically occurs a few days or weeks after ICU discharge, the model may be treated as a predictive model.

2.2 Visualizing the Data

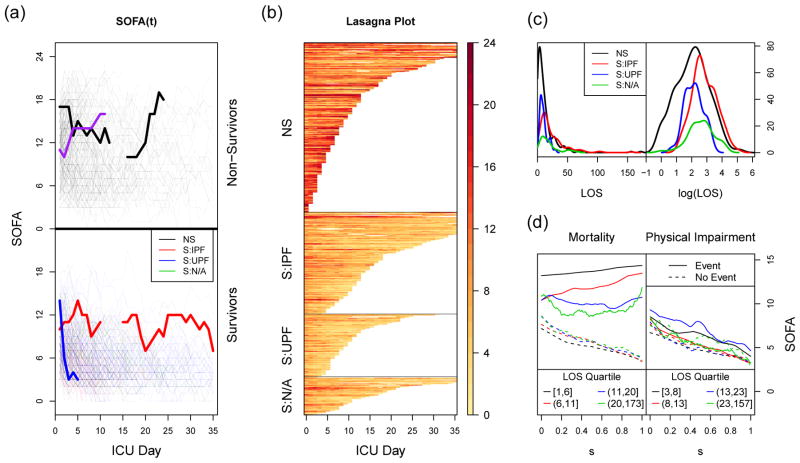
Exploratory plots of the data are presented in Figure 1. Plots (a) and (b) contain two depictions of the first 35 days of SOFA data. Both plots are stratified by the two outcomes: in-hospital mortality, and impaired physical function. Subjects are aligned according to the day of their onset of ALI/ARDS, which also corresponds to the first recorded SOFA measurement; this time point is indicated as day 0. We highlight four individual subjects in the spaghetti plot (Figure 1a) to provide some context. The patient indicated by the purple line entered the ICU with a moderate SOFA score of 11, but his health steadily declined (as indicated by an increasing SOFA score) until his death on the 11th day. The blue subject, on the other hand, started with a more severe initial score of 14, but his health rapidly improved, and he was discharged alive from the ICU on the fifth day without impaired physical function. The black and red subjects are examples of subjects with gaps in their curves. This occurs when a subject is discharged from the ICU to a hospital ward and later readmitted to the ICU; SOFA is not collected in the ward. The black subject entered the ICU with a score of 17, but improved enough to be discharged from the ICU to a hospital ward on his 12th day. However, he was re-admitted to the ICU four days later, and rapidly deteriorated until dying on the 24th day from baseline. The red subject was discharged from the ICU on his 10th day, was re-admitted 5 days later, and eventually was discharged a final time from the ICU on his 35th day.

Figure 1.

Exploratory plots. In plots (a), (b), and (c), NS = non-survivors, S:IPF = survivors with impaired physical function, S:UPF = survivors with unimpaired physical function, and S:N/A = survivors not assessed for physical function. The first two panels display the first 35 days of SOFA data as (a) a spaghetti plot and (b) a lasagna plot. Both subjects are separated into four groups, based on their values for the two outcomes (in-hospital mortality and physical impairment). In the spaghetti plot, color indicates outcome category. Four subjects are highlighted, and lines are used to connect adjacent measurements on the same subject, with gaps representing days where SOFA information was not available. In the lasagna plot, rows correspond to individual subjects, and darker colors are indicative of higher SOFA scores, i.e., poorer health. (c) Density estimates of the length of stay, stratified by the two outcomes, multiplied by the number of subjects in each stratum. (d) Mean SOFA functions that have been linearly compressed to a common domain, stratified by both outcome and ICU length of stay, for both mortality and physical function. Each LOS stratum contains approximately one quarter of the subjects for each outcome.

At least one gap similar to those observed in the black and red highlighted curves occurs in 33 of the 520 subjects (6%), causing 364 of the 8879 potential patient days (4%) to be missing (Table 1). The missingness is potentially informative, as patients are healthier when outside of the ICU than inside it, but models that account for the missing data mechanism are outside of the scope of this paper. Instead, since our method requires dense and equally spaced data, we impute these days using last observation carried forward (LOCF) based on advice from clinical experts. We conducted a number of sensitivity analyses, such as excluding the 33 subjects whose data contained gaps, and results remained relatively unchanged (supplemental material). This leads us to believe that any bias introduced by the LOCF imputation has minimal effect on our results.

Table 1.

Summary statistics regarding the distribution of lengths of stay, within-subject mean SOFA score, and ICU gaps in the ICAP data, stratified by outcome. An ICU gap occurs when a subject is discharged from the ICU to a hospital ward, but later readmitted to the ICU prior to hospital discharge. Mean SOFA Score refers to the average SOFA score observed for each subject.

	All Subjects (N=520)	Mortality		Physical Function
		Non-survivors (N=237)	Survivors (N=283)	Impaired (N=142)	Unimpaired (N=89)
Length of Stay:
Mean (SD)	17.1 (19.0)	14.2 (19.3)	19.5 (18.4)	24.6 (22.3)	11.2 (6.4)
Median (IQR)	11.0 (6.0, 20.0)	8.0 (4.0, 17.0)	13.0 (8.5, 23.0)	16.5 (11.0, 32.0)	10.0 (6.0, 13.0)
Range	(1, 173)	(1, 173)	(2, 157)	(4, 157)	(3, 31)
Mean SOFA Score:
Mean (SD)	8.5 (4.6)	11.9 (4.3)	5.6 (2.5)	6.0 (2.6)	4.9 (2.0)
Median (IQR)	7.2 (4.6, 11.6)	12.0 (8.3, 14.9)	5.0 (3.7, 7.2)	5.3 (4.0, 7.4)	4.6 (3.4, 6.1)
Range	(1.2,22.0)	(2.7,22.0)	(1.2,14.8)	(1.9,14.8)	(1.6,11.2)
ICU Gaps:
Subjects Affected (%)	33 (6%)	12 (5%)	21 (7%)	13 (9%)	2 (2%)
Patient Days Affected	364/8879 (4%)	132/3362 (4%)	232/5517 (4%)	174/3494 (5%)	17/1001 (2%)

Density estimates for the ICU length of stay, T_i, are displayed in Figure 1c, with summary statistics presented in Table 1. We see that subject-to-subject variability in terms of length of stay is quite extreme. There are several subjects for whom only a single SOFA measurement is available (all of whom died on that day), while others remained in the ICU for over 100 days. The median length of stay is 11 days, with survivors tending to remain in ICU longer than non-survivors. Accounting for this heterogeneity in the length of stay will be a key challenge that our method must address.

Some trends in the data are easy to see; for example, higher SOFA scores, shorter times in the ICU, and greater SOFA variability (both within and between subjects) are more common among the non-survivors than survivors. Indeed, a simple logistic regression of in-hospital mortality on each subject’s mean SOFA score performs well in terms of discrimination, resulting in a cross-validated area under the receiver operating characteristic curve (AUC) of 0.89. However, the question remains whether we could do better by considering the entire SOFA curve, without collapsing the values into a single summary statistic such as the mean. It is much more difficult to visually identify patterns that differentiate SOFA scores between impaired and unimpaired physical function, except that those with impaired physical function tend to remain in the ICU for longer than those who are unimpaired.

An alternative way of exploring SOFA trends across different lengths of stay is displayed in Figure 1d. Here, individual SOFA functions have been linearly compressed to a common domain from 0 to 1, a procedure that we refer to as domain-standardization (this will be discussed in more detail in Section 4.2). We then plot the mean SOFA function for each outcome category, stratified into four groups by length of stay. For mortality, we see a clear separation in the mean functions of the survivors (dashed lines) as compared to those who died (solid lines). Interestingly, the mean function of the survivors is quite consistent regardless of T_i. We do see differences in the mean function of the non-survivors according to T_i, with the functions decreasing and becoming more “U-shaped” as T_i increases. We do not see nearly as strong of a differentiation between those with (solid lines) and without (dashed lines) impaired physical function. In fact, the mean functions for those with and without physical impairment are virtually indistinguishable from each other in the (8, 13] and (23, 157] strata. In the other two strata there is a tendency for those who had impaired physical function on hospital discharge to have elevated SOFA scores. We do not observe a strong pattern in these functions as T_i increases.

2.3 Approach

Our goal is to explore the data in order to understand how patterns of SOFA scores differ among subjects with different levels of the two outcomes, in-hospital mortality and physical impairment. We are investigating regression procedures that take each subject’s entire set of covariates, {X_i(t_ij), Z_i, T_i}, t_ij ∈ [0, 1, …, T_i], and produce a single number that is most predictive of outcome; e.g., the log odds of mortality. In particular, this procedure must be flexible enough to account for a functional covariate of varying length. Note that by conditioning on the domain width T_i, our model cannot be used to dynamically predict when the curve will terminate (e.g., when a subject will die). Instead, our focus is a retrospective analysis that explores differences in SOFA patterns and how they relate to each outcome.

For potential solutions, we incorporate ideas from the field of functional regression, which we briefly describe here. Standard functional regression models focus on the association between a scalar outcome and a functional covariate of fixed width (i.e., functional domain). Suppose that {Y_i} are a set of scalar outcomes, {X_i(t)} are functional covariates all defined on the interval [0, T], and {Z_i} are non-functional covariates, where i ∈ {1, 2, …, N}. Then the generalized functional linear model (GFLM) to relate a functional covariate to a scalar outcome is

$$g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^T{X}_i(t)\beta (t)dt$$ (1)

where Y_i follows an exponential family distribution with mean μ_i, and g(·) is a link function. The functional parameter β(t) represents the optimal way of weighting each X_i(t) across the domain t ∈ [0, T], to obtain the total contribution of X_i(t) towards g(μ_i). β(t) is typically constrained to be smooth across the domain t.

Model (1) has been studied extensively (Marx and Eilers, 1999; Cardot et al., 1999; James, 2002; Cardot and Sarda, 2005; Müller and Stadtmüller, 2005; Ramsay and Silverman, 2005; Reiss and Ogden, 2007; James et al., 2009). Incorporating non-Gaussian outcomes, producing confidence intervals, and incorporating multiple noisy and heterogeneous functional predictors has proven to be difficult. Using a penalized likelihood approach and the connection with mixed effects models, Goldsmith et al. (2011) introduced penalized functional regression (pfr), a simple fitting approach that solved these outstanding problems. The method is implemented in the namesake function pfr() deployed in the R (R Development Core Team, 2011) package refund (Crainiceanu et al., 2012).

All these fundamental contributions have only considered the case when subject-specific functions have the same fixed domain. We now propose a new model that relates variable-domain functions to a scalar outcome.

3 Variable-Domain Functional Regression

3.1 Model Specification

We propose the following model to regress a scalar outcome on a function with subject-specific domain, which we refer to as variable-domain functional regression (VDFR):

$$g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+\frac{1}{T_i}{\int }_0^{T_i}{X}_i(t)\beta (t,T_i)dt$$ (2)

The model contains two important modifications from (1). The first is that the bounds of integration, previously fixed to be from 0 to T, are now subject-specific. The second is to replace the univariate coefficient function β(t) with the bivariate coefficient function β(t, T_i). We now describe this bivariate coefficient function in more detail to provide intuition. For any fixed domain width T₀, β(t, T₀) is a univariate function of length T₀, defined over the t-domain. This function serves as the optimal weight function for X_i(t) to express its contribution towards g(μ_i), just as β(t) did in (1). However, one typically would not want to assume that the weight function for a subject who remained in the ICU for 5 days, for example, would be the same as that for a subject who stayed in the ICU for 20 days. The bivariate coefficient function allows these weights to change as the width of the domain changes. We require that these weights change smoothly in both the t and T_i directions.

The VDFR model is similar in spirit to the varying-coefficient model (Hastie and Tibshirani, 1993), also referred to as a continuous-by-continuous interaction model (Ruppert et al., 2003). The interaction describes the way in which one variable (i.e. the domain width, T_i) modifies the association between the outcome and our covariate of interest X_i(t). Varying-coefficient models have previously been extended to the functional regression setting by Wu et al. (2010), who allow for a coefficient function that changes with any fixed covariate Z_i. The unique feature of our model is that the fixed covariate that we interact with X_i(t) is the domain width, T_i, and the integration only occurs over that domain width. Note that the term $\frac{1}{T_i}$ which appears in front of the integral sign is unnecessary, as it could easily be absorbed by the nonparametric coefficient function β(t, T_i). Its inclusion causes the estimate of the coefficient function to have similar magnitude across different levels of T_i.

3.2 Estimation

The domain of the coefficient function β(t, T_i) is {t, T_i: 0 ≤ t ≤ T_i ≤ max_i T_i}, which is a triangular or trapezoidal surface. Most common functional regression methods use a B-spline basis to approximate the coefficient function, but a tensor-product B-spline basis is defined over a rectangular surface and is thus not appropriate for variable-domain data. Instead, we use a thin plate regression spline basis (Wood, 2003), which adapts well to the non-rectangular regression surface covered by the data. A potential disadvantage of such a basis choice is that each basis function is symmetric in all directions (isotropic). In our scenario the two coordinates (t and T_i) have fundamentally different interpretations, and we may want to control the shape and degree of smoothness in each direction separately. Nonetheless, when a large number of basis functions are used the estimated surface can adapt quite flexibly to the data, and we have found them to work remarkably well in practice. An alternative basis choice would be the finite element basis (Brenner and Scott, 2002; Braess, 2007) that has been used to estimate the trapezoidal coefficient function of the historical functional linear model (Malfait and Ramsay, 2003; Harezlak et al., 2007). This basis was not chosen due to its increased computational complexity, though we do suggest it as an area for future research.

Basis coefficients are penalized with a second-order derivative penalty in order to ensure that estimates are visually smooth in both the t and T_i directions. We take advantage of the well-known connection between penalized likelihood and mixed models (Ruppert et al., 2003; Reiss and Ogden, 2009), which allows us to estimate the parameters of (2) using standard mixed model software, such as the gam function of the mgcv package in R (Wood, 2006). In addition to the software being readily available and well-tested, this allows us to take advantage of the inferential machinery for mixed models to obtain covariance estimates for all parameters. These estimates may then be used to obtain pointwise confidence intervals for β(t, T_i) using standard sandwich estimators; see Goldsmith et al. (2011) for details. All model parameters are estimated using restricted maximum likelihood (REML) to simultaneously estimate both the coefficients and the smoothing parameters (Wood, 2011).

3.3 Computational Issues

In scalar-on-function regression, it is often common practice to subtract the overall mean function from each raw covariate function, and use the resulting de-meaned functions as predictors in the regression model (Ramsay and Silverman, 2005; Goldsmith et al., 2011). In the standard scalar-on-function regression model (1), doing so does not effect the model other than in the interpretation of the intercept, but it can lead to increased numerical stability in the computation. In the case of variable-domain data, the overall mean function is not clearly defined. However, we can estimate the conditional mean of X_i(t) given T_i, which we denote μ_X|Ti(t), by fitting the generalized additive model X_i(t) = μ_X|Ti(t) + ε_i(t, T_i), ε_i(t, T_i) ~ N (0, σ²I). The bivariate mean function falls on a triangular or trapezoidal surface (the same surface as the associated coefficient function β(t, T_i), and may be fit using a thin plate regression spline basis.

Unlike in the standard scalar-on-function regression model (1), de-meaning the predictor functions will lead to different estimates of the bivariate coefficient function in the VDFR model (2). This is because de-meaning introduces an “offset” into the model that is dependent on T_i:

$$\begin{array}{l}\frac{1}{T_i}{\int }_0^{T_i}\{X_i(t)-\mu (t,T_i)\}\beta (t,T_i)dt=\frac{1}{T_i}{\int }_0^{T_i}{X}_i(t)\beta (t,T_i)dt-\frac{1}{T_i}{\int }_0^{T_i}\mu (t,T_i)\beta (t,T_i)dt\\ =\frac{1}{T_i}{\int }_0^{T_i}{X}_i(t)\beta (t,T_i)dt-h(T_i)\end{array}$$

If one includes the additive term f(T_i) in the model, this term would capture the offset h(T_i), and de-meaning will not have an effect on the estimate of β(t, T_i). If one does not include this term, the decision of whether to de-mean can be based on the desired interpretation of the resulting coefficient function, i.e., whether one believes that it is an individual’s deviation from the mean predictor function, rather than their predictor function itself, that is most associated with the outcome. Alternatively, the decision may be data-driven, for example by comparing cross-validated prediction errors.

We also note that isotropic smoothers such as the one we employ here were designed to model surfaces for which the arguments of the smoother are measured in the same units, such as points in space. If all of the predictor functions are of similar width, we may be faced with a situation where the coordinates in the t direction span a much wider range than the coordinates in the T_i direction. For these situations, we follow the suggestion of Wood (2003) and scale the coordinates to the unit triangle (i.e., the “upper-left corner” of the unit square).

Example code for all steps of the estimation for this model (as well as the extensions proposed in the next section) is provided in the supplemental material.

4 Expanded Class of Variable-Domain Models

In this section we show how we can use simple change of variables and re-parameterization of some of the terms in (2) to expand the class of models for variable-domain functional regression. The models in this section are theoretically equivalent to (2). However, in practice, each model will give different results due to choice of basis set, smoothness assumptions, and the scale of the numerical approximation of the integral term. We will compare these models more thoroughly in Section 5.

4.1 Lagged Time

Let u = t − T_i denote the “negative lagged” time, i.e. the time remaining until the end of one’s function, T_i, expressed as a negative number. This is the scale that one would obtain if each function was aligned according to their final measurement rather than their first, and this time was denoted as time u = 0. (2) becomes

$$\begin{array}{l}g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+\frac{1}{T_i}{\int }_{-T_i}^0{X}_i(u+T_i)\beta (u+T_i,T_i)du\\ =\alpha +{\mathit{Z}}_i\mathit{\gamma }+\frac{1}{T_i}{\int }_{-T_i}^0{X}_i^{\ast }(u){\beta }^{\ast }(u,T_i)du\end{array}$$ (3)

where $X_i^{\ast }(u)=X_i(u+T_i)$ and β*(u, T_i) = β(u + T_i, T_i), and the functions { $X_i^{\ast }(u)$} fall on the domain [−T_i, 0]. The main advantage of this approach is that it assumes smoothness based on the lagged-time as opposed to the original time, which may be more appropriate in certain applications. For example, if X_i(t) is a longitudinally-measured covariate and it is assumed that the most recent measurements will have a stronger effect than the earlier ones, then it makes more sense to impose smoothness based on the lagged time. The coefficient function still falls on a triangular or trapezoidal domain, defined by {u, T_i: min_i −T_i ≤ −T_i ≤ u ≤ 0}. Although this domain is the mirror image of that of β(t, T_i) in (2) (projected over the T_i-axis), the functions $X_i^{\ast }(u)$ are translations, rather than reflections, of the original functions X_i(t). The model may be estimated using a thin plate regression spline basis, in much the same way as we proposed to fit (2).

4.2 Domain-Standardization

In Section 1, we noted that a common approach in the functional regression literature for handling variable-domain data is to transform each function to a common domain. With the change of variable transformation s = t/T_i, model (2) becomes

$$g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^1{\stackrel{\sim }{X}}_i(s)\stackrel{\sim }{\beta }(s,T_i)ds$$ (4)

where X̃_i(s) = X_i(sT_i) and β̃ (s, T_i) = β(sT_i, T_i). The new covariate functions {X_i(s)} all fall on the common domain [0, 1], and the new domain variable s has the interpretation of representing the proportion of the way through the function. Thus, X̃_i(.5) is equal to X_i(t₀) at t₀ = T_i/2 (i.e., halfway between 0 and T_i), and X̃_i(1) is the final recorded value of X_i(t).

The coefficient function β̃ (s, T_i) still allows for a weight function β̃(s, ·) that changes with T_i. In fact, model (4) is a particular instance of a varying coefficient functional regression model (Wu et al., 2010), one for which the functional coefficient varies with T_i. The domain of the coefficient function is the rectangle {s, T_i: 0 ≤ s ≤ 1, 0 ≤ T_i ≤ max_i T_i}, which allows us to approximate the surface with an anisotropic basis suited for a rectangular surface, such as a tensor-product basis. Since B-splines are the most common basis found in the functional regression literature (Marx and Eilers, 1999; Cardot et al., 2003; Cardot and Sarda, 2005; Marx and Eilers, 2005), we apply a tensor-product B-spline basis to the surface. For comparison, we also fit the model using thin plate regression splines over the same surface.

4.3 Parametric Interactions

Domain standardization provides another benefit by allowing us to easily parametrize how T_i affects the weight function β̃(s, ·). For example, if we assume β̃ (s, T_i) = β₁(s) + β₂(s)T_i, the model becomes a linear interaction model. Letting X̃_i(s)T_i = A_i(s), (4) becomes

$$\begin{array}{l}g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^1{\stackrel{\sim }{X}}_i(s)\{{\beta }_1(s)+{\beta }_2(s)T_i\}ds\\ =\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^1{\stackrel{\sim }{X}}_i(s){\beta }_1(s)ds+{\int }_0^1{A}_i(s){\beta }_2(s)ds\end{array}$$ (5)

Thus, restricting β(s, T_i) to be linear in T_i reduces the problem to a standard scalar-on-function regression model with two functional predictors, X̃_i(s) and A_i(s). Similarly, if we assume $\stackrel{\sim }{\beta }(s,T_i)={\beta }_1(s)+{\beta }_2(s)T_i+{\beta }_3(s)T_i^2$, we obtain a quadratic interaction model. Technically, there is little difference between the linear and quadratic interaction models. Indeed, if ${\stackrel{\sim }{X}}_i(s)T_i^2=B_i(s)$ then the model becomes

$$\begin{array}{l}g({\mu }_i)=\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^1{\stackrel{\sim }{X}}_i(s)\{{\beta }_1(s)+{\beta }_2(s)T_i+{\beta }_3(s)T_i^2\}ds\\ =\alpha +{\mathit{Z}}_i\mathit{\gamma }+{\int }_0^1{\stackrel{\sim }{X}}_i(s){\beta }_1(s)ds+{\int }_0^1{A}_i(s){\beta }_2(s)ds+{\int }_0^1{B}_i(s){\beta }_3(s)ds\end{array}$$ (6)

which is a standard scalar-on-function regression model with three functional predictors. Alternatively, we can make the stricter assumption that β̃ (s, T_i) does not change with T_i, that is β̃ (s, T_i) = β(s). The resulting model, which is not an interaction model at all, is equivalent to the standard functional regression model (1) using the domain-standardized predictor functions.

Any of the models presented in this section may be fit using existing functional regression software that accepts multiple functional predictors, such as pfr (Goldsmith et al., 2011). To maintain consistency across all models, our implementation does not use existing functional regression software, but instead calls mgcv::gam directly, as was done for the non-parametric models discussed previously. As all models are fit using mixed model software, pointwise confidence intervals are available. We use a penalized B-spline basis to approximate the univariate coefficient functions in (1), (5), and (6) above.

5 Simulation Studies

5.1 Simulation Design

We now investigate the performance of these models via simulations, under a variety of true coefficient functions β(t, T_i). For simplicity, we consider the scenario where there are no non-functional covariates Z, and only a single functional predictor X(t). We consider every combination of the following simulation parameters, resulting in 3 × 2 × 2 × 4 × 2 = 96 total scenarios:

1. Three choices for the sample size, N: 100, 200, and 500

2. Two distributions for T_i: uniform or right-skewed

3. Four different possibilities for the true coefficient function, β(t, T_i), defined below

4. Two different types of outcomes: continuous and binary. We fit gaussian models to the continuous outcomes, and logistic models to the binary outcomes

5. Two choices for measurement error in X(t): none vs. some.

For notational convenience, we will assume that our functions are observed at whole-numbered time points, {t_j = 0, 1, …, J = 100}. For each value of N, we generate R = 1000 datasets of functional covariates according to the following model, which is adapted from Goldsmith et al. (2011):

$$\begin{array}{l}{W}_i(t_j)=X_i(t_j)+{\delta }_i(t_j)\\ X_i(t_j)=u_i+\sum _{k=1}^{10}\left\{v_{ik1}sin\left(\frac{2\pi k}{100}{t}_j\right)+v_{ik2}cos\left(\frac{2\pi k}{100}{t}_j\right)\right\}\end{array}$$

where ${\delta }_i(t_j)~N(0,{\sigma }_X^2)$, u_i ~ N (0, 1), and v_ik1, v_ik2 ~ N (0, 4/k²). In this notation, {X_i(·)} are the true underlying functions, whereas {W_i(·)} are the observed functions. We consider ${\sigma }_X^2\in \{0,1\}$, corresponding to no measurement error and some measurement error.

The domain width T_i is generated for each function independently, either from a Uniform(0, 100) distribution, or from a NegBin(1, p = 0.04) distribution that is truncated at a maximum T_i of 100. The latter distribution is right-skewed so as to produce more values of T_i that are small, such as those we observe in the ICAP data. Each function X_i(t_j) and W_i(t_j) is then truncated to only allow for t_j ≤ T_i.

We generate both continuous and binary outcomes for each dataset of functional covariates, based on the model ${\eta }_i=\frac{1}{T_i}{\sum }_{t_j=0}^{T_i}{\beta }_b(t_j,T_i)X_i(t_j)$, where b indexes the particular true coefficient function used. The continuous outcomes are simulated as Y_i = η_i + ε_i, ε_i ~ N (0, 1), whereas the binary outcomes are simulated from a Bernoulli(p_i) distribution, p_i = exp(η_i)/(1 + exp(η_i)).

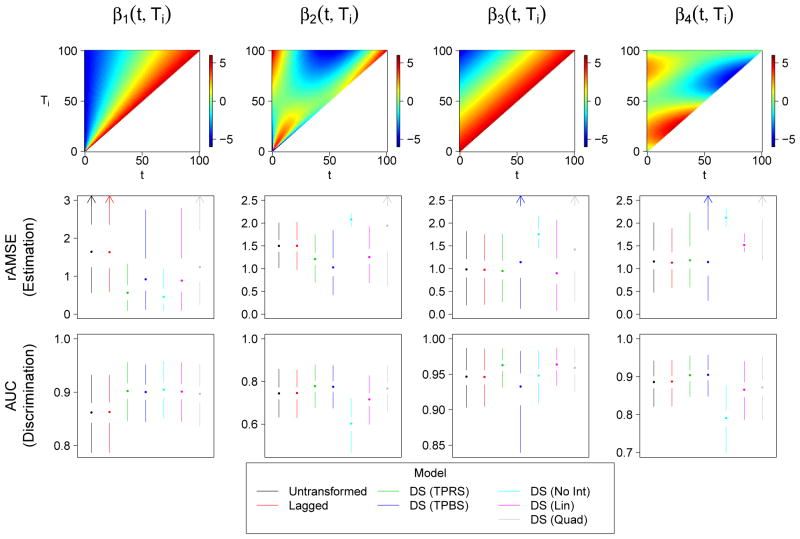
Four possible bivariate coefficient functions β_b(t, T_i) are considered:

$$\begin{array}{l}{\beta }_1(t,T_i)=10\frac{t}{T_i}-5\\ {\beta }_2(t,T_i)=\left(1-\frac{2T_i}{J}\right)\times \left(5-40{\left(\frac{t}{T_i}-0.5\right)}^2\right)\\ {\beta }_3(t,T_i)=5-10\left(\frac{T_i-t}{J}\right)\\ {\beta }_4(t,T_i)=sin\left(\frac{2\pi T_i}{J}\right)\times \left(5-10\left(\frac{T_i-t}{J}\right)\right)\end{array}$$

These coefficient functions all fall within the range [−5, 5], similar to what we will observe in our application, and are plotted as heat maps in Figure 2. The coefficient functions are meant to reflect one of two realistic scenarios. The first of these scenarios corresponds to a situation in which the relative position (t/T_i) within the function drives the association between X_i(t) and g(μ_i). This scenario is reflected in β₁(t, T_i) and β₂(t, T_i). The remaining two coefficient functions reflect a scenario in which the lag, T_i − t, drives the strength of the association.

Figure 2.

Simulation results for the case when N = 200, T_i is skewed, measurement error is present, and the outcome is binary. The top row depicts a heat map of the true coefficient functions. The second and third rows depict the root average mean squared error (rAMSE) of β●(t, T_i) and 10-fold cross-validated area under the ROC curve (AUC), respectively, for each of the seven models. Smaller rAMSE and larger AUC indicate better model performance. Results are presented as Tufte box plots, with the median represented by a dot, the interquartile range by the white space around the dot, and the smallest and largest non-outlying points by the endpoints of the lines. Outliers are defined as values not within 1.5 times the interquartile range of the nearest quartile. Arrows indicate lines that extend outside the plotting range.

We fit seven versions of the VDFR model to each simulated data set. The first one, which uses the untransformed predictor functions as described in Section 3, will be referred to as the “Untransformed” model. The second uses the lagged predictor functions as described in Section 4.1, and is referred to accordingly as the “Lagged” model. The remaining five models use the domain-standardized predictor functions. The first two allow for the interaction with T_i to be non-parametric (Section 4.2), either with a thin plate regression spline basis or a tensor-product B-spline basis. We refer to them as “DS (TPRS)” and “DS (TPBS)”, respectively. The final three models parametrize the interaction as described in Section 4.3. We refer to the models with no interaction, linear interaction, and quadratic interaction as “DS (No Int)”, “DS (Lin)”, and “DS (Quad)”, respectively.

In addition to the seven functional models, we fit 14 “non-functional” models to the simulated data (Table 2). The first five of these models were simple linear or logistic regressions of the outcome against a single summary statistic of each subject’s predictor function. The remaining nine were more complicated parametric or semi-parametric models involving the within-subject mean X̄_i and the domain width T_i. Variables and parameterizations of each model are listed in Table 2. All smooth functions are modeled using a thin-plate regression spline basis.

Table 2.

Median cross-validated AUC for all models applied to the simulated data, for the case when N=200, T_i is skewed, measurement error is present, and the outcome is binary. Models include seven functional models, five simple logistic regressions on the indicated summary statistic, and nine more complicated parametric or semi-parametric functions of the within-subject mean (X̄_i) and the domain width (T_i).

	β1(t, Ti)	β2(t, Ti)	β3(t, Ti)	β4(t, Ti)
Functional Models:
Untransformed	0.862	0.744	0.947	0.886
Lagged	0.863	0.746	0.946	0.887
DS (TPRS)	0.902	0.778	0.963	0.904
DS (TPBS)	0.900	0.775	0.933	0.905
DS (No Int)	0.905	0.602	0.948	0.790
DS (Lin)	0.901	0.716	0.964	0.866
DS (Quad)	0.897	0.767	0.959	0.872
Summary Statistic Models:
Mean	0.434	0.634	0.955	0.854
Median	0.436	0.637	0.949	0.847
Maximum	0.439	0.601	0.842	0.776
Cumulative	0.431	0.646	0.915	0.817
Slope	0.820	0.429	0.438	0.431
Additional Models:
β1X̄i + β2Ti	0.459	0.631	0.954	0.850
β1X̄i + f2(Ti)	0.466	0.628	0.951	0.846
f1(X̄i) + β2Ti	0.466	0.621	0.953	0.845
f1(X̄i) + f2(Ti)	0.472	0.620	0.949	0.842
f(X̄i, Ti)	0.465	0.720	0.938	0.865
β1X̄i + β2Ti + β3X̄iTi	0.458	0.636	0.958	0.864
β1X̄i + f2(Ti) + f3(X̄iTi)	0.468	0.647	0.953	0.856
f1(X̄i) + β2Ti + f3(X̄iTi)	0.472	0.650	0.955	0.857
f1(X̄i) + f2(Ti) + f3(X̄iTi)	0.475	0.649	0.952	0.852

5.2 Evaluation criteria

Performance of models was evaluated in two ways. First, we measure the ability of each model to predict the outcome in each scenario. For the models fit to the continuous outcomes, this is measured through the cross-validated root mean squared error (rMSE), whereas for the binary outcome models, we calculated the cross-validated area under the receiver operating characteristic curve (AUC). All cross-validation is 10-fold. Good predictive accuracy is indicated by low rMSE or high AUC.

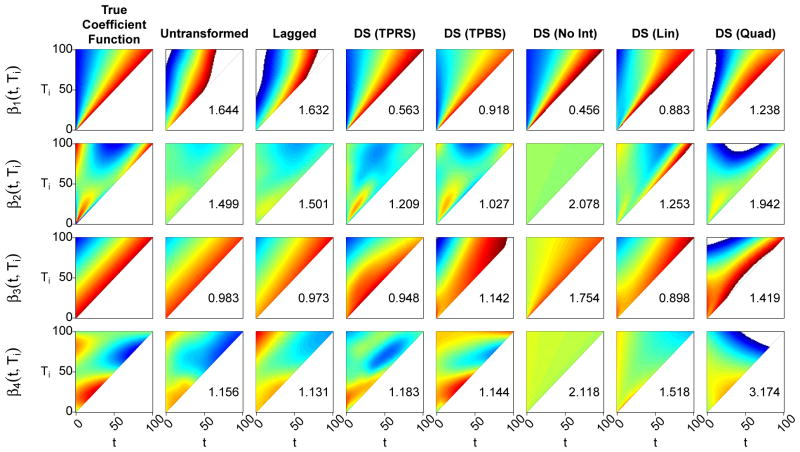
For the seven models that produce functional estimates, we also measure the ability of each model to estimate the true coefficient function. This ability is evaluated using the average mean squared error (AMSE) of the estimate over all possible values of t_j and T_i. More precisely,

$${\text{AMSE}}^{(r)}\left({\widehat{\beta }}_b(·,·)\right)=\frac{1}{J(J+1)}\sum _{k=0}^J\sum _{j=0}^k{\left\{{\widehat{\beta }}_b^{(r)}(t_j,k)-{\beta }_b(t_j,k)\right\}}^2,$$

where ${\widehat{\beta }}_b^{(r)}(t_j,k)$ is the estimated coefficient function from the r^th simulated dataset evaluated at t = t_j, T_i = k, and β_b(t_j, k) is the value of the true coefficient function at this location. Before this calculation is performed, all estimates (other than the one from the Untransformed model) are converted back to the original (triangular) domain. For the Lagged model, this is a simple translation of the estimates. For the five models fit using the domain-standardized predictor functions over a rectangular grid, we stratify estimates for each T_i into T_i + 1 bins, and calculate the mean value in each bin.

5.3 Simulation results

The median cross-validated AUC statistics for the case when N = 200, T_i is chosen from a skewed distribution, measurement error is present, and the outcome is binary are presented in Table 2. This scenario is presented because it is most similar to our application; results from other scenarios appear in the supplemental material. For the presented scenario and in nearly every other scenario, the model with the lowest median cross-validated mean squared error (continuous outcome) or highest median cross-validated AUC (binary outcome) was one of the seven functional models. In many cases, the performance of the non-functional models was extremely poor, resulting in cross-validated AUC statistics around 0.5 or even below, indicating that the given model does not help predict the outcome at all. The only cases where the best model was one of the non-functional models occurred with the smallest sample size, binary outcome, and skewed distribution for T_i, under β₃(t, T_i). In these cases there were a number of models that all predicted outcome very well, and the best-performing model happened to be one of the non-functional ones.

The results for the seven functional models under the above scenario are presented more fully in Figures 2 and 3. The former presents the rAMSE and cross-validated AUC values across the 1000 iterations as box plots, whereas the latter depicts the estimated coefficient function for the estimate with median AMSE among the 1000 iterations, as a heat map. The four nonparametric models seem to perform well regardless of the true coefficient function. For β₁(t, T_i) and β₂(t, T_i), the domain-standardized models tend to perform better than the Untransformed and Lagged models. The DS (TPRS) and DS (TPBS) models tend to perform similarly for all coefficient functions other than β₃(t, T_i), where there appears to be much more variability in the performance of the DS (TPBS) model. The reasons for this are not clear, and this effect does not occur when the outcome is gaussian (supplemental material). The Untransformed and Lagged models tend to perform similarly for all four coefficient functions, including β₃(t, T_i) and β₄(t, T_i), which were designed to be lag-based.

Figure 3.

Heat maps of the estimate with median AMSE across the 1000 simulated datasets, for each model and coefficient function, in the case where N = 200, T_i is skewed, measurement error is included, and the outcome is binary. The range for each plot is from −6 (blue) to 6 (red), with values outside of this range indicated by white space. The numbers in the lower-right corner of each plotting area are the rAMSE statistics for each estimate.

The parametric functional models are among the best-performing models in the cases when the interaction with T_i is simple enough to be accounted for by the parametric assumption. For example, all three parametric models perform well under β₁(t, T_i), which contains no interaction on the domain-standardized scale. However, the DS (No Int) model cannot account for the linear interactions that are present in the other three coefficient functions, resulting in an estimate that is quite homogenous in both the t and T_i directions. The three parametric models are outperformed by the domain-standardized nonparametric models for both β₂(t, T_i) and β₄(t, T_i), which contain more complicated interactions. The quadratic model especially produces estimates that are quite unstable in the region with high T_i. Recalling that these estimates are from the scenario where T_i is chosen from a right-skewed distribution, this observation reflects the instability of extrapolating higher-order polynomial functions to regions outside the bulk of the data.

Tables and plots of the rAMSE, rMSE, and AUC under other scenarios (different sample sizes, distribution of T_i, amount of measurement error, and continuous outcomes) are available in the supplemental material. In general, we found the results discussed above to hold true under these scenarios as well. As expected, both estimation and prediction error tend to be lower as the sample size increases, when the distribution of T_i is uniform, and when measurement error is not present. rAMSE values tended to be much lower when the outcome was continuous as opposed to binary. They were also much less variable, resulting in more clear differentiation between models. Overall patterns of comparative model performance were similar to the binary case.

6 Application to ICAP Data

6.1 Model Specification

For both binary outcomes in the ICAP data, we fit each of the seven VDFR models discussed in the preceding sections. Each model includes SOFA as a functional covariate and controls for age, gender, Charlson comorbidity index (a commonly used index of baseline health, (Charlson et al., 1987)), and the log of the ICU length of stay T_i, as fixed (non-functional) effects.

We investigated whether de-meaning the functional predictors and/or modeling log(T_i) as a smooth term rather than a linear term improved model performance. Based on cross-validated AUC statistics, we found the optimal performance for the mortality outcome occurred when the SOFA functions were not de-meaned and when log(T_i) was modeled smoothly. For physical function, highest cross-validated AUC scores occurred without de-meaning when log(T_i) was included as a linear term. It is these results that we present below. Additionally, since the domain width T_i is highly right-skewed, we investigated whether the interaction in the functional models should occur with a transformation of this variable. In other words, instead of estimating the coefficient function β(t, T_i), we estimate β*(t, w(T_i)), where w(·) is a monotonic transformation function. The two w(·) functions considered were the log function, and the empirical quantiles of T_i. In addition to evening out the amount of data over the estimated surface on these scales, this approach assumes that the true interaction takes place on the transformed scale. Since the w functions are monotonic, the resulting models are theoretically equivalent, but in practice may be different due to the choice of basis and level of smoothness. However, we found that differences between the three methods were quite small in the ICAP dataset. Since the lengths of stay are approximately log-normally distributed, we present the results using the log-transformed T_i.

In addition to the seven functional models, we fit 13 non-functional models to the data, similar to those fit to the simulated data. All models are adjusted for the same covariates (age, gender, Charlson index, and log(T_i)) as the functional models.

6.2 Model Performance

AUC statistics for each model are presented in Table 3, both in-sample and under cross-validation, with 95% confidence intervals based on 1000 bootstrapped samples. The in-sample statistic measures the discriminative ability of each model on the existing dataset, whereas the cross-validated statistic estimates discriminative ability for a new sample, and is more relevant for model selection as it is less prone to over-fitting. The cross-validated statistics are based on leave-one-out (i.e., N-fold) cross-validation, but the confidence intervals are based on 10-fold cross-validation to reduce the computation time. This will likely produce slightly wider confidence intervals than if we had used N-fold cross-validation.

Table 3.

AUC statistics for each model, applied to the binary outcomes of in-hospital mortality and physical function in the ICAP dataset. Results are presented as _LX_R, where X is the estimate, and (L, R) are the lower and upper bounds, respectively, of a 95% confidence interval based on 1000 bootstrapped samples. Both in-sample and cross-validated AUC statistics are presented. Cross validation is N-fold for the estimates, and 10-fold for the bootstrapped confidence intervals. All models are adjusted for age, gender, Charlson comorbidity index, and the log length of stay. Log length of stay is included as a smooth term for mortality and as a linear term for physical impairment.

	Mortality		Physical Impairment
	In-sample	Cross-validated	In-sample	Cross-validated
Functional Models:
Untransformed	0.9400.9480.977	0.9130.9190.955	0.8130.8380.911	0.7560.7840.871
Lagged	0.9410.9470.977	0.9110.9180.955	0.8120.8360.911	0.7600.7900.875
DS (TPRS)	0.9420.9490.983	0.9220.9330.960	0.8250.8470.943	0.7660.7900.888
DS (TPBS)	0.9420.9500.981	0.9200.9360.961	0.8110.8290.945	0.7500.7840.883
DS (No Interaction)	0.9340.9460.971	0.9160.9340.957	0.7670.8260.886	0.7270.7970.860
DS (Linear)	0.9370.9470.973	0.9140.9330.957	0.7730.8310.902	0.7250.7940.862
DS (Quadratic)	0.9430.9500.977	0.9190.9350.959	0.7890.8300.907	0.7350.7880.863
Summary Statistic Models:
Mean	0.8770.8990.927	0.8700.8930.922	0.7550.8200.870	0.7190.7980.854
Median	0.8760.8980.929	0.8680.8910.923	0.7520.8200.872	0.7160.7980.852
Maximum	0.8600.8850.913	0.8530.8790.908	0.7570.8190.874	0.7280.7990.858
Cumulative	0.8050.8420.876	0.7930.8330.868	0.7600.8180.872	0.7310.7970.854
Slope	0.7440.7950.856	0.7280.7850.847	0.7500.8100.868	0.7230.7900.851
Additional Models:
β1X̄i + f2(Ti)	0.8800.9010.930	0.8710.8920.922	0.7960.8210.892	0.7470.7920.862
f1(X̄i) + β2Ti	0.8770.8990.927	0.8680.8930.920	0.7670.8200.879	0.7130.7960.852
f1(X̄i) + f2(Ti)	0.8800.9010.930	0.8690.8920.920	0.7970.8210.895	0.7400.7900.862
f(X̄i, Ti)	0.8780.8990.933	0.8650.8930.921	0.7670.8200.917	0.7270.7980.865
β1X̄i + β2Ti + β3X̄iTi	0.8760.9000.927	0.8690.8930.922	0.7530.8180.871	0.7170.7950.851
β1X̄i + f2(Ti) + f3(X̄iTi)	0.8820.9010.933	0.8690.8910.921	0.8020.8200.905	0.7450.7810.858
f1(X̄i) + β2Ti + f3(X̄iTi)	0.8800.9010.930	0.8690.8910.922	0.7730.8200.899	0.7360.7910.859
f1(X̄i) + f2(Ti) + f3(X̄iTi)	0.8840.9010.934	0.8680.8910.921	0.8090.8200.915	0.7450.7810.858

Comparing the seven functional models for the mortality outcome, we see that the five models that used the domain-standardized functions all performed quite similarly by both metrics. The Untransformed and Lagged models both performed slightly worse under cross-validation. Each of the functional models resulted in higher AUC statistics than the non-functional ones, both in-sample and cross-validated. While the absolute differences in AUC between the functional and non-functional models may not be very large, we note that a perfectly discriminating model would have an AUC of 1. Thus, the difference between each AUC and 1 offers a measure of the “imperfection” of each model. From this perspective, the best-performing functional model (Domain-standardized B-splines) offers an improvement over the best-performing summary statistic model (mean SOFA) of 40% in terms of cross-validated AUC.

For physical function, AUC statistics were quite a bit lower than those for the mortality outcome, reflecting the weaker association between SOFA patterns and impaired physical function. Additionally, we do not see the same benefit in using a functional modeling approach. Although the functional models result in higher in-sample AUC statistics than the non-functional models, this does not hold under cross-validation. This result indicates that the functional nature of the SOFA curves is not a strong predictor of impaired physical function. The functional model with no interaction performs quite well under cross-validation in both of the two outcome scenarios, indicating that there is not much benefit in terms of discriminative ability to allowing β(t, T_i) to change with T_i.

6.3 Estimated Coefficient Functions

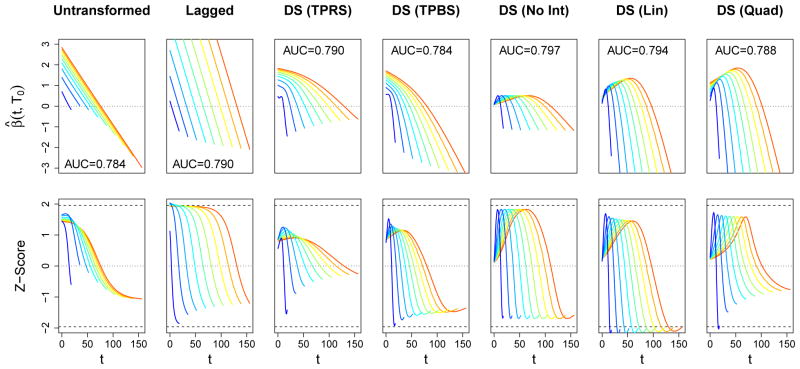
The estimates for the coefficient functions for mortality and physical function are presented in Figures 4 and 5, respectively. Rather than presenting the triangular surface β̂(t, T_i) estimated by each model as a heat map, we present the univariate weight functions β̂ (t, T₀) for 10 different values of T₀ spread evenly across the domain of T_i. The top row in these figures displays these estimates, with T₀ indicated by color as well as the support along the t-axis, and the bottom row of plots displays the corresponding pointwise Z-scores, β̂ (t, T₀)/SE(β̂ (t, T₀)).

Figure 4.

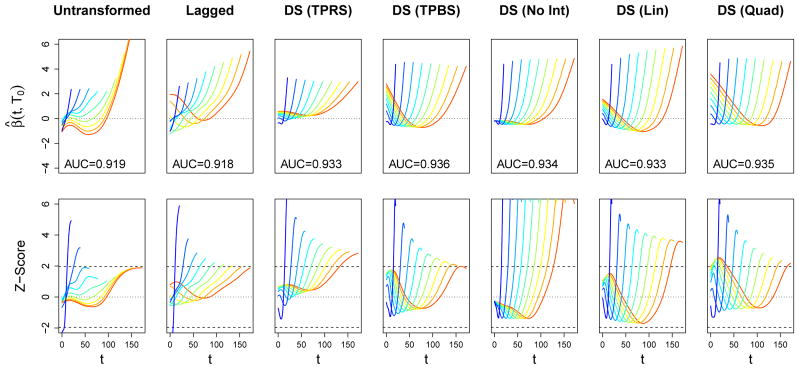
Estimated coefficient functions for the association between daily SOFA score and in-hospital mortality in the ICAP dataset. Each column corresponds to one of our six functional models. In the top row of plots, estimates are depicted as β● (t, T₀) for 10 evenly-spaced values of T₀. AUC statistics subject to 10-fold cross-validation are also provided. The bottom row displays the corresponding pointwise Z-scores, β● (t, T₀)/SE(β● (t, T₀)), as a function of t. The value of T₀ is indicated both by color and by the support of each function. The zero line is indicated with a horizontal dotted line, and dashed lines correspond to Z-scores of ±1.96.

Figure 5.

Estimated coefficient functions for the association between daily SOFA score and impaired physical function in the ICAP dataset, presented similarly to Figure 4.

For mortality, we see a consistent pattern among all models of a strong, positive spike in the association between death and high SOFA scores at the end of one’s ICU stay, regardless of T_i. In most cases, the pointwise associations in these regions is statistically significant, according to a Wald test with α = 0.05. This pattern is expected: subjects with higher SOFA scores (i.e., more severe organ failure) right before the end of their ICU stay are likely to have their ICU stay end in death, rather than be discharged alive. Moreover, increasing SOFA scores have been associated with withdrawal of life support, leading to subsequent mortality (Turnbull and Ruhl, 2014). The linear and quadratic models show a tendency for this spike to move later into one’s ICU stay when T_i is long. This pattern suggest that the last few days in the ICU are most important for predicting mortality, regardless of T_i. The models that allow for a more flexible interaction with T_i also estimate a positive association between early SOFA scores and mortality for subjects with long lengths of stay, resulting in “U-shaped” weight functions. Although there may be some effect on mortality related to the severity of the event that caused the onset of ALI/ARDS, we note that there are very few subjects that have these high lengths of stay (only seven subjects with T_i > 75), and this effect may be spurious. This hypothesis is supported by the fact that the pointwise associations in these regions are not statistically significant.

For physical function, one might be tempted to ignore the coefficient estimates from the functional models, which had lower cross-validated AUC statistics than some of the simpler, parametric models. However, these estimates may still be revealing, as they are able to estimate types of associations that are not possible to be estimated by traditional approaches, and still may identify important trends in the data. For this outcome, we find that the functional association decreases over one’s ICU stay, quite linearly in each case. However, the magnitude of these associations is relatively small, and the pointwise 95% confidence intervals cover 0 in every region of all models, except for some very small locations in the Untransformed and DS (TPRS) models. This lack of a strong association reflects our observations from Figure 1 and Table 3, each of which showed weak functional relationships between SOFA and physical impairment.

For both mortality and physical impairment, there are certain features in the estimates that were somewhat unexpected, and these features have fundamental implications on the interpretation of the coefficient functions. For mortality, we were initially surprised that there were regions of each estimate that lied below the zero line. This means that, for two subjects with the same SOFA scores during the regions where the coefficient function is positive, the model predicts that the one with lower scores (i.e., the healthier patient) in the region with negative coefficient function is more likely to die. Similarly, even though the estimates for physical impairment were not statistically significant (in a pointwise sense), we were surprised the the predominant trend was for the weight functions to decrease over one’s ICU stay. According to these models, a subject whose condition gradually deteriorates throughout their hospitalization will be less likely to have impaired physical function upon hospital discharge than a subject who improves.

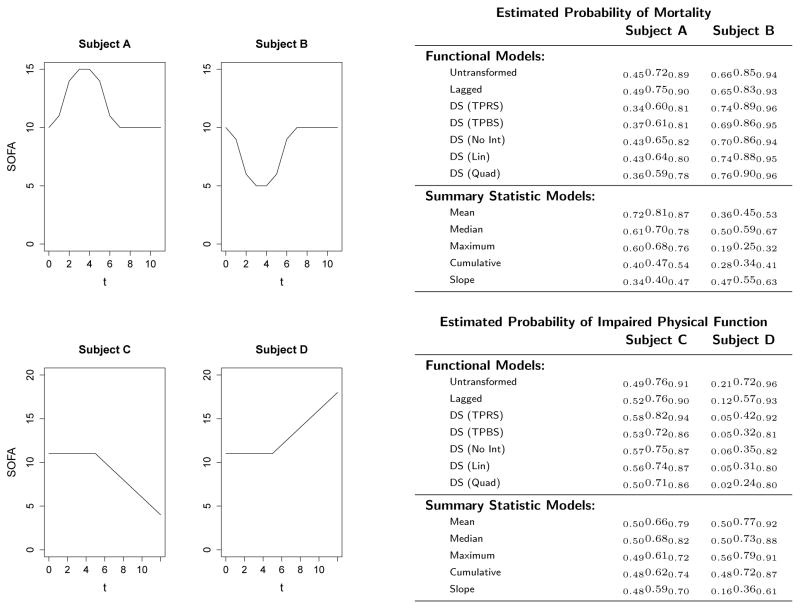
To further illustrate these points, consider the hypothetical SOFA curves plotted in Figure 6. Subjects A and B have the same SOFA scores during the latter portion of their hospitalization, but Subject A experiences a temporary spike in his SOFA scores during the middle of his hospitalization, whereas Subject B experiences a temporary drop during this same time period. Both subjects were assigned the same values for their non-functional covariates (age, gender, Charlson index, and length of stay). According to each of the functional models, the subject who experienced the lower scores is more likely to die than the subject with higher scores. High SOFA scores, in the early and middle portion of one’s ICU stay, appear to be associated with higher likelihood of survival. Similarly, in the lower plots both subjects had the same SOFA scores for the first 7 days of their ICU stay, but then Subject C’s condition improved over the final 6 days whereas Subject D’s health declined. However, the functional models predict that the subject whose health improved is more likely to leave the ICU with impaired physical function than the one whose condition deteriorated. The lone exception is the Lagged model, whose estimate has a shorter period where it is negative compared to the other models.

Figure 6.

Trajectories of four hypothetical patients, along with their predicted probabilities of outcome according to each model. Top row corresponds to the mortality outcome, and bottom corresponds to impaired physical function.

At first glance these observations may appear counter-intuitive, but each may be explained in the context of the full model. Since subjects similar to Subject A contain peaks in their SOFA scores early in their ICU stay, it means that they survived a serious episode that caused a temporary peak (worsening of health); if they did not, then their SOFA function would end at this point. Thus, subjects whose SOFA scores peak early in their ICU stay might have greater baseline physiological reserve than those who did not experience this peak, as demonstrated by their ability to survive this severe organ failure. Moreover, for two subjects who have the same SOFA pattern towards the end of their ICU stay, the one whose scores peaked earlier during their hospitalization must have experienced improvement since then. Thus, although Subject A was quite sick in the middle of his ICU stay, the trend in the latter half of hospitalization indicates relative improving health. In contrast, Subject B may have improved early on, but since that point their condition declined. The negative estimated coefficient function early in one’s ICU stay captures this effect, whereas the non-functional models do not.

The high predicted probabilities of physical impairment for Subject C relative to D may be explained by recognizing that the subjects eligible for this outcome not only survived their ICU stay, but were also deemed healthy enough to be discharged from the ICU. If a subject has experienced a rapid improvement in their physiological metrics, a physician may be more likely to allow the subject to leave the ICU, even if he is still has some physical limitations as measured by the ADL scale. Conversely, a subject who still has some evidence of poor organ function will likely only be discharged from the ICU if he has demonstrated tremendous improvement in his outward appearance, such as proving to be unrestricted in daily activities. Though it is possible that these effects are only spurious, as these models were outperformed by some of the non-functional ones, we feel these trends are noteworthy and should perhaps be investigated in future studies.

7 Discussion

In this paper, we investigated methods to capture the effect of a functional predictor, where the domain of this predictor may vary widely from subject-to-subject. Such a situation is most commonly encountered when the domain variable is time, and each subject (or unit) is measured for a different length of time, as in our application. This investigation motivated our development of the variable-domain functional regression model (VDFR), which estimates a weight function to capture the effect of a functional predictor, but allows this weight function to vary (smoothly) based on the total follow-up time for each subject.

The VDFR models were able to identify features of the association between a longitudinally collected covariate and an outcome that traditional multivariate regression methods are not equipped to handle. In the analysis of ICAP mortality, we saw specifically how the functional models incorporate information related to both the magnitude of one’s SOFA score and their trajectory over time to provide better discriminative ability than naive (non-functional) approaches. They also allow us to ask previously unanswerable questions, such as whether or not it is optimal to treat a longitudinal covariate with subject-specific domain as a function, and how the domain width affects the covariate-outcome relationship. Although we were not able to identify any evidence for a strong functional relationship between SOFA score and physical function at hospital discharge, without these methods we would not have known how to answer such a question.

It is important to recognize that the models that we fit are not causal models, and we do not employ them to try to identify a causal relationship between the covariate function and outcome. For example, we identified a pattern in the data that increasing SOFA scores towards the end of one’s hospitalization, which indicate a decline in one’s overall health, are associated with a higher likelihood that a surviving subject has limitations in their activities of daily living. We do not believe that organ failure causes a subject to have improved physical function; such a claim would run contrary to logic. One must take care in the interpretation of the coefficient functions not only in the VDFR models, but in any functional regression model. The magnitude of the coefficient function at any particular point (t, T_i) = (t₀, T₀) should only be interpreted conditional on the rest of the curve, the domain width T_i, and the patient population under consideration.

Among the various VDFR models, we observed an advantage in domain-standardization as compared to the Untransformed and Lagged models, both in our simulations and when applied to the ICAP data. The key difference between the fit via the domain-standardized models and the Untransformed/Lagged models is the scale on which the smoothness is applied. The Untransformed/Lagged models apply the same degree of smoothness between adjacent time points regardless of the domain width, T_i. The domain-standardized models, on the other hand, implicitly relax the amount of smoothness between adjacent days when T_i is short, as compared to when T_i is long, because these points are stretched further apart on the domain-standardized scale. It is quite likely that one would want to allow for a greater separation in the estimated weights on days 1 and 2 when a subject is only followed for 3 only days, for example, than when he is followed for 30 or 100. A potential solution would be to employ a smoothness criterion that allows the degree of smoothness to vary with T_i, which we do not attempt in this paper.

It may seem unnatural to stretch a function with a domain of only a few days to be the same width as a function with a domain of 100 or more days, however we remind the reader that we avoid any problems by allowing the coefficient function to change with T_i. We are unsure whether or not we would see the same advantage to domain-standardization if there was not such a large amount of variability in T_i, or if the minimum T_i was greater than just a single day, as is the case in the ICAP data. These questions should be explored in future work. Another advantage of domain-standardization is that it easily allowed us to implement three parametric interaction models (no interaction, linear interaction, and quadratic interaction). These models were usually outperformed by their nonparametric counterparts, but they did offer a number of potential benefits, including more robust estimates, tighter confidence intervals, and greater interpretability.

Our proposed methodology is not without limitations. First and foremost is its inability to dynamically predict mortality during one’s ICU stay. The ability to predict whether a subject is likely to survive while they are in the ICU would be quite useful for patient prognostication and treatment. We intend to investigate whether this methodology can be extended to this scenario in future work, perhaps by incorporating ideas from joint models for longitudinal and survival data. Additionally, our methods currently fail to account for missing observations, or sparse or unevenly sampled functional covariates. For the SOFA data, we avoid this scenario by imputing SOFA scores to fill the gaps in our functions. This approach ignores the informative missingness of this data, but we were encouraged by the fact that our sensitivity analyses, including a complete-case-only analysis, produced similar results. This is likely in part due to the fact that only 4% of possible patient days are missing. In cases where the missing data mechanism is assumed uninformative, a preferred approach is to approximate each function using a functional principal components expansion, which would impute each function by borrowing strength from similar functions that do not contain gaps. This procedure has not yet been developed for variable-domain functions. We hope to explore these issues in future work.