Differences and Comparisons of the Properties and Reactivities of Iron(III)–hydroperoxo Complexes with Saturated Coordination Sphere

Abstract

Heme and nonheme monoxygenases and dioxygenases catalyze important oxygen atom transfer reactions to substrates in the body. It is now well established that the cytochrome P450 enzymes react through the formation of a high-valent iron(IV)–oxo heme cation radical. Its precursor in the catalytic cycle, the iron(III)–hydroperoxo complex, was tested for catalytic activity and found to be a sluggish oxidant of hydroxylation, epoxidation and sulfoxidation reactions. In a recent twist of events, evidence has emerged of several nonheme iron(III)–hydroperoxo complexes that appear to react with substrates via oxygen atom transfer processes. Although it was not clear from these studies whether the iron(III)–hydroperoxo reacted directly with substrates or that an initial O–O bond cleavage preceded the reaction. Clearly, the catalytic activity of heme and nonheme iron(III)–hydroperoxo complexes is substantially different, but the origins of this are still poorly understood and warrant a detailed analysis. In this work, an extensive computational analysis of aromatic hydroxylation by biomimetic nonheme and heme iron systems is presented, starting from an iron(III)–hydroperoxo complex with pentadentate ligand system (L₅²). Direct C–O bond formation by an iron(III)–hydroperoxo complex is investigated, as well as the initial heterolytic and homolytic bond cleavage of the hydroperoxo group. The calculations show that [(L₅²)Fe^III(OOH)]²⁺ should be able to initiate an aromatic hydroxylation process, although a low-energy homolytic cleavage pathway is only slightly higher in energy. A detailed valence bond and thermochemical analysis rationalizes the differences in chemical reactivity of heme and nonheme iron(III)–hydroperoxo and show that the main reason for this particular nonheme complex to be reactive comes from the fact that they homolytically split the O–O bond, whereas a heterolytic O–O bond breaking in heme iron(III)–hydroperoxo is found.

Introduction

Heme and nonheme iron monoxygenases and dioxygenases are unique classes of biological catalysts, which drive vital reactions for human health and as a consequence they are found in most biosystems ranging from bacteria to mammals. The nonheme iron dioxygenases bind and utilize molecular oxygen on an iron center and transfer both oxygen atoms to one or more substrates.[1] For instance, a well-studied nonheme iron dioxygenase is taurine/α-ketoglutarate dioxygenase (TauD), which uses molecular oxygen to decarboxylate α-ketoglutarate to succinate and thereby generates a high-valent iron(IV)–oxo intermediate.[2] The latter species acts as the oxygen-atom transfer agent to substrates, such as taurine. Yet other nonheme iron dioxygenases, such as cysteine dioxygenase (CDO),[3] transfer both oxygen atoms to the same substrate. In both TauD and CDO, an initial iron(III)-superoxo intermediate is formed that, in an electrophilic reaction step, is converted into an iron(IV)–oxo species. By contrast, isopenicillin N synthase reacts with four consecutive hydrogen atom abstraction steps, whereby the iron(III)-superoxo is converted into iron(III)–hydroperoxo, subsequently into iron(IV)–oxo, and finally into an iron(III)-hydroxo complex in each of these hydrogen atom abstraction reactions.[4] Therefore, in this particular system, the nonheme iron(III)-superoxo, iron(III)–hydroperoxo, iron(IV)–oxo, and iron(III)-hydroxo intermediates are all catalytically competent oxidants of hydrogen atom abstraction reactions from aliphatic groups. Chemically, the nonheme iron dioxygenases are, therefore, quite different from heme enzymes like the cytochromes P450, where a catalytic cycle that uses two electrons and two protons generates an iron(IV)–oxo heme cation radical, which is the sole active species.[5] All other catalytic cycle intermediates of P450 so far have been ruled out as possible oxidants in such demanding reactions.

Despite differences in reactivity, the above-mentioned nonheme iron enzymes have structural features of the active site in common. Figure 1 shows the active-site structure of isopenicillin N synthase (IPNS) as taken from the protein databank (pdb) file 1BK0.[6] The active site of the enzyme contains an iron atom that is linked to the protein through two histidine side chains (His₂₁₄ and His₂₇₀) and the carboxylic acid group of Asp₂₁₆. This 2His/1Asp ligand feature is a general structural motif of most nonheme iron dioxygenases[7] but CDO differs from this template due to a 3His ligand system. In some nonheme iron enzymes, such as IPNS and CDO, the substrate binds covalently to the metal center, whereas in others, such as TauD, it binds in its vicinity. Substrate δ-(l-α-aminoadipoyl)-l-cysteinyl-D-valine (ACV) in IPNS binds to the iron through the thiolate group, and the fifth ligand position of the metal is occupied by a water molecule, which is replaced by molecular oxygen during the catalytic cycle.

Figure 1.

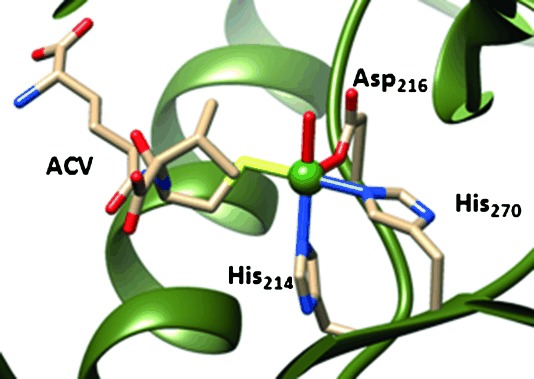
Active site structure of IPNS as taken from the pdb file 1BK0. Amino acids are labelled as in the pdb.

Another known biochemical system with an iron(III)–hydroperoxo intermediate that exhibits catalytic activity is the glycopeptide antibiotic bleomycin, which is able to degrade double-stranded DNA in the presence of oxygen and iron. It forms an iron(III)–hydroperoxo intermediate that either reacts directly with substrate or initially splits heterogeneously or homogeneously via the formation of iron(IV/V)–oxo intermediates.[8]

In contrast to the nonheme iron dioxygenases, heme enzymes such as the cytochromes P450 cannot bind substrate directly to the cofactor as the tetradentate heme ligand blocks its access. P450 enzymes are important heme monoxygenases in the human body involved in the biosynthesis of hormones, such as oestrogen, but also catalyze the biodegradation of xenobiotics and drug molecules.[9] The P450 enzymes undergo a catalytic cycle starting from the resting state that requires molecular oxygen binding and two reductive steps to form an iron(III)–peroxo, which is protonated to form iron(III)–hydroperoxo or Compound 0 (Cpd 0). This intermediate was trapped and characterized using various spectroscopic methods, such as electron nuclear double resonance (ENDOR) and resonance Raman spectroscopy at low temperature.[10] A final proton delivery step in the catalytic cycle converts Cpd 0 into the active species, namely an iron(IV)–oxo heme cation radical (Compound I, Cpd I). Cpd I is highly reactive,[11] but Rittle and Green managed to trap and characterize it recently.[12]

In P450 chemistry, there has been a controversy for many years regarding the catalytic activity of Cpd 0 with respect to that of Cpd I.[13] Site-directed mutations that supposedly blocked one of the proton transfer channels in the catalytic cycle, however, still gave activity of the enzyme in olefin epoxidation, which was attributed to Cpd 0 acting as an active oxidant.[14] Initial computational modelling, however, contradicted these studies and established sluggish reactivity for Cpd 0, and hence implicated that Cpd I is the sole oxidant of P450 enzymes.[15] Subsequent biomimetic model studies on synthetic analogues, that is, iron(III)–hydroperoxo porphyrin complexes, confirmed the conclusions from theory and found little activity in substrate epoxidation and sulfoxidation reactions.[16] Further biomimetic studies by van Eldik and co-workers[17] generated Cpd I and Cpd 0 models of iron meso-tetramesitylporphyrin and measured rate constants for hydrogen atom abstraction reactions. They unequivocally identified Cpd I as the superior oxidant of hydrogen atom abstraction, double bond epoxidation, and sulfoxidation reactions with substrates. Subsequently, Ohta, Naruta, and co-workers synthesized an iron(III)–hydroperoxo porphyrin complex and spectroscopically characterized it with resonance Raman, UV/Vis spectroscopy and electron paramagnetic resonance spectroscopy.[18] Also their reactivity studies with selected substrates gave little activity and hence proved that the iron(III)–hydroperoxo porphyrin complex cannot be an active oxidant.

Despite the fact that heme/porphyrin iron(III)–hydroperoxo complexes are poor oxidants of oxygen atom transfer reactions, in recent years evidence has accumulated of the opposite trend in some nonheme iron(III)–hydroperoxo complexes. Thus, combined experimental and computational studies on nonheme iron(IV)–oxo versus nonheme iron(III)–hydroperoxo complexes with N4Py ligand system (N4Py=N,N-bis(2-pyridylmethyl)-N-bis(2-pyridyl)methylamine) found efficient oxygen atom transfer reactivity with halides and sulfides for both oxidants.[19] Clearly, heme and nonheme oxidants have structural and electronic features that may be responsible for the fact that in the former the iron(III)–hydroperoxo is unreactive, but in the latter it can be reactive. It should be noted here that many studies on iron(III)–alkylperoxo complexes also found little catalytic activity in reactions with substrates and,[20] therefore, iron(III)–alkylperoxo may not always be a good mimic for iron(III)–hydroperoxo. Furthermore, it has been suggested that changes in environmental factors, such as solvent polarity, may affect the spin-state ordering and the ability of the homolytic versus heterolytic cleavage pathways of nonheme iron(III)–hydroperoxo complexes.[21]

Initial studies of the aromatic hydroxylation by hydrogen peroxide catalyzed by nonheme iron(II) complexes suggested that iron(III)–hydroperoxo may be the active oxidant in this demanding reaction.[22] Recently, Banse and co-workers[23] reported aromatic hydroxylation by a nonheme iron(III)–hydroperoxo complex for the first time using the pentadentate ligand L₅² (Scheme 1; L₅²=N-methyl-N,N′,N′-tris(2-pyridylmethyl)ethane-1,2-diamine).[24] Complex [(L₅²)Fe^III(OOH)]²⁺ was isolated and spectroscopically characterized[25] and it was shown to react with benzene and anisole in an acetonitrile solution with first-order kinetics to produce the corresponding phenols. Although these studies definitely demonstrated the implication of the iron(III)–hydroperoxo species, it was not clear whether the catalytic activity was from the iron(III)–hydroperoxo or not. Alternatively, a homolytic O–O bond cleavage of the iron(III)–hydroperoxo bond to yield an iron(IV)–oxo and a hydroxyl radical was a plausible scenario to account for the observed catalytic activity. Clearly, the work raises several questions that can only be answered from a detailed computational study. Herein we aim to answer the following questions: What is the active oxidant in the reaction mechanism of [(L₅²)Fe^III(OOH)]²⁺ with substrates and why is the nonheme iron(III)–hydroperoxo reactive whereas its heme counterpart is a sluggish oxidant?

Scheme 1.

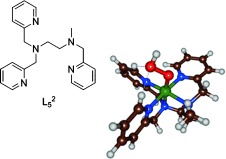
Iron(III)–hydroperoxo model with drawing of the ligand system investigated here.

Although some experimental studies have been reported on the catalytic activity of nonheme iron(III)–hydroperoxo complexes, there are very few computational studies in the field and none of the computational studies explains the differences between heme and nonheme iron(III)–hydroperoxo.[26, 27] In order to gain insight into the ability of nonheme iron(III)–hydroperoxo intermediates in aromatic hydroxylation processes and the relative activity versus an iron(IV)–oxo species, we decided to do a density functional theory (DFT) study on the catalytic activity of [(L₅²)Fe^III(OOH)]²⁺ with aromatic substrates and perform a general analysis of nonheme versus heme iron(III)–hydroperoxo complexes and their potential reactivity in oxygen atom transfer. Our calculations show, for the first time, that nonheme iron(III)–hydroperoxo complexes can react with substrates efficiently through OH transfer to aromatic rings. A thermochemical and valence bond analysis further shows that this is due to homolytic O–O bond cleavage of the hydroperoxo bond, whereas in heme Cpd 0 the cleavage is heterolytic.

Results

Experimental studies characterized [(L₅²)Fe^III(OOH)]²⁺ with a broad range of spectroscopic methods, including Mössbauer,[28] resonance Raman and UV/Vis techniques.[29] To establish appropriate methods for the DFT calculations on these complexes, we decided to calculate the low-lying spin states of [(L₅²)Fe^III(OOH)]²⁺, ^2,4,6A, in the doublet, quartet, and sextet spin states and evaluate their spectroscopic properties. Technically, there are at least four possible isomers of hydroperoxo binding to the iron(III)–L₅² complex: i) With the distal oxygen atom hydrogen bonded to the two C–H protons of pyridine groups (A₁); ii) with the proximal oxygen atom hydrogen-bonded to the two C–H protons of the pyridine groups (A₂); iii) with the distal oxygen atom hydrogen-bonded to one C–H pyridine group and one methyl group (A₃); iv) with the hydroperoxo proton in hydrogen-bonding interaction to one of the nitrogen atoms of the L₅² ligand (A₄). Our initial studies focused on characterizing these four isomers, however, all attempts to optimize structures ²A₃ and ²A₄ converged to either structure ²A₁ or ²A₂. This is different from heme iron(III)–hydroperoxo complexes, as previous calculations characterized it with the terminal proton in hydrogen-bonding interaction with one of the nitrogen atoms of the heme ligand.[15, 30] In [(L₅²)Fe^III(OOH)]²⁺ a more stable solution is possible with hydrogen-bonding interactions with C–H protons. Figure 2 gives optimized geometries of ²A₁ and ²A₂ as obtained with UB3LYP/BS2.

Figure 2.

Optimized geometries of ²A₁ and ²A₂ as obtained with UB3LYP/BS2. Bond lengths are given in angstroms and relative energies in kcal mol⁻¹.

Although the optimized geometries give bond lengths that are very similar, structure ²A₂ is slightly lower in energy due to four weak C–H hydrogen-bonding interactions to oxygen atoms of the hydroperoxo group, while there are only three in ²A₁. The characterization of two close-lying isomers is in agreement with experimental EPR studies that gave evidence of at least two stable structures.[25]

Subsequently we investigated the consistency and reproducibility of the DFT methods and reoptimized one set of isomers, namely ^2,4,6A₁, with several different methods and basis sets: UB3LYP/BS1, UB3LYP/BS2, UPBE0/BS1, and UPBE0/BS2. Table 1 summarizes optimized geometries of ^2,4,6A₁ as obtained with these methods. All optimized structures, regardless of computational method and basis set for the iron(III)–hydroperoxo complex, converge to similar geometries with the hydroperoxo proton trans to the iron, as depicted in Figure 2. The distal oxygen atom undergoes hydrogen-bonding interactions with two protons of the L₅² ligand that hold it in a specific orientation with the proton of the OOH group trans to the iron. Although we made several attempts to optimize the structures with the hydroperoxo proton in hydrogen-bonding interaction with one of the nitrogen atoms of the L₅² scaffold, all geometry optimizations converged back to either A₁ or A₂.

Table 1.

Key geometric features and spin state energies of [(L₅²)Fe^III(OOH)]²⁺ as obtained from geometry optimized structures using different density functional theory methods and basis sets

Spin state	Variable[a,b]	B3LYP/BS1	B3LYP/BS2	PBE0/BS1	PBE0/BS2
2A1	rFeO/rOO	1.811/1.506	1.797/1.443	1.802/1.448	1.785/1.421
	ΔE	0.0	0.0	0.0	0.0
4A1	rFeO/rOO	1.808/1.507	1.789/1.445	1.801/1.489	1.777/1.424
	ΔE	10.1	6.3	7.1	2.7
6A1	rFeO/rOO	1.886/1.471	1.871/1.418	1.871/1.454	1.855/1.399
	ΔE	6.2	−0.9	−1.2	−9.0

[a] Bond lengths (r) in angstroms; [b] spin state energies in kcal mol⁻¹ and include zero-point energy (ZPE) corrections.

In general, the data in Table 1 show that improving the basis set from BS1 to BS2 gives a small bond shortening for the Fe–O distances by about 0.01–0.02 Å and a somewhat larger effect on the O–O distances. Geometrically, replacing the DFT method gives no dramatic changes to the optimized geometries. Nevertheless, the calculated Fe–O distances are in excellent agreement with 1.81 Å value obtained from EXAFS.[31]

Subsequently, the analytical frequencies were analyzed in detail to find out whether our calculated geometries are in good agreement with experiment. Following previous experience in the field, the vibrational frequencies were scaled with a value of 0.9257.[32] Resonance Raman spectroscopic studies characterized the O–O stretch vibration (ν_OO) of [(L₅²)Fe^III(OOH)]²⁺ at 796 cm⁻¹.[29] In addition, a large down-shift of 45 cm⁻¹ was measured for the replacement of ¹⁶O₂ by ¹⁸O₂. Our B3LYP/BS1 calculations give a value of ν_OO=786 cm⁻¹ in the doublet spin state, whereas in the sextet spin state the O–O vibration is at a significantly lower value. The same trends are observed when geometry optimizations are performed at UB3LYP/BS2, UPBE0/BS2, and UPBE0/BS1. The O–O stretch vibration, therefore, reproduces experiment reasonably. Note that a geometry optimization of ²A₁ and ²A₂ at UB3LYP/BS2 gives very similar vibrational frequencies and structures; ν_FeO is increased in A₁ by 9 cm⁻¹, whereas ν_OO is identical in both structures.

Replacement of the oxygen isotopes from ¹⁶O₂ to ¹⁸O₂ in ²A₁ results in a down-shift of −46 cm⁻¹ for the O–O stretch vibration, in agreement with experiment, where a value of −45 cm⁻¹ was reported. Also the Fe–O stretch vibration is affected by replacement of ¹⁶O₂ by ¹⁸O₂, albeit by a smaller extent (−24 cm⁻¹), which compares well with the experimentally determined resonance Raman difference spectrum of −17 cm⁻¹.[29] As a matter of fact, experimental resonance Raman spectra on nonheme iron(III)–hydroperoxo complexes with various ligands characterized the Fe–O stretch vibration between 609 and 632 cm⁻¹ and the O–O stretch vibration between 788 and 808 cm⁻¹.1b, [33] Our calculated vibrational frequencies fit these windows perfectly. For P450 Cpd 0, values of ν_OO=799 cm⁻¹ and ν_FeO=559 cm⁻¹ were measured.[34] Subsequent DFT calculations on the iron(IV)–oxo species, [(L₅²)Fe^IV(O)]²⁺, gave vibrational frequencies in line with those obtained for analogous complexes.[35]

The spin-state ordering varies between the four computational methods and a doublet spin ground state is found at UB3LYP/BS1 level of theory, whereas all other methods give a sextet spin ground state. Note that, at UB3LYP/BS2 and UPBE0/BS1 level of theory, the spin-state splitting between doublet and sextet is within 1.2 kcal mol⁻¹, hence they are degenerate. Experimental studies characterized a doublet spin ground state;[28] within the error of the DFT calculations, this is reproduced here with B3LYP.

Using a slightly different ligand system, Rajaraman and co-workers27a calculated a sextet spin ground state for an iron(III)–hydroperoxo complex with a free energy of 14.5 kcal mol⁻¹ less than the doublet spin state. Their chemical system had a hydrogen-bonding interaction between the proximal oxygen atom and a coordinated carboxylic acid group, which may have induced differences in orbital interactions. Because of this interaction, they also found an elongated Fe–O bond.

In a P450 Cpd 0 model, Fe–O and O–O distances of 1.86 and 1.52 Å were calculated for a doublet spin state that is well below the quartet and sextet spin states.[36] Clearly, iron(III)–hydroperoxo complexes have spin-state ordering, spin-state energies, and geometric features that are dependent on the axial and equatorial ligands bound to the iron as well as local interactions, that is, hydrogen-bonding interactions. This may also affect the catalytic properties, as will be shown below.

To further establish the key spectroscopic parameters and benchmark and calibrate our methods and basis sets, we calculated Mössbauer parameters for the UB3LYP/BS1 optimized doublet, quartet, and sextet geometries in ORCA.[37] The doublet spin state gives an asymmetry parameter (η) of 0.38 and a quadrupole splitting (ΔE_Q) of −1.69 mm s⁻¹. In the quartet spin state these values change to η=0.76 and ΔE_Q=−1.52 mm s⁻¹, whereas they are η=0.39 and ΔE_Q=0.66 mm s⁻¹ for the sextet spin state. The Mössbauer parameters calculated for ²A₂ are very similar to those found for ²A₁, that is, ΔE_Q differs by 0.07 mm s⁻¹ and η by 0.05, and therefore do not distinguish these two species. Experimentally, Mössbauer parameters of ΔE_Q=−2.01 mm s⁻¹ and η=0.4 were found.[28] Consequently, our calculated doublet spin Mössbauer parameters give the closest agreement to experiment of all the spin states and confirm a doublet spin ground state for this chemical system.

Subsequently, we investigated the possible mechanisms of aromatic hydroxylation of benzene and anisole by ^2,4,6A (Scheme 2). The reaction mechanism starts off with the approach of the substrate onto ^2,4,6A with the formation of a reactant complex (Re). Three different mechanisms of aromatic hydroxylation were tested. The direct pathway (top part of Scheme 2) leads to direct attack of the substrate on the iron(III)–hydroperoxo complex and the acting of this species as the oxidant. The other two pathways start with either a homolytic O–O bond splitting of the iron(III)–hydroperoxo complex or the heterolytic O–O bond breaking (bottom parts of Scheme 2). In the homolytic and heterolytic O–O bond splitting, the iron(III)–hydroperoxo species first splits into an iron(IV)–oxo or iron(V)–oxo by release of either OH^. or OH⁻, respectively. The actual substrate activation in these pathways, therefore, proceeds via either the iron(IV)–oxo or iron(V)–oxo species.

Scheme 2.

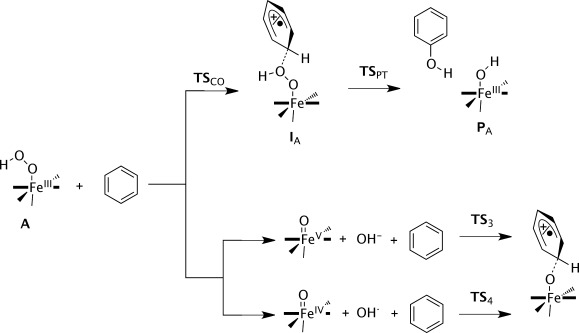
Reaction Scheme calculated in this work with nomenclature of local minima and transition states. Substrates benzene and anisole were investigated.

In the direct mechanism, the substrate attacks the distal oxygen atom of the iron(III)–hydroperoxo group and via an electrophilic transition state (TS_CO) an intermediate is formed where the OH group is bound to the substrate ring (I_A). As the attacked carbon atom is involved in four covalent interactions, this disturbs the aromaticity of the phenyl ring and the rest of the ring now contains either a radical or a cation. In the next step, the hydrogen atom (or proton) of the ipso position is transferred to the proximal oxygen atom via a transition state TS_PT to form phenol and an iron(III)-hydroxo complex (P_A).

Before discussing the direct oxygen atom transfer to substrate from the iron(III)–hydroperoxo complex, we investigated the homolytic and heterolytic bond cleavage of the iron(III)–hydroperoxo species. To this end, the structures of [(L₅²)Fe^V(O)]³⁺, [(L₅²)Fe^IV(O)]²⁺, OH⁻, and OH^. were calculated at UB3LYP/BS2 level of theory and the free energy difference with respect to ^2,4,6A was determined. Scheme 3 gives the free energy values (with solvent corrections included) for the homolytic and heterolytic bond breaking of the O–O bond in ²A. Both reactions are endergonic, especially the heterolytic bond splitting leading to an iron(V)–oxo species, which in solvent is energetically costly by ΔG_solv=73.9 kcal mol⁻¹. Consequently, the heterolytic bond breaking of the hydroperoxo bond in ²A is an unlikely process and the iron(V)–oxo species is not expected to play a role in the catalytic mechanism.

Scheme 3.

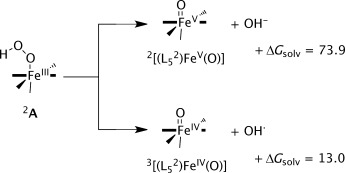
Free energies in kcal mol⁻¹ for homolytic and heterolytic O–O bond splitting in the iron(III)–hydroperoxo complex A₁.

The homolytic bond cleavage of the O–O bond in the iron(III)–hydroperoxo complex, by contrast, is endergonic by only ΔG_solv=13.0 kcal mol⁻¹. At this stage, therefore, this pathway cannot be ruled out as a possibility of substrate activation. Therefore, we calculated the C–O bond activation of benzene by ^1,3[(L₅²)Fe^IV(O)] and the optimized geometry is displayed in Figure 3. As follows from the optimized geometries and relative energies, a considerable barrier is encountered for aromatic hydroxylation by ^1,3[(L₅²)Fe^IV(O)]²⁺ of 24.0 and 40.5 kcal mol⁻¹ for the triplet and singlet pathways, respectively, which confirms the inability of these complexes at oxidizing arenes.[39] These barriers are considerably lower than those reported before for the reaction of benzene with ³[(N4Py)(Fe^IV(O)]²⁺, because of lesser stereochemical repulsions between the approaching substrate and the ligand system.[38] Thus, in ³TS₄ the ipso proton of benzene hydrogen-bonds with one of the nitrogen atoms of the L₅² ligand and hence stabilizes the TS structure. Nevertheless, starting from ²[(L₅²)Fe^III(OOH)]²⁺ the total free energy of homolytic O–O bond cleavage followed by C–O bond formation to the substrate will be ΔG_solv=37 kcal mol⁻¹. We, therefore, decided to assess whether a direct pathway from the iron(III)–hydroperoxo would be possible or competitive.

Figure 3.

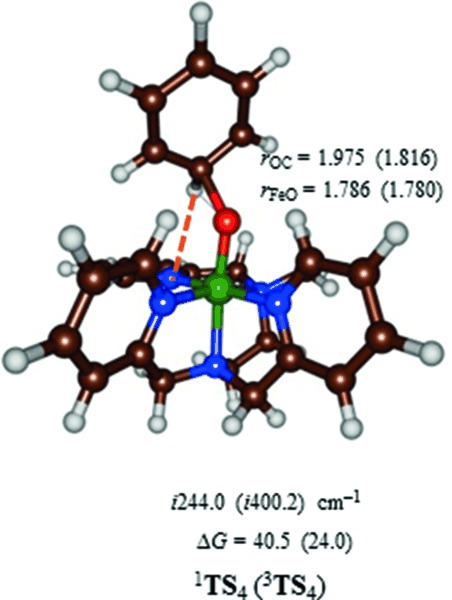
UB3LYP/BS2-optimized geometries of ^1,3TS₄ with bond lengths in angstroms and the imaginary frequency in wave numbers. Barriers (free energies in solvent) relative to a reactant complex of ³[(L₅²)Fe^IV(O)]+C₆H₆ are given in kcal mol⁻¹.

Our calculated homolytic bond cleavage free energy compares well with the temperature-dependent reaction rates determined by Que and co-workers,[40] which established values of about 15 kcal mol⁻¹ for the homolytic cleavage of the iron(III)–alkylperoxo complexes [(TPA)Fe^III(OOR)] and [(BPMCN)Fe^III(OOR)] (TPA=(tris(2-pyridylmethyl)amine; BPMCN=N,N-bis(2-pyridylmethyl)-N,N-dimethyl-trans-1,2-diaminocyclohexane).

Early studies by the Siegbahn group on naphthalene-1,2-dioxygenase investigated the cis-dihydroxylation of substrate by an iron(III)–hydroperoxo intermediate.[41] They found, in agreement with what we report here, that the target reaction was performed by the iron(III)–hydroperoxo complex. However, their gas-phase results did implicate a small exothermicity of a homolytic pathway to form an iron(IV)–oxo species, but this pathway would require an additional electron transfer, which is not possible in our system.

It should be noted here that, in the case of iron(III)–hydroperoxo complexes with tetradentate ligands system or less, the heterolytic cleavage pathway could lead to an iron(V)–oxo(hydroxo) complex, which is considerably lower in energy than an iron(V)–oxo with isolated OH⁻ group.[42] To gain further insight into the generality of homolytic versus heterolytic cleavage pathways by nonheme iron(III)–hydroperoxo complexes, we also calculated the free energies for [(N4Py)Fe^III(OOH)]²⁺, [(Bn-tpen)Fe^III(OOH)]²⁺, and [(6-Me₃-TPA)Fe^III(OOH)]²⁺ (Bn-tpen=N-benzyl-N,N′,N′-tris(2-pyridylmethyl)ethane-1,2-diamine; 6-Me₃-TPA=tris-[(6-methyl-2-pyridyl)methyl]amine). For these chemical systems, homolytic cleavage free energies of 9.7, 12.1, and 4.1 kcal mol⁻¹, respectively, are found, whereas the heterolytic cleavage was found to be much higher in energy. However, the energy difference between the homolytic and heterolytic pathways is found to vary by more than 25 kcal mol⁻¹ in these cases, therefore, the preference of homolytic over heterolytic cleavage may be ligand dependent.

Next we investigated the direct pathway for aromatic hydroxylation by iron(III)–hydroperoxo complexes (top part of Scheme 2) and the results are displayed in Figure 4. We calculated the full potential energy profile for aromatic hydroxylation by the A₁ and A₂ isomers. Energetically, there is little difference in the catalytic activity of the two isomers. As described above, the doublet and sextet reactants are close in energy and small external perturbations or solvent change the ordering slightly. Note as well that energies obtained at B3LYP/BS2 level of theory are within 1 kcal mol⁻¹ of those calculated with B3LYP-D3/BS2, hence the effect of dispersion is small here.

Figure 4.

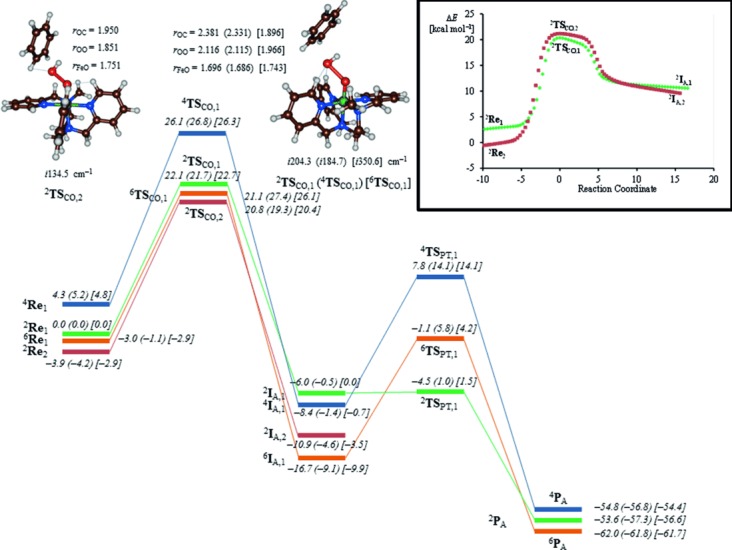
UB3LYP-D3/BS2//UB3LYP/BS2-calculated free energy landscape of benzene hydroxylation by ^2,4,6Re with energies in kcal mol⁻¹. Values in parentheses and square brackets contain solvent corrected free energies using UB3LYP-D3/BS2 and UB3LYP/BS2 energies, respectively. Optimized geometries of ^2,4,6TS_CO are reported with bond lengths in angstroms and the imaginary frequency in the TS_CO in wave numbers. The inset gives the IRC scan from ²TS_CO,1 and ²TS_CO,2 leading to reactants in one direction and to ²I_A in the other direction.

Approach of substrate on the terminal oxygen atom of the iron(III)–hydroperoxo group leads to electrophilic addition of the OH group to the arene via a transition state TS_CO. In the gas phase, three of those (²TS_CO,2, ²TS_CO,1, and ⁶TS_CO,1) are within ΔG=1.3 kcal mol⁻¹ of each other. These transition states are characterized by simultaneous C–O bond formation and O–O breaking and give an imaginary frequency of i 134.5 (²TS_CO,2), i 204.3 (²TS_CO,1), i 184.7 (⁴TS_CO,1), and i 350.6 (⁶TS_CO,1) cm⁻¹. Geometrically, the transition states occur later on the potential energy surfaces and long O–O bonds of 2.116 and 1.966 Å are found for ²TS_CO,1 and ⁶TS_CO,1, respectively. At the same time, the Fe–O distances have elongated significantly from about 1.5 Å in the reactants to about 1.7 Å in the transition states.

For isomer A₂ the electrophilic attack of benzene on the hydroperoxo group results in a transition state (²TS_CO,2) with considerably shorter C–O and O–O distances than those for ²TS_CO,1. The reason derives from the angle under which the substrate approaches the terminal oxygen atom of the iron(III)–hydroperoxo unit. Thus, in ²TS_CO,1 the bulky upwards-pointing pyridine rings repel the approaching substrate and as a consequence it attacks under an angle Fe-O_p-C (with O_p the proximal oxygen atom) of 133.3°. By contrast, in ²TS_CO,2 the Fe-O_p-C angle is 122.7°, and enables a closer approach of the substrate without incurring stereochemical interactions with the L₅² ligand.

Intrinsic reaction coordinate (IRC) scans starting from ²TS_CO,1 and ²TS_CO,2, inset of Figure 4, connect the transition states to reactants in one direction and to a cationic intermediate (I_A) in the reverse direction. Thus, the group spin densities of ²I_A,1 give values of ρ_Fe=0.89 and ρ_O=0.20 and negligible spin density on the OH group and the substrate. This implies that the iron is in oxidation state iron(III) and the arene is cationic. In previous aromatic hydroxylation studies, close lying intermediates were found with the substrate either radical or cationic.[43] Attempts were made to swap molecular orbitals to find the radical intermediate, but during the SCF convergence the wave function converged back to the cationic state instead and thereby implicates that the radical intermediate is substantially higher in energy.

In the gas phase, the free energy of activation on the sextet and doublet spin states are very similar (22.1 vs. 21.1 kcal mol⁻¹ for ²TS_CO,1 vs. ⁶TS_CO,1), but solvent effects destabilize the sextet pathway by almost 5 kcal mol⁻¹. However, the cationic intermediate on the sextet spin-state surface (⁶I_A,1) is more stable than either the doublet or quartet spin-state structures by 10.7 or 8.3 kcal mol⁻¹, respectively. In the cationic intermediate the ipso carbon atom of the substrate is tetrahedral with sp³ hybridization, which has disrupted the aromaticity of the substrate. Although we focus in this work only on the rate-determining C–O bond activation, for completeness we also calculated the subsequent steps leading to either phenol or cyclohexanone products. We will go into more detail on these bifurcation pathways in a follow-up paper and focus only on the rate-determining step here. In the final reaction step, the ipso proton is shuttled from substrate to proximal oxygen atom via a barrier TS_PT,1, which brings the aromaticity back into the substrate and gives a phenol hydrogen-bonded to an iron(III)–hydroxo complex.

On the doublet spin-state surface, the proton-transfer barrier via TS_PT,1 is small with a value of less than 1.5 kcal mol⁻¹, whereas the analogous barriers are about 15 kcal mol⁻¹ in the quartet and sextet spin states. This matches previous computational studies of aromatic hydroxylation by heme and nonheme iron(IV)–oxo complexes that were shown to proceed with a rate-determining electrophilic addition and small subsequent barriers for proton shuttle to form phenol products.[39, 43, 44]

Thereafter, we calculated the aromatic hydroxylation of anisole by ^2,4,6A₁ and found a potential energy landscape that shows similarity to the one observed for benzene, see Supporting Information. The electrophilic addition step via TS_CO,1,AN is again rate determining and values of ΔG=20.2 (15.4) kcal mol⁻¹ in the gas phase for ²TS_CO,1,AN (⁶TS_CO,1,AN) are found, whereas in solvent these values are raised to 22.5 (21.6) kcal mol⁻¹. Experimental studies of aromatic hydroxylation of anisole by [(L₅²)Fe^III(OOH)]²⁺ determined a rate constant of 1.165 min⁻¹,[23] which, according to transition state theory, can be converted into a ΔG^{294 K}=19.5 kcal mol⁻¹. Our calculated free energy of activation at the doublet spin state, therefore, is in excellent agreement with the experimental value.

Optimized geometries of the rate-determining transition states ^(2,4,6TS_CO,1,AN) for electrophilic attack of anisole on ^2,4,6A₁ are given in Figure 5. These transition states have elongated Fe–O and shortened C–O distances as compared to those for benzene hydroxylation shown in Figure 4. Consequently, the sextet spin anisole barriers are later on the potential energy surface than the benzene activation barriers. Due to stereochemical interactions of the ortho-hydroxylation mechanism, the C–O bond formation barrier with anisole is of similar magnitude to that for benzene. Previous aromatic hydroxylation studies of iron(IV)–oxo porphyrin complexes showed that late transition states generally correspond with lower reaction barriers.[43–45] Indeed, that is what is seen here as well in the sextet spin state and to a lesser extent in the doublet spin state.

Figure 5.

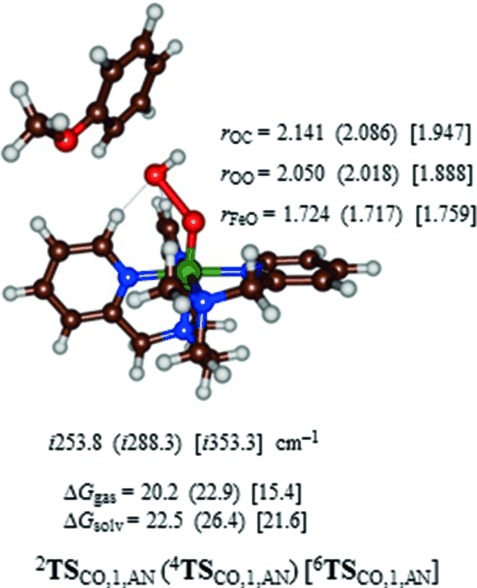
Optimized geometries of ^2,4,6TS_CO,1,AN as obtained with UB3LYP/BS1. Dispersion-corrected free energies in the gas phase and with solvent model included are given in kcal mol⁻¹. Optimized geometries of ^2,4,6TS_CO,1,AN are reported with bond lengths in angstroms and the imaginary frequency in the TS in wave numbers.

Discussion

In this work, we have investigated the possibility of a nonheme iron(III)–hydroperoxo complex to act as an oxidant of aromatic hydroxylation reactions. The work reveals that indeed nonheme iron(III)–hydroperoxo complexes can activate arenes and convert them to phenols with a free energy of activation in solvent of 21.7 (benzene) and 22.5 (anisole) kcal mol⁻¹ on a doublet spin state. The alternative homolytic and heterolytic dissociation pathways were also tested but ruled out as thermodynamically unfeasible. These studies contrast experimental and computational studies of heme iron(III)–hydroperoxo complexes and porphyrin analogues that all identified it as a sluggish oxidant.[13, 15–18] So what is so special about the nonheme iron(III)–hydroperoxo complexes A₁ and A₂ that they can hydroxylate aromatic rings, whereas P450 Cpd 0 cannot do this?

Let us start with an analysis of the molecular orbitals of the reactant species, that is, A, and how these orbitals change during the reaction mechanism. Figure 6 displays the molecular orbitals of A₁. Note that the orbitals for the two isomers are very similar. The set of relevant valence orbitals in Figure 6 is dominated by the metal 3d interactions and π orbitals on the hydroperoxo moiety. The orbital lowest in energy and nonbonding is the π*_xy orbital in the plane of four nitrogen atoms of the L₅² ligand. The 3d_xz orbital on iron mixes with the π/π* pair of orbitals on the hydroperoxo group along the z axis in a bonding and antibonding set, designated π_xz and π*_xz. Similarly, the 3d_yz orbital on iron mixes with the π/π* pair of orbitals along the y axis, designated π_yz and π*_yz. Two antibonding orbitals, σ* and σ*, represent the antibonding interactions of the metal with ligands along the z axis and the xy plane, respectively. In the doublet spin ground state the metal is in oxidation state iron(III) and its orbitals shown in Figure 6 have the following occupation: π_xz² π_yz² π*_xy² π*_xz² π*_yz¹. The quartet and sextet spin states of A₁ have orbital occupation π_xz² π_yz² π*_xy² π*_xz¹ π*_yz¹ σ*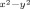¹ and π_xz² π_yz² π*_xy¹ π*_xz¹ π*_yz¹ σ*¹ σ*¹, respectively.

Figure 6.

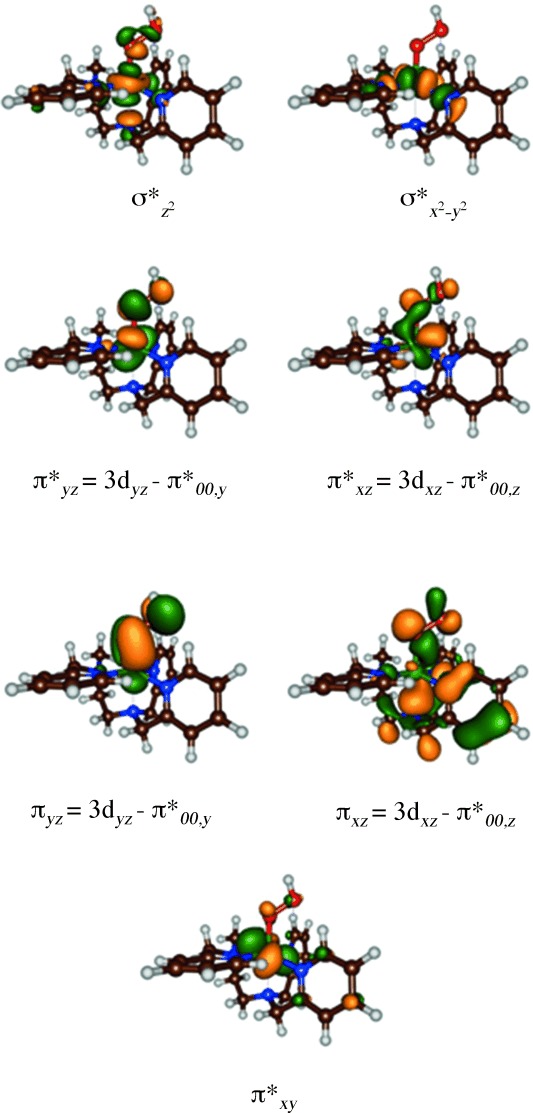
High-lying occupied and low-lying virtual orbitals of [(L₅²)Fe^III(OOH)]²⁺, A₁.

To understand the electron transfer processes and the substrate activation pathway, we devised a valence bond (VB) diagram for the rate-determining reaction step in the aromatic hydroxylation by iron(III)–hydroperoxo complexes (Figure 7). The VB curve-crossing diagram was used previously to rationalize hydrogen atom abstraction barriers of Cpd I models and explains the electron transfer processes during the rate-determining step, but also can be used as a means to predict barrier heights from physicochemical properties of oxidant and substrate.[46] The VB diagram starts on the left-hand side with the reactant complexes, that is, ²A and substrate (PhH), in the reactant geometry with wave function ²Ψ_Re and continues to the product complexes, namely the cationic intermediates ²I_A, with wave function ²Ψ_I.

Figure 7.

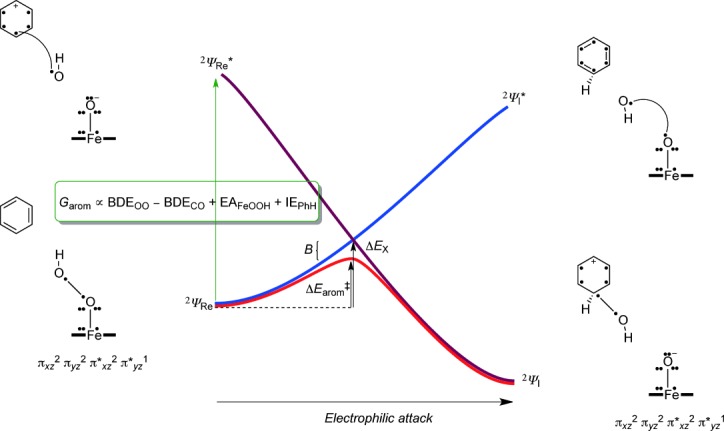
Valence bond curve-crossing diagram for the electrophilic addition of an OH group to an aromatic ring. Dots represent valence electrons and a line (straight or curved) between dots represents a chemical bond.

In VB theory, it has been shown[47] that the reactant wave function (²Ψ_Re) connects to an excited state in the product geometry, that is, ²Ψ_I*(blue curve in Figure 7). At the same time, the product wave function (²Ψ_I) connects to an excited state in the reactant geometry, that is, ²Ψ_Re*(dark red curve in Figure 7). The two curves cross and lead to an avoided crossing and hence a transition state with barrier height ΔE_arom^≠. The properties and height of the transition states are, therefore, determined by the reactant and product wave functions and the electronic changes that occur during the reaction. The extent of the mixing can be determined from the excitation energy from ²Ψ_Re to ²Ψ_Re* in the reactant geometry, which is called the promotion gap (G). Thus, the curve crossing point (ΔE_X) is a fraction (f) of the promotion gap in the reactant geometry. Furthermore, the transition-state energy (ΔE_arom^≠) is below the curve-crossing energy by an amount that accounts for the resonance energy (B). Therefore, the VB descriptions of the ground and excited states in the reactant geometry reflect the quantum mechanical changes during the reaction mechanism and the nature of the transition state.

To understand the changes along the reaction mechanism from A+PhH to I_A, we give valence bond descriptions of the molecules/clusters involved in the process for reactants and products as well as the relevant excited states. Thus, the excited state configuration (²Ψ_Re*) has the geometry of the reactants, but electronic description of the products, and vice versa for ²Ψ_I*. In the VB structures, valence electrons are identified with a dot and bonds with a line (straight or bend). The reactant structure has π_xz² π_yz² π*_xy² π*_xz² π*_yz¹ configuration with 7 electrons along the Fe–O bond for occupation of the π_xz/π*_xz and π_yz/π*_yz orbitals, and in addition the O–O bond has two electrons. After electrophilic attack of the aromatic group on the distal oxygen atom, the O–O bond breaks and an iron(III)–oxo group stays behind with configuration π_xz² π_yz² π*_xy² π*_xz² π*_yz¹.

Thus, one electron that originates from the O–O bond forms a new bond with one of the π-electrons of the aromatic ring from the nearest carbon atom of the substrate. At the same time, an electron transfer from the C₆H₆OH^. to oxyl group takes place to give the corresponding C₆H₆OH⁺ cation and an iron(III)–oxo. The electrophilic addition of the OH group to the substrate, therefore, involves a homolytic O–O bond breaking, the formation of a new C–O bond, and an electron transfer during the rate-determining reaction event. As the excited state wave function ²Ψ_Re* has the same VB description as the product ²Ψ_I this implies that the promotion gap G will also include a homolytic bond cleavage of the hydroperoxo bond, the bond formation of a new C–O bond and an electron transfer [Eq. (1)]. The homolytic O–O bond breaking of the hydroperoxo bond is described via the bond dissociation (free) energy BDE_OO, whereas the bond dissociation (free) energy of the C–O bond between the arene and OH is given as BDE_CO. In addition, the promotion gap results in the electron transfer from arene to oxo group, and hence includes the ionization potential of the substrate (IE_PhH) and the electron affinity of the iron(III)–hydroperoxo complex (EA_FeOOH).

(1)

Scheme 3 reports a value of 13.0 kcal mol⁻¹ for the homolytic bond breaking of the O–O bond in [(L₅²)Fe^III(OOH)]²⁺, that is, BDE_OO=13.0 kcal mol⁻¹. Furthermore, a calculation of the BDE_CO from C₆H₆OH^., benzene and an OH radical gives a free energy of −4.4 kcal mol⁻¹ in solution. Similarly, an IE_PhH=157.2 kcal mol⁻¹ and IE_anisole=150.7 kcal mol⁻¹ were calculated in solution. Figure 7 and Eq 1, therefore, show that the difference in reactivity between nonheme iron(III)–hydroperoxo and heme iron(III)–hydroperoxo can only result from oxidant-related thermochemical properties, namely through differences in BDE_OO and EA_FeOOH.

A correlation between barrier height and the bond energy of the bond that is broken is a common principle and follows the Polanyi correlation and has been noted before, for instance, in hydrogen atom abstraction reactions, where the bond dissociation energy of the C–H bond that is broken correlates with the natural logarithm of the rate constant for the hydrogen atom abstraction.[48]

To understand the thermodynamics and kinetics of the electrophilic addition of an OH group to benzene as the initial step for the reaction of iron(III)–hydroperoxo with arenes, we calculated the individual bond energies and electron transfer energies for all possible steps (Scheme 4). Moreover, the bond formation and electron transfer mechanisms do not necessarily happen simultaneously in the transition state. We tested three different pathways that are described from top to bottom in Scheme 4: i) Initial electron transfer (ET) followed by homolytic O–O bond cleavage with energy E_homol,II and attack of the OH^. radical on the ionized substrate with bond dissociation energy BDE_CO,cat; ii) initial homolytic O–O bond cleavage with energy E_homol,III, followed by OH addition to the substrate (BDE_CO,rad) and a final electron transfer; iii) initial homolytic O–O bond cleavage followed by electron transfer and addition of OH to the ionized substrate. To find out why heme iron(III)–hydroperoxo is a sluggish oxidant, whereas nonheme iron(III)–hydroperoxo can activate substrates, we calculated the energetics of each individual reaction step via pathways i, ii, and iii for nonheme iron(III)–hydroperoxo (Scheme 4) and heme iron(III)–hydroperoxo (Scheme 5).

Scheme 4.

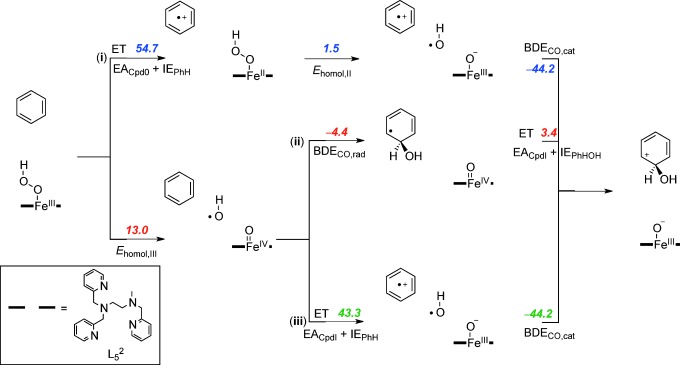
Thermochemical reaction scheme for the electrophilic addition step for the reaction of [(L₅²)Fe^III(OOH)]²⁺ with benzene split into individual components. All reaction energies are dispersion-corrected. ΔG_solv values are given in kcal mol⁻¹.

Scheme 5.

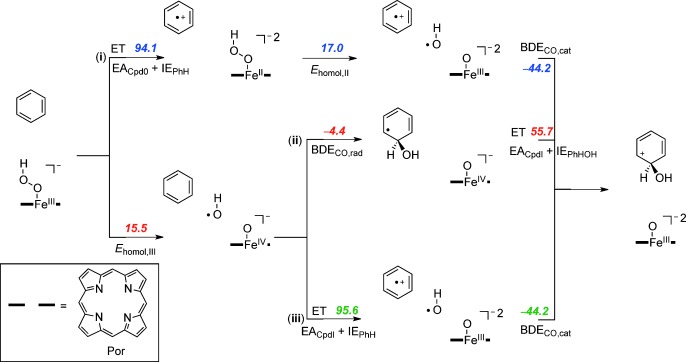
Thermochemical reaction scheme for the electrophilic addition step for the reaction of [(Por)Fe^III(OOH)(SH)]⁻ with benzene split into individual components. All reaction energies are dispersion-corrected. ΔG_solv values are given in kcal mol⁻¹.

Pathway i considers an initial long-range electron transfer from iron(III)–hydroperoxo to substrate. These pathways are highly endergonic with 54.7 kcal mol⁻¹ for ²A and 94.1 kcal mol⁻¹ for ²Cpd 0. Obviously, with endergonicities of that order of magnitude, a reaction starting with a long-range electron transfer is unlikely to take place. Furthermore, the reaction is followed by a homolytic bond cleavage of the iron(II)–hydroperoxo bond that is still endergonic for both heme and nonheme complexes.

The two alternative pathways start with an initial homolytic O–O bond cleavage. As discussed above in nonheme iron(III)–hydroperoxo complexes, in agreement with the literature[40] a value of 13.0 kcal mol⁻¹ was found. Subsequent addition of the OH^. radical to the benzene ring gives a weak C–O bond due to the loss of the aromaticity in the arene. However, the C₆H₆OH^. radical has a very low ionization potential, much lower than benzene or anisole and rapidly transfers an electron to the metal. Pathway ii, therefore, is a low-energy aromatic hydroxylation pathway due to a weak homolytic O–O bond cleavage, a low C₆H₆OH^. ionization potential, a weak C–O bond that is formed (BDE_CO,rad), and an almost thermoneutral final electron transfer.

In a final thermochemical test, we investigated pathway iii, whereby the homolytic O–O bond breaking is followed by an initial electron transfer from benzene to iron(IV)–oxo prior to the C–O bond formation step. As aromatic groups have relatively large ionization potentials, the corresponding electron transfer free energy is high; 43.3 kcal mol⁻¹ for the nonheme system and 95.6 kcal mol⁻¹ for the heme model.

The thermochemical landscapes for heme Cpd 0 show some similarities to those found for nonheme iron(III)–hydroperoxo, but also dramatic differences that we will highlight in the following. Thus, the data in Schemes 4 and 5 implicates that both nonheme and heme iron(III)–hydroperoxo should be able to homolytically cleave the O–O bond in the iron(III)–hydroperoxo complex to initiate an oxygen atom transfer reaction, with E_homol,III values of 13.0 and 15.5 kcal mol⁻¹, respectively. As the subsequent binding of OH to benzene does not involve the metal center it is identical for both heme and nonheme iron(III)–hydroperoxo with a value of −4.4 kcal mol⁻¹.

The final step then includes an electron transfer from C₆H₆OH^. to the metal–oxo group, which is almost thermoneutral for nonheme systems (+3.4 kcal mol⁻¹) but strongly endergonic for heme systems (+55.7 kcal mol⁻¹). The origin behind this disparity results from differences in overall charge of the two complexes that stabilize a heterolytic pathway over a homolytic pathway in one case. Thus homolytic bond cleavage of a nonheme iron(III)–hydroperoxo complex, that is, [(L₅²)Fe^IIIOOH]²⁺, gives an OH radical and an iron(IV)–oxo species [(L₅²)Fe^IV(O)]²⁺ that in a later step is reduced to [(L₅²)Fe^III(O)]⁺. In heme Cpd 0, the overall charge of the chemical system is −1 due to a double negative charge on the heme and an anionic axial ligand. Homolytic splitting of the O–O bond of Cpd 0 gives an OH radical and an iron(IV)–oxo heme with overall charge −1. Further reduction in the final reaction step then leads to an iron(III)–oxo heme with overall charge −2. The latter is highly unstable due to the excess negative charges and consequently the final reduction is highly endergonic. Because of this, Cpd 0 cannot react with substrates through oxygen atom transfer via a homolytic bond cleavage of the hydroperoxo O–O bond.

To ascertain that no pathways were missed for heme iron(III)–hydroperoxo we also calculated the heterolytic O–O bond cleavage. Although, in heme Cpd 0, the homolytic bond cleavage is of similar magnitude to nonheme iron(III)–hydroperoxo (15.5 vs. 13.0 kcal mol⁻¹), actually the heterolytic cleavage is much lower in energy, namely 10.2 kcal mol⁻¹ for heme Cpd 0 [Eq. (2)], whereas the nonheme iron(III)–hydroperoxo has a highly endergonic heterolytic O–O bond cleavage of 73.9 kcal mol⁻¹ (Scheme 3). This implies that the heme system is more likely to react via a heterolytic pathway and release of a hydroxide anion, whereas in nonheme iron(III)–hydroperoxo a homolytic cleavage occurs. As heme Cpd 0 is an intermediate in the catalytic cycle that needs to generate Cpd I by proton abstraction, it heterolytically cleaves the O–O bond to form Cpd I and an OH⁻ anion. The enzymatic binding site of the heme is accommodated for release of OH⁻ and has several proton relay channels available to assist in this process.[49]

(2)

A reaction pathway starting with heterolytic cleavage of the O–O bond of heme Cpd 0 (pathway iv), however, has a large endergonicity of OH⁻ transfer to the arene (ΔG_solv=36.7 kcal mol⁻¹). Consequently, due to a dominant heterolytic O–O bond cleavage in heme Cpd 0, the formed OH⁻ group is too weak a base to abstract protons from aliphatic substrates and it also cannot do an electrophilic addition to an aromatic substrate. Because nonheme iron(III)–hydroperoxo reacts by homolytic bond cleavage and heme iron(III)–hydroperoxo by heterolytic bond cleavage, these intermediates can act differently in biology and have been given different functions. Thus, heme Cpd 0 is a catalytic intermediate in the biosynthesis of Cpd I, while nonheme iron(III)–hydroperoxo can act as a catalytic oxidant of various oxygen atom transfer processes. To further confirm the hypothesis of Scheme 5, we calculated the C–O bond activation of benzene by ²[Fe^III(OOH)(Por)(SH)], see supporting information for details. However, upon approach of substrate onto the iron(III)–hydroperoxo species, the heterolytic cleavage occurs and our obtained transition state essentially is the C–O bond formation from OH⁻ to benzene with still a high barrier of ΔG_solv=26.5 kcal mol⁻¹. Clearly, heme iron(III)–hydroperoxo is unable to act as an oxidant able to activate aromatic substrates such as benzene.

The studies presented herein are also in line with those reported on the nonheme iron glycopeptide antibiotic Bleomycin, whereby an iron(III)–hydroperoxo complex was found to be able to abstract a hydrogen atom from substrate with a low barrier, whereas considerably larger barriers were encountered if the complex either heterolytically or homolytically splits first.[50]

To further ascertain the established reaction mechanisms and find evidence of our thermochemical and valence bond hypothesis, we analyzed the group spin densities of the rate-determining transition states. Figure 8 gives group spin densities of ²TS_CO,1 for the benzene (PhH) and anisole (AN) reaction mechanisms. As follows from the group spin densities and orbital analysis for both ²TS_CO,1 structures the FeO group has two unpaired electrons in π*_xz and π*_yz orbitals and hence corresponds to a triplet iron(IV)–oxo species. In addition, the departing OH group has significant unpaired spin character. Accordingly, the transition state for aromatic hydroxylation has spin densities that assign the structure as a homolytic O–O bond cleavage and the formation of a partial radical on the leaving OH group. In the anisole transition state already some radical character starts to appear on the substrate group in a sign that electron transfer also starts to happen here. The spin densities, therefore, implicate that the reaction involves an initial homolytic O–O bond cleavage and only after the transition state the electron is transferred from substrate to oxidant to form the cationic intermediate.

Figure 8.

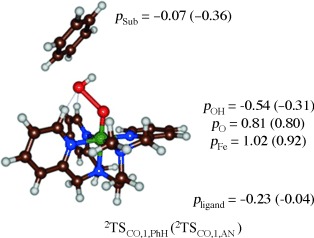
Group spin densities of ²TS_CO,1 optimized geometries for benzene (PhH) and anisole (AN) activation by ²A₁.

In summary, the calculations presented herein establish that heme-iron(III)–hydroperoxo complexes split heterolytically into Compound I and a hydroxo anion, whereas [(L₅²)Fe^III(OOH)]²⁺ splits homolytically into an hydroxyl radical and an iron(IV)–oxo species. Electronic differences are the reason why P450 Cpd 0 is unreactive with substrates, whereas nonheme iron(III)–hydroperoxo complexes are able to catalyze oxygen atom transfer reactions.

To understand the origin behind this difference in O–O bond breaking and to further establish the chemical differences between these two iron(III)–hydroperoxo complexes, we analyzed the molecular valence orbitals. Figure 9 displays the orbital relative energies of [(heme)Fe^III(OOH)]⁻, that is, P450 Cpd 0 and [(L₅²)Fe^III(OOH)]²⁺. In both systems, the valence orbitals are dominated by the interactions of the metal 3d orbitals with neighboring atoms. The two σ* orbitals (σ* and σ*) are virtual, whereas the π*_xz and δ_xy orbitals are low lying and doubly occupied. In both structures the π*_yz molecular orbital is singly occupied in the doublet spin state. In the heme system the π*_OO,y orbital strongly mixes with the a_2u orbital (shown on the right-hand-side of Figure 9) and the bonding combination is stabilized, whereas the antibonding combination is destabilized and virtual. By contrast, in the nonheme iron system the interaction of the π*_OO,y orbital with those on the ligand is much weaker and instead the π*_OO interacts with π orbitals on two nitrogen atoms of the equatorial ligand (shown on the right-hand-side of Figure 9). As a consequence, the π*_OO,y orbital becomes the HOMO orbital in [(L₅²)Fe^III(OOH)]²⁺. The π*_OO,y orbital in heme iron(III)–hydroperoxo mixes with the a_2u orbital on the heme ligand, which is its HOMO orbital. Nonheme iron(III)–hydroperoxo does not have high lying ligand orbitals and as a consequence the ligand cannot be oxidized in the reaction process. The orbital energy splittings in Figure 9 show that heme iron(III)–hydroperoxo will split heterolytically through the formation of Compound I (Cpd I), whereas a more likely homogeneous splitting will occur in the nonheme iron(III)–hydroperoxo complex.

Figure 9.

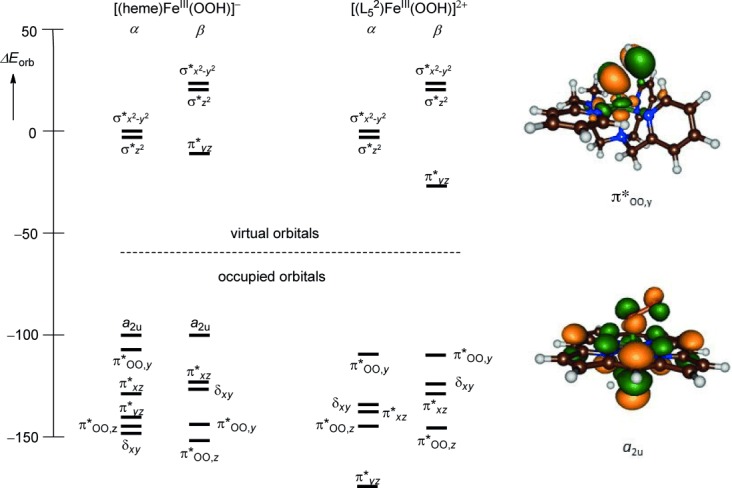
Relative orbital energy levels (in kcal mol⁻¹) for [(heme)Fe^III(OOH)]⁻ and [(L₅²)Fe^III(OOH)]²⁺ as established at UB3LYP/BS2. Also shown are LUMO orbitals of both species.

Conclusion

This work reports a detailed computational study into the reactivity differences of nonheme and heme iron(III)–hydroperoxo complexes with saturated coordination sphere. We show that aromatic hydroxylation of model substrates, including benzene, is feasible at room temperature. In support of this, we did a thorough valence bond, thermodynamic and electronic analysis of nonheme versus heme iron(III)–hydroperoxo complexes. The studies show that heme complexes thermodynamically lead via heterolytic O–O bond cleavage to a high-valent iron(IV)–oxo heme cation radical intermediate (Cpd I), whereas [(L₅²)Fe^III(OOH)]²⁺ has a low energy homolytic O–O bond breaking pathway. The origin of this difference was determined and assigned to key orbital interactions in the process. Our study finally established the key geometric and electronic components of a highly reactive nonheme iron(III)–hydroperoxo complex for oxygen atom transfer reactions.

Experimental Section

The calculations presented here used density functional theory methods as implemented in the ORCA and Gaussian 09 program packages.[37, 51] Our model uses an iron(III)–hydroperoxo complex with pentadentate ligand L₅² (Scheme 1). The geometry of [(L₅²)Fe^III(OOH)]²⁺ was initially optimized in Gaussian (without constraints) in the doublet, quartet and sextet spin states and characterized by a frequency calculation. We optimized all geometries with two density functional theory (DFT) methods, namely B3LYP and PBE0.[52, 53] In addition, we tested the effect of the basis set and ran one set of calculations with a double-ζ type LANL2DZ basis set on iron (with core potential) and 6–31G on the rest of the atoms; basis set BS1, whereas a second set of calculations used a triple-ζ LACV3P+ basis set on iron (with core potential) and 6–31+G* on the rest of the atoms; basis set BS2.[54]

After the reactant structures were studied, we explored the potential energy surface between reactants, intermediates and products. Initially, constraint geometry scans were performed at UB3LYP/BS1 where all degrees of freedom were fully optimized except the one for the reaction coordinate, which was kept fixed at regular intervals to mimic a pathway between two local minima. The maxima of these geometry scans were used as starting points for the transition state optimizations. Local minima and transition states reported here were the result of a full geometry optimization (without constraints) and were characterized by frequency analyses. All local minima had real frequencies only and the transition states had one imaginary frequency for the correct mode. Intrinsic reaction coordinate (IRC) calculations were performed on all transition states and confirmed these as first-order saddle points that connect the reactants to intermediates. The potential energy surface of benzene and anisole hydroxylation was studied at B3LYP/BS1, B3LYP/BS2 and PBE0/BS1 level of theory and all geometries were reoptimized using each of these methods. In addition for a selection of local minima (^2,6Re₁, ^2,6TS_CO,1) we performed full geometry optimization at UB3LYP-D3/BS2, UPBE0/BS2 and UBP86/BS2 levels of theory. Regardless of the computational method the optimized geometries are reproduced well (see the Supporting Information, Figure S2) and the energetics follow the same trends. Furthermore, little effect of the basis set and density functional method is obtained; for instance, UB3LYP/BS2//UB3LYP/BS1 gives almost identical energy landscape to UB3LYP/BS2.

Free energies reported here use energies calculated with either B3LYP/BS2 or B3LYP-D3/BS2, and include zero-point energies, thermal and entropic corrections from the frequency file obtained at 1 atm pressure and a temperature of 298 K. Solvent corrections were obtained through a single point calculation with the conductor polarized continuum model with acetonitrile as a solvent (dielectric constant of 35.688) and with dispersion (D3) corrected B3LYP.[55]

Subsequently, we calculated spectroscopic parameters (Mössbauer and EPR parameters) in ORCA from single-point calculations on the optimized geometries using the B3LYP method[49] in combination with the TZVP basis set with LANL core potential on iron coupled to a 6–31+G* basis set on the rest of the atoms.[56] The electric field gradients V_i (i=x, y, or z) were used to calculate the quadrupole splitting (ΔE_Q) with the help of Equations (3) and (4), whereby e represents the elementary charge of a proton/electron, Q the nuclear quadrupole moment, Q(⁵⁷Fe)=0.16 barn and η the asymmetry parameter of the nuclear quadrupole tensor.[57]

(3)

(4)

The isomer shift δ was evaluated from the spin density at the iron nucleus ρ₀(Fe) with fit parameters determined previously in ORCA.[37] Magnetic hyperfine parameters, A_i (i=x, y, or z), were obtained using the scalar relativistic zero-order regular approximation (ZORA) at the B3LYP level of theory. These methods were shown to reproduce experimentally determined Mössbauer and EPR parameters of transition metal complexes well.[58]

As transition metal complexes have many close-lying spin states, the choice of the density functional method is important and may affect spin-state ordering.[59] We did a series of single-point calculations on the UB3LYP/BS2 optimized geometries using BP86,[60] M06,[61] and B3LYP-D3.[55] These computational methods and procedures were carefully benchmarked and calibrated against experimental data in the past and, for instance, reproduced experimental free energies of activation within 3 kcal mol⁻¹.[62]

Thermochemical cycles were calculated for individual reactants and products at UB3LYP/BS2 with solvent and dispersion corrections included.

Supporting Information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

miscellaneous_information