Comparison of electromyography and force as interfaces for prosthetic control

Abstract

The ease with which persons with upper-limb amputations can control their powered prostheses is largely determined by the efficacy of the user command interface. One needs to understand the abilities of the human operator regarding the different available options. Electromyography (EMG) is widely used to control powered upper-limb prostheses. It is an indirect estimator of muscle force and may be expected to limit the control capabilities of the prosthesis user. This study compared EMG control with force control, an interface that is used in everyday interactions with the environment. We used both methods to perform a position-tracking task. Direct-position control of the wrist provided an upper bound for human-operator capabilities. The results demonstrated that an EMG control interface is as effective as force control for the position-tracking task. We also examined the effects of gain and tracking frequency on EMG control to explore the limits of this control interface. We found that information transmission rates for myoelectric control were best at higher tracking frequencies than at the frequencies previously reported for position control. The results may be useful for the design of prostheses and prosthetic controllers.

INTRODUCTION

To a person who has sustained an upper-limb amputation, the control interface between her- or himself and the prosthesis is critical to the success of the device. The capability of the interface to communicate intended movements to the prosthesis sets the upper limit for its performance. A wide variety of control systems for powered upper-limb prostheses is used today. Typically, the user generates the command signal with myoelectric control, the application of force, or a measurement of excursion of the body. However, the relative extent to which these interfaces limit the prosthetic use is unknown. The goal of this study was to quantify the efficacy of two control interfaces that could be used to provide input to a powered prosthetic arm. Detailed descriptions of conventional prosthesis control methods are given by Williams [1] and Muzumdar [2].

Electromyogram (EMG), or myoelectric, control is by far the most common user interface for powered prostheses and generally is used when possible. Among its many advantages are its relative ease of use, comfort, and promotion of muscle tone. The physical effort for operation is low because the muscle activity needed is relatively small [3]. For persons with transradial amputations, no harnessing is required, and control using residual wrist muscles is intuitive. EMG also provides access to the muscle activation process and can provide a large amount of information about the user’s intentions as he or she manipulates the muscles of the residual limb [4]. However, EMG is an indirect means to estimate the forces and positions generated by the motor system that people use to interact with their environments. It is a noisy signal and is far less directly related to the control of force or position, which is required during functional tasks. Furthermore, filtering properties of the limb tissue affect the surface myoelectric signal, and movement of the skin beneath the electrode may cause a motion artifact that can be confused with the signal [2].

Powered prostheses controlled directly by force use the proximal motion of the shoulder of the residual limb instead of any remaining distal musculature. A force-based interface is a natural means for a human to interact with the environment and provides more direct sensory information than EMG, potentially increasing control performance. Force transducers are often operated by persons with transhumeral amputations, capturing shoulder motion using a harness. This procedure requires minimal body movement, because the tension is applied at the residual limb. For persons with shoulder disarticulation amputations, force-sensing resistor touch pads at the shoulder can measure force without the use of cables. Control schemes are discussed in detail by Williams [5]. Persons with transradial amputations rarely use force transducers to control a powered prosthesis, but all body-powered systems use force directly.

To quantify the effectiveness of a prosthesis control interface, one must model the human-machine system in the context of how it affects user performance. As McRuer and Krendel noted, closed-loop transfer characteristics of the human operator influence the response measurements of interest [6]. These characteristics will vary according to the operator’s ability to adapt to the dynamic characteristics of the controlled elements, influencing the stability and performance of the entire closed-loop system. Because of these interactions, one cannot examine changes in the system characteristics due to independent changes in either the human operator or the controlled element. Other factors influencing the human operator’s transfer characteristics are physiological differences, task experience, motivation, and the type of input driving the system. Because the sources of performance differences are difficult to separate, a quantification of the complete user-prosthetic system is usually most appropriate.

The system can be concisely represented with a linear model of the human operator, as previously used to study human-operator dynamics in manual control systems [6–11]. In this analysis, the closed-loop system is represented by a linear transfer function and a generator of random noise, or “remnant,” which represents all output content that cannot be explained by a linear operation on the input. The linear closed-loop transfer function provides information about the system performance and may be used to compare multiple control interfaces, provided it reasonably describes the data and the remnant is small.

The objective of this study was to evaluate the use of EMG as a control interface, comparing it with force and position. The ability of the person with an amputation to control the prosthesis is a limiting factor for its performance. By comparing EMG, force, and position interfaces, we can examine the capabilities of these control paradigms. We implemented the linear model of the human-operator system to compare wrist control of position, force, and EMG during a one-dimensional (1-D) tracking task. While, in practice, force control is more commonly used at the shoulder, we selected the wrist to compare the interfaces as fairly as possible. Velocity was controlled in the EMG and force experiments, because control of the device velocity is commonly used in current powered prostheses [3]. This method of control gives the prosthetic user added flexibility; he or she controls both the motion of the device and the time to complete that motion. This study compared the control interfaces at 1 Hz, a tracking frequency known to be optimal for the direct-position control, which served as a gold standard against which to compare the force and EMG interfaces. We evaluated performance in terms of tracking error, human-operator bandwidth, and information transmission rate. Furthermore, we examined the effects of gain and tracking frequency for the EMG interface. The quantification of EMG-controlled tracking performance, in particular, may be useful in specifying limits for prosthetic design.

METHODS

Subjects

Eight able-bodied subjects (five male, three female), aged 22 to 30, participated in this study. While testing a wider range of ages may have been useful to reflect the varied population with an upper-limb amputation more accurately, we considered that the effect of age would be minimal compared with the differences in musculature because of the damage amputation caused.

All subjects were right-arm dominant and had participated in preliminary experiments of the same nature. Hence, they were experienced with all three protocols before commencing the experiments. This experience was important to ensure that the results were not biased by the order in which the interfaces were tested, because strong learning effects were observed during the preliminary experiments.

Experimental Setup

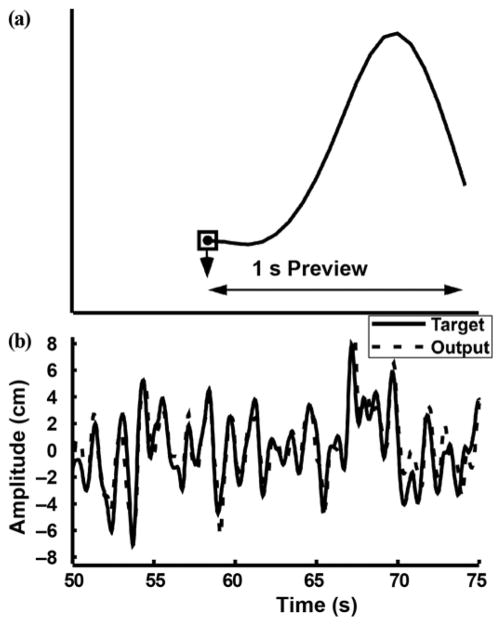
We presented a 1-D tracking task to the subjects on a computer screen by means of a MATLAB (MathWorks Inc; Natick, Massachusetts) graphical user interface. A square target was displayed on the screen. We chose a preview system as the input display type in this study (Figure 1). The target input and the system output were displayed independently to the operator; this paradigm has been shown to be more effective than compensatory displays, where only the difference between the two signals, or error term, is shown [7]. In addition, the target signal from the current time to a set time in the future was displayed. We selected this type of input because it more closely represents everyday prosthesis use. In most situations, a prosthesis user knows the desired path of the prosthesis for some time into the future.

Figure 1.

Experimental task. (a) Subject could move dot vertically either up or down as computer advances box along with target signal. Preview of 1 s was displayed. Task goal was to keep dot in box. One of three control sources controlled motion of dot: electromyography, force, or position. (b) 25 s sample from example trial of 3 min. Dashed signal was subject’s attempt to follow target.

We generated the target signal from white noise low-pass-filtered by a fourth-order Butterworth filter. Low-pass-filtered Gaussian white noise has been used previously in similar experiments [7–8,12], because the assumption of linearity of the human-operator system has been found to be fair for randomly appearing inputs [11]. We selected four different cutoff frequencies, including three practice frequencies (0.5, 0.7, and 0.9 Hz), which we used to establish a certain task performance level. We performed test trials using a target signal with a 1 Hz cutoff frequency. The target moved vertically on the screen, and a preview of the oncoming second was visible to the subject at all times. The subjects controlled a cursor (dot). The aim of the task during the trial was to keep the cursor as close to the center of the target as possible.

User Control Interfaces

During the position control experiment, the angle of the wrist was mapped directly to the cursor position. In these experiments, the subject’s wrist joint was securely attached to a custom-made electrogoniometer, which was placed on the worktable and supported by padding at the forearm (Figure 2(a)). Deviations of ±30° in flexion and extension were mapped to the full range of cursor displacements. This range of excursions was found to result in performance at least as good as larger and smaller ranges in a set of preliminary experiments. Cursor displacements were updated every 50 ms and set proportional to the average joint angles measured over the previous 100 ms. This choice of time window low-pass-filtered the data with a cutoff frequency of approximately 5 Hz, above the highest frequencies typically used in voluntary movement [13].

Figure 2.

Experimental setup. (a) Position setup: arm was free to move and wrist angle was measured. (b) Electromyography (EMG): electrodes were placed on wrist flexor and extensor muscles. (c) Force: forces were measured at hand, and movement at wrist was restricted.

Activation of the subjects’ forearm muscles provided the input for the EMG-controlled task. Contractions were isometric: the subjects gripped a metal rod using a palmar grasp while the forearm was fixed to the table in front of them (Figure 2(b)). We chose this paradigm to minimize proprioceptive feedback from the wrist joint, which would not be available to person with an amputation; persons with amputations perform prosthesis control using isometric contractions. However, eliminating tactile feedback from the hand was impossible with able-bodied subjects. The use of a task that required palmar grasp minimized this effect, relative to a task that involved the fingers more directly since the tactile acuity of the palm is less than that of the fingertips.

We collected EMG data from the wrist flexor and extensor muscles in the dominant forearm. To emulate a real prosthetic interface, we did not specifically target muscles. However, the electrodes were positioned such that the flexor carpi radialis and extensor carpi ulnaris contributed significantly to control. Two single differential-surface EMG sensors (Bagnoli DE-2.1, Delsys; Boston, Massachusetts) were placed parallel to the muscle fibers. The signals were amplified with a two-channel Delsys Bagnoli-2 signal conditioning unit with a 20 to 450 Hz bandwidth and sent to a computer by way of a National Instruments card (PCI-6031E; Austin, Texas), which performed the analog-to-digital conversion. After the subject’s forearm was secured in the experimental rig, the subject performed a 3 s isometric maximum voluntary contraction (MVC) for both flexion and extension. We used the MVC to normalize the magnitude of the EMG during proportional velocity control. The EMG signals were sampled at 1,000 Hz, and any linear trend was removed from each incoming 50 ms of data. The mean absolute value of a 100 ms window was calculated for each channel, and the windows were updated every 50 ms, a rate more than adequate for EMG control [14].

During control, we set the flexor and extensor EMG channels to zero when they were below a threshold of 2 percent of MVC to minimize the effects of spurious movement and measurement noise. We also normalized each channel by the EMG recorded during MVCs to provide a relative measure of muscle activation. To determine the velocity of the cursor, we then considered the larger of the two normalized channels active and multiplied it by a gain factor, G. Flexion moved the cursor down, and extension moved it up. If neither channel was above threshold, the velocity was set to zero.

In the force control system, we modulated the velocity of the cursor by isometric flexion and extension forces at the wrist. A load cell at the hand was used; both the hand and wrist muscles likely contributed to the control. The subject’s hand was securely strapped to the sensor, and a padded brace restricted movement of the forearm and wrist so that contractions were isometric (Figure 2(c)). In contrast to the EMG setup, where prosthetic control was emulated as much as possible, the force setup represented the best-case scenario for the control. Force control in powered upper-limb prostheses is most commonly performed at the shoulder, which (while more applicable for a wider range of amputees) is less effective than wrist control [15]. We decided, however, to compare EMG and force using the same neural command signal: that to the wrist flexor and extensor muscles.

We recorded forces for MVCs in both flexion and extension. As we just described for the EMG-controlled cursor, we used MVCs to scale the forces measured during cursor control. The velocity of the force-controlled cursor was set proportional to the mean force recorded over the prior 100 ms. The velocity of the cursor was updated every 50 ms. Flexion forces moved the cursor down, and extension forces moved it up.

Protocols

Comparison of Control Interfaces

All subjects performed an experiment with each interface. Each interface was evaluated separately, and the order of the evaluated interfaces was randomized across subjects. To allow the subject to become familiar with the control interface, we held a training session at the beginning of each experiment. Subjects completed a sequence of trials with a gradual progression of increasing target signal cutoff frequency within the range of optimal human-tracking bandwidths (0.5, 0.7, and 0.9 Hz); the subject advanced to the next frequency when a normalized root-mean-square tracking error of 30 percent or lower was achieved. The training trials were 30 s in duration, avoiding an excessively long protocol.

The selection of an optimal gain factor, G, is extremely important for subject performance in velocity control tasks [12]. Therefore, we performed an optimization procedure before the test trials to ensure the appropriate choice. Generally, if the gain is too low, the subjects will struggle to keep up with the task signal, and fatigue might occur. However, if the gain is too high, control interfaces become too responsive and often unstable. We selected the gain using 30 s trials with continuous random signals with cutoff frequencies of 1 Hz; this was the same frequency used in the trials for comparing control interfaces, because the optimal gain depends on the frequency content of the task. We selected the gain that produced the lowest tracking error.

The subjects performed at least one 30 s trial at the selected gain immediately before testing to ensure that they were comfortable and familiar with the task. Otherwise, we (the experimenters) ensured the subject was comfortable with the task. Trials continued at this setting until subjects reached a performance plateau. A plateau was recognized when the tracking error did not decrease by more than 5 percent in subsequent trials. This entire procedure took an average of 30 min. Once we finished the setup and tuning, each subject completed three 3 min evaluation trials that we used to compare the interfaces.

Electromyogram Controller Gain Variation

In many situations, EMG is the most practical choice of interface for a powered prosthesis, because of intuitive control and comfort, as just described. For this reason, we performed further experiments to examine the effect of changing the EMG controller gain, G, on tracking performance. The human operator is remarkably able to adapt to many different systems, and we expected that the subjects’ performance would remain stable for a reasonably wide range of gain selections. However, because we selected the gain based solely on tracking error, its effect on human-operator bandwidth and information transmission rate was unknown. Because it ultimately limited the velocity at which the cursor could be manipulated, the bandwidth of the human-operator system could possibly be limited as well. This limitation would have resulted in an unfair disadvantage for the EMG and force control interfaces, because the position interface was not constrained in this way. We performed four experiments using the EMG interface. We also performed the training and gain selection processes exactly as just described. Once the optimal gain, G, had been selected, the 3 min trials commenced. Three full-length trials were performed at each of four different gains: G, G × 1.1, G × 1.2, and G × 1.4, in random order. Subjects rested liberally, as needed.

Electromyogram Task Frequency Variation

The tracking cutoff frequency was a parameter that was certain to affect task performance, since higher bandwidth signals are more difficult to track. Of particular interest was seeing the effect of this parameter on the information transmission rate of the EMG interface. The effect of the target signal cutoff frequency on the information transmission rates of position control has been well documented, and the optimal range (0.5–1.0 Hz) for tracking is known [8,12]. However, an EMG velocity-based control interface of the kind used in most current prostheses may provide different results. We performed four experiments with experienced subjects using the EMG interface. Three full-length trials were performed at six different tracking target cutoff frequencies, ranging from 0.3 to 2.3 Hz. We selected a single gain, which was high enough that the trial at 2.3 Hz could be performed without fatiguing the subjects. We performed the first six trials sequentially in order of increasing frequency to allow gradual learning to take place. We performed the trials in the last two sets in a pseudorandom order; slow and fast trials were alternated in such a way that fatigue could be avoided. Subjects also rested liberally, as needed.

Analysis

We evaluated task performance using three different measures. Accuracy of the task performance was measured with the normalized mean square error between the target signal and the path followed by the cursor. This measure of tracking error is independent of any assumptions about the human-operator system. We calculated the bandwidths and the information transmission rates of the human-machine systems using techniques developed for the study of manual control tasks [6–9,16]. The human-operator bandwidth is the highest frequency at which the user can track the target while capturing at least 70 percent of the proportion of input signal components that were captured at the lowest frequencies with the specific human-operator-controller system. Information transmission rate allows us to examine the capabilities of humans in the context of the machines they operate by modeling the human as a noisy information channel. Elkind and Sprague first used the information transmission rate to quantify continuous tracking performance [8]. The quasilinear model of the human operator is equivalent to that of an information channel with additive noise, as described by Shannon [17]. For a tracking task, the objective of reproducing a signal from the input to the output is analogous to transmitting information across a channel while minimizing error. Doubler and Childress first applied this analysis to upper-limb prostheses [12,15]. They based the analysis on the premise that the ability of the user to communicate motor intent to his or her prosthesis is a large component of its effectiveness. Both of these analyses (human-operator bandwidth and information transmission rate) assume the quasilinear model of the human-machine system.

We calculated the power spectral densities of the input and output signals using Welch’s averaged periodogram method [18]. From these spectra, we calculated the transfer and coherence functions [19]. For each subject, the three transfer functions for a control interface’s test trials were computed and averaged, after which the bandwidth was calculated as the frequency at which the transfer function dropped to –3 dB from its maximum value. We calculated the maximum value by taking the mean value of the transfer function for all frequencies up to half of the cutoff frequency of the target signal for the particular trial. We selected this method because, for the control experiments with high cutoff frequencies, the transfer functions were sometimes noisy and the bandwidths were difficult to estimate. By observing this procedure, we confirmed that it produced reasonable estimates for trials of all cutoff frequencies tested. We calculated the information transmission rate of the human-machine system for each 3 min trial by integrating Shannon’s channel capacity over the frequency spectrum [8,12].

RESULTS

Comparison of Control Interfaces

During test trials for each interface, subjects tracked the target signals with varying degrees of accuracy (Figure 3). Power spectra and transfer and coherence functions are shown in Figure 4. For each interface, subjects performed three 3 min trials at a tracking cutoff frequency of 1 Hz. We used the results of these trials to compare the tracking performance of the three control interfaces. We performed a three-way analysis of variance (ANOVA) for each performance measure, treating subject as a random factor. The two fixed factors were the type of interface (position, force, EMG) and the order in which these interfaces were presented. We found that the order in which we tested the interfaces was not significant for any of the quantified outcome measures (all p > 0.18), indicating that the combination of previous task experience and a thorough training protocol was effective. This factor was then removed from the analysis, and two-way ANOVAs were performed. We then used a Tukey test for post hoc comparisons. In all statistical comparisons, we used α = 0.05 to test for significance.

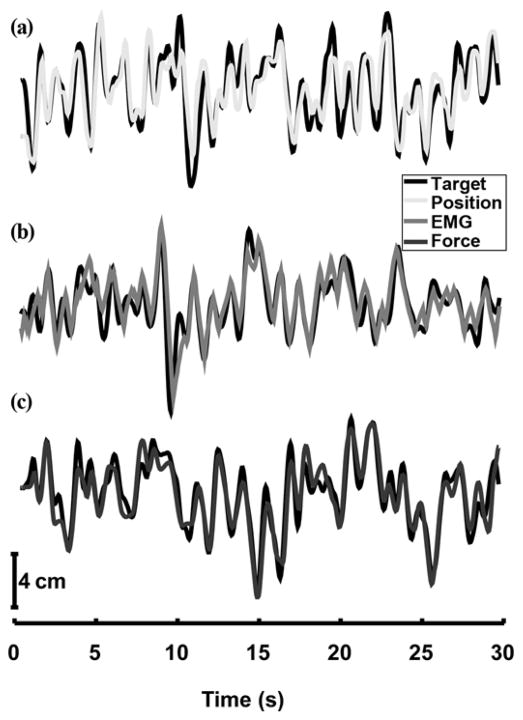
Figure 3.

Sample tracking trials for each interface. One subject, 30 s samples from 3 min trials with target cutoff frequency of 1 Hz. Both target signal and output are shown. (a) Position: tracking error = 23.8%, information transmission rate = 4.23 b/s; (b) electromyography (EMG): tracking error = 32.7%, information transmission rate = 3.13 b/s; (c) force: tracking error = 35.4%, information transmission rate = 3.3 b/s.

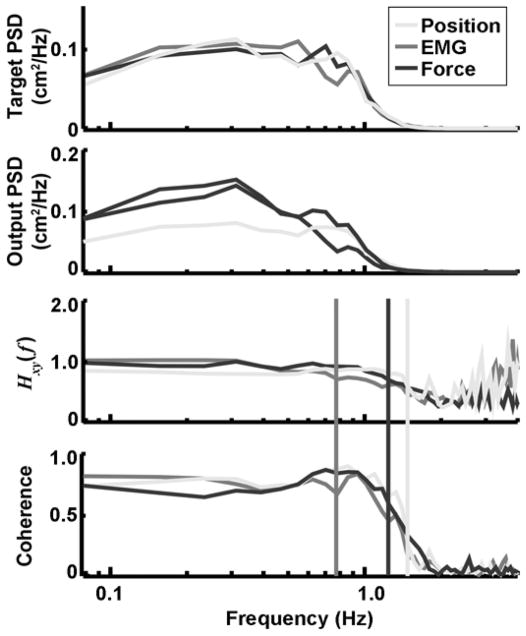
Figure 4.

Frequency domain analyses of tracking performance. Data are from same subject shown in Figure 3, except that all three trials are used in these calculations. Power spectra were calculated with frequency resolution of 0.08 Hz. From top: Power spectral densities (PSD) of targets (x) and outputs (y), followed by transfer (H_xy) and coherence functions, all as function of frequency (f). Bandwidths of 1.50, 0.80, and 1.25 are marked by corresponding vertical lines for position, electromyography (EMG), and force, respectively.

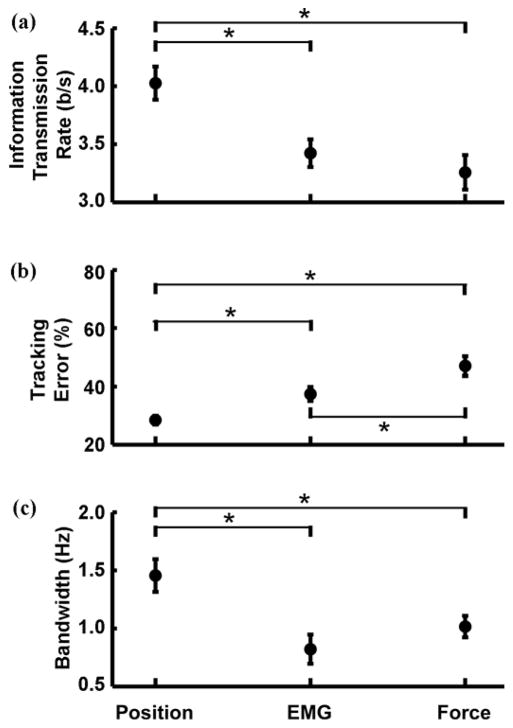
Information transmission rate, tracking error, and human-operator bandwidth were significantly affected by the choice of interface. The information transmission rate (Figure 5(a)) of the position control was superior to the EMG (p = 0.008) and force interfaces (p < 0.001), with no statistically significant difference between the latter two (p = 0.67). The tracking error (Figure 5(b)) for the position interface was lower than that for the EMG (p = 0.04) and force (p < 0.001) interfaces, and the tracking error for the EMG was lower than that for the force interface (p = 0.03). The mean bandwidth (Figure 5(c)) for the position interface was significantly higher than that for the EMG (p = 0.003) and force interfaces (p = 0.046). The latter two interfaces were not statistically different (p = 0.5).

Figure 5.

Control interface comparison (eight subjects). Group mean and standard errors of (a) information transmission rate, (b) tracking error, and (c) human-operator bandwidth for each interface. Stars indicate statistically significant differences. Target signal cutoff frequency was 1 Hz. EMG = electromyography.

Electromyogram Controller Gain Variation

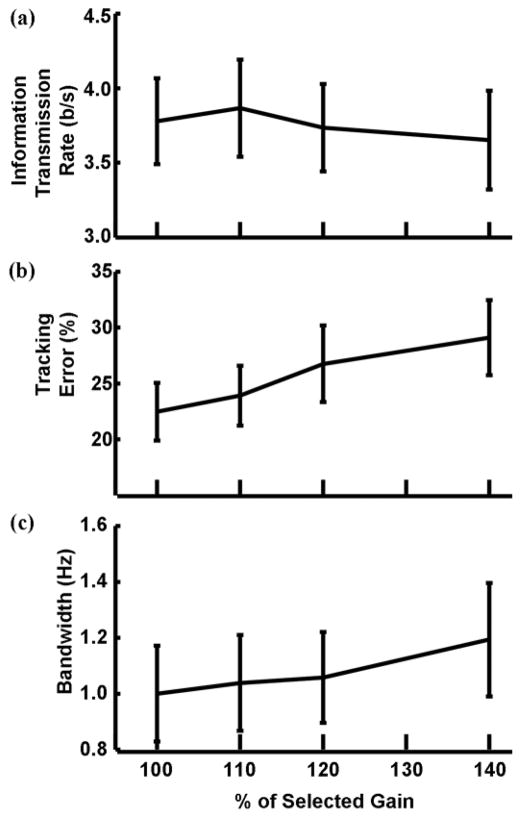
Increasing the EMG controller gain significantly affected the task performance for two of the three outcome measures (Figure 6). We performed a two-way analysis of covariance (ANCOVA) for each outcome measure, treating the subject as a random factor and gain as a fixed continuous variable. The gain did not significantly affect the information transmission rate (p = 0.27). A significant positive effect was found on both the tracking error (p = 0.003) and the human-operator bandwidth (p = 0.01).

Figure 6.

Effect of gain on electromyogram interface (four subjects). Group mean and standard errors of (a) information transmission rate; (b) tracking error; and (c) human-operator bandwidth, all versus % of selected gain.

Electromyogram Task Frequency Variation

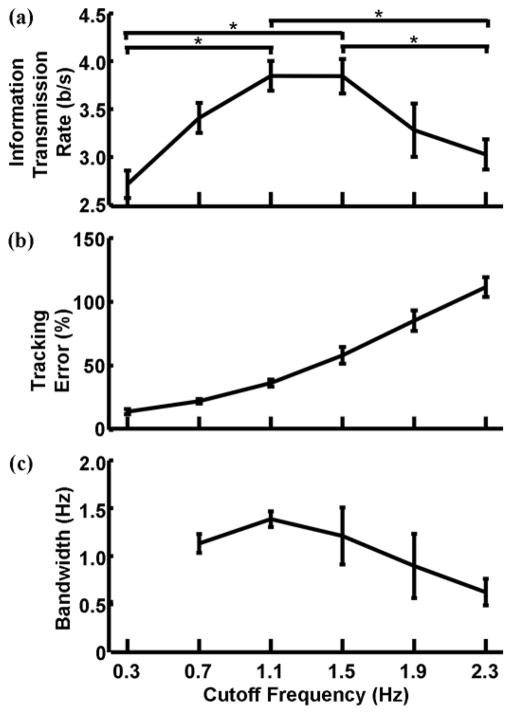
For EMG control, all three of the performance measures depended highly on the bandwidth of the target signal presented (Figure 7). The human-operator bandwidth at 0.3 Hz is not shown, since for three of the four subjects, the frequency content of these data was too low for estimating the human-operator bandwidth (Figure 7(c)). For the tracking error and human-operator bandwidth, we performed two-way ANCOVAs, treating the subject as a random factor and target signal cutoff frequency as a fixed continuous variable. A significant positive effect was found on the tracking error (p < 0.001) and a negative effect on the human-operator bandwidth (p = 0.03). We assessed the effect on information transmission rate using a two-way ANOVA, treating the subject as a random factor and target signal cutoff frequency as a fixed factor. The highest information transmission rates occurred at 1.1 and 1.5 Hz, which were both statistically significantly different from those at 0.3 and 2.3 Hz, the cutoff frequencies that produced the lowest information transmission rates (p < 0.05). No other statistical differences were found between cutoff frequencies (all p > 0.08). Both the information transmission rate (Figure 7(a)) and the human-operator bandwidth (Figure 7(c)) were highest at the target signal bandwidths of 1.1 and 1.5 Hz. Below the optimal range, the information content of the target signal was low, and above it, the tracking error was so high that the performance deteriorated (Figure 7(b)). The maximum information transmission rates (3.9 ± 0.6 b/s) were close to those found for position control (4.0 ± 0.7 b/s) in the original experiment when the target signal bandwidth was 1 Hz, which has been shown to be optimal for position control [8,11,16].

Figure 7.

Effect of target bandwidth on electromyogram control interface (four subjects). Group mean and standard errors of (a) information transmission rate; (b) tracking error; and (c) human-operator bandwidth, all versus target cutoff frequency. Stars indicate statistically significant differences.

DISCUSSION

As prosthetics research progresses, devices are being developed with increasing degrees of freedom (DOFs). To identify clearly the differences between them, we need to explore the limits of the available control interfaces, whether due to physical constraints or to the mental burden involved in their use. This study demonstrated that EMG performs at least as well as a force control interface at 1 Hz tracking. The limits of the EMG control interface were explored for tracking frequency; the optimal range of frequencies found was higher than that reported for position control [8,11,16]. Evidently, EMG, despite being a noisy signal, provides a control interface for prostheses that does not limit information transmission from the user any more than force control, which is a natural means to interact with the environment. The capability of the EMG interface to transfer information at high frequencies should be considered in the future design of prosthetic limbs.

Comparison of Control Interfaces

This study extracted the neural command signal at three different stages of processing by the human-operator system (Figure 8). The limb mechanics subsystem is effectively bypassed when EMG or force is used as the control signal. For the point of extraction and subsequent processing of the neural command signal, the force and EMG control interfaces are similar in nature. Both signals are related to muscle force and are used to control the velocity of the cursor. As just discussed, their performance is not as good as that of the position control. However, they are generally more practical for use with prostheses, requiring less excursion of the residual limb.

Figure 8.

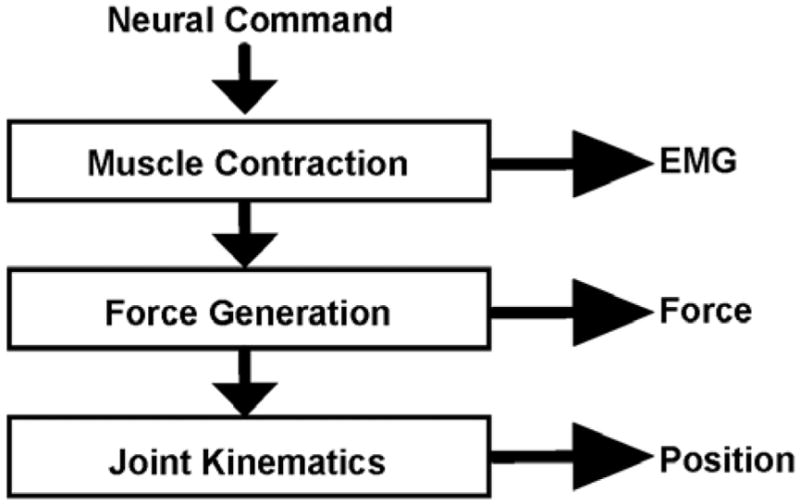
Decomposition of neural command signal processed by human operator. EMG = electromyography.

Intuitively, the use of joint kinematics for position control results in better tracking accuracy and information transmission than the velocity-based methods of EMG and force sensing. Muscle spindles provide proprioceptive feedback from the forearm and wrist joint, enabling precise control of wrist position. As position is controlled, the one-to-one relationship between the physical controlling process and the cursor position on the screen further simplifies the subject’s mental processing task. Generally, researchers believe that, despite the constraints of the neuromuscular system, central delays rather than input/output information transmission delays limit the bandwidth of a human operator [20]. However, Mesplay and Childress found that the highest information transmission rates were obtained by the joints with the lowest moments of inertia [21]. This finding suggests that the constraints of the neuromuscular system may also affect performance. Research has found that wrist goniometer control is superior to the use of more proximal joints [12], and thus its selection for an upper bound for human-operator capabilities is appropriate. The information transmission rates found for the position control interface in this study are similar to those rates found previously for 1-D pursuit position tracking at 1 Hz (4–5 b/s) [8,12].

We expected that the differences in how the command signal is obtained and the nature of proprioceptive feedback that EMG and force control interfaces provide would be reflected in their respective performances. For both paradigms, force feedback was available from the flexor and extensor muscles and tendons. For the force sensor, the amount of force applied could be directly sensed by way of mechanoreceptors in the skin of the hand. In contrast, EMG is only a by-product of muscle force. A relationship still existed between the EMG signal production and hand-skin force perception, but it was perhaps less direct than for the force interface. The positioning of the electrodes on the skin affects the relative influence of specific muscles on the control signal. One may have also expected that the user would find mastering complete control of the cursor more challenging, because the EMG signal is stochastic and is much noisier than the force signal.

Despite the many potential problems of EMG velocity control, subjects were just as effective with EMG as they were with force velocity control. The tracking error was actually slightly lower for the EMG interface. Evidently, the filtering and integration of the noisy EMG signal were effective in producing a well-behaved velocity at the output.

The efficacy of EMG as a control interface is a much-debated topic in the prosthetics field. As just discussed, the muscle activation properties on which the signal depends are stochastic in nature. In addition, the EMG-force relationship is not stationary because of issues such as fatigue. Nonetheless, the argument for the use of EMG as a prosthesis control interface is supported by the fact that EMG does not limit the operator’s ability to transmit user intent any more than force.

Effect of Gain: Speed/Accuracy Trade-Off

We performed further experiments using the EMG control interface to examine whether the gain selection in our experiments affected the results in any way. Since the human-operator bandwidth calculated for the velocity control systems had been found to be significantly lower than the bandwidth for the position control, we were interested in whether they had been limited by the choice of gain. Increasing the gain of the EMG-based controller did increase human-operator bandwidth. In fact, the human-operator bandwidth at the highest gain was closer to that bandwidth computed for the position control than to the bandwidth computed for the EMG in the original experiments. However, the tracking error also increased with gain. These results demonstrate a trade-off between speed and accuracy in human tracking, which many researchers have described [22–23].

The information transmission rates, however, were not affected by the choice of controller gain. This insensitivity to controller tuning demonstrates that the information transmission rate is a more comprehensive performance measure than tracking error or human-operator bandwidth. It incorporates both the accuracy of the system and the speed at which it can operate. The use of low gains will result in slow and accurate movements of a prosthesis. Increasing the gain will increase speed at the expense of accuracy. One could find an optimal balance of these two factors as appropriate for the task by ensuring that the information transmission rate remains high while the speed and accuracy are balanced. The insensitivity of information transmission rate over a wide range of tracking frequencies also suggests that it may be useful as a tool in assessing the trade-off between speed and accuracy for a particular task.

Effect of Target Signal Cutoff Frequency

Many researchers have shown that the information transmission rate of the human operator is maximal in one DOF for target signal bandwidths between 0.5 and 1.0 Hz [8,11,16]. Chan and Childress developed a fundamental relationship to show that the variance of the human-machine noise is proportional to the mean-square velocity of its output [22,24]. They found that this relationship could be used to predict information transmission rates and that a maximum rate exists at which humans could respond. This maximum sets the processing limit of human-machine control. Information transmission rates increase with target bandwidth until this maximum rate is achieved, after which they decrease as the bandwidth of the target is increased.

Of great interest was the range of tracking frequencies for which the EMG control interface is effective. The bandwidth of the signal presented to the user dramatically affected the human-operator system response. The mean human-operator bandwidths calculated at all possible tracking frequencies increased as the cutoff frequency was increased from 0.7 to 1.5 Hz and decreased as it was increased further. This decrease in human-operator bandwidth with increasing target signal bandwidth is somewhat counterintuitive. One might expect a faster target to induce a faster response. However, as the signals became more difficult to track, the response was so poor (error too high) at all frequencies that the human-operator bandwidth became difficult to estimate.

As would naturally be expected, tracking error increased as the movements became faster. Once again, the trade-off between speed and accuracy is evident from these results. Information transmission rates were consistently good across a wide range of target frequencies; they were highest at 1.1 and 1.5 Hz. This range is higher than the reported range of optimal bandwidths in position control (0.5–1.0 Hz). Interestingly, the information transmission rates of the EMG interface at these higher frequencies were comparable to the position control system in the original experiments, which were performed at the optimal frequency for position control, according to the literature. The high rate of information transmission found in this study at high frequencies may be relevant for the design of future devices. However, the appropriate balance between speed and accuracy must be selected based on both the user of the prosthesis and the task. Taylor et al. stressed the need to balance a high information transmission rate with the “cost” of an error [25]. Specifically, if a large number of errors need to be corrected, the overall information transmission rate will be reduced significantly. The cost of an error depends on the function being performed. This trade-off must be considered, and therefore, the average user is unlikely to use the maximal measured information transmission rates most of the time.

The relative importance of speed and accuracy is highly task-dependent. At peak rates of information transmission from the experiment summarized in Figure 7, the tracking error appears to be quite high (36%–58%). We should note, however, that a high tracking error, as defined in this study, does not indicate a complete failure in tracking. A 100 percent tracking error corresponds to an error between the target and output equal in magnitude to the target itself. High errors may not be a huge problem for tasks in which the workspace is large and precision is not vital, such as during rapid movements. As in natural control, one could increase precision near the target by decreasing terminal velocity [26].

When extending to two-dimensional and three-dimensional tasks more relevant to everyday life, we would expect to see further trade-offs between DOFs, movement frequency, and accuracy. The addition of further DOFs would naturally increase the overall information transmission rates, though not necessarily linearly. The exact increase that could be expected depends on a number of factors, including the independence with which the individual DOFs could be controlled and the maximum limit for human-information transmission.

CONCLUSIONS

For this high-speed tracking task, the use of EMG to sense the user command signal does not limit the information transmission capabilities or bandwidth of the human operator more than the use of force does. This result is promising for upper-limb prostheses, because the human sets the performance limits for control. As would be intuitively expected, position control provided an upper bound for human-operator capabilities. It was more effective and produced higher operator bandwidths, lower information transmission rates, and a lower tracking error.

Tracking error and human-operator bandwidth were sensitive to changes in the controller gain, whereas information transmission rate was not. We found that, for this paradigm, the frequency range for optimal information transmission is higher for an EMG velocity control interface than the previously reported optimal frequency range for the position-tracking task. Information transmission rates are consistent for a wide range of target frequencies. This frequency response of the EMG control interface may be useful when one is specifying limits for prosthetic design, because the information transmission rate provides a tool for balancing the trade-off between speed and accuracy that must be considered in prosthetic control.

Abbreviations

1-D

one-dimensional

ANCOVA

analysis of covariance

ANOVA

analysis of variance

DOF

degree of freedom

EMG

electromyogram and electromyography

MVC

maximum voluntary contraction