Abstract
We have synthesized and characterized, using X-ray crystallographic, spectroscopic, and computational techniques, a six-coordinate diazide Fe3+ complex, LFe(N3)2 (where L is the tetradentate ligand 7-diisopropyl-1,4,7-triazacyclononane-1-acetic acid), that serves as a model of the azide adducts of Fe3+ superoxide dismutase (Fe3+SOD). While previous spectroscopic studies revealed that two distinct azide-bound Fe3+SOD species can be obtained at cryogenic temperatures depending on protein and azide concentrations, the number of azide ligands coordinated to the Fe3+ ion in each species has been the subject of some controversy. In the case of LFe(N3)2, the electronic absorption and magnetic circular dichroism spectra are dominated by two broad features centered at 21 500 cm−1 (ε ≈ 4000 M−1 cm−1) and ~30 300 cm−1 (ε ≈ 7400 M−1 cm−1) attributed to N3− → Fe3+ charge transfer (CT) transitions. A normal coordinate analysis of resonance Raman (RR) data obtained for LFe(N3)2 indicates that the vibrational features at 363 and 403 cm−1 correspond to the Fe–N3 stretching modes (νFe–N3) associated with the two different azide ligands and yields Fe–N3 force constants of 1.170 and 1.275 mdyne/Å, respectively. RR excitation profile data obtained with laser excitation between 16 000 and 22 000 cm−1 reveal that the νFe–N3 modes at 363 and 403 cm−1 are preferentially enhanced upon excitation in resonance with the N3− → Fe3+ CT transitions at lower and higher energies, respectively. Consistent with this result, density functional theory electronic structure calculations predict a larger stabilization of the molecular orbitals of the more strongly bound azide due to increased σ-symmetry orbital overlap with the Fe 3d orbitals, thus yielding higher N3− → Fe3+ CT transition energies. Comparison of our data obtained for LFe(N3)2 with those reported previously for the two azide adducts of Fe3+SOD provides compelling evidence that a single azide is coordinated to the Fe3+ center in each protein species.
Introduction
Superoxide dismutases (SODs) are a family of enzymes responsible for the protection of aerobic organisms against cellular damage caused by the superoxide radical anion, O2•−. SODs can be classified on the basis of the metal ion(s) they require for activity, namely, Mn, Fe, Cu/Zn, or Ni.1,2 Mn- and FeSODs, like all other SODs, disproportionate the superoxide radical anion into dioxygen and hydrogen peroxide in a two-step ping-pong-type mechanism (eqs 1a and 1b, where M = Fe or Mn) during which the metal ion cycles between the 2+ and 3+ oxidation states.3–5 While structurally unrelated to the Cu/Zn- and NiSODs, Mn- and FeSODs possess nearly identical protein folds and highly homologous active sites.6 In the resting states of both proteins, the metal ions are in five-coordinate, distorted trigonal bipyramidal ligand environments with a histidine (His) and a solvent molecule in the axial positions and two His residues and an aspartate (Asp) in the equatorial plane (Figure 1, left).6–11 The substrate is proposed to bind trans to the Asp ligand (i.e., between the two equatorial His residues) to yield a six-coordinate, roughly octahedral complex.
| (1a) |
| (1b) |
Figure 1.
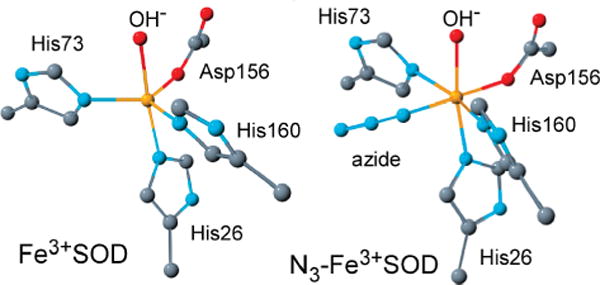
Active-site structures of Fe3+SOD (left) and N3−Fe3+SOD (right) from E. coli, based on PDB files 1ISB and 1ISC, respectively.6 H atoms are omitted for clarity.
The rate constants for the reaction of Mn- and FeSODs with superoxide approach the diffusion-controlled limit, thus largely preventing direct studies of catalytic intermediates. Various substrate analogues have therefore been used to generate geometric and electronic structural models of the substrate-bound protein active sites. Azide (N3−) is a particularly well-suited substrate analogue, because it possesses the same charge and similar frontier orbitals as O2•−. The reaction of Fe3+SOD with azide results in the formation of a yellow species (N3−Fe3+SOD) that has been the subject of spectroscopic and X-ray crystallographic studies, which revealed that azide binds to the putative substrate-binding site located between the two equatorial His ligands (Figure 1, right). Interestingly, however, two differently colored N3−Fe3+SOD species can be obtained at low temperatures depending on the protein and azide concentrations:12 a pink adduct is formed upon the freezing of a solution low in protein concentration and where [N3−]/[FeSOD] > 2, whereas a yellow adduct is observed in all other instances.
Initially, these results were interpreted as indication for one and two azides binding to the Fe3+ center in the yellow and pink N3−Fe3+SOD species, respectively, with the second azide potentially displacing the metal-bound OH− ligand (Figure 1, right), thus yielding octahedral complexes in both cases.12 The possibility that anions can displace the Fe-bound solvent is quite intriguing, as this finding would imply that two substrate molecules could simultaneously bind to the active site under turnover conditions. However, we have recently proposed alternative descriptions of the two distinct N3−Fe3+SOD species, namely, that both contain a single, though somewhat differently oriented, azide ligand.13 Specifically, we have shown computationally that an increase in the Fe–azide bond angle by ~30° would be sufficient to cause a change in color of N3−Fe3+SOD from yellow to pink. Such a modulation in the Fe–azide bond angle could be caused, for example, by the binding of a second azide ion (in addition to the one already coordinated to the metal) to a residue near the active site so as to perturb the hydrogen-bonding network that involves the coordinated solvent and several second-sphere residues.
To explore the spectroscopic properties of the putative diazide Fe3+ core originally proposed for the pink N3−Fe3+SOD species, we have synthesized a model complex, LFe(N3)2 (where L is the tetradentate ligand 7-diisopropyl-1,4,7-triazacyclononane-1-acetic acid), in which two azides are bound to a high-spin Fe3+ center (Figure 2). We have characterized this complex using X-ray crystallography as well as X-band electron paramagnetic resonance (EPR), electronic absorption (Abs), magnetic circular dichroism (MCD), variable-temperature/variable-field (VTVH) MCD, and resonance Raman (RR) spectroscopies. Additionally, we have employed density functional theory (DFT), semiemperical INDO/S-CI, and time-dependent (TD) DFT calculations to generate an experimentally validated electronic structure description for this diazide Fe3+ model complex. When compared to the spectroscopic data of the yellow and pink N3−Fe3+SOD species reported in the literature, our results obtained for LFe(N3)2 provide compelling evidence that only one azide ion can bind to the Fe3+ center of the enzyme active site.
Figure 2.

Molecular structure of LFe(N3)2 as determined by X-ray crystallography (H atoms are omitted for clarity). The INDO/S-CI computed D-tensor orientation is shown on the right.
Experimental Section
Synthesis. Materials and Methods
All reagents were obtained from commercial sources and used as received unless noted otherwise. Solvents were purified according to standard methods. Isotopically labeled sodium azide (1−15N, 98%) was obtained from Cambridge Isotope Laboratories. The ligand precursor 1,4-diisopropyl-1,4,7-triazacyclononane was prepared as described previously.14 All reactions and products were handled under an inert atmosphere using standard Schlenk techniques, or in a Vacuum Atmospheres inert atmosphere glovebox. Nuclear magnetic resonance (NMR) spectra were obtained using a JEOL Eclipse 400 spectrometer. 1H and 13C{1H} chemical shifts are reported versus tetramethylsilane and are referenced to residual solvent peaks. Infrared spectra were obtained using a Nicolet Avatar 360 spectrometer as KBr dispersions using a diffuse reflectance accessory. Electronic absorption spectra were measured using a Hewlett-Packard 8453 spectrophotometer (190–1100 nm range). Elemental analyses were performed by Atlantic Microlabs (Norcross, GA).
HL·2HBr
To a stirred solution of 1,4-diisopropyl-1,4,7-triazacyclononane (8.37 g, 39.2 mmol) in CH3CN (100 mL) was added t-butylbromoacetate (7.86 g, 40.3 mmol), Na2CO3 (41.35 g, 390 mmol), and Bu4NBr (20 mg). The mixture was heated at reflux for 6 h, after which time it was cooled to room temperature and filtered. The filter cake was washed with CHCl3, and the combined filtrates were evaporated to yield a tan residue. This residue was suspended in acetone (250 mL), and the mixture stirred rapidly while 33% HBr in CH3CO2H (40 mL) was added. This procedure resulted in the deposition of a tan solid, which was filtered, washed with acetone until the washings were colorless, and then dried. The crude product was recrystallized from a mixture of CH3OH and toluene to yield the pure ligand as colorless needles. Yield: 14.47 g (85%). mp 224–228 °C. 1H NMR (400 MHz, CD3OD): 3.81 (heptet, J = 6.6 Hz, 2H), 3.74 (s, 3H), 3.66 (s, 2H), 3.55−3.52 (m, 2H), 3.47−3.42 (m, 2H), 3.30−3.24 (m, 2H), 3.06−3.02 (m, 2H), 1.53 (d, J = 6.6 Hz, 6H), 1.46 (d, J = 6.6 Hz, 6H) ppm. 13C{1H} NMR (100 MHz, CD3OD): 174.1, 61.7, 55.9, 49.5, 48.9, 46.7, 18.4, 15.9 ppm.
[LFeCl]2
A stirred suspension of HL·2HBr (0.260 g, 0.600 mmol) in tetrahydrofuran (THF) (60 mL) was treated with excess NaH for 2 h. The insoluble material (excess NaH and NaBr) was filtered away and the filtrate evaporated to provide a white solid (NaL). This solid was dissolved in CH2Cl2 (4 mL) and treated with a solution of FeCl2 (0.080 g, 0.63 mmol) dissolved in CH3CN (4 mL). The resulting mixture was stirred for 1 h, then filtered, and the filtrate evaporated to dryness. The crude solid product was redissolved in a mixture of CH3OH (3 mL) and CH2Cl2 (3 mL) and precipitated as a white solid by the addition of excess Et2O. Yield: 0.140 g (64%). Recrystallization by diffusion of Et2O into a solution of [LFeCl]2 in 1:1 CH3OH/CH2Cl2 provided colorless block crystals of the product suitable for crystallographic analysis. Anal. calcd. for C28H56N6O4Fe2Cl2: C, 46.49, H, 7.80; N, 11.61. Found: C, 45.98; H, 7.75; N, 11.25.
LFe(N3)2
A sample of [LFeCl]2 (0.033 g, 0.046 mol) was suspended in CH3OH (5 mL) and treated with excess NaN3. The resulting mixture was gently heated in the air until a clear, red-orange solution resulted. The solution was then cooled and evaporated to dryness. The crude product was extracted into hot CH3CN, filtered, and the filtrate cooled to −20 °C, depositing the product as a red crystalline solid. Yield: 0.015 g (40%). Recrystallization by diffusion of Et2O into a solution of LFe(N3)2 in CH3OH provided red plate crystals of the product suitable for crystallographic analysis. UV − vis (CH3CN) [λmax, nm (ε, M−1cm−1)]: 332 (7400), 417 (3500), sh. 495 (2300). FTIR (KBr): 2068, 2043 (15NN2: 2060, 2034), 1666 (νCO2) cm−1. Anal. calcd. for C14H28N9O2Fe: C, 40.99; H, 6.88; N, 30.72. Found: C, 40.92; H, 6.80; N, 30.80.
Crystal Structure Data
Single crystals were mounted in thin-walled glass capillaries and transferred to a Bruker-Nonius MACH3S X-ray diffractometer for room temperature data collection using graphite monochromated Mo Kα (λ = 0.71073 Å) radiation. Unit cell constants were determined from a least-squares refinement of the setting angles of 25 intense, high-angle reflections. Intensity data were collected using the ω/2θ scan technique to a maximum 2θ value of ~50°. Absorption corrections were applied on the basis of azimuthal scans of several reflections for each sample. The data were corrected for Lorentz and polarization effects and converted to structure factors using the teXsan for Windows crystallographic software package.15 Space groups were determined on the basis of systematic absences and intensity statistics. Successful direct-methods solutions were calculated for each compound using the SHELXTL suite of programs.16 Any non-hydrogen atoms not identified from the initial E-map were located after several cycles of structure expansion and full matrix least-squares refinement on F2. Hydrogen atoms were added geometrically. Non-hydrogen atoms were refined with anisotropic displacement parameters, while hydrogen atoms were refined using a riding model with group isotropic displacement parameters. Relevant crystallographic data for the compounds are summarized in Table 1. Complete crystallographic information for each complex is provided as Supporting Information in CIF format.
Table 1.
X-Ray Crystallographic Data for [LFeCl]2 and LFe(N3)2a
| [LFeCl]2 | LFe(N3)2 | |
|---|---|---|
| empirical formula | C28H56Cl2Fe2N6O4 | C14H28FeN9O2 |
| fw | 723.39 | 410.30 |
| cryst syst | monoclinic | orthorhombic |
| space group | P21/c | Pna21 |
| a (Å) | 8.066(2) | 15.605(3) |
| b (Å) | 14.749(7) | 9.740(1) |
| c (Å) | 13.621(2) | 12.757(1) |
| ß (deg) | 98.28(2) | |
| V (Å3) | 1603.5(9) | 1939.0(4) |
| Z | 2 | 4 |
| dcalcd (mg m−3) | 1.498 | 1.406 |
| cryst size (mm) | 0.30 × 0.30 × 0.25 | 0.38 × 0.22 × 0.06 |
| abs. coeff. (mm−1) | 1.115 | 0.807 |
| 2θ max (deg) | 49.94 | 49.90 |
| transmission range | 1.0 − 0.8954 | 0.9532 − 0.7492 |
| no. of reflns collected | 3018 | 6650 |
| no. of ind. reflns | 2807 | 3398 |
| no. of obsd reflns [I > 2σ(I)] | 1974 | 2508 |
| no. of variables | 190 | 239 |
| R1 (wR2)b [I > 2σ(I)] | 0.0593 (0.1565) | 0.0388 (0.0706) |
| goodness of fit (F2) | 1.041 | 0.981 |
| diff. peaks (e− Å−3) | 0.119, −0.701 | 0.268, −0.212 |
See Experimental Section for additional data collection, reduction, and structure solution and refinement details.
R1 = Σ|| Fo| − |Fc||/Σ| Fo|; wR2 = [Σ[w(Fo2 − Fc2)2]]1/2 where w = 1/σ2(Fo2) + (aP)2 + bP.
X-Band EPR Spectroscopy
Samples for EPR experiments were prepared by dissolving LFe(N3)2 in methanol (32 mM final concentration) and were immediately frozen in liquid N2. EPR spectra were collected on a Bruker ESP 300E spectrometer equipped with an Oxford ESR 900 continuous-flow liquid helium cryostat and an Oxford ITC4 temperature controller. The spectra were obtained at 4.6 K using the following instrument settings: frequency = 9.36 GHz, microwave power = 0.4 mW, gain = 1.25 × 10−3, modulation amplitude = 9.5 G, conversion time = 163.84 ms, time constant = 10.24 ms, sweep width = 3000 G, and resolution = 1024 points. The spectrum presented in this paper represents the average of seven scans. EPR spectral simulations were carried out using the WinEPR program (Bruker BioSpin).
Low-Temperature Abs, MCD, and VTVH MCD Spectroscopies
Low-temperature Abs and MCD spectra were collected using a CD spectropolarimeter (Jasco J-715) in conjunction with a superconducting magnetocryostat (Oxford Instruments SM4-8T). VTVH MCD data were obtained by measuring the signal intensity as a function of the magnetic field at 2, 4, 8, and 15 K. CD contributions to the MCD data were removed by taking the difference between data measured with the magnetic field applied parallel and antiparallel to the light propagation axis. All low-temperature data were collected on a solid-state mull sample that was prepared by grinding approximately 4 mg of solid LFe(N3)2 with polydimethylsiloxane. The extinction coefficients (ε) for the low-temperature Abs data were estimated from a comparison to the room-temperature solution Abs spectrum. The MCD intensity (Δε) was calculated using the estimated “effective” concentration of the mull sample from the low-temperature Abs data.
RR Spectroscopy
Samples for RR experiments were prepared by grinding a 1:1 ratio of LFe(N3)2 and Na2SO4 in the presence of an excess of KBr. RR spectra were obtained by using Ar+ (Coherent I-305) and Kr+ (Coherent I-90) ion lasers. All spectra were collected with ~20 mW of laser power at the sample using a ~135° backscattering arrangement. The scattered light was dispersed using a triple monochromator (Acton Research, equipped with 300, 1200, and 2400 grooves/mm gratings) and analyzed with a deep-depletion, back-thinned CCD detector (Princeton Instruments Spec X: 100BR). RR excitation profile data were obtained by averaging three separate data sets and were quantified using the 984 cm−1 scattering peak of Na2SO4 that was added to the sample as an internal standard.
Normal Coordinate Analysis
A normal coordinate analysis (NCA) was performed on both the crystal-structure and DFT geometry-optimized coordinates for the diazide–Fe3+ fragment of LFe(N3)2 using the Wilson FG matrix method.17 The analysis was carried out using the General Vibrational Analysis System program package (QCPE program 576) developed by McIntosh and Peterson.18
DFT Calculations
Spin-unrestricted (S = 5/2) DFT geometry optimizations of a complete model of LFe(N3)2 were performed using the Amsterdam density functional (ADF) 2003.01 software package19–22 and ORCA 2.223 developed by Dr. Frank Neese (University of Bonn, Germany). In each case, the input geometry was based on the crystal-structure coordinates of LFe(N3)2. The ADF geometry optimization was carried out using uncontracted triple-ζ Slater-type orbitals with a single set of polarization functions (ADF basis set IV), an integration constant of 3.0, and the Vosko, Wilk, and Nusair local density approximation,24 along with the nonlocal gradient corrections of Becke25 and Perdew.26 The core orbitals were frozen through 1s (O, C, and N) and 2p (Fe). Two additional geometry optimizations were performed in ORCA 2.2, one using Becke’s three-parameter hybrid functional27,28 for exchange and the correlation functional of Lee, Yang, and Parr (B3LYP)29 and the second employing the Vosko, Wilk, and Nusair local density approximation24 along with the nonlocal gradient corrections of Becke25 and Perdew.26 The SV(P) (Ahlrichs polarized split valence) basis30 and SV/C auxiliary basis31 were used for all atoms except Fe, for which the TZVP (Ahlrichs polarized triple-ζ valence)32 basis was employed.
Calculation of Ground- and Excited-State Properties
Semiempirical INDO/S-CI and TD DFT calculations were also performed using the ORCA 2.2 software package. INDO/S-CI calculations employed the model of Zerner and co-workers,33,34 the valence shell ionization potentials and Slater–Condon parameters listed by Bacon and Zerner,35 and the standard interaction factors fpσpσ = 1.266 and fpπpπ = 0.585. Restricted open-shell Hartree–Fock self-consistent field calculations were tightly converged on the sextet (S = 5/2) ground state, which served as the reference state for configuration interaction (CI) calculations. Ground-state properties were computed by including single electron excitations among the 39 highest-energy doubly occupied molecular orbitals (MOs), the five singly occupied MOs, and the 21 lowest-energy virtual MOs along with double electron excitations between the 25 highest-energy doubly occupied MOs, the five singly occupied MOs, and the nine lowest-energy virtual MOs for the sextet states. Additionally, single electron excitations among the five singly occupied MOs were considered for the quartet states. Larger active spaces did not yield significant changes to the calculated parameters.
Electronic transition energies and intensities were computed using the TD-DFT method36–38 within the Tamm–Dancoff approximation39,40 as implemented in ORCA, employing the same basis sets as those used for the geometry optimizations described above and the one-parameter hybrid functional PBE0/G.41 This functional was used because it yielded the best agreement with our experimental data; however, similar results were obtained in TD-DFT calculations with the BP and B3LYP functionals. A total of 50 excited states were calculated within an energy range of ±3 hartree of the highest occupied molecular orbital–lowest unoccupied molecular orbital gap. Isosurface plots of the MOs and electron difference density maps (EDDMs) were generated using the gOpenMol program with isodensity values of 0.06 au and 0.04 au, respectively.42,43
Vibrational frequencies, as well as infrared (IR) and Raman spectra, were also calculated using the ORCA 2.2 software package. In these calculations, the nonlocal gradient corrections of Becke25 and Perdew26 and the Vosko, Wilk, and Nusair local density approximation24 were used together with the basis sets described above for the TD-DFT computations.
Results and Analysis
A. Synthesis and Crystal-Structure Data
The sterically hindered, carboxylic acid pendant triazacyclononane derivative HL was prepared by a method that differs from that described previously by Pecoraro and co-workers.44 In the present work, the ligand precursor 1,4-diisopropyl-1,4,7-triazacyclononane was alkylated with t-butylbromoacetate to provide a synthetic intermediate bearing a pendant t-butyl ester group (Scheme 1),14 which was readily hydrolyzed by HBr in acetone to yield HL·2HBr as a colorless crystalline solid. This ligand, prepared in 85% overall yield from 1,4-diisopropyl-1,4,7-triazacyclononane, was characterized by spectroscopic methods, and its structure and composition were confirmed by X-ray crystallography.45
Scheme 1.
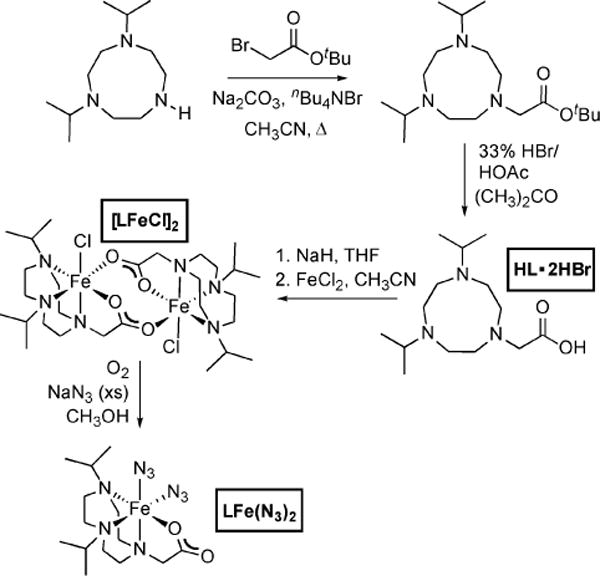
To introduce Fe2+ into this ligand framework, the protonated ligand HL · 2HBr was deprotonated by reaction with excess NaH in THF, followed by reaction of “NaL” (not characterized) with anhydrous FeCl2 in CH3CN. This reaction yielded the iron(II) complex [LFeCl]2 as colorless block crystals in 64% overall yield. The X-ray crystal structure of this complex (Figure 3, top) reveals a dimeric complex in which two distorted octahedral Fe2+ ions are bridged by two pendant carboxylate groups that link the two iron centers in a syn–anti bridging mode. The resulting eight-membered ring that incorporates the two iron centers has a long Fe⋯Fe distance of 5.284(1) Å.
Figure 3.
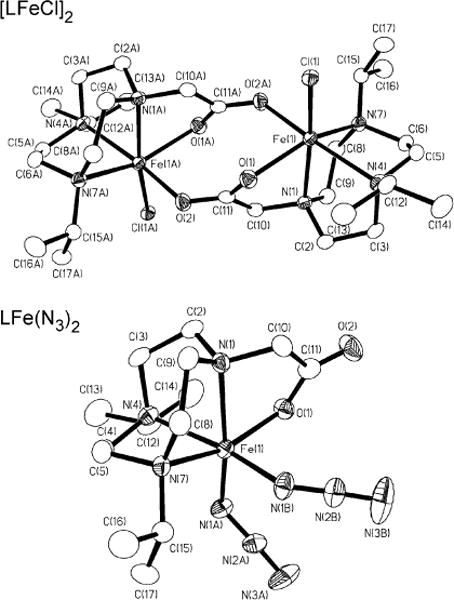
Thermal ellipsoid representation (35% probability boundaries) of the X-ray crystal structures of [LFeCl]2 and LFe(N3)2. Top: Significant interatomic distances (Å) and angles (deg) of [LFeCl]2: Fe1–O1, 2.200(4); Fe1–O2a, 2.175(4); Fe1–Cl1, 2.372(2); Fe1–N1, 2.232(4); Fe1–N4, 2.320(4); Fe1–N7, 2.270(5); C11–O1, 1.267(7); C11–O2, 1.257(7); Fe1⋯Fe1a, 5.284(1); O2a–Fe1–O1, 86.8(2); O1–Fe1–N4, 103.4(2); N4–Fe1–N7, 80.0(2); N7–Fe1–O2a, 85.4(2); C11–Fe1–O2a, 93.6(1); Cl1–Fe1–N7, 114.9(1); Cl1–Fe1–N4, 97.3(1); Cl1–Fe1–O1, 93.8(1); N1–Fe1–O1, 73.3(2); N1–Fe1–N4, 77.7(2); N1–Fe1–N7, 79.2(2); N1–Fe1–O2a, 94.5(2); N1–Fe1–Cl1, 164.4(1); O1–C11–O2a, 124.1(6). Bottom: Significant interatomic distances (Å) and angles (deg) of LFe(N3)2: Fe1–O1, 1.998(3); Fe1–N1a, 1.981(4); Fe1–N1b, 1.999(3); Fe1–N1, 2.187(3); Fe1–N4, 2.283(3); Fe1–N7, 2.238(3); N1b–Fe1–O1, 90.3(1); O1–Fe1–N4, 103.7(1); N4–Fe1–N7, 80.5(1); N7–Fe1–N1b, 84.3(1); N1–Fe1–N1b, 99.4(1); N1–Fe1–O1, 76.9(2); N1–Fe1–N4, 78.4(1); N1–Fe1–N7, 79.5(1); N1a–Fe1–N1b, 97.1(1); N1a–Fe1–O1, 95.5(1); N1a–Fe1–N4, 87.7(1); N1a–Fe1–N7, 109.8(2); N1–Fe1–N1a, 161.8(1); Fe1–N1a–N2a, 121.4(3); Fe1–N1b–N2b, 131.2(3); N1a–N2a–N3a, 177.4(5); N1b–N2b–N3b, 176.7(5).
While solutions of [LFeCl]2 are not particularly air-sensitive, the reaction of [LFeCl]2 with O2 in the presence of excess NaN3 rapidly provided an intensely colored redorange solution, from which red crystals of LFe(N3)2 were isolated in 40% yield. The X-ray crystal structure of this mononuclear complex (Figure 3, bottom) reveals a distorted octahedral Fe3+ center featuring a mutually cis triad of two azide ligands and the macrocyclic ligand’s pendant carboxylate group. The Fe–ligand bond lengths exhibit the contraction that is expected upon oxidation of the metal center from +2 in [LFeCl]2 (average Fe–O = 2.188 Å; average Fe–NTACN = 2.274 Å) to +3 in LFe(N3)2 (Fe–O = 1.988 Å; average Fe–NTACN = 2.236 Å). Each of the azide ligands binds to the Fe3+ center in a bent fashion, with Fe–N–N2 bond angles of 121.4(3)°and 131.2(3)°.
B. Spectroscopy
B.1. X-Band EPR Data
The X-band EPR spectrum of LFe(N3)2 in a frozen methanol solution at 4.6 K exhibits two features at geff ≈ 4.3 and 9.8 (Figure 4, top), characteristic of a high-spin d5 complex possessing nearly rhombic symmetry.46,47 This spectrum could be simulated reasonably well using the zero-field splitting (ZFS) parameters of D = 1.0 cm−1 and E/D = 0.32 (Figure 4, bottom). The highly rhombic EPR spectrum of LFe(N3)2 reflects the similar donor strength of the three anionic ligands located in the fac position of this complex (Figure 2), which also rotates the principal axes of the D tensor away from the metal–ligand bond vectors as revealed by INDO/S-CI computations (vide infra).
Figure 4.
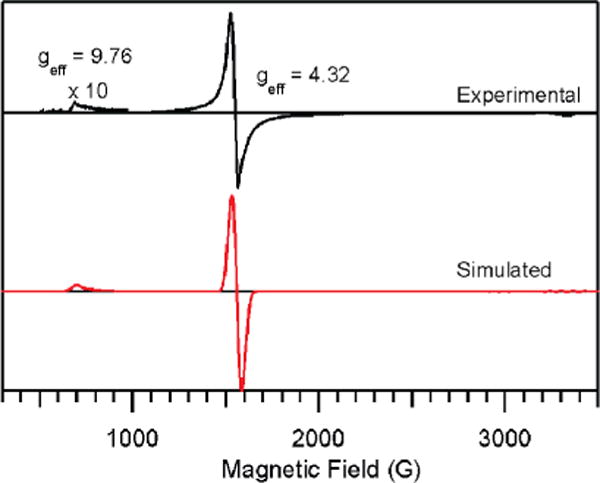
Top: Experimental X-band EPR spectrum of a frozen methanol solution of LFe(N3)2 at 4.6 K. Bottom: Simulated spectrum, obtained with D = 1.0 cm−1 and E/D = 0.32.
B.2. Low-Temperature Abs and MCD data
Abs spectra of LFe(N3)2 were collected both at room temperature (solution spectrum, Figure S1, Supporting Information) and at 4.5 K (solid-state mull spectrum, Figure 5). Both spectra are qualitatively similar, indicating that the crystallographically determined molecular structure of this complex is preserved in solution. In the 4.5 K Abs spectrum (Figure 5, top), two broad features are discernible, one centered at 21 500 cm−1 (ε ≈ 4000 M−1 cm−1) and a more intense one with a maximum at ~30 300 cm−1 (ε ≈ 7400 M−1 cm−1). On the basis of their large intensities, these features can be assigned as ligand-to-metal charge transfer (LMCT) transitions.
Figure 5.
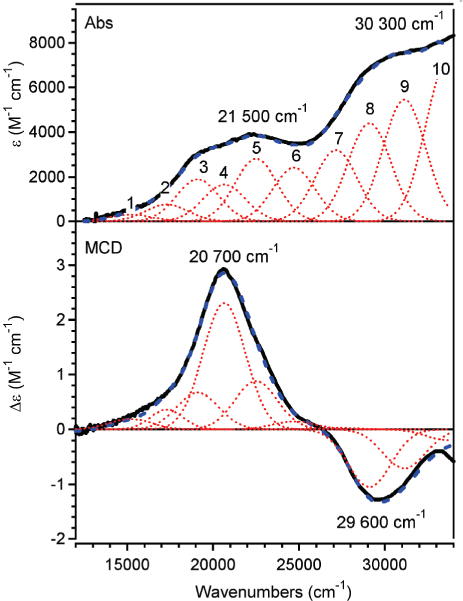
Abs (top) and MCD (bottom) spectra at 4.5 K of a solid-state mull sample of LFe(N3)2. Individual Gaussian bands (numbered 1–10) are shown as red, dotted lines and the simulated spectra are shown as blue, dashed lines.
To resolve the individual LMCT transitions contributing to the Abs spectrum, MCD spectroscopy was used. As shown in Figure 5 (bottom), the MCD spectrum of LFe(N3)2 is dominated by two oppositely signed bands centered at 20 700 cm−1 and at 29 600 cm−1, both of which exhibit temperature-dependent C-term behavior, as expected for this paramagnetic species (Figure S2, Supporting Information). By iteratively fitting the 4.5 K Abs and MCD spectra with the lowest acceptable number of Gaussian bands of constant width, the energies of the individual LMCT transitions could be determined (Table 2 and Figure 5). Good agreement between the simulated and experimental spectra over the entire 15 000–34 000 cm−1 range was achieved by using a total of 10 Gaussian bands.
Table 2.
| band | energy (cm−1) | ε (M−1 cm−1) | f × 103b |
|---|---|---|---|
| 1 | 15200 | 300 | 3.3 |
| 2 | 17300 | 760 | 8.5 |
| 3 | 19100 | 1900 | 21 |
| 4 | 20650 | 1660 | 19 |
| 5 | 22500 | 2790 | 31 |
| 6 | 24700 | 2400 | 27 |
| 7 | 27150 | 3190 | 36 |
| 8 | 29100 | 4410 | 49 |
| 9 | 31130 | 5470 | 61 |
| 10 | 33600 | 7060 | 79 |
Because only LMCT transitions are expected to contribute significantly to the Abs and MCD spectra of LFe(N3)2, the same full-width-at-half-maximum of 2426 cm−1 (which falls within the typical range for this type of transition) was used for all Gaussian bands.
Oscillator strengths, f.
By performing VTVH MCD saturation experiments, in which the MCD signal intensity is measured as a function of applied magnetic field at several fixed temperatures,48 additional insight was obtained into the ground-state properties as well as the LMCT transition polarizations of LFe(N3)2. VTVH MCD data collected at 20 661 cm−1 (Figure 6) exhibit significant nesting behavior, characteristic of an S > 1/2 transition metal complex. Fits of the VTVH MCD data were performed by systematically varying the ZFS parameters and using the three transition dipole moment products (Mij) as adjustable parameters. For each set of D and E/D values, the goodness of fit was assessed by the χ2 value, which corresponds to the sum of the squares of the differences between the experimental and predicted data.49 Acceptable fits were obtained for ZFS parameters in the range of −0.5 < D < 1.0 cm−1 and E/D > 0.1. All fits indicated that the LMCT transition at 20 661 cm−1 is polarized primarily along an axis that roughly bisects the two Fe–azide bond vectors (corresponding to the x axis of the INDO/S-CI computed D tensor in Figure 2). Hence, on the basis of our VTVH MCD data analysis, the prominent Abs feature at 20 661 cm−1 is assigned as an N3− → Fe3+ CT transition with contributions from both azide ligands.
Figure 6.
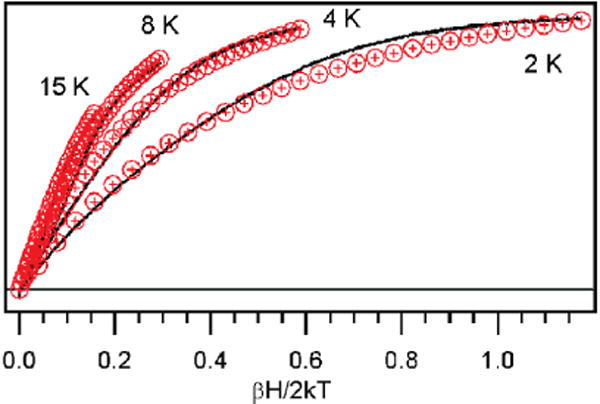
Experimental VTVH MCD data (black lines) of LFe(N3)2 collected at 20 661 cm−1 and 2, 4, 8, and 15 K and simulated data (black circles) obtained with D = 1.0 cm−1 and E/D = 0.32.
B.3. RR Spectroscopy
In the RR spectrum of LFe(N3)2 obtained with 17 606 cm−1 (568 nm) laser excitation (Figure 7 and Table 3), two pairs of features can be discerned at 363 and 403 cm−1 and at 2047 and 2071 cm−1. On the basis of their frequencies, we attribute these features to the Fe–N(azide) (νFe–N3) and antisymmetric intra-azide (νas(N3−)) stretching modes, respectively, associated with the two different azide ligands.50 In support of these assignments, both pairs of RR features shift to lower frequency upon 14N → 15N isotopic labeling of one of the terminal nitrogen atoms of each azide ligand (Figure 7, insets). Although the RR spectrum of LFe(15NN2)2 has contributions from four different isotopologues, the vibrational features are too broad to allow for the individual components to be resolved.
Figure 7.
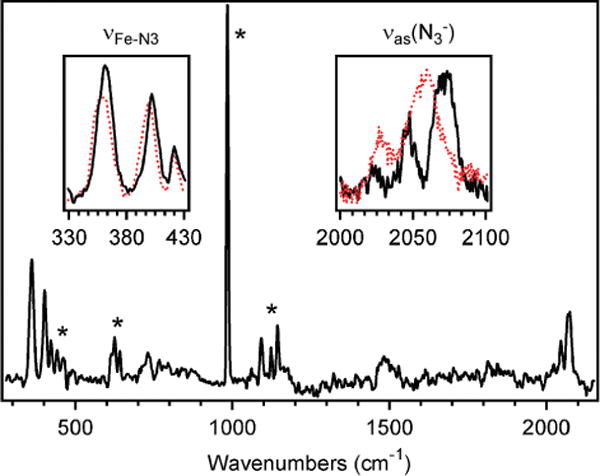
RR spectrum at 77 K of a solid-state sample of LFe(N3)2 obtained with 17 606 cm−1 (568 nm) laser excitation. Peaks associated with Na2SO4, which was added as an internal standard, are designated by an asterisk (*). The insets are expanded views of the νFe–N3 and νas(N3−) features of LFe(N3)2 and LFe(15NN2)2 (solid black and dotted red lines, respectively). All data were taken using 20 mW laser power at the sample.
Table 3.
RR Peak Positions (in cm−1) for LFe(N3)2 and LFe(15NN2)2
| species | νFe–N3 | νas(N3−) |
|---|---|---|
| LFe(N3)2 | 363, 403 | 2047, 2071 |
| LFe(15NN2)2a | 355, 398 | 2028, 2057 |
Each feature has contributions from four different isotopologues.
To obtain further insight into the nature of the LMCT transitions that dominate the Abs spectrum of LFe(N3)2, RR spectra were collected over a range of different laser excitation wavelengths. These experiments revealed that the νFe–N3 stretching modes at 363 and 403 cm−1 display larger relative enhancement for excitation below and above 20 500 cm−1, respectively (Figure 8). Note that, even though for laser excitation in the higher-energy region, particularly above 22 000 cm−1, the absolute RR peak intensities are likely underestimated due to photodegradation of the sample, the relative intensities can still be compared in this region because a CCD camera was used for data collection. The fact that both νFe–N3 stretching modes are resonance-enhanced in the 15 000–22 000 cm−1 range indicates that the broad Abs feature centered at 21 500 cm−1 has contributions from LMCT transitions involving both azide ligands. This result is consistent with the transition polarization obtained from our VTVH MCD data analysis presented above and suggests that strong electronic coupling exists between the two azide ligands.
Figure 8.
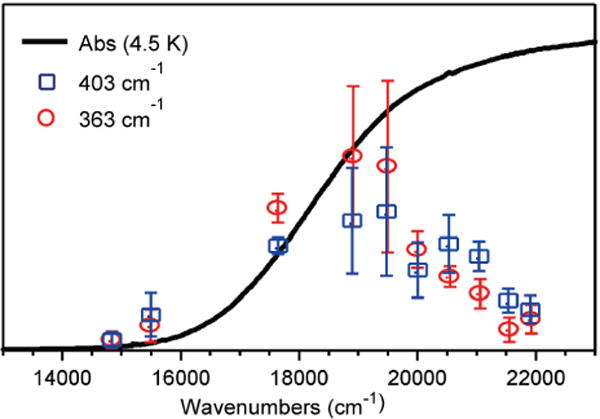
RR excitation profiles of LFe(N3)2 collected at 77 K for the νFe–N3 stretching modes at 363 and 403 cm−1 (red circles and blue boxes, respectively) shown with error bars representing the standard deviation. The 4.5 K solid-state Abs spectrum is also shown for comparison (black line).
C. Computations
Electronic structure calculations were used to assist in the interpretation of the spectroscopic data and to develop a quantitative bonding description for LFe(N3)2. For the majority of these calculations, a model derived from the crystal-structure coordinates was used. However, to obtain a model of LFe(N3)2 suitable for a frequency calculation, the experimental structure was used as the starting point for two separate geometry optimizations that employed either pure (BP) or hybrid (B3LYP) DFT exchange-correlation functionals to ensure that our calculations were not functional-dependent. As shown in Table 4, the salient features observed in the crystal structure are preserved in both geometry-optimized models. In particular, the Fe–N(azide) bond is consistently shorter for azide1 than for azide2, and the Fe–N–N bond angle involving azide1, α(Fe–azide1), remains smaller than α(Fe–azide2). The only notable deviations from the crystal structure data are a minor shortening of the Fe–N(azide) and Fe–O bonds (by <0.03 and 0.05 Å, respectively) along with a significant lengthening of the other Fe–N bonds (by up to 0.17 Å). Additionally, the difference between the two Fe–N−N bond angles, α(Fe–azide2) − α(Fe–azide1), is ~50% smaller in the geometry-optimized models than in the crystal structure. Despite these differences, the computed ground-state and excited-state properties were found to be similar for all three models (see the Supporting Information for a complete summary of the computational results). The computational results presented below were obtained using the crystal-structure coordinates, with the exception of the vibrational frequencies that were computed for the BP optimized model.
Table 4.
Bond Lengths (Å) and Bond Angles (deg) for LFe(N3)2 as Obtained by X-ray Crystallography and DFT Geometry Optimizations
| crystal structure | DFT/BP | DFT/B3LYP | |
|---|---|---|---|
| Bond Lengths | |||
| Fe–O | 2.00 | 1.98 | 1.96 |
| Fe–N(azide1) | 1.98 | 1.96 | 1.96 |
| Fe–N(azide2) | 2.00 | 1.97 | 1.97 |
| Fe–N(trans carboxylate) | 2.24 | 2.37 | 2.37 |
| Fe–N(trans azide1) | 2.19 | 2.31 | 2.32 |
| Fe–N(trans azide2) | 2.28 | 2.44 | 2.45 |
| Bond Angles | |||
| α(Fe–azide1) | 121 | 123 | 123 |
| α(Fe–azide2) | 131 | 128 | 129 |
| α(azide1−Fe–azide2) | 97 | 102 | 101 |
D. Ground-State Properties
D.1. Normal Coordinate Analysis
A NCA was carried out for LFe(N3)2 to assign the 14N → 15N isotopically sensitive features observed in the corresponding RR spectrum (Figure 7) and to determine the relevant force constants. To minimize the number of adjustable parameters, this analysis was restricted to the [Fe(N3)2]+ fragment using the metric parameters provided by the X-ray crystal structure, and only the six Fe–N and N−N stretching motions were considered. The corresponding force constants (i.e., six parameters) were determined by fitting the NCA-predicted frequencies to those observed experimentally for the two sets of νFe–N3 and νas(N3−) vibrational modes (four observables). In this fitting procedure, initial estimates for the Fe–N(azide) and intra-azide force constants were based on values reported for similar complexes.13,51
The fitted Fe–N(azide) force constants, kFe–N, of 1.275 and 1.170 mdyne/Å for azide1 and azide2, respectively (Table 5), lie in the range of kFe–N values reported for similar species.13,51 Moreover, these values are consistent with the structural parameters obtained by X-ray crystallography, as the Fe–N(azide1) bond is shorter by 0.02 Å than the Fe–N(azide2) bond (Table 4). Similarly, the two intra-azide1 force constants, kN−N, are larger than the corresponding intra-azide2 force constants, also in agreement with our X-ray crystallographic data. Hence, it is reasonable to use the NCA results for assigning the 403 and 2071 cm−1 vibrational features of LFe(N3)2 to the νFe–N3 and νas(N3−) stretches, respectively, associated with azide1 and the 363 and 2047 cm−1 features to νFe–N3 and νas(N3−), respectively, associated with azide2 (Table 5).
Table 5.
Experimental Frequencies, NCA-Predicted Frequencies and Force Constants (mdyne/Å), and DFT-Computeda Vibrational Frequencies for LFe(N3)2 and LFe(15NN2)2 for All Normal Modes Associated with the Two Azide Ligands (Frequencies Are Given in cm−1)
| exptl frequencies
|
NCA frequencies and force constants
|
DFT computed frequencies
|
|||||
|---|---|---|---|---|---|---|---|
| normal mode | Fe(N3)2+ | Fe(15NN2)2+ | Fe(N3)2+ | Fe(15NN2)2+ | force constants | LFe(N3)2 | LFe(15NN2)(N3)b |
| Azide1 | |||||||
| νFe–N3 | 403 | 398 | 403 | 394 | kFe–N = 1.275 | 405 | 397, 405 |
| νs(N3−) | 1201 | 1180 | kN−N = 11.06, | 1277 | 1269, 1277 | ||
| νas(N3−) | 2071 | 2057 | 2071 | 2061 | 12.45c | 2080 | 2078, 2078 |
| Azide2 | |||||||
| νFe–N3 | 363 | 355 | 363 | 355 | kFe–N = 1.170 | 374 | 370, 374 |
| νs(N3−) | 1192 | 1171 | kN−N = 10.95, | 1303 | 1295, 1303 | ||
| νas(N3−) | 2047 | 2028 | 2043 | 2033 | 11.95c | 2063 | 2060, 2061 |
From a DFT computation on the geometry-optimized model obtained with the BP functional.
The first and second columns list the computed νFe–N3 stretching frequencies for two different isotopologues, the first having 15N adjacent to Fe and the second possessing a terminal 15N.
Intra-azide N−N force constants are given in the order adjacent, terminal.
D.2. Frequency Calculation
To corroborate the NCA-based RR assignments of the vibrational features for LFe(N3)2, a frequency calculation was performed on the DFT geometry-optimized model obtained using the BP functional. As shown in Table 5, the DFT-computed frequencies agree well with our experimental data, correctly predicting the frequency of the νFe–N3 mode to be lower for azide2 than for azide1. Additionally, two vibrational modes are predicted at 2063 and 2080 cm−1 that correspond to the in-phase and out-of-phase motions of the two antisymmetric intra-azide stretches (note that both azides contribute almost equally to these two modes). To calculate the 14N → 15N isotopic shift of each normal mode, we alternately changed the masses of the four noncentral azide nitrogen atoms from 14 to 15 g/mol and recalculated the vibrational frequencies. In agreement with our NCA-based assignments, the νFe–N3 modes at 405 and 374 cm−1 are predicted to downshift upon terminal 15N labeling of azide1 and azide2, respectively. Due to the strong coupling of the intra-azide vibrations, the computed isotope shifts for the two νas(N3−) modes are similar in magnitude regardless of which azide’s terminal N atoms are labeled.
D.3. Spin-Hamiltonian Parameters
To complement our EPR and VTVH MCD data analyses, the ground-state properties of LFe(N3)2 were computed using semiempirical INDO/S-CI calculations. The calculated ZFS parameters of D = −0.34 cm−1 and E/D = 0.23 are in qualitative agreement with those determined from our EPR data (|D| ≈ 1.0 cm−1 and E/D ≈ 0.33). Hence, it is reasonable to use the INDO/S-CI computed D-tensor orientation for defining the molecular coordinate system of LFe(N3)2. Accordingly, the z axis lies primarily along the Fe–carboxylate bond vector, the x axis roughly bisects the two Fe–N(azide) bond vectors, and the y axis is rotated approximately 15° from the Fe–N(azide1) bond vector (Figure 2).
D.4. Electronic Structure of LFe(N3)2
MO energies and compositions for LFe(N3)2 were calculated using spin-unrestricted DFT computations with the one-parameter hybrid functional PBE0.52 Due to the large spin polarization inherent to high-spin S = 5/2 metal ions, the occupied Fe3+ 3d-based spin-up MOs of LFe(N3)2 are significantly stabilized in energy relative to their unoccupied spin-down counterparts and thus exhibit considerable mixing with ligand-based orbitals. For ease of analysis, only the spin-down MOs will thus be considered here (Table 6). The unoccupied Fe3+ 3d- based spin-down MOs display a pseudo-octahedral splitting pattern, with the 3dxy-, 3dyz-, and 3dxz-based MOs (106b, 107b, and 108b, respectively) at lower energies than the - and -derived MOs (109b and 110b, respectively) (Figure 9). The highest-energy occupied azide-based MOs (101b and 103b–105b) are of azide π-nonbonding, πnb, character and oriented either in-plane (ip) or out-of-plane (op) with respect to the Fe–N(azide) plane. The azide1 πnb-based MOs (101b and 103b) are at lower energy than the azide2 πnb-based MOs (104b and 105b), and in both cases, the azide πnb(ip)-based MOs (101b and 104b for azide1 and azide2, respectively) are stabilized relative to their respective azide πnb(op)-based MOs (103b and 105b, respectively). Note that the stabilization of the azide1 πnb-based MOs relative to the azide2 πnb-based MOs correlates nicely with the difference in the corresponding Fe–N(azide) bond strengths as revealed by our NCA (Table 5).
Table 6.
Energies and Percent Compositions of the Relevant Spin-Down MOs Obtained from a Spin-Unrestricted DFT Calculation Using the X-ray Crystal Structure Coordinates of LFe(N3)2 and the One-Parameter Hybrid Functional PBE0
| Fe 3d orbitals
|
Azide1
|
Azide2
|
|||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MO | E (eV) | main contributor | occ | xy | yz | xz | x2−y2 | z2 | px | py | pz | px | py | pz | |
| 110b | −1.2938 |
|
0 | 8 | 1 | 3 | 5 | 54 | 0 | 6 | 0 | 0 | 0 | 0 | |
| 109b | −1.3684 |
|
0 | 26 | 0 | 2 | 24 | 13 | 0 | 3 | 0 | 6 | 2 | 4 | |
| 108b | −2.3156 | Fe 3dxz | 0 | 1 | 0 | 80 | 1 | 7 | 0 | 0 | 1 | 2 | 0 | 1 | |
| 107b | −2.3665 | Fe 3dyz | 0 | 5 | 62 | 0 | 14 | 1 | 1 | 0 | 6 | 1 | 2 | 0 | |
| 106b | −2.4590 | Fe 3dxy | 0 | 34 | 16 | 0 | 29 | 0 | 1 | 0 | 6 | 1 | 9 | 0 | |
| 105b | −6.2105 | Azide2 πnb(op) | 1 | 1 | 1 | 0 | 5 | 1 | 14 | 7 | 8 | 13 | 44 | 4 | |
| 104b | −6.4888 | Azide2 πnb(ip) | 1 | 2 | 0 | 2 | 2 | 1 | 1 | 2 | 2 | 26 | 9 | 28 | |
| 103b | −6.5349 | Azide1 πnb(op) | 1 | 1 | 6 | 0 | 3 | 0 | 3 | 4 | 44 | 0 | 11 | 1 | |
| 101b | −7.0574 | Azide1 πnb(ip) | 1 | 6 | 1 | 0 | 0 | 1 | 9 | 54 | 0 | 0 | 15 | 0 | |
Figure 9.
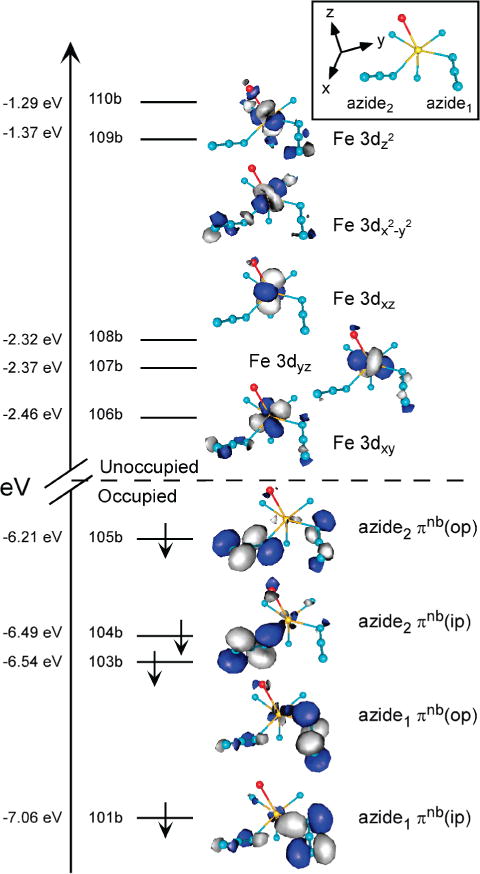
Energy-level diagram showing the occupied azide πnb and unoccupied Fe3+ 3d-based spin-down MOs, as obtained from a spin-unrestricted DFT calculation on the LFe(N3)2 model complex. Boundary surface plots of the corresponding MOs are shown on the right. The molecular coordinate system (which is aligned according to the INDO/S-CI computed D-tensor orientation) is shown in the inset.
E. Excited State Properties
E.1. Time-Dependent DFT Computations and Spectral Assignments
TD-DFT computations employing the PBE0 functional were used to calculate electronic transition energies and intensities for LFe(N3)2 (Table 7), to develop specific assignments of the dominant Abs features observed experimentally, and to obtain further insight into the electronic structure of this species. As shown in Figure 10, the dominant features in the experimental Abs spectrum are reasonably well reproduced by the TD-DFT computation, which predicts two clusters of bands centered at 21 000 and ~31 000 cm−1. In agreement with our RR excitation profile data (Figure 8), the low-energy Abs feature in the computed spectrum arises from azide πnb → Fe3+ 3d “ ”’-type CT transitions (bands 2–5) and azide πnb(op) → Fe3+ 3d “eg”-type CT transitions (bands 6 and 7). The higher-energy Abs features are attributed to carboxylate → Fe3+ 3d “ ”-type CT transitions (bands 8 and 9) and an azide1 πnb(ip) → Fe3+ 3d “eg”-type CT transition (band 10).
Table 7.
Calculated and Experimental Transition Energies (cm−1), Oscillator Strengths f × 103, and Band Assignments for LFe(N3)2
| banda | experimentalb | calculatedb | band assignments | |
|---|---|---|---|---|
| 1 | 15200 (3.3) | |||
| 2 | 17300 (8.5) | 17534 (2.2) | azide2 πnb(op) → Fe3+ 3dxz | |
| 17992 (6.5) | azide2 πnb(op) → Fe3+ 3dxy | |||
| 3 | 19100 (21) | 20349 (2.4) | azide2 πnb(ip) → Fe3+ 3dyz | |
| 20630 (27) | azide2 πnb(ip) → Fe3+ 3dxz | |||
| 4 | 20650 (19) | 21 280 (22) | azide1 πnb(op) → Fe3+ 3dxy | |
| 5 | 22500 (31) | 23088 (1.0) | azide1 πnb(ip) → Fe3+ 3dxy | |
| 24202 (2.0) | azide1 πnb(ip) → Fe3+ 3dyz | |||
| 6 | 24700 (27) | 24879 (1.0) |
|
|
| 25297 (1.0) | ||||
| 25393 (4.9) | ||||
| 25411 (1.3) | ||||
| 7 | 27 150 (36) | 27138 (3.0) |
|
|
| 27785 (11) | ||||
| 28905 (1.8) | ||||
| 8 | 29100 (49) | 29586 (1.4) | O → Fe3+ 3dxz | |
| 30106 (4.4) | ||||
| 30530 (27) | ||||
| 9 | 31130 (61) | 31379 (32) | O → Fe3+ 3dxy | |
| 32537 (41) | ||||
| 10 | 33600 (79) | 33559 (20) |
|
Band numbers refer to the experimental Abs spectrum in Figure 10.
Oscillator strengths, f × 103, are given in parentheses for each transition.
Figure 10.
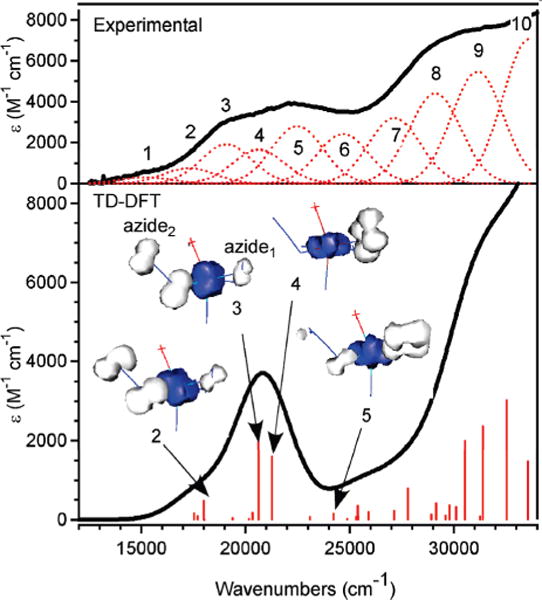
Experimental (top) and TD-DFT calculated (bottom) Abs spectra of LFe(N3)2. Electron density difference maps (EDDMs) for the dominant LMCT transitions corresponding to Gaussian bands 2–5 in the experimental spectrum are shown above the computed spectrum, where white and blue indicate electron density loss and gain, respectively.
The TD-DFT computational results for LFe(N3)2 reveal that the azide1 πnb → Fe3+ CT transitions (bands 4 and 5) occur at higher energies than the azide2 πnb → Fe3+ CT transitions (bands 2 and 3) and that, in each case, the transitions originating from the azide πnb(ip)-based MO are blue-shifted relative to those involving the azide πnb(op)-based MO (Table 7). These band assignments are corroborated by the corresponding EDDMs, which provide a visual representation of the change in electron density that occurs upon LMCT excitation. The EDDMs for the LMCT transitions associated with bands 2–5 (Figure 10, bottom) indicate that these excitations lead to a simultaneous decrease in electron density on both azide ligands. Thus, the TD-DFT computational results correlate well with our RR excitation profile data (Figure 8), which revealed that (i) the νFe–N3 stretching modes involving azide1 and azide2 are preferentially enhanced by using higher and lower laser excitation energies, respectively, and (ii) both νFe–N3 stretching modes are strongly enhanced upon laser excitation across the entire region of the Abs spectrum comprising bands 2−5 (thus signifying that the donor MOs involved in these transitions contain orbital character from both azide ligands). Collectively, our experimental and DFT computational results provide strong evidence that the azide1 πnb-based MOs are stabilized relative to those associated with azide2 (Table 6), thereby indicating that the Fe–N(azide1) bond is stronger than the Fe–N(azide2) bond.
E.2. Excited-State Distortions
To gain further insight into the nature of the LMCT transitions that dominate the Abs spectrum of LFe(N3)2, the excited-state distortions along the Fe–N(azide) and intra-azide bonds were estimated from a simultaneous fit of the Abs and RR excitation profile data using TD Heller theory.53–55 Specifically, the dimensionless excited-state distortions |∆363| and |∆403| along the νFe–N3 normal modes involving azide2 and azide1, respectively, were varied to achieve the best agreement between the simulated and experimental Abs and RR excitation profile data in the region of Gaussian bands 2–4 (Figures 5 and 11), while the relative distortions along the νas(N3−) modes, |∆2047| and |∆2071|, were determined using eq 2. In this expression, In and Ik are the relative intensities, ∆n and ∆k are the dimensionless distortions, and ωn and ωk are the frequencies associated with normal modes n and k, corresponding to νas(N3−) and νFe–N3, respectively. It should be noted that the RR excitation profiles of the features at 2047 and 2071 cm−1 roughly follow those of the 363 and 403 cm−1 modes, indicating that self-absorption was negligible and thus warranting the use of eq 2.
| (2) |
Figure 11.
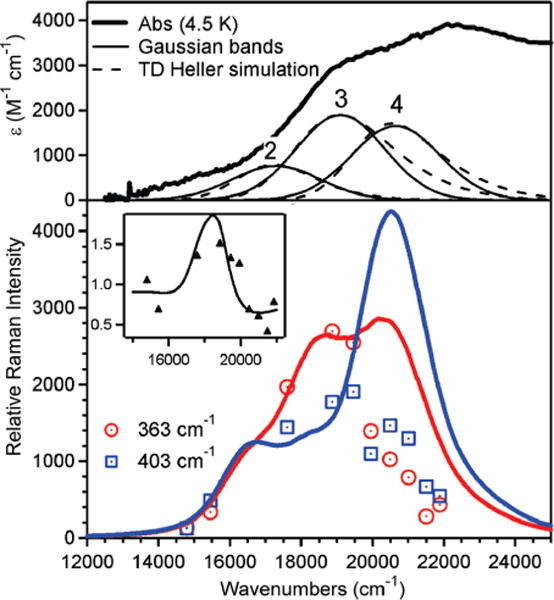
Experimental and simulated Abs and RR excitation profile data for LFe(N3)2 (see Table 8 for a summary of the parameters used in the simulations). Top: Experimental Abs spectrum at 4.5 K (thick solid line), Gaussian bands (thin solid lines) from Figure 5, and simulated Abs bands (dashed lines). Bottom: Experimental RR excitation profiles for the 363 and 403 cm–1 modes (red circles and blue boxes, respectively) along with the simulated RR profiles (red and blue lines for the 363 and 403 cm–1 modes, respectively). The inset shows the intensity ratio of the 363 and 403 cm–1 modes, where the experimental and simulated ratios are represented by solid triangles and a continuous line, respectively.
Due to photodecomposition of the sample in RR experiments employing laser excitation energies >20 000 cm−1, the dimensionless distortions in this region were obtained by fitting the ratio |∆363|/|∆403| to the experimental RR profiles (inset of Figure 11) while the Abs data were used for determining the magnitudes of the ∆n values (Figure 11, top). A comparison of the experimental and simulated Abs and RR data is provided in Figure 11, and the parameters obtained from this fitting procedure are summarized in Table 8. Taking into account that the RR excitation profiles above 20 000 cm−1 are skewed by sample photodegradation, the agreement between the experimental and simulated data is satisfactory.
Table 8.
Fit Parameters Obtained from TD Heller Analysis of Abs and RR Excitation Profile Data for LFe(N3)2
| parameter | band 2 | band 3 | band 4 |
|---|---|---|---|
| Δ363 | 1.92 | 3.02 | 1.61 |
| Δ403 | 2.12 | 2.20 | 2.51 |
| Δ2047 | 0.19 | 0.42 | 0.35 |
| Δ2071 | 0.36 | 0.43 | 0.49 |
| E00 (cm–1)a | 15700 | 16400 | 18800 |
| μrel2b | 1.00 | 2.74 | 1.99 |
E00 is the energy difference between the minima of the ground state and excited state potential energy surfaces.
μrel are the relative transition dipole moments for the transitions associated with bands 2–4.
From the fitted excited-state distortion parameters, the internal coordinate changes, ∆ri, upon electron excitation can be calculated using eq 3, where Li,n is the ith element of the mass-weighted eigenvector, Ln, for the nth normal mode (as obtained from the NCA).56
| (3) |
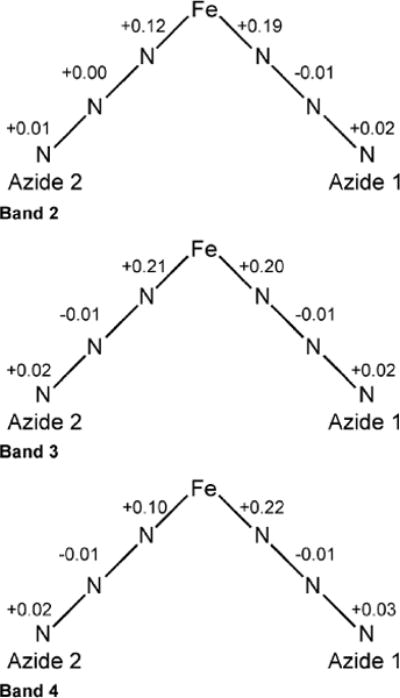
The results from this excited-state distortion analysis are summarized in Scheme 2. Consistent with our assignment of bands 2–4 to LMCT transitions causing a net loss of electron density from an azide πnb-based MO (Figure 10, bottom), the intra-azide excited-state distortions are significantly smaller than those along the Fe–N(azide) bonds. For the excited-state corresponding to band 4, the TD Heller analysis yields a larger elongation of the Fe–N(azide1) bond than of the Fe–N(azide2) bond (Scheme 2), lending further support to our assignment of this band to an azide1 πnb(op) → Fe3+ 3d CT transition. In the case of band 3, the TD Heller analysis indicates that the corresponding excited state undergoes similar distortions along both Fe–N(azide) bonds, which agrees well with our assignment of this band to an azide2 πnb(ip) → Fe3+ 3d CT transition possessing significant azide1 πnb(op) → Fe3+ 3d CT character (Figure 10). Lastly, while our TD-DFT computational results suggest that an azide2 πnb(op) → Fe3+ 3d CT transition is the dominant contributor to band 2, the corresponding excited state actually undergoes a slightly larger distortion along the Fe–N(azide1) bond than along the Fe–N(azide2) bond due, presumably, to the strong electronic coupling between azide1 and azide2.
Scheme 2.
Discussion
Because azide possesses the same charge and similar frontier orbitals as the superoxide radical anion, this substrate analogue has been used extensively for investigating the molecular mechanism of FeSOD. Previous spectroscopic and crystallographic studies revealed that the reaction of Fe3+SOD with azide results in the formation of a yellow species in which azide occupies the putative substrate-binding site that is located between the two equatorial His ligands (Figure 1, right).6,12,57 A particularly puzzling feature of this N3−Fe3+SOD complex is that, when [N3−]/[FeSOD] > 2 and the protein concentration is low, it converts to a pink species upon freezing. Initially, this color change was interpreted as indicating that the protein undergoes a conformational change at low temperatures, so as to allow the binding of a second azide ion to the Fe3+ center via displacement of one of the five original protein−ligands,12 presumably the axially coordinated solvent molecule. By analogy, it would thus be anticipated that two substrate molecules could simultaneously bind to the active site under turnover conditions.4,5,58–63
However, other evidence suggests that only one azide can actually bind to the Fe3+ center in Fe3+SOD. First, a single azide ligand (Fe–N(azide) bond length of 2.12 Å) is observed in the X-ray crystal structure of N3−Fe3+SOD (Figure 1, right), even though a high concentration of azide (100 mM NaN3) was used in the corresponding mother liquor solution.6 Second, in a more recent combined spectroscopic and computational study of N3−Fe3+SOD, we have shown that relatively subtle perturbations to the Fe–N(azide) bonding interaction, such as a variation in the Fe–N(azide) bond angle, could also cause the observed color change from yellow to pink.13 Moreover, our RR and MCD spectroscopic data obtained for the pink N3−Fe3+SOD species did not provide any evidence for the presence of two distinct azide ligands. Nevertheless, because an analogous spectroscopic/ computational study of a structurally characterized diazide−Fe3+ complex had not previously been completed, it remained unknown whether RR and MCD spectroscopic techniques provide sufficiently sensitive probes for identifying individual azide ligands in N3−Fe3+SOD species. The primary goals of the present study, therefore, were (i) to establish if the presence of two structurally distinct azide ligands in an Fe3+ complex can indeed be unveiled using spectroscopic tools and (ii) to use the results obtained for a structurally characterized diazide−Fe3+ complex as the basis for an unambiguous determination of the number of azide ligands in the pink N3−Fe3+SOD species.
Spectroscopic Evidence for the Presence of Two Azide Ligands in LFe(N3)2
As mentioned above, a major goal of this study was to determine whether RR and MCD spectroscopic data provide an adequate basis for determining the number of azide ligands in a given Fe3+ complex. Both the Abs and MCD spectra of LFe(N3)2 (Figure 5) exhibit rather broad, poorly resolved features that are not necessarily characteristic of either a mono- or diazide Fe3+ species. This finding can be understood on the basis of our RR excitation profile data (Figure 8) and TD-DFT computational results (Figure 10), which reveal that the electronic transitions producing the dominant Abs and MCD spectral features involve MOs that contain significant contributions from both azide ligands. Importantly, however, two sets of νFe–N3 and νas(N3−) vibrational features are clearly discernible in the RR spectrum of LFe(N3)2 (Figure 7), each of which can be correlated with one of the two distinct azide ligands within the framework of a NCA (Table 5). Consequently, two sets of νFe–N3 and νas(N3−) features should be observed in the RR spectra of N3−Fe3+SOD species possessing two symmetry-inequivalent azide ligands (which would necessarily be the case given the low symmetry of the enzyme active site). In further support of this hypothesis, the IR spectrum of cis-[Fe3+(cyclam)(N3)2]ClO4, a complex with two structurally distinct azide ligands, exhibits two well-resolved features in the region of the νas(N3−) mode, at 2047 and 2078 cm−1.64
Nature of Fe–N(azide) Bonds in LFe(N3)2
Consistent with the conclusions drawn from our recent study of the yellow N3−Fe3+SOD complex,13 the spectroscopic and computational results obtained here for LFe(N3)2 indicate that the azide πnb(ip) and Fe3+ 3d orbitals develop a relatively strong σ-bonding interaction, the magnitude of which decreases as the Fe–N(azide) bond angle increases. Specifically, the increase in the Fe–N(azide) bond angle from 123.7° to 132.8° for azide1 and azide2, respectively, correlates with a decrease in both the NCA-determined force constant kFe–N, from 1.28 to 1.17 mdyne/Å, and the DFT-computed Mayer bond order, from 0.76 to 0.74. The difference in the Fe–N(azide) σ-bonding interactions and, hence, bond strengths for azide1 and azide2 is also evident from the X-ray crystal structure of LFe(N3)2, which shows that the two Fe–N(azide) bond distances differ by 0.02 Å (1.98 and 2.00 Å, respectively, see Table 4).
As a further consequence of the different strengths of the two Fe–N(azide) σ-bonding interactions in LFe(N3)2, our DFT calculations predict that the azide1 πnb-based MOs are stabilized by ~0.5 eV relative to those derived from azide2 (see Table 6 and Figure 9). It is this difference in relative MO energies that causes the azide1- and azide2-based LMCT transitions to occur at different energies. Specifically, both our TD-DFT computational results and RR excitation profile data indicate that the azide2 πnb → Fe3+ 3d “t2g”-type CT transitions are shifted to lower energy relative to those originating from the azide1 πnb-based MOs (Table 7 and Figure 8). It should be noted, however, that these transitions are significantly mixed due to the strong electronic coupling between the two azide ligands, as revealed by our VTVH MCD and RR spectroscopic data as well as our DFT computational results.
Implications for Pink N3−Fe3+SOD Species
The experimental and computational results obtained for LFe(N3)2 provide an excellent framework within which to interpret the spectroscopic data reported previously for the yellow and pink N3−Fe3+SOD complexes. Importantly, having shown for LFe(N3)2 that the presence of two symmetry-inequivalent azide ligands can be readily discerned using RR spectroscopy, the fact that the published RR data for both N3−Fe3+SOD complexes exhibit only one set of νFe–N3 and νas(N3−) features provides compelling evidence that in each species a single azide ligand is bound to the Fe3+ center.13 Our data are thus consistent with the proposal that the temperature-induced conversion from the yellow to the pink N3−Fe3+SOD complex is caused by the binding of an azide ion to the putative outer-sphere substrate prebinding site, which could perturb the Fe–N(azide) bonding interaction involving the azide ligand that is already present in the yellow species via the conserved active-site hydrogen-bond network. Independent evidence for the existence of an outer-sphere prebinding site in FeSOD has been obtained in azide-binding studies of Fe3+SOD at room temperature5,65,66 as well as NO-binding studies of Fe2+SOD at cryogenic temperatures.67
As discussed above, Abs and MCD spectroscopic data alone do not permit an unambiguous determination of the number of azide ligands in the LFe(N3)2 complex due to the strong mixing between the azide1 and azide2 πnb → Fe3+ CT transitions. It is thus not surprising that the MCD spectra of the model complex and the yellow and pink N3−Fe3+SOD species are quite similar, each displaying a positively signed intense feature in the visible spectral region due to azide πnb → Fe3+ 3d CT transitions.13 Although the peak position of this feature exhibits a significant red-shift from the yellow and pink N3−Fe3+SOD species (νmax ≈ 22 240 and 22 570 cm−1, respectively) to the LFe(N3)2 model complex (νmax ≈ 20 661 cm−1), a similar red-shift has been previously reported for the singly azide-bound Q69E N3−Fe3+SOD mutant (νmax ≈ 20 150 cm−1).13 This finding suggests that the position of the dominant azide πnb → Fe3+ 3d CT feature in the Abs and MCD spectra correlates with the strength of the Fe–N(azide) bonding interaction(s) rather than the number of azide ligands.62
It is interesting to note that azide was also originally believed to be capable of displacing one of the five original active-site ligands upon coordination to the Mn3+ center of the closely related enzyme MnSOD.68,69 In this case, variable-temperature Abs spectroscopic studies definitely showed that the N3−Mn3+SOD active site displays thermochromism, converting from a six-coordinate azide adduct at cryogenic temperatures to a five-coordinate species at room temperature (for Escherichia coli MnSOD, this transition occurs at 225 K). However, a more recent spectroscopic/ computational study of N3−Mn3+SOD revealed that it is, in fact, the azide ligand that dissociates from the Mn3+ ion and instead binds to the second-sphere Tyr34 residue above the transition temperature.70 Consequently, neither in FeSOD nor in MnSOD does azide actually displace any of the original active-site ligands, which implies that (i) the coordinated solvent and the Asp ligand are likely to play a crucial role in tuning the redox potential of the active site metal ion in the key reaction intermediates and (ii) a single substrate molecule can coordinate to the metal ion under turnover conditions.4,5,58–63
Supplementary Material
Acknowledgments
T.C.B. thanks the NIH (GM 64631) for financial support. J.A.H. acknowledges support from the NSF (CHE-0615479).
Footnotes
Supporting Information Available: Cartesian coordinates of crystal-structure and DFT geometry-optimized LFe(N3)2 models, INDO/S-CI calculated ZFS parameters for all models of LFe(N3)2, DFT predicted MO energies and compositions for LFe(N3)2 models, TD-DFT calculated electronic excitation energies, Abs and MCD data of LFe(N3)2 collected at 4.5 K, and analysis of VTVH MCD data collected at 20 661 cm−1. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Choudhury SB, Lee JW, Davidson G, Yim YI, Bose K, Sharma ML, Kang YM, Cabelli DE, Maroney MJ. Biochemistry. 1999;38:3744–3752. doi: 10.1021/bi982537j. [DOI] [PubMed] [Google Scholar]
- 2.Fridovich I. Acc Chem Res. 1972;5:321–326. [Google Scholar]
- 3.McAdam ME, Fox RA, Lavelle F, Fielden EM. Biochem J. 1977;165:81–87. doi: 10.1042/bj1650081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bull C, Niederhoffer EC, Yoshida T, Fee JA. J Am Chem Soc. 1991;113:4069–4076. [Google Scholar]
- 5.Bull C, Fee JA. J Am Chem Soc. 1985;107:3295–3304. [Google Scholar]
- 6.Lah MS, Dixon MM, Pattridge KA, Stallings WC, Fee JA, Ludwig ML. Biochemistry. 1995;34:1646–1660. doi: 10.1021/bi00005a021. [DOI] [PubMed] [Google Scholar]
- 7.Stoddard BL, Howell PL, Ringe D, Petsko GA. Biochemistry. 1990;29:8885–8893. doi: 10.1021/bi00490a002. [DOI] [PubMed] [Google Scholar]
- 8.Stoddard BL, Ringe D, Petsko GA. Protein Eng. 1990;4:113–119. doi: 10.1093/protein/4.2.113. [DOI] [PubMed] [Google Scholar]
- 9.Wagner UG, Pattridge KA, Ludwig ML, Stallings WC, Werber MM, Oefner C, Frolow F, Sussman JL. Protein Sci. 1993;2:814–825. doi: 10.1002/pro.5560020511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cooper JB, McIntyre K, Badasso MO, Wood SP, Zhang Y, Garbe TR, Young D. J Mol Biol. 1995;246:531–544. doi: 10.1006/jmbi.1994.0105. [DOI] [PubMed] [Google Scholar]
- 11.Edwards RA, Baker HM, Whittaker MM, Whittaker JW, Jameson GB, Baker EN. J Biol Inorg Chem. 1998;3:161–171. [Google Scholar]
- 12.Slykhouse TO, Fee JA. J Biol Chem. 1976;251:5472–5477. [PubMed] [Google Scholar]
- 13.Xie J, Yikilmaz E, Miller AF, Brunold TC. J Am Chem Soc. 2002;124:3769–3774. doi: 10.1021/ja016254h. [DOI] [PubMed] [Google Scholar]
- 14.Halfen JA, Tolman WB. Inorg Synth. 1998;32:75–81. [Google Scholar]
- 15.TeXsan for Windows. Vol. 1.02. Molecular Structure Corporation, Inc; The Woodlands, TX: [Google Scholar]
- 16.SHELXTL for Windows NT. Vol. 5.1. Bruker AXS; Madison, WI: [Google Scholar]
- 17.Wilson EB, Jr, Decius JC, Cross PC. Molecular Vibrations, The Theory of Infrared and Raman Vibrational Spectra. McGraw-Hill Book Co: New York; 1955. [Google Scholar]
- 18.McIntosh DF, Peterson MR. General vibrational analysis system, Quantum Chemistry Program Exchange, QCPE 576. University of Toronto; Toronto, Canada: 1988. [Google Scholar]
- 19.Baerends EJ, Ellis DE, Ros P. Chem Phys. 1973;2:41. [Google Scholar]
- 20.Versluis L, Ziegler T. J Chem Phys. 1988;88:322–328. [Google Scholar]
- 21.te Velde G, Baerends EJ. J Comput Phys. 1992;99:84–98. [Google Scholar]
- 22.Guerra CF, Snijders JG, te Velde G, Baerends EJ. Theor Chem Acc. 1998;99:391–403. [Google Scholar]
- 23.Solomon EI, Brunold TC, Davis MI, Kemsley JN, Lee SK, Lehnert N, Neese F, Skulan AJ, Yang YS, Zhou J. Chem Rev. 2000;100:235–349. doi: 10.1021/cr9900275. [DOI] [PubMed] [Google Scholar]
- 24.Vosko SH, Wilk L, Nusair M. Can J Phys. 1980;58:1200. [Google Scholar]
- 25.Becke AD. J Chem Phys. 1986;84:4524–4529. [Google Scholar]
- 26.Perdew JP. Phys Rev B: Condens Matter Mater Phys. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 27.Becke AD. J Chem Phys. 1993;98:1372–1377. [Google Scholar]
- 28.Becke AD. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 29.Lee C, Yang W, Parr RG. Phys Rev B: Condens Matter Mater Phys. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 30.Schäfer A, Horn H, Ahlrichs R. J Chem Phys. 1992;97:2571–2577. [Google Scholar]
- 31.Weigand F, Häser M. Theor Chem Acc. 1997;97:331–340. [Google Scholar]
- 32.Schäfer A, Huber C, Ahlrichs R. J Chem Phys. 1994;100:5829–5835. [Google Scholar]
- 33.Ridley J, Zerner MC. Theor Chem Acc. 1973;32:111. [Google Scholar]
- 34.Zerner MC, Loew GH, Kirchner RF, Mueller-Westerhof UT. J Am Chem Soc. 1980;102:589. [Google Scholar]
- 35.Bacon AD, Zerner MC. Theor Chem Acc. 1979;53:21. [Google Scholar]
- 36.Bauerschmitt R, Ahlrichs R. Chem Phys Lett. 1996;256:454–464. [Google Scholar]
- 37.Casida EM, Jamorski C, Casida KC, Salahub DR. J Chem Phys. 1998;108:4439–4449. [Google Scholar]
- 38.Stratman RE, Scuseria GE, Frisch MJ. J Chem Phys. 1998;109:8218–8224. [Google Scholar]
- 39.Hirata S, Head-Gordon M. Chem Phys Lett. 1999;302:375–382. [Google Scholar]
- 40.Hirata S, Head-Gordon M. Chem Phys Lett. 1999;314:291–299. [Google Scholar]
- 41.Adamo C, Barone V. J Chem Phys. 1999;110:6158–6170. [Google Scholar]
- 42.Laaksonen L. J Mol Graphics. 1992;10:33–34. doi: 10.1016/0263-7855(92)80007-z. [DOI] [PubMed] [Google Scholar]
- 43.Bergman D, Laaksonen L, Laaksonen A. J Mol Graphics Modell. 1997;15:301–306. doi: 10.1016/s1093-3263(98)00003-5. [DOI] [PubMed] [Google Scholar]
- 44.Scarpellini M, Wu AJ, Kampf JW, Pecoraro VL. Inorg Chem. 2005;44:5001–5010. doi: 10.1021/ic050281h. [DOI] [PubMed] [Google Scholar]
- 45.Colorless blocks of HL · 2HBr are monoclinic, P21/n, with a = 12.150(2) Å, b = 12.703(2) Å, c = 13.952(3) Å, b = 115.10(3), V = 1950 0(7) Å3, Z = 4, and 298(2) K. Full-matrix least-squares refinement of 2270 reflections with I > 2(I) against 190 variable parameters yielded residuals R1 = 0.0786 and wR2 = 0.1991.
- 46.Pilbrow JR. Transition ion electron paramagnetic resonance. Clarendon Press; Oxford, U.K.: 1990. [Google Scholar]
- 47.Solomon EI, Lever ABP. Inorganic Electronic Structure and Spectroscopy. Wiley; New York: 1999. [Google Scholar]
- 48.Johnson MJ. In: Physical Methods in Bioinorganic Chemistry: Spectroscopy and Magnetism. Que L Jr, editor. University Science Books; Sausilito, CA: 2000. pp. 233–285. [Google Scholar]
- 49.Neese F, Solomon EI. Inorg Chem. 1999;38:1847–1865. doi: 10.1021/ic981264d. [DOI] [PubMed] [Google Scholar]
- 50.Note that features attributable to the symmetric intra-azide stretching modes (νs(N3−)) would be expected to appear in the 1200–1350 cm−1 range. However, the only discernible features near this range (at ~1100–1150 cm−1) are not isotope-sensitive and arise from the that was used as an internal standard.
- 51.Tsubaki M, Srivastava RB, Yu NT. Biochemistry. 1981;20:946–952. doi: 10.1021/bi00507a047. [DOI] [PubMed] [Google Scholar]
- 52.Similar results were obtained using the B3LYP hybrid functional; see the Supporting Information, Figure S4 and Table S5.
- 53.Zink JI, Shin K-SK. In: Advances in Photochemistry. Volman DH, Hammond GS, Neckers DC, editors. Vol. 16. John Wiley; New York: 1991. pp. 119–214. [Google Scholar]
- 54.Heller EJ. J Chem Phys. 1975;62:1544–1555. [Google Scholar]
- 55.Heller EJ. Acc Chem Res. 1981;14:368–375. [Google Scholar]
- 56.The signs of all ∆n’s were taken as positive on the basis of the following reasoning. Excitation in resonance with the N3− → Fe 3+ CT transitions formally involves promotion of an electron from an azide π-nonbonding-based MO (which is σ-bonding with respect to the Fe–N(azide) bond) to an Fe3+ 3d-based MO that is σ-antibonding with respect to the Fe–N(azide) bond. We would therefore expect a weakening, and thus a lengthening, of the Fe–N(azide) bond in the corresponding excited state. Only positive values of ∆363 and ∆403 yielded this result. For the intra-azide stretches, the bond length changes are expected to be much smaller, as the MO involved in the N3− → Fe3+ CT transitions is formally π-nonbonding. However, for the same reasoning as above, the ∆2047 and ∆2071 values were also taken as positive.
- 57.Tierney DL, Fee JA, Ludwig ML, Penner-Hahn JE. Biochemistry. 1995;34:1661–1668. doi: 10.1021/bi00005a022. [DOI] [PubMed] [Google Scholar]
- 58.Vance CK, Miller AF. J Am Chem Soc. 1998;120:461–467. [Google Scholar]
- 59.Vance CK, Miller AF. Biochemistry. 2001;40:13079–13087. doi: 10.1021/bi0113317. [DOI] [PubMed] [Google Scholar]
- 60.Yikilmaz E, Xie J, Brunold TC, Miller AF. J Am Chem Soc. 2002;124:3482–3483. doi: 10.1021/ja011220v. [DOI] [PubMed] [Google Scholar]
- 61.Schwartz AL, Yikilmaz E, Vance CK, Vathyam S, Miller AF. J Inorg Biochem. 2000;80:247–256. doi: 10.1016/s0162-0134(00)00086-6. [DOI] [PubMed] [Google Scholar]
- 62.Grove LE, Xie J, Yikilmaz E, Karapetyan A, Miller AF, Brunold TC. Inorg Chem. 2008 doi: 10.1021/ic702414m. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Grove LE, Xie J, Yikilmaz E, Miller AF, Brunold TC. Inorg Chem. 2008 doi: 10.1021/ic702412y. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Meyer K, Bill E, Mienert B, Weyhermuller T, Wieghardt K. J Am Chem Soc. 1999;121:4859–4876. [Google Scholar]
- 65.Benovic J, Tillman T, Cudd A, Fridovich I. Arch Biochem Biophys. 1983;221:329–332. doi: 10.1016/0003-9861(83)90151-0. [DOI] [PubMed] [Google Scholar]
- 66.Fee JA, McClune GJ, Lees AC, Zidovetzki R, Pecht I. Isr J Chem. 1981;21:54–58. [Google Scholar]
- 67.Jackson TA, Yikilmaz E, Miller AF, Brunold TC. J Am Chem Soc. 2003;125:8348–8363. doi: 10.1021/ja029523s. [DOI] [PubMed] [Google Scholar]
- 68.Whittaker MM, Whittaker JW. Biochemistry. 1996;35:6762–6770. doi: 10.1021/bi960088m. [DOI] [PubMed] [Google Scholar]
- 69.Whittaker MM, Whittaker JW. J Biol Inorg Chem. 1997;2:667–671. [Google Scholar]
- 70.Jackson TA, Karapetian A, Miller AF, Brunold TC. J Am Chem Soc. 2004;126:12477–12491. doi: 10.1021/ja0482583. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


