Logical Analysis of Data in Structure-Activity Investigation of Polymeric Gene Delivery

Abstract

To date semi-empirical or surrogate modeling has demonstrated great success in the prediction of the biologically relevant properties of polymeric materials. For the first time, a correlation between the chemical structures of poly(β-amino esters) and their efficiency in transfecting DNA was established using the novel technique of logical analysis of data (LAD). Linear combination and explicit representation models were introduced and compared in the framework of the present study. The most successful regression model yielded satisfactory agreement between the predicted and experimentally measured values of transfection efficiency (Pearson correlation coefficient, 0.77; mean absolute error, 3.83). It was shown that detailed analysis of the rules provided by the LAD algorithm offered practical utility to a polymer chemist in the design of new biomaterials.

Introduction

Logical analysis of data (LAD) has been recently utilized to build data mining/machine learning models, which were successfully applied to the development of diagnostic and prognostic systems in medicine as well as to the focused design of polymeric biomaterials.^[1] The medical applications of LAD vary from differential diagnosis of selected types of pneumonias and prognosis in ovarian and breast cancer research^[2] to risk assessment among cardiac patients.^[3] In the field of biomaterials design, combinatorial computational models can be of utmost importance for prediction of the cellular response to implanted medical devices.^[4] In particular, LAD was applied to examine cell growth on the surface of polymers comprising a library of 112 polyarylates.^[5] LAD identified patterns of physicochemical parameters, adequately classified each polymer as high, medium, or low cell growth substratum, and established correlations between cellular response and polymer properties that are uniquely relevant to the specific polymer chemistry.

Since LAD already has a well-established reputation in solving of a large number of data analysis problems, it would be invaluable to test its applicability to more sophisticated tasks in the design of novel biomaterials. During the past fifteen years, gene therapy has attracted considerable attention in the field of chemistry, medicine, pharmaceutical sciences, and biotechnology due to its great potential in treating various types of genetic disorders and cancer.^[6] Despite the significant promise and advances in gene therapy research, results of numerous clinical trials have yet to attain a compelling record of success. As an alternative to the viral gene delivery systems, recent studies suggest that nonviral gene delivery systems may hold advantages due to their low immunogenecity, the absence of endogenous virus recombination, reproducibility and lower costs.^[7] Additional benefits include unlimited DNA size for packaging and the possibility of chemical modifications for specific tissue or cell targeting. However, the efficiency of nonviral delivery systems is noticeably lower than that of viral vectors.

Among known categories of nonviral gene delivery (e.g., naked DNA delivery and lipid-based delivery), polymer-based delivery has attracted considerable attention.^[6] Self-assembled complexes of DNA and synthetic polymers termed “polyplexes”^[8] are stabilized by electrostatic interactions between the anionic phosphate groups of the DNA and the cationic groups of the polymer.^[8] Diverse types of polycationic polymers have been studied extensively, including linear, branched, dendritic, and block or graft copolymer architectures.

Recent advances in cationic polymer-based gene delivery include incorporation of biodegradability into the polymer design to decrease toxicity, and the development of combinatorial approaches to synthesis and screening of these materials.^[9] The backbone of most nondegradable polymeric gene carriers contains a carbon–carbon or amide bond, which do not degrade under physiological conditions. Such carriers cannot be completely removed by physiological clearance systems, which leads to their accumulation in cells and therefore, increased cytotoxicity.^[6] In contrast, biodegradable polycations contain a degradable region represented by a hydrolysable ester linkage. As a consequence, they exhibit lower cytotoxicity and higher (or comparable) transfection efficiency relative to nondegradable polycations such as poly(l-lysine) or polyethyleneimine (PLL and PEI, respectively). It has been shown in several publications by Langer and co-workers^[9-11] that poly(β-amino esters) are a particularly promising biodegradable class of polymers due to their high in vitro transfection efficiency and relatively straightforward synthesis. This group of authors pioneered^[12] the solution-phase parallel synthesis and characterization of a large, structurally diverse library of degradable poly(β-amino esters). The most promising candidates in terms of transfection efficiency were successfully identified by high-throughput screening of all polymers in the library.^[9]

Kohn and co-workers^[13-16] have demonstrated in several publications that quantitative structure-activity relationship (QSAR) data modeling, described as surrogate modeling, is a useful tool for prediction of both protein adsorption on, and cellular response to, the surface of polymeric materials. Moreover, surrogate modeling may serve as a guide for the rational design of candidate materials for further investigation and focused applications. The purpose of the present study was to assess the utility of logical analysis of data (LAD), a novel surrogate modeling tool for prediction of polymeric DNA carriers using the gene delivery data obtained by Anderson et al.^[9]

Methods and Models

Gene Delivery by Poly(β-amino esters)

As described in detail by Anderson et al.,^[10] transfection assays were performed in vitro with all polymers at six different polymer/DNA ratios to investigate the influence of the ratio itself, molecular weight, and chain end group on the transfection efficiency of each polymer.^[9] COS-7 cells were used in conjunction with plasmid DNA encoding the firefly luciferase reporter gene (pCMV-Luc). Overall 12 000 transfection experiments were carried out by means of high-throughput methods.^[9] The specific dataset used in this work was reported in Supplemental Table 2 of ref.^[9]

LAD Methodology

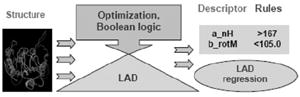
LAD was originally developed by Hammer and coauthors.^[17,18] This method uses combinatorics, optimization, and Boolean logic to detect structural information present in datasets. Classification is the major application of LAD, directly comparable and competitive with other machine-learning methods. One of the distinctive features of LAD is its ability to explain the classification of new observations in a way consistent with previous classifications archived by the algorithm.^[19] The other specific feature of LAD is the recognition of hidden logical patterns that distinguish observations in one class from the all other observations and that govern the phenomena of interest. LAD identifies patterns expressed in terms of input variables or predictors (e.g., molecular descriptors) and renders the prediction in terms of positive or negative outcomes. The LAD approach was developed such that it is equally amenable to datasets contain numerical or binary variables.^[19]

The conventional LAD methodology, primarily designed for the detection of patterns and classification, has been recently extended to deal with regression problems.^[20] The resulting algorithm can be viewed as the iterative construction of a set of binary predictors. The form of the binary predictors resulting from the LAD regression function may suggest relations between the original variables that may not be apparent at first glance. The additional set of generated binary predictors is unattainable by most regression approaches, where numerical products of two or three of the original variables are used as additional predictors. The present study is an initial attempt to apply this methodology to the nontrivial problem of polymeric gene delivery. All LAD results reported in this paper were obtained using the RUTCOR software.^b

Cross-Validation

The results presented in this paper were cross-validated by means of the k-folding method of statistics. The total set of observations was randomly partitioned into k (using k = 10) approximately equal subsets. One of these subsets was defined as the test set. The model was built using the remaining k − 1 subsets, which formed the training set, and then tested on the k-th subset. This process was repeated k times by changing a subset taken as a test set. The quality of the method was gauged by the calculated average accuracy for the entire iterative process.^[1]

Selection of Modeling Variables

The multitude of experimental variables introduced in ref.^[9] and Supplemental Table 1, 3, and 4 (e.g., polymer molecular weight, particle size, and complex surface charge) represents a serious challenge for surrogate modeling even in the case of high quality experimental measurements. Therefore, to avoid excessive complexity of our models and to make the consequent data analysis feasible, we restricted ourselves to structure-related variables such as stoichiometric ratio, the nature of end groups and the number and type of molecular descriptors.

Alternative Predictive Techniques

Several alternative predictive techniques were employed in the present study for comparison with LAD to assess its superiority in solving the nontrivial problem of gene delivery prediction. These were neural networks represented by polynomial neural network (PNN)^[21,22] and artificial neural network (ANN), support vector regression (SVR), and linear regression (LR) method.^[23] The ANN used in this study is represented by feed-forward network with one hidden layer. The software included in the Weka package^[23] was used for LR, SVR, and ANN methods. The custom-made simulation package was adopted to build PNN models.^[21,22]

Computational Models

Accurate prediction of physical and biorelevant polymer properties based on their chemical structure still remains a challenge for quantitative structure-activity relationship (QSAR) approaches. Conventional QSAR approaches use various modes of regression such as simple linear regression and neural networks, which require input of fixed-size numerical vectors usually represented by molecular descriptors. Descriptors can be derived from experimental properties or computed from chemical structure. In the present study only conformation independent, two-dimensional (2D) descriptors were utilized for the sake of computational efficiency and due to their previous success in building surrogate models for prediction of bioresponse.^[13-15]

Two modeling approaches hereafter referred to as linear combination and explicit representation models were proposed to provide a quantification of polymers from the poly(β-amino esters) library.^[9]

Linear Combination Model

Each polymer was represented by its composite monomers (i.e., amino and diacrylate monomers) and their stoichiometric ratio. For example, diacrylate monomer C and amino monomer 32 were denoted as C32-1.0, C32-1.20, etc. A set of molecular descriptors for each of these polymers was generated as follows.

First, the set of descriptors was calculated for the individual amino and diacrylate monomers. These descriptors were denoted as

$${\mathrm{Damino}}_i\mathrm{and}{\mathrm{Ddiacrylate}}_i\mathrm{for}i=1\dots n,$$ (1)

where n is the total number of descriptors. For example, descriptors for the polymer C32 were defined as

$$\mathrm{D}{\mathrm{C}}_i\mathrm{and}\mathrm{D}{32}_i\mathrm{for}i=1\dots n.$$ (2)

The stoichiometric ratio was included by means of parameter ν

$$\nu =1/(1+\mathrm{amine}/\mathrm{acrylate})$$ (3)

and the descriptors were computed for each specific polymer at certain amine/acrylate ratio as a linear combination, i.e.,

$$\begin{array}{l}\mathrm{Dpolymer}­\mathrm{amine}/{\mathrm{acrylate}}_i\\ =(1-\nu ){\mathrm{Damino}}_i+\nu {\mathrm{Ddiacrylate}}_i\\ \mathrm{for}i=1\dots n.\end{array}$$ (4)

Thus, descriptors were computed using the Dragon software package^[24] for a total of 30 (18 amino and 12 diacrylate) monomers that comprised 76 polymers listed in Supplemental Table 2.^[9] For the linear combination model, two sets of descriptors were generated. The extended set comprised 472 descriptors, which were organized into 12 groups ranging from constitutional descriptors to Eigenvalue-based indices according to the default classification of the Dragon software. The selected set consisted of 42 empirical descriptors representing the group of molecular properties (the general rational for this type of selection is outlined in the section “Selected descriptor set”).

Explicit Representation Model

For the explicit representation model,68or60(depending on availability and the quality of experimental data) polymers of 10–11 monomers length were built by means of the polymer builder module provided in the MOE modeling package.^[25] The basic structures of poly(β-amino esters) that originated from the conjugate addition of primary or bis(secondary amines) to diacrylates^[10] were computationally reproduced accounting for amine–amine and (for the sake of comparison) amine–diacrylate terminal groups. In this case the extended and selected sets comprised 184 (i.e., the total number of 2D descriptors in MOE package) and 21 descriptors, respectively, where the later set was formed from the entire (i.e., extended) one by focused selection (see the section “Selected descriptor set” for more details).

For both models monomer subunits were sketched using a molecular editor (ISIS/Draw, MDL) and then 2D structures were transferred to MOE and geometry optimized using the MM94 molecular mechanics force field. The optimization procedure was carried out with gradient of 0.05, cutoff of 8, and dielectric constants of 1 and 80 for molecular interior and exterior, respectively. Convergence was achieved on average after 5 000 iteration steps. Finally, the 2D descriptors mentioned above were calculated for the extended and selected sets of the linear combination and explicit representation models by means of the Dragon and MOE programs, respectively. Additionally, all computational models presented here were built for only two stoichiometric ratios: 1:1 and 1.2:1. Since the most successful poly(β-amino esters) in terms of transfection efficiency were C32, JJ28, and C28, identified at these specific compositions, the corresponding datasets contained the largest number of experimental data points and these stoichiometric ratios were the most suitable for both computational models. Results from the computational models are summarized in Table 1. Structure of polymers in sdf format are available on-line as Supporting Information from the journal website.

Table 1.

Characteristics of models and datasets employed in the present study.

Model	Stoichiom. ratio	Number of polymersa)	Number of descriptors	Dataset
Linear combination	1.2:1	76	472	Extended
Linear combination	1.2:1	76	42	Selected
Explicit	1:1	60	21	Selected
Explicit	1.2:1	68	21	Selected
Explicit	1.2:1	68	184	Extended

^a)Number of polymers was selected depending on availability of experimental data.

Results and Discussion

Characterization and Comparison of Predictive Models

The predictive ability of the surrogate regression models obtained from LAD, LR, SVR, and ANN were characterized by calculating the average Pearson correlation coefficient which can vary from −1 to 1,^[26] and the mean absolute error (MAE) between the predicted and actual values of transfection efficiency. The MAE was computed as the average difference in absolute value between the predicted and the actual transfection efficiency of each polymer over the entire dataset. The results obtained by these algorithms for the linear combination and explicit representation computational models built for the extended and selected descriptor sets are shown in Table 2 and 3. Four data sets that differ with respect to model representation, descriptor set, and stoichiometric ratio are presented in these two tables. The results attained for the linear combination model using PNN and LAD are compared in Table 4 To elucidate possible advantages (or disadvantages) of LAD in performing analysis of complex biorelevant data, we included for comparison several regression algorithms that have significantly different biases for comparative assessment of the results obtained for given datasets.

Table 2.

Correlations obtained for linear combination (stoichiometric ratio 1.2:1, 76 polymers) and explicit (stoichiometric ratio 1:1, 60 polymers) models. The selected descriptor sets are shown.

Model	Linear combination		Explicit
Method	Pearson r	MAE	Pearson r	MAE
LAD	0.26	10.30	0.77	3.83
LR	−0.32	13.07	0.01	4.59
SVR	0.32	19.27	−0.04	4.71
ANN	0.30	18.95	−0.15	10.29

Table 3.

Correlations obtained for the explicit representation model (stoichiometric ratio 1.2:1, 68 polymers). The selected and extended descriptor sets are shown.

Dataset	Selected		Extended
Method	Pearson r	MAE	Pearson r	MAE
LAD	0.14	12.87	0.21	9.76
LR	−0.09	14.42	0.37	11.22
SVR	0.06	12.08	0.13	13.97
ANN	0.28	15.26	0.03	23.88

Table 4.

PNN and LAD correlations obtained for the linear combination model (results for 76 polymers are shown).

Method	Stoichiom. ratio	Pearson r		Number of descriptors	Dataset
		Model	X-validation
PNN	1:1	0.53	–	472	Extended
	1.2:1	0.54	–	472	Extended
LAD	1.2:1	0.94	0.22	472	Extended
	1.2:1	0.91	0.26	42	Selected

It is worth mentioning that the Pearson correlation and the MAE criteria, although related, suggest two different ways of interpreting the results in Table 2 and 3. While the MAE criterion tells how close (on average) the predicted values are to the actual transfection efficiency values, the correlation coefficient indicates the degree of linearity of the relationship between the predicted and experimental values of transfection efficiency. Therefore, among the four datasets examined, both datasets shown in Table 2 were identified as the best in terms of average absolute correlation and MAE. Indeed, the absolute average correlation of 0.77 obtained for the explicit model dataset after applying the 10-fold cross-validation is the highest among the other datasets and it is associated with the lowest MAE, which confirms superiority of this particular model representation (see also Figure 1 and 2). It is a common practice in the field of surrogate modeling to prioritize the MAE criterion.^[13] From this perspective the overall statistical performance was better for the explicit representation model than for the linear combination model (see Table 2).

Figure 1.

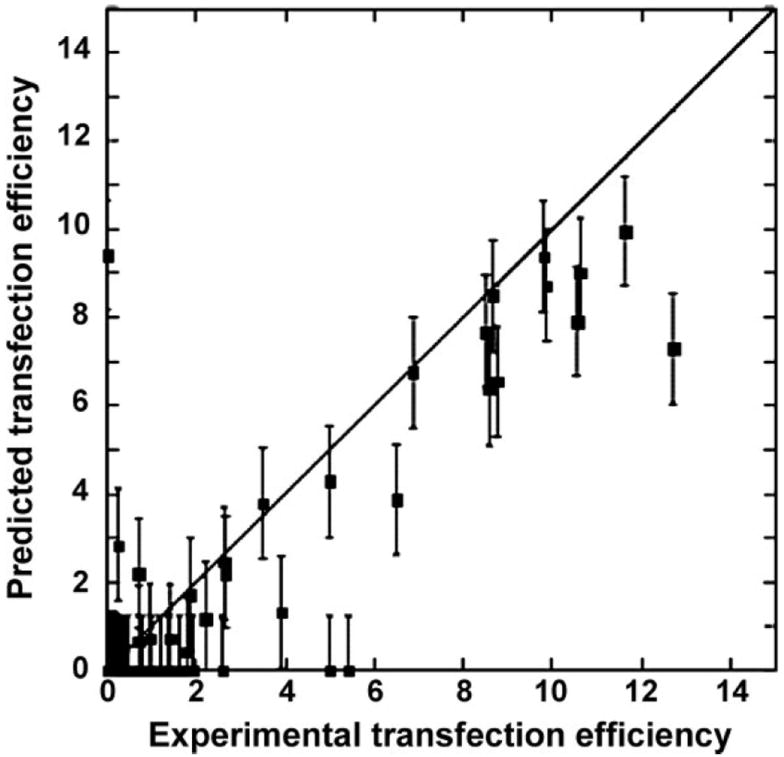
LAD predictions are shown versus experimental results on transfection efficiency for the set of 60 polymers (two polymers with the highest values of transfection efficiency are omitted for the clarity of the graphical image). Error bars represent MAE.

Figure 2.

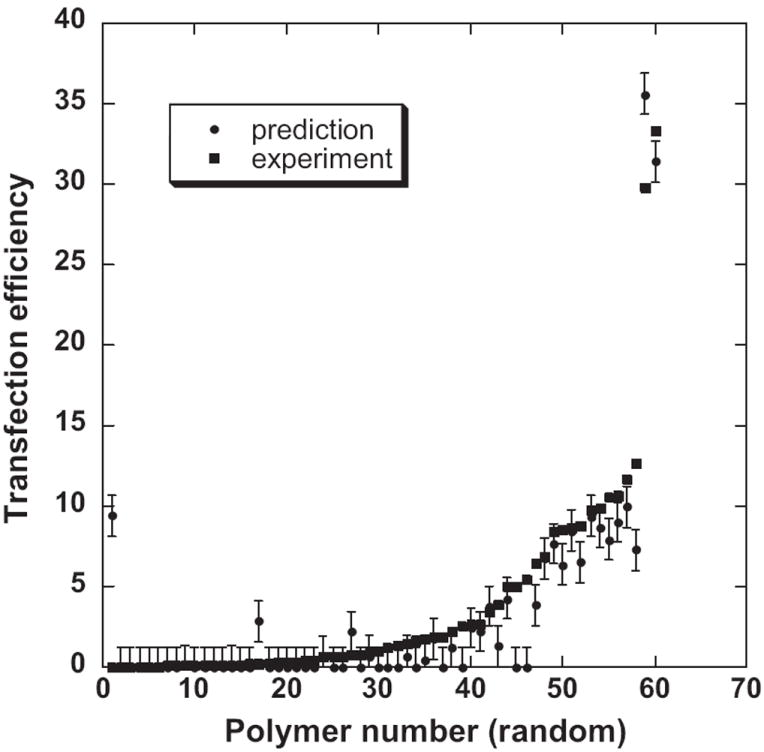
Comparison of predicted and experimental results for the dataset of 60 polymers. Error bars represent MAE.

The absolute average correlation obtained by LAD for the datasets used in conjunction with the linear combination model compare favorably with those obtained using PNN. However, the cross-validation decreases the accuracy of LAD results by about 70% for the linear combination model based on both extended and selected descriptor sets (Table 4).

It needs to be emphasized that a feature selection procedure was employed to improve the performance of linear combination model in the case of the extended descriptor set(s). The feature selection (or rather feature construction) protocol adopted in the LAD regression is completely automatic and guided by the optimization process. The algorithm uses a technique called column generation that allows identifying binary logical predictors that should be added to the set of currently known features in order to improve the quality of the regression function. The issue of variable selection was also addressed in PNN modeling. In the training part of the computational protocol, PNN was constrained to use no more than 5–7 descriptors from the entire pool of 472 descriptors initially included in the linear combination model. As one can see from Table 4, use of the feature selection procedure, however, did not improve the resulting LAD and PNN correlations. All the above demonstrates a weakness of the linear combination model and suggests that the explicit representation model is more advantageous in the case of poly(β-amino esters).

The next question to be addressed is: how does the specific size of a descriptor set and chemical “nature” of the chosen descriptors influence the accuracy of the predictive models? In Table 3 results for the explicit model are compared for (a) the much smaller extended set of descriptors (i.e., 184) and (b) the selected set of geometrical descriptors, which consists of 21 structure and property related quantities. It is somewhat surprising that there was no significant difference in correlation coefficient obtained by LAD, LR, and SVR algorithms for the extended and selected set of descriptors. Noticeable improvement in correlation and MAE was observed only for the ANN algorithm while overall quality of prediction for all four tested algorithms was rather poor. On other hand, the LAD results for the explicit model based on the selected 21 descriptors demonstrated high correlation and very low MAE when stoichiometric ratio of 1:1 was included in the model and the corresponding experimental data set has been employed.

The influence of the chemical composition of poly(β-amino esters) on modeling results requires special consideration. According to experimental findings^[9] the highest transfection efficiency was obtained for polymers C32, JJ28, and C28, which were synthesized at monomer ratios with an excess of the amino components. The highest transfection efficiency for these, the most effective, polymers corresponds to the stoichiometric ratio 1.2:1 (see Supplemental Table 2 of ref.^[9]). These results deviate from the trend reflected in the correlations obtained for the explicit model with the selected descriptor set (see Table 2 and 3): the correlation coefficient is much lower for amino terminated polymers at monomer ratio of 1.2:1 (i.e., 0.14) than for amino- and diacrylate-terminated polymers at stoichiometrically equivalent contribution from both types of monomers (i.e., 0.77). A possible explanation for this deviation can be found in the experimental observations. Anderson et al.^[9] have shown that only polymers with molecular weights above 10 000 Da, but none of the low molecular weight polymers, were able to transfect efficiently. These differences in the size or molecular weight of poly(β-amino esters) were not included in the present computational models and therefore the influence of experimental stoichiometry on transfection efficiency could not be captured.

It is still remains somewhat questionable what key factor is responsible for such a noticeable difference in correlation for two relatively similar datasets. Numerical analysis of experimental data from both 1.2:1 and 1:1 datasets has revealed that the observed inconsistency in correlations can also be related to the quality of experimental data employed in modeling. Relatively high “numerical noise” and the absence of uniformity in the 1.2:1 experimental dataset (so called classification errors) get reflected in significant lowering of the overall accuracy of prediction.

Prediction of Transfection Efficiency by LAD Regression

Results of the LAD prediction of transfection efficiency obtained for the explicit representation model with the selected set of descriptors (stoichiometric ratio 1:1, 60 polymers) are compared with experimentally determined values in Figure 1-3. We recall that due to the small size of experimental data sets, it was not possible to separate a subset of polymers for external validation without significant reduction of the accuracy of prediction. Thus, the k-folding cross-validation approach described in the “Methods” section was adopted to validate the LAD regression.

Figure 3.

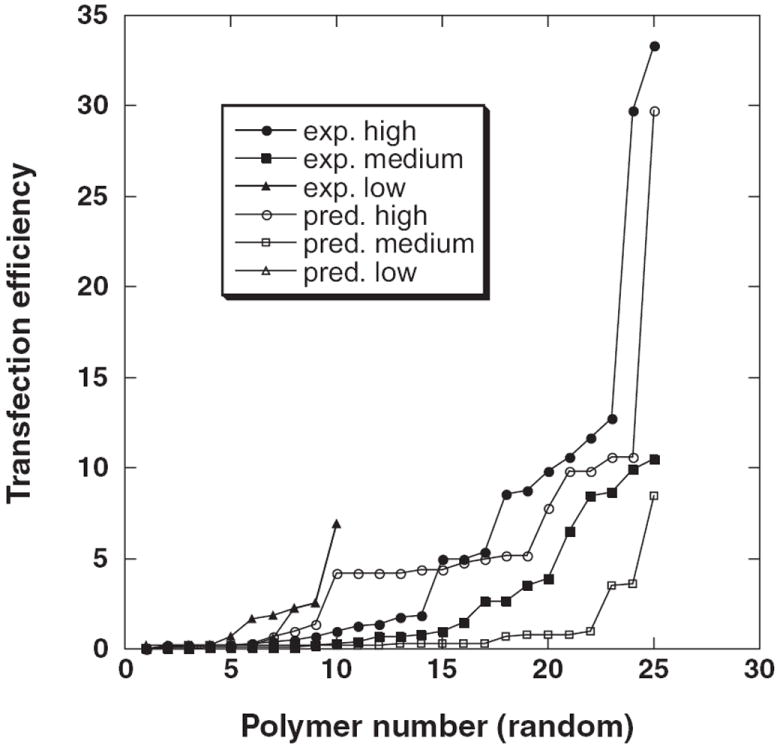
Results of standard 3-means clustering procedure for the dataset of 60 polymers projected in the rule-based 0–1 space.

LAD regression yielded good agreement between the experimental and predicted estimates of bioresponse with average Pearson correlation coefficient r = 0.77 (Figure 1). One can see nearly even distribution of data points along the 45-degree bisector in the regions of medium and high transfection efficiency while a certain tendency for clustering can be observed in the less significant region of low transfection. Anexcellent agreement between actual and predicted values (aside for a few outliers) can be noted in Figure 2, where the error bar corresponds to MAE.

The LAD algorithm adopted in the present work constructs an optimal set of rules in such a way that the least absolute error of a linear regression function is minimized in the associated 0–1 vector space. Once a set of rules has been identified LAD performs mapping of each polymer to 0–1 vector space^[1] that can be regarded as a transformation procedure similar to that implemented by the SVR algorithm.^[27] Projecting the polymers in this rule-based 0–1 space appears to be especially useful because it renders the data amenable to a more accurate analysis. The present study exploited this feature by performing standard 3-means clustering^[28] in the 0–1 representation of polymers. The actual and predicted values of transfection efficiency for the clusters were obtained (Figure 3). The entire set of 60 polymers is represented by three clusters that include the polymers with high, medium, and low transfection efficiency. One can see satisfactory agreement between experimental and predicted values that belong to the clusters with high and low DNA transfection, while predicted values of the medium range cluster are slightly lowered.

From the analysis given above one can see that LAD has the obvious advantage in finding good correlation for the 1:1 dataset compared with the other well-known predictive methodologies due to its ability to handle numerically and phenomenologically challenging datasets. Its success is associated with the exceptional ability of LAD to deal with three of the most common datasets problems, such as classification errors, missing attributes (i.e., experimental values), and small errors in the measurements of numerical attributes.^[19]

Selected Descriptor Set

Conventional machine-learning methods from linear regression to neural networks utilize as inputs fixed-size numerical vectors. Therefore, the chemical substances must be represented by the numerical vectors of the same dimension known as descriptors, which are usually derived by means of different encoding techniques (e.g., group contribution, topological methods,^[29,30] etc.) or obtained experimentally. Computation of descriptor values can vary from trivial (e.g., molecular weight) to complex and time-consuming (quantum chemical properties).

There are several approaches that can be used to select the descriptors, which are inexpensive to compute and which capture the most relevant physical or chemical features of molecular systems or/and the process of interest.^[31] The approach adopted by Landrum et al.^[31] to build predictive models for virtual library of polymer catalysts can be defined as intuitive. The authors limited the descriptor set to descriptors that are presumably important in determining the properties of catalyst or the identity of ligands. Their final descriptor set contained ten descriptors such as electrotopological state indices, connectivity and shape descriptors, as well as surface factor descriptors responsible for the degree of steric crowding. Abramson et al.^[5] applied a similar tactic to identify the most significant descriptors for prediction of cell growth on polymeric biomaterials using LAD models. In this case the authors combined experimentally derived descriptors such as glass transition temperature (T_g) and air–water contact angle (θ) with three new structural descriptors that captured information about the chemical composition of the specific class of polymers (i.e., polyarylates). Correlations between the chemical composition of polyarylates and the selected descriptors were established previously.^[5]

Alternative approaches to the selection of descriptors can be called rational, as successfully employed by Smith et al. in a series of publications devoted to prediction of bioresponse to the surface of biodegradable polymers using ANN and PNN.^[13-15] In these studies, a decision tree algorithm was used to rank descriptors in order of their correlation to fibrinogen adsorption and cell growth data and to select 3–5 descriptors. Including a multitude (i.e., about 800) of descriptors in the networks would have been impractical and even meaningless in view of the problem of data overfitting. It became an essential part of the modeling approach developed by Smith and co-authors to identify a priori descriptors that were relevant to the specific type of bioresponse.

In the present work, we have adopted an approach that can be defined as focused. On the one hand, the challenging nature of gene delivery problem does not allow one to make a reasonably educated guess regarding the correlation of the QSAR descriptors to transfection efficiency. Therefore an intuitive choice in this case is infeasible. On the other hand, the rational approach can provide a set of automatically chosen (even if they are relevant) descriptors that may not allow one to gain desirable and comprehensive insight into relationships between chemical structure of the polymers and their performance in terms of gene delivery. Hence, the descriptors chosen for this case must reflect the structural specificity of the polymers and contain information about their physicochemical characteristics that can be modified, if there is a need, in the process of combinatorial synthesis. The total list of such descriptors includes descriptors from two groups: geometrical descriptors (in the MOE definition – atom and bond counts^[25]) and physical properties (Table 5). Representatives of these descriptor groups encode information about the hydrophilic or hydrophobic nature of polymers, their chain flexibility, number and type of hydrogen bonds, molecular weight and surface area which are of utmost importance for focused polymer design. As discussed in the next section, we have demonstrated how descriptor-based rules of LAD can be used to identify and characterize the most and least successful poly(β-amino esters) in terms of DNA transfection.

Table 5.

Total list of descriptors chosen for the selected descriptor set.

Name	Definitiona)
	Atom and bond counts
a_nH	Number of hydrogen atoms
a_nC	Number of carbon atoms
a_nN	Number of nitrogen atoms
a_nO	Number of oxygen atoms
a_acc	Number of hydrogen bond acceptor atoms
a_don	Number of hydrogen bond donor atoms
a_hyd	Number of hydrophobic atoms
lip_acc	Number of acceptors (i.e., O and N atoms)
lip_don	Number of OH and NH atoms
b_double	Number of double bonds (non aromatic)
b_rotN	Number of rotatable bonds
b_rotR	Fraction of rotatable bonds (with respect to heavy atoms)
	Physical properties
density	Molecular mass density
logP(o/w)	Log of the octanol/water partition coefficient (from linear atom type model)
SlogP	Log of the octanol/water partition coefficient (from atomic contribution model)
mr	Molecular refractivity (from linear atom type model)
SMR	Molecular refractivity (from atomic contribution model)
TPSA	Polar surface area (from group contribution model)
vdw_area	Area of van der Waals surface (in connection table approximation)
vdw_vol	van der Waals volume (in connection table approximation)
Weight	Molecular weight

^a)Definitions in this table correspond to those adopted in MOE simulation package.^[25]

LAD identification and Characterization of Poly(β-amino esters)

The LAD regression (or Pseudo-Boolean regression)^[20] is based on a set of rules. Each rule is described in terms of constraints^[2] on the values of one or two predictors (in our case descriptors). Once a set of rules has been identified, each polymer can be represented as a 0–1 vector, with each entry corresponding to one the rules in the following way: if a rule is satisfied by the polymer, then its corresponding entry is equal to 1, otherwise, it is equal to 0. In this representation, each rule can be defined as a synthetic descriptor, constructed from values of original descriptors. The LAD regression function is given by a sum of the rules where each rule is multiplied by a coefficient. A prediction value for each polymer, which is derived from this LAD function, is a sum of coefficients of the rules that are satisfied by a polymer.

Table 6 summarizes results of application of the LAD regression function for the explicit representation model built for 60 polymers at 1:1 stoichiometric ratio using the selected descriptor set (i.e., the best among all models in its predictive accuracy). In the first column numerical values of the coefficients of the LAD rules were substituted by a general description of the contribution of the rules to transfection efficiency of selected poly(β-amino esters). “Positive” specifies contribution to high transfection and “negative” indicates contribution to low transfection. Each row in Table 6 corresponds to a rule: the second column gives the rule’s definition and the last column (i.e., prevalence) shows the number of polymers satisfying that rule.

Table 6.

Summary of LAD rules for explicit representation model (stoichiometric ratio 1:1, 60 polymers) with the selected descriptor set employed. Significance of contribution to transfection efficiency (TE) is shown in descending order.

Contribution to TE	Rulesa)	Prevalence
Positive	a_nN > 10	5
	a_nH ≤ 167 AND	31
	a_hyd ≤ 95
	vdw_area ≤ 2 240.18	31
	a_nC > 110	17
	SMR > 54.6295	23
	a_nO > 30	19
	a_nH > 167	28
	Weight ≤ 2059.51	34
	a_acc ≤ 30 AND	16
	SMR > 54.6295
	b_rotN > 100.5	29
Negative	SlogP > 6.6284	37
	a_nH ≤ 167 AND	9
	TPSA > 443.39
	Density > 0.714308	39
	TPSA ≤ 443.39	31
	b_double > 12.5	5
	b_rotR > 0.627451	44
	vdw_vol ≤ 2 842.91	34
	mr > 55.9334	25
	vdw_vol ≤ 2 842.91	25
	AND logP(o/w) ≤ 6.9525
	logP(o/w) > 6.9525	29
	a_hyd > 95	21
	a_nH ≤ 167 AND	29
	vdw_vol ≤ 2 842.91
	a_acc ≤ 30	51
	a_nN > 10 AND	2
	b_rotN ≤ 100.5
	lip_acc > 40	13

^a)Numerical values associated with each rule are given for 10 monomers length polymer chains.

The rules in Table 6 can be interpreted as indicators of specific features of polymers that related to a high or low value of transfection efficiency. For example, the first rule defined as “the number of nitrogen atoms is at most 10” is associated with five polymers, namely, AA24, D24, F94, E86, II28, which support high transfection efficiency. A similar positive contribution to the transfection level comes from 31 polymers which satisfy the simultaneous rule: “the number of hydrogen atoms is at least 167” and “the number of hydrophobic atoms is at least 95.” The same approach can be used to identify structural features of the least effective polymers in terms of DNA transfection efficiency.

Alternatively, one can consider the role of a specific descriptor in the rules in which this descriptor participates. For instance, the descriptor SMR appears in two rules of Table 6. In both rules, the large value of SMR (in one of these rules it is combined with a smaller value of the a_acc descriptor) implies a positive contribution to the predicted value. Similarly, small values of the vdw_vol descriptor contribute to low predicted values of transfection efficiency. In the case of the a_hyd descriptor, the trend is inverted: a value of a_hyd above 95 contributes negatively to the predicted value, while a value smaller than or equal to 95, combined with a low value of a_nH, contributes positively to the predicted value of transfection.

LAD analysis also makes use of the so-called incidence matrix of the rules. This matrix shows which polymers are influenced by which rules. Each entry of this matrix is either 1 or 0, depending whether the polymer in that row satisfies the rule in that column or not. Such information allowed us to extract rules that are satisfied by the three best performing polymers reported in ref.,^[9] particularly polymers C32, JJ28, and C28 (see Figure 4). First, the rules were extracted for C32, JJ28, and C28 from datasets corresponding to 1:1 and 1.2:1 stoichiometric ratios. Next, the rules, which exhibit similar trends for both compositions were identified and summarized in Table 7.

Figure 4.

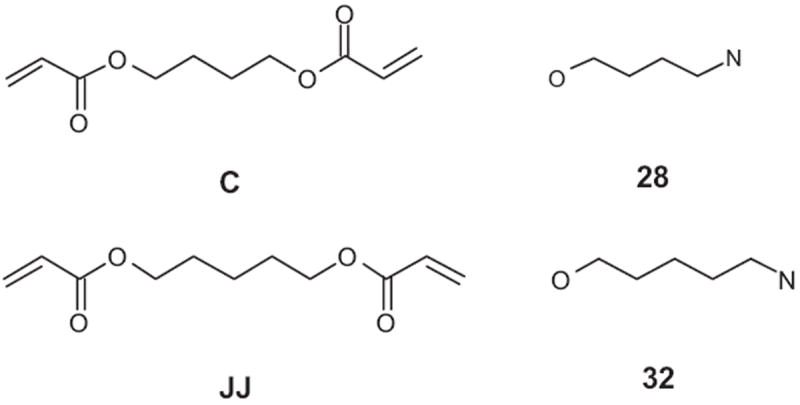
Chemical structures of acrylate and amino monomers which compose the most effective polymers from the poly-(β-amino ester) library, namely C32, JJ28, and C28.

Table 7.

Summary of the LAD rules covering C₃₂, JJ₂₈ and C₂₈ polymers for stoichiometric ratios 1:1 and 1.2:1.

Descriptor	Rules for 1:1	Rules for 1.2:1
a_nH	>167	>172
a_nC	>110	>111.5
a_acc	≤30	≤33
b_rotN	>105.0	>100.5
b_rotR	>0.62	>0.63
density	>0.71	>0.71
logP(o/w)	>5.20	>6.95
SlogP	>4.62	>6.62
mr	>56.98	>55.93
vdw_vol	≤28.93	≤28.42

The value of the information summarized in Table 7 is two-fold. On the one hand, the numerical estimates obtained can serve as an excellent guide to a synthetic chemist in his search of specific geometrical and physical parameters for polymers with high propensity to DNA delivery. On the other hand, the descriptors identified can help one to gain useful insights into the physicochemical nature of potentially successful polymer candidates. The structural descriptors such as number of carbon and hydrogen atoms capture information about chemical composition and, if considered together, may indicate the importance of aliphatic chains. The number of hydrogen bond acceptors indirectly emphasizes the role of nitrogen and oxygen atoms (see Figure 4) in hydrogen bonding interactions between polymers and DNA. The number of rotatable bonds shows the necessity for polymer chains of interest to possess a certain degree of conformational flexibility.

In focused polymer design a researcher attempts to correlate biological response with structural characteristics as well as with specific physicochemical properties of a polymer. The physicochemical properties reflect different types of intramolecular forces (e.g., hydrophobic, ionic, van der Waals), which are involved in interactions between a polymer and biochemical environment. In the case of poly(β-amino esters) the appearance of logP(o/w) and SlogP descriptors clearly indicates the importance of hydrophobic interactions. Molecular refractivity, which is calculated using Lorentz–Lorentz function,^[30] encodes the molecular volume and the strength of London dispersive forces in intermolecular interactions.^[32] Molecular volume also appears in Table 7 as the vdw_vol descriptor, although the summary of the rules for the entire set of polymers (see Table 6) reveals that this property contributes to low transfection efficiency of selected poly(β-amino esters). In contrast, the descriptor associated with polymer surface area (vdw_area) contributes positively to bioresponse. This positive association concurs with the presence of surface effects (e.g., DNA condensation) that were found experimentally.^{[ 9]} The later examples emphasize the necessity of thorough analysis of the rules obtained by LAD to ensure successful rational biomaterials design.

Conclusion

Since the basic concepts of LAD were introduced by Hammer and co-workers,^[17,18] there have been a number of applications that demonstrated the competitive performance and great flexibility of the LAD methodology. The utility of LAD has been established in pattern detection, support set selection, theory formation, etc.; however, classification appears to be the most widely used application of LAD that is comparable with other well established methods in this field. Recently Bonates and Hammer^[20] developed a new LAD algorithm that employs principles of combinatorial optimization and mathematical programming to extend the LAD methodology to the regression setting. This algorithm has been tested in preliminary computational experiments and was shown to be comparable to standard regression algorithms in terms of mean absolute error and correlation. The major advantage of the new LAD regression algorithm is its ability to capture hidden correlations similar to how the conventional LAD algorithm discovers hidden patterns.

Polymeric gene delivery provides a unique opportunity to examine the ability of the LAD algorithm to deal with a challenging biological problem. The experimental measurements reported by Langer and co-authors that formed data sets analyzed in the present work preclude unambiguous identification of the parameter(s) that most control DNA transfection. It is very likely that the relationship between polymer structure and transfection efficiency is an extremely complex biological process that challenges computational approaches that adopt descriptor-based surrogate modeling.

Accuracy of the prediction reported here can probably be improved by performing external validation on additionally synthesized and characterized sets of poly(β-amino esters) or including such measured parameters as actual molecular weight, particle size and surface charge as descriptors into the predictive model. Including the latter characteristic would also illuminate the role of electrostatic interactions in spontaneous binding and condensation of DNA by poly(β-amino esters).

Despite the many challenges presented by the experimental data itself, the LAD regression algorithm demonstrated clear superiority in establishing good correlation with Pearson coefficient of 0.77 and MAE of 3.83 when its performance was compared with that of other traditional regression algorithms. It has also apparent that the degree of success depends significantly on the modeling representation and the molecular descriptors selected for this particular case. The predicted values of the transfection efficiency obtained by means of LAD regression function are in strong agreement with reported experimental values.^[9]