Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Feb 4.
Published in final edited form as: Epidemics. 2013 Nov 19;6:37–45. doi: 10.1016/j.epidem.2013.11.002

Probabilistic uncertainty analysis of epidemiological modeling to guide public health intervention policy

Jennifer A Gilbert a, Lauren Ancel Meyers b,c, Alison P Galvani a,d, Jeffrey P Townsend d,e,*
PMCID: PMC4316830  NIHMSID: NIHMS656278  PMID: 24593920

Abstract

Mathematical modeling of disease transmission has provided quantitative predictions for health policy, facilitating the evaluation of epidemiological outcomes and the cost-effectiveness of interventions. However, typical sensitivity analyses of deterministic dynamic infectious disease models focus on model architecture and the relative importance of parameters but neglect parameter uncertainty when reporting model predictions. Consequently, model results that identify point estimates of intervention levels necessary to terminate transmission yield limited insight into the probability of success. We apply probabilistic uncertainty analysis to a dynamic model of influenza transmission and assess global uncertainty in outcome. We illustrate that when parameter uncertainty is not incorporated into outcome estimates, levels of vaccination and treatment predicted to prevent an influenza epidemic will only have an approximately 50% chance of terminating transmission and that sensitivity analysis alone is not sufficient to obtain this information. We demonstrate that accounting for parameter uncertainty yields probabilities of epidemiological outcomes based on the degree to which data support the range of model predictions. Unlike typical sensitivity analyses of dynamic models that only address variation in parameters, the probabilistic uncertainty analysis described here enables modelers to convey the robustness of their predictions to policy makers, extending the power of epidemiological modeling to improve public health.

Keywords: Infectious disease, Epidemiology, Mathematical modeling, Health policy, Uncertainty

Introduction

Epidemiological models can serve as powerful tools to predict and understand the dynamics of infectious diseases. These models allow us to target control measures and use limited resources more efficiently. However, the predictions of a model are highly dependent on the quality of the data used for parameterization. Therefore, it is crucial that proper care is given to the provenance and precision of data available, and that uncertainty in model outcomes be addressed. Epidemiological models can be broadly classified as deterministic or stochastic, where deterministic models have fixed parameter values and stochastic models have probabilistic values (Anderson and May, 1991; Keeling and Rohani, 2008; Vynnycky and White, 2010). Although stochastic simulations of disease transmission more often convey uncertainty by characterizing the probability of an epidemiological outcome as part of an uncertainty analysis (e.g. Fraser et al., 2009), deterministic models typically do not. As a case in point, the study of influenza has been markedly advanced by a number of insightful deterministic models (e.g. An der Heiden et al., 2009; Chen and Liao, 2008; Crowe et al., 2011; Flahault et al., 2006; Krumkamp et al., 2010; Medlock and Galvani, 2009; Mercer et al., 2011; Mylius et al., 2008; Nuño et al., 2007; Roberts et al., 2007; Tracht et al., 2011;Tuite et al, 2010). However, while sensitivity analysis is performed on these models and the relative importance of parameters' contributions to uncertainty in the model outcomes determined, global outcome uncertainty has not been examined. Uncertainty analysis and its representation of the total possible uncertainty in model outcomes would strengthen policy makers' confidence in the interpretation of results and enhance their ability to act accordingly. Indeed, uncertainty analysis has been previously applied to infectious disease models without public health interventions (Blower and Dowlatabadi, 1994; Chowell et al., 2004; Coelho et al., 2008; Matser et al., 2009; Samsuzzoha et al., 2013; Sanchez and Blower, 1997) and has been recommended by experts for many fields of mathematical modeling, including medical decision making, as an optimal approach to presenting model predictions (Briggs et al., 2012). In the case of dynamic transmission modeling, however, authoritative best practices have not included uncertainty analyses (Pitman et al., 2012). General modeling guidelines recommend the methodology used in a probabilistic sensitivity analysis, in which both global parameter uncertainty and output uncertainty are addressed, as the best practice method for uncertainty analysis (Briggs et al., 2012) but that ideal has not been extended to dynamic transmission models, for which its implementation has been challenging (Pitman et al., 2012). Moreover, previous applications of uncertainty analysis methodology to dynamic models have not extended the technique to the evaluation of public health interventions that are important for reducing diseases transmission or avoiding epidemics altogether.

One challenge to the estimation of epidemiological parameters is the imprecision of the relevant data, stemming from hurdles to acquisition, privacy restrictions, and/or the need for analysis during outbreaks. Unfortunately, parameterizing a deterministic epidemiological model with the best point estimates based on minimal data can convey a misleading degree of certainty to policy makers. Conversely, policy makers who are aware that models are parameterized with weakly supported point estimates may be overly dismissive of deterministic predictions that might yet have significant validity. These issues can be addressed by incorporating the uncertainty of parameters directly into an analysis by probabilistically re-sampling data or likely distributions of parameters to calculate a distribution of predictive outcomes given the model as part of a probabilistic uncertainty analysis (Blower and Dowlatabadi, 1994; Elderd et al., 2006; Helton and Davis, 2003; Marino et al., 2008; Sanchez and Blower, 1997).

One of the most common modeling approaches for evaluating interventions in dynamic systems is the construction of a differential equation model of a disease, such as the standard deterministic Susceptible-Infected-Recovered (SIR) model (Anderson and May, 1991; Keeling and Rohani, 2008; Vynnycky and White, 2010). From the differential equation model, a closed-form solution can be calculated for the basic reproductive number, R0, the average number of secondary infections that would follow upon a primary infection in a naïve host population (Anderson and May, 1991; Keeling and Rohani, 2008; Van den Driessche and Watmough, 2002; Vynnycky and White, 2010). In a population where there is pre-existing immunity due to either vaccination or previous infection, the effective reproductive number, Re, is defined as the average number of secondary infections following a primary infection in a population that is not completely naïve, as is true when vaccination or treatment is implemented (Keeling and Rohani, 2008; Vynnycky and White, 2010). Re is of particular interest in public health because interventions that bring its value below one are predicted to eradicate the disease (Keeling and Rohani, 2008; Vynnycky and White, 2010). Thus, the Re = 1 threshold often serves as a target for designing effective intervention policies (Keeling and Rohani, 2008; Vynnycky and White, 2010).

While deterministic SIR models can provide valuable estimates of the impact of interventions, they are often hampered by two critical limitations. First, the model often lacks realism and stands as just one of several competing models that are compatible with the same empirical evidence. This concern is typically addressed by comparing model predictions to real-world data (Helton and Davis, 2002, 2003; Keeling and Rohani, 2008; Vynnycky and White, 2010), but can also be addressed using Bayesian model averaging, model selection, and expert elicitation (Hoeting et al., 1999; Lloyd, 2009; Kass and Raftery, 1995; Saltelli et al., 2004). Second, the best parameter estimates (needed for the closed-form solution of Re) are often inexact. To address this concern, sensitivity analyses are used to explore the relationship between model parameters and outcomes. Specifically, one or more parameters are perturbed and the corresponding effects on outcomes are examined (Marino et al., 2008). The perturbation can be done either by evaluating the effect of arbitrarily small changes in parameter values (e.g. ±1%, as in Massad et al., 2009) or by evaluating the effects across a range of values defined by plausible probability density functions (e.g. Amaku et al., 2003, 2009). However, because the values of other parameters are held fixed at best point estimates, these strategies do not account for interaction effects in non-linear dynamic models, and do not assess global uncertainty in parameters or outcome.

A global probabilistic sensitivity analysis allows the contribution of each parameter to model outcomes to be investigated while also taking into account the uncertainty of other model parameters (Blower and Dowlatabadi, 1994; Marino et al., 2008; Sanchez and Blower, 1997; Wu et al., 2013). Uncertainty in parameter values can be accounted for by sampling randomly from empirical data or from probability density functions fit to empirical data. Such sampling techniques include bootstrapping, Monte Carlo sampling, and Latin hypercube sampling (Blower and Dowlatabadi, 1994; Hastings, 1970; Helton and Davis, 2002, 2003; Metropolis et al., 1953; Marino et al., 2008; Sanchez and Blower, 1997). The model output generated from parameter samples can then be analyzed using linear (e.g. partial correlation coefficients), monotonic (e.g. partial rank correlation coefficients) and non-monotonic statistical tests (e.g. sensitivity index) to determine the contribution of each parameter to the variation in output values (Blower and Dowlatabadi, 1994; Helton and Davis, 2002, 2003; Marino et al., 2008; Sanchez and Blower, 1997; Wu et al., 2013). The model itself may also be treated as an uncertain parameter and varied in the sensitivity analysis to determine the effect that the choice of model has on the output. This technique, known as Bayesian model averaging, can be computationally infeasible (Hoeting et al., 1999; Kass and Raftery, 1995; Saltelli et al., 2004). Even the most thoroughly data-driven studies often only report the results of a global sensitivity analysis in terms of a ranking of parameters' relative contributions to outcome uncertainty, without reporting the outcome uncertainty itself. Probabilistic uncertainty analysis provides additional utility, carrying data-driven parameter uncertainty through to the model outcomes, yielding probabilistic distributions rather than single value estimates of possible outcome values (Blower and Dowlatabadi, 1994; Elderd et al., 2006; Helton and Davis, 2003; Marino et al., 2008; Sanchez and Blower, 1997). A probabilistic outcome distribution serves as a gold standard for conveying the robustness and uncertainty of model results to policy makers that has yet to be widely adopted by the epidemiological modeling community.

Here, we illustrate methodology by which parameter uncertainty can be incorporated into model predictions using an example of influenza antiviral and vaccination intervention, comparing model predictions that include uncertainty analysis to predictions that only include sensitivity analysis in order to reveal the importance of analyzing both parameter and output uncertainty in deterministic modeling studies. Performing a probabilistic sensitivity analysis and extending parameter uncertainty into the model predictions, we assess uncertainty in outcome, a procedure that allows researchers to provide public health officials with fundamentally important information – especially for key threshold considerations such as the probability of disease eradication at each level of an intervention – so that decision makers may precisely weigh the cost of the intervention against the potential for and extent of success.

Methods

Mathematical model

We implemented a compartmental model of influenza transmission that divides individuals into susceptible (S), latent (E), infected (I), recovered (R), treated (T), vaccinated (V), and hospitalized (H) states (Fig. 1). Values for parameters relevant to the calculation of Re, which included secondary attack rate θ, duration of infectiousness 1/δ, treatment efficacy εT, vaccine efficacy εV, contact rate c and probability of hospitalization from influenza infection pH, were obtained from literature on seasonal influenza (Table 1; Belshe et al, 1998; Cauchemez et al, 2004; Halloran et al., 2007; Longini et al., 1982; Mossong etal., 2008; Sullivan et al., 1993; Thompson et al., 2003, 2004). Susceptible individuals acquire infection following contact with an infectious individual (I or T) with a force of infection λ, given by λ = β((I/N) + (1 − εT)(T/N)), where β is the product of the contact rate c and the probability of infection given contact with an infectious individual 1 − (1 − θ)δ, θ is the secondary attack rate or the proportion of individuals who will become infected upon contact with an infectious individual during the total infectious period, δ is one divided by the duration of infectiousness, N is the total number of individuals in the population, and εT is the efficacy of antiviral treatment at reducing infectiousness. A proportion 1 − εV of vaccinated individuals (V) become infected following contact with an infectious individual with a force of infection λ, where εV is the efficacy of the vaccine at reducing susceptibility. A proportion pT of individuals who become infected (E) are treated with antivirals, proceeding into the treated class (T) at a rate σ. These individuals (T) have a reduced ability to infect susceptible individuals, based on the efficacy of antivirals εT. The remaining infected individuals (1 − pT)E proceed to the infected class (I) at a rate σ. Infected (I) and treated (T) individuals recover from infection at a rate δ and proceed to the recovered class (R). Infected individuals (I) are also hospitalized (H) at a rate η, from which they recover (R) at a rate κ, or die from infection at a rate μ. The flow of individuals from one compartment to another is described by the ordinary differential equations:

Fig 1.

Fig 1

Open in a new tab

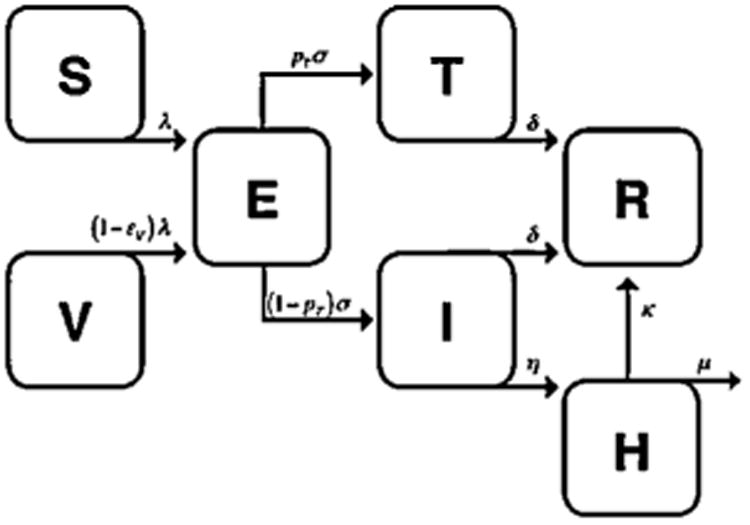
Diagram of compartmental model of influenza transmission. Compartments correspond to susceptible [S], latently infected [E], infectious [I], recovered [R], vaccinated [V], treated [T] and hospitalized [H] individuals. λ corresponds to force of infection, 1/σ to duration of incubation period, η to rate of hospitalization, κ to rate of recovery following hospitalization, and μ to flu mortality rate. The remaining rates are described in Table 1.

Table 1.

Parameter descriptions, values, distributions, and sources.

Parameter Point estimate Distribution Reference
Infectious perioda 1/δ 3.8 days Normalb Cauchemez et al. (2004)
Secondary attack rate θ 0.147 Truncated normalc,d Longini et al. (1982)
Contact rate c 13.4 contacts/day Empirical Mossong et al. (2008)
Vaccine efficacy εV 0.95 Betae Belshe et al. (1998)
Antiviral treatment efficacy εT 0.808 Betaf Halloran et al. (2007)
Proportion of infected individuals hospitalized pH 0.005 Betag Sullivan et al. (1993), Thompson et al. (2003, 2004)
Open in a new tab

SD, standard deviation.

a

1/recovery rate.

b

Standard deviation = 0.4.

c

All values greater than 0.

d

Standard deviation = 0.037.

e

From 1−Beta(7,163)Beta(64,468)

f

From 1−Beta(4,176)beta(22,168)

g

From [Beta(1441,14687)/(1441/16128)](167812/226545805)Beta(120,694)

dSdt=−λS,dEdt=λS+(1−ɛV)λV−σE,dIdt=(1−pT)σE−(δ+η)I,dTdt=pTσE−δT,dRdt=δI+δT+κH,dVdt=−(1−ɛV)λV,dHdt=ηI−(κ+μ)H.

Reproductive number

Our outcome of interest was the probability with which Re was suppressed below one for a given set of parameter values. To facilitate direct evaluation of outcome under uncertainty based on our model, we derived an expression for Re using the next generation matrix method (Van den Driessche and Watmough, 2002) from this model:

Re=(1−pTδ+η+pTδ(1−ɛT))(βS0N+(1−ɛV)βV0N), (1)

where η = pHδ/(1 – pH), S = S0, V = V0, and E = I = T = H = R = 0.

Uncertainty analysis

We evaluated outcomes from Eq. (1), incorporating parameter uncertainty, to assess whether different levels of treatment (pT) and vaccination (V0/N) would effectively lower Re to below one, thus achieving the termination of transmission. Treatment (pT) and vaccination (V0/N) are considered to be controllable variables that can be changed based on the intervention approach, in contrast to the model parameters that have known values and do not change with intervention. To compare with the typical approach, we first calculated Re using the best point estimates – the mean of the data or distribution from the literature – for the values of the parameters, without incorporating parameter uncertainty (see Table 1 for parameter values and distributions). We then performed an uncertainty analysis (Saltelli et al., 2008): for each parameter, we sought to use the most informative data available in the literature, in the form of data from an experiment or a distribution that had been fitted to such data. We sampled from each parameter's distribution to perform the uncertainty analysis. The methods for estimating the uncertainty distributions for secondary attack rate θ, duration of infectiousness 1/δ, vaccine efficacy εV, treatment efficacy εT, proportion of infected individuals hospitalized pH, and contact rate c from available data are detailed in the Appendix. The probability that Re was less than one was then calculated across the full range of combinations of the variables pT and V0/N. We performed this calculation by computing Re for fixed variables pT and V0/N while randomly sampling the other parameters from their uncertainty distributions. Repeating this process of Monte Carlo sampling for the other parameters and calculating Re 10,000 times enabled us to generate a distribution of all possible values for our outcome Re for each pair of variables pT and V0/N. The probability that Re was below one for each pair of variables pT and V0/N was therefore equal to the number of Re values less than one divided by 10,000.

We assumed that the parameter distributions were independent of each other because joint distribution data were not available. In reality, it is unlikely that all model parameters are independent. In general, correlation between parameters would be expected to reduce the overall uncertainty in outcome predictions. To assess whether issues of parameter independence would significantly impact our outcome, we repeated our analysis while imposing complete inverse correlation between the parameters θ and δ. These parameters correspond to pathogen virulence and duration of infectiousness, which theory suggests may be correlated (Galvani, 2003).

Sensitivity analysis

To assess the contribution of each parameter to the overall uncertainty in Re, we performed one-way and global probabilistic sensitivity analyses. For the one-way sensitivity analysis, we varied each parameter individually across the 90% confidence interval of its uncertainty distribution and determined the minimum and maximum Re value achieved at various combinations of vaccination and treatment coverages. The coverages were chosen to correspond to potential plausible levels achievable in the United States (Centers for Disease Control and Prevention, 2009). We plotted the results of the one-way sensitivity analysis in a series of tornado diagrams, corresponding to the different combinations of treatment and vaccination levels. For the global sensitivity analysis, we performed both partial rank correlation coefficient (PRCC) and sensitivity index calculation at different combinations of fixed treatment and vaccinations levels. Detailed methodology on PRCC calculation can be found in Blower and Dowlatabadi (1994), as well as Wu et al. (2013). To calculate the sensitivity index for the parameters in Xi (i.e. c, δ, pH, εT, θ, and εV), while fixing the proportion of individuals treated and vaccinated, we evaluated the following equation (Saltelli et al., 2008) for each parameter:

Si=VXi(EX~i(Re|Xi))V(Re), (2)

where VXi (EX∼i (Re|Xi)) is the variance of the expected value of model output Re when holding Xi fixed across all its possible values and allowing the other parameters to vary, and V(Re) is the variance of Re. This sensitivity index quantifies the degree to which our outcome Re is expected to vary when a given parameter is known exactly. It ranges from zero to one, with higher values indicating greater sensitivity of an outcome to the parameter uncertainty.

Results

Model predictions without uncertainty

When point estimates of parameter values were used, our compartmental model predicted that proportions of influenza vaccination above 0.54 or treatment above 0.64 would reduce Re below one regardless of the value of the other proportion (Fig. 2). A combination of lower vaccination and lower treatment levels were also predicted to reduce Re below one (Fig. 2), indicating that vaccinating less than 54% of susceptible individuals and treating less than 64% of infected individuals could prevent an epidemic provided these interventions are implemented at the same time.

Fig. 2.

Fig. 2

Open in a new tab

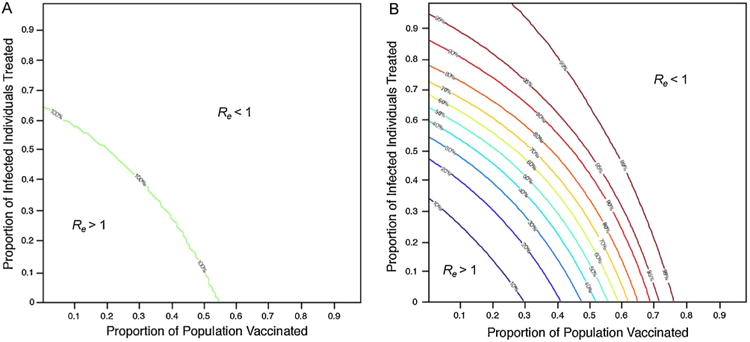
Probability (%) that Re is below one for different levels of vaccination and treatment (A) without and (B) with the incorporation of parameter uncertainty.

Model predictions with uncertainty

Inclusion of parameter uncertainty demonstrated that higher treatment and vaccination levels were required to reduce Re below one with a probability greater than 50% (Fig. 2). When intervention was based exclusively on vaccination, only proportions of vaccination above 0.69 reduced Re below one with a probability above 90% (Fig. 2). Reducing Re below one with a probability above 99% requires a minimum of 0.76 vaccine coverage (Fig. 2). When intervention was based exclusively on treatment, even higher levels of treatment were required to reduce Re below one with the same probability as that for vaccination. Proportions of treatment above 0.87 could reduce Re below one with a probability above 90% (Fig. 2). No level of treatment was alone able to reduce Re below one with a probability above 99% (Fig. 2). The levels of vaccination and treatment previously estimated to achieve eradication (Re<1) without uncertainty analysis are predicted to only do so with probability 50% with uncertainty analysis. These findings indicate that, compared to the model's predictions without the inclusion of parameter uncertainty, increased levels of intervention are required to reduce Re below one with a high probability.

When the maximum level of treatment or vaccination achievable is known, the probability of the reduction of Re below one can be depicted with a fixed level of the known variable and varying levels of the unknown variable (Fig. 3). For example, about three out often people choose to be vaccinated for influenza in a given year (Centers for Disease Control and Prevention, 2009). For this situation, the outcomes can be depicted with varying levels of treatment and a fixed proportion of vaccination of 0.3 (Fig. 3). With this level of vaccination, proportions of treatment above 0.66 could reduce Re below one with a probability above 90%, and proportions of treatment above 0.94 could reduce Re below one with a probability above 99%. Conversely, if it is already known that there are only enough antivirals in a country's stockpile to treat 3 out of 10 infected people during an outbreak, policy makers can be best served by information on the probability of eliminating an epidemic of influenza when the proportion of infected individuals who are treated is 0.3 (Fig. 3). With this level of treatment, proportions of vaccination above 0.57 could reduce Re below one with a probability above 90%, and proportions of vaccination above 0.66 could reduce Re below one with a probability above 99%. These results provide a basis for decision-making regarding mitigating an epidemic that incorporates probability of successful eradication given existing and potential levels of intervention.

Fig. 3.

Fig. 3

Open in a new tab

Probability that Re is below one (A) for varying levels of treatment when proportion vaccinated is 0.3 and (B) for varying levels of vaccination when proportion treated is 0.3.

Imposing an anticorrelation between parameters θ and δ moderately reduced the level of vaccination needed to reduce Re below one relative to that depicted in Fig. 2. However, the breadth of uncertainty around the effect of treatment remained the same. In addition, the breadth of uncertainty around the effect of vaccination remained high as well as centered around the deterministic prediction. Accordingly, correlation between parameters appears not to impact our conclusion that a full uncertainty analysis reveals key information for evaluating the predictions of epidemiological models.

Sensitivity analysis

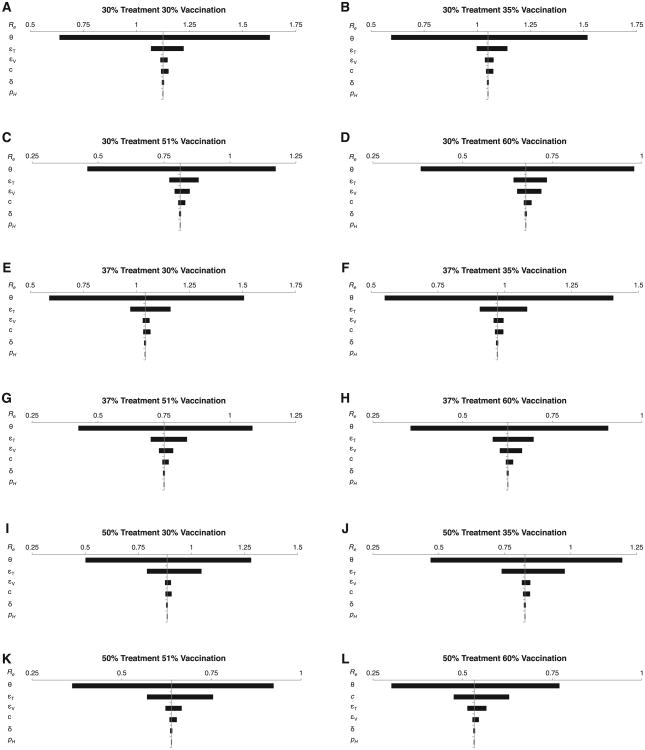
Our sensitivity analysis to determine the sources of uncertainty in our outcome Re demonstrated that we need more data (in order of priority) on secondary attack rate θ, treatment efficacy εT, vaccine efficacy εV, contact rate c, duration of infectiousness 1/δ and probability of hospitalization from influenza infection pH, respectively, to provide greater predictive power to estimate Re (Fig. 4 and Tables 2 and 3). Secondary attack rate θ and treatment efficacy εt have the greatest contributions to uncertainty in Re. The one-way sensitivity analysis demonstrated that when θ was varied across the 90% confidence interval of its uncertainty distribution and all other parameters are held fixed, the greatest range in Re was achieved, with a minimum value of 0.4 and maximum of 1.6, depending on the level of vaccination and treatment implemented (Fig. 4). The next widest ranges of Re values occurred when εT and εV were varied across the 90% confidence interval of their uncertainty distributions (Fig. 4). The difference between the minimum and maximum Re values when varying εT or εV was greatest when treatment or vaccination coverage, respectively, was highest (Fig. 4).

Fig 4.

Fig 4

Open in a new tab

One-way, local sensitivity analysis of parameter contributions to model outcome uncertainty at different combinations of vaccination and treatment levels. (A) 30% treatment and 30% vaccination coverage, (B) 30% treatment and 35% vaccination coverage, (C) 30% treatment and 51% vaccination coverage, (D) 30% treatment and 60% vaccination coverage, (E) 37% treatment and 30% vaccination coverage, (F) 37% treatment and 35% vaccination coverage, (G) 37% treatment and 51% vaccination coverage, (H) 37% treatment and 60% vaccination coverage, (I) 50% treatment and 30% vaccination coverage, (J) 50% treatment and 35% vaccination coverage, (K) 50% treatment and 51% vaccination coverage, and (L) 50% treatment and 60% vaccination coverage.

Table 2.

PRCC for each model parameter at different combinations of treatment and vaccination coverages. Higher absolute values indicate that a parameter contributes a greater amount to the uncertainty in Re.

30% Vaccinated 35% Vaccinated 51% Vaccinated 60% Vaccinated
Parameter PRCC p-Value PRCC p-Value PRCC p-Value PRCC p-Value
30% treated Secondary attack rate θ 0.996 <0.001 0.996 <0.001 0.996 <0.001 0.995 <0.001
Antiviral treatment efficacy εT −0.862 <0.001 −0.860 <0.001 −0.845 <0.001 −0.826 <0.001
Vaccine efficacy εV −0.353 <0.001 −0.422 <0.001 −0.623 <0.001 −0.727 <0.001
Contact rate c 0.354 <0.001 0.350 <0.001 0.328 <0.001 0.304 <0.001
1/(Duration of infectious period) δ −0.098 <0.001 −0.097 <0.001 −0.091 <0.001 −0.085 <0.001
Proportion of infected individuals hospitalized pH −0.029 0.003 −0.030 0.002 −0.033 0.001 −0.033 0.001
37% treated Secondary attack rate θ 0.994 <0.001 0.994 <0.001 0.994 <0.001 0.993 <0.001
Antiviral treatment efficacy εT −0.871 <0.001 −0.870 <0.001 −0.861 <0.001 −0.849 <0.001
Vaccine efficacy εV −0.286 <0.001 −0.346 <0.001 −0.551 <0.001 −0.661 <0.001
Contact rate c 0.284 <0.001 0.282 <0.001 0.268 <0.001 0.254 <0.001
1/(Duration of infectious period) δ −0.079 <0.001 −0.078 <0.001 −0.075 <0.001 −0.072 <0.001
Proportion of infected individuals hospitalized pH −0.024 <0.017 −0.025 0.013 −0.027 0.006 −0.029 <0.001
50% treated Secondary attack rate θ 0.988 <0.001 0.988 <0.001 0.987 <0.001 0.987 <0.001
Antiviral treatment efficacy εT −0.887 <0.001 −0.886 <0.001 −0.883 <0.001 −0.878 <0.001
Vaccine efficacy εV −0.204 <0.001 −0.250 <0.001 −0.425 <0.001 −0.540 <0.001
Contact rate c 0.199 <0.001 0.198 <0.001 0.192 <0.001 0.185 <0.001
1/(Duration of infectious period) δ −0.057 <0.001 −0.060 <0.001 −0.055 <0.001 −0.054 <0.001
Proportion of infected individuals hospitalized pH −0.018 0.072 −0.019 0.064 −0.021 0.037 −0.023 0.023
Open in a new tab

Table 3.

Sensitivity index (SI) for each model parameter at different combinations of treatment and vaccination coverages. Higher values indicate that a parameter contributes a greater amount to the uncertainty in Re.

30% Vaccinated 35% Vaccinated 51% Vaccinated 60% Vaccinated
Parameter SI SI SI SI
30% treated Secondary attack rate θ 0.966 0.966 0.961 0.955
Antiviral treatment efficacy εT 0.025 0.025 0.025 0.024
Vaccine efficacy εV 0.001 0.002 0.006 0.012
Contact rate c 0.001 0.001 0.001 0.001
1/(Duration of infectious period) δ <0.001 0.001 <0.001 <0.001
Proportion of infected individuals hospitalized pH <0.001 0.001 <0.001 <0.001
37% treated Secondary attack rate θ 0.946 0.945 0.941 0.935
Antiviral treatment efficacy εT 0.043 0.043 0.043 0.042
Vaccine efficacy εV 0.001 0.002 0.006 0.012
Contact rate c 0.001 0.001 0.001 0.001
1/(Duration of infectious period) δ <0.001 0.001 <0.001 <0.001
Proportion of infected individuals hospitalized pH <0.001 0.001 <0.001 <0.001
50% treated Secondary attack rate θ 0.881 0.881 0.877 0.872
Antiviral treatment efficacy εT 0.101 0.100 0.100 0.099
Vaccine efficacy εV 0.001 0.002 0.006 0.011
Contact rate c 0.001 0.001 0.001 0.001
1/(Duration of infectious period) δ <0.001 0.001 <0.001 <0.001
Proportion of infected individuals hospitalized pH <0.001 0.001 <0.001 <0.001
Open in a new tab

The global sensitivity analyses (PRCC and sensitivity index) confirmed that θ and εT had the greatest influence on Re, even when uncertainty in the other parameters was controlled for (Tables 2 and 3). The PRCCs for θ and εT were positive and negative, respectively, greater than the PRCCs for the remaining parameters, and statistically significant, indicating that there is a strong monotonic relationship between the parameters and Re (Table 2). Lower values of Re were achieved, regardless of vaccination or treatment coverage, when θ was decreased or εT increased. Parameter εV had the next highest absolute PRCC value and was inversely and monotonically correlated with Re, with εV becoming more influential as vaccination coverage increased. Sensitivity index calculations confirmed that θ and εT were the most influential parameters, with θ contributing to between 87.2% and 96.6% of the uncertainty in Re estimates and εT to between 2.4% and 10.1% (Table 3). The remaining parameters contributed to less than 1% of the uncertainty in Re.

The relative importance of parameters is partly determined by the lack of data on these parameters, but is also in accord with the important roles played by θ, εT, and εV in the calculation of Re (Eq. (1)): θ is raised to the power of δ and multiplied by the proportion of individuals who are susceptible S0/N. Parameters εT and εV additionally serve as multipliers in Eq. (1).

Discussion

Here we demonstrated that incorporation of parameter uncertainty into the analysis of deterministic models provides a key tool for policy decisions regarding levels of public health interventions needed to halt an epidemic. These results hold true even for a relatively well-investigated disease such as influenza. Without the inclusion of parameter uncertainty, mathematical analysis often yields a single threshold value corresponding to the level of an intervention that presumably leads to a successful outcome. We have shown that such a threshold value for an intervention suggests an undue level of robustness for a model's predictions regarding the mitigation of a potential epidemic. In reality, the levels of vaccination and treatment indicated by deterministic modeling halt an outbreak only about half of the time. Procuring a more palatable chance of success will take greater levels of intervention, the amount of which depends critically on the data available on key parameters. Quantifying the relationship between levels of interventions and the probabilities of success requires uncertainty analysis, and communicating this probabilistic understanding to policy makers is of vital importance.

For instance, we found that without the inclusion of parameter uncertainty, our model predicted that levels of vaccination above 54% or treatment coverage above 64% could successfully control a flu epidemic. These results may mislead a decision maker into thinking that an influenza epidemic would definitely be avoided if 54% of a population were vaccinated or 64% treated and the subsequent development of public policy to promote this coverage level. However, we saw that when parameter uncertainty was incorporated and uncertainty in the model outcome was analyzed, predicted intervention levels would only successfully control an epidemic 50% of the time; much higher coverage levels – closer to 70% for vaccination and 90% for treatment – were needed to be 90% certain these interventions would successfully control an epidemic. The same principle holds true for stochastic epidemiological models that do not perform uncertainty analysis, since often these models alone do not capture the full plausible range of parameter values and therefore do not convey the total uncertainty in model outcomes. Quantification of uncertainty provides policy makers the opportunity to weigh deployment of resources against risks in choosing the appropriate combination of vaccination and treatment coverage levels at the beginning of or potentially before the start of an epidemic in order to successfully mitigate the number of infections and deaths.

Sources of outcome uncertainty can additionally be identified by deterministic sensitivity analysis to indicate where to direct further empirical research efforts. Typically, in epidemiological modeling of disease transmission, deterministic sensitivity analyses are performed by taking the derivatives of outcome variables at best point estimates or by analyses of slight perturbations without explicit regard to sampling error. This approach is not ideal when the parameters are not precisely known or when the model is nonlinear, as the analysis is only informative at the point estimates from which it is computed. The one-way sensitivity analysis performed on our influenza model is an example of a deterministic, local sensitivity analysis. While the one-way sensitivity analysis ranked each parameter in order of importance, as well as gave ranges of possible Re values, it did not control for uncertainty in the other parameters, account for interactions between parameters, or quantify the probability that Re would be less than one. A global sensitivity analysis that takes the uncertainty of all parameters into account is more appropriate for epidemiological models of disease transmission. The global sensitivity analyses performed on our influenza model also ranked the parameters in order of importance, but controlled for global parameter uncertainty. They demonstrated that secondary attack rate most influenced our outcome Re. Accordingly, to model influenza transmission more precisely, additional research studies should focus on precise estimation of the secondary attack rate. However, PRCC and sensitivity index calculation did not indicate the potential ranges of Re that were achieved at the different vaccination and treatment levels, nor did it give an indication regarding how likely different intervention levels were to succeed (i.e. reduce Re below one). The information regarding the total uncertainty in Re estimates for each intervention level and the probability of intervention success was only gained through the probabilistic uncertainty analysis.

While we used a relatively basic model of influenza to illustrate our methodology, the approach that we advocate can be applied more generally by incorporating additional details into the model structure. For example, age structure would be highly appropriate to include when investigating potential vaccination policies for influenza. Moreover, other disease models might not require a recovered compartment because recovery is either not possible (e.g. HIV/AIDS) or immunity is not acquired (e.g. gonorrhea; Vynnycky and White, 2010). The model structure should reflect the important disease characteristics. However, regardless of model complexity, parameter uncertainty will always exist and will always impact model predictions. Therefore, an uncertainty analysis is necessary for all types of dynamic transmission models.

Because it is not always clear what the model structure for a disease should be, uncertainty in model specification also exists. Uncertainty in model specification, if incorporated into an analysis (Hoeting et al, 1999), would be expected to further increase the uncertainty of model predictions. In our model, for example, we could have instead allowed infected individuals to be infectious for a period of time before being treated. Under this alternate scenario, the outcome Re would have to be calculated by a different equation, potentially leading to a different uncertainty in outcome. Our sensitivity analysis might also have identified a different parameter as most influential of our outcome Re. As with many other studies, however, our ultimate choice of model structure was dictated in part by the data available for parameter values. While this more complex model would be a more realistic portrayal of the natural history of influenza, we could not find any dataset to create an appropriate distribution for the amount of time an individual was infected before treatment and therefore we did not incorporate the additional complexity to predict proportions of vaccination and treatment required to prevent or forestall an epidemic. Our study is not intended to directly influence policy but rather to demonstrate the importance of uncertainty analysis. Furthermore, because we focus on a single strain of influenza, we have structured our analysis to address uncertainty associated with the statistical measurement of parameters in research studies. Additional uncertainty exists in the biological variation between strains of influenza, which is important when considering more than one season of influenza transmission. For diseases other than influenza, variation in parameter estimates between studies conducted at different times or in different populations may also need to be addressed. Ideally, a single study that is viewed as the best dataset can be selected for parameterization of a model. When it is not clear which data source is most appropriate to use, study variation can be addressed with meta-analysis, sampling from multiple distributions for a parameter, or imposing a uniform distribution on the minimum and maximum values found in literature.

In summary, sensitivity analysis of our influenza model identified the secondary attack rate as the parameter that most influenced our outcome Re. Accordingly, to model influenza transmission more precisely, additional research studies should focus on estimating precise values of the secondary attack rate. Moreover, because policy makers are interested in the predicted impact of different types and levels of interventions on an epidemic, estimated effects of an intervention should be presented to policy makers along with the degree of credibility that these effects will occur in light of uncertainty in the model parameters. Thereby, policy makers can make a well-informed decision with an understanding of the probability of success or failure based on the decision taken. Our study demonstrates that this uncertainty can be incorporated into analyses seamlessly by re-sampling from distributions of likely parameter values, calculating the outcome of interest, and determining the probability that the outcome is achieved, as we illustrated here for a model of influenza vaccination and treatment.

Acknowledgments

This work was supported by the National Institutes of Health (grant number 1R01AI072706-01) and the National Science Foundation (award number 0624117). We thank Joel Mossong and Erik Volz for supplying the contact data. We also thank Jan Medlock, Angelika Hofmann, and Meagan Fitzpatrick for their helpful insights and commentary and Cristen Pallante for assistance with graphic design.

Appendix A

Uncertainty Distributions

Vaccine efficacy εV

Belshe et al.(1998) performed a clinical study on the efficacy of a live attenuated vaccine against influenza. They found that 7 out of 1070 vaccinated participants became infected with influenza, whereas 64 out of 532 unvaccinated participants became infected. This yielded a vaccine efficacy of about 95%. We then calculated 10,000 values to describe the uncertainty distribution for vaccine efficacy by randomly drawing from beta distributions for each proportion infected and evaluating the equation ɛV=1−P(infection|vaccinated)P(infection|unvaccinated)=1−AB, where A ∼ Beta (7, 170−7) and B ∼ Beta (64, 532−64). Beta distributions were chosen for the probabilities of infection not only because they are constrained by [0,1], but also because they are appropriate to describe the probability of an event (i.e. infection) given a certain number of trials (i.e. population of individuals).

Treatment efficacy εT

Halloran et al.(2007) analyzed clinical data on the efficacy of antiviral treatment for preventing the development of influenza disease in exposed individuals. They found that 4 out of 180 treated participants became infected with influenza, whereas 22 out of 190 untreated participants became infected. We then calculated 10,000 values to describe the uncertainty distribution for treatment efficacy by randomly drawing from beta distributions for proportion infected and evaluating the equation ɛT=1−P(infection|treated)P(infection|untreated)=1−CD, where C ∼ Beta (4, 180−4) and D ∼ Beta (22, 190−22). Beta distributions were chosen for the probabilities of infection not only because they are constrained by [0,1], but also because they are appropriate to describe the probability of an event (i.e. infection) given a certain number of trials (i.e. population of individuals).

Proportion hospitalized pH

Because data on the proportion of infected individuals hospitalized for influenza were not directly available from literature, we obtained the proportion of infected individuals hospitalized by taking the ratio of the proportion of individuals in a population hospitalized for influenza-like illnessby the proportion of individuals in a population infected with influenza. Thomson et al.(2003, 2004) estimated annual influenza-associated hospitalizations in the United States. They found that 167,812 / 226,545,805 or approximately 73.1 per 100,000 persons were hospitalized during a single influenza season. Additionally they reported that 1441 of 16,128 isolates of those with suspected influenza infection tested positive for influenza. Sullivan et al.(1993) conducted a clinical study in the United States to determine the number of individuals infected annually with influenza. They found that 120 of 814 all individuals were infected with influenza during a single influenza season. The uncertainty distribution for the proportion of individuals hospitalized for influenza can be described by sampling from beta distributions for probability of influenza-associated hospitalization and probability of influenza infection in a population, and evaluating the following equation:

pHP(hospitalization|population)P(infection|population)=E/(1441/16128)(167812/226545805)F

where E ∼ Beta (1441, 16128−1441) and F ∼ Beta (120, 814−120). The proportion of influenza-associated hospitalizations is multiplied by the proportion of influenza suspects with confirmed influenza infection, and then divided by the proportion of people who come down with true influenza, in a season. The components of this calculation subject to significant uncertainty were the proportion of individuals with flu-like symptoms who actually were infected with influenza, and the proportion of individuals who came down with flu during a season. Both of these proportionswere estimated from binomial sampling studies. Thus, both were resampled from beta distributions in serial calculations of pH, holding as fixed the proportion of influenza-associated hospitalizations.

Contact rate c

Mossong et al.(2008) collected survey data from 7,290 participants on the number of contacts each individual had during one day. They found that individuals had on average 13.4 contacts per day. We used bootstrapping to obtain an uncertainty distribution. First we randomly sampled from the dataset with replacement to generate a new dataset of equal size. We then calculated the mean number of contacts per day from the new dataset. We repeated this process 10,000 times to generate 10,000 values to constitute the uncertainty distribution of the mean contact rate.

Duration of infectiousness 1δ

Cauchemez et al.(2004) used a Bayesian MCMC approach to estimate the posterior probability distribution for the mean duration of infectious period for influenza from household data. They found that a normal distribution with a mean of 3.8 days and standard deviation of 0.4 days best fit the data. We used Monte Carlo sampling to draw 10,000 random samples from a normal probability distribution with mean 3.8 and standard deviation 0.4. By calculating the inverse of each sampled value, we generated 10,000 values to constitute the uncertainty distribution for θ.

Secondary attack rate θ

Longini et al.(1982) used maximum likelihood estimation to estimate the secondary attack rate from household data. They found that a normal distribution with mean 0.147 and standard deviation 0.037 best fit the data. We used Monte Carlo sampling to draw 10,000 random samples from a normal distribution with mean 0.147 and standard deviation 0.037. Because SAR cannot be negative, we truncated the normal distribution at 0. We generated 10,000 values to constitute the uncertainty distribution for θ.

Footnotes

Appendix A. Supplementary data: Supplementary material related to this article can be found, in the online version, at doi:10.1016/j.epidem.2013.11.002.

References

  1. Amaku M, Coutinho FAB, Azevedo RS, Burattini MN, Lopez LF, Massad E. Vaccination against rubella: analysis of the temporal evolution of the age-dependent force of infection and the effects of different contact patterns. Phys Rev E. 2003;67:051907. doi: 10.1103/PhysRevE.67.051907. [DOI] [PubMed] [Google Scholar]
  2. Amaku M, Azevedo RS, de Castro RM, Massad E, Coutinho FAB. Relationship among epidemiological parameters of six childhood infections in a non-immunized Brazilian community. Mem Inst Oswaldo Cruz. 2009;104:897–900. doi: 10.1590/s0074-02762009000600013. [DOI] [PubMed] [Google Scholar]
  3. An der Heiden M, Bucholz U, Krause G, Kirchner G, Claus H, Haas WH. Breaking the waves: modeling the potential impact of public health measures to defer the epidemic peak of novel influenza A/H1N1. PLoS One. 2009;4:e8356. doi: 10.1371/journal.pone.0008356. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Anderson RM, May RM. Infectious Diseases of Humans: Dynamics and Control. Oxford University Press; Oxford: 1991. [Google Scholar]
  5. Belshe RB, Mendelman PM, Treanor J, King J, Gruber WC, Piedra P, et al. The efficacy of live attenuated cold-adapted, trivalent, intranasal influenza virus vaccine in children. N Engl J Med. 1998;338:1405–1421. doi: 10.1056/NEJM199805143382002. [DOI] [PubMed] [Google Scholar]
  6. Blower SM, Dowlatabadi H. Sensitivity and uncertainty analysis of complex models of disease transmission: an HIV model, as an example. Int Stat Rev. 1994;62:229–243. [Google Scholar]
  7. Briggs AH, Weinstein MC, Fenwick EAL, Karnon J, Sculpher MJ, Paltiel AD. Model parameter estimation and uncertainty analysis: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group – 6. Med Decis Making. 2012;32:722–732. doi: 10.1177/0272989X12458348. [DOI] [PubMed] [Google Scholar]
  8. Cauchemez S, Carrat F, Viboud C, Valleron AJ, Boëlle PY. A Bayesian MCMC approach to study transmission of influenza: application to household longitudinal data. Stat Med. 2004;23:469–3487. doi: 10.1002/sim.1912. [DOI] [PubMed] [Google Scholar]
  9. Centers for Disease Control and Prevention. Adult Vaccination Coverage, National Health Interview Survey. [accessed 16.10.2012];2009 http://www.cdc.gov/vaccines/stats-surv/nhis/2009-nhis.htm.
  10. Chen SC, Liao CM. Modelling control measures to reduce the impact of pandemic influenza among schoolchildren. Epidemiol Infect. 2008;136:1035–1045. doi: 10.1017/S0950268807009284. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Chowell G, Castillo-Chavez C, Fenimore PW, Kribs-Zaleta CM, Arriola I, Hyman JM. Model parameters and outbreak control for SARS. Emerg Infect Dis. 2004;10:1258–1263. doi: 10.3201/eid1007.030647. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Coelho FC, Codeco CT, Struchiner CT. Complete Treatment of Uncertainties in a Model for Dengue R0 Estimation. Cad Saude Publica, Rio de Janeiro. 2008;24:853–961. doi: 10.1590/s0102-311x2008000400016. [DOI] [PubMed] [Google Scholar]
  13. Crowe S, Utley M, Walker G, Grove P, Pagel C. A model to evaluate mass vaccination against pneumococcus as a counter measure against pandemic influenza. Vaccine. 2011;29:5065–5077. doi: 10.1016/j.vaccine.2011.04.034. [DOI] [PubMed] [Google Scholar]
  14. Elderd BD, Dukic VM, Dwyer G. Uncertainty in predictions of disease spread and public health responses to bioterrorism and emerging diseases. Proc Natl Acad Sci USA. 2006;103:15693–15697. doi: 10.1073/pnas.0600816103. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Flahault A, Vergu E, Coudeville L, Grais RF. Strategies for containing a global influenza pandemic. Vaccine. 2006;24:6751–6755. doi: 10.1016/j.vaccine.2006.05.079. [DOI] [PubMed] [Google Scholar]
  16. Fraser C, Donnelly CA, Cauchemez S, Hanage WP, Van Kerkhove MD, Hollingsworth TD, et al. Pandemic potential of a strain of influenza A (H1N1): early findings. Science. 2009;324:1557–1561. doi: 10.1126/science.1176062. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Galvani AP. Epidemiology meets evolutionary ecology. Trends Ecol Evol. 2003;18:132–139. [Google Scholar]
  18. Halloran ME, Hayden FG, Yang Y, Longini IM, Monto AS. Antiviral effects influenza viral transmission and pathogenicity: observations from household-based trials. Am J Epidemiol. 2007;165:212–221. doi: 10.1093/aje/kwj362. [DOI] [PubMed] [Google Scholar]
  19. Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57:97–109. [Google Scholar]
  20. Helton JC, Davis FJ. Illustration of sampling-based methods for uncertainty and sensitivity analysis. Risk Anal. 2002;22:591–622. doi: 10.1111/0272-4332.00041. [DOI] [PubMed] [Google Scholar]
  21. Helton JC, Davis FJ. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems. Reliab Eng Syst Saf. 2003;81:23–69. [Google Scholar]
  22. Hoeting JA, Madigan D, Raftery AE, Volinsky CT. Bayesian model averaging: atutorial. Stat Sci. 1999;14:382–417. [Google Scholar]
  23. Kass RE, Raftery AE. Bayes factors. J Am Stat Assoc. 1995;90:773–795. [Google Scholar]
  24. Keeling MJ, Rohani P. Modeling Infectious Diseases in Humans and Animals. Princeton University Press; Princeton, NJ: 2008. [Google Scholar]
  25. Krumkamp R, Kretzschmar M, Rudge JW, Ahmad A, Hanvoravongchai P, Westenhoefer J, et al. Health service resource needs for pandemic influenza in developing countries: a linked transmission dynamics, interventions and resource demand model. Epidemiol Infect. 2010;139(59):67. doi: 10.1017/S0950268810002220. [DOI] [PubMed] [Google Scholar]
  26. Lloyd AL. Sensitivity of model-based epidemiological parameter estimation to model assumptions. In: Chowell G, Hyman JM, Bettencourt LMA, Castillo-Chavez C, editors. Mathematical and Statistical Estimation Approaches in Epidemiology. Springer; New York: 2009. pp. 123–142. [Google Scholar]
  27. Longini IM, Koopman JS, Monto AS, Fox JP. Estimating household and community transmission parameters for influenza. Am J Epidemiol. 1982;115:736–751. doi: 10.1093/oxfordjournals.aje.a113356. [DOI] [PubMed] [Google Scholar]
  28. Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254:178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Massad E, Behrens RH, Burattini MN, Coutinho FAB. Modeling the risk of malaria for travelers to areas with stable malaria transmission. Malar J. 2009;8:296. doi: 10.1186/1475-2875-8-296. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Matser A, Hartemink N, Heesterbeek H, Galvani A, Davis S. Elasticity analysis in epidemiology: an application to tick-borne infections. Ecol Lett. 2009;12:1298–1305. doi: 10.1111/j.1461-0248.2009.01378.x. [DOI] [PubMed] [Google Scholar]
  31. Medlock J, Galvani AP. Optimizing influenza vaccine distribution. Science. 2009;325:1705–1708. doi: 10.1126/science.1175570. [DOI] [PubMed] [Google Scholar]
  32. Mercer GN, Barry SI, Kelly H. Modelling the effect of seasonal influenza vaccination on the risk of pandemic influenza infection. BMC Public Health. 2011;11:S11. doi: 10.1186/1471-2458-11-S1-S11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Metropolis N, Rosenbluth AW, Rosenbluth MN, Teller AH, Teller E. Equations of state calculations by fast computing machines. J Chem Phys. 1953;21:1087–1092. [Google Scholar]
  34. Mossong J, Hens N, Jit M, Beutels P, Auranen K, Mikolajczyk R, et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5:e74. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Mylius SD, Hagenaars TJ, Lugner AK, Wallinga J. Optimal allocation of pandemic influenza vaccine depends on age, risk and timing. Vaccine. 2008;26:3742–3749. doi: 10.1016/j.vaccine.2008.04.043. [DOI] [PubMed] [Google Scholar]
  36. Nuño M, Chowell G, Gumel AB. Assessing the role of basic control measures, antivirals and vaccine in curtailing pandemic influenza: scenarios for the US, UK and the Netherlands. J R Soc Interface. 2007;4:505–521. doi: 10.1098/rsif.2006.0186. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Pitman R, Fisman D, Zaric GS, Postma M, Kretzschmar M, Edmunds J, Brisson M. Dynamic transmission modeling: a report of the ISPOR-SMDM Modeling Good Research Practices Task Force Working Group – 5. Med Decis Making. 2012;32:712–721. doi: 10.1177/0272989X12454578. [DOI] [PubMed] [Google Scholar]
  38. Roberts MG, Baker M, Jennings LC, Sertsou G, Wilson N. A model for the spread and control of pandemic influenza in an isolated geographic region. J R Soc Interface. 2007;4:325–330. doi: 10.1098/rsif.2006.0176. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, et al. Global Sensitivity Analysis: The Primer. Wiley; West Sussex, England: 2008. [Google Scholar]
  40. Saltelli A, Tarantola S, Campolongo F, Ratto M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. Wiley; Hoboken, NJ: 2004. [Google Scholar]
  41. Samsuzzoha M, Singh M, Lucy D. Uncertainty and sensitivity analysis of the basic reproduction number of a vaccinated epidemic model of influenza. Appl Math Model. 2013;37:908–915. [Google Scholar]
  42. Sanchez MA, Blower SM. Uncertainty and sensitivity analysis of the basic reproductive rate, tuberculosis as an example. Am J Epidemiol. 1997;145:1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. [DOI] [PubMed] [Google Scholar]
  43. Sullivan KM, Monto AS, Longini IM. Estimates of the US health impact of influenza. Am J Public Health. 1993;83:1712–1716. doi: 10.2105/ajph.83.12.1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Thompson WW, Shay DK, Weintraub E, Brammer L, Cox N, Anderson LJ, et al. Mortality associated with influenza and respiratory syncytial virus in the United States. J Am Med Assoc. 2003;289:179–186. doi: 10.1001/jama.289.2.179. [DOI] [PubMed] [Google Scholar]
  45. Thompson WW, Shay DK, Weintraub E, Brammer L, Bridges CB, Cox N, et al. Influenza-associated hospitalizations in the United States. J Am Med Assoc. 2004;292:1333–1340. doi: 10.1001/jama.292.11.1333. [DOI] [PubMed] [Google Scholar]
  46. Tracht SM, Del Valle SY, Hyman JM. Mathematical modeling of the effectiveness of facemasks in reducing the spread of novel influenza A (H1N1) PLoS One. 2011;5:e9018. doi: 10.1371/journal.pone.0009018. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Tuite AR, Fisman DN, Kwong JC, Greer AL. Optimal pandemic influenza vaccine allocation strategies for the Canadian population. PLoS One. 2010;5:e10520. doi: 10.1371/journal.pone.0010520. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Vanden Driessche P, Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
  49. Vynnycky E, White RG. An Introduction to Infectious Disease Modeling. Oxford University Press; New York: 2010. [Google Scholar]
  50. Wu J, Radhika D, Gambhir M, Remais JV. Sensitivity analysis of infectious disease models: methods, advances and their application. J R Soc Interface. 2013;10:20121018. doi: 10.1098/rsif.2012.1018. [DOI] [PMC free article] [PubMed] [Google Scholar]

RESOURCES