Spatial resolution in depth for time-resolved diffuse optical tomography using short source-detector separations

Abstract

Diffuse optical tomography for medical applications can require probes with small dimensions involving short source-detector separations. Even though this configuration is seen at first as a constraint due to the challenge of depth sensitivity, we show here that it can potentially be an asset for spatial resolution in depth. By comparing two fiber optic probes on a test object, we first show with simulations that short source-detector separations improve the spatial resolution down to a limit depth. We then confirm these results in an experimental study with a state-of-the-art setup involving a fast-gated single-photon avalanche diode allowing maximum depth sensitivity. We conclude that short source-detector separations are an option to consider for the design of probes so as to improve image quality for diffuse optical tomography in reflectance.

1. Introduction

Diffuse optical tomography (DOT) is a medical imaging technique providing three-dimensional maps of the distribution of absorption and diffusion optical coefficients inside an organ. These maps are obtained thanks to non-invasive measurements by placing sources of near-infrared light and detectors around the organ and analyzing the collected light. In the past twenty years, DOT has been used to image a large variety of organs and tissues and in particular broadly applied to breast and brain imaging [1–3]. Most DOT instruments consist in spherical or cylindrical configurations of sources and detectors placed around the organ to image. Nevertheless, for some organs like the prostate [4], the anatomy does not allow this geometry. In other cases, for practical reasons, a compact instrument easy to install on the patient can be preferred to one featuring a large number of optical fibers to attach all over the imaged organ. This is the case of premature infants brain imaging. An alternative is a single “optical probe”: it consists of a pad holding a combination of optical fibers for illumination and detection distributed on a few cm² and enabling reflectance measurements at short source-detector separation. Such a probe can be positioned at the surface of an organ to image locally its optical properties. However, reflectance measurements at short source-detector separation (SD) are not commonly used because the dynamic range to exploit is too large in order to specifically measure photons carrying depth information. Such a dynamic range is not achievable with conventional setups like continuous wave (CW) or conventional time-resolved setups with time-correlated single-photon counting (TCSPC).

We have shown in a previous paper [5] that a time-resolved setup combining TCSPC and fast-gated single-photon avalanche diodes (SPADs) enabled to exploit the late photons carrying depth information for DOT with reflectance measurements at short source-detector separations (SD = 5 and 15 mm). This setup can detect and localize in depth a single buried absorbing inclusion better than conventional non-gated TCSPC setups. Having shown that depths of 2 to 3 cm can be reached with DOT at such short interfiber distances thanks to the fast-gated SPADs, we now investigate the imaging potential of this configuration. More specifically, we show here that short source-detector separations are not only a constraint for DOT but can also become an advantageous tool to improve spatial resolution to a certain depth in the imaged medium.

Several studies have already discussed the issue of spatial resolution in DOT using a time-resolved approach (TR-DOT) [6, 7]. Yet, only recently, the proposal of time-gated acquisition to suppress early photons [8] opened the way to the full exploitation of short source-detector distances. With a theoretical and general approach, a previous simulation study compared the contrast profiles of time-resolved measurements at null versus SD = 3 cm [9]. Nevertheless, the impact of short SD on the attainable resolution in a full 3D tomographic reconstruction is yet to be investigated. In this context, our approach is empirical: conclusions are drawn in the precise case of tomographic reconstructions of an object and its corresponding source-detector separations for image acquisition.

So far, we have presented results only on 2D DOT [5, 10, 11]. In the present paper, we show our first results with a full 3D problem and 3D reconstruction algorithm. We compare reconstruction results obtained with two fiber optic probes having the same design but different scale factors. In the first probe, featuring nine source-detector pairs, sources and detectors are separated by SD = 15 mm. The second probe contains the same number and similar distribution of sources- detectors pairs, but separated by SD = 10 mm. We compare the ability of these two probes to separate and localize two absorbing inclusions deeply embedded in a diffusive medium.

First, we study the intrinsic spatial resolution of the two probes on simulations, without adding photonic noise, in order to identify the sole effect of geometry and photon migration. Secondly, we confirm our conclusions with experimental data containing real photonic noise and other sources of experimental noise. As measurements at short source-detector separations are relevant only when a high dynamic range (DR) is available, we test it with a state-of-the art setup including a fast-gated SPAD, enabling a large DR and depth sensitivity [5, 12]. Our goal is to demonstrate that such a setup enables to consolidate the simulated performances and to show what can be achieved with optical probes and state-of-the-art time-resolved instruments.

2. Simulation study

2.1 Methods

Optical probes. There are an unlimited number of possible acquisition geometries. A simple configuration often used in TR-DOT consists in regularly alternating a source and a detection fiber. This type of probe is used in a study on spatial resolution of TR-DOT versus CW-DOT, as reported in [7]. We focus on this type of probe and analyze the spatial resolution in depth obtained with probes featuring the same configuration of sources and detectors, but with a different scale factor. Both acquisition geometries consist of 9 source-detector pairs with SD = 15 and 10 mm (Fig. 1 ).

Fig. 1.

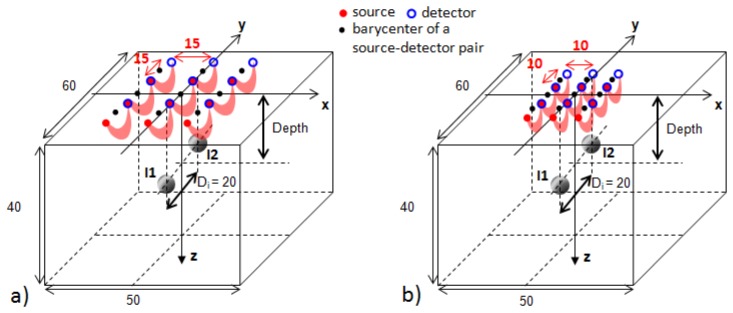
Acquisition geometries: a) probe with SD = 15 mm, b) probe with SD = 10 mm. Red areas schematically depict the “banana shapes” or sensitivity matrices of the measurements between pairs used for DOT reconstructions (9 in total for each probe). For both probes, the barycenter of the central source-detector pair is aligned with the barycenter of the two inclusions along the y axis. The parallelepiped of 50 x 60 x 40 mm depicts the volume employed in the DOT reconstructions. All dimensions are in mm.

Object to image. We focus on the spatial resolution in one direction (y axis on Fig. 1) and on the ability of the probes to separate two absorbing inclusions in this direction. In the whole study, the inclusions I1 and I2 are two spheres of 1 cm diameter, aligned along the y axis and separated by the distance D_i = 20 mm center to center. We illustrate the differences in spatial resolution obtained with the two probes for the following cases: I1 and I2 both positioned at the same depth, varying between 10 and 25 mm with steps of 5 mm. The absorption coefficient µ_a is set to 0.1 cm⁻¹ for the background and 0.8 cm⁻¹ for the inclusions, while the reduced scattering coefficient µ_s’ is set to 10 cm⁻¹ in the whole object.

Direct model. The measurements or time-point spread functions (TPSFs) are simulated by solving the diffusion equation in 3D with the finite-volume method. They are calculated from 0 to 4 ns with a time step of dt = 4.1 ps. No statistical noise is added in order to strictly evaluate the impact on spatial resolution of photon migration for each acquisition geometry.

Inverse problem. The DOT image reconstruction method is the same as described previously in [11]. In summary, for both probes, a set of the first 25 orders of the Mellin-Laplace transform (with p = 3 ns⁻¹) is used to extract data from different time-windows of the TPSFs [10]. The solution to the inverse problem is then approached by an iterative method in which the 3D absorption maps and the calculated sensitivity matrix are updated at each step. The algorithm converges with the stabilization of the reconstructed depth of the inclusions after 15 iterations. All images presented in this section were extracted from the 15th iteration of the algorithm.

2.2 Results

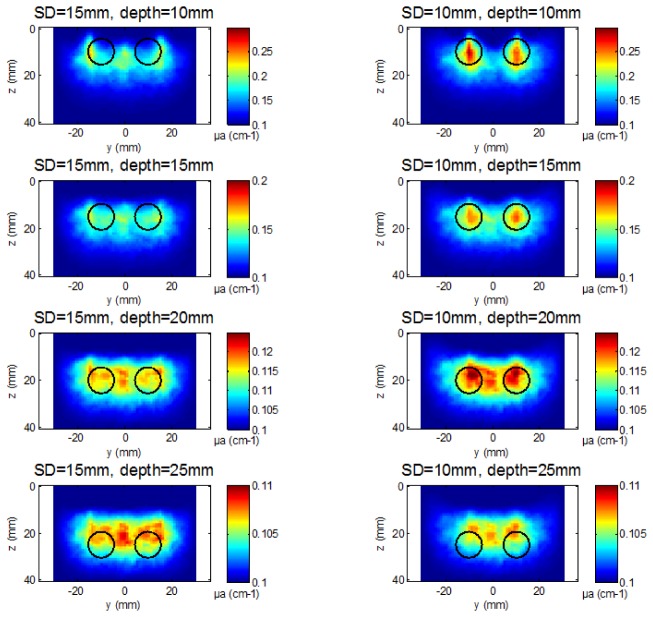
Figure 2 displays cut views of the reconstructed 3D images along the plane (y, z) at x = 0, for both probes at all tested depths. By observing these images, one can already obtain a qualitative impression of the difference in spatial resolution achieved with the two probes. Moreover, as we study the spatial resolution along the y axis, we specifically analyze the µ_a profiles along the y axis at x = 0 mm. More particularly, we seek the presence of maxima of µ_a at y = + 10 and – 10 mm and a local minimum at y = 0 mm, suggesting the possibility to separate the two inclusions. Figure 3 depicts for each 3D image the profiles of dµ_a (µ_a minus background value) along the y axis at x = 0 mm and z equal to the mean reconstructed depth. To calculate this mean reconstructed depth for each tested case, we isolate the pixels above the threshold of 50% of the maximum reconstructed dµa and calculate the z coordinate of the barycenter of these pixels. For a better readability, all profiles are normalized by the maximum value of dµ_a. These profiles enable to better quantify the variations in absorption and precisely localize the peaks.

Fig. 2.

Reconstructed µ_a maps (cut views along plane (y,z) at x = 0) for both probes at all tested depths. Black circles indicate the real position and size of the two inclusions.

Fig. 3.

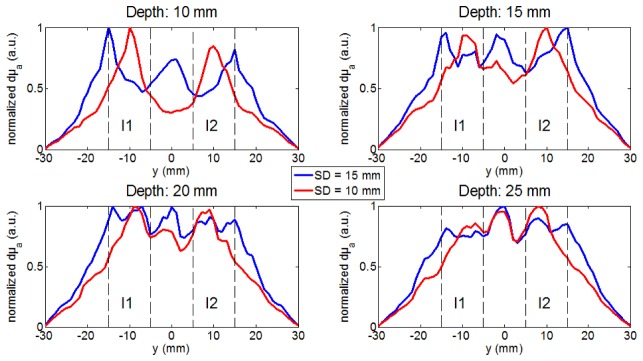
dµ_a profiles (normalized by maximum) along y axis at x = 0 and z = mean depth extracted from Fig. 2. The dotted lines delimit the width of I1 and I2 along the y axis.

Firstly, when looking at the depths of 10 and 15 mm, the results are significantly different for the two probes. With the probe using SD = 10 mm, one can clearly distinguish the presence of two different absorbing blobs (Fig. 2) centered at y = −10 mm and + 10 mm (Fig. 3). On the contrary, with the probe using SD = 15 mm, these two blobs are not visible (Fig. 2). Instead, there is an almost continuous large absorbing blob featuring three spots with slightly higher absorption, located at y = −15, 0 and + 15 mm (Fig. 3), corresponding to the center of the 3 source-detector pairs along the y axis. In other words, only the probe with SD = 10 mm is able to separate the two inclusions.

Secondly, for the deepest positions of the inclusions, 20 and 25 mm, the results get closer for both probes. In the absence of added noise, the signal to noise ratio (SNR) is infinite and therefore sufficient to detect the two inclusions at these two depths with both probes. However, a single blob is seen, the two inclusions cannot be separated anymore (Fig. 2 and 3). This is a direct effect of photon migration: the sensitivity maps at late times (and therefore high orders of Mellin-Laplace transform) penetrate deep in the medium but are also broader than the ones at early times.

3. Experimental validation

Having characterized the intrinsic spatial resolution of the two probes with simulations, we now test them experimentally with a high DR system enabling to have a good SNR on late photons and to image deeper than conventional setups [5].

3.1 Materials and methods

Phantom. The two absorbing inclusions are made of resin, TiO₂ particles and black ink in order to reach µ_a = 0.8 cm⁻¹ and µ_s’ = 10 cm⁻¹. They are molded in the shape of a cylinder of 8 mm diameter and 12 mm height, yielding almost the same volume of the simulated spheres. The inclusions are inserted in a liquid background made of water, Intralipid® and black ink, prepared to reach µ_a = 0.1 cm⁻¹ and µ_s’ = 10 cm⁻¹ at λ = 820 nm. These two inclusions are placed on top of two white needles inserted in a white plate. This holding system can be moved automatically inside the liquid background; its influence on the optical measurements was proved to be negligible (data not shown). Differently from simulations, the inclusions are now constructed in the shape of a cylinder (almost rectangular) instead of a sphere. We have previously shown in the case of totally absorbing objects, that the two shapes yields a comparable perturbation as far as the volume is kept the same [13].

Probe. We mimic the probes of simulations (Fig. 1) by using a single source-detector pair at the surface of the phantom with two interfiber distances, either 15 mm or 10 mm. This single source-detector pair is fixed at the surface of the liquid and the object to image (the two inclusions) is scanned in the background liquid. For each probe, the measurements are carried out in 9 positions in order to mimic the desired probes of featuring 9 source-detector pairs.

Measurement chain. The chosen setup aims at maximizing the DR of the TPSFs to increase the depth sensitivity. A fast-gated SPAD is associated to TCSPC [12]. The fast-rise time of the detector (< 200 ps) enables it to be in the OFF state when numerous early photons arrive and in the ON state to count late photons. The procedure consists in measuring each TPSF in different time-portions by temporally moving the gate with a programmable delayer. For each time-gate, a variable optical attenuator adjusts the incident source power to reach the maximum count of 10⁶ photons per second. The source power is a fiber-based 4-wave mixing laser (Fianium, UK), operating at λ = 820 nm and providing pulses of 26 ps full width at half maximum at 40 MHz. All details on this setup and acquisition of the TPSFs with high dynamic range can be found in [5]. Here, for each TPSF, 6 time-gates of 5 ns temporal width are measured. The temporal positions of the gates and the corresponding attenuation values are tuned to each source-detector separation. In all cases, the acquisition time is 1 second per time-gate. In this experiment, the power is increased between the first and last gate by a factor of 500 for SD = 15 mm and of 3000 for SD = 10 mm.

Acquisition protocol. We first choose one of the 9 positions of the x-y scan and acquire the measurements at all gates for the first depth of the two inclusions. We then repeat it for the other tested depths and for a “homogeneous” case (the inclusions are both positioned “out of sight”, at the depth of 5 cm). We repeat these series for all other positions of the x-y scan. Let us note that the “homogeneous” measurement is required by our DOT reconstruction algorithm [11], since it is used as a reference unperturbed state. We acquire this reference at each x-y position of the scan in order to minimize the influence of the experimental drifts (laser power, phantom settling).

Pre-processing. Each TPSF is reconstituted by using the 6 time-gated measurements rescaled with the attenuation values used for their acquisition. All details on this procedure can be found in [5].

Data analysis. After pre-processing the TPSFs with high DR, we apply the same 3D DOT reconstruction algorithm as described earlier for simulations (2.1). As the TPSFs are now degraded by statistical noise, we use only the 15 first orders of the Mellin-Laplace transform with p = 3 ns⁻¹ for both probes because higher orders are affected too much by noise.

3.2 Results

In the first place, we present results with the two inclusions positioned at the same depth, as in simulations. We focus on the depths of 15 mm – deepest case for which the two inclusions can be separated with SD = 10 mm – and 25 mm – deepest position that could be detected with this setup. We finish this section by looking at a more difficult case in which one inclusion (I1) is positioned 5 mm lower than the other (I2).

Inclusions at the same depth. At the depth of 15 mm, the DOT images obtained with the two probes are significantly different. The separation and localization of the two inclusions is clearly better with the smallest probe (SD = 10 mm). This is clear on the reconstructed image (Fig. 4 ) and on the profiles of µ_a in depth (Fig. 5 ). Moreover, as seen on simulations, with the largest probe (SD = 15 mm), the two inclusions are not localized at their real positions but below the barycenter of the two source-detector pairs at the extremity of the probe (y = −15 mm and + 15 mm). There is also an artifact showing a third false local maximum at y = 0 mm (Fig. 4 and 5). Therefore the probe with SD = 10 mm allows a better spatial resolution than the one with SD = 15 mm when the object to image is located at the depth of 15 mm. Finally one can note that the separation of the two inclusions obtained in this experimental case is better than in simulation (Fig. 3). Indeed, even if both spherical (simulation) and cylindrical (experimental) inclusions have been inserted at the same depth for comparison purpose, the object is a little higher in the latter case (12mm rather than 10mm); thus it’s nearer to the surface at some point, which explains the difference between experimental and simulation results.

Fig. 4.

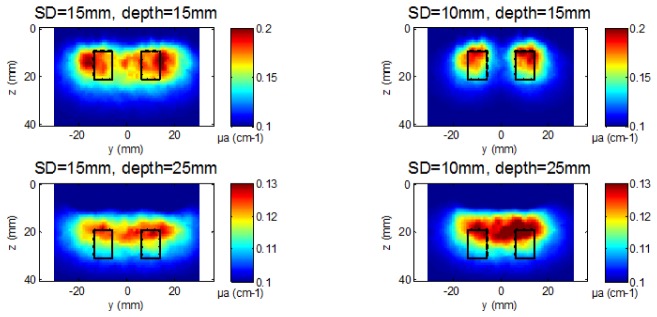
Reconstructed µ_a maps with experimental data (cut views along plane (y,z) at x = 0) for both probes at the depths of 15 and 25 mm. Black rectangles indicate the real position and size of the two inclusions.

Fig. 5.

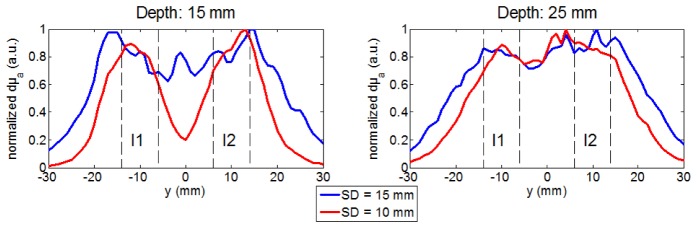
dµ_a profiles (normalized by maximum) along y axis at x = 0 and z = mean depth extracted from Fig. 4. The dotted lines delimit the width of I1 and I2 along the y axis.

At the depth of 25 mm, we can detect the two inclusions down to the depth of 25 mm thanks to the high DR of the TPSFs acquired with the fast-gated SPAD. However, the spatial resolution is degraded with both probes. The reconstructed images and the profiles of dµ_a show that a single inclusion is reconstructed with both probes: the two inclusions cannot be separated (Fig. 4 and 5).

Inclusions at different depths. We complete and finish this experimental study with a more complex object constituted of the two absorbing inclusions positioned at different depths (case 1: I1 at 15 mm and I2 at 10 mm, case 2: I1 at 20 mm and I2 at 15 mm). This configuration is more challenging because the algorithm inherently tends to detect and localize the shallowest inclusions. Here, more iterations (i.e. 20) of the reconstruction algorithm are used in order to properly reconstruct the deepest inclusion.

When I1 is positioned at the depth of 15 mm and I2 at 10 mm, the obtained DOT images show the same trends as seen with the two inclusions at the same depth. With the smallest probe, the two inclusions are better separated and localized in y and z than with the largest one (Fig. 6 and 7 ). The advantage of the smallest probe is also visible for deeper positions of the inclusions (I1 at 20 mm and I2 at 15 mm) as it can be seen on the images (Fig. 6) and on the profiles of dµ_a in depth (Fig. 7). Indeed, in Fig. 6 and 7, we show that an artifact appears in between when using the largest SD distance while the two inclusions are clearly resolved with the shortest distance SD = 10 mm.

Fig. 6.

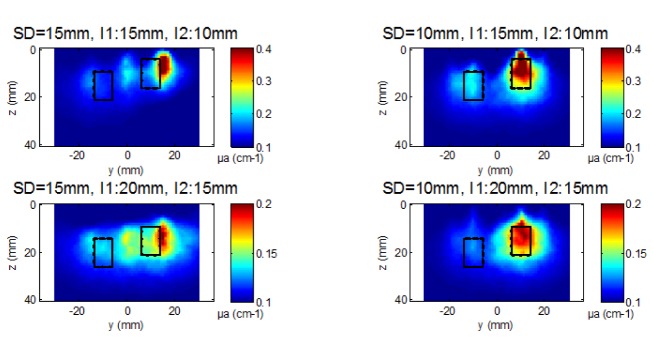
Reconstructed µ_a maps with experimental data (cut views along plane (y,z) at x = 0) for both probes for the depth of 15 mm for I1 (left inclusion) and 10 mm for I2 (right inclusion) on the top row and the depth of 20 mm for I1 and 15 mm for I2 on the bottom row. Black rectangles indicate the real position and size of the two inclusions.

Fig. 7.

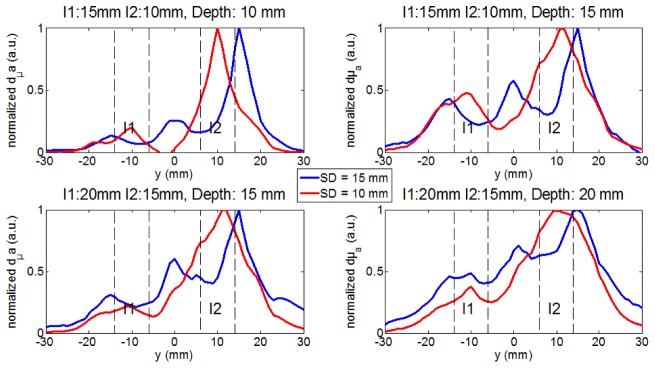
dµ_a profiles (normalized by maximum) along y axis at x = 0 and at the real depths of I1 and I2, extracted from Fig. 6. The dotted lines delimit the width of I1 and I2 along the y axis.

These results confirm that, with a proper probe design, our DOT algorithm based on the Mellin-Laplace transform can identify a deep inclusion in the presence of a more superficial one. However, more iterations of the algorithm are needed in order to detect the deepest inclusion on the DOT image. In any case, the deepest inclusion is reconstructed with a lower µ_a than the superficial inclusion. Further algorithms developments should tackle the quantification problem of objects located at different depths.

4. Discussion

Simulations without added statistical noise confirm the intrinsic limitation of spatial resolution in depth due to the broadening of the sensitivity maps [10], which is a direct physical effect of photon migration. Down to a certain depth (here 15 mm), shorter interfiber distances enable to obtain a better spatial resolution than larger ones but this advantage is lost when observing deeper layers (here starting from 20 mm). Of course, benefitting from this advantage of short source-detector separations requires access to detection techniques allowing the measurement of late photons. Our study is limited to a reduced set of source-detector pairs, for compact probes and instruments. A better outcome is expected with dense optode coverage, as clearly demonstrated for CW measurements in the case of brain imaging [14]. To finish, this non-exhaustive simulation study also shows the need for a compromise between the size of imaged area and the spatial resolution, when designing an optical probe for a dedicated medical application.

Our experimental study has shown consistent results with the simulations. State-of-the art instruments allowing the acquisition of TPSFs with a large dynamic range have increased the relevancy of configurations with short interfiber distances, limited by depth sensitivity with previous instruments. Let us note that similar experimental studies could also be carried out with other types of detectors like photomultiplier tubes (PMTs) or hybrid PMTs. However, the smallest dynamic range would limit the imaged depth in the medium. In our study, we have shown that configurations with short interfiber distances can now realistically be included in the design of compact instruments and improve the spatial resolution, until a certain depth. However, the DR of current fast-gated SPADs setups is still limited by the intrinsic noise in the detector [15]. Further improvements on this technology should benefit directly TR-DOT.

5. Conclusion

In reflectance DOT, spatial resolution is inherently degraded when depth increases, due to the physical phenomenon of photon migration in turbid media. However, we have shown on a specific example that using optical fiber arrangements with short interfiber distances could improve the spatial resolution down to a certain depth. This was first illustrated with simulations studying the intrinsic limitations of each probe configuration. It was then confirmed by an experimental study carried out on a state-of-the art setup chosen for its large depth sensitivity.

We have seen that the smallest probe involving the shortest source-detector separation has an advantage over the larger one: it offers an improved spatial resolution down to a certain depth. When the two inclusions are positioned at the same depth, the probe with the smallest scale factor enables a better spatial resolution down to the depth of 15 mm. For deeper positions of the inclusions, neither the large probe nor the small one can separate them. In the most complex case with the two inclusions positioned at different depths, the smallest probe also provides a better spatial resolution in depth than the largest one.

Concretely, our setup combining a fast-gated SPAD and TCSPC enabled to detect the two absorbing inclusions with robust contrast down to 25 mm with both tested probes, featuring source-detector separations of 10 and 15 mm. The imaged depth range was comparable with both tested interfiber distances. We remind here that these results were obtained using a time-gated setup. The maximum depth would be smaller with the smallest interfiber distance adopting more standard non-gated setups [5].

To conclude, this non-exhaustive study on realistic probe designs has shown that short source-detector separations should not only be seen as a constraint for DOT. Using them to design a small probe can improve the spatial resolution down to a certain depth (in the conditions tested here, down to 15 mm). Therefore, with measurement chains allowing a large dynamic range for the TPSFs, short source-detector separations can be used to image a large depth range and improve spatial resolution down to a certain depth. This study brings new elements for the design of probes dedicated to a specific medical application. It underlines the compromise to make between size of the imaged area, spatial resolution and number of optical fibers (linked to total acquisition time). Further studies with other probe designs should complement these conclusions to give a broader view on the issue of fiber optic probe design for time-resolved DOT.