Optimization of multimodal spectral imaging for assessment of resection margins during Mohs micrographic surgery for basal cell carcinoma

Abstract

Multimodal spectral imaging (MSI) based on auto-fluorescence imaging and Raman micro-spectroscopy was used to detect basal cell carcinoma (BCC) in tissue specimens excised during Mohs micrographic surgery. In this study, the MSI algorithm was optimized to maximize the diagnosis accuracy while minimizing the number of Raman spectra: the segmentation of the auto-fluorescence images was optimized according to the type of BCC, sampling points for Raman spectroscopy were generated based on auto-fluorescence intensity variance and segment area, additional Raman spectra were acquired when performance of the segmentation algorithm was sub-optimal. The results indicate that accurate diagnosis can be achieved with a sampling density of ~2,000 Raman spectra/cm², based on sampling points generated by the MSI algorithms. The key benefit of MSI is that diagnosis of BCC is obtained based on intrinsic chemical contrast of the tissue, within time scales similar to frozen-section histopathology, but without requiring laborious sample preparation and subjective interpretation of stained frozen-sections.

1. Introduction

Basal cell carcinoma (BCC) is the commonest cancer in humans. Annually there are 700,000 new patients diagnosed with BCC in Europe [1] and more than 2,800,000 in the USA [2]. While most BCCs on the body are low risk and are commonly treated by standard excision, certain BCCs can have invisible tumor spread, and are therefore at higher risk of incomplete excision. “High-risk” BCCs include tumors located in the so-called H-zone of the face (ear, eyelid, eyebrow, nose, temple), tumors larger than 2 cm diameter, BCCs with poorly defined edges, morphoeic/infiltrative or aggressive histological subtypes [1]. Recurrent or previously incompletely excised BCCs are also considered “high-risk” [1]. The gold-standard treatment for these “high-risk” BCCs is Mohs micrographic surgery (MMS) [3]. In MMS, sequential layers of skin tissue are excised and the entire resection margin is assessed during the surgery by frozen-section histopathology. This procedure maximizes the removal of tumor cells, while sparing as much healthy tissue as possible. The 10-year tumor recurrence rates for high-risk primary BCCs treated by standard excision are 12.2% and 4.4% for MMS; for recurrent BCCs, 10-year recurrence rates are 3.9% for MMS and 13.5% and surgical excision [4]. Although MMS provides improved treatment outcome compared to other treatment options, the need for a pathologist or specialized surgeons to diagnose frozen-sections during surgery has limited the widespread use of MMS, leading to cases of inappropriate inferior treatment and healthcare inequalities. In addition, the frozen-section histopathology requires laborious and time-consuming procedures, increasing the costs compared to standard excision.

Raman micro-spectroscopy (RMS) is an analytical technique based on the interaction of light with the molecules in a sample and can accurately measure the chemical composition of cells and tissue. Changes in the molecular spectra of tissues measured by RMS can be used to build multivariate classification models, which allow objective diagnosis of independent tissue samples obtained from new patients. Recently, diagnosis with sensitivity and specificity higher than 90% was demonstrated for many cancer types, including skin [5–8]. Nevertheless, achieving objective diagnosis images of skin specimens with high spatial resolution (20-50 μm) required long data acquisition and analysis times (~5-hour per 1 mm × 1 mm area) [6, 8]. To reduce the data acquisition time and make Raman spectroscopy suitable for intra-operative diagnosis of cancer, selective sampling strategies have been proposed [9], including multimodal spectral imaging (MSI) based on auto-fluorescence imaging and Raman microscopy [10, 11]. First, tissue auto-fluorescence imaging, which has high sensitivity and speed but low specificity, was used to determine the main spatial features of the sample. Then, the information obtained from the auto-fluorescence images was used in an automated manner to select and prioritize the sampling points for Raman spectroscopy. This sampling strategy made it possible to obtain diagnosis of nodular BCC in skin samples as larger as 1 cm × 1 cm skin with only 500-1500 Raman (~20-40 minutes) [10]. While this initial study demonstrated the potential of selective-sampling Raman microscopy based on integrated auto-fluorescence and Raman spectroscopy for diagnosis of resection specimens, the algorithms for generating sampling points was not optimized (considered a fixed number of sampling points per segments).

In this paper, we optimized the MSI algorithm to increase the diagnosis accuracy while minimizing the number of Raman spectra. The segmentation algorithms for the auto-fluorescence images were optimized for nodular/micro-nodular BCC and infiltrative BCC, as in practice this information is known prior to surgery. The number of sampling points for Raman spectroscopy for each segment was determined based on the auto-fluorescence intensity variance and area of the segment. Given that the segmentation of auto-fluorescence images does not delineate perfectly the tumor regions from healthy tissue, iterative steps for additional Raman measurements were introduced for the segments in which the classification of the Raman spectra identified as BCC but BCC was not the dominant class.

2. Materials and methods

2.1 Multimodal spectral imaging algorithm

The optimized MSI algorithm proposed in this study is schematically described in Fig. 1 .

Fig. 1.

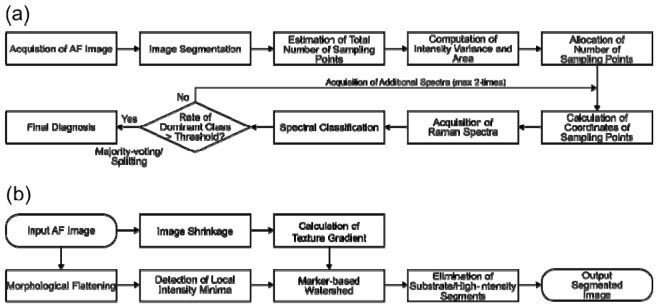
(a) Schematic flowchart of the MSI algorithm based on auto-fluorescence imaging (AF) and Raman spectroscopy. (b) Flow chart for the segmentation algorithm for the AF intensity images of skin tissue.

The MSI algorithm commences by recording an auto-fluorescence intensity image for the entire tissue area (excitation 365 nm, emission 447 nm). Then, the auto-fluorescence image is segmented so that the entire area of the tissue is divided into a set of disconnected segments. A typical segmented image consists of hundreds of closed segments, and each segment ideally corresponds to individual distinctive tissue structures. The total number of sampling points for Raman spectroscopy was computed based on the total area of the sample, Area_total, and the sampling density, σ_sampling: N_{sampling, total} = σ_sampling × Area_total. The value of σ_sampling was selected so that the entire diagnosis of a typical tissue specimen can be completed within the time-scale compatible with MMS (e.g., 20-60 min per tissue layer).

The auto-fluorescence intensity variance, Var, and area, Area, of each segment were then calculated. Using these two values, the number of sampling points for each segment was estimated based on:

$$N_{sampling}\left(i\right)=N_{min}+\frac{Var\left(i\right)\times Area (i)}{{{\displaystyle \sum }}_{i=1}^k\left[Var\left(i\right)\times Area(i)\right]}\times N_{rest} ,$$ (1)

where N_sampling(i) is the number of sampling points allocated to the segment i, N_min is the minimum number of sampling points for each segment, k is the total number of segments, Var(i) is the intensity variance in the segment i, Area(i) is the area of the segment i, and N_rest = N_{sampling, total} – k × N_min is the dditional sampling points that can be allocated to segments after the allocation of the minimum sampling points required for each segment.

Equation (1) is based on two assumptions: 1) if the segmentation algorithm provides well-discriminated tissue structures, the intensity variance of such segments is low (segments are likely to be homogenous), therefore fewer Raman spectra are needed to establish the diagnosis; 2) if the area of a segment is large, the segment has a higher probability to have a more complex structure, thus the segment is allocated more sampling points. In order to avoid the case in which certain segments have no sampling points, each segment is allocated at least a minimum number of sampling points, N_min. As anticipated, if N_min or k are large, the number of sampling points which is distributable to each segment in addition to the N_min sampling points becomes small and, in the worst case, it ends up with N_rest = 0 (i.e., no additional sampling, just the minimum number of sampling). In this study, we tested two values for this minimum sampling number: N_min = 2 and 3.

For each segment i, N_sampling(i) Raman spectra were measured and then assigned a class based on a multivariate classification model (see section 2.3). The coordinates of the sampling points for each Raman spectra were calculated using a k-mean clustering algorithm. After classifying each spectrum, the percentage of the Raman spectra corresponding to each class was calculated for each segment. If this percentage of spectra classified as BCC was above a certain threshold, t, then this class was set as the “dominant class” and the diagnostic of the entire segment was BCC. If the classification model identified BCC in a segment but the BCC class was not the dominant class in the segment (percentage of BCC spectra was below the threshold t), an additional N_sampling(i) sampling points were generated for the segment and a new set of Raman spectra were acquired. The aim of this additional step, which was performed maximum twice, was to increase the number of Raman spectra measured in the areas of the tissue where the auto-fluorescence image were sub-optimally segmented. For these cases, there is a high probability that the segments contain multiple tissue structure, and therefore no dominant class can be obtained. Therefore, at the end of the two cycles of additional Raman spectra, the segments are split into n smaller segments, where n is the number of classes identified inside the segment.

The size of tumor regions in a skin specimen can vary, from 20 to 200 μm in the case of morphoeic/infiltrative BCC, to more than 1 mm in the case of nodular BCC. This wide range makes it difficult to establish a single segmentation algorithm to account for all types of BCC. Because the type of BCC is known prior to Mohs surgery, it is possible to optimize separate segmentation algorithms based on the expected size of the tumors. In this study, the tissue samples were divided into two groups: i) samples expected to contain tumors larger than 300 μm (e.g., nodular, superficial, micronodular, and pigmented BCCs), which usually appear as blocks of tumors, and ii) samples expected to have a large number of smaller tumors (e.g., 20-200 μm for morphoeic/infiltrative BCCs). A schematic description of the segmentation algorithms is presented in Fig. 1(b).

The core of the segmentation algorithm is the marker-controlled (or marker-based) watershed algorithm [12], to which the texture-enhanced gradient and the local intensity minima of morphologically flattened tissue auto-fluorescence image were adopted [13]. First, the raw auto-fluorescence image was shrunk to a resolution of 1024 × 1024 pixels and the texture-enhanced gradient was computed. In parallel, the raw auto-fluorescence image was flattened by morphological opening and then by closing, and the local intensity minima were detected [12]. The two images were then combined and the locations of local intensity minima were marked with minus infinity value. Using this marked texture-enhanced gradient image, watershed segmentation of the combined image was performed. The segments were ranked in order of increasing average fluorescence intensity. Progressive linear regressions of the intensity on the ranks were carried out to identify a transition from a linear to a nonlinear trend. The transition was determined as the point at which the coefficient of determination R² fell below 0.98. All segments with intensity higher than this threshold were classified as dermis and excluded from the Raman measurements [10].

The software code for the computation of the texture-enhanced intensity gradient followed O’Callaghan et al.’s algorithm [13] and was based on the code shared by Naidu [14]. For the computation of the texture-gradient with dual-tree complex wavelet transform was used [15], and the auto-fluorescence images were reduced to 1024 × 1024 pixels, regardless of the size, aspect ratio, and resolution of the raw images. The aspect ratio of the raw images was restored after the computation of the texture-enhanced gradient with the fixed resolution: 13.8 μm pixel⁻¹ for the images containing large tumors and 6.9 μm pixel⁻¹ for small tumors. These resolutions were chosen so that the resulting segmented images of large tumor samples had fewer than 1,000 segments (assuming that the sample area was 1 cm × 1 cm) and those of small tumors had ~1,000 segments (the area of out two morphoeic/infiltrative samples are 5.5 mm² and 11 mm²).

As BCC areas have lower auto-fluorescence intensity compared to healthy dermis, local intensity minima were used as markers. In order to detect the local intensity minima in an original auto-fluorescence image, the image was first resized into the same resolution: 13.8 μm pixel⁻¹ for the image with large tumors and 6.9 μm pixel⁻¹ for small tumors. Then, the resized image was treated by morphological processing (opening and successive closing) using disk-structuring elements with optimized radius r (units defined in pixels), for small and large tumors [12]. The purpose of this morphological processing was to flatten the noisy signals and enhance the detection of local intensity minima. These radii of disk-structuring elements were chosen by comparing the results of the successive watershed segmentation. In general, if the structuring element is too large, it leads to under-segmentation, if r is selected too small, the image is over-segmented.

2.2 Skin tissue samples

All skin tissue samples used in this study were obtained from patients undergoing MMS for treatment of BCC on the face and neck areas at Nottingham University Hospitals (consent was obtained). Ethical approval was granted by the Nottingham Research Ethics Committee (07/H0408/172). After excision, tissue specimens were soaked in optimal cutting temperature medium (OCT) and then frozen with a cryogenic spray (Frostbite, Surgipath). For MSI experiments, microsections (20 μm thickness) were cut and deposited on an MgF₂ cover-slip. An adjacent microsection (5-10 μm thickness) was deposited on a glass coverslip and stained with hematoxylin and eosin (H&E). This stained section was used for diagnostic by the Mohs surgeon and a pathologist. A total of 20 tissue samples were used in this study (10 for the optimization of the segmentation algorithms and 10 for evaluation of the complete algorithms).

2.3 Instrumentation and multivariate classification model

The instrument used in this study was described in detail previously [10]. The instrument consisted of a Raman microscope based on an inverted optical microscope (Eclipse Ti, Nikon). A 50 × /0.55 objective (Leica), spectrometer (77200, Oriel), back-illuminated deep-depletion CCD (DU401-A-BR-DD, Andor Technology), and a movable stage (H107 ProScan II, Prior Scientific) is equipped to this microscope. A 785 nm wavelength diode laser (StarBright XM, Torsana) with 2-μm diameter is equipped. An autofluorescence imaging system was integrated to the Raman microscopy: LED (Mounted High-Power LEDs, Thorlabs), CCD (01-QIClick-F-M-12 Mono, QImaging). Throughout all the Raman measurements conducted in this study, the laser power was consistently set to 200 mW at the output of the 50 × objective lens.

The multivariate classification model based on Raman spectroscopy used in this study has been described in detail previously [10]. This model classifies a newly acquired Raman spectrum of a skin specimen into one of seven tissue classes: BCC, muscle, fat, dermis, inflamed dermis, epidermis, and substrate. The sensitivity and specificity for discriminating BCC from healthy tissue (all other classes combined) was 100% and 92% respectively [10].

3. Results and discussion

3.1 Image segmentation

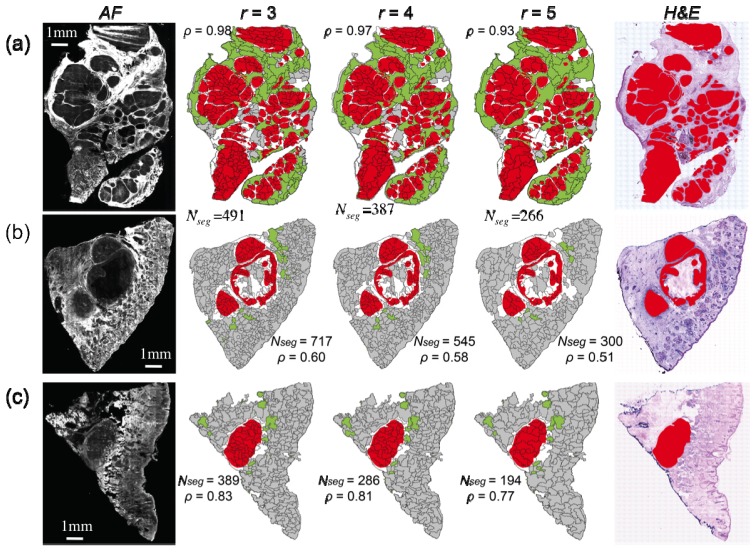
The segmentation algorithms for the auto-fluorescence intensity images were optimized according the type of BCC by adjusting the radius r of the disk-structuring element. Figure 2 shows the segmentation results for skin tissue samples with nodular BCC with tumour areas larger than 1 mm, and compares the segmented images with H&E images after staining (tumors highlighted in red color).

Fig. 2.

Segmentation of auto-fluorescence intensity (AF) images for skin samples with large nodular BCC (tumours larger than 1mm). r: radius of disk structuring element used for the morphological processing of AF images. Color code for segmented images: red = tumor regions (diagnostic provided by histopathology - for clarity not all tumors are highlighted), white = segment containing residual tumor, green = segments with AF intensity above threshold, gray = segment without tumor. N_seg = the number of segments.

The auto-fluorescence images have a high sensitivity for detection of BCC as all tumors can be identified as regions of low emission intensity. Nevertheless, the specificity of the auto-fluorescence intensity was low as other tissue structures commonly found in healthy skin have similar auto-fluorescence emission intensity and similar morphology, such as sebaceous glands and hair follicles. The image segmentation was carried out using r = 3, 4, and 5 and the ratio ρ of the total tumor area over the total area of the segments containing tumor was calculated for all samples $(\rho =Are{a}_{Red}/(Are{a}_{Red}+Are{a}_{White})$ in Figs. 2–5). The value of ρ can be interpreted as an indicator of the effectiveness of the segmentation algorithm to delineate the tumor regions. For ρ = 1 the segmentation could be considered perfect, and for a Raman classification model with perfect diagnostic accuracy (100% sensitivity and 100% specificity), a single Raman spectrum per segment would be required. Figure 2 shows that decreasing r, i.e. smaller segments, the segmentation performance increases as indicated by the higher values of ρ. However, as the value of r is decreased the total number of segments increases, and the implementation of multimodal spectral imaging would require a larger number of sampling points for Raman spectroscopy.

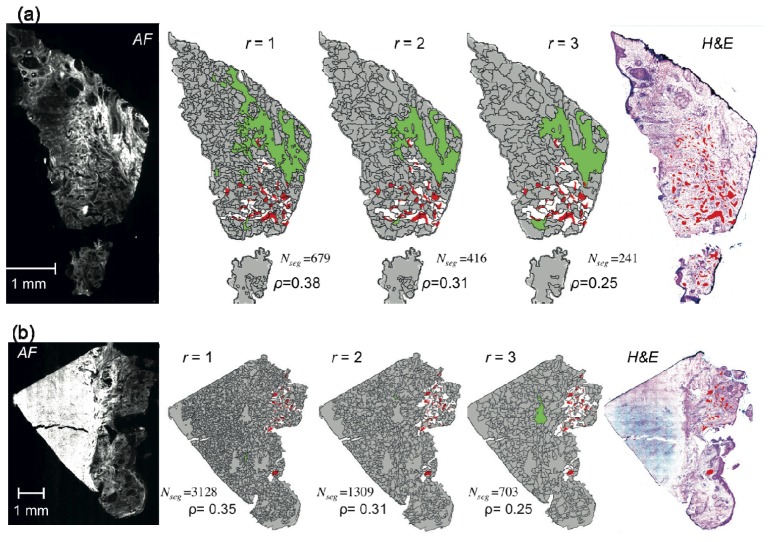
Fig. 5.

Generation of sampling points for Raman spectropscopy based on AF intensity images for two tissue samples. (a), (f) AF images, (b), (g) the intensity variance maps for the segmented AF images (gray scale) with estimated sampling points (cyan), segment-boundary (orange) and segments AF intensity above threshold (green). (c), (h): H&E-stained skin tissue image with BCC highlights in red. (d), (e) and (i), (j): zoom-in images of the red square region in (b) and (g). In (e) and (j), BCCs are additionally highlighted in red. For both skin tissue samples, the segmentation function optimized for large BCC was applied with N_min = 2 and σ_sampling = 2,000 spectra cm⁻².

Figure 2 shows that for nodular BCC with tumors larger than 1 mm, the performance of the segmentation algorithm is very high for all values of r. When r = 3, for certain samples, values of ρ close to unity can be achieved (Fig. 2(a)). High segmentation performance call also be achieved with r = 5 (ρ >0.5) while the number of segments was found to reduce typically to half (from 500 to 700 when r = 3 to 250-300 when r = 5).

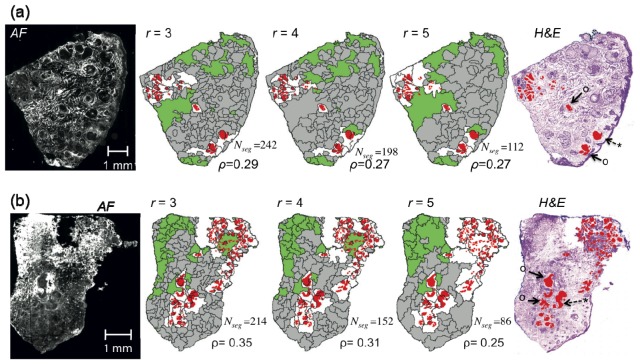
The segmentation performance was lower when the size of the tumours became smaller than ~1mm. Figure 3 shows examples of segmentation results for skin tissue samples with nodular, micro-nodular and superficial BCC with tumours in the 300 −1000 μm range.

Fig. 3.

Segmentation of auto-fluorescence intensity (AF) images for skin samples with nodular, micro-nodular and superficial BCC with tumour sizes within 300-1000 μm. r: radius of disk structuring element used for the morphological processing of AF images. Color code for segmented images: red = tumor regions (diagnostic provided by histopathology - for clarity not all tumors are highlighted), white = segment containing residual tumor, green = segments with AF intensity above threshold, gray = segment without tumor. Symbols “o” indicate segments for which the tumour accounted for more than half of the segment area, and “*” segments that can be observed clearly in the AF but the tumour accounted for less than a quarter of the segmentation area. . N_seg = the number of segments.

In this case, the typical values of ρ ranges in between 0.2 and 0.4 depending on the size of the structural element. By setting a target of maximum of 2,000 spectra cm⁻² (corresponds to a total diagnostic time of ~1-hour for the current instrument, ~15-min for an optimized automated instrument), selecting r = 4 represents a good compromise between the segmentation performance (ρ>0.25) and the number of segments (80 to 250 per sample).

Although the segmentation function optimized for nodular and micro-nodular BCCs provide ρ = 0.3-0.98, the performance of this algorithm is significantly poorer for smaller tumors, such as morphoeic/infiltrative BCC (e.g., ρ < 0.1). Therefore, the segmentation algorithm was modified for samples containing tumors smaller than 300 μm by setting a higher resolution (6.8 μm pixel⁻¹) for the input texture-enhanced gradient image and selecting r < 4. Figure 4 shows that the resulting segment density was higher compared to large tumors, while ρ > 0.25. In order to provide a trade-off between the number of segments (700 to 3000) and segmentation performance (ρ>0.25), this study adopted r = 2.

Fig. 4.

Segmentation of auto-fluorescence intensity (AF) images for skin samples with small BCC (morphemic/infiltrative BCC). r: radius of disk structuring element used for the morphological processing of tissue AF image. Color code for segmented images: red = tumor regions (diagnostic provided by histopathology) (for clarity not all tumors are highlighted), white = segment containing residual tumor, green = segments with AF intensity above threshold, gray = segment without tumor. N_seg = the number of segments.

3.2 Sampling point estimation and allocation

After optimizing the size of the structure elements and image resolution, the segmented auto-fluorescence intensity images were used to generate sampling points for Raman spectroscopy measurements based on Eq. (1). The hypothesis underpinning this algorithm is that larger segments with higher auto-fluorescence intensity variance are more likely to have a higher chemical heterogeneity and contain multiple tissue structure, therefore they should be allocated more sampling points for Raman spectroscopy. The higher number of Raman spectra for segments with higher chemical heterogeneity would then account for sub-optimal segmentation and provide correct diagnostic of BCC.

Figures 5(a) -5(e) show the location of the generated sampling points for Raman spectroscopy for a skin sample with BCC for which the performance of the segmentation algorithm was high (ρ = 0.35).

For smaller segments with low auto-fluorescence variance (below 0.2), the number of sampling points equals to the minimum number N_min. For segments with higher intensity variance or large area, the number of sampling points is increased. For the majority of the skin samples with large BCC tumors (8 out of the 10 samples used for this part of the study), the tumors were well-delineated by the boundaries of segments and most of the initial sampling points overlapped with the tumor regions. For such tissue samples, it is expected that the a dominant class can be established after the acquisition of the Raman spectra and diagnosis based on the multivariate classification model.

However, Figs. 5(f)-5(j) show that for certain samples, the performance of the segmentation algorithms can be lower, and many tumor regions were not delineated by the boundary of segments. It is also interesting to note that in these cases the anatomical heterogeneity did not increase the variance of the auto-fluorescence intensity to the level to increase the number of sampling points for Raman spectroscopy to account for such segmentation imperfection. While this sample would still be diagnosed as BCC positive as for the majority of the segments the sampling points coincided with the location of the BCC (symbol “o”), Fig. 5(j) shows that for several large BCC-positive segments (symbol “*”), the majority of the sampling points for Raman spectroscopy did not match the location of the tumors, therefore such segments would be misdiagnosed as BCC-negative.

In order to reduce such errors caused by imperfections in the segmentation algorithm, the multimodal spectral imaging algorithm was modified to provide additional sampling of Raman spectra for segments in which BCC was detected by Raman spectroscopy but BCC was not the dominant class. This additional sampling of Raman spectra was carried out maximum twice, and if no single dominant class was identified, then the segment was divided into smaller segments.

3.3 Comparison optimized multimodal spectral imaging (MSI) and raster-scanning Raman spectroscopy

To estimate the performance of the optimized MSI algorithms to detect residual BCC in skin tissue excised during Mohs micrographic surgery, MSI was compared to raster-scanning Raman microscopy (same tissue sample) and histopathology (adjacent H&E stained sections) for 10 new skin samples (7 with nodular/micro-nodular BCC and 3 with infiltrative BCC). To allow comparison with raster-scanning, measurements were limited to 4 mm × 4 mm areas of the sample. Raman spectra were recorded by raster-scanning at 20 μm step size and the MSI diagnostic was obtained by pulling out the Raman spectra at the locations corresponding to the sampling points generated by the MSI algorithm according to Fig. 1. The radius of the disk-shaped structuring element was selected to r = 4 for large tumors (nodular and micro-nodular) and r = 2 for smaller tumors (infiltrative BCC). Several regimes were investigating, including N_min = 2 and 3, and sampling densities, σ_sampling of 1500 spectra cm⁻², 2000 spectra cm⁻² and 2500 spectra cm⁻². To account for errors in segmentation accuracy, several values for the thresholds defining the dominant class, t, were investigated: 50%, 70% and 90%.

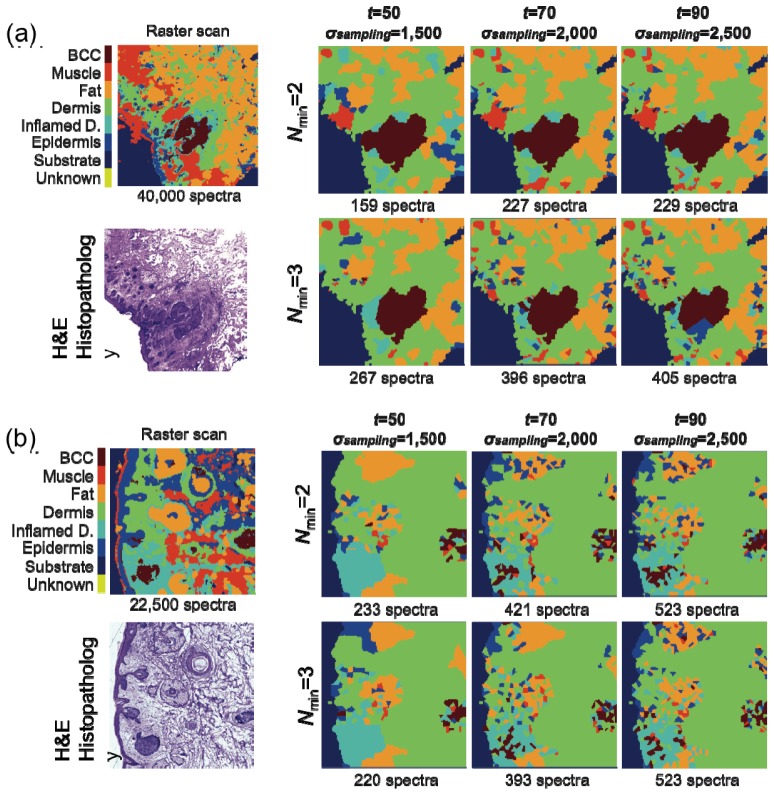
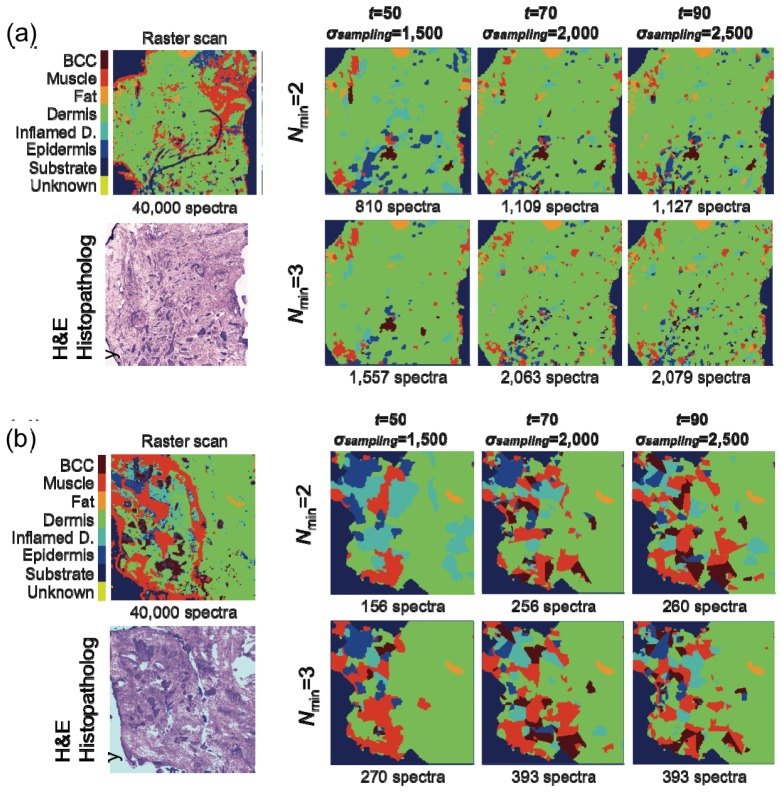
Figure 6 shows typical MSI results for tissue sections from patients with BCC on face or neck that were characterized by larger tumors (> 300 μm). Figure 6(a) presents the MSI diagnostic for a sample with superficial BCCs for which the size of the tumor is ~1 mm. In this case, the result of the segmentation algorithm was very good (ρ = 0.49) and the quality of diagnosis seems not to depend on the parameters N_min, t, and σ_sampling. The result in the regions around the tumor is very stable and in all six conditions the diagnostic image captures accurately the tumor. In this case, the most efficient algorithm corresponds to N_min = 2, σ_sampling = 1,500 spectra cm⁻² and t = 50%, which requires the acquisition of only 159 Raman spectra (equivalent ~3 minutes) compared to 40,000 for raster scanning. Even for the most detailed regime based on N_min = 3, σ_sampling = 2,500 spectra cm⁻² and t = 90%, that provides improved detail for the tumor, MSI requires only 405 Raman spectra (~1% of the raster-scanning data set).

Fig. 6.

Evaluation of the MSI algorithms for nodular and superficial BCC (tumors larger than 300 μm). H&E-stained adjacent section is included for comparison. Tissue size: (a) 4 mm × 4 mm and (b) 3 mm × 3 mm.

Figure 6(b) presents a case of skin sample containing nodular and superficial BCCs with tumors ~300-500 μm, for which the performance of the segmentation algorithm was poor (ρ = 0.14). In this case, the quality of the MSI diagnosis shows distinctive differences when adjusting the values of N_min, σ_sampling and t. When t = 50% and σ_sampling = 1,500 spectra cm⁻², the nodular BCC tumor on the right side of the tissue is detected but the large tumor and superficial tumor at the left of the area, as well as the small tumor in the center, are misdiagnosed. Increasing t = 70% and σ_sampling = 2,000 spectra cm⁻², which approximately doubles the number of Raman spectra, the larger tumors are correctly classified; only the small tumor at the center of the sample is missed. Increasing further the threshold t and the sampling density, improves only marginally the quality of diagnosis. This case demonstrates the effectiveness of the algorithm for measuring additional Raman spectra for samples for which the segmentation is sub-optimal. As the segmentation fails to delineate the tumor accurately, increasing the threshold t means that no class becomes dominant class and additional Raman spectra were recorded. Finally, the segment was divided in several smaller segments, which were labeled according to the dominant class of each sub-segment, thus allowing detection of BCC. These results show that even if the segmentation of the auto-fluorescence intensity images is sub-optimal, the accuracy of BCC diagnosis can be improved by increasing the number of Raman spectra in the segments lacking a dominant class. Based on the evaluation of 7 independent tissue samples with nodular, micro-nodular and superficial BCC, the best compromise between diagnostic accuracy and speed for samples was achieved by selecting N_min = 2, t = 70%, σ_sampling = 2,000 spectra cm⁻². For 5 samples, the value of ρ ranged between 0.25 and 0.5 and all tumor regions were detected (100% detection). For 2 samples, for which the segmentation accuracy was lower (ρ = 0.1 and ρ = 0.15), the percentage of detected tumor regions were 30% and 75% respectively. For these samples, the algorithm for measuring additional Raman spectra led to increased detection rates for BCC.

In the case of skin samples with smaller tumors (infiltrative BCC), the performance of the segmentation algorithm was significantly lower (ρ≈0.1). Figure 7 presents a comparison between the diagnostic obtained by MSI and raster-scanning Raman micro-spectroscopy for two skin samples with BCC tumors smaller than 300 μm (infiltrative BCC on the face and neck areas). In Fig. 7(a) raster-scanning Raman micro-spectroscopy provides BCC diagnostic in good agreement with histopathology based on H&E-staining and indicates the presence of one tumor of ~300 μm and ~25 tumors smaller than 300 μm. For the MSI regimes based on the minimum sampling density and lowest threshold for the dominant class (t = 50%), only the larger BCC tumors were detected and their size was slightly exaggerated. When t = 70% and σ_sampling = 2,000 spectra cm⁻², the diagnostic quality was significantly improved: more than 10 tumors smaller than 200 μm were detected when N_min = 2 (1,109 total Raman spectra) and more than 20 tumors smaller than 200 μm are detected when N_min = 3 (2,063 total Raman spectra). Increasing t to 90% does not provide further detail in diagnostic as the number of Raman spectra reached the maximum value. For the case presented in Fig. 7(b), similar to Fig. 6(b), only 3 out of 13 tumors were detected when t = 50% and σ_sampling = 1,500. Nevertheless, the MSI regime corresponding to t = 70% and σ_sampling = 2,000 spectra cm⁻², was able to detect successfully 12 out the 13 tumors with only 256 Raman spectra (N_min = 2). Further detail was obtained when t = 90% and σ_sampling = 2,500 as all tumor regions were correctly diagnosed requiring only 393 Raman spectra (~1% from the number of spectra required for raster scanning Raman micro-spectroscopy). By comparing the results for all three samples, the regime with N_min = 2, t = 70%, σ_sampling = 2,000 spectra cm⁻² provides a good trade-off between diagnosis accuracy and speed, parameters similar to the optimal MSI algorithm for larger BCCs. Despite of the sub-optimal segmentation of the AF images (ρ≈0.1), the re-sampling routine improved the diagnosis accuracy for the three samples with infiltrative BCC. The percentage of the individual tumour regions correctly classified was 50-90%. Improved results may be obtained by reducing the size of the structural element in the segmentation algorithm, but this would increase the number of segments, hence increase the diagnosis time. Although it is desirable to detect all individual tumor regions, in practice it is sufficient to provide an answer on whether the resection margins are clear of tumor or not. The large number of such tumor regions in samples with infiltrative BCC, in particular in the 1st or 2nd resected layers, increases the probability to detect positive resection margins, even if the detection rate for individual tumor regions is not 100%.

Fig. 7.

Evaluation of the MSI algorithms for morphoeic/infiltrative BCC (tumors smaller than 300 μm). H&E-stained adjacent section is included for comparison. Tissue size: (a) 4 mm × 4 mm and (b) 2 mm × 2 mm.

5. Conclusion

Multimodal spectral imaging based on auto-fluorescence imaging and Raman micro-spectroscopy is a powerful technique that can detect residual BCC in tissue specimens resected during Mohs micrographic surgery. In this paper the MSI algorithms was optimized in order to maximize diagnosis accuracy while minimizing the number of Raman spectra. The size of the structuring element in the segmentation algorithm for the auto-fluorescence intensity images was optimized for large tumors (nodular, micro-nodular and superficial BCC) and smaller tumors (infiltrative/morphemic BCC). This optimization based on histological subtype is relevant clinically because the type of BCC is known prior to surgery. The sampling points for Raman spectroscopy for each segment were allocated base on a new algorithm that considered the area of the segment and the variance of the auto-fluorescence intensity. In order to account for errors due to sub-optimal segmentation, additional sampling points were allocated to segments where the multivariate classification model based on Raman spectroscopy detected a BCC spectrum but failed to identify BCC as the dominant class. The results of this study indicate that the best compromise between diagnostic accuracy and speed was achieved when the size of the structuring element in the segmentation algorithm was when r = 4 for nodular, micro-nodular and superficial BCC, and r = 2 for infiltrative/morphemic BCC, while selecting N_min = 2, t = 70%, σ_sampling = 2,000 spectra cm⁻². When using these parameters, accurate diagnosis of BCC was achieved for all samples, requiring typically only ~1-2% of the Raman spectra recorded in raster-scanning. At the optimized σ_sampling = 2,000 spectra cm⁻², diagnosis of typical skin samples of 1 cm × 1 cm can be achieved in ~60 minutes with our laboratory-based instrument (2 seconds integration time for each Raman spectrum, ~3 min for acquisition and segmentation of fluorescence images ~3 min, ~5 s for analysis of Raman spectra). Using higher-throughput Raman spectrometers with shorter integration times (e.g. 1 seconds/spectrum [8]) could allow intra-operative diagnose of tissue layers and blocks within 30 minutes for all types of BCC, which is similar or shorter to frozen-section histopathology (20-30 minutes for micro-sectioning and staining, followed by 5-10 minutes for microscopic examination and diagnostic). Although in this study we used tissue micro-sections (20 µm thickness) to allow a direct comparison between MSI and histopathology (avoid changes during handling and micro-sectioning), it is important to note that MSI does not require micro-sectioning because both AF and Raman measurements can be carried out on thick tissue specimens without compromising diagnosis performance [10]. Therefore, MSI is an attractive technique for assessment of resection margins during surgery because it does not require laborious tissue preparation procedures and is not based on subjective interpretation of stained sections.