Automatic segmentation of microcystic macular edema in OCT

Abstract

Microcystic macular edema (MME) manifests as small, hyporeflective cystic areas within the retina. For reasons that are still largely unknown, a small proportion of patients with multiple sclerosis (MS) develop MME—predominantly in the inner nuclear layer. These cystoid spaces, denoted pseudocysts, can be imaged using optical coherence tomography (OCT) where they appear as small, discrete, low intensity areas with high contrast to the surrounding tissue. The ability to automatically segment these pseudocysts would enable a more detailed study of MME than has been previously possible. Although larger pseudocysts often appear quite clearly in the OCT images, the multi-frame averaging performed by the Spectralis scanner adds a significant amount of variability to the appearance of smaller pseudocysts. Thus, simple segmentation methods only incorporating intensity information do not perform well. In this work, we propose to use a random forest classifier to classify the MME pixels. An assortment of both intensity and spatial features are used to aid the classification. Using a cross-validation evaluation strategy with manual delineation as ground truth, our method is able to correctly identify 79% of pseudocysts with a precision of 85%. Finally, we constructed a classifier from the output of our algorithm to distinguish clinically identified MME from non-MME subjects yielding an accuracy of 92%.

1. Introduction

Multiple sclerosis (MS) is an inflammatory demyelinating disorder of the central nervous system. As noninvasive retinal imaging has promise for tracking more widespread neurologic disease, the retina is of growing interest to neurologists who are treating and studying MS [1]. As well, optical coherence tomography (OCT) is being used as a primary modality to explore the effects of the disease on the eye [2]. OCT uses near-infrared light to image the reflective properties of the retina enabling high resolution cross-sectional images of the retinal layers. Previously, OCT has been used to show that the thickness of the retinal nerve fiber layer around the optic disc is correlated with visual function in MS [3]. It is also known that MS patients have atrophy in the deeper retinal layers, which is best quantified by imaging the macula [4].

Microcystic macular edema (MME) is a condition found in a subset of MS patients whereby small cystic changes occur in the inner nuclear layer (INL) of the macula [5,6]. These cystic lesions, which are called pseudocysts, appear in approximately 5% of MS patients [5]. Although the biological origin of these pseudocysts is not known, their presence has been found to correlate well with disease severity (MS severity score) and to predict an increased recurrence of MS attacks [5, 6]. While many patients with MME have had previous episodes of optic neuritis (ON), pseudocysts do not appear in all patients who have had ON [5, 7, 8]. Additionally, the appearance of MME is not restricted to MS patients. It has been noticed in eyes of patients suffering from neuromyelitis optica, Leber’s hereditary optic neuropathy, glaucoma, and several other diseases [9]. Such a diversity of conditions further adds to the uncertainty surrounding MME. Therefore, the ability to accurately identify, localize, and quantify the presence of the pseudocysts found in MME is an important step in understanding how and why these changes occur. Both identifying the initial appearance of MME and tracking the changes over time will be crucial to this process.

To the best of our knowledge, there are no reports outside of our own prior work [10] describing the automatic segmentation of pseudocysts in MME. A variety of methods for the segmentation of more general cystic changes in the retina have been reported, however. In particular, methods have been developed for segmentation in diabetic macular edema, retinal detachment, and age-related macular degeneration [11–16]. These methods use a variety of techniques to segment the cystoid spaces. Two semi-automatic algorithms were described, where one uses a deformable model [11] and the other uses a split Bregman segmentation algorithm to generate candidate fluid spaces [12]. Several fully automatic algorithms have been presented. One uses a k-nearest neighbor (k-NN) classification plus a graph cut segmentation [13], and another uses using a dynamic programming algorithm on polar transformed data of pilot estimates of the lesions [14]. The method of [15] uses bilateral filtering followed by thresholding while the method of [16] uses k-means clustering and k-NN. The cysts found using these algorithms for their targeted diseases are generally much larger than the pseudocysts found in MS and therefore these existing methods are inappropriate for application to MME in MS.

As an additional challenge, the primary focus with respect to MME has been on data acquired from a Heidelberg Spectralis scanner which uses multi-frame averaging to improve the quality of each image. Unfortunately, this feature has the negative impact of averaging away the pseudocysts which reduces the contrast with the surrounding retinal tissue.

In this paper, we present a segmentation algorithm for the detection of pseudocysts due to MME in macular OCT scans acquired on the Spectralis scanner. Our algorithm leverages the ability of a random forest classifier (RFC) to learn the probability that a pixel belongs to a pseudocyst given a set of features. Classifiers like ours have previously been used in a variety of OCT specific applications including layer segmentation [17, 18], neural canal opening localization [19], and drusen classification [20]. The presented method improves on our previous algorithm [10] and includes a validation study on a larger cohort of subjects. Section 2 describes the algorithm including pre-processing steps. Section 3 covers the experiments and results and finally, Section 4 provides a brief discussion and conclusions.

2. Methods

2.1. OCT data

Macular OCT data from nine MME subjects totaling twelve scans was used for this study (three subjects had MME in both eyes). All data was acquired on a Heidelberg Spectralis scanner (Heidelberg Engineering, Heidelberg, Germany). Each scan covered a 6 × 6 mm area of the macula using 49 B-scans (cross-sectional images), each with 1024 A-scans (vertical scan lines) and 496 pixels per A-scan. The axial resolution was 3.9 μm. The scanner’s automatic real-time (ART) setting was used to average at least 12 B-scans at each location.

Manual segmentation of the MME data was generated by a trained rater who delineated all of the pseudocysts in each of the 12 scans. A second rater delineated five scans for comparison with the first rater. Pseudocysts were defined as small, hypointense, cystic lesions with identifiable boundaries and with other MME areas appearing locally in at least one adjacent B-scan (i.e. no isolated pseudocysts) [5]. Note that due to the large spacing between adjacent B-scans, the individual pseudocysts are generally only visible in one image (i.e. we rarely see the same pseudocyst spanning multiple B-scans). Due to the averaging done by the scanner, the degree to which the pseudocysts appear ‘dark’ is highly variable. Thus, areas which were only slightly darker than the surrounding tissue were not labeled as pseudocysts since minute intensity or texture differences may be artifactual. Table 1 provides an overview of all of the manually segmented data. Since a dichotomy of low and high pseudocyst count emerged from the data, we additionally classified subjects into these two groups for analytical purposes.

Table 1.

Overview of the data used for this study including the statistics of the pseudocysts as labeled by the first manual rater. (OD - right eye, OS - left eye)

Low pseudocyst density subjects
Subject	Eye	# of pseudocysts	# of pseudocyst pixels	Median size (px)	Size range [min, max]
1	OD	7	79	14	[6, 14]
2	OD	29	442	14	[4, 50]
2	OS	10	121	11	[5, 23]
3	OS	20	246	11	[6, 22]
4	OD	5	81	18	[4, 27]
4	OS	27	374	12	[5, 40]
Mean		16.3	224	13.3

High pseudocyst density subjects
Subject	Eye	# of pseudocysts	# of pseudocyst pixels	Median size (px)	Size range [min, max]
5	OD	239	3342	12	[3, 48]
6	OD	528	16793	24	[4, 444]
7	OS	301	7858	20	[3, 209]
7	OD	87	1578	15	[3, 92]
8	OD	214	5081	19	[4, 152]
9	OS	707	28621	32	[6, 254]
Mean		346	10546	20.3

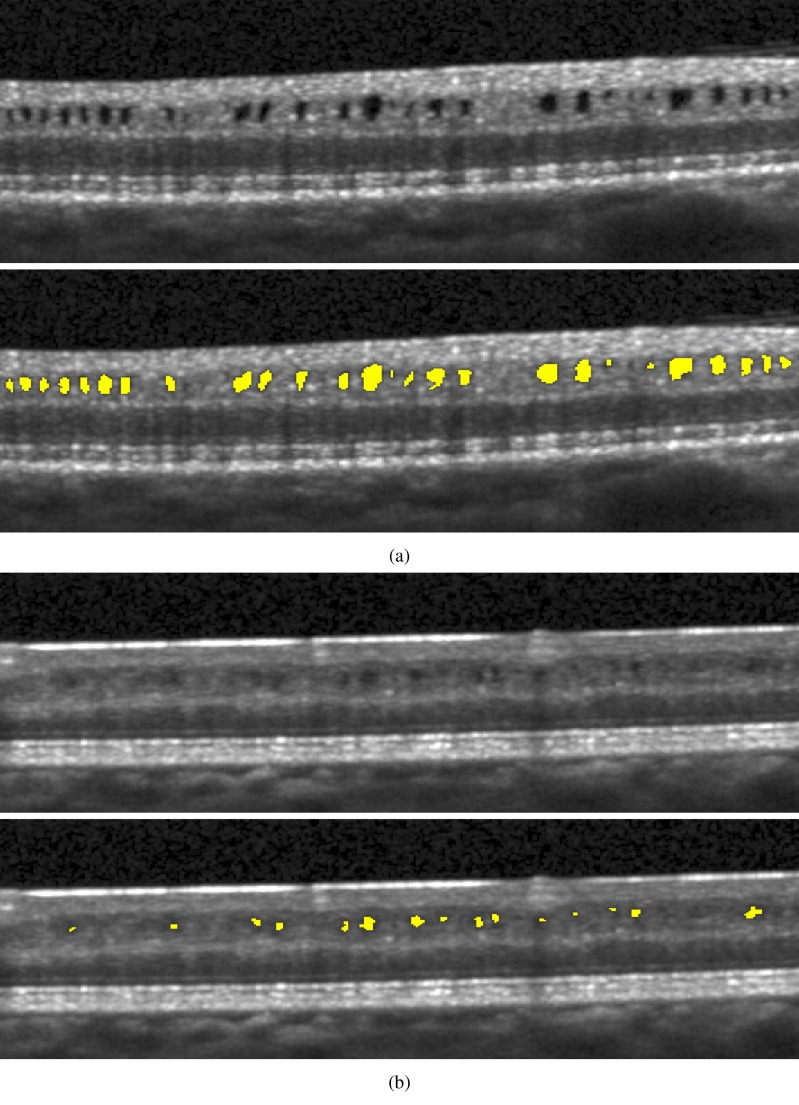
Illustrative B-scans from two separate MME subjects and their corresponding manual segmentations are shown in Fig. 1. In Fig. 1(b), we see that the ART can have the effect of averaging away some of the pseudocysts from the image, making them difficult to identify.

Fig. 1.

B-scan images and corresponding pseudocyst manual segmentations from two different subjects. The averaging done by the scanner makes the pseudocysts in (b) more difficult to distinguish.

2.2. MME segmentation overview

We now overview our algorithm for automatically segmenting pseudocysts from macular OCT images. Details on specific aspects of the algorithm will follow. Our overall method follows a pixel classification approach. For each pixel in a given B-scan, we compute several different features which a classifier then uses to decide which class the pixel belongs to — the two classes being pseudocyst or background. We use an RFC to do this classification [21]. The RF algorithm was chosen for several reasons including its comparable accuracy to other state-of-the-art algorithms, its simplicity and efficiency, the relatively small number of tunable parameters, and a history of successful use for image segmentation tasks, including OCT-related applications [17,18]. Also, the RFC outputs a soft classification, or probability, instead of only a binary result, providing a measure of confidence at each pixel that we will take advantage of.

Before classifying the pixels, we first normalize the intensities of each volume to provide better consistency both between subjects and between B-scans of the same subject (see Sec. 2.3 for details). After this normalization, we compute a set of 18 features at each pixel (see Sec. 2.5 for a description) which are used by the RFC to generate MME probability maps for each image. Details of training the RFC will be discussed in Sec. 2.6. We then follow a three-stage thresholding scheme to produce the final segmentation of the data. First, the resulting RFC probabilities are thresholded at a value of 0.5 to generate candidate cystic lesions. This threshold was empirically chosen to represent a majority voting scheme commonly used for binary classification problems. A second threshold is used to remove any connected regions (defined using 8-connectivity) that do not have any pixels with a probability of greater than 0.85. Thus, we encourage only those pseudocysts that are highly probable. Due to the noise and variability of the pseudocyst appearance, we do not expect a high probability everywhere within a given lesion. As a final step, we remove all connected components with fewer than 5 pixels thus removing spurious areas potentially found due to noise. All remaining pixels are then classified as pseudocysts. This final threshold makes sense since there were very few (25 total) manually delineated pseudocysts smaller than this threshold.

2.3. Intensity normalization

Intensity inhomogeneity in retinal OCT data arises due to a variety of reasons and causes the intensities of each layer to be inconsistent both between and within images. Since the pseudocysts appear strictly darker than the surrounding INL tissue, it is important to normalize these intensities to make them more consistent. In the ideal case where we have the boundaries of the INL, we could normalize the intensities of this layer directly. Unfortunately, without running a layer segmentation algorithm, which may have trouble due to the appearance of the pseudocysts, we must rely on another method of normalization. Since the outer boundary of the retina is simple to find due to the high contrast between the RPE and choroid, we use the RPE as the basis of our normalization. Finding this boundary is briefly described in Sec. 2.5.

To normalize the data, we scale the intensity values of each A-scan such that the RPE has an approximately uniform intensity across the entire volume. We assume that this scaling factor, or bias field, is smoothly varying between and across each B-scan. Using the convention that x, y, and z are the lateral, through-plane, and axial directions, respectively, this transformation can be given as

$$\hat{I}(x,y,z)=\frac{I(x,y,z)}{N(x,y)},$$ (1)

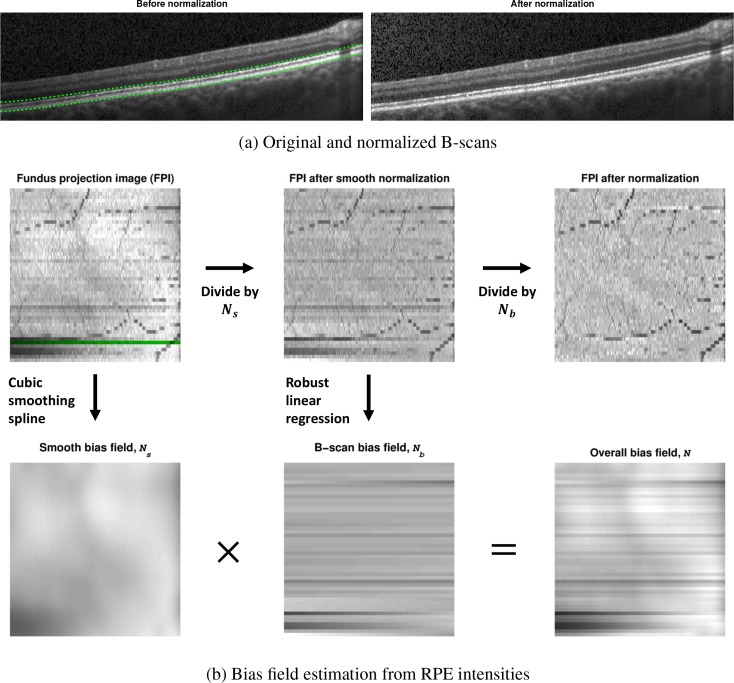
where I and Î are the original and normalized intensities, respectively, and N is the bias field correction. This bias field is given by the product N(x, y) = N_s(x, y) N_b(x, y), where N_s and N_b are components which vary smoothly over the entire volume and over each B-scan, respectively. We estimate N(x, y) from the underlying RPE intensities in each A-scan, which are given as the median value within 80 μm of the lower RPE boundary. This region is shown between the dashed green lines in Fig. 2(a). In 2D, we denote this RPE intensity map as a fundus projection image (FPI)—an example of which is shown on the top left in Fig. 2(b). Notice that the blood vessel locations appear due to the shadow they produce in the data, a feature which we would like to preserve after normalization.

Fig. 2.

(a) B-scan images before and after intensity normalization. The dashed lines in the original image represent the area used to compute the fundus projection image (FPI) shown in (b). (b) Estimation of the bias field and its decomposition into two components using the FPI. The green line on the FPI shows where the B-scan in (a) was acquired.

The steps for estimating the bias field are shown in Fig. 2(b). To estimate N_s from the FPI, we fit a bivariate tensor cubic smoothing spline to the data. A fixed value of 0.9 was used for the regularization weight, which removes higher frequency variations. To estimate N_b, we fit a robust linear regression to the intensity data in each B-scan (each row of the FPI), after normalizing by N_s, using a bisquare weighting function. The use of a robust linear regression is important to preserve the blood vessels and accurately model the intensity change. The final FPI after normalization and the bias field are shown in the right of Fig. 2(b). We see that the FPI contains only a uniform intensity in addition to the blood vessels remaining intact. An example of the resulting intensity normalized B-scan is shown on the right of Fig. 2(a).

2.4. Random forest classifier

A random forest is a classification method that uses the results of multiple decision trees to make an aggregated outcome about the most likely class. The outcome for a given tree is produced by sequentially propagating an input feature vector through a series of nodes in the tree until it reaches a leaf node. The input is then classified with most common label of the training data which ended at that leaf node. Each node of the tree makes a binary decision about which direction to propagate by thresholding the value of a single feature. Both the threshold value and which feature to choose are determined during training by maximizing the information gain of the split. Randomness is injected into each tree to reduce the correlation between them and to improve the overall accuracy. The first source of randomness is that each tree is built using a random sampling of the data with replacement. The other source is that only a random subset of features are examined at each node within the decision tree. Finally, we note that class probabilities are generated by averaging the decisions over N trees as $p(y|x)=\frac{1}{N}{\sum }_{i=1}^{N}I(h_i(x),y)$ where x is the input feature vector, h_i(x) is the classification result of decision tree i, y ∈ {1,...,L} is a label of interest, and I(h_i(x), y) is an indicator function for whether or not h_i(x) equals y.

2.5. Classifier features

In total, 18 features are used to identify the pseudocysts, with 16 of those being derived from intensities and 2 from the spatial position. The list of features used is given in Table 2. Since the pseudocysts are generally identified by their dark intensity, several multi-scale intensity-based features were included (features 1–12). For the morphological operators, the closing operator acts to remove the pseudocysts from the image, providing a contrast to the opening operator which enhances the pseudocysts. Examples of these features can be found in Figs. 3(a)–(f). Features 15 and 16 are computed for each A-scan and thus have the same value for each pixel in an A-scan. The FPI (Fig. 3(g)) is useful since the MME regions show up darker due to the pseudocysts producing a shadow below them. The signal-to-noise ratio (SNR) feature is used to learn where the quality of the data is particularly poor. Using this feature helps to reduce the number of false positives in low SNR areas since these areas are generally very dark.

Table 2.

List of the 18 features used by the random forest classifier.

#	Feature	Details
1–4	Intensity	Gaussian smoothed at 4 scales (σ = 0, 5, 10, 15 μm)
5–8	Gradient magnitude
9–12	Laplacian
13	Morphological opening	20 μm disc structuring element
14	Morphological closing	20×20 μm square structuring element
15	Fundus projection image	Single value for each A-scan
16	Signal-to-noise ratio
17	Retina distance	See text
18	Radial distance to fovea	Computed in the x–y fundus plane

Fig. 3.

Example images for several of the features used by the classifier to find the MME. The SNR feature is not shown since it was fairly uniform for this subject.

Finally, we augment the 16 previously described intensity features with 2 spatial features. The first measures the relative distance each pixel lies between the inner and outer retina boundaries, with the boundaries estimated using a simple gradient-finding algorithm [17]. An example is shown in Fig. 3(h). The second measures the radial distance in the x–y plane of each pixel from the fovea (Fig. 3(i)). Together these features help to identify the MME based on where the pixel is in the retina. For example, the fact that MME is generally only found within the INL means that the first feature will be particularly helpful to identify where the pseudocysts are. The pseudocysts also mostly appear within an annulus around the fovea. Thus, the radial distance will discourage the algorithm from finding pseudocysts outside of this region.

2.6. Classifier training

For the RFC, we used 60 trees, each grown with a minimum terminal leaf size of 10. At each node in the tree, four features were randomly chosen and used to determine the best split. The algorithm’s performance was fairly robust to the selection of these parameters. For training, all of the pseudocyst pixels from the manual segmentations were included along with a random selection of 20% of all background pixels taken from within a mask region described as follows. Given the position of the fovea, the background mask included all pixels within a radial distance of between 0.45 and 3 mm of the fovea (from feature 18) along with all pixels within a relative distance of 40% and 90% of the axial position from the outer to inner retina boundaries (from feature 17). Overall, this region encompassed all pseudocysts that were manually delineated.

3. Experiments and results

To explore the performance of our algorithm, we used a leave-one-out approach for training the classifier. Since we had data from nine subjects, we left one subject out instead of one scan to avoid any bias that including the opposite eye may introduce. Thus, each classifier was trained on data from eight scans. For subjects with scans from both eyes, either the left or right eye was randomly used. However, evaluations were done on all 12 scans.

To additionally show how the algorithm performs on data without MME, we ran the algorithm on 10 healthy control (HC) subjects and 10 MS patients, with each scan manually examined and found to not have any pseudocysts. The classifier for these experiments was trained on data from all of the subjects (9 scans).

To evaluate our experiments, we looked at several different measures based on the number of pseudocysts found including precision (Pr), recall (Re), and F-measure (F-m). These are defined as follows:

$$\begin{array}{ll}\hfill \text{Pr}& =\frac{\text{TP}}{\text{TP}+\text{FP}}=\frac{\#\hspace{0.17em}\text{correct}}{\#\hspace{0.17em}\text{found}}\hfill \\ \hfill \text{Re}& =\frac{\text{TP}}{\text{TP}+\text{FN}}=\frac{\#\hspace{0.17em}\text{correct}}{\#\hspace{0.17em}\text{true}}\hfill \\ \hfill \text{F-m}& =\frac{2\cdot \text{Pr}\cdot \text{Re}}{\text{Pr}+\text{Re}}\hfill \end{array}$$

where the true positive (TP), false positive (FP), and false negatives (FN) were computed on a per cyst manner (as opposed to per pixel). If any portion of a pseudocyst found by the algorithm overlapped with one from the ground truth, it was counted as a TP. We can interpret precision as the probability that a pseudocyst found by the algorithm is real and recall as the probability that a real pseudocyst is found by the algorithm. The F-measure is an overall measure of overlap similar to the popular Dice coefficient with the difference being that it is computed over all pseudocysts found instead of all pixels found.

3.1. Results

Table 3 lists the results of the algorithm both divided into the low and high density groups as well as the overall results. The measures are generally lower for the low density subjects with a larger spread as measured by the interquartile range (IQR).

Table 3.

Median precision, recall, and F-measure values over all cross-validation runs with IQR in parentheses.

Group	Precision	Recall	F-measure
Low density	0.84 (0.75, 0.90)	0.63 (0.45, 0.78)	0.73 (0.60, 0.81)
High density	0.88 (0.77, 0.92)	0.86 (0.80, 0.88)	0.85 (0.80, 0.88)
Overall	0.85 (0.76, 0.91)	0.79 (0.63, 0.87)	0.80 (0.73, 0.85)

Next, we looked at the total MME volume computed as the total number of MME pixels in each scan. Comparing the manual and automatic segmentation, we get a correlation coefficient of 0.98 (p < 1 × 10⁻⁷) which indicates excellent agreement. Table 4 shows a comparison of the differences between the algorithm and ground truth where we see that the algorithm consistently underestimates the volume for the low density subjects and overestimates for the high density subjects. Since the low density subjects generally have smaller pseudocysts (see Table 1) which are more difficult to segment, the total volume from the algorithm is generally smaller than the truth. The large value for the volume difference in the high density subjects can also partially be attributed to overestimation of the pseudocyst size by the algorithm.

Table 4.

The total difference in number of pseudocysts found and the overall difference in MME volume. Differences were computed as (algorithm − truth). Values represent the median over all scans with IQR in parentheses.

	Difference in # of pseudocysts found	Volume difference (px)	Volume difference (%)
Low density	−4 (−10, −1)	−19 (−75, 40)	−11.6 (−22.9, 26.7)
High density	3 (−14, 28)	413 (−1058, 458)	9.6 (−6.3, 25.3)
Overall	−4 (−12, 7)	15.5 (−88, 413)	0.0 (−14.6, 26.0)

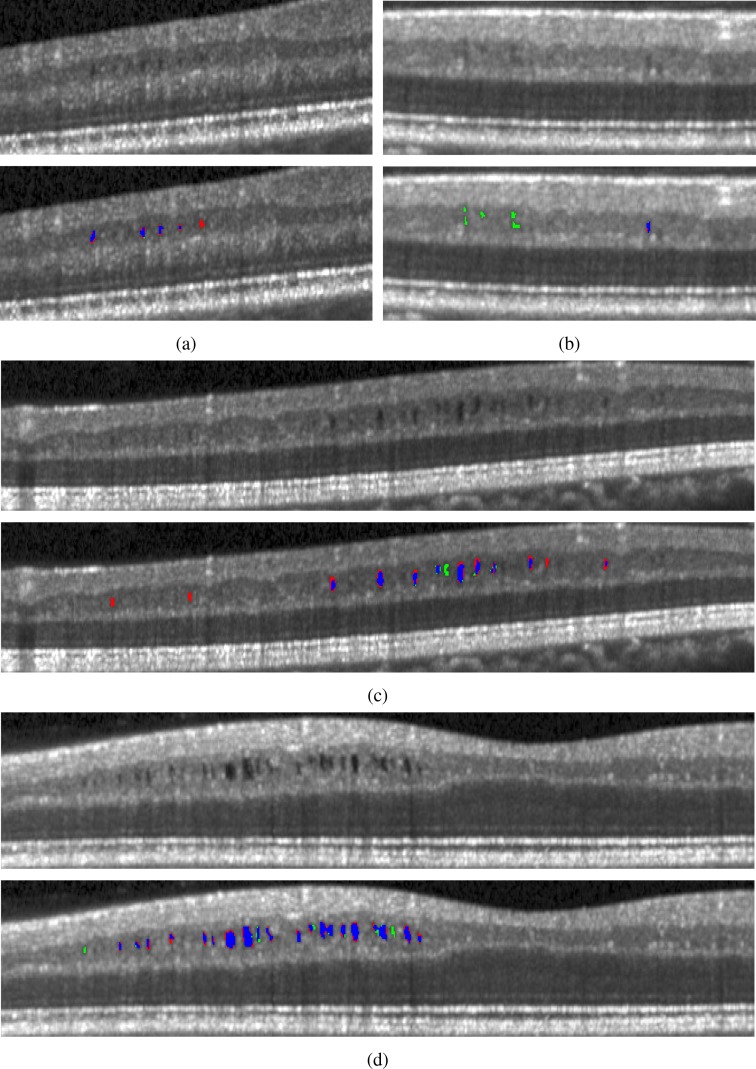
In Fig. 4, we display the results of the algorithm on one B-scan each from four subjects, two low and two high density subjects. While the algorithm clearly has no trouble finding the larger, darker pseudocysts, many of the false negatives and false positives are due to having a much lighter appearance. Indeed, many of the false positives could be argued to actually be pseudocysts but were simply not designated so by the rater. Also note the general appearance of a red ring around the pseudocysts indicating that the algorithm found slightly larger lesions.

Fig. 4.

B-scan images showing the original images and those with the results overlaid. The algorithm is shown in red, the manual segmentation in green, and the agreement of the two in blue. Images (a) and (b) are from low pseudocyst density subjects while (c) and (d) are from high density subjects.

3.2. Non-MME data

The results of running the segmentation algorithm on the non-MME data are shown in Table 5. The median number of pseudocysts found was the same for the HC and MS subjects with the IQR being slightly larger for the MS subjects.

Table 5.

The results of running the algorithm on non-MME data. Shown are the total number of estimated pseudocysts found and the total MME volume.

	# of Pseudocysts		Volume (px)
	Median (IQR)	[Min, Max]	Median (IQR)	[Min, Max]
HC	1 (0, 1)	[0, 5]	3 (0, 8)	[0, 52]
MS	1 (0, 2)	[0, 5]	4 (0, 20)	[0, 103]

Given all of the data analyzed, a simple classifier for predicting whether or not a subject has MME can be created based on the number of pseudocysts found by the algorithm. If we set the minimum number of pseudocysts found at 6 in order to classify a subject as having MME, we get a true positive rate (TPR) of 11/12 = 0.92 and a true negative rate (TNR) of 20/20 = 1, correctly predicting all of the non-MME as non-MME. Since thresholding in this way can misidentify those with a few pseudocysts early in the disease, we can instead look at the total probability of all high probability pixels in each volume (e.g. the sum of the probability of all pixels with a probability > 0.85). In this case, setting a threshold on the total probability in each volume at 16, we can get the same TPR and TNR as with the threshold based on number of pseudocysts.

3.3. Rater comparison

For an inter-rater comparison, each rater manually segmented five of the MME scans. Under the assumption that the first rater is the ground truth, recall, precision, and F-measure values are 0.99, 0.53, and 0.68, respectively, for the second rater. This means that the second rater found nearly all of the same pseudocysts as the first rater, but was much more lenient in their definition of what a pseudocyst is. In total, 1182 pseudocysts were found by the first rater and 1977 were found by the second rater, with median pseudocyst sizes of 19 and 27, respectively. Therefore, the second rater found more pseudocysts and they were larger as well. Another common measure of delineation overlap is the Dice coefficient, which produces values between 0 and 1, varying from no agreement and to complete agreement, respectively. Comparing the two raters, the average value over all scans was 0.53. Note that this measure is on a per-pixel basis as opposed to per-pseudocyst like the other measures. Overall, these differences highlight the difficulty in the task at hand. The most likely explanation is that the averaging done by the scanner blurs the boundaries, as is shown in Fig. 1(b), which creates uncertainty about what should be called a pseudocyst.

3.4. Algorithm design

Here, we explore the importance of different aspects and parameters of the algorithm. In the first step, we normalize the intensities of the OCT data using an estimate of the intensity values in the RPE. Comparing against a previously developed method that uses a linear contrast stretching on each B-scan [17], we find that the median F-measure is higher for the presented method (0.80 vs. 0.78), although the difference is not significant (p = 0.13, one-sided paired t-test). The difference in precision, however, is significant (0.85 vs. 0.80, p = 0.013). Additionally, when comparing performance on the non-MME data, the number of pseudocysts found were significantly fewer with the RPE normalization (p = 0.025).

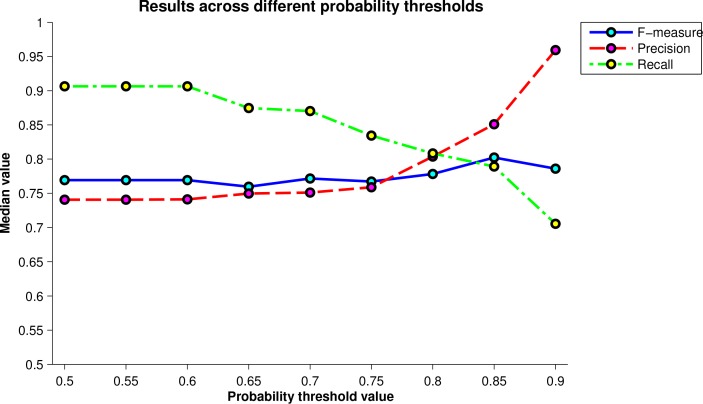
Another important parameter of the algorithm is the value of the threshold for the second stage of the segmentation algorithm where only the high probability pseudocysts are retained. Fig. 5 shows a plot comparing the F-measure, precision, and recall values across a set of thresholds from 0.5 to 0.9 in increments of 0.05. The final threshold used was chosen as the one that maximized the F-measure. There is a trade-off between precision and recall as the threshold changes. At a value of 0.5, the recall is largest since no pseudocysts are removed. As the threshold increases, the recall decreases and precision increases until the F-measure peaks at a threshold of 0.85. We also note that this peak value also has the smallest IQR.

Fig. 5.

Plot of the median F-measure, precision, and recall values over all scans for varying values of the high probability threshold. The maximum F-measure value was used to determine the final threshold.

One of the most important aspects of the algorithm is the choice of features used by the classifier. Some features are clearly more important than others. Looking at the variable importance measure output by the RFC, the four most important features were the Laplacian of Gaussian with σ = 15 and σ = 10, pixel intensity, and A-scan distance. Some features like the estimated SNR had little effect on the overall accuracy of the algorithm, but were useful specifically in segmenting the poor quality scans. For instance, when we exclude this feature, the maximum number of pseudocysts found in the non-MME data jumps from 5 to 79.

4. Discussion and conclusion

In this work, we developed an automated algorithm for segmentation of MME in macular OCT scans with a focus on data from the Spectralis scanner. The performance was quite good, finding 79% of the pseudocysts within the data. Using a simple classifier based only on the number of pseudocysts found, the classifier correctly labeled all of the non-MME data. While the algorithm is straightforward, using an RFC in a pixel-wise fashion, the addition of a novel intensity normalization method proved to increase the performance of the algorithm. The major limitation of this study is the number of scans available for validation. Since MME appears in only a small percentage of all MS subjects, the number of available scans was small. Additionally, several datasets had to be excluded due to poor quality, further reducing the number of usable scans. More data would not only allow us to do a more comprehensive evaluation and increase our understanding of the variability of the algorithm, but it would also allow us to include more data in the training of the RFC. More training data could improve both the accuracy and robustness of the algorithm.

As a word of caution with respect to segmentation of MME in Spectralis data: longitudinal analysis may prove to be difficult because each scan is averaged differently at each visit. The amount of averaging can directly influence the number of pseudocysts found by the algorithm since they can be “averaged away”. We still believe the algorithm and the data to be useful, however, as we are able to detect the presence and severity of MME. While previous authors have suggested that ART values larger than 12 are sufficient for detecting MME [5, 22], this value proved to limit the ability of the algorithm to find all of the true pseudocysts. While some degree of averaging is important to reduce the amount of noise, the best practice for acquiring data to quantify MME would be to reduce the amount of averaging performed. Alternatively, the raw data could be used to do averaging in a smarter way that would not remove the pseudocysts.

In the future, we hope to explore two avenues of extending the presented work. First, the algorithm will be adapted to segment MME in data from other scanners, in particular, the Zeiss Cirrus-HD OCT. Since these images do not undergo any averaging, the data from this scanner has a significant amount of noise making the pseudocysts more difficult to identify. More robust pre-processing may be necessary including additional denoising. Second, we hope to use the results of the algorithm to improve the performance of previously developed layer segmentation algorithms on MME subjects [17]. The performance of this algorithm and others have been found to be inadequate to assess the thickness changes of the INL in these subjects, which is important since a thickened INL might be related to the presence of MME [6, 8].

Finally, we note that although the proposed algorithm has been developed for segmentation of MME specifically, it should be able to identify larger cysts found in other eye diseases. Removal of the spatial features may be necessary in these cases, especially if the cysts are not expected to appear in a consistent location within the retina.