Abstract
Polarization mode dispersion (PMD) degrades the performance of Jones-matrix-based polarization-sensitive multifunctional optical coherence tomography (JM-OCT). The problem is specially acute for optically buffered JM-OCT, because the long fiber in the optical buffering module induces a large amount of PMD. This paper aims at presenting a method to correct the effect of PMD in JM-OCT. We first mathematically model the PMD in JM-OCT and then derive a method to correct the PMD. This method is a combination of simple hardware modification and subsequent software correction. The hardware modification is introduction of two polarizers which transform the PMD into global complex modulation of Jones matrix. Subsequently, the software correction demodulates the global modulation. The method is validated with an experimentally obtained point spread function with a mirror sample, as well as by in vivo measurement of a human retina.
OCIS codes: (110.4500) Optical coherence tomography, (110.5405) Polarimetric imaging, (120.5410) Polarimetry, (170.4500) Optical coherence tomography, (170.4460) Ophthalmic optics and devices, (170.4470) Ophthalmology
1. Introduction
Optical coherence tomography (OCT) [1] is a noninvasive imaging modality that provides high axial resolution cross-sectional images at micrometer scales. Because of its noninvasiveness, OCT has been widely applied for clinical fields including ophthalmology [2], dermatology [3], dentistry [4], gastroenterology [5], and cardiology [6]. Among them, ophthalmology is one of the most successful field of OCT, because of the difficulty of performing ocular biopsy [2].
Functional extensions of OCT, including Doppler OCT [7–9] and polarization-sensitive OCT (PS-OCT) [10–15], have been demonstrated to obtain additional information over the morphological information. Doppler OCT can detect moving particles in a sample, and as a clinical application, it has been used to measure blood flow and velocity and also to visualize vasculature [8, 16–22]. On the other hand, PS-OCT measures the polarization properties of a sample [10, 11, 13–15]. As an ophthalmic application, it has been utilized to visualize fibrous tissues [23, 24] and the retinal pigment epithelium (RPE) [25, 26].
Recently, we demonstrated Jones-matrix-based multifunctional OCT (JM-OCT) [27, 28]. This system simultaneously measures OCT, Doppler shift, and the polarization properties of a sample, and it enables simultaneous imaging of tissue structure, vasculature, and birefringent tissue. This system has been applied for imaging of the posterior eye [29], where the integrity of the vasculature and RPE of exudative macular disease were noninvasively investigated. Measurement speed is important for in vivo ophthalmic imaging, because eye motion and its related artifacts are problematic. Hence, it was natural to continue development of faster JM-OCT techniques. In the present work, we adopt optical buffering [18, 30–32] to JM-OCT. The optical buffering enables a scan rate of 200,000 A-lines per second with a commercially available 100-kHz wavelength swept laser, and high-speed Jones matrix imaging of the posterior eye is demonstrated.
When significant length of optical fiber is used in an OCT system, a non-negligible amount of polarization mode dispersion (PMD) is incurred. This can be classified into two types: PMD in non-common paths of an interferometer or that in a common path. The first type of PMD occurs in probe and reference arms, whose lengths are typically a few meters. It mainly appears as a small additional dispersive phase in the OCT signals. Although this small dispersive phase is not a problem in non-PS-OCT, it can degrade the image quality and polarimetric accuracy of PS-OCT [33]. So far, several methods have been devised to eliminate this type of PMD in PS-OCT. For instance, Zhang et al. [34] demonstrated numerical compensation of PMD with three calibration signals in the sample arm, and Villiger et al. [35] numerically mitigated PMD artifacts by spectral binning. Recently, Braaf et al. [36] demonstrated another sophisticated numerical correction method.
The second type of PMD becomes problematic if it is induced by a very long optical fiber of the order of a few hundreds to thousands of meters. This PMD is substantial and affects not only the phase but also the envelope of the spectrum if the OCT is equipped with polarization-sensitive components such as polarizers, polarizing beam splitters, or polarization-sensitive semiconductor optical amplifiers (SOAs). Hence, it significantly degrades the imaging performance of PS-OCT. Bonesi et al. [37] employed an actively controlled booster SOA to compensate for the slowly fluctuating spectral envelope that is mainly due to the temporally drifting PMD at the buffering fiber spools. A similar method was also used to cancel the spectral distortion induced by a long fiber spool in a Fourier-domain mode-locking laser, where the injection current of the primary SOA in a cavity was actively controlled [38].
In this work, a specialized method to correction for the substantial PMD induced by an optical buffering module in JM-OCT is presented. This method is purely numerical, and no active SOA control is required. Thus, it is compatible with commercially available standard light sources. We first mathematically formulate the PMD in JM-OCT, and then derive a method to correct for it. This method is applied to an optically buffered high-speed swept-source JM-OCT system with an A-line scan rate of 200 kHz. By using this JM-OCT, in vivo retinal imaging is demonstrated.
2. Optically buffered JM-OCT system
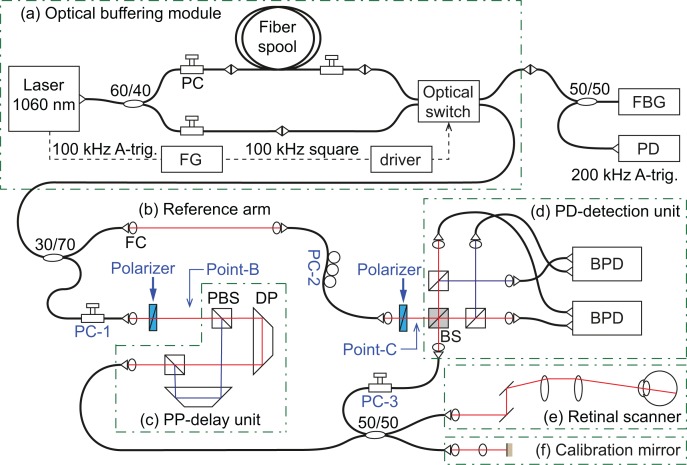
Figure 1 is a schematic of the system. The source arm is equipped with an optical buffering module built with a fast optical switch (FOS), which is similar to that demonstrated by Dhalla et al. [32]. Aside from the buffering module, it is nearly identical to a JM-OCT system that we have previously demonstrated [28].
Fig. 1.
Schematic diagram of the optically buffered JM-OCT system. An (a) optical buffering module makes a 200 kHz laser sweep. The JM-OCT system is composed of a (b) reference arm, (c) passive polarization delay unit (PP-delay unit), (d) polarization diversity detection unit (PD-detection unit), (e) retinal scanner, and (f) calibration mirror. PC: polarization controller, FG: function generator, FBG: fiber Bragg grating, PD: photo-detector, FC: fiber collimator, PBS: polarizing beam-splitter, DP: dove prism, BS: non-polarizing beam splitter, BPD: balanced photo-detector. Point-B and -C indicate particular points which are discussed in Section 6.3 and PC-1 and -2 correspond to those in Fig. 6.
The light source is a wavelength-sweeping laser (Axsun Technologies, Massachusetts, USA) with a scanning frequency of 100 kHz, a center wavelength of 1040 nm, and a −10-dB bandwidth of 111 nm, and an output optical power of 31 mW. The swept laser has a duty cycle of around 50% and hence has a dead time between wavelength scans of approximately 5 μs. A subsequent buffering module doubles the scanning frequency into 200 kHz. A 60 : 40 fused fiber coupler is used to split the beam into buffered and unbuffered fiber paths. A 1027 m fiber spool (HI1060, Corning) is used in the buffered path to create a 5 μs delay. The 60% port of the coupler is used for the buffered line to compensate the optical loss of −1.5 dB at the fiber spool. A 2 × 2 FOS (Nanona, Boston Applied Technologies, Massachusetts, USA) is utilized to switch between the buffered and unbuffered paths. The FOS has insertion losses at each switching mode as −1.05 dB (cross state, for buffered path) and −0.99 dB (bar state, for unbuffered path). The net insertion loss in the continuous switching drive mode is −1.61 dB. The transition time between the switching modes is around 60 ns, and it corresponds to 30 sampling points of spectral detection. 100 kHz driving signal for the FOS is generated by a function generator (AFG3252, Tektronix), which is synchronized with the light source by using an A-trigger from the source. The switch timing was fine tuned with the function generator to match the delay timing of the buffering module. Three in-line polarization controllers (PCs) (PolaRITE, PLC-006-S-25, General Photonics) were used in the buffering module to maximize the optical power throughput. The optical loss of the buffering module was −2.65 dB.
The 200 kHz A-trigger is generated by a fiber Bragg grating (reflection at 996.3 nm, full width at half-maximum (FWHM) of the reflection band of 0.1 nm, Tatsuta Electric Wire & Cable Co. Ltd., Osaka, Japan) attached to the sub-port of the FOS through a 50 : 50 coupler. A weak cross-talk light from the FOS is sufficient to generate the A-trigger. Reflected light from the FOS is received by a photo-detector (PDA10A-EC, Thorlabs) and amplified with a signal amplifier (AA020-0S, R&K, Shizuoka, Japan). The amplified signal is fed into the trigger channel of a digitizer (ATS9350, Alazar Technologies, Quebec, Canada).
The JM-OCT interferometer consists of a reference arm, a passive polarization delay unit (PP-delay unit), a polarization diversity detection unit (PD-detection unit), a retinal scanner, and a calibration mirror [Figs. 1(b)–1(f)]. Light from the optical buffering module is split by a 30 : 70 fiber coupler; the 30% portion feeds the reference delay arm, and the 70% portion is guided to the probe arm. In the probe arm, the light enters to the PP-delay unit after passing through a polarizer oriented at 45°. In the PP-delay unit, the two orthogonal polarization states are split, travel through different paths with different lengths, and are recombined at the output port. This results in passive multiplexing of the incident polarization states in depth. P-polarization state is delayed compared to the S-polarization state, and the delayed depth difference was 2.8 mm in air. The output from the PP-delay unit is split by a 50 : 50 single-mode fiber coupler. One portion is guided to the retinal scanner, and the other is reflected by a calibration mirror. The scanning mirrors in the retinal scanner are clocked by the 200-kHz trigger. The back-scattered light from a sample and a reflected beam from the calibration mirror are guided to the PD-detection unit through the 50 : 50 fiber coupler. The optical probe power on the cornea is 1.48 mW. And the sensitivity of the PS-OCT system was measured as 84.3 dB at 0.5 mm depth of J11 channel (undelayed polarization input and horizontal polarization detection channel). The reference beam passes through a reference arm consisting of single-mode optical fiber and a bulk optical delay unit and is introduced into the PD-detection unit after passing a 45°-oriented polarizer.
Interference signals are detected by balanced photo-detectors (BPDs; PDB430C, Thorlabs). The analog output from each BPD is sent through a 1-MHz high-pass and a 250-MHz low-pass filter (HP1CH3-0S and LP250CH3-0S, 7th-order type I Chebyshev, R&K, Shizuoka, Japan) and digitized by the ATS9350 with a sampling rate of 500 MS/s and 12-bit resolution. Each spectral interference signal is sampled with 2,368 points, which corresponds to a wavelength range of 104 nm. Spectral shifts among the spectra, which are due to timing jitter in the A-trigger, are estimated and corrected by use of the calibration signal [28]. The sampled interference signals are numerically rescaled to be linear in the wave-number using predefined rescaling parameters determined by a time-frequency calibration method [39]. The spectral shift is compensated during this rescaling process.
For OCT reconstruction, first the spectral distortion due to PMD is numerically corrected, as described in detail in Section 3.2, and then OCT signals are obtained by numerically inverse-Fourier transforming the interference signals. The sampled spectral range and the windowing function finally yield the measured −6-dB depth-resolution of 14.6 μm in air, corresponding to 10.6 μm in tissue. This depth resolution was measured based on the unbuffered A-lines. And as described in Section 5.1, a significant difference was not observed for −6-dB depth resolution.
3. Polarization mode dispersion in JM-OCT
3.1. Formulation
A 1-km single-mode fiber is used in the optical buffering module to create a 5-μs delayed laser sweep, and it causes a significant amount of PMD. As the first step of PMD correction, we mathematically describe the effect of PMD in the optically buffered JM-OCT system.
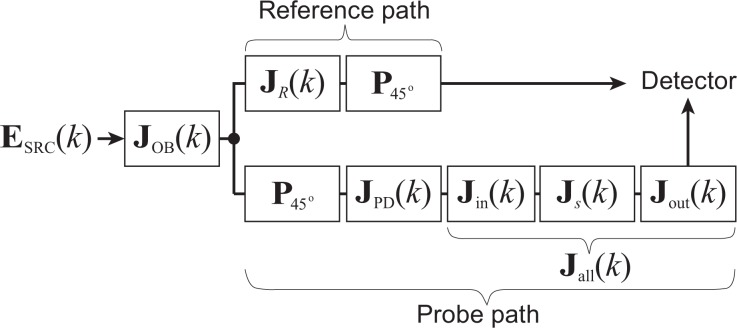
The polarization properties of our JM-OCT are modeled as depicted in Fig. 2. The light from the source is first introduced into the buffering module, which consists not only of optical fiber but also an FOS, which has significant diattenuation at one of its two switching modes. Hence the Jones matrix of the optical buffering module is modeled as a general matrix, as
| (1) |
where a(k), b(k), a′(k), and b′(k) and their subscripted versions with B and U are arbitrary complex functions of wavenumber k. Note that JOB(k) has two realizations, as described on the right-hand side. One realization is for a buffered mode in which the light passes through a long fiber spool, and the other is for a unbuffered mode.
Fig. 2.
Schematic model of the polarization properties of the JM-OCT interferometer. JOB(k), JR(k), and JPD(k) are the Jones matrices of the buffering module, the reference arm, and the PP-delay unit, respectively. Jin(k) and Jout(k) are the Jones matrices of the illumination and the collection paths of the probe arm, and Js(k) is the Jones matrix of the sample. P45° represents a polarizer oriented at 45°. ESRC(k) is the Jones vector of the source light.
After the buffering module, a portion of the light is led to the reference arm, which consists of optical fiber and nonbirefringent free-space optics. The reference arm is treated as a general elliptic retarder, which can have an arbitrary eigenpolarization state but has no diattenuation. Since the Jones matrix of a general elliptic retarder is a matrix in the special unitary group of degree 2, i.e., SU(2), the Jones matrix of the reference arm can be expressed in general form as
| (2) |
where α(k) and β(k) are arbitrary complex functions of k and the superscript of * denotes complex conjugation. According to the property of SU(2) matrix, |α(k)|2 + |β(k)|2 = 1. After passing through the reference arm, the reference beam passes a 45°-oriented linear polarizer ( ) at the entrance of the PD-detection unit. Hence the Jones vector of the reference beam at the photo-detectors becomes
| (3) |
where ESRC(k) is the Jones vector of the source light and the bulk phase on the right-hand side is a phase slope corresponding to the bulk length of the reference arm, zr.
On the other hand, the probe beam passes through the optical buffering module, another 45°-oriented linear polarizer (P45°), the PP-delay unit (JPD(k)), an illumination path (Jin(k)), the sample (Js(k)), and a collection path (Jout(k)). So the Jones vector of the probe beam at the photo-detectors becomes
| (4) |
where zp is the bulk length of the probe arm and Jall(k) = Jout(k)Js(k)Jin(k), which is also expressed as [J11(k) J12(k) ; J21(k) J22(k)] in the later part of this paper. The Jones matrix of the PP-delay unit is JPD(k) = [1 0 ; 0 d(k)] where d(k) = exp(−ikzd) with zd the path-length difference generated by the PP-delay unit between two incident polarization states.
It should be noted that the model of the PP-delay unit does not account for depth dependent signal roll-off. The signal roll-off can cause different signal strengths between two OCT signals corresponding to the two incident polarization states. This signal roll-off is not corrected in our method, since the effect of signal roll-off to the polarization measurement is not significant as far as the roll-off speed is similar for the both incident polarizations as discussed in Section 5.4 of [28]. Although it was not implemented in our system, additional numerical correction of the signal roll-off [36] would further enhance the accuracy of polarization measurement.
Without loss of generality, the source light can be assumed to be horizontally polarized: ESRC(k) = [S(k) 0]T, where S(k) is a complex spectral amplitude of the source. With this light source, the Jones vectors of the probe and the reference beam at the PD-detection unit respectively become
| (5) |
| (6) |
The spectral interference signal is obtained by entrywise operations of these Jones vectors as
| (7) |
where | · |2 and ○ denote the entrywise absolute square and multiplication, respectively. The first and second entries of this vector expression are the interference signals detected by the horizontal and vertical detectors of the PD-detection unit, respectively. The third term of this equation is a polarization-sensitive spectral interference signal corresponding to an OCT signal, expressed as
| (8) |
where Δz = zp − zr is the bulk path-length difference between the probe and reference arms. Here ε(k) is a complex modulation defined as
| (9) |
Because of the presence of d(k), the OCT signals corresponding to J12(k) and J22(k) appear at a different depth from those for J11(k) and J21(k). Hence, the four entries of the Jones matrix can be properly demultiplexed [28], and the spectrum of a raw measured Jones matrix is obtained as
| (10) |
This equation indicates that the Jones matrices are globally modulated by |S(k)|2 ε(k). The inverse Fourier transform of this modulation, ℱ−1[|S(k)|2] * ℱ−1[ε(k)], is the point spread function (PSF) of the JM-OCT system, with ℱ−1 the inverse Fourier transform and * denoting convolution. Since a(k) and b(k) have different realizations for the buffered and unbuffered modes, the PSFs for these two modes are different. On the other hand, all four entries of the Jones matrix are concurrently modulated, and their PSFs are identical. This difference in PSFs between the buffered and unbuffered modes — but not among the four entries of Jones matrix — is the main inadequacy induced by the optical buffering in our JM-OCT system. This relatively simple effect of PMD is due to the two 45°-oriented polarizers. The benefits of the polarizers are discussed in detail in Section 6.1.
In our JM-OCT system, this buffering-mode-dependent modulation is numerically corrected using the method described in the next section.
In this section, the orientations of polarizers are assumed to be 45°. It is to ensure equal optical power between two incident polarization states and between two reference powers of horizontal and vertical detectors. This particular configuration of polarizers are selected mainly to simplify the formulation, and, in practice, the orientations do not need to be 45° as to be discussed in Section 6.2.
3.2. Numerical correction of polarization mode dispersion
As described in the previous subsection, the PMD, which is due mainly to the buffering module, appears as a global complex modulation of the measured Jones matrix [Eq. (10)]. This section describes a numerical method to cancel this modulation. In this method, the envelope of the modulation is corrected first. The phase of the modulation is then corrected after the envelope correction, together with polarization-independent chromatic dispersion.
By scanning a sample with the optically buffered JM-OCT system, two sets of spectra are obtained, corresponding to two horizontal and vertical detection polarization states. To estimate the envelope of the modulation, we utilized the spectra of a B-scan, which typically consists of 490 A-lines. For PMD correction of a volumetric data set, only the first B-scan of the volume is used. The two (horizontal and vertical) spectral sets consist of interlaced buffered and unbuffered spectra. These are deinterlaced, and the buffered and unbuffered spectra are then processed independently.
First, the spectral shift correction and spectral rescaling were performed as described in Section 2. Note that the set of spectra are function not only of k but also of the transversal scanning position x. The wavelength-dependent DC-offset is removed by subtracting a spectrum averaged over x. These processes are applied to the horizontal and vertical polarization spectral sets independently, and two sets of rescaled spectra, fH (k, x) (horizontal) and fV (k, x) (vertical), are obtained.
These spectra are inversely fast Fourier transformed (IFFT’ed) into the depth domain, and OCT signals corresponding to J11 and J21 are cropped with Hanning windows from the inverse Fourier transforms of fH (k, x) and fV (k, x), respectively. These spectra are then fast Fourier transformed (FFT’ed) back into the k-domain. This process provides two sets of complex spectra: f11(k, x) for J11, and f21(k, x) for J21. These are expressed as
| (11) |
where n is 11 or 21. It is noteworthy that J11 and J21 are functions of k and x while S(k) and ε(k) are independent of x.
The joint envelope of the modulation function ε(k) and the source spectrum |S(k)|2 are then obtained as following computation.
| (12) |
where 〈·〉x represents averaging along x. The square root part in the second line becomes a constant C in the third line, because of the statistical nature of J11(k, x) and J21(k, x). In practice, the Ie(k) obtained in this computation is further smoothed by a median filter with a width of 30 spectral sampling points, corresponding to 1.3 nm. The median filter width was selected based on the appearance of the reference beam, which had a typical modulation frequency of around 10 cycles per full spectral range.
The spectral reshaping filter to demodulate the modulation envelope is then defined as
| (13) |
where G(k) is a Gaussian function that defines the depth resolution. In our particular implementation, the FWHM of the Gaussian window is 45.3 nm, which results in a theoretical depth resolution of 10.8 μm in air. Two reshaping filters are independently defined for buffered and unbuffered modes.
After obtaining the spectral reshaping filter, all the rescaled spectra in the volume (fH (k, x) and fV (k, x)) are reshaped. This reshaping modifies the spectral interference signal of OCT [Eq. (8)] to
| (14) |
where ∠ε(k) is the phase of the modulation function ε(k). In the second line, the polarization-independent chromatic dispersion, ϕ(k), is unlinked from the entries of the Jones matrix so that Jn(k, x) = eiϕ(k) (k) with n = 11, 12, 21, and 22. This equation indicates that the reshaping filter corrects the envelope of the spectral interference signal to Gaussian. The remaining unwanted factor is thus the global phase modulation ei{∠ε(k)+ϕ(k)}, which is removed in the subsequent numerical process.
Before removing the global phase, fixed pattern noise (FPN) is removed by complex median subtraction [40]. In this process, the spectra are IFFT’ed into the depth domain once, the complex median along the x-direction is subtracted from each depth-domain complex signal at each depth, and the signals are FFT’ed back into the k-domain.
After correcting the spectral envelope and removing FPN, the modulation phase is estimated by using an iterative numerical method originally developed for polarization-independent chromatic dispersion correction [41], which determines the modulation phase to minimize the information entropy of the OCT image. In our implementation, the dispersion phase is estimated by minimizing the information entropy of the J11 and J12 images obtained from the horizontal spectra. This dispersion phase is used to correct the dispersion in both the horizontal and vertical spectra.
The dispersion phase estimation and correction are performed independently for the buffered and unbuffered spectra. This yields a PMD-corrected spectral Jones vector G(k) C[ (k) + d(k) (k) (k) + d(k) (k)]T exp(−ikΔz). Each entry of the spectral Jones vector is then IFFT’ed, and a set of four OCT images forming the Jones matrix OCT is obtained.
The computation of spectral reshaping filter and the dispersion phase estimation are performed with the first B-scan of a volumetric data set. This set of spectral filter and the dispersion phase is utilized for the entire volumetric processing.
4. Image formation
In our scanning protocol, four cross-sectional frames are sequentially acquired at each location on the sample. Several types of OCT images, including intensity, power Doppler, phase retardation, and degree-of-polarization uniformity (DOPU) [25, 42], are obtained from a set of four PMD-corrected Jones matrices.
The intensity and power Doppler images are obtained by the same means as in Section 3.7 of [28]. The intensity image is a global-phase-corrected, sensitivity-enhanced, scattering OCT, described in detail in Section 3.8 of [28]. The power Doppler image is a power-of-Doppler-shift image, as described in Section 3.7 of [28]. In our particular implementation, the time separation for Doppler phase shift determination is 3.2 ms. In the image formation, four A-lines are combined to yield an intensity A-line and a power Doppler A-line. Our scanning protocol is designed to ensure that all four A-lines in the set are solely buffered or unbuffered. It is in order to ease the implementation of numerical correction of PMD which should be applied separately to the buffered and unbuffered data sets.
To compute the phase retardation and DOPU images, the four PMD-corrected Jones matrices are first averaged by the adaptive Jones-matrix averaging method (Section 3.4 of [28]). For DOPU computation, Makita’s modified DOPU [42] is computed with a kernel size of 8 pixels (transverse) by 3 pixels (depth). Two of the four entries of the Jones matrix (J11 and J21) represent the Jones vector of an output probe beam generated from horizontal incident polarization, while the other entries (J12 and J22) represent vertical polarization. Hence, two Stokes vectors are obtained from a single Jones matrix. In addition, since the buffered and unbuffered A-lines are interlaced, the kernel consists of 4 × 3 buffered and unbuffered Jones matrices for each. Hence, the Stokes vectors obtained within the kernel are subdivided into four groups according to the combinations of buffering modes and the incident polarization states. The Stokes vectors are then corrected for noise error [Eq. (1) of [42]]. This correction is done independently for each group by using the estimated noise energies of each group. Finally, modified DOPU with multiple incident polarization states (M-DOPU′) is computed by use of Eq. (3) of [42] from the noise-error-corrected Stokes vectors.
For computation of the phase retardation, the buffered and unbuffered A-lines are first deinterlaced into two frames of Jones-matrix images. The phase retardation is then computed for each frame independently as described in [28]. Briefly, each Jones-matrix pixel in the image is multiplied by the inverse of the averaged Jones matrix of the sample surface. This operation transforms the Jones matrix into the similar matrix of the sample Jones matrix [28, 43]. The phase retardation is obtained as the phase difference between the two eigenvalues of the similar matrix. The phase retardation images obtained from the buffered and unbuffered frames are then reinterlaced to form a phase retardation image.
5. Results
5.1. Validation of PMD correction
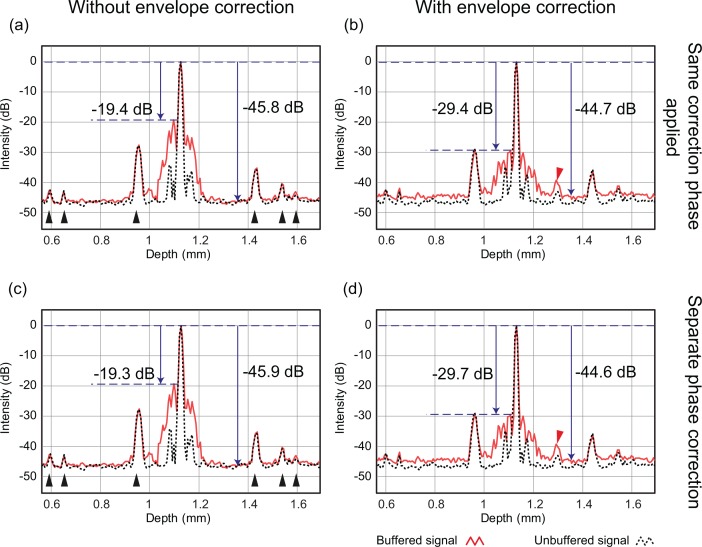
To validate the numerical PMD correction, a mirror sample was measured by JM-OCT. The mirror was sampled for 512 A-lines (256 each for of buffered and unbuffered modes) without transversal scanning. Since transversal scanning was not performed, FPN removal was not applied. For the same reason, wavelength-dependent DC-offset removal was performed not by averaged spectrum subtraction but by frequency filtering, such that ± 30 pixels around the zero-delay position in the depth domain were masked. Figure 3 shows the averaged A-lines of the buffered (red solid lines) and unbuffered (black dotted lines) modes with different combinations of processing. The modulation envelope correction filter [Eq. (13)] was applied only to Figs. 3(b) and 3(d) (the right panels), but not applied to Figs. 3(a) and 3(c) (the left panels). In Figs. 3(c) and 3(d) (the bottom panels), the modulation phase was separately estimated and corrected for buffered and unbuffered spectra. For Figs. 3(a) and 3(b) (the top panels), the modulation phase was obtained from the buffered spectra and the same phase correction was applied to both buffered and unbuffered spectra. Thus, Fig. 3(d) shows the signal with the full PMD correction.
Fig. 3.
Averaged A-line signals of a mirror sample with different processing options for PMD correction. The black dotted and the red solid lines indicate unbuffered and buffered Alines, respectively. The panels on the right were processed with envelope correction, while the left panels were not. The dispersion and modulation phase were corrected separately for buffered and unbuffered modes in the bottom panels, while the same correction phase was applied for the both modes in the top panels. Black arrowheads indicate FPN, and red arrowheads indicate a side peak created by the envelope correction.
Without envelope correction (Fig. 3, left), the SNR of the mirror signal was around 46 dB and strong side peaks were observed. The maximum side peak of the buffered spectra was around −19 dB compared with the main signal peak of the mirror. With the envelope correction, the maximum side peaks were decreased to −29.7 [Figs. 3(b)] and −29.4 dB [Fig. 3(d)]. A small side peak appears, as indicated by red arrowheads in Figs. 3(b) and 3(d). However, since its strength is −42.1 dB for unbuffered mode and −39.3 dB for buffered mode, it can be neglected for in vivo measurements. The unbuffered signal was not significantly altered by the envelope correction, as expected from the insignificant amount of PMD in the unbuffered path. Spectral reshaping slightly decreased the SNR by around −1 dB. However, considering the reduction of side peaks by more than 10 dB, it is worth applying the envelope correction. The reduction of the side peak was measured at five depth locations at 0.57 mm, 0.83 mm, 1.12 mm, 1.40 mm, and 1.66 mm and corresponding reductions were −9.3 dB, −10.2 dB, −10.2 dB, −9.5 dB, and −9.1 dB, respectively.
In contrast to envelope correction, there was no significant difference between separate (bottom) and non-separate (top) phase correction. This is due to appropriate alignment of the fiber polarization, as discussed in detail in Section 6.3. Although separate versus non-separate phase correction makes no difference if the fiber polarization is well aligned, this will slowly alter over time. Hence, the phase should be corrected separately for the two buffering modes to ensure mid- to long-term stability.
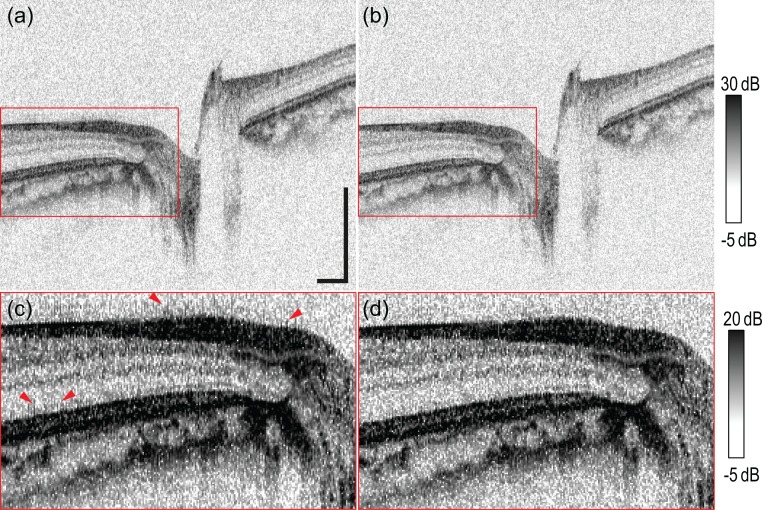
Figure 4 shows the typical difference in OCT intensity images of in vivo human retina. The PMD is not corrected in Figs. 4(a) and 4(c) while the PMD is corrected in Figs. 4(b) and 4(d). Figures 4(c) and 4(d) are magnified images of red rectangle area of Figs. 4(a) and 4(b), respectively, and their dynamic range was reduced to show the improvement of the PMD correcton. Without PMD correction, comblike smearing appears around hyper-scattering layers, such as the retinal nerve fiber layer and RPE complex, as indicated by red arrowheads in Fig. 4(c). This appearance is due to the different PSFs between buffered and unbuffered modes, which are caused by different PMD in the optical buffering module. PMD correction removes this smearing, as shown in Figs. 4(b) and 4(d).
Fig. 4.
Comparison of in vivo retinal OCT images (a), (c) without and (b), (d) with PMD correction. Panels (c) and (d) are magnified images of the red rectangular regions in (a) and (b), respectively. The scale bar in (a) represents 0.5 mm × 0.5 mm
5.2. High-speed JM-OCT imaging of in vivo human eye
Figure 5 summarizes the high-speed in vivo JM-OCT images of the human optic nerve head (ONH) obtained at 200,000 A-lines per second with PMD correction. The imaged eye was myopic (−7.25 D) and the subject was a 28-year-old Japanese male. A 6 mm × 6 mm area around the ONH was scanned with 512 A-lines × 256 B-scans × 4 repeated B-scans at a single location in 3.3 seconds. For this in vivo imaging, the polarizer in the sample arm was realigned to minimize the measurement error of the phase retardation, by which the polarizer is aligned to 37°. This realignment is compatible with the PMD correction, as discussed in Section 6.2. The SNRs of two PD-detection channels are roughly equalized for each subject by aligning the polarization controller in the probe arm (PC-3 of Fig. 1).
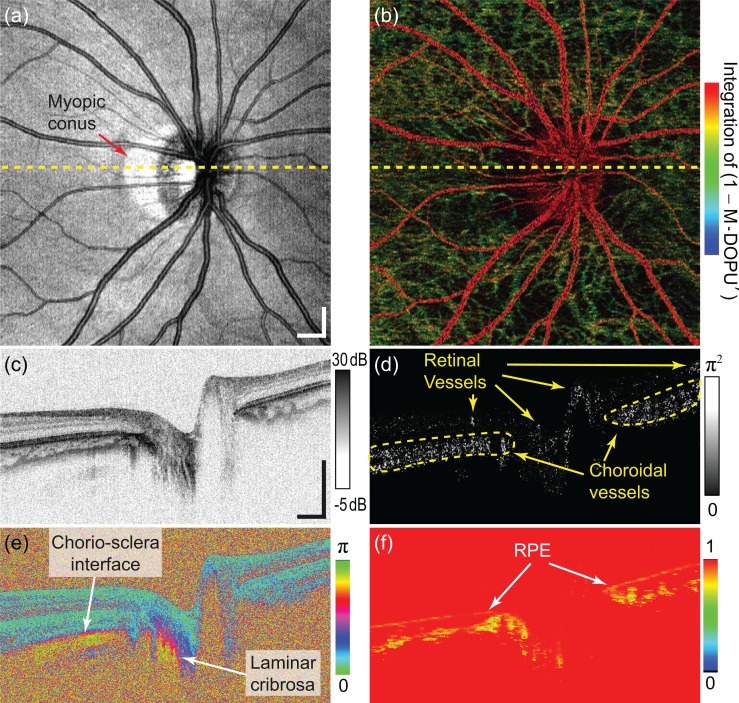
Fig. 5.
An example of our high-speed multifunctional OCT images of in vivo human optic nerve head. (a), (c) En face projection and a representative cross section of scattering (intensity) OCT, respectively; (d)–(f) power Doppler, phase retardation, and M-DOPU′ cross-sections, respectively; (b) an en face pseudo-color composite of power Doppler and M-DOPU′ signals. Yellow dashed lines in (a) and (b) represent the location of the cross-sectional images. The scale bars in (a) and (c) represent 0.5 mm × 0.5 mm.
Even with a shorter measurement time, the high-speed JM-OCT yields contrast similar to a previous system based on nearly the same configuration but without optical buffering and, hence, scanning at 100,000 A-lines per second [28]. Figure 5(a) is an en face projection of the scattering (intensity) OCT, and Fig. 5(c) is a representative scattering OCT B-scan. Figures 5(d)–5(f) are power Doppler, phase retardation, and DOPU (M-DOPU′) images, respectively. Figure 5(b) is a volume rendered en face view of power Doppler signals which are pseudo-colored by DOPU signals [42]. The voxel color is defined by the integrated values of (1–M-DOPU′) over the voxel. The voxel brightness is first defined by the power Doppler signal intensity and then attenuated by the integrated values of (1–M-DOPU′) over the voxel. This numerical attenuation emulates the obscuration of the vessels by melanin in RPE and the choroid. Then, the pseudo-colored en face power Doppler image is created by integrating the voxels along depth. In this en face image, blood vessels anterior to the RPE appear as red, while those beneath the RPE appear as green.
A myopic conus is well recognized in the en face scattering OCT image [Fig. 5(a), red arrow]. The OCT B-scan [Fig. 5(c)] shows clear retinal and choroidal structures. The phase retardation image [Fig. 5(e)] exhibits rapid alterations around the chorio-scleral interface and the lamina cribrosa, which indicate high birefringence of the sclera and lamina cribrosa, respectively. The DOPU image [Fig. 5(f)] discriminates the RPE clearly as a low-DOPU line. Some regions in the choroid also appear with low DOPU values, which is consistent with our previous clinical study based on 100,000 A-lines per second JM-OCT [29]. The power Doppler B-scan [Fig. 5(d)] contrasts not only the retinal vessels but also choroidal vessels. The retinal and choroidal vessels can be distinguished by its color in the en face pseudo-color composite [Fig. 5(b)], where the retinal vessels are red and choroidal vessels are green. It is noteworthy that this distinguishing between retinal and choroidal vessels was done without RPE segmentation. Hence, the technique will be applicable even to pathologic cases with severe RPE damage.
6. Discussion
6.1. Roles of polarizers in probe and reference arms
In our JM-OCT system, two polarizers are used in the probe and reference arms, while some other JM-OCT systems do not [36, 44]. These polarizers play an important role in simplifying the effect of PMD.
By removing the polarizers from Eqs. (3) and (4), the polarization-sensitive spectral signal corresponding to OCT [Eq. (8)] becomes
| (15) |
where (k) and (k) are probe and reference fields without polarizers in Jones-vector form, respectively, and
| (16) |
Evidently, the four entries of the measured Jones matrix are differently modulated. In addition, the modulation differs between the buffered and unbuffered modes. Hence, eight different modulations appear in total, while there are only two if the polarizers are employed. As shown by these equations, the polarizers dramatically simplify the treatment of PMD.
As a reference, Baumann et al. has built a similar JM-OCT but without polarizers [45]. As the authors described, the dispersion had to be numerically corrected independently for each polarization channel in this case.
Even without linear polarizers, the complex modulations of four entries of the measured Jones matrix can be corrected by separately applying the numerical PMD correction method to each entry. In this case, we should accept additional computational load. In addition, it should be noted that the result of dispersion correction should be consistent among four entries. It is not always assured because the numerical dispersion correction method utilized in the present method is heuristic. So the property of this numerical method should be carefully examined and the algorithm should be modified if necessary.
6.2. Orientation of polarizers
In Section 3, the orientations of the polarizers were assumed to be 45° for simplicity. However, the orientations do not significantly affect JM-OCT measurements.
Let the polarizer orientations be θP and θR in the probe and reference paths, respectively. The Jones matrices of the polarizers become PP = R (θP)[1 0; 0 0]R (−θP) for the probe arm and PR = R (θR)[1 0; 0 0]R (−θR) for the reference arm, where R (θ) is a rotation matrix defined as [cosθ − sinθ; sinθ cosθ]. By replacing P45° in Eq. (3) with PR and that in Eq. (4) with PP, Eq. (8) is generalized as
| (17) |
where (k) and *(k) are the probe and reference fields in Jones-vector form with arbitrary polarizer rotation angles, respectively, and
| (18) |
According to this equation, the measured Jones matrix becomes
| (19) |
It is evident that all entries of the Jones matrix are only globally modulated. Hence, the method described in Section 3.2 can remove the modulation.
This equation also shows that (k) is decomposed into the products of a diagonal matrix of ΘR (θR), Jall(k) = Jout(k)Js(k)Jin(k), and a diagonal matrix of ΘP (θP). By regarding ΘRJout(k) as the Jones matrix of a collection optics (k) and Jin(k)ΘP as that of an illumination optics (k), the measured Jones matrix can be expressed as (k) = |S(k)|2 ε″(k) (k)Js(k) (k). Since this form of (k) is covered by the generality of Eq. (10), ΘR and ΘP have no significant effect on JM-OCT measurements.
Although the theory suggests that the orientations of the polarizers do not affect the result, this does not take measurement noise into account. It is known that such noise results in significant bias in phase retardation measurements [46]. This bias can be reduced by increasing the signal energy of OCT. When the total signal energy of OCT is fixed, as in the case of practical JM-OCT measurements, the bias is minimized by equalizing the SNRs of OCT signals originating from the two incident polarization states. Hence, for practical in vivo measurement (Section 5.2), θP and θR were aligned to satisfy this condition. In our particular case, θP and θR were aligned to 37° and 45°, respectively.
6.3. Alignment of polarization controllers
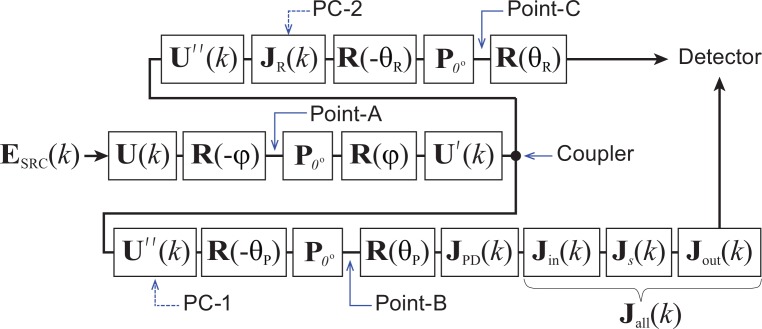
There was no significant difference between two sets of PSFs; when the modulation phase were corrected separately for the buffered and unbuffered modes [Figs. 3(c) and 3(d)], and when the same correction phase was applied to both modes [Figs. 3(a) and 3(b)], respectively. This insensitivity to separate or non-separate phase correction is a result of proper alignment of the polarization controllers. In this section, this fact is elucidated with a mathematical description of the alignment process.
By considering the strong diattenuation of the FOS, the polarization model of our JM-OCT interferometer in unbuffered mode can be illustrated as in Fig. 6. In this schematic, U(k), U′(k), and U″(k) are Jones matrices of the optical fibers and can be treated as SU(2) matrices; φ is the orientation of the diattenuation of the FOS, which is modeled by a polarizer; θP and θR are the orientations of the polarizers in the probe and reference arms, respectively. By comparison with the polarization model in Fig. 2, It can be seen that the Jones matrices from U(k) to U″(k) form the Jones matrix of a buffering module, JOB. Note that in the practical optical setup, a coupler splits the beam after U′(k) and before U″(k). This departure from the practical setup is compensated by accounting for the same matrix U″(k) in both the probe and reference arms. The polarization controller in the probe arm (PC-1) alters U″(k), while that in the reference arm (PC-2) alters JR(k).
Fig. 6.
Schematic model of the polarization properties of the JM-OCT interferometer with a specific FOS model and polarizers with arbitrary orientations. U(k), U′(k), and U″(k) are SU(2) matrices representing the Jones matrices of the optical fibers. R(θ) is a rotation matrix with rotation angle θ and P0° represents a polarizer oriented at 0°.
In the first step of the alignment, PC-1 is aligned to maximize the optical throughput from point-A to point-B indicated in Fig. 6. This yields
| (20) |
where p(k) is an arbitrary complex function. Since U″(k)U′(k) is a Jones matrix of optical fiber and is SU(2) matrix, thus the condition |p(k)|2 = 1 is ensured.
After the alignment of PC-1, the polarization of the reference arm (JR(k)) is modified by PC-2 to maximize the optical throughput from point-A to point-C. This alignment establishes
| (21) |
where q(k) is an arbitrary complex function and |q(k)|2 = 1.
By combining Eqs. (20) and (21), it can be known that the alignment process ensures
| (22) |
where γ(k) = p*(k)q(k).
By substituting JR(k) into Eq. (18) as [α(k) − β*(k); β(k) α*(k)] = JR(k), the spectral modulation function under this alignment condition is given by
| (23) |
The phase of this modulation function is
| (24) |
As is evident from this equation, the phase of the modulation function does not depend on a(k) and b(k), the phase functions defining the polarization properties of the buffering module. This suggests that the phase of the modulation becomes independent from the buffering mode under this alignment condition. It properly explains why the PSFs presented in Section 5.1 are equally good no matter whether the modulation phase correction was applied separately or not for the buffered and unbuffered modes.
Equation (24) suggests that the dispersion correction can be performed at once for buffered and unbuffered spectra if the system polarization is properly aligned. However, in practice, the polarization properties of optical fibers varies slowly but continuously. Hence, it is still important to separately correct the modulation phase to ensure mid- to long-term stability.
In this section, Eq. (23) was derived by directly substituting Eq. (22) into Eq. (18). Although this simplifies the explanation, it results in elaborate manipulations of the equations. Alternatively, Eq. (23) can be derived more simply by substituting JOB(k) = U″(k)U′(k)R(φ)P0° R(−φ)U(k) and JR(k) obtained in this section into Eqs. (3) and (4).
6.4. Polarization mode dispersion of buffering module
Dhalla et al. reported that, with their non-PS-OCT, the PMDs of the fiber spool and the FOS in the buffering module result in two distinctive types of side peaks with different separations from the main peak [32]. In our PSF measurement (Fig. 3), these two types of side peaks were overlapped each other.
As it was done by Dhalla et al., we also carefully aligned the polarization controllers in the buffering module to minimize the PMDs of the fiber spool and the FOS at an initial time point. Although this alignment condition is slowly corrupted by temporal drifting of fiber birefringence, the PMDs of both the fiber spool and the FOS are corrected by the present numerical correction method. It is assured by the fact that the birefringence model of the buffering module [Eq. (1)], which is the bases of our method, properly models the PMD of both sources.
6.5. Polarization mode dispersion in probe arm
In this paper, we assumed that PMD in the probe arm optics is negligible, i.e., Jin(k) and Jout(k) have only polarization-independent chromatic dispersion. This assumption is rational if the optical fibers in the probe arm are short.
In our particular case, the optical fibers in the illumination and collection paths are 5 m and 4 m, respectively. Thus, the assumption would be rational.
In the case that PMD in the probe arm is not negligible, other methods can be additionally applied to correct this PMD. For instance, a method recently presented by Braaf et al. [36] can be combined with the present method. Villiger et al. [35] have also presented a spectral binning method to reduce PMD. This method could be applicable with little modification for Jones-matrix formulation.
7. Conclusion
We have described JM-OCT based on optical buffering. Although the long optical fiber in the optical buffering module induces strong PMD and a consequent strong spectral modulation, it can be corrected numerically. Validation experiments showed that the numerical method successfully corrected the PMD.
In vivo measurement of a non-pathologic eye was employed to demonstrate the practical imaging performance of a high-speed JM-OCT system. This system was designed for the investigation of the posterior eye and uses a probe wavelength of 1 μm. A high-speed measurement with 200,000 A-lines per second was achieved with a commercially available wavelength-sweeping light source with a wavelength scanning rate of 100 kHz. The quality of the OCT intensity, Doppler, cumulative phase retardation, and DOPU images were found to be similar to a previous JM-OCT system with half the measurement speed. This decreased measurement time would enhance the clinical utility of JM-OCT by reducing motion artifacts.
Acknowledgments
This research was supported in part by Topcon Corp. and Tomey Corp.
References and links
- 1.Huang D., Swanson E., Lin C., Schuman J., Stinson W., Chang W., Hee M., Flotte T., Gregory K., Puliafito C., Fujimoto J., “Optical coherence tomography,” Science 254, 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Sakata L. M., DeLeon-Ortega J., Sakata V., Girkin C. A., “Optical coherence tomography of the retina and optic nerve a review,” Clinical & Experimental Ophthalmology 37, 90–99 (2009). 10.1111/j.1442-9071.2009.02015.x [DOI] [PubMed] [Google Scholar]
- 3.Pierce M. C., Strasswimmer J., Park B. H., Cense B., de Boer J. F., “Advances in optical coherence tomography imaging for dermatology,” Journal of Investigative Dermatology 123, 458–463 (2004). 10.1111/j.0022-202X.2004.23404.x [DOI] [PubMed] [Google Scholar]
- 4.Otis L. L., Everett M. J., Sathyam U. S., Colston B. W., “Optical coherence tomography: A new imaging technology for dentistry,” The Journal of the American Dental Association 131, 511–514 (2000). 10.14219/jada.archive.2000.0210 [DOI] [PubMed] [Google Scholar]
- 5.Gora M. J., Sauk J. S., Carruth R. W., Gallagher K. A., Suter M. J., Nishioka N. S., Kava L. E., Rosenberg M., Bouma B. E., Tearney G. J., “Tethered capsule endomicroscopy enables less invasive imaging of gastrointestinal tract microstructure,” Nature Medicine 19, 238–240 (2013). 10.1038/nm.3052 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tearney G. J., Waxman S., Shishkov M., Vakoc B. J., Suter M. J., Freilich M. I., Desjardins A. E., Oh W.-Y., Bartlett L. A., Rosenberg M., Bouma B. E., “Three-dimensional coronary artery microscopy by intracoronary optical frequency domain imaging,” J Am Coll Cardiol Img 6, 752–761 (2008). 10.1016/j.jcmg.2008.06.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Chen Z., Milner T. E., Dave D., Nelson J. S., “Optical doppler tomographic imaging of fluid flow velocity in highly scattering media,” Opt. Lett. 22, 64–66 (1997). 10.1364/OL.22.000064 [DOI] [PubMed] [Google Scholar]
- 8.White B., Pierce M., Nassif N., Cense B., Park B., Tearney G., Bouma B., Chen T., de Boer J., “In vivo dynamic human retinal blood flow imaging using ultra-high-speed spectral domain optical coherence tomography,” Opt. Express 11, 3490–3497 (2003). 10.1364/OE.11.003490 [DOI] [PubMed] [Google Scholar]
- 9.Leitgeb R., Schmetterer L., Drexler W., Fercher A., Zawadzki R., Bajraszewski T., “Real-time assessment of retinal blood flow with ultrafast acquisition by color doppler fourier domain optical coherence tomography,” Opt. Express 11, 3116–3121 (2003). 10.1364/OE.11.003116 [DOI] [PubMed] [Google Scholar]
- 10.Hee M. R., Huang D., Swanson E. A., Fujimoto J. G., “Polarization-sensitive low-coherence reflectometer for birefringence characterization and ranging,” J. Opt. Soc. Am. B 9, 903–908 (1992). 10.1364/JOSAB.9.000903 [DOI] [Google Scholar]
- 11.de Boer J. F., Milner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22, 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 12.Hitzenberger C., Goetzinger E., Sticker M., Pircher M., Fercher A., “Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography,” Opt. Express 9, 780–790 (2001). 10.1364/OE.9.000780 [DOI] [PubMed] [Google Scholar]
- 13.Yasuno Y., Makita S., Sutoh Y., Itoh M., Yatagai T., “Birefringence imaging of human skin by polarization-sensitive spectral interferometric optical coherence tomography,” Opt. Lett. 27, 1803–1805 (2002). 10.1364/OL.27.001803 [DOI] [PubMed] [Google Scholar]
- 14.Yamanari M., Makita S., Madjarova V. D., Yatagai T., Yasuno Y., “Fiber-based polarization-sensitive fourier domain optical coherence tomography using b-scan-oriented polarization modulation method,” Opt. Express 14, 6502–6515 (2006). 10.1364/OE.14.006502 [DOI] [PubMed] [Google Scholar]
- 15.Yamanari M., Makita S., Yasuno Y., “Polarization-sensitive swept-source optical coherence tomography with continuous source polarization modulation,” Opt. Express 16, 5892–5906 (2008). 10.1364/OE.16.005892 [DOI] [PubMed] [Google Scholar]
- 16.Yang V. X. D., Gordon M., jiang Tang S., Marcon N., Gardiner G., Qi B., Bisland S., Seng-Yue E., Lo S., Pekar J., Wilson B., Vitkin I., “High speed, wide velocity dynamic range doppler optical coherence tomography (part iii): in vivo endoscopic imaging of blood flow in the rat and human gastrointestinal tracts,” Opt. Express 11, 2416–2424 (2003). 10.1364/OE.11.002416 [DOI] [PubMed] [Google Scholar]
- 17.Makita S., Hong Y., Yamanari M., Yatagai T., Yasuno Y., “Optical coherence angiography,” Opt. Express 14, 7821–7840 (2006). 10.1364/OE.14.007821 [DOI] [PubMed] [Google Scholar]
- 18.Baumann B., Potsaid B., Kraus M. F., Liu J. J., Huang D., Hornegger J., Cable A. E., Duker J. S., Fujimoto J. G., “Total retinal blood flow measurement with ultrahigh speed swept source/fourier domain oct,” Biomed. Opt. Express 2, 1539–1552 (2011). 10.1364/BOE.2.001539 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hendargo H. C., McNabb R. P., Dhalla A.-H., Shepherd N., Izatt J. A., “Doppler velocity detection limitations in spectrometer-based versus swept-source optical coherence tomography,” Biomed. Opt. Express 2, 2175–2188 (2011). 10.1364/BOE.2.002175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Braaf B., Vermeer K. A., Vienola K. V., de Boer J. F., “Angiography of the retina and the choroid with phase-resolved oct using interval-optimized backstitched b-scans,” Opt. Express 20, 20516–20534 (2012). 10.1364/OE.20.020516 [DOI] [PubMed] [Google Scholar]
- 21.Blatter C., Coquoz S., Grajciar B., Singh A. S. G., Bonesi M., Werkmeister R. M., Schmetterer L., Leitgeb R. A., “Dove prism based rotating dual beam bidirectional doppler oct,” Biomed. Opt. Express 4, 1188–1203 (2013). 10.1364/BOE.4.001188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hong Y.-J., Miura M., Makita S., Ju M. J., Lee B. H., Iwasaki T., Yasuno Y., “Noninvasive investigation of deep vascular pathologies of exudative macular diseases by high-penetration optical coherence angiography,” Investigative Ophthalmology & Visual Science 54, 3621–3631 (2013). 10.1167/iovs.12-11184 [DOI] [PubMed] [Google Scholar]
- 23.Pircher M., Götzinger E., Leitgeb R., Sattmann H., Findl O., Hitzenberger C., “Imaging of polarization properties of human retina in vivo with phase resolved transversal ps-oct,” Opt. Express 12, 5940–5951 (2004). 10.1364/OPEX.12.005940 [DOI] [PubMed] [Google Scholar]
- 24.Miura M., Yamanari M., Iwasaki T., Elsner A. E., Makita S., Yatagai T., Yasuno Y., “Imaging polarimetry in age-related macular degeneration,” Investigative Ophthalmology & Visual Science 49, 2661–2667 (2008). 10.1167/iovs.07-0501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Götzinger E., Pircher M., Geitzenauer W., Ahlers C., Baumann B., Michels S., Schmidt-Erfurth U., HitzenbergerAdi C. K., “Retinal pigment epithelium segmentation by polarization sensitive optical coherencetomography,” Opt. Express 16, 16410–16422 (2008). 10.1364/OE.16.016410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ahlers C., Gtzinger E., Pircher M., Golbaz I., Prager F., Schtze C., Baumann B., Hitzenberger C. K., Schmidt-Erfurth U., “Imaging of the retinal pigment epithelium in age-related macular degeneration using polarization-sensitive optical coherence tomography,” Investigative Ophthalmology & Visual Science 51, 2149–2157 (2010). 10.1167/iovs.09-3817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Lim Y., Hong Y.-J., Duan L., Yamanari M., Yasuno Y., “Passive component based multifunctional jones matrix swept source optical coherence tomography for doppler and polarization imaging,” Opt. Lett. 37, 1958–1960 (2012). 10.1364/OL.37.001958 [DOI] [PubMed] [Google Scholar]
- 28.Ju M. J., Hong Y.-J., Makita S., Lim Y., Kurokawa K., Duan L., Miura M., Tang S., Yasuno Y., “Advanced multi-contrast jones matrix optical coherence tomography for doppler and polarization sensitive imaging,” Opt. Express 21, 19412–19436 (2013). 10.1364/OE.21.019412 [DOI] [PubMed] [Google Scholar]
- 29.Hong Y.-J., Miura M., Ju M. J., Makita S., Iwasaki T., Yasuno Y., “Simultaneous investigation of vascular and retinal pigment epithelial pathologies of exudative macular diseases by multifunctional optical coherence tomography,” Investigative Ophthalmology & Visual Science 55, 5016–5031 (2014). 10.1167/iovs.14-14005 [DOI] [PubMed] [Google Scholar]
- 30.Huber R., Adler D. C., Fujimoto J. G., “Buffered fourier domain mode locking: Unidirectional swept laser sources for optical coherence tomography imaging at 370,000 lines/s,” Opt. Lett. 31, 2975–2977 (2006). 10.1364/OL.31.002975 [DOI] [PubMed] [Google Scholar]
- 31.Potsaid B., Baumann B., Huang D., Barry S., Cable A. E., Schuman J. S., Duker J. S., Fujimoto J. G., “Ultrahigh speed 1050nm swept source / fourier domain oct retinal and anterior segment imaging at 100,000 to 400,000 axial scans per second,” Opt. Express 18, 20029–20048 (2010). 10.1364/OE.18.020029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dhalla A.-H., Shia K., Izatt J. A., “Efficient sweep buffering in swept source optical coherence tomography using a fast optical switch,” Biomed. Opt. Express 3, 3054–3066 (2012). 10.1364/BOE.3.003054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang E. Z., Vakoc B. J., “Polarimetry noise in fiber-based optical coherence tomography instrumentation,” Opt. Express 19, 16830–16842 (2011). 10.1364/OE.19.016830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Zhang E. Z., Oh W.-Y., Villiger M. L., Chen L., Bouma B. E., Vakoc B. J., “Numerical compensation of system polarization mode dispersion in polarization-sensitive optical coherence tomography,” Opt. Express 21, 1163–1180 (2013). 10.1364/OE.21.001163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Villiger M., Zhang E. Z., Nadkarni S. K., Oh W.-Y., Vakoc B. J., Bouma B. E., “Spectral binning for mitigation of polarization mode dispersion artifacts in catheter-based optical frequency domain imaging,” Opt. Express 21, 16353–16369 (2013). 10.1364/OE.21.016353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Braaf B., Vermeer K. A., de Groot M., Vienola K. V., de Boer J. F., “Fiber-based polarization-sensitive oct of the human retina with correction of system polarization distortions,” Biomed. Opt. Express 5, 2736–2758 (2014). 10.1364/BOE.5.002736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Bonesi M., Sattmann H., Torzicky T., Zotter S., Baumann B., Pircher M., Götzinger E., Eigenwillig C., Wieser W., Huber R., Hitzenberger C. K., “High-speed polarization sensitive optical coherence tomography scan engine based onfourier domain mode locked laser,” Biomed. Opt. Express 3, 2987–3000 (2012). 10.1364/BOE.3.002987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Torzicky T., Marschall S., Pircher M., Baumann B., Bonesi M., Zotter S., Götzinger E., Trasischker W., Klein T., Wieser W., Biedermann B., Huber R., Andersen P., Hitzenberger C. K., “Retinal polarization-sensitive optical coherence tomography at 1060 nm with 350 khz a-scan rate using an fourier domain mode locked laser,” Journal of Biomedical Optics 18, 026008 (2013). 10.1117/1.JBO.18.2.026008 [DOI] [PubMed] [Google Scholar]
- 39.Yasuno Y., Madjarova V. D., Makita S., Akiba M., Morosawa A., Chong C., Sakai T., Chan K.-P., Itoh M., Yatagai T., “Three-dimensional and high-speed swept-source optical coherence tomography for in vivo investigation of human anterior eye segments,” Opt. Express 13, 10652–10664 (2005). 10.1364/OPEX.13.010652 [DOI] [PubMed] [Google Scholar]
- 40.Moon S., Lee S.-W., Chen Z., “Reference spectrum extraction and fixed-pattern noise removal in optical coherence tomography,” Opt. Express 18, 24395–24404 (2010). 10.1364/OE.18.024395 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yasuno Y., Hong Y., Makita S., Yamanari M., Akiba M., Miura M., Yatagai T., “In vivo high-contrast imaging of deep posterior eye by 1-um swept source optical coherence tomography andscattering optical coherence angiography,” Opt. Express 15, 6121–6139 (2007). 10.1364/OE.15.006121 [DOI] [PubMed] [Google Scholar]
- 42.Makita S., Hong Y.-J., Miura M., Yasuno Y., “Degree of polarization uniformity with high noise immunity using polarization-sensitive optical coherence tomography,” Opt. Lett. 39, 6783–6786 (2014). 10.1364/OL.39.006783 [DOI] [PubMed] [Google Scholar]
- 43.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Jones matrix analysis for a polarization-sensitive optical coherencetomography system using fiber-optic components,” Opt. Lett. 29, 2512–2514 (2004). 10.1364/OL.29.002512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wang Z., Lee H.-C., Ahsen O. O., Lee B., Choi W., Potsaid B., Liu J., Jayaraman V., Cable A., Kraus M. F., Liang K., Hornegger J., Fujimoto J. G., “Depth-encoded all-fiber swept source polarization sensitive OCT,” Biomedical Optics Express 5, 2931–2949 (2014). 10.1364/BOE.5.002931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Baumann B., Choi W., Potsaid B., Huang D., Duker J. S., Fujimoto J. G., “Swept source / fourier domain polarization sensitive optical coherence tomography with a passive polarization delay unit,” Opt. Express 20, 10229–10241 (2012). 10.1364/OE.20.010229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Makita S., Yamanari M., Yasuno Y., “Generalized jones matrix optical coherence tomography: performance and local birefringence imaging,” Opt. Express 18, 854–876 (2010). 10.1364/OE.18.000854 [DOI] [PubMed] [Google Scholar]