Abstract
Ptychography is an imaging method whereby a coherent beam is scanned across an object, and an image is obtained by iterative phasing of the set of diffraction patterns. It is able to be used to image extended objects at a resolution limited by scattering strength of the object and detector geometry, rather than at an optics-imposed limit. As technical advances allow larger fields to be imaged, computational challenges arise for reconstructing the correspondingly larger data volumes, yet at the same time there is also a need to deliver reconstructed images immediately so that one can evaluate the next steps to take in an experiment. Here we present a parallel method for real-time ptychographic phase retrieval. It uses a hybrid parallel strategy to divide the computation between multiple graphics processing units (GPUs) and then employs novel techniques to merge sub-datasets into a single complex phase and amplitude image. Results are shown on a simulated specimen and a real dataset from an X-ray experiment conducted at a synchrotron light source.
OCIS codes: (100.5070) Phase retrieval, (110.3010) Image reconstruction techniques, (200.4960) Parallel processing, (170.7440) X-ray imaging
1. Introduction
Traditional microscopes measure changes in specimen optical response via a lens-based direct mapping to pixels in a detector. Such microscopes have a resolution limited by the numerical aperture of the lens used according to the Abbe diffraction limit [1]. While one can exceed this limit by using special properties of certain fluorophores in visible light microscopy [2–5], another approach is to record far-field diffraction patterns without optics-imposed resolution limits and use them to recover the structure of the specimen. Coherent diffractive imaging (CDI) is a technique using a highly coherent beam to image interesting specimens, ranging from inorganic materials such as metals and polymers to organic ones such as cells, protein molecules, and viruses. The process of determining structure from diffraction patterns is not straightforward. In practice, far-field diffraction data are the squared modulus of the Fourier transform of the sample’s exit wave function. This gives rise to the well-known phase problem, in that the (unmeasured) Fourier phases are also needed for direct Fourier inversion to produce an image. The phase problem is considered an ill-posed inverse problem, meaning its solution is non unique [6]. There are an infinite number of functions whose Fourier transforms have the same modulus. Phase retrieval algorithms are designed to solve the phase problem by iteratively trying to find phases for the measured amplitudes that satisfy a set of constraints. Once the phases are correctly estimated, the object’s complex wave function can be obtained using an inverse Fourier transform.
This paper focuses on ptychography [7–9] as a coherent diffraction imaging method that is able to image extended, non-isolated samples. Ptychography involves recording a set of diffraction patterns recorded from multiple overlapping coherent probe locations. Because of the redundancy of information in the object among many diffraction patterns, iterative methods are able to converge quickly on a robust solution for the object, and one can also recover one or more probe distributions [10, 11] (such as for imaging with partially coherent illumination). Because there are no optics-imposed limits to collecting large scatter angle diffraction patterns, ptychography can be used for imaging at a spatial resolution limited only by the scattering strength of the optic and detector geometry.
The majority of phase retrieval algorithms resemble iterative optimization methods, where the objective error function to be minimized combines candidate phase values with the measured intensities of the diffraction pattern. Applying a set of constraints in both real and reciprocal spaces typically leads to a convergence to a solution that aligns the acquired data with the a priori constraints [12]. In this regard, the reciprocal space is the domain in which the Fourier transform of the specimen’s two-dimensional spatial function (real space) is represented.
Faster area detectors, brighter X-ray sources, increasingly higher resolution nanofocusing condenser optics, and larger scan fields are leading to a rapid increase in the size of ptychography datasets. In practice these large ptychography datasets must be reconstructed in near real-time in order to inform the progress of the experiment. As stated earlier, phase retrieval methods involve the computation of multiple Fast Fourier Transforms (FFTs) over thousands of diffraction patterns, making them suitable for parallel analysis. Moreover, extending ptychography to 3D comes at the expense of an increase in the computational and memory requirements of the phase retrieval software.
2. Phase retrieval
In order to make the phase problem uniquely solvable, a set of constraints can be iteratively enforced [12]. Most practical implementations of phase retrieval algorithms use a finite support constraint that corresponds to a finite region bounding the specimen in the physical experiment where the reconstructed image should be zero-valued. Support-based phase retrieval has been used in many X-ray microscopy experiments [13–15]. Ptychography has recently gained popularity because it removes the need for a finite object support, has been shown to be more robust, and has faster convergence rates than traditional finite support based methods [16, 17].
2.1. Ptychography
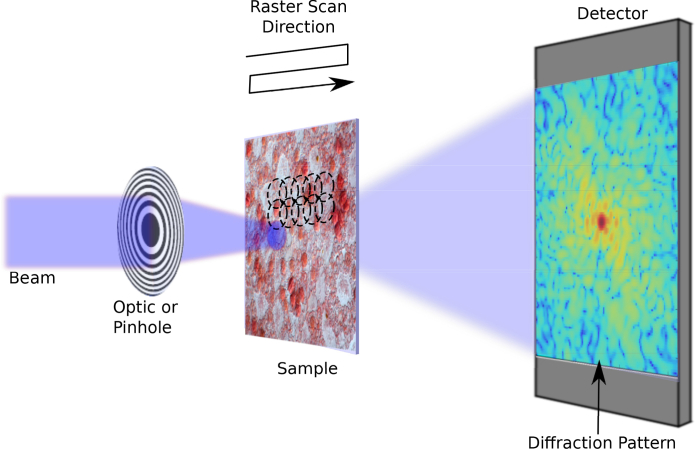
Ptychography was first introduced by Hoppe [7] to solve the phase problem using a set of interfering diffraction patterns. Thus, the finite support constraint is replaced by the redundancy resulting from overlapping an illumination function at different positions across a sample. This redundancy helps solve the phase problem by changing the relative position of the illumination with regard to the sample position. In an actual experiment, this scanning is often achieved by moving the sample relative to the incident beam in a predefined pattern as in Fig. 1. There are many alternative ptychography reconstruction algorithms in the literature. The difference map (DM) method [11, 18], which is similar to the HIO method by Fienup [12], can process all the diffraction patterns in parallel to retrieve the sample transmission function. The ptychographical iterative engine (PIE) [19], later extended by Maiden and named ePIE [20], requires fewer iterations to converge and is robust to noise. Ptychography, and CDI in general, originally required highly coherent beams, which are experimentally difficult to obtain and often lead to flux reduction. Relaxing the strict coherence requirements for ptychography, Thibault and Menzel recently demonstrated that one can reconstruct an illumination function from multiple mixed states or modes to compensate for and capture decoherence of the incident beam [21].
Fig. 1.
Simplified ptychography experiment setup showing a Cartesian grid used for the overlapping raster scan positions.
The DM algorithm is suitable for a parallel implementation, but since it calculates the exit wavefronts of all scan points at once, while keeping a copy of the previous iteration calculations in memory, DM has about five times the memory footprint of ePIE. For example, if a dataset consists of 1 GB of raw floating point diffraction pattern intensities, DM will require two buffers to hold current and previous iteration exit wavefronts, each amounting to 2 GB of complex valued data. In this case, the minimum memory footprint of DM is 5 GB, whereas ePIE only needs to store the actual dataset plus two small buffers each of the same size as one diffraction pattern in complex format (∼1 GB). Memory footprint is the main reason why we chose to implement ePIE first, with DM left for future work. The implementation also employs multiple illumination modes in the reconstruction to allow the use of partially coherent beams with higher flux.
2.1.1. ePIE
The ePIE algorithm tries to recover two distinct quantities:
the illuminating “probe” wavefront P(r), which is the complex-valued scalar wave function describing the beam incident on a sample over a set of real space coordinates r; and
the object transmission function O(r) describing the actual sample under investigation.
Before the reconstruction starts, the only given data is the far-field diffraction pattern set denoted by I(u), where u is a vector in reciprocal space coordinates. I(u) is composed of a collection of J diffraction patterns formed from the product of the object transmission function and the probe function. Each exit wavefront at a given raster scan position j is termed ψj. The interaction of the probe and object wavefronts can be given as their complex Hadamard product; this exit wave is propagated to the detector plane through a Fourier transform and recorded by the detector as the squared magnitude of the Fourier transform. This can be written as:
| (1) |
| (2) |
where R is a vector of size J listing all the relative shifts between the probe and the object. The ePIE algorithm starts with an initial guess for the probe and object wavefronts. It is also desirable to process the diffraction patterns in random order, to remove any starting position bias (this random order is recomputed at the beginning of every ePIE iteration). The algorithm then proceeds with calculating the exit wave function using the current object and probe guesses, as in Eq. (1). The estimate Ψj is then updated by replacing the modulus of the Fourier transform of the current exit wave with the square root of the measured diffraction pattern intensity, such that
| (3) |
The exit wave can be updated by means of an inverse Fourier transform, as in
| (4) |
Finally, the object and probe wavefront guesses can be updated using the following functions:
| (5) |
| (6) |
where * denotes the complex conjugate operation. The update of the object function is normalized by the maximum squared magnitude of the probe wave function while the probe function is normalized by the maximum object function intensity in order to keep the values in a proportional range between both functions. These steps are repeated for every diffraction pattern j, and for a number of predefined ePIE iterations, or until a certain convergence criterion is reached.
2.1.2. Probe modes
In the fully coherent case, a single mode probe function is adequate to converge to a faithful reconstruction of the sample. A perfectly coherent incident beam can be described by a single pure state, while, to account for the partial coherence of the light source, P(r) can be modeled as a mixture of K independently coherent but mutually incoherent probe modes. Amending the ePIE algorithm with a probe function consisting of multiple modes entails adjusting Eq. (1) such that for every probe mode k a separate exit wave is generated. The modulus constraint calculation in Eqs. (3) and (4) is subsequently transformed into
| (7) |
where the summation operation here is the incoherent sum over all modes. The update functions in Eq. (6) are also changed to account for the multiple modes
| (8) |
| (9) |
For all the reconstructions presented, each secondary probe mode was initialized to 5% of the primary mode illumination, and made orthogonal to all other modes using a GPU implementation of the Gram-Schmidt process.
3. Parallel implementation
Our parallel phase retrieval software is written entirely in C++ using the CUDA platform [22] by nVIDIA. It also uses the DIY [23] data-parallel programming library for the multi-GPU extension, the HDF5 library for data I/O, and the Simple DirectMedia Layer (SDL) [24] library for OpenGL visualization.
The programming language used within CUDA (CUDA-C) is an extension of the C programming language which allows one to implement GPU-based parallel functions, called kernels, which, when called, are executed n times in parallel by n different CUDA threads. The CUDA programming model requires the problem to be partitioned into subproblems that are solved independently in parallel by blocks of threads. In turn, each subproblem is also partitioned into finer pieces that can be solved cooperatively in parallel by all threads within the same block. Blocks are organized into a one-, two-, or three-dimensional grids of thread blocks. Kernel thread configuration is an important factor affecting the performance of a CUDA implementation.
According to nVIDIA’s best practices guide [25], global memory accesses should be coalesced to achieve maximum cache utilization, and to perform memory read/write operations in as few transactions as possible. Memory requests by threads of a warp are grouped by the hardware to a single instruction, if one cache line is enough to serve these concurrent requests. Since different devices have different cache architectures, it is useful to align matrix memory to a multiple of the specific device’s warp size (Fig. 2). Ensuring that each warp performing matrix operations will request adjacent memory addresses also significantly reduces cache misses.
Fig. 2.
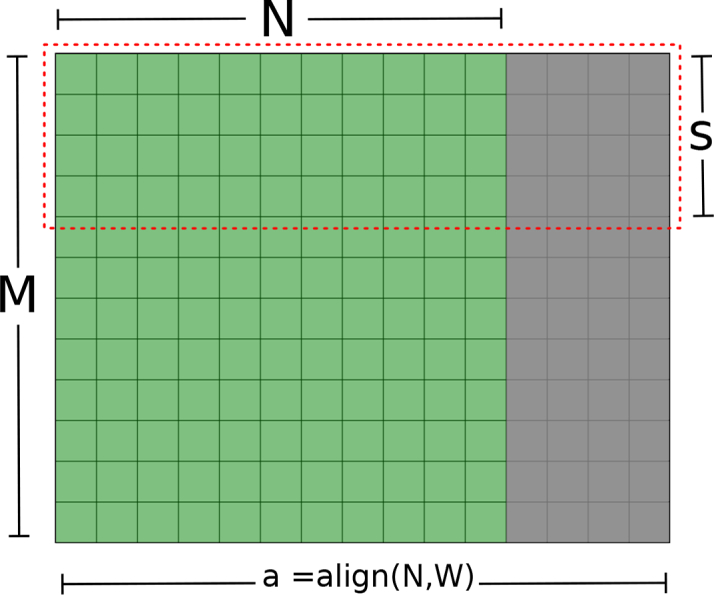
GPU memory layout of a 2D M×N matrix. The gray area represents the aligned matrix zero padding, where W = warp size (32 threads on most devices). The padded area is always ignored in matrix operations. CUDA blocks operate on matrix slices of size s such as the region outlined by the dashed red line. Memory requests for a row of the padded matrix are served by a single cache line.
Ptychography relies on complex-valued matrix operations and Fourier transforms. Implementing each ptychography algorithm using large, method specific, GPU kernels would markedly increase development and debugging efforts, while also sacrificing customization and extensibility. For this reason, we rely on compact efficient kernels for matrix operations, such as complex multiplication, addition, normalization, phase and magnitude calculation, and so forth. As for CUDA kernels thread configuration, we refer once more to Fig. 2. A kernel operating on an M×N matrix will be launched with a one-dimensional grid, of size ⌈M ÷ s⌉, where s = ⌊maxThreads ÷ a⌋, a = (N aligned to the GPU warp size), and maxThreads is the maximum number of threads supported by the GPU to run concurrently within a block. The blocks are configured as two-dimensional thread grids having a threads in the first dimension, and s threads in the second. This configuration automatically balances the computation load so that each block is using the maximum allowed number of threads, with the fewest possible idle threads given the memory coalescing constraint. Although the kernels are limited by N ≤ maxThreads, with the multi-GPU implementation, the theoretical reconstruction size can reach (maxThreads × G)2, where G is the number of GPUs available. For the FFT computation, we use nVIDIA’s CUFFT library [26] provided with the CUDA platform.
3.1. Multi-GPU algorithm
New multimodal imaging techniques and devices are generating large amounts of data at high rates. For instance, experiments are now combining ptychography with fluorescence detectors to deduce a specimen’s structure and elemental composition at the same time. Such experiments typically require smaller beams and therefore more raster scan points than single mode experiments. Furthermore, tomographic datasets composed of multiple two-dimensional scans at different angles around the specimen’s axis of rotation can easily exceed hundreds of gigabytes of raw data [27,28]. To date, the maximum amount of device memory on a single nVIDIA GPU is 12 GB of RAM. In order to keep all raw data on the device memory without the need for swapping from disk or host RAM, a dataset can be subdivided and processed on multiple GPUs.
In an experiment setup, the overlapping probe raster scan points can be arranged in a variety of configurations, such as Cartesian grids, concentric circles [29], Fermat spirals [30], or any other arbitrarily shaped pattern. Given any of these patterns, spatially contiguous scan subregions can be defined such that the degree of overlap between adjacent scan points is preserved. Data partitioning is achieved using the DIY parallel programming library [23] that is written on top of MPI to facilitate communication between parallel processes. In DIY terminology, we assign a DIY block (not to be confused with CUDA blocks) to each GPU. The 2D domain size here is the number of scan points in each dimension. The DIY block extents are mapped to the subset of file names from which the block can read its own portion of diffraction patterns. The raw data of each subregion is then loaded from disk, transfered to GPU memory, and processed separately from the other subregions residing on other GPU memory spaces. Sub-dataset reconstructions can either be merged to form a final reconstruction after phase retrieval, or shared between separate GPUs every iteration or every few iterations of the phase retrieval method.
3.1.1. Asynchronous parallel ptychography
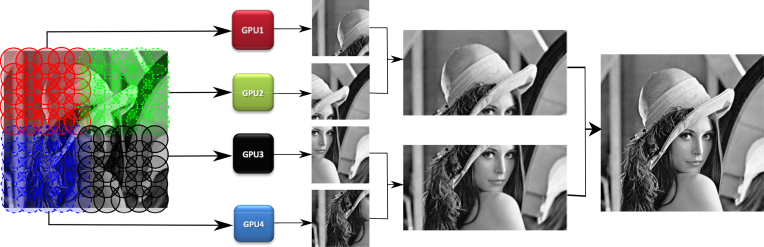
The fastest approach to parallel ptychography is to subdivide the dataset and phase sub-datasets asynchronously, then merge the results to form a final reconstruction, without the need for data sharing or synchronization. The final reconstructions from the phase retrieval algorithm running on separate GPUs are stitched back in parallel, between pairwise subsets because their relative orientation is already known. A parallel reduction-with-merge algorithm [31] is utilized to achieve the stitched mosaic of the whole sample final reconstruction, as shown in Fig. 3.
Fig. 3.
The diffraction patterns are subdivided and distributed among available GPUs. Pairwise stitching is performed on the separate reconstructions attained by phase retrieval.
Stitching independent phase retrieval reconstructions has two main difficulties. First, the reconstructed wavefronts exhibit arbitrary phase shifts, which is an inherent problem with all phase retrieval algorithms [32]. Second, the probe and object functions are usually not centered within their respective arrays because they are not constrained in real space coordinates. In order to address these problems, normalization must compensate for the different overall phase shifts of the reconstructions. In addition, a registration method is required to find the relative translation between reconstructed wavefronts. In order to solve for phase shifts between two object wavefronts, phase values from a common area present in both wavefronts can be used. It is not, however, straightforward to calculate the amount of overlap between the resulting reconstructed wavefronts in real 2D image space. An extension to phase correlation [33] is employed for rigid registration, and once a translative offset is found, a modulation factor can be calculated from the common part. This modulation factor can be subsequently used to normalize the participating complex wavefronts into one coherent reconstruction.
Phase correlation is based on the Fourier shift theorem, which states that a relative translation between two images is represented as a linear phase difference in reciprocal space. We adopt phase correlation because it is an accurate rigid registration method, and because a GPU FFT implementation is available through CUFFT. Phase correlation, like all Fourier based methods, suffers from jump discontinuities caused by image boundaries. A tapering function, such as the Hamming window, can be used to reduce edge artifacts from the Fourier domain. In most cases, however, the features required for an effective registration reside near the edges, especially with finer data partitions. An alternative solution is to use the gradient of the original images, as suggested by Argyriou and Vlachos [34].
The mathematical formulation of the registration method used begins with computing the horizontal and vertical gradients, gh(x, y) and gv(x, y) respectively, using central differencing, such that
| (10) |
| (11) |
where f (x, y) is the phase of the reconstructed wavefront. The gradients are then put into a complex representation in the form
| (12) |
Using the magnitudes of the complex gradients g1(x, y) and g2(x, y) of reconstructed waves, the cross-power spectrum S(r) is calculated by
| (13) |
| (14) |
| (15) |
where ○ is the element-wise matrix multiplication operation. The inverse Fourier transform of the cross-power spectrum is the cross-correlation function that peaks at the registration point Δx, Δy, defined as
| (16) |
The registration point can then be used to find the exact overlapping regions, R1(x, y){x ∈ [Δx, M], y ∈ [Δy, N]} and R2(x, y){x ∈]0, M − Δx], y ∈]0, N − Δy]}, of the two reconstructed wavefronts of equal sizes M×N. Employing a method similar to the gain compensation technique used for photographic image stitching [35], the overlapping regions are approximated by their respective complex-valued means μ1 and μ2. Then a ratio of the calculated means is used to modulate one of the retrieved object functions to match the other, giving
| (17) |
where Oi(x, y) is the ith partial reconstruction of the 2D object wavefront. Finally, a stitched object wavefront O(x, y) is formed from the two partial reconstructions O1(x, y) and (x, y) in the form
| (18) |
Here each partial reconstruction contributes to the stitching with its own distinct features in addition to half of the overlapping region. Therefore, the output O(x, y) has a new size of (M + Δx) × (N + Δy). Subsequently, the stitched wavefront O(x, y) can, in turn, be considered a partial reconstruction input for another pairwise stitching as shown in Fig. 3.
3.1.2. Synchronous parallel ptychography
The synchronous variant of our multi-GPU parallel ptychography method is inspired by the work done by Guizar-Sicairos et al. [36]. There, multiple datasets were acquired from a single extended sample by tiling a 7×4 rectangular grid with concentric circles pattern scans and some amount of overlap between individual datasets. The final reconstruction of the entire sample is achieved by sharing the object function array among the datasets, while solving a separate probe function for each scan. In so doing, the phase retrieval method should converge to a common object transmission function, benefiting from the increased statistics found where the scan regions overlap. In our work, instead of acquiring multiple datasets, a single dataset is split into multiple sub-datasets, and their respective reconstructions, residing on separate GPUs, are synchronized during the course of the phase retrieval algorithm.
Sharing the whole object array among multiple GPUs would incur a significant overhead from broadcasting a large amount of data across the network interface every single iteration, or few iterations, of the phase retrieval algorithm. For this reason, a local sharing method is utilized, where each GPU shares the current reconstruction only with its immediate neighbors as depicted in Fig. 4. This effectively decreases the message size sent at every synchronization point without sacrificing reconstruction quality. At a synchronization step t, each GPU replaces its object function array O(r) with an averaged array Ot (r), such that
| (19) |
where L is the size of neighboring reconstructions set, N(r) = {N1(r), ..., NL(r)}, found in the immediate local neighborhood of a sub-dataset.
Fig. 4.

Object array sharing through neighborhood exchange between 16 GPUs. The overlap (halo), highlighted in blue, is defined in terms of additional scan points assigned to each GPU sub-dataset.
The multi-GPU implementation that relies on splitting the scan dataset into a number of sub-datasets has a drawback of creating artificial scan borders with less overlap at the outermost scan points. The asynchronous version of the implementation overcomes artificial border artifacts by using half of the common region from each of the stitched reconstructions, thus avoiding the areas near the artificial borders where the reconstruction is unreliable. The synchronous version is essentially working with a single dataset; the object array sharing forces the sub-dataset reconstructions to agree on common phase and spatial offsets. Hence, it increases the information around the subdivision borders to overcome the artificial borders problem. Both versions retrieve separate probe functions for each GPU, which is useful when the beam properties are not constant during a scan, especially for longer exposures. Solving a separate illumination function for each GPU has the potential to compensate for fluctuations in the motorized stage positions, beam intensity, and sample temperature, particularly when these changes happen on a longer timescale than the data subset scan time.
3.2. Related work
Several authors have been trying to parallelize CDI reconstruction algorithms to run near real-time. In the work of Falch et al. [37], an optimized parallel difference map algorithm was implemented using thread pools and SIMD instructions. The code optimizations were based on array merging, expression rewriting, and loop unrolling. Python and C serial versions were developed for comparison; the parallel implementation achieved approximately one order of magnitude speedup over those sequential implementations. A GPU implementation was left as future work, although the same authors used multiple GPUs for visualizing diffraction data based on a parallel volume ray casting technique [38].
The authors of the ePIE algorithm present another extension to the ptychographical iterative engine method called 3PIE [39], providing a three-dimensional ptychographical reconstruction without the need for multiple tomographic measurements, but rather by modeling the sample in terms of layers or slices, propagating exit waves of one slice as the incident illumination on the next. 3PIE was demonstrated experimentally with a MATLAB implementation making use of the GPU-based acceleration offered by MATLAB. However, no speedup or scaling information was provided. Similarly, Claus et al. [40] show the use of visible-light ptychography to distinguish between healthy and tumorous unstained cells in a MATLAB implementation. In that work, CUDA is used solely to compute 2D FFT and Fourier shift functions, essentially transferring data back and forth between CPU memory and GPU memory, which is very expensive.
Schroer et al. used a complete ePIE GPU implementation for the purpose of deducing X-ray beam characteristics, such as shape and size [41]. Their parallel implementation achieved two orders of magnitude speedup over a serial one but only used a single GPU (nVIDIA Tesla C2050) for the beam focus reconstruction. The Hawk package [42] focuses on finite support based methods relying on a single diffraction pattern for phase retrieval. Hawk is a publicly available open-source software toolkit that uses CUDA to implement numerous phasing algorithms.
4. Testing
Our parallel methods were evaluated on two datasets: a synthetic sample simulating the diffraction patterns from known images, and on real data acquired using the Bionanoprobe [43] at beamline 21-ID-D of the Advanced Photon Source at Argonne National Laboratory. Experiments were run on the Tukey cluster at the Argonne Leadership Computing Facility (ALCF). Tukey is a visualization platform consisting of 96 compute nodes; each node has two 2 GHz AMD Opteron 6128 processors (8 cores per CPU, 16 cores total), and two nVIDIA Tesla M2070 GPUs. Each GPU has 6 GB of memory and a CUDA compute capability of 2.0; the code was built and run with CUDA v6.0.
4.1. Synthetic sample
A simulated dataset was generated to assess both the accuracy and performance of the parallel phase retrieval reconstructions. Two known images (Baboon and Lena) were used to represent the object phase and magnitude profiles. The magnitude image was scaled to values in the [0.1, 1] range, and the phase to values in the [0, ] range. A regular 175 × 120 Cartesian grid was used for the probe positions, generating 21,000 far-field diffraction patterns, totaling 5.12 GB of single precision floating point raw data. The diffraction patterns were generated with a single-pixel detector point-spread function, with no added noise. A randomized Gaussian kernel was used to represent the probe function, simulating a 5 keV X-ray beam having a theoretical width of 110 nm and a step size (the distance between scan points on the raster grid) of 50 nm, providing 54% overlap between adjacent scan points in the horizontal and vertical directions. The synthetic sample was 1 m away from the detector, which had 256×256 pixels of size 172 μm. Results were obtained for different numbers of GPUs after 200 iterations of the ePIE algorithm. The probe estimate was not updated for the first 10 iterations, as recommended in the literature.
Since the actual object wavefront, O(r), is known in the synthetic sample case, the convergence of a reconstructed result On(r) can be measured directly employing the normalized RMS error [20]
| (20) |
| (21) |
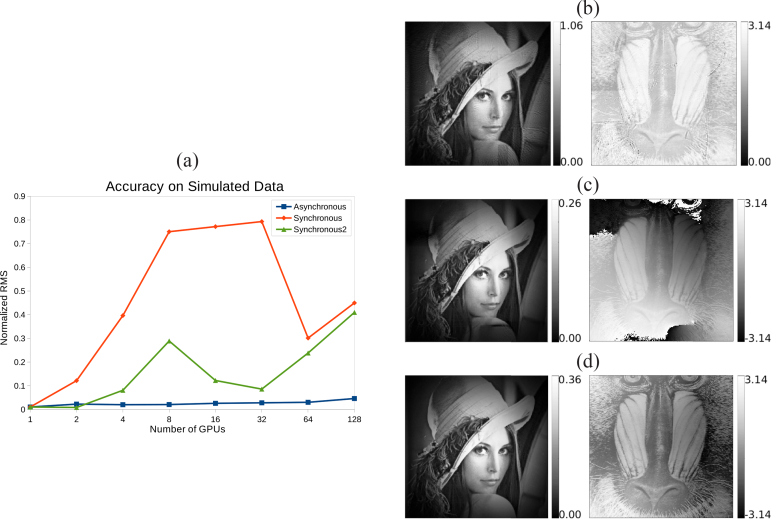
where γ is a modulation factor compensating for a constant phase offset between O(r) and On(r), and n is the number of GPUs used for the reconstruction. Values of n were only set to multiples of 2. Therefore tests were run taking advantage of up to 128 GPUs, to evaluate the asynchronous and synchronous implementations performance and convergence. Object array sharing was carried out at every iteration of the phase retrieval method. The error between the final reconstructions and the ground truth was calculated using Eq. (21) over the central 200×200 pixel area of the reconstruction to avoid border artifacts and using a subpixel registration method [44] to align the reconstruction with the ground truth. The plot in Fig. 5 shows the normalized RMS error comparing the asynchronous and synchronous versions of the multi-GPU implementation. Clearly, the asynchronous variant is superior to the synchronous one in terms of reconstruction error. This is mainly attributed to two reasons: first, the additional statistics introduced to a GPU object array at any given synchronization step do not directly relate to any scan point of this GPU’s sub-dataset, but rather slow its convergence. Second, our simple averaging method of the shared arrays results in linear phase ramps that arise when the phase retrieval algorithm tries to reconcile phase offsets of multiple object functions. Figure 5 shows the worst performing GPU configurations: the 128 GPU configuration for the asynchronous implementation, and 32 GPUs for the synchronous. Another 32 GPU reconstruction of the synchronous implementation (Synchronous2) is also shown in the figure, where the sub-dataset scan region overlap has been set to 2 rows and columns of diffraction pattern data (halo=2). Increasing the halo region helps counter the effects of object array sharing, which is evident from the quality of the shown reconstruction. This reconstruction, however, still exhibits an overall phase gradient and thus a higher RMS error than the asynchronous implementation. Stitching artifacts can be seen in the magnitude image of the asynchronous reconstruction, also some artifacts from the phase profile are also visible. Image contrasts were not equalized; therefore the phase image has overall low contrast because of the outliers caused by interference from the magnitude profile of the simulated sample wavefront.
Fig. 5.
(a) Normalized RMS error of final reconstructions achieved by different GPU configurations using the asynchronous, synchronous, and synchronous with halo=2 implementations. (b) Magnitude and phase of the object wavefront retrieved from simulated data using the asynchronous version and 128 GPUs. (c) Magnitude and phase of the object wavefront retrieved from simulated data using the synchronous version and 32 GPUs. (d) Magnitude and phase of the object wavefront retrieved from simulated data using the synchronous version, 32 GPUs, and a halo region of 2 additional scan point rows and columns.
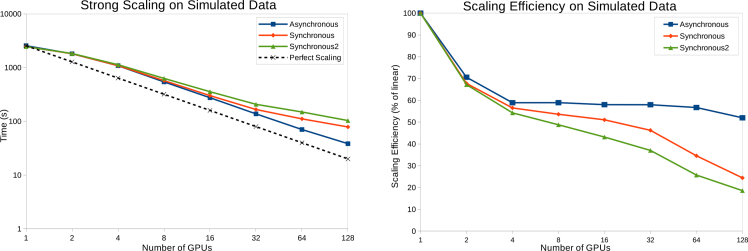
To evaluate the performance and scalability of our algorithms, the total running time of different GPU configurations is reported in Fig. 6. The first plot shows that scaling of the three multi-GPU variants is almost linear for configurations of more than 2 GPUs. The simulated problem size was chosen carefully to be able to fit all the raw data on one GPU, in order to study how well the code scales when adding more GPUs to process the same amount of raw data. Suboptimal GPU occupancy may be the cause of the deviation from linear scaling that is found when the number of GPUs is increased from one to two. Occupancy is the percentage of active thread warps of a given device at a one time. Changes in the problem size can lead to divergence in the code path and different kernel scheduling, that in turn increase thread idling time and lead to suboptimal GPU occupancy. The second plot of Fig. 6 outlines the strong scaling efficiency with respect to the phase retrieval algorithm run time on one GPU. The asynchronous version, by definition, does not require communication among the running GPUs, except at the end of reconstruction in the stitching step. The effect of synchronization becomes more prominent when a higher number of GPUs is used, due to increased network latencies and data copying overhead.
Fig. 6.
Performance plots on synthetic data. Left: Total running time (in seconds) of different GPU configurations. Right: The scaling efficiency plotted as a percentage of linear scaling.
4.2. Real sample
In addition to the simulated test case, we evaluate the performance on real data acquired at a synchrotron radiation facility; not only to validate the applicability and performance with domain scientists, but also because such data is usually compromised with noise resulting from thermal drifts in the motorized stages, fluctuations in the beam intensity, and distortions in the diffraction patterns caused by air scattering, changes in sample temperature, and bad or missing detector pixels.
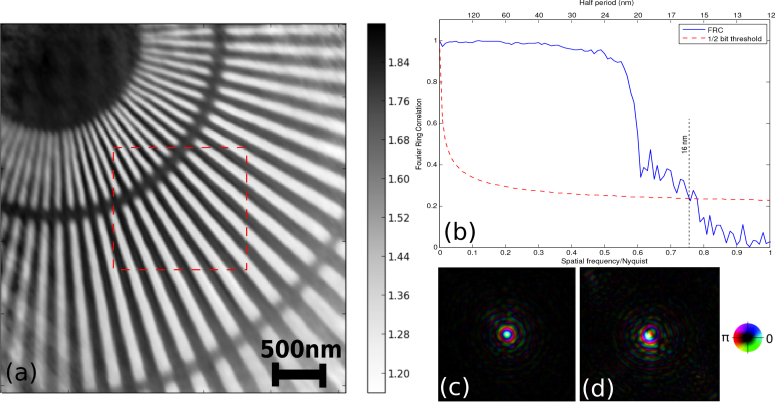
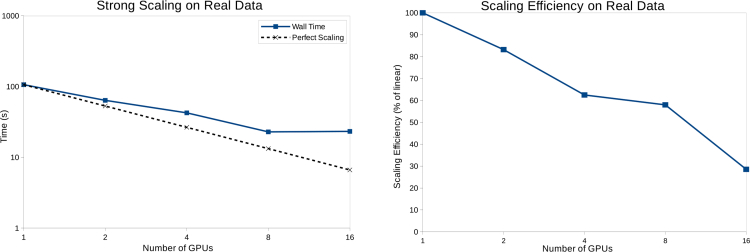
The experiment was carried out at the Bionanoprobe [43] at the 21-ID-D beamline of the Advanced Photon Source. A 5.2 keV X-ray beam was focused by a Fresnel zone plate with 85 nm theoretical Rayleigh resolution onto a gold test pattern with 30 nm finest feature. The test pattern was raster scanned through a 26×26 grid using a step size of 40 nm. A photon counting hybrid pixel array detector (PILATUS 100K, 195×487 pixels with 172 μm pixel size) was placed 2.2 m downstream of the sample to record coherent diffraction patterns with an exposure time of 0.6 s per scan point. The central 195×256 pixels of each diffraction pattern were cropped and zero padded in a 256×256 array for reconstructions. The total measurement time was about 20 minutes, including positioning and computer overheads. Two independent datasets were acquired and reconstructed respectively. After subpixel image registration of the two independent reconstructed phase images, the quality and the spatial resolution of the measurements were evaluated by Fourier ring correlation (FRC) [45]. Figure 7 shows an estimated half-period resolution of 16 nm given by the intersection of the FRC curve and 1/2-bit threshold curve [46]. The reconstructed phase of the transmission function was retrieved using 200 iterations, on one nVIDIA Tesla M2070 GPU, using two probe modes. The primary probe mode was updated after 10 iterations of the phase retrieval method, while the second mode was initialized and updated after 20 iterations. Multi-GPU reconstructions were also run employing the asynchronous implementation on 2, 4, 8, and 16 GPUs with little quality degradation in the phase image. An overview of the different GPU configurations’ performance on real experiment data is shown in Fig. 8. For the 16 GPU configuration, data blocks had to be expanded with a halo along the data subdivision boundaries to increase sub-dataset reconstruction accuracies. However, this redundancy led to an overall performance drop resulting from the additional load for each GPU to process its halo of diffraction patterns. The point at which the overhead of data distribution among multiple GPUs outweighs the performance gain depends on the dataset size and hardware used and is currently found empirically.
Fig. 7.
(a) Phase image of the reconstructed object transmission function, with the 1 μm×1 μm scan region highlighted in red. (b) Fourier ring correlation (FRC) plot showing a spatial resolution of 16 nm in the phase of the exit surface wave. (c,d) The recovered illumination function of two probe modes.
Fig. 8.
Performance plots on real data. Left: Total running time (in seconds) of different GPU configurations. Right: The scaling efficiency plotted as a percentage of linear scaling.
Prior to the development of the parallel methods presented here, scientists at the APS used an unoptimized sequential implementation for phase retrieval. The running time of our asynchronous algorithm using one GPU on the data set presented here is 106.37 seconds, which is an order of magnitude faster than the data acquisition time. This marks the first time that our users have been able to reconstruct results while their imaging experiments were still running.
5. Conclusions and future work
In this paper we presented a parallel multi-GPU software for ptychographic reconstruction through iterative phase retrieval. It provides a generalized platform enabling ptychographic dataset analysis in real-time. In order to overcome the hardware memory limitation of GPUs, the code follows a hybrid approach where the raw data is divided and analyzed on separate GPUs, and each GPU in turn is managed by one MPI process. The results are merged into a coherent specimen complex transmission function, either at the end of the reconstruction, or by information sharing during the reconstruction, solving for discontinuities caused by relative phase and spatial shifts in the sub-dataset reconstructions. Our methods were evaluated on synthetic and real data to assess their accuracy and performance, and are currently being used by the physicists conducting ptychography experiments at the APS.
The asynchronous multi-GPU implementation has better running time and scalability performance than the synchronous one. Also, in our simulations, the stitching approach was more accurate than the object array sharing method. This may be due to the high contrast features present in the sub-dataset reconstructions, which facilitated correct registration and modulation of a final reconstruction. Moreover, linear phase ramps in the reconstructed transmission function phase profile resulted in higher calculated RMS error, despite the reconstructions being of better visual quality when increasing the sub-dataset halo size. With the addition of linear phase ramp corrections [47], we expect the synchronous implementation to be robust and applicable to samples of varying materials, regardless of their scattering strength and feature contrast. More desirable features to be included in the future are: correcting for positioning errors caused by temperature changes or motor drifts [48, 49], the maximum-likelihood refinement method for post-processing the results [50], and additional phase retrieval algorithms such as the difference map method.
Acknowledgments
We gratefully acknowledge the use of the resources of the Argonne Leadership Computing Facility at Argonne National Laboratory. We also would like to thank our reviewers for their constructive comments. This work was supported by Advanced Scientific Computing Research, Office of Science, U.S. Department of Energy, under Contract DE-AC02-06CH11357. Work is also supported by DOE with agreement No. DE-FC02-06ER25777. The Bionanoprobe is funded by NIH/NCRR High End Instrumentation (HEI) grant (1S10RR029272-01) as part of the American Recovery and Reinvestment Act (ARRA). Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. Department of Energy (DOE) Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. Development of ptychography for cryo microscopy applications is supported by NIH under grant R01 1GM104530.
The submitted manuscript has been created by UChicago Argonne, LLC, Operator of Argonne National Laboratory (“Argonne”). Argonne, a U.S. Department of Energy Office of Science laboratory, is operated under Contract No. DE-AC02-06CH11357. The U.S. Government retains for itself, and others acting on its behalf, a paid-up nonexclusive, irrevocable worldwide license in said article to reproduce, prepare derivative works, distribute copies to the public, and perform publicly and display publicly, by or on behalf of the Government.
References and links
- 1.Born M., Wolf E., Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (CUP Archive, 1999). 10.1017/CBO9781139644181 [DOI] [Google Scholar]
- 2.Hell S. W., Wichmann J., “Breaking the diffraction resolution limit by stimulated emission: stimulated-emission-depletion fluorescence microscopy,” Opt. Lett. 19, 780–782 (1994). 10.1364/OL.19.000780 [DOI] [PubMed] [Google Scholar]
- 3.Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313, 1642–1645 (2006). 10.1126/science.1127344 [DOI] [PubMed] [Google Scholar]
- 4.Rust M. J., Bates M., Zhuang X., “Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (storm),” Nature Methods 3, 793–796 (2006). 10.1038/nmeth929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hell S. W., “Far-field optical nanoscopy,” Science 316, 1153–1158 (2007). 10.1126/science.1137395 [DOI] [PubMed] [Google Scholar]
- 6.Huiser A., Van Toorn P., “Ambiguity of the phase-reconstruction problem,” Opt. Lett. 5, 499–501 (1980). 10.1364/OL.5.000499 [DOI] [PubMed] [Google Scholar]
- 7.Hoppe W., “Beugung im inhomogenen primarstrahlwellenfeld. i. prinzip einer phasenmessung von elektronen-beungungsinterferenzen,” Acta Crystallogr., Sect. A 25, 495–501 (1969). 10.1107/S0567739469001045 [DOI] [Google Scholar]
- 8.Faulkner H., Rodenburg J., “Movable aperture lensless transmission microscopy: a novel phase retrieval algorithm,” Phys. Rev. Lett. 93, 023903 (2004). 10.1103/PhysRevLett.93.023903 [DOI] [PubMed] [Google Scholar]
- 9.Rodenburg J., Hurst A., Cullis A., Dobson B., Pfeiffer F., Bunk O., David C., Jefimovs K., Johnson I., “Hard-x-ray lensless imaging of extended objects,” Phys. Rev. Lett. 98, 034801 (2007). 10.1103/PhysRevLett.98.034801 [DOI] [PubMed] [Google Scholar]
- 10.Thibault P., Dierolf M., Menzel A., Bunk O., David C., Pfeiffer F., “High-resolution scanning x-ray diffraction microscopy,” Science 321, 379–382 (2008). 10.1126/science.1158573 [DOI] [PubMed] [Google Scholar]
- 11.Thibault P., Dierolf M., Bunk O., Menzel A., Pfeiffer F., “Probe retrieval in ptychographic coherent diffractive imaging,” Ultramicroscopy 109, 338–343 (2009). 10.1016/j.ultramic.2008.12.011 [DOI] [PubMed] [Google Scholar]
- 12.Fienup J. R., “Phase retrieval algorithms: a comparison,” Appl. Opt. 21, 2758–2769 (1982). 10.1364/AO.21.002758 [DOI] [PubMed] [Google Scholar]
- 13.Miao J., Charalambous P., Kirz J., Sayre D., “Extending the methodology of x-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens,” Nature 400, 342–344 (1999). 10.1038/22498 [DOI] [Google Scholar]
- 14.Chapman H. N., Barty A., Marchesini S., Noy A., Hau-Riege S. P., Cui C., Howells M. R., Rosen R., He H., Spence J. C. H., Weierstall U., Beetz T., Jacobsen C., Shapiro D., “High-resolution ab initio three-dimensional x-ray diffraction microscopy,” J. Opt. Soc. Am. A 23, 1179–1200 (2006). 10.1364/JOSAA.23.001179 [DOI] [PubMed] [Google Scholar]
- 15.Abbey B., Nugent K. A., Williams G. J., Clark J. N., Peele A. G., Pfeifer M. A., De Jonge M., McNulty I., “Keyhole coherent diffractive imaging,” Nature Phys. 4, 394–398 (2008). 10.1038/nphys896 [DOI] [Google Scholar]
- 16.Zhang F., Pedrini G., Osten W., “Phase retrieval of arbitrary complex-valued fields through aperture-plane modulation,” Phys. Rev. A 75, 043805 (2007). 10.1103/PhysRevA.75.043805 [DOI] [Google Scholar]
- 17.Bao P., Zhang F., Pedrini G., Osten W., “Phase retrieval using multiple illumination wavelengths,” Opt. Lett. 33, 309–311 (2008). 10.1364/OL.33.000309 [DOI] [PubMed] [Google Scholar]
- 18.Thibault P., Dierolf M., Menzel A., Bunk O., David C., Pfeiffer F., “High-resolution scanning x-ray diffraction microscopy,” Science 321, 379–382 (2008). 10.1126/science.1158573 [DOI] [PubMed] [Google Scholar]
- 19.Rodenburg J. M., Faulkner H. M., “A phase retrieval algorithm for shifting illumination,” Appl. Phys. Lett. 85, 4795–4797 (2004). 10.1063/1.1823034 [DOI] [Google Scholar]
- 20.Maiden A. M., Rodenburg J. M., “An improved ptychographical phase retrieval algorithm for diffractive imaging,” Ultramicroscopy 109, 1256–1262 (2009). 10.1016/j.ultramic.2009.05.012 [DOI] [PubMed] [Google Scholar]
- 21.Thibault P., Menzel A., “Reconstructing state mixtures from diffraction measurements,” Nature 494, 68–71 (2013). 10.1038/nature11806 [DOI] [PubMed] [Google Scholar]
- 22.nVIDIA Corporation , CUDA C Programming Guide v. 6.0 (2014).
- 23.Peterka T., Ross R., Gyulassy A., Pascucci V., Kendall W., Shen H.-W., Lee T.-Y., Chaudhuri A., “Scalable parallel building blocks for custom data analysis,” in “Large Data Analysis and Visualization (LDAV), 2011 IEEE Symposium on,” (IEEE, 2011), pp. 105–112. [Google Scholar]
- 24.Lantinga S., “The simple directmedia layer library,” http://www.libsdl.org.
- 25.nVIDIA Corporation , CUDA C Best Practices Guide v. 6.0 (2014).
- 26.nVIDIA Corporation , CUFFT Library User’s Guide v. 6.0 (2014).
- 27.Dierolf M., Menzel A., Thibault P., Schneider P., Kewish C. M., Wepf R., Bunk O., Pfeiffer F., “Ptychographic x-ray computed tomography at the nanoscale,” Nature 467, 436–439 (2010). 10.1038/nature09419 [DOI] [PubMed] [Google Scholar]
- 28.Holler M., Diaz A., Guizar-Sicairos M., Karvinen P., Färm E., Härkönen E., Ritala M., Menzel A., Raabe J., Bunk O., “X-ray ptychographic computed tomography at 16nm isotropic 3D resolution,” Sci. Rep. 4, 3857 (2014). 10.1038/srep03857 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dierolf M., Thibault P., Menzel A., Kewish C. M., Jefimovs K., Schlichting I., Von Koenig K., Bunk O., Pfeiffer F., “Ptychographic coherent diffractive imaging of weakly scattering specimens,” New J. Phys. 12, 035017 (2010). 10.1088/1367-2630/12/3/035017 [DOI] [Google Scholar]
- 30.Huang X., Yan H., Harder R., Hwu Y., Robinson I. K., Chu Y. S., “Optimization of overlap uniformness for ptychography,” Opt. Express 22, 12634–12644 (2014). 10.1364/OE.22.012634 [DOI] [PubMed] [Google Scholar]
- 31.Peterka T., Goodell D., Ross R., Shen H.-W., Thakur R., “A configurable algorithm for parallel image-compositing applications,” in “Proceedings of the Conference on High Performance Computing Networking, Storage and Analysis,” (ACM, 2009), p. 4. [Google Scholar]
- 32.Bunk O., Dierolf M., Kynde S., Johnson I., Marti O., Pfeiffer F., “Influence of the overlap parameter on the convergence of the ptychographical iterative engine,” Ultramicroscopy 108, 481–487 (2008). 10.1016/j.ultramic.2007.08.003 [DOI] [PubMed] [Google Scholar]
- 33.Kuglin C., “The phase correlation image alignment method,” in “Proc. Int. Conf. on Cybernetics and Society, 1975,” (1975). [Google Scholar]
- 34.Argyriou V., Vlachos T., “Using gradient correlation for sub-pixel motion estimation of video sequences,” in “Acoustics, Speech, and Signal Processing, 2004. Proceedings.(ICASSP’04). IEEE International Conference on,”, vol. 3 (IEEE, 2004), vol. 3, pp. iii–329. [Google Scholar]
- 35.Brown M., Lowe D. G., “Automatic panoramic image stitching using invariant features,” International J. Comp. Vis. 74, 59–73 (2007). 10.1007/s11263-006-0002-3 [DOI] [Google Scholar]
- 36.Guizar-Sicairos M., Johnson I., Diaz A., Holler M., Karvinen P., Stadler H.-C., Dinapoli R., Bunk O., Menzel A., “High-throughput ptychography using eiger: scanning x-ray nano-imaging of extended regions,” Opt. Express 22, 14859–14870 (2014). 10.1364/OE.22.014859 [DOI] [PubMed] [Google Scholar]
- 37.Falch T. L., Fløystad J. B., Elster A. C., Breiby D. W., “Optimization and parallelization of ptychography reconstruction code,” Norsk informatikkonferanse 2012 (2012). [Google Scholar]
- 38.Falch T. L., “3D visualization of x-ray diffraction data,” NTNU (2012). [Google Scholar]
- 39.Maiden A. M., Humphry M. J., Rodenburg J., “Ptychographic transmission microscopy in three dimensions using a multi-slice approach,” J. Opt. Soc. Am. A 29, 1606–1614 (2012). 10.1364/JOSAA.29.001606 [DOI] [PubMed] [Google Scholar]
- 40.Claus D., Maiden A. M., Zhang F., Sweeney F. G., Humphry M. J., Schluesener H., Rodenburg J. M., “Quantitative phase contrast optimised cancerous cell differentiation via ptychography,” Opt. Express 20, 9911–9918 (2012). 10.1364/OE.20.009911 [DOI] [PubMed] [Google Scholar]
- 41.Schroer C. G., Hnig S., Goldschmidt A., Hoppe R., Patommel J., Samberg D., Schropp A., Seiboth F., Stephan S., Schder S., Burghammer M., Denecke M., Wellenreuther G., Falkenberg G., “Hard x-ray nano-beam characterization by ptychographic imaging,” in “SPIE Optical Engineering+ Applications,” (International Society for Optics and Photonics, 2011), p. 814103. [Google Scholar]
- 42.Maia F. R., Ekeberg T., Van Der Spoel D., Hajdu J., “Hawk: the image reconstruction package for coherent x-ray diffractive imaging,” J. Appl. Crystallogr. 43, 1535–1539 (2010). 10.1107/S0021889810036083 [DOI] [Google Scholar]
- 43.Chen S., Deng J., Yuan Y., Flachenecker C., Mak R., Hornberger B., Jin Q., Shu D., Lai B., Maser J., Roehrig C., Paunesku T., Gleber S. C., Vine D. J., Finney L., VonOsinski J., Bolbat M., Spink I., Chen Z., Steele J., Trapp D., Irwin J., Feser M., Snyder E., Brister K., Jacobsen C., Woloschak G., Vogt S., “The bionanoprobe: hard x-ray fluorescence nanoprobe with cryogenic capabilities,” J. Synchrotron Radiat. 21, 66–75 (2014). 10.1107/S1600577513029676 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Guizar-Sicairos M., Thurman S. T., Fienup J. R., “Efficient subpixel image registration algorithms,” Opt. Lett. 33, 156–158 (2008). 10.1364/OL.33.000156 [DOI] [PubMed] [Google Scholar]
- 45.Saxton W., Baumeister W., “The correlation averaging of a regularly arranged bacterial cell envelope protein,” J. Microsc. 127, 127–138 (1982). 10.1111/j.1365-2818.1982.tb00405.x [DOI] [PubMed] [Google Scholar]
- 46.van Heel M., Schatz M., “Fourier shell correlation threshold criteria,” J. Struct. Biol. 151, 250–262 (2005). 10.1016/j.jsb.2005.05.009 [DOI] [PubMed] [Google Scholar]
- 47.Guizar-Sicairos M., Diaz A., Holler M., Lucas M. S., Menzel A., Wepf R. A., Bunk O., “Phase tomography from x-ray coherent diffractive imaging projections,” Opt. Express 19, 21345–21357 (2011). 10.1364/OE.19.021345 [DOI] [PubMed] [Google Scholar]
- 48.Zhang F., Peterson I., Vila-Comamala J., Diaz A., Berenguer F., Bean R., Chen B., Menzel A., Robinson I. K., Rodenburg J. M., “Translation position determination in ptychographic coherent diffraction imaging,” Opt. Express 21, 13592–13606 (2013). 10.1364/OE.21.013592 [DOI] [PubMed] [Google Scholar]
- 49.Maiden A., Humphry M., Sarahan M., Kraus B., Rodenburg J., “An annealing algorithm to correct positioning errors in ptychography,” Ultramicroscopy 120, 64–72 (2012). 10.1016/j.ultramic.2012.06.001 [DOI] [PubMed] [Google Scholar]
- 50.Thibault P., Guizar-Sicairos M., “Maximum-likelihood refinement for coherent diffractive imaging,” New J. Phys. 14, 063004 (2012). 10.1088/1367-2630/14/6/063004 [DOI] [Google Scholar]