Sample Size Calculations for Prevalent Cohort Designs

Abstract

Cross-sectional prevalent cohort design has drawn considerable interests in the studies of association between risk factors and time-to-event outcome. The sampling scheme in such design gives rise to length-biased data that require specialized analysis strategy but can improve study efficiency. The power and sample size calculation methods are however lacking for studies with prevalent cohort design, and using the formula developed for traditional survival data may overestimate sample size. We derive the sample size formulas that are appropriate for the design of cross-sectional prevalent cohort studies, under the assumptions of exponentially distributed event time and uniform follow-up for cross-sectional prevalent cohort design. We perform numerical and simulation studies to compare the sample size requirements for achieving the same power between prevalent cohort and incident cohort designs. We also use a large prospective prevalent cohort study to demonstrate the procedure. Using rigorous designs and proper analysis tools, the prospective prevalent cohort design can be more efficient than the incident cohort design with the same total sample sizes and study durations.

1 Introduction

Incident and prevalent cohort designs are two primary types of epidemiological study designs that have been widely used to investigate the natural history of a disease and to assess the association between a risk factor and the disease prognosis. ^1–4 An incident cohort comprises individuals who are at risk for the initiating event (e.g., the onset or diagnosis of a disease) and will be followed to observe a subsequent event of interest (e.g., death or recurrence). An incident cohort study typically requires the follow-up of thousands of individuals to observe the initiating and failure events. A prevalent cohort consists of individuals who have already experienced the initiating event but have not experienced the failure event at the time of ascertainment, and will be followed to observe the failure event. Incident cohort studies are usually preferred approach to estimating the incidence of a disease and studying the natural history of the disease. However, incident studies often require large cohorts with lengthy follow-up. In contrast, a prevalent cohort design is a cost-effective alternative to study the natural history of the disease. While the prevalent cohort design has gained popularity in recent years with economic and efficiency advantages over the incident cohort design, data observed from a prevalent cohort study are typically subject to selection bias and not representative of the target population for the purpose of estimation and inference. Standard methods for survival analysis and study design developed for incident cohort studies are not appropriate for prevalent cohort studies in general. ^5–9 As adeptly demonstrated in the study of ischemic heart disease by Buckley et al., ¹⁰ a considerable difference in distribution of disease prognosis existed between the prevalent and incident cohorts using the same naïve estimation method, even though both cohorts were derived from the same population.

As an example to illustrate the two sampling schemes, consider the Canadian Study of Health and Aging (CSHA), a multicenter observational study of dementia and other chronicle diseases for people aged 65 years and over in five regions of Canada. ¹¹ Between 1991 and 1992, 14,026 individuals were randomly selected from the community and institutions, and 10,263 agreed to participate in the study. Among them, 1132 were identified with dementia by cognitive impairment screening and clinical examination, and their dates of onset for dementia were ascertained via a review of their medical records. These dementia patients were recruited to the prevalent cohort and prospectively followed for subsequent death (or censoring). One primary outcome of interest is the duration from the onset of dementia to death. From the schema presented in Figure 1, time 0 is defined as the time of enrollment for dementia individuals to the CSHA study. The length of each line defines the duration from the onset of dementia to death or right censoring. For an incident cohort study to evaluate the same outcome, the randomly selected individuals (e.g., cases 5, 6, and 7 in Figure 1) would be followed prospectively for the onset of dementia and death. In contrast to the incident cohort, a sample of cases who experienced the initiating event but not the event of failure (e.g., cases 1, 2, and 3 in Figure 1) are recruited and prospectively followed for the failure event in a cross-sectional prevalent cohort. Cross-sectional sampling captures prevalent cases only. Such individuals often have a longer time gap between the initiation and failure events than individuals from the incident cohort. This bias in prevalent cohort studies is referred to as length-bias, when the incidence of the initiating event follows a stationary Poisson process. It is recognized that such bias is difficult to remove by study design and may confound the interpretation of analysis results.

Figure 1.

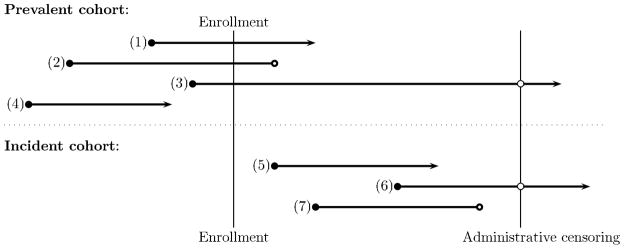
Incident and Prevalent Cohort Sampling Schemas, where (1) through (7) represent individuals (cases); ○ represents censoring

While the prevalent cohort design has been popular with epidemiology research, it has been noted the consequences that using conventional analysis and inference methods for survival data obtained from a prospective prevalent cohort leads to severely biased estimates due to biased sampling. ^12–15 In other words, a claim of finding an association between the risk factors and failure event in a prevalent cohort study using standard analytic methods may be spurious. Recently, there has been increasing interest and advances made in developing statistical methodology to correct the estimation bias in association studies. ^16–19 Practical statistical methods have been developed to obtain unbiased inference and estimation using observed biased data. However, corresponding developments in the design of prevalent cohort studies has been lacking. Researchers generally use the power and sample size calculation tools for incident cohort studies, which are not suited for prevalent cohort studies. Valid tools designed for prevalent cohort studies are needed for estimating the required sample size and/or the length of follow-up to detect an expected association between a risk factor and a failure event. The objective of this paper is to consider formal aspects of prevalent cohort study designs, in particular power and sample size calculations. We present basic methods and practical tools for power and sample size calculations of a prospective prevalent cohort study under the stationary assumption, and compare the empirical results with those from the incident cohort design under similar settings. We also demonstrate how to analyze the observed right-censored from a prevalent cohort study under the proportional hazards model using CSHA as an example.

2 Methods

2.1 Setup

Participants in a prevalent cohort are recruited according to the cross-sectional sampling method, in which one ascertains risk factors (e.g., smoking or a genetic variant) and disease status at the time of enrollment, and then prospectively follows the individuals with the disease to observe the events of interest (e.g. death). Subjects with the initiating event prior to time 0 (time of enrollment to the study) who are still at risk for the failure event (e.g. alive) at time 0 are sampled to the prevalent cohort, and are followed up to time τ.

The difference in sampling scheme between a prevalent cohort study and an incident cohort study is illustrated graphically in Figure 2. Let T̃ be the population duration time from an initiating event to a failure event. In the incident cohort, the event time T̃ can be observed unbiasedly. Let à be the duration time measured from the time of the initiating event to study enrollment. In the prevalent cohort, the observed time (T, A) are length biased sampled; they are (T̃, Ã) observed among those with T̃ > à (see for example, cases 1 to 3 depicted in Figure 1). Cases with an initiating event prior to time 0 (time of enrollment to the study) who are still at risk for the failure event (e.g. alive) at time 0 are sampled to the prevalent cohort, and we record the truncation time A, and residual survival time V or residual right-censoring time C if it is less than the maximum follow-up time, τ. Here, T = A + V is the failure time measured from the initiating event.

Figure 2.

Observed Data from Incident and Prevalent Cohorts

Suppose that the goal of a study is to test the association between unbiased failure time T̃ and a risk (exposure) factor, X. Without loss of generality, we compare the hazard rates for the unbiased failure time T̃ between the exposed and unexposed groups. Let λ₀ and λ₀ be the constant hazard rates of the unexposed (X=0) and exposed (X=1) groups, respectively. Comparing hazards rates is equivalent to testing whether the log-hazard ratio between the two groups θ = log(λ₁/λ₀), where the null hypothesis of no association is

$$H_0:\theta =0\text{vs}.H_1:\theta \ne 0.$$

2.2 Sample size calculations: Incident cohort

Various methods for estimating sample size have been proposed for time-to-event outcomes in standard incident cohort designs with different censoring distributions. ^{2, 20–21} Most of these calculations are based on the exponential distribution assumption for T̃. For illustration, we present the sample size calculation equation, assuming that T̃ follows an exponential distribution with parameter λ₀ for the unexposed group, and λ₁ for the exposed group. Using the maximum likelihood estimation method as approximated by Lachin, ²² the sample size estimation is derived from the score test statistic and Fisher’s information. Assume that all participants are followed for a fixed study duration τ. Let n₀ and n₁ be the respective sample sizes for the unexposed and exposed groups, and z_α/2 and z_β be the upper α/2- and upper β-th quantile of the standard normal distribution. The total sample size n = n₀ + n₁ required to achieve (1 − β) power at the significance level α for a two-sided test can be obtained from the following equation:

$$n_I=\frac{{(z_{\alpha /2}+z_{\beta })}^2}{{\theta }^2}\left\{\frac{1}{\gamma (1-e^{-{\lambda }_0\tau })}+\frac{1}{(1-\gamma )(1-e^{-{\lambda }_{0}exp(\theta )\tau })}\right\},$$ (1)

where γ = n₀/n. In practice, it is common that participants are recruited uniformly over (0, τ). Then a similar formula for sample size calculation can be found, but with different variance estimators,

$$n_I=\frac{{(z_{\alpha /2}+z_{\beta })}^2{\lambda }_0\tau }{{\theta }^2}\left\{\frac{1}{\gamma \{{\lambda }_0\tau -(1-e^{-{\lambda }_0\tau })\}}+\frac{exp(\theta )}{(1-\gamma )\{{\lambda }_0{\mathrm{e}}^{\theta }\tau -(1-e^{-{\lambda }_{0}exp(\theta )\tau })\}}\right\}.$$ (2)

2.3 Sample size calculations: Prevalent cohort

We derive the formulas for power and sample size calculations for a prevalent cohort study based on the maximum likelihood approach. The derivations can be found in the appendix. Under the exponential distribution assumption, the equation that derives the total sample size and power for testing the equality of hazards is based on the asymptotic score test statistic. If all participants can be potentially followed for a fixed time τ, then the total sample size has the following explicit form

$$n_P={\left\{\frac{z_{\alpha /2}+z_{\beta }}{\theta }\right\}}^2\left\{\frac{1}{\gamma (2-e^{-{\lambda }_0\tau })}+\frac{1}{(1-\gamma )(2-e^{-{\lambda }_{0}exp(\theta )\tau })}\right\}.$$ (3)

If the losses to follow-up are uniformly distributed over (0, τ), then the above formula needs to be modified. The corresponding sample size formula can be found in Appendix I. We also derive the sample size formula when the population duration time follows a Weilbull distribution assumption. The detail of the formula for testing the hazard rates at a fixed time t between two independent groups can be found in a supplementary material from the authors.

2.4 Comparison between prevelent cohort design and incidence cohort design

Comparing formula (1) and formula (3), it is evident that the sample size requirement for prevalent cohort design is smaller than the sample size requirement for incidence cohort design, i.e. n_P < n_I, under the same design consideration including the same type I/II errors, the same follow-up duration τ and the same null hazard rate λ₀. In fact, the sample size difference is

$$n_I-n_P={\left\{\frac{z_{\alpha /2}+z_{\beta }}{\theta }\right\}}^2\left\{\frac{1}{\gamma (2-e^{-{\lambda }_0\tau })(1-e^{-{\lambda }_0\tau })}+\frac{1}{(1-\gamma )(2-e^{-{\lambda }_1\tau })(1-e^{-{\lambda }_1\tau })}\right\}.$$

Intuitively, prevalent cohort design can use the extra information on the backward time A, compared to the incident cohort design. When failure time T̃ follows an exponential distribution, the observed truncation time A and residual survival time V follow the same exponential distribution and independently contribute information to the likelihood. Moreover, the truncation time A is not subject to right censoring, but V may be. Hence, it is not surprising that the gain in power for the prevalent cohort study can be more than double that of its counterpart incident cohort study.

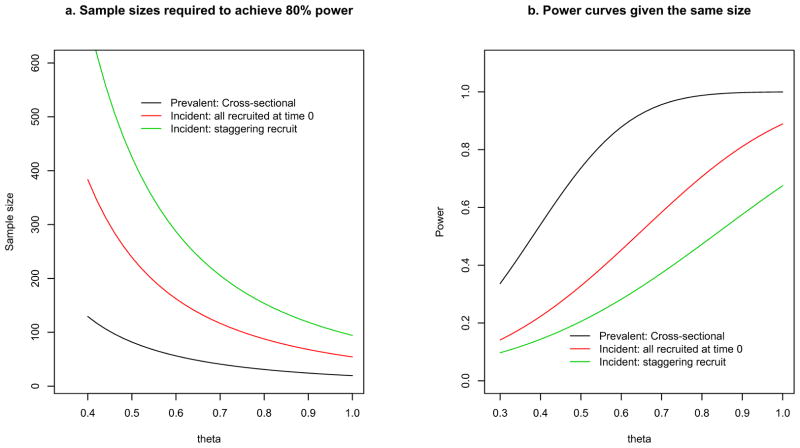
To further illustrate the difference, we compare the sample sizes and powers of the two types of design, as shown in Figure 3. We consider two sampling methods for the incident cohort study. The first method assumes that all participants are recruited at the beginning of the study -- this is parallel to the cross-sectional sampling of the prevalent cohort design presented in Figure 1. The second method assumes that participants are recruited on a staggered fashion during the interval (0, τ). We consider a range of values for the log hazard ratio θ, while assuming α = 0.05, total follow-up duration τ = 4 years, and γ = 0.5.

Figure 3.

(a) Sample Size and (b) Power Comparisons Between Prevalent and Incident Cohort Designs

Using sample size estimation equations (1) and (2) for the incident designs and equation (3) for the prevalent design, we can estimate the total sample sizes required to achieve 80% power for the designs, keeping all other design parameters the same. For example, when θ=0.5, and λ₀=0.6, the total sample size required to achieve 80% power at a significance level of 0.05 is 82 for the prevalent cohort design, and 240 for the incident cohort design, with 1 year follow up. The required sample size for the incident cohort study is almost 3 times as high as the required sample size for the prevalent cohort study (when all participants are recruited at time 0). The difference in sample size requirements is especially large when the hazard ratio is small. The difference becomes small when the hazard ratio increases. With the same total sample size (n = 70) and follow-up duration, the power (Figure 3b) for the prevalent cohort design can be up to 2.4 times higher than the power for the corresponding incident design. The difference in power is even larger when the comparison is made between the prevalent cohort design and the incident design with staggered entry. The advantage of the prevalent design is more evident when the hazard ratio is small to moderate.

3 Numerical studies

3.1 Simulations

The power and sample size considerations are based on the most efficient test statistics under parametric models, while assuming every patient can be followed for a fixed time. We conduct simulation studies to compare the powers of incidence cohort deign and prevalent cohort deign, when the data are analyzed instead by nonparametric test statistics, when the sample size is small, and when more general censoring mechanisms are considered. For incident cohort studies, the standard log-rank (LR) test is the asymptotically most efficient test under proportional hazards alternatives. For prevalent cohort studies, Ning et al. proposed an asymptotically most efficient permutation (PM) test under proportional hazards alternatives. ¹⁸ As shown in Ning et al., the naïve log-rank test is also a valid test statistic, but only when censoring distributions are the same across different groups for analyzing length-biased data. ¹⁸ We consider two underlying distributions of T̃: exponential and Weibull, and two types of censoring mechanisms, as shown in Table 1. The total sample size used is 80, with equal numbers in each risk group. For each scenario, we present the statistical power for testing the effect of exposure using the PM test, log-rank (LR) test, and the conditional test for general left- truncated data (denoted as LT) observed from a prevalent cohort. ²³ We compare the power against that of the log-rank test for traditional survival data observed from an incident cohort with the same sample size and follow-up duration. Under the null hypothesis (θ = 0), all test statistics in both designs lead to a type I error rate of around 0.05 (not presented in Table 1).

Table 1.

Empirical Power Based on 1000 Simulated Cohorts for Incident and Prevalent Designs with the Same Sample Size and the Same Follow-up Duration. Cens %, censoring percentage; LT, conditional test for left-truncated data; ²³ LR, log-rank test; PM, permutation test. ¹⁸

	Incident Design				Prevalent Design
θ	Cens%a	LRa	Cens%b	LRb	Cens%	PM	LR	LT
Exp: λ0 = 0.15, τ1 = 4, type I censoring at τ = 8
0.4	34	30.7	23	33.7	23	64.2	64.6	29.9
0.5	32	44.4	22	52.5	22	82.2	82.9	44.9
0.6	31	59.2	21	67.6	21	91.7	92.3	58.7
0.7	29	75.3	20	77.9	19	98.3	98.5	71.4
Exp: λ0 = 0.15, τ1 = 4, Uniform censoring (0,8)
0.4	70	17.4	52	25.7	52	55.3	50.3	18.9
0.5	68	22.7	51	36.3	51	74.5	71.7	30.7
0.6	67	31.6	49	48.7	49	85.5	82.6	40.3
0.7	66	41.6	48	59.6	48	95.4	93.9	52.7
Weibull: shape=1.5, scale=2, τ1 = 1, type I censoring at τ = 3
0.4	32	30.7	23	37.1	13	57.9	59.5	37.0
0.5	34	43.8	24	50.4	14	75.2	77.0	51.5
0.6	36	57.7	26	66.0	15	88.8	90.2	63.5
0.7	38	67.6	28	76.7	17	96.8	97.1	77.0
Weibull: shape=1.5, scale=2, τ1 = 1, Uniform censoring (0, 3)
0.4	72	13.2	60	21.5	46	45.0	44.8	21.7
0.5	73	19.8	61	29.1	47	65.0	62.0	30.6
0.6	74	24.0	62	38.3	48	80.5	78.9	41.5
0.7	75	33.6	64	43.0	49	89.4	88.3	50.9

^aparticipants are recruited with staggering entry from (0, τ₁) in incident cohort

^bparticipants are recruited at the beginning of the study at time 0, similar to prevalent cross-sectional sampling.

With the specified alternatives, the power of the PM test (similar to the LR test) for the prevalent cohort is about 1.3 to 1.9 times higher than that of the LR test for the incident cohort when all participants are recruited at the beginning of a study. With staggered entry during (0, τ₁) years for the incident design, it is not surprising that the power is even lower for each scenario. When participants in both cohorts are subject to right censoring, which follows a uniform distribution, the gain in power for the prevalent design compared to the incident design is more substantial than that with type I censoring. Under the Weibull distributions, we observe a similar trend of efficiency advantage for the prevalent design over the incident design. In summary, the asymptotically most efficient permutation test achieves the highest power (similar to the LR test) for the prevalent cohort; whereas the power of the conditional LT test from the prevalent cohort can be as low as (or lower than) that from the parallel incident cohort.

3.2 An example: CSHA prevelent cohort study

In the CSHA study as mentioned in Introduction, it is of interest to investigate how different types of dementia may impact long-term survival measured from the disease diagnosis, after adjusting for length-biased data obtained from the prevalent cohort. Specifically, one focus is to evaluate whether patients with possible Alzheimer’s disease have similar survival as those with vascular dementia or probable Alzheimer’s diseases. The conventional survival analysis methods in the standard statistical software may result in false interpretation on the association between the type of dementia and time to death.

The observed data from CSHA consist of 818 individuals with a diagnosis of possible Alzheimer’s disease (252 subjects), probable Alzheimer’s disease (392 subjects), or vascular dementia (173 subjects). We first show how the prevalent cohort data can be analyzed by valid statistical methods under the most popular Cox model with length-bias assumption, and then illustrate the sample size calculations based on the estimated hazard ratios.

To compare the survival distribution of possible Alzheimer’s disease with that of vascular dementia or probable Alzheimer’s disease, we consider statistical methods that are valid for length-biased data including the conditional test, ^8,23 which is an efficient inverse weighted estimating equation method with easily modified existing statistical software, ¹⁹ and asymptotically most efficient permutation test. ¹⁸ Denote the data by {(A_i, T_i, δ_i, X_i)}, where A_i is the time measured from dementia diagnosis to the study enrollment, T_i is the time measured from dementia diagnosis to death or right-censoring, X_i =1 for possible Alzheimer’s disease and 0 otherwise, and δ_i= I(T_i−A_i<C_i) is a censoring indicator. The conditional test (LT) for general left-truncated data can be used to model the observed data using SPlus or R, ^8,23 where the function and its data input are provided in Box 1. The corresponding output gives the estimated hazard ratio (HR) of 0.94 (95% CI 0.79–1.12; P=0.47) between possible Alzheimer’s disease and other dementia types, which does not show a statistically significant difference in survival distributions by diagnosis type.

Box 1. Use R/SPlus to estimate HR from the prevalent cohort study.

Conditional Test

> coxph(Surv(A, T, Δ) ~ X, data=data.name)

where

A= the time measured from dementia diagnosis to the study enrollment

T= the time measured from demential diagnosis to death or right-censoring

Δ= censoring indicator

X= disease type indicator

Inverse weighted estimation

> coxph(Surv(Ym, rep(1, m)) ~ Xm + offset(log(W)), data=data.name)

where

m= the total number of the observed failure times

Y_m= sorted failure times

X_m= the corresponding group indicator associated with Y_m

W= (W₁, …, W_m), where $W_i={\int }_0^{Y_i}\widehat{S_C}(u)du$ is the integral of the Kaplan-Meier estimator of residual censoring time C.

The inverse weighted estimation algorithm developed in Qin and Shen can be directly linked to existing S-PLUS or R function for the Cox model by adding appropriate weights using “offset” option, ¹⁹ see Box 1. Similarly, one can use “PROC PHREG” in SAS with “offset” to include the weight function W. The estimated HR of 0.84 between possible Alzheimer’s disease and other dementia types has the same interpretation as LT model. However, the standard error of HR should be obtained from the bootstrap method, which shows a statistically significant difference between the groups (95% CI 0.73 to 0.95; P=0.03). Given the censoring distributions across two groups are the same in the CSHA study, both the permutation test of Ning et al ¹⁸ and the traditional logrank test are valid, while both show that patients with possible Alzheimer’s disease had significantly longer survival than the other types of dementia with a p-value of .010 and .018, respectively.

Suppose now that we design a prevalent cohort study on Alzheimer’s disease, and the sample size calculation is based on the hazard ratio θ=0.84 of overall survival between possible Alzheimer’s disease (POA) and vascular dementia or probable Alzheimer’s disease (VD+PRA). Assume that the sample size ratio between POA and total study sample is similar to that of the CSHA study, i.e., γ = 252/818 ≈ 0.31. Consider a follow up τ = 6 years, which is the maximum follow up in the CSHA study. Using the prevalent cohort design, a sample size of 818 subjects would have 80% power to detect a hazard ratio of θ=0.84 with a significance level of 0.05, assuming that the hazard rate of death is λ₀ = 0.114 among the subjects with vascular dementia or probable Alzheimer’s disease. In contrast, under the same design considerations, the incidence cohort design would require 2,538 subjects, three times higher than the sample size requirement using the prevalent cohort design.

4 Discussion

Most sample size calculations in clinical trials and incident cohort studies are approximations based on simple parametric distribution assumptions. Similarly, we propose sample size calculation tools for a cross-sectional prevalent cohort design assuming that the failure times follow exponential or Weibull distribution. We also compare the empirical power of the two types of designs with the same total sample sizes and design parameters under commonly used parametric forms such as exponential and Weibull distributions. The prevalent cohort design achieves higher efficiency/power than the incident cohort design with the same total sample size and study duration. The power advantage for the prevalent design is more evident when the hazard ratio of the two groups is small.

The likelihood for length-biased data is calculated under the assumption that the onset of the initiating event follows a stationary Poisson process ⁶, which has a connection to queuing theory that may lead to future works. For length-biased data obtained from a prevalent cohort study, the naïve log-rank test is a valid test statistic if the censoring distributions are the same in the exposed and unexposed groups. Otherwise, the naïve log-rank test could inflate the type I error rate. A related cautionary note is that estimating hazard ratio using standard software for the Cox model will be severely biased for length-biased data from a prevalent cohort. Instead, proper estimation methods for length-biased data should be used. ^17,19,24 We demonstrated some existing methodologies using the example of CSHA cohort study.

Another interesting observation is that a prevalent cohort design will not lead to any improved power if one uses an inefficient test statistic. The conditional test, which is a valid test statistic that has been widely used for analyzing data observed from prevalent cohort studies over the past decades ^8,23,25 leads to substantial loss of power because the information of the backward recurrence time A (in Figure 2) is not properly utilized. For the conditional test, the risk set at each failure time is defined to include participants with survival times that extend beyond that time point and truncation times that are shorter than that time point, which results in few summands compared to that for the logrank test. Gains and losses of power are two sides of the same coin in prevalent cohort designs. When using the asymptotically most efficient test statistic for both cohort studies, it is evident that the prevalent cohort design is more efficient than the incident cohort design because the extra “free” information on A is properly utilized. Again, the gain in power for the prevalent cohort design depends on the design as well as the use of efficient test statistics.

Sample size estimations are ubiquitously approximated using methods under simplified parametric assumptions. For a cross-sectional prevalent cohort study, more precise sample size and power estimations may be proposed as a two-stage design. Using the observed truncation times A, we may estimate the distribution parameters and the corresponding distribution in the first stage. At the second stage, given the estimated parameters, we can determine the length of the prospective follow-up for a fixed total sample size to achieve the desired power. Alternatively, we may increase the sample size during the prospective follow-up. Moreover, the sample size calculation for parametric distributions other than exponential can be obtained similarly.

In summary, while efficient statistical analysis methods have been developed to obtain unbiased estimator of hazard ratio and to test the equality of survival distributions using biased data observed from a prevalent cohort study, it is critical to provide practical design tools by estimating the sample size/power for the prospective prevalent cohort study.

Appendix

The derivation of sample size formulas under the exponential distribution assumption

Suppose that the unbiased duration time T̃ follows an exponential distribution with hazard λ. The probability density function for time T̃ is f_T(t) = λ exp(−λt). The joint probability density function of observed variable (A, T) and marginal probability density function of T under the stationarity assumption are as follows:

$$f_{A,T}(a,t)={\lambda }^{2}exp(-\lambda t)I(0<a<t),g_T(t)={\lambda }^{2}texp(-\lambda t).$$

Note that f_{A, V}(a, v) = λ² exp(−λ(a + v)), which implies the independence of A and V under the exponential distribution.

Consider the determination of the total sample size n = n₀ + n₁, where n₀ and n₁ are the sizes of unexposed and exposed groups, respectively. The sample size estimation is based on the assumption that the underlying survival time for an individual in the kth group (k = 0 or 1) follows an exponential distribution with hazard rate λ_k for k = 0, 1 in the unexposed and exposed groups, respectively.

Let (T_ki, δ_ki) denote the observed length-biased event-time data for i = 1, …, n_k and k = 0, 1. The likelihood function for the observed length-biased data is

$${\lambda }_0^{{\sum }_{i=1}^{n_0}(1+{\delta }_{0i})}{\lambda }_1^{{\sum }_{i=1}^{n_1}(1+{\delta }_{1i})}exp\left(-{\lambda }_0\sum _{i=1}^{n_0}{T}_{0i}\right)exp\left(-{\lambda }_1\sum _{i=1}^{n_1}{T}_{1i}\right).$$

The most efficient estimator for λ_k is the maximum likelihood estimator that can be solved by maximizing the likelihood function,

$${\widehat{\mathrm{\lambda }}}_k=\frac{{\sum }_{i=1}^{n_k}(1+{\delta }_{ki})}{{\sum }_{i=1}^{n_k}{T}_{ki}},k=0,1.$$

The equation that derives the total sample size and power for testing the equality of hazards is based on the asymptotic score test statistic θ̂/σ̂, where θ̂ is the log hazards ratio, and λ̂₀ and λ̂₁ are the maximum likelihood estimations for λ₀ and λ₁, respectively. When assuming right censoring occurs only at the end of study τ,

$${\widehat{\sigma }}^2=\frac{1}{n_0[2-exp(-{\widehat{\mathrm{\lambda }}}_0\tau )]}+\frac{1}{n_1[2-exp(-{\widehat{\mathrm{\lambda }}}_1\tau )]}.$$

Using the standard large sample theory with an application of the delta method, we can show that $\sqrt{n_k}(log{\widehat{\mathrm{\lambda }}}_k-log{\lambda }_k)$ is asymptotically normal with mean 0 and variance σ²(λ_k) = 1/[1 + λ_kE{min(T̃_k, C)}], where C is the time to the loss of follow up, assumed to follow the same distribution for both groups. If right censoring only occurs at the end of study τ, then σ²(λ_k) = {2 − exp(−λ_kτ)}⁻¹.

Consider testing the null hypothesis H₀:log λ₀ = log λ₁. The sample size calculation can be based on the following asymptotic test statistic

$$Q_n({\widehat{\mathrm{\lambda }}}_1,{\widehat{\mathrm{\lambda }}}_0)=\frac{log{\widehat{\mathrm{\lambda }}}_1-log{\widehat{\mathrm{\lambda }}}_0}{{\{{\sigma }^2({\widehat{\mathrm{\lambda }}}_1)/n_1+{\sigma }^2({\widehat{\mathrm{\lambda }}}_0)/n_0\}}^{1/2}}.$$

Under H₀, Q_n(λ̂₁, λ̂₀) approximates to the standard normal when min{n₁, n₂} is large. The null hypotheses thus will be rejected at approximate α level of significance if |Q_n(λ̂₁, λ̂₀)| is greater than z_α/2. Under the alternative hypothesis λ₁ ≠ λ₀, the sample size to achieve a power of 1 − β can be found by solving the equation |Q_n(λ₁, λ₀)| − z_α/2 = z_β, or equivalently,

$$n_P={\left(\frac{z_{\alpha /2}+z_{\beta }}{\theta }\right)}^2\left\{\frac{{\sigma }^2({\lambda }_0)}{\gamma }+\frac{{\sigma }^2({\lambda }_0)}{(1-\gamma )}\right\}.$$ (4)

If right censoring only occurs at the end of study τ, then the sample size formula can be explicitly expressed as in (3). If losses to follow-up are uniformly distributed over (0, τ), the corresponding sample size is determined by equation (4), where

$${\sigma }^2({\lambda }_k)=\frac{2{\lambda }_k\tau exp({\lambda }_k\tau )}{2-{\lambda }_k^2{\tau }^2+2exp({\lambda }_k\tau )(2{\lambda }_k\tau -1)}.$$