The effect of low b-values on the intravoxel incoherent motion (IVIM) derived pseudodiffusion parameter in liver

Abstract

Purpose

To examine the effect of low b-values (0<b<50 s/mm²) on the calculation of the intravoxel incoherent motion (IVIM) derived pseudodiffusion parameter in the normal liver.

Methods

Simulations were performed to examine the effects of adding low b-values on the pseudodiffusion parameter. Low b-values were cumulatively added to the distribution and the IVIM signal was generated with varying pseudodiffusion values. The signal was fit with the IVIM model after the addition of Gaussian noise, and the simulated values were compared to the true values. In addition, the livers of eight control subjects were imaged using respiratory-triggered DWI. Pseudodiffusion was calculated with and without low b-values and compared.

Results

Pseudodiffusion tended to be underestimated when low b-values were not included in the b-value distribution as predicted by simulations and confirmed with in vivo imaging. The number of outlier values was also reduced as more low b-values were added.

Conclusion

In conclusion, this study showed pseudodiffusion in the liver tended to be underestimated when too few low b-values (0<b<50 s/mm²) were included in the distribution. Therefore, it is recommended to include at least two low b-values when performing liver IVIM studies.

INTRODUCTION

Diffusion weighted MRI (DWI) has been gaining prominence in abdominal imaging (1,2). The intravoxel incoherent motion (IVIM) analysis technique, which uses a biexponential model to extract perfusion-related information from the DWI signal, has been used to diagnose liver cirrhosis (3–6). The IVIM theory was originally proposed by Le Bihan and colleagues (7,8). The basic premise is that diffusion within in vivo tissue is more complex than the simple random Brownian motion of water molecules and is therefore better described by faster and slower diffusing components (7,8). The faster component is thought to represent the microcirculation of blood through capillaries, with the relatively faster moving blood causing a sharper decrease in the signal with diffusion weighting (b-value) (7,8). Therefore, the model requires the collection of both low and high b-values as the IVIM effect becomes largely negligible as the b-value is increased beyond about 200 s/mm² (7–9). The IVIM model is a two-compartment model and includes terms for the fraction of received signal attributed to moving blood (fractional perfusion, f_p), the diffusion caused by moving blood (pseudodiffusion, D_p), and a diffusion component free of perfusion effects (true molecular diffusion, D_t) (Equation 1). Here, S_b is the signal as a function of b-value and S₀ is the signal from the b = 0 s/mm² image.

$$\frac{S_b}{S_0}=\left(1-f_p\right)·e^{-b·D_t}+f_p·e^{-b·D_p}$$ (1)

Recent studies have shown that organs in the abdomen, including the liver (3–6), pancreas (10), and kidney (11) have relatively high fractional perfusion and pseudodiffusion values compared to other organs, such as the brain (12,13). It is in this high perfusion regime that choice of b-values becomes paramount. As pseudodiffusion increases, the influence of low b-values becomes greater. Pseudodiffusion has been shown to be lower in cirrhotic livers compared to normal livers (3–5). One study found pseudodiffusion to be more predictive of cirrhosis than traditional ADC and suggested decreases in pseudodiffusion may actually explain the decreased ADC (4).

IVIM studies in the liver have used different b-value distributions and obtained different values for IVIM parameters (3,4,6,14,15). For example, Patel et al. used a b-value distribution of b = (0, 50, 100, 150, 200, 300, 500, 700, and 1000) s/mm² and obtained values for f_p, D_t, and D_p of 0.32, 1.2 μm²/ms, and 40 μm²/ms respectively in normal liver (3). Luciani et al. used a b-value distribution of b = (0, 10, 20, 30, 50, 80, 100, 200, 400, and 800) s/mm² and obtained values for f_p, D_t, and D_p of 0.26, 1.2 μm²/ms, and 85 μm²/ms respectively in normal liver (4). Luciani et al. found pseudodiffusion values twice as high as Patel et al. and used three additional b-values between b = 0 and 50 s/mm². Furthermore, studies have shown relatively poor repeatability for D_p and, to a lesser extent, f_p with coefficients of variation (CV) ranging from 14.6–59% for D_p and 7.7–25% for f_p in normal livers (3,16).

Therefore, the goal of this study was to examine the effect of very low b-values (0<b<50 s/mm²) on the value and repeatability of the IVIM-derived pseudodiffusion parameter. It was hypothesized that pseudodiffusion calculated in the high perfusion regime of the liver, without any b-values between b = 0 and 50 s/mm² would underestimate the true pseudodiffusion value. It was also hypothesized that the addition of b-values less than b = 50 s/mm² would lead to IVIM parameters with higher repeatability than parameters calculated with no b-values between b = 0 and 50 s/mm². To accomplish this, simulations were performed that looked at the effect of b-value on the error and value of the calculated IVIM parameters. These results were compared to IVIM data collected in the liver of normal control subjects.

METHODS

Simulations

Simulations were performed to look at the effects of low b-values on IVIM calculations. All simulations were implemented in Matlab (17) (Mathworks, Natick, MA). The procedure was as follows: First, starting with a b-value distribution of b = (0, 50, 100, 150, 200, 400, 800 s/mm²), b-values were added cumulatively in the range 0<b<50 s/mm² in the following order: b = 25, 10, 40 s/mm². The signal was generated using Equation 1 with common values for IVIM parameters reported for liver (3,4) of f_p = 0.3, D_t = 1.2 μm²/ms and D_p = 20, 40, 60, 80, and 100 μm²/ms. Gaussian noise was added so the SNR of the b = 0 s/mm² image was 30. The noisy signal was then fit with Equation 1 using a Levenberg Marquardt algorithm. This was repeated 10000 times and the error was computed from Equation 2, where N = the number of iterations, x_i = the simulated parameter value, and x = the true parameter value. In addition, the mean and median values of each parameter, as well as the percentage of outliers (defined as iterations where the Jacobian matrix was ill-conditioned), were computed for each b-value distribution and IVIM parameter set.

$${\sigma }_x=\frac{\sqrt{\frac{1}{2}{\displaystyle \sum _{i=1}^N}{\left(x_i-x\right)}^2}}{x}$$ (2)

In-vivo Studies

Eight subjects with no known history of abdominal disease participated in this study (4 male, 4 female, mean age 33.6 years, range 18–55 years). Written informed consent was obtained for each subject in accordance with our Institutional Review Board policies. Food intake prior to scanning was not controlled for.

Each subject underwent two consecutive imaging sessions on a GE 1.5T scanner. Each session consisted of a multiple b-value respiratory-triggered (RT) single-shot spin-echo EPI DWI scan, which lasted around 6 minutes. The FOV ranged from 36–40cm with a slice thickness of 8mm skip 2mm, matrix size of 96×160 zero-filled to 192×256, partial k-space factor of 0.9, and echo train length equal to the number of acquired phase encode lines.. Additional imaging parameters were as follows: TE = 63.4ms, TR = one breathing cycle (~4–8 s), b = (0, 10, 25, 50, 100, 150, 200, 400, 800), NEX = (3, 3, 3, 2, 2, 2, 2, 6, 6), and three diffusion directions applied simultaneously (3in1). All b-values had the same respiratory trigger delay. The NEX was higher for high b-values to obtain higher SNR images. The NEX for b-values less than 50 s/mm² was higher than the NEX for the middle b-values because these b-values have been shown to be more important for the calculation of pseudodiffusion (18).

For this analysis, IVIM parameters were calculated using a segmented approach and applying methods previously published (3,4). The segmented approach takes advantage of the fact that, since D_p ≫ D_t, its effect can be neglected when b > 200 s/mm². Thus, D_t can be estimated by linearly fitting the natural log of Equation 3, where S_int is the y-intercept of the fit. Likewise, f_p can be estimated by evaluating Equation 4, where S₀ is the signal of the b = 0 s/mm² image. D_p can then be calculated by fitting Equation 1 with f_p and D_t already known. IVIM parameters were calculated using the acquired b-value distribution and then were recalculated after eliminating the b = 10 and 25 s/mm² images. All curve-fitting analyses were performed in Matlab using a Levenberg-Marquardt algorithm.

$$S_b=S_{int}·e^{-b·D_t}$$ (3)

$$f_p=\frac{\left(S_0-S_{int}\right)}{S_0}$$ (4)

Circular regions of interest (ROIs) with 20mm radii were drawn in segments V and VI in the lower right lobe of the liver. ROIs were placed to avoid large intrahepatic vessels. Mean and median values of each parameter were extracted on a voxelwise basis within the ROI (voxelwise method). The DWI signal was also averaged within the ROI and the averaged signal was then fit to obtain one value for each IVIM parameter within an ROI (ROI method). Repeatability was assessed using the within subject coefficient of variation (CV) defined as the standard deviation divided by the mean.

Data Analysis

Mean and median values of IVIM parameters, as well as the percentage of outliers, were compared for each b-value distribution and IVIM parameter set. A histogram analysis was performed for the simulation portion of the study to examine the effect of b-value set on the distribution of IVIM parameter values.

For the in-vivo studies, mean and median values for the ROI and voxelwise calculations of IVIM parameters and the percentage of outliers were compared between b-value distributions with a paired two-sample t-test. For the voxelwise analysis, only voxels where both D_p calculations were not outliers were included in the analysis.

RESULTS

Simulations

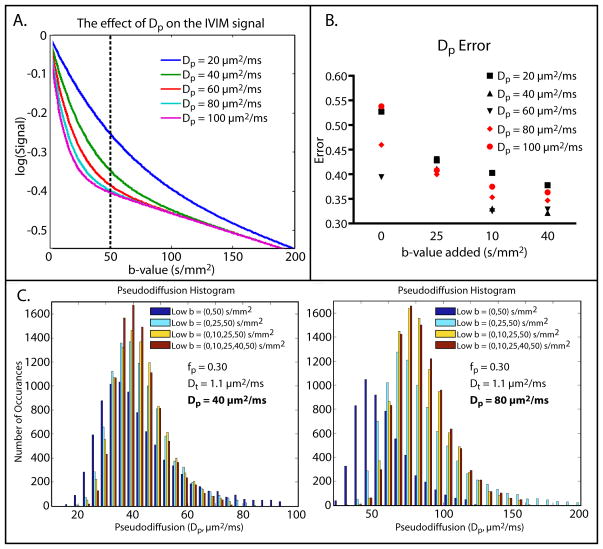
Mean and median values for the D_p term, as well as the percentage of outliers, were computed for four b-value distributions and five different simulated D_p values. The results are shown in Table 1. Starting with D_p = 60 μm²/ms, the simulated D_p was less than the true D_p when there were no b-values between 0 and 50 s/mm². When b = 25 s/mm² was added to the distribution, the simulated D_p values approached the true values. The percentage of outliers dropped drastically when b = 25 s/mm² was added and tended to level off at about 1–2% once b = 10 s/mm² was also included. The effects of varying D_p on the IVIM signal as well as histograms of the simulated D_p for two D_p values and varying b-value distributions are shown in Figure 1A, C.

Table 1.

Simulated pseudodiffusion values compared with the true values and the percentage of outliers for different b-value distributions

	Dp = 20 μm2/ms			Dp = 40 μm2/ms			Dp = 60 μm2/ms			Dp = 80 μm2/ms			Dp = 100 μm2/ms
	Mean Dp	Med Dp	% Out	Mean Dp	Med Dp	% Out	Mean Dp	Med Dp	% Out	Mean Dp	Med Dp	% Out	Mean Dp	Med Dp	% Out
Low b=(0,50)	23	21	5.3	41	36	20.4	47	43	37.7	49	45	46.2	50	46	49.0
Low b=(0,25,50)	22	21	1.5	44	41	3.3	65	59	9.1	80	73	18.8	91	82	28.7
Low b=(0,10,25,50)	22	21	1.1	43	41	1.3	64	61	1.5	86	81	1.4	108	101	2.0
Low b=(0,10,25,40,50)	22	21	0.9	43	41	1.3	64	61	1.3	85	81	1.5	107	101	2.1

The units of the b-values are s/mm². True pseudodiffusion values are shown above of the simulated pseudodiffusion values. Each set of low b-values was in addition to a b-value distribution of b=(100,150,200,400,800) s/mm².

Abbreviations: D_p = Pseudodiffusion, % Out = Percentage of voxels excluded due to an ill-conditioned Jacobian matrix (i.e. percentage of outliers), Med = median.

Figure 1. Simulation Results.

A. The effect of increasing pseudodiffusion on the IVIM signal. As pseudodiffusion increases, the change in signal is driven by b-values less than 50 s/mm². B. Simulated pseudodiffusion error for different pseudodiffusion values and b-value distributions. Each b-value was added cumulatively to the original distribution of b = (0,50,100,150,200,400,800) s/mm². In all cases, error was reduced as b-values were added and appeared to level off once b = 10 s/mm² was added. C. Simulated pseudodiffusion histograms for true D_p = 40 μm²/ms (left) and 80 μm²/ms (right). When the true D_p = 40 μm²/ms, the distribution of simulated pseudodiffusion values was centered on the true pseudodiffusion value for all b-value distributions. On the other hand, when the true D_p = 80 μm²/ms, the distribution of simulated pseudodiffusion values was pushed to the left when no b-values between 0 and 50 s/mm² were included in the b-value distribution. As low b-values were added the simulated pseudodiffusion distribution became tighter and centered around the true pseudodiffusion value.

The error in the calculated D_p values tended to decrease as more b-values between 0 and 50 s/mm² were added to the distribution and leveled off once b = 10 s/mm² was included (Figure 1B). This trend was observed for all D_p values, but the largest changes in error were seen for D_p = 40 μm²/ms (0.21) and D_p = 100 μm²/ms (0.17).

In-vivo

Mean and median values of D_p were calculated with two different b-value distributions in the liver of eight healthy volunteers who were scanned twice in the same session. Results are shown in Table 2. For both the voxelwise and ROI analyses, D_p calculated without b-values between 0 and 50 s/mm² was significantly lower than D_p calculated with b = 10 and 25 s/mm² included in the distribution (paired two-sample t-test, P < 0.001). The percentage of outliers calculated without b-values between 0 and 50 s/mm² was significantly higher than the percentage of outliers calculated with b = 10 and 25 s/mm² included in the distribution (paired two-sample t-test, P < 0.001).

Table 2.

In vivo pseudodiffusion calculations for the ROI-based and voxelwise methods in normal volunteers

		Low b=(0,50)	Low b=(0,10,25,50)
ROI	Dp	37.0 (9.7)	85.9 (25.1)	P < 0.001
	CV	0.26	0.28
Voxelwise	Mean Dp	25.2 (6.0)	61.3 (18.3)	P < 0.001
	CV	0.11	0.10
	Median Dp	19.0 (6.6)	35.0 (13.3)	P < 0.001
	CV	0.25	0.18
	% Outliers	31.3 (7.9)	10.1 (5.5)	P < 0.001

The units of the b-values are s/mm². The units of the pseudodiffusion values are μm²/ms. Each set of low b-values was in addition to b=(100,150,200,400,800) s/mm². Standard deviations are shown in parentheses. P-values are the result of a paired two-sample t-test.

Abbreviations: D_p = pseudodiffusion, CV = coefficient of variation.

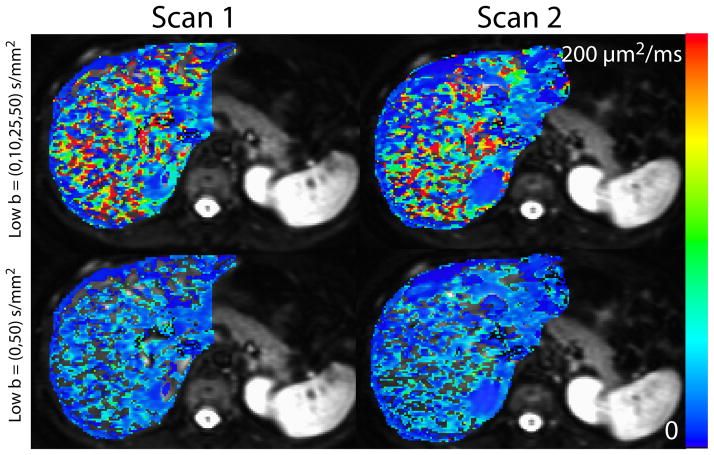
Repeatability was analyzed with the coefficient of variation (CV). For the voxelwise analysis, the CV was similar for the case where no b-values between 0 and 50 s/mm² were included and the case with b = 10 and 25 s/mm² included. This was the true for both the mean (0.11 vs. 0.10) and median (0.25 vs. 0.18) calculations. A similar trend was seen for the ROI analysis (0.26 vs. 0.28). Example parametric maps for one representative subject are shown in Figure 2.

Figure 2. Liver pseudodiffusion images from one representative subject.

The left column shows results from the first scan from one subject. The right column shows the second scan from that same subject conducted in the same scan session. The top row depicts pseudodiffusion maps calculated with b = 10 and 25 s/mm² included in the b-value distribution while the bottom row shows pseudodiffusion maps calculated without b-values between 0 and 50 s/mm² included in the b-value distribution. Images in the top row have more fitted voxels as well as a wider range of pseudodiffusion values. The images in the bottom row have more outlier values shown as blank voxels on the images.

DISCUSSION AND CONCLUSIONS

This study calculated the IVIM-derived pseudodiffusion parameter with and without b-values between 0 and 50 s/mm². Simulations showed that pseudodiffusion tended to be underestimated when no b-values between 0 and 50 s/mm² were included in the b-value distribution for pseudodiffusion values greater than or equal to D_p = 60 μm²/ms. Furthermore, the percentage of outliers, defined as the percentage of iterations where the Jacobian matrix was ill-conditioned, and the parameter error decreased as more b-values between 0 and 50 s/mm² were added to the b-value distribution. In vivo MRI results in the liver of normal controls showed that the measured pseudodiffusion value was lower when calculated with no b-values between 0 and 50 s/mm² compared to when calculated with b = 10 and 25 s/mm² included in the distribution.

For the simulation portion of this study, Gaussian noise was added to the simulated signal so the b = 0 s/mm² had a signal to noise ratio of 30. Literature-reported SNR values for the b = 0 s/mm² image in normal liver parenchyma range from 14.0 – 84.8 (6,18–21). An SNR of 30 was chosen as the majority of studies reported SNR around this value. Previous work has shown MRI magnitude images with low SNR (SNR < 2) are governed by a Rician, not Gaussian, noise distribution (22). Noise distributions were shown to be nearly Gaussian for SNR > 2 (22). For the simulations undertaken in this study, the SNR of the b = 800 s/mm², D_p = 100 μm²/ms image (i.e. the image with the lowest SNR) was 8.7. Therefore, we contend that the use of a Gaussian noise model was appropriate.

This study also showed relatively high pseudodiffusion repeatability (low CV) for b-value distributions both including b = 10 and 25 s/mm² and those without b = 10 and 25 s/mm². The CV values ranged from 10% for the voxelwise mean of the parameters to 28% for the case of the average signal within an ROI. These values are lower than those reported in the literature. For example, Patel et al. used an ROI based analysis method and found a mean CV of 24% in five subjects who underwent free breathing DWI, navigator triggered DWI or a combination of the two (3). One study found a pseudodiffusion CV of 59% for RT-DWI (14), while another found pseudodiffusion CV ranging from 30 to 56% for FB and RT sequences with varying diffusion gradient polarity (6). Repeatability was calculated using voxelwise mean and median values or calculated using the averaged signal. The pseudodiffusion parametric maps themselves, though improved, still look noisy relative to the fractional perfusion and molecular diffusion maps and may therefore benefit from even more averaging and/or better respiratory triggering techniques. One recent paper used a data driven Bayesian modeling approach and achieved vastly improved parameter maps (23). Despite the extra processing time, these results suggest the voxelwise mean should be used when comparing scans across time.

Furthermore, no marked decrease in repeatability was seen when b = 10 and 25 s/mm² were included in the distribution. This is in disagreement with simulations that predicted a reduction in error when more low b-values were included, which would imply an increase in repeatability. One explanation for this discrepancy is that a larger range of pseudodiffusion values could be distinguished when fitting data obtained with b-value distributions containing more low b-values. This leads to higher variability in pseudodiffusion values and thus could lower repeatability. Despite the similar CV, there were far less outliers when b = 10 and 25 s/mm² were included in the distribution compared to when they were not. This is evident in the parametric maps shown in Figure 2.

Food intake was not controlled for in this study. Portal venous blood flow is known to increase postprandially, and could potentially increase D_p values. However, since D_p comparisons were made between different b-value combinations within the same scans, and not between subjects, these effects should be minimal in this study. Food intake may also have negatively affected repeatability. Since repeat scans were done shortly after initial scans, these effects should also be minimal.

Another potential issue in this analysis is bias from large blood vessels. Voxels that contained a sharp drop off in signal at low b-values tended to have ill-conditioned Jacobian matrices that would be excluded from further analysis when fit with a b-value distribution with no b-values between 0 and 50 s/mm². These same voxels fit with a b-value distribution that included b = 10 and 25 s/mm² resulted in more accurate fits and reasonable pseudodiffusion values. To account for this potential bias, the data was masked by the D_p map with no b-values between 0 and 50 s/mm². Thus, only voxels that were not outliers for both b-value distributions were included in the analysis. Including all non-outlier voxels for both distributions still resulted in significantly different pseudodiffusion values. Mean pseudodiffusion calculated from a b-value distribution that included b = 10 and 25 s/mm² and all non-outlier values was higher than the mean pseudodiffusion calculated from the same b-value distribution when voxels were limited to just those that were non-outliers when no b-values between 0 and 50 s/mm² were included in the distribution.

Additionally, studies have shown decreased D_p in cirrhotic patients compared to controls (3,4). Luciani et al. found D_p values around 60 μm²/ms in cirrhotic livers (4). Simulation results from the current study suggest this value is high enough to be underestimated by a b-value distribution with no b-values between 0 and 50 s/mm².

Finally, the b-value distribution is not the only thing that can be different between IVIM studies. Other issues include the use or non-use of respiratory or navigator triggering, the effect of diffusion direction, ROI versus voxelwise analysis techniques, and IVIM fitting technique. IVIM fitting can be accomplished using the segmented or full models. This study used respiratory triggering, diffusion in all three directions simultaneously (3in1), both voxelwise and ROI based analysis techniques, and the segmented IVIM fitting model.

In conclusion, this study showed pseudodiffusion in the liver tends to be underestimated when very low b-values (0<b<50 s/mm²) are excluded from the distribution. Therefore it is recommended to include at least two very low b-values when performing liver IVIM studies.