Remembering Complex Objects in Visual Working Memory: Do Capacity Limits Restrict Objects or Features?

Abstract

Visual working memory stores stimuli from our environment as representations that can be accessed by high-level control processes. This study addresses a longstanding debate in the literature about whether storage limits in visual working memory include a limit to the complexity of discrete items. We examined the issue with a number of change-detection experiments that used complex stimuli which possessed multiple features per stimulus item. We manipulated the number of relevant features of the stimulus objects in order to vary feature load. In all of our experiments, we found that increased feature load led to a reduction in change-detection accuracy. However, we found that feature load alone could not account for the results, but that a consideration of the number of relevant objects was also required. This study supports capacity limits for both feature and object storage in visual working memory.

Working memory (WM) is a capacity-limited store for information that is actively in use or which must be maintained over a short interval (Baddeley, 2003; Cowan, 2001). One concern of WM researchers has been to specify how the constituent features of objects are integrated in visual WM into coherent internal representations of the external objects (Fougnie, Asplund, & Marois, 2010; Luck & Vogel, 1997; Treisman, 1988; Wheeler & Treisman, 2002). This study is primarily focused on the issue of whether there is a cost to processing (encoding, storing, and/or retrieving) stimuli for which there is a high feature load. In an influential study, Luck and Vogel manipulated feature load by varying the number of task-relevant features of the stimulus objects. Their finding was that no loss in accuracy resulted from an increase in feature load. We are following up on this result due to a number of results in the literature that find an effect of feature load on accuracy (Alvarez & Cavanagh, 2004; Cowan, Blume, & Saults, 2013; Delvenne & Bruyer, 2004; Fougnie et al., 2010; Oberauer & Eichenberger, 2013; Wheeler & Treisman, 2002).

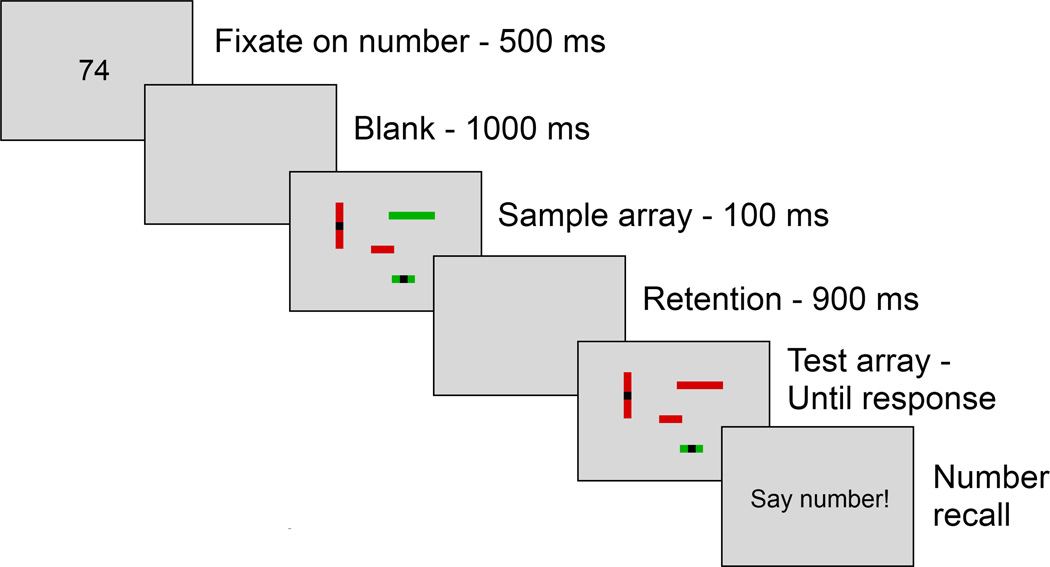
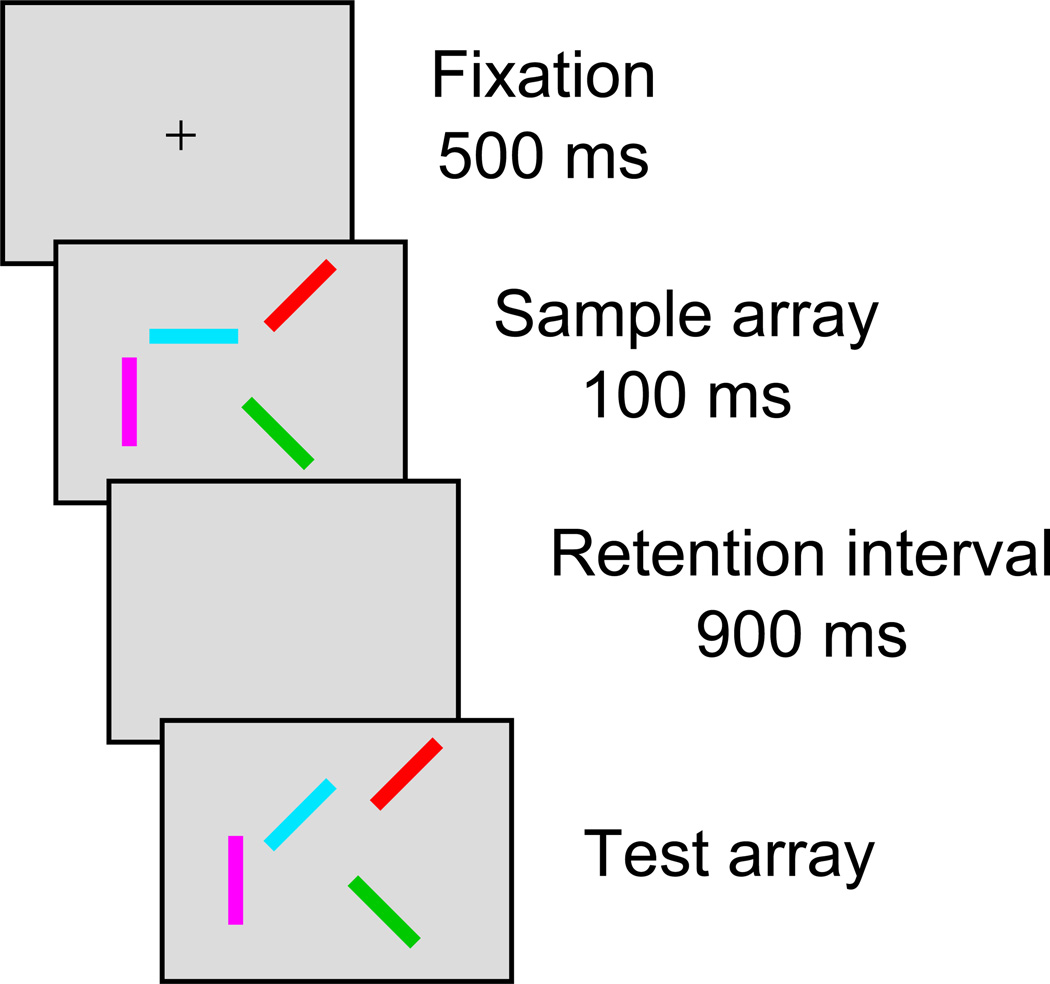
In this study, we will use the change-detection paradigm to measure our participants’ memory abilities (Luck & Vogel, 1997; Wheeler & Treisman, 2002). In the change-detection paradigm, participants are presented with a sample array of visual objects which must be retained in memory for a brief interval before a test array (or sometimes a single test object) is presented. The participant is required to respond to the test array by indicating whether or not anything has changed between the sample array and the test array. We are primarily focused on a particular experiment performed by Luck and Vogel in which objects possessed four features: length, orientation, color, and the presence or absence of a black "gap" in the middle of the object (this experiment was republished as Experiment 14 in Vogel, Woodman, & Luck, 2001 with additional methodological information; see Figure 1 for an example of the stimuli). In some conditions of their experiment, participants were informed that only one of the features could change between the sample and test arrays (which we term the "single-feature" conditions in this study). For example, in the color single-feature condition, only the color of the objects was allowed to change. In the critical multi-feature condition, participants knew that any of the features of the objects could change. The difference between the single- and multi-feature conditions is strictly in terms of feature load: the number of objects is held constant.

Figure 1.

An example of a single trial in Experiment 1. Each trial began with a two-digit number that participants were instructed to remember. Then a sample array of visual objects was presented. The objects were rectangular bars which possess a color, orientation, length, and the presence or absence of a black gap in the middle of the bar. Following a brief retention interval, participants were shown a test array of objects in which one of the features of one of the objects may have changed from its value in the sample array. In this example, one of the rectangles changed from green to red, so the participant should say that there was a change. After making their response to the test array, participants spoke the number they were remembering from the beginning of the trial.

The striking result that Luck and Vogel (1997) found was that there was no difference in accuracy between the multi-feature condition and any of the single-feature conditions. This finding was important evidence for the argument that the features of an object are effortlessly bound to the representation of that object without any cost for additional features (Luck & Vogel, 1997; Zhang & Luck, 2008). The model that came out of this finding is often described as the slot model of WM, in which visual WM has a limited number of slots, each of which can be filled with a single object until there are no more slots available (Zhang & Luck, 2008). The results of Luck and Vogel have often been used as evidence that coherent objects with strongly integrated features are the sole limiting factor of storage in WM, with the implication that the number and/or complexity of the features which make up an object can be ignored when interpreting results because – although it possesses multiple features – a multi-featured object still only takes up one object slot in WM. Based on the results of Luck and Vogel, it seemed clear that objects were the sole limiting factor of storage in WM and that feature capacity was very high – potentially unlimited.

Although the results of Luck and Vogel (1997) are very striking, they are not without controversy. Both Wheeler and Treisman (2002) and Delvenne and Bruyer (2004) failed to replicate the results of one of the feature-conjunction experiments of Luck and Vogel (1997) in which bicolored squares were used, with feature load manipulated by requiring participants to attend to either one or both of the colors of each object. Although Luck and Vogel found no difference in accuracy whether participants were held responsible for one or both of the colors of each square, Wheeler and Treisman and Delvenne and Bruyer both found a deficit when both colors of each square were needed. Thus, it seems that there is support for a feature load effect in the case of objects possessing two features from the same feature dimension.

The present study examines the somewhat different situation in which the features of the objects are drawn from different dimensions (e.g. objects have a color and an orientation). In this particular area, there have been a number of studies using different methodologies which have found costs related to feature load (Alvarez & Cavanagh, 2004; Cowan et al., 2013; Fougnie et al., 2010). These results suggest that even if the results of Luck and Vogel replicate, they may not generalize to other experimental conditions that are theoretically equivalent.

Importantly, we know of no experiments which have attempted a direct replication of a critical result of Luck and Vogel (1997), in which objects possessing four features drawn from different feature dimensions resulted in equivalent accuracy regardless of the number of the features that participants were required to remember. A recent addition to the literature explored tasks in which participants were required to store multiple features per object, including objects with four features (Oberauer & Eichenberger, 2013). In that study, the authors found that accuracy in a change-detection task decreased as the number of relevant features of the objects increased. This decrease in accuracy occurred even when the number of relevant features increased from one to four features. Although Oberauer and Eichenberger included in their manipulations conditions very similar to those used by Luck and Vogel, the visual stimuli and methodology differed in some important ways between the experiments, preventing Oberauer and Eichenberger from being considered a direct replication.

Given the recent focus on problems with replicability of results in psychology (Pashler & Wagenmakers, 2012), another attempt to replicate the results of Luck and Vogel seems warranted. If the results of Luck and Vogel can be replicated, we could examine what attributes of their methods allowed them to obtain such a result while others could not with different methods. If the boundary conditions in which Luck and Vogel were able to find their results could be determined, that knowledge could inform some theoretical aspects of WM.

We are interested in the question of whether visual WM is limited solely by the number of objects that can be held, or if it is also limited by the complexity of these objects (operationally defined as the number of features of the object that must be known in order to perform perfectly on the task). If fully-integrated objects are the sole limiting factor of storage in WM, it would be expected that, as long as the number of objects in the array is the same, participant accuracy would not vary with the number of features they are required to remember, which was the result observed by Luck and Vogel (1997). In that study, no differences in accuracy were found between the single- and multi-feature conditions or between any of the single-feature conditions. If object complexity (i.e. feature load) matters, it would be expected that accuracy would decrease as feature load increases.

We tested these predictions by attempting a direct replication of the four-feature experiment of Luck and Vogel (1997), which we did in Experiment 1. As far as we could ascertain, this experiment used the same change-detection task, stimuli, timings, and secondary verbal load task as the original experiment. Then in Experiments 2 through 6 we performed several confirmatory experiments using the same stimuli in order to rule out effects of a variety of nuisance variables that could have explained our results. Finally, in Experiments 7 and 8 we attempted to extend our findings to somewhat different stimuli by attempting to replicate the results of another feature-conjunction experiment of Luck and Vogel.

Experiment 1

This experiment was our best attempt to perform a direct replication of the four-feature experiment performed by Luck and Vogel (1997; see also Experiment 14 of Vogel et al., 2001 for additional methodological detail). We made a serious effort to perform an accurate replication and believe that the only methodological discrepancies are minor. One potentially important methodological uncertainty, regarding the luminance of the background, was further investigated in Experiment 4. The discrepancies of which we are aware are discussed.

Method

The experiments reported in this article involve a change-detection procedure with a number of methodological features in common, for which reason some statements about general methodological details are made in this section. Most of the experiments hew closely to the method of this first experiment and details specific to each experiment are described in that experiment’s method section.

Participants

Participants were recruited from introductory psychology courses at the University of Missouri – Columbia campus and received partial course credit for participation.

For all of the experiments in this study, participants were removed from the sample if their accuracy fell below 55% on at least one trial block. This criterion was designed to remove participants who were performing near chance in at least some conditions. The focus on individual blocks was decided on because while overall accuracy on the tasks tended to be relatively high, there was a distinct pattern of accuracy in many participants’ data that seemed to indicate that those participants were not making an attempt to perform the task to the best of their abilities in a consistent manner (i.e. very good performance on some trial blocks while performance on other trial blocks was very near chance level). This pattern generally involved at least one trial block on which accuracy was very near chance, which informed our use of the 55% cutoff.

For this experiment, two participants were removed for meeting this low accuracy criterion. An additional participant was removed for having a very high error rate on the secondary verbal load task (37% of their responses were errors compared with a 6% overall average error rate). This left 19 participants (12 female; mean age 19.3) who were used in the analysis.

Materials

The experiments were performed using E-Prime 2 experimental software (Psychology Software Tools, Pittsburgh, PA) on PCs using CRT monitors set to a resolution of 1024 × 768 pixels. For this experiment, the monitor used a refresh rate of 75 Hz. Given that the monitor’s refresh period was 13.3 ms, it was not possible to use presentation times in increments of 100 ms as used in the original experiment. The most important timing difference was that the sample array was presented for only 93.3 ms. However, because each participant was presented with every combination of conditions, there is little potential for this presentation time difference to affect the differences between conditions, although overall accuracy may be slightly shifted. In all other experiments, the refresh rate of the monitors varied between 60 Hz and 75 Hz. Again, because each participant completed all conditions on a single computer, there is no potential for the conditions to be differentially affected by the variations in refresh rate. In the procedure section, nominal presentation durations – as would have been achieved by 60 Hz monitors – are given.

In each trial, participants were presented with a sample array of 2, 4, or 6 visual objects about which they would be tested later. The objects possessed four features: orientation (vertical or horizontal), color (red or green), length (short or long), and the presence or absence of a black "gap" in the middle of the rectangle. The objects were rectangles with a length of 2.0° (long objects) or 1.0° (short objects) and a width of 0.15° of visual angle. The gaps were the same width as each object and 0.25° long. Objects were separated by at least 2.0° of visual angle center-to-center to reduce the chance of objects touching. The objects were presented in an area of the screen taking up 9.8° (horizontal) by 7.3° (vertical).

The colors of the objects will be reported as an ordered triple of the red, green, and blue components of the colors, which were 8-bits per component and so varied from 0 to 255 for each component, where a higher number indicates a greater amount of that component. In all experiments the background on which the objects were presented was a shade of grey and the gaps in the objects were always the darkest black that the monitors we used were able to display (RGB: 0, 0, 0). For this experiment, the background was a light grey (214, 214, 214) and the objects were either red (255, 21, 37) or green (66, 181, 70). These values were identical to those used in Figure 1 of the digital version of Luck and Vogel (1997). However, as reported in Vogel et al. (2001), originally the background was a dark grey with luminosity 8.2 cd/m². We had not noticed this difference until after this experiment was performed. When measured on a representative monitor used for experiments in our lab using a TSL2561 luminosity sensor (Texas Advanced Optoelectronic Solutions, Plano, TX), the luminosity of the background used in this experiment was 123 cd/m², which was much brighter than the value reported by Vogel et al.. In Experiments 4 and 5, we used a darker background and found no meaningful effect of background luminosities on the results.

A sample array and a test array of visual objects were presented on each trial (see Figure 1). The test array was identical to the sample array on half of the trials. On the other half of the trials, a single feature of a single object was changed to a different value. For some trial blocks, only one of the four features was allowed to change (single-feature blocks). In the critical multi-feature block, any of the features were allowed to change, but it was still the case that only one feature of one object was allowed to change on any given trial. Object location was held constant between sample array and test array.

Procedure

Participants were tested in a sound-attenuated booth under observation of an experimenter who read the instructions for the task to the participant. Once participants had completed the first set of practice trials, the experimenter left the booth and monitored the rest of the session by way of a video camera and microphone in the booth. The instructions fully informed the participants about the rules governing the presentation of stimuli in order to assist them to perform optimally.

To begin each trial, participants fixated on a two-digit number presented centrally for 500 ms before the screen was blanked for 1000 ms. Then the sample array was presented for 100 ms before the screen was again blanked for 900 ms. After this retention interval, the test array was presented until participants made a same/different response by pressing "S" or "D" on a standard US keyboard. After giving their response, participants were cued to say the number they had seen at the beginning of the trial, with responses coded correct or incorrect by the experimenter. This secondary verbal load task was intended to prevent verbal recoding of visual stimuli. The effect of this verbal load task is further examined in Experiment 2. The procedure for a single trial is shown in Figure 1.

The presentation of the test array in this experiment was slightly different than the presentation used by Luck and Vogel (1997). In their experiments, the test array was removed after 2000 ms, but the participant was still required to make a response. In all of our experiments, the test array was presented until a response was made. This is very unlikely to have had any effect because in this experiment only 6% of response times were longer than 2000 ms. This percentage was similar across our experiments.

Participants performed four single-feature trial blocks and one multi-feature trial block, the order of which was counterbalanced across participants using a Latin square. Each trial block began with a screen of instructions indicating which feature (for the single-feature conditions) or features (for the multi-feature condition) of the objects should be attended in the coming trial block. Upon reading the instructions and indicating their intent to continue, participants were given six practice trials after which they were presented with an indication that they had finished the practice trials and were starting the main block. Within a trial block, the number of objects in the arrays varied unpredictably from trial to trial but there were always the same number of trials at each array size. In this experiment, there were 96 trials per trial block, 32 trials at each of the three array sizes. For all experiments, each participant’s experimental session lasted no more than one hour.

Results

In keeping with the data analysis procedure of Luck and Vogel (1997), we removed trials on which the spoken number was incorrect, which resulted in the removal of 6% of trials.

The data were analyzed in order to determine how accuracy changed as a function of the number of features and objects that were relevant to the task, where number of relevant features and objects were treated as continuous independent variables rather than categorical variables. Using linear regression gives us more information than a standard ANOVA, because in addition to informing us about the existence of object and feature effects, linear regression allows us to directly compare the magnitude of the object and feature effects, whereas ANOVA would simply note the existence of such effects. This analysis was performed using a Bayesian regression technique provided by the BayesFactor package (R. D. Morey & Rouder, 2013) for R (R Core Team, 2013). In the analysis, proportion correct was predicted based on object count and feature count fixed effects, plus a random effect for participant. Treating participants as random effects makes this a within-participants regression. For the single-feature conditions, object count and feature count were both equal to the array size. In the multi-feature condition, object count was the array size and feature count was four times the array size. Three models were estimated: a full model with effects of both object count and feature count and two reduced models, one with an object count effect and the other with a feature count effect. The full model is

$${\widehat{A}}_i=\alpha +F{\beta }_F+O{\beta }_O+{\pi }_i$$

where Â_i is the predicted accuracy for the i^th participant, α is the intercept, F is the number of features, β_F is the feature effect, O is the number of objects, β_O is the object effect, and π_i is the participant effect for the i^th participant. The reduced models lack either the Fβ_F term or the Oβ_O term.

The full model was compared with both reduced models in order to determine if there was sufficient evidence to support the full model over each of the reduced models. This model comparison allows us to determine if we can account for the data by only using information about the number of relevant objects or features alone, without incorporating both object count and feature count into the model. The result of a model comparison is a Bayes’ factor (BF), which provides an indication of which model is preferred. For these comparisons, the full model was in the numerator of the ratio, which means that a BF greater than 1 is evidence for the full model. For this experiment, the full model was clearly preferred to both the reduced model with only an object effect (BF_FR = 3.86 * 10⁶) and the reduced model with only a feature effect (BF_FR = 1.25 * 10⁵). The subscript FR indicates that the Bayes factor is for the full model (F) over the reduced model (R).

Given that the full model is preferred, estimates for the change in accuracy as a function of object and feature count are drawn from the full model. These estimates were obtained by taking the mean of 1,000,000 samples drawn from the posterior distributions of the object and feature count parameters (using the "posterior" function of the BayesFactor package), yielding an object effect of −0.0287 (β_O in the above equation) and a feature effect of −0.0070 (β_F in the above equation). These values can be thought of as the slope of accuracy versus object count and feature count: if one object is added, accuracy decreases by 2.87% and if one feature is added, accuracy decreases by 0.70%. The estimates for these effects are reported, along with the model comparison BFs, for each experiment in Table 1. This table also includes a brief summary of the defining characteristics of each experiment.

Table 1.

Experiment Descriptions and Primary Results

Experiment number and description	Object BFaFR	Feature BFbFR	Object slope (%)c	Feature slope (%)d
1: Direct replication of four-feature experiment of Luck and Vogel (1997).	3.86 * 106	1.25 * 105	−2.87	−0.70
2: Same as 1, except no verbal suppression task.	4.91 * 1012	3.01 * 106	−3.14	−0.99
3: Same as 2, except 500 ms sample array presentation.	3.02 * 108	6.06 * 102	−2.11	−0.78
4: Same as 2, except different stimulus and background colors.	6.49 * 109	6.82 * 105	−2.76	−0.79
5: Same as 4, except only a single object was tested.	4.80 * 1011	7.05 * 107	−2.92	−0.79
6: Similar to 5, but participants were cued to specific features of the objects.	3.59 * 1011	2.31 * 103e	−3.09	−0.39e
7: Similar to 2, except that objects only had a color and orientation.	1.75 * 100	5.88 * 104	−2.83	−0.62
8: Same as 7, except that color and orientation were matched in difficulty.	6.02 * 103	3.57 * 1015	−3.40	−0.85

The full model is Â_i = α + Fβ_F + Oβ_O + π_i; see the results section of Experiment 1 for explanation of all the parameters.

^aBayes factor (BF) of model with both feature and object effect over model with only a feature effect. The FR subscript indicates that the BF is for the full model over the reduced model.

^bSame as ^a, but over model with only an object effect.

^cEstimate of change in accuracy with the addition of one object (in percent; β_O).

^dSame as ^c, but change in accuracy with addition of one feature (β_F).

^eFor this experiment, the Feature BF and Feature slope refer to the effect of relevant features at encoding, not including the effect of relevant features at test.

Implicit in the design of this statistical analysis is the fact that the single-feature conditions are collapsed together because they all share identical object and feature counts. Thus, the evidence that accuracy decreases with the addition of more relevant features is equivalent to there being a difference in accuracy between the average of the single-feature conditions and the multi-feature condition. Still, in order to clearly show the discrepancy from the statistical result of Luck and Vogel (1997), for this experiment we performed a 5-way univariate within-participants ANOVA on the attended feature conditions (i.e. an ANOVA on the four single-feature and one multi-feature trial blocks). This analysis showed a main effect of attended feature condition, F(4, 72) = 21.94, MSE = 0.0169, p < .001, ${\eta }_p^2=.55$, which goes against the failure to reject the null hypothesis reported by Luck and Vogel.

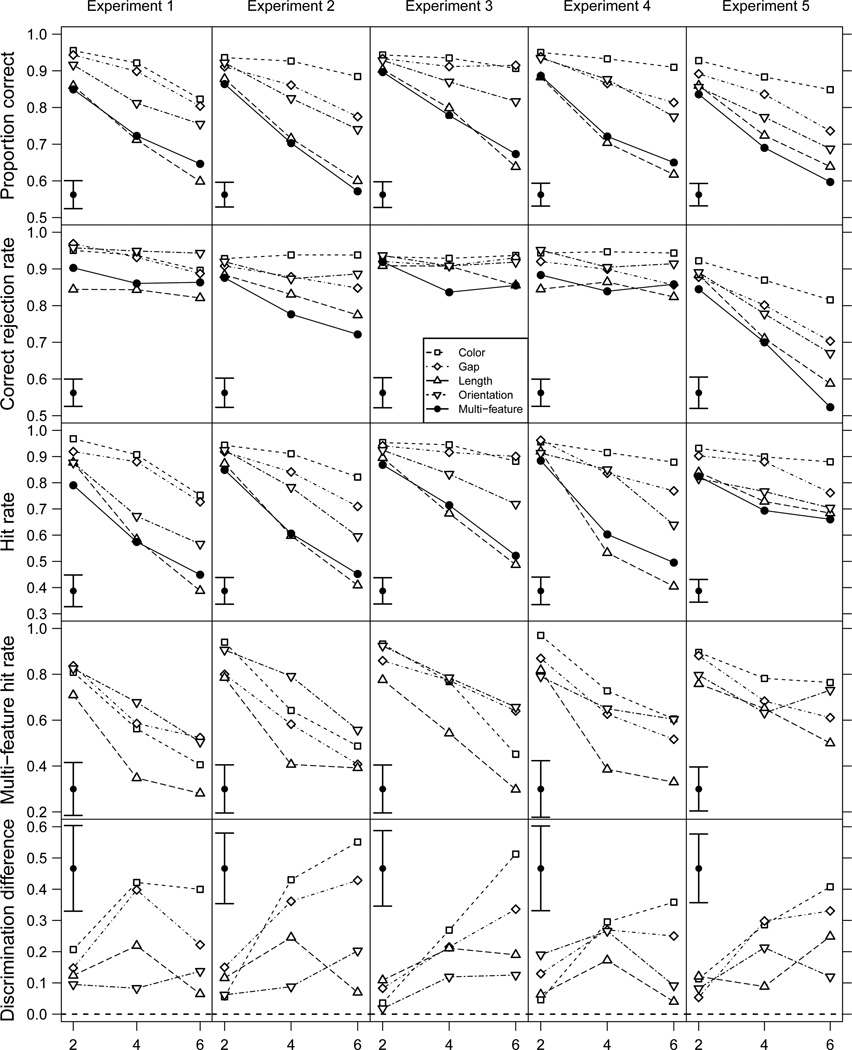
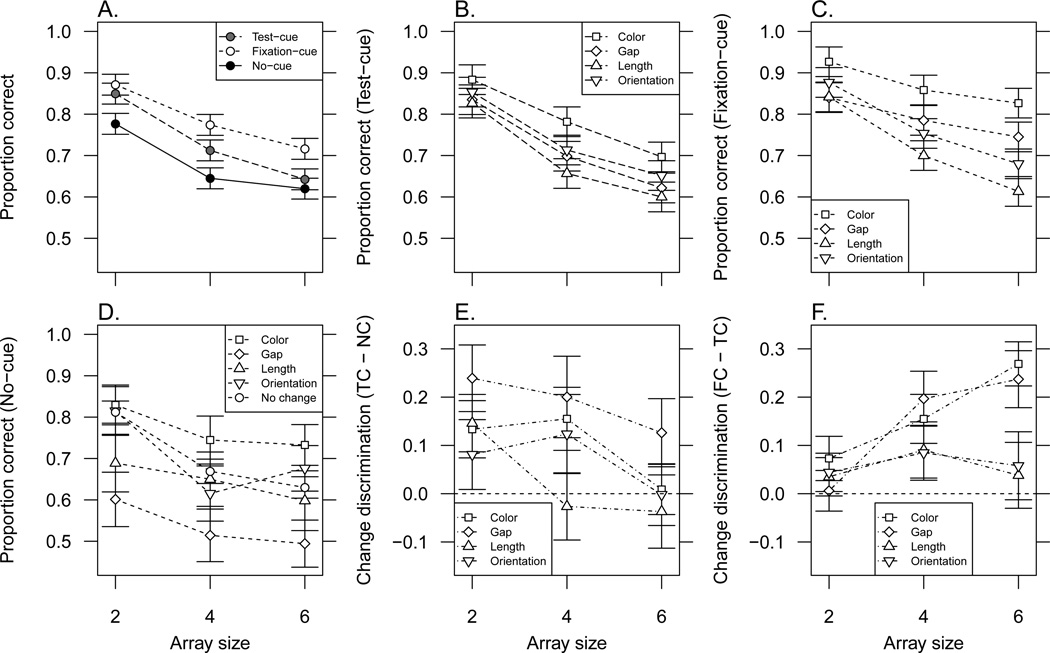
The data for this experiment are visually summarized in Figure 2. Because most of the experiments in this study are very similar in design, Figure 2 shows the data from several experiments in a standardized form. The data are presented in several ways. All dependent measures are plotted as a function of array size and grouped by some feature condition. For each experiment, proportion correct, correct rejection rate, and hit rate are plotted for each attended feature condition. Additionally, within the multi-feature condition, hits for trials on which there was a change are grouped by which feature changed. Finally, a compound measure of the difference in the ability to detect changes when accounting for response bias is used to compare each single-feature condition and the corresponding feature within the multi-feature condition.

Figure 2.

Plots of data from Experiments 1 to 5. Array size is plotted on the X-axis. Rows of panels, from top to bottom, show overall proportion correct on the task, correct rejection rate, hit rate, hit rate for each feature within the multi-feature condition, and change discrimination difference for each feature (see the results section of Experiment 1 for more detail). Note that the scale of the Y-axis varies. In a corner of each panel is an error bar showing a 95% repeated measures confidence interval (see Hollands and Jarmasz, 2010 for a summary of the method) that applies to each data point in the panel. The legend applies to all panels in the figure.

The compound measure was calculated in the following way: In each single-feature condition, the hit rate minus the false alarm rate was calculated, giving the single-feature change discrimination. Then, within the multi-feature condition, the hit rate for each single feature minus the overall false alarm rate was calculated (note that there are no false alarms for any given single feature because if no change occurs, it is not possible to assign the response to that trial to a specific feature). Finally, the difference between the single-feature change discrimination and the multi-feature change discrimination was taken and plotted. This compound measure is labeled "Discrimination difference" in the figure.

The logic behind examining the discrimination difference is as follows. For full array change detection tasks, the trade-off between hits and false alarms (receiver operating characteristic or ROC) is known to be linear (Rouder et al., 2008). Consequently, by taking the difference between the hit rate and the false alarm rate, any difference in response criterion between attended feature conditions is subtracted out, leaving only the participant’s change discrimination ability. Taking the difference in discrimination between each single-feature condition and the corresponding feature in the multi-feature condition, it can be seen for each feature if there was a deficit in discrimination for that feature in the multi-feature condition relative to the single-feature condition. If the discrimination difference is positive, it means that participants were better able to discriminate between change and no change trials for that feature in the single-feature condition than in the multi-feature condition.

In order to make it possible to find evidence for the null hypothesis that the discrimination difference was zero, we used a Bayesian t-test (Rouder, Speckman, Sun, Morey, & Iverson, 2009) for each feature collapsed across array sizes. For the Bayes factors that are reported, the alternative hypothesis was in the numerator for the model comparison, which means that Bayes factors greater than one are support for the existence of a discrimination difference not equal to zero. In this experiment, there was evidence that the discrimination difference was greater than zero for color (1.94 * 10⁴), gap (85.5), and length (5.75). There was a small amount of evidence that the discrimination difference was zero for orientation (0.67), although a BF this close to 1 is not very strong evidence for either hypothesis. Results of the discrimination difference tests for all experiments are reported in Table 2. The discrimination difference results are not necessarily reported in the results section of each experiment individually. A summary of the discrimination difference results is provided in the discussion of Experiment 8.

Table 2.

Bayes factors for change-discrimination difference for each feature versus null model of no difference.

Experiment	Color	Gap	Length	Orientation
1	1.94 * 103	85.5	5.75	0.67
2	2.40 * 104	50.0	12.8	13.0
3	2.02 * 104	8.13	10.4	2.91
4	472	67.9	0.59	5.99
5	1.71 * 104	107	22.5	5.02
6 (FC - TC)a	4.21 * 104	175	0.92	0.92
6 (TC - NC)b	23.3	89.7	0.28	0.48
7	0.64	N/A	N/A	0.88
8	38.5	N/A	N/A	12.2

^aFixation-cue minus test-cue.

^bTest-cue minus no-cue.

Discussion

The results of this experiment were clearly dissimilar from those of Luck and Vogel (1997), who found no effect of feature load. Using the same stimuli and methods as the original experiment, we found a clear effect of feature load. We cannot attribute our failure to replicate Luck and Vogel to our choice of statistical techniques because when we performed the same statistical analysis on our data as was performed by Luck and Vogel, we obtained a result that was incompatible with theirs. This result contradicts the results of Luck and Vogel and contradicts the hypothesis that visual WM always stores the same number of objects with all of the features of those objects intact. At the same time, we also found support for the importance of object load to performance. We do not have any interest in arguing against the importance of objects, just in showing evidence for the importance of features. In fact, our estimated object load effect is larger than the feature load effect.

Because we used a linear regression approach with both object and feature effects in the model, our analysis examined the effect of object load while statistically controlling for feature load. Our results showed that it does not seem to be possible to support the idea that feature load by itself is able to fully account for accuracy in our task. This is in contrast to the finding of Wheeler and Treisman (2002) that object load does not affect accuracy if feature load is equated. One plausible reason for the difference in findings is that the experiment in which Wheeler and Treisman obtained their result differed meaningfully from ours in that their objects possessed two different colors. In our experiments, the features of each object are drawn from different feature dimensions. By drawing features from the same feature dimension, they may be examining a different effect than we are. What we can say is that it may not be generally true that feature load can wholly account for performance in WM tasks.

Our analysis leaves open the possibility that there is a separate capacity limit for each type of feature. It is possible that in the multi-feature condition at array size two, participants are able to fill all four feature-specific stores with a small amount of information relative to the capacity of the stores. On the other hand, in the single-feature conditions they may run out of storage for that particular feature, resulting in poorer performance in the single-feature conditions. This possibility could explain why we did not find the same substantial result as Wheeler and Treisman (2002). In their task, participants would have had to fill the same feature store (color) in both the single- and multi-feature conditions, which could result in equivalent performance regardless of object load if the color store was fully filled at the smallest array size.

One visually striking result is the apparent equivalence in proportion correct between the multi-feature condition and the length condition, which can be seen in the top row of Figure 2. If those conditions are in fact equally difficult, one interpretation is that performance in the multi-feature condition is limited by the most difficult single feature of the objects. One reason why we think the weakest link interpretation is wrong is our change discrimination difference analysis. We found reasonable evidence that the change discrimination difference for length was not zero, which indicates that there was a loss in the ability to detect length changes in the multi-feature condition relative to the length single-feature condition. This goes against the weakest link hypothesis, because performance for the weakest link should not be able to go down in the context of other features. Additionally, in Experiment 8 we found that the multi-feature condition was more difficult than either of the single-feature conditions, which was caused by adjusting the relative difficulties of the individual features.

It is not clear to us why our results were discrepant from those of Luck and Vogel. We made every attempt to bring our methods in line with those reported by Luck and Vogel, even extracting additional methodological detail from Vogel et al. (2001). Over the next several experiments, we attempt to replicate our own result using a variety of minor (and major) changes to the method in order to rule out the possibility that we obtained an unusual sample in this experiment or that there was an error in our methods that caused us to obtain results discrepant from the results of Luck and Vogel.

Experiment 2

The purpose of this experiment was to determine if the verbal load task has a meaningful effect on accuracy in this particular task. Research by C. C. Morey and Cowan (2004) showed that secondary verbal loads consisting of two digits do not have an effect on accuracy in visual WM tasks similar to those used in this study. However, C. C. Morey and Cowan did not investigate how verbal load affected accuracy in a task that used visual objects with multiple features. Multi-featured objects in visual WM may be affected differently by secondary verbal loads than simple, single-featured objects. If this is the case, the choice to use secondary verbal loads and the nature of those loads must be carefully considered for these confirmatory experiments. If not, the use of such a task may be discontinued.

This experiment differed from Experiment 1 by the removal of the verbal load task. Instead of fixating on a number, participants in this experiment fixated on a small cross in the center of the screen. The blank interval following fixation in Experiment 1 was important as it allowed time for participants to begin passively rehearsing the number. Because this experiment had no such secondary task, this blank interval was removed in order to increase trial density. As the results will show, this manipulation had no meaningful effect on the pattern of results. Because no secondary task was used, there was no need for an experimenter to monitor participants during their session, so the monitoring was discontinued for this and all following experiments. In this experiment, participants performed 120 trials per attended feature condition for a total of 600 trials. In this experiment, data from 16 new participants (10 female, mean age 18.6 years) drawn from the same population of those in Experiment 1 were used.

The data from this experiment are plotted in Figure 2. As in Experiment 1, the full model with both object and feature effect was strongly supported over either reduced model (see Table 1 for model comparison results and slopes). To test whether the slopes of the object and feature effects were the same between this experiment and Experiment 1, some between-experiment models were compared. A between-experiments full model was created that had the same object and feature effects as the standard full model. In addition, the between-experiments full model also had a categorical effect for experiment (with two conditions, one per experiment) and interaction terms for experiment by object and experiment by feature. This model was compared with two between-experiments reduced models that lacked either the object by experiment interaction term or feature by experiment interaction term. If the slopes of the object or feature effects differ between the experiments, then we would expect the corresponding interaction term to substantially improve the fit of the model to the data. In that case, the model with the interaction term should be preferred to the model without the interaction term. The reduced model without the object by experiment interaction term was preferred over the full model (BF_RF = 10.7), suggesting that there was no meaningful difference in the object effect between experiments. The reduced model without the feature by experiment interaction term was marginally preferred to the full model (BF_RF = 1.79). This suggests that for the feature effect there was no difference between experiments, although this result is nearly equivocal about the existence or non-existence of a difference. This analysis suggests that if there are differences in slopes observed between this experiment and Experiment 1, they are too small to be easily detected, but the evidence is against a difference.

This result indicates that there is no clear reason to continue using the verbal load task in its current form in this type of experiment, as it does not seem to have an effect on the parameters of interest. We have chosen to discontinue the use of such a task for further experiments in this study. Although we had the option of increasing the verbal load and examining the effects of such a manipulation, we chose instead to neglect the contributions of verbal memory for this set of experiments with the possibility of continuing this line of research in the future. Due to the rapid presentation of stimuli and short maintenance period, it is questionable if verbal recoding is generally an effective strategy at all. It is even more questionable whether any advantage in accuracy achieved through verbal recoding would be worth the cost of the additional effort required in order to enact such a strategy.

Experiment 3

The purpose of this experiment was to determine what effect sample array presentation time has on the pattern of results we have observed so far. Although sample array presentation time was previously ruled out by Luck and Vogel (1997) as an important contributor to accuracy, because of the striking differences between our results and theirs we were interested to see what effect it might have on the patterns of results we were obtaining.

The relationship between accuracy in the multi-feature condition and the most difficult single-feature condition (length) might be explained by the results of Vogel, Woodman, and Luck (2006), who found that there was a minimum amount of time needed to consolidate a WM representation. If the amount of time it takes to encode an object is limited by the most-difficult-to-encode feature, it could be that when participants are attempting to encode all the features of each object in the multi-feature condition, their accuracy is limited by the amount of time it takes to encode the lengths of the objects, length being the most difficult single feature in our experiments. If participants are given a much longer encoding time, then encoding should no longer be a bottleneck and accuracy in the multi-feature condition would not be limited by the most difficult single feature if encoding time is in fact a limiting factor of accuracy.

This experiment differed from Experiment 2 by increasing the sample array presentation time to 500 ms. The blank interval between sample and test was maintained at 900 ms. Data from 15 participants (7 female, mean age 20.6 years) were used in this experiment. Three additional participants’ data were removed for failing to meet the single-block accuracy cutoff (less than 55% correct).

As in the previous experiments, the full model with both object and feature effects was strongly supported over either reduced model (see Table 1 for results and Figure 2 for plots of the data). The slopes of the object and feature effects were similar to those found in Experiment 2. When this experiment was compared with Experiment 2 using the same method that was used to compare Experiments 1 and 2, the between-experiments reduced model without an object by experiment interaction term was preferred to the full between-experiments model (BF_RF = 3.81), as was the reduced model without a feature by experiment interaction term (BF_RF = 4.54). Thus, increasing the encoding time fivefold did not meaningfully affect the feature or object effects. The encoding rate suggested by Vogel et al. (2006) was about 50 ms per item, which would mean that a 500 ms encoding interval should be sufficient for encoding enough items to fill the WM of most participants. The fact that we still observe a loss in accuracy with increasing feature count suggests that our pattern of results is not caused by an encoding time bottleneck.

Experiment 4

This experiment was performed in order to determine if the background color on which the objects were presented affected accuracy. As mentioned in the method for Experiment 1, the background colors initially used by us differed from the values reported by Vogel et al. (2001) because we based our color values on a figure in Luck and Vogel (1997). Presumably, the figure was modified for better visibility in a print format and did not reflect the actual color values that were used. The most important difference was that the background color we used for Experiments 1 through 3 was far brighter than was reported in Vogel et al. (2001). We performed this experiment to determine what effect changing the brightness of the background would have. Of primary concern was the ability to distinguish the black gap in objects from the background. With the lighter background colors used in the previous experiments, the gap and background were clearly distinguishable. In this experiment, as in the original experiments (Vogel et al.), it is possible that the gap might not be distinguishable from the background, which would result in participants perceiving objects with gaps as two separate objects. The color values for the red and green objects were also changed somewhat in order to maintain high contrast between the objects and the background.

The method of this experiment was identical to 2 except for which stimulus color values were used. The RGB values of the colors used in this experiment were as follows: background (50, 50, 50), red (255, 0, 0), and green (0, 255, 0). Data from 13 participants (12 female; mean age 18.4 years) who took part in this experiment were used in the analysis. Three additional participants failed to meet the accuracy criterion and their data were removed from the analysis.

As Table 1 shows, the results of this experiment are similar to previous experiments. The slopes of the object and feature effects were similar to those found in Experiment 2. When compare with that experiment, the between-experiments reduced model without an object by experiment interaction term was preferred to the full between-experiments model (BF_RF = 10.6), as was the reduced model without a feature by experiment interaction term (BF_RF = 4.87). The result of this experiment indicates that our results are not dependent on the specific lightness of the background that is used. Of course there still exists the possibility that another color combination would result in a different outcome, but this experiment indicates that our results are not fully stimulus-bound. Moving forward, we will not continue to pursue the issue of background color and will instead focus on how the decision phase of the task might affect our results.

Experiment 5

In this experiment we presented a single object from the sample array as a probe, with a possible change in one feature, rather than presenting the entire array again as a probe with a possible change in a feature of one object. As Luck and Vogel (1997) pointed out, this method limits to one the number of objects for which a decision must be made. Of course, this method still requires decisions about multiple features on a single trial in the multi-feature condition, an issue we will address in the following experiment.

This experiment is identical to Experiment 4 (dark background) except for the way in which participants were tested. In order to present a single object to participants at test, all of the irrelevant objects from the sample array were replaced with a placeholder in that location. This was done by replacing all but one of the objects in the test array with an unfilled white circle in the location of the original objects that were presented in the sample array. The presentation of location information about the irrelevant objects would allow participants to identify the target object in the context of the array. This was important because features were allowed to repeat within a given array, leaving location as the only unique identifier of each object. The single object that was not replaced with a placeholder was the critical object about which a change-detection decision was required. On any given trial, there was a 50% probability that one feature of the critical object would change. Of the 26 participants who participated in this experiment, eight were removed for falling below the 55% single-block accuracy criterion, leaving 18 (10 female; mean age 18.9 years) to be used in the analysis.

As shown in Table 1, the main results of this experiment are very similar to previous experiments. When a between-experiments comparison was performed with Experiment 4, the reduced model without an object by experiment interaction term was preferred to the full between-experiments model (BF_RF = 12.0), as was the reduced model without a feature by experiment interaction term (BF_RF = 12.4).

Although in this experiment there was a constraint on the number of decisions that had to be made, the pattern of accuracy change with features and objects is very similar to all of the preceding experiments. Examination of hits and correct rejections shows that participants were more likely to respond that there had been a change in this experiment when compared with our previous experiments (see Figure 2 for plots of hit and correct rejection rates). This criterion shift can only be attributed to the use of a single-item probe in this experiment (as this was the only change from Experiment 4), so it is not of interest when considering storage processes. Although this experiment reduced the number of decisions participants were required to make, participants were still required to make more decisions in the multi-feature condition relative to the single-feature conditions. As a result, this experiment does not fully control for decision errors and the issue will be explored in more detail in Experiment 6.

Experiment 6

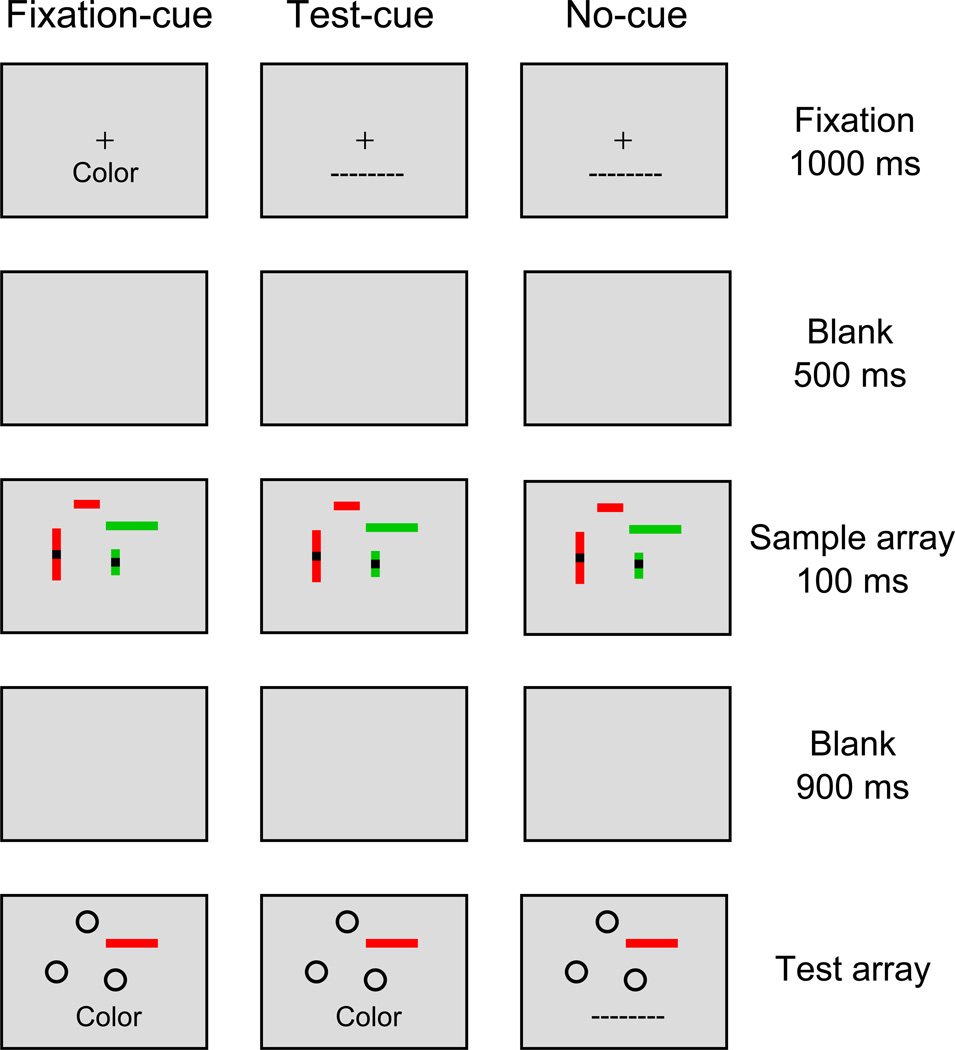
This experiment is intended to extend the results of the previous experiments by presenting a cue to indicate which feature will be tested (see Figure 3). The method is similar to that used by Cowan et al. (2013) in which participants were cued at test to a specific feature dimension in which a change may have occurred. In this experiment we will sometimes present feature cues at test and sometimes before presentation of the sample array, which will allow for a direct comparison of accuracy between conditions in which participants are able to use information about the target feature at encoding versus conditions in which participants are only made aware of the target feature at test. This comparison is a direct test of whether or not objects are the sole limiting factor of storage in visual WM. If objects are the sole limiting factor of storage, there would be no advantage for the condition in which participants are cued before seeing the sample array because the same number of objects would be stored regardless of when the cue is given. However, if objects are not the sole limiting factor of storage, and there is also a limit to the amount of featural information that can be stored, it is expected that selective attention to the target feature at encoding would allow more information about that feature to be stored, resulting in improved accuracy.

Figure 3.

Example of the task used in Experiment 6. The three cuing conditions are demonstrated by showing the combinations of cues shown at fixation and at test for each condition. The post-fixation blank, sample array, and retention interval were the same for each condition.

We have chosen to use a single-item probe as it has the advantage of limiting the number of decisions that a participant must make when giving a response. By cuing both a feature and an item, only a single decision will have to be made at test. A benefit of this design is that it allows us to examine the possibility that the limiting factor in the multi-feature conditions was that participants had to perform a feature-by-feature search of the test array. If participants do not know what feature might have changed, they may have needed to perform a serial search of the test array for a difference from the representation they held, which would result in reduced accuracy if the search was slow enough for the representation to lose fidelity before search terminated. If this were the case, the difference between the single- and multi-feature conditions could have been due to memory search, not storage. In this experiment, because participants are only required to make a single decision about one feature of one object, the differences between test conditions is eliminated. The comparison of conditions which differ in terms of when participants are cued to the target feature will show more clearly the effect of feature load in memory, while controlling for test differences.

Method

Participants

Thirty participants (19 female; mean age 18.4 years) who participated in this experiment were used in the analysis. Two additional participants were removed for falling below the accuracy criterion.

Materials

The stimulus objects in Experiment 6 possessed the same four feature dimensions as in the previous experiments. The colors of the stimuli modified slightly in order to match the colors on luminance. For the red objects, the RGB values were (255, 0, 0) and for the green objects, the RGB values were (0, 246, 0). The L* value in the L*A*B* color space was 80 for both of these colors. Like in Experiment 5, only a single object was presented at test and all other objects were replaced with white (255, 255, 255), unfilled circles (as in Experiment 5; see Figure 3). The background was a medium-dark grey (60, 60, 60).

The placement of the stimulus objects in arrays were changed in order to reduce collisions between objects, with a new distance of 2.25° between the centers of objects. Collisions were possible using the previous settings because although the objects were at most 2.0° long and center-to-center distance was held at 2.0°, the long rectangles were greater than 2.0° long when measured from diagonally opposite corners. This led to some occurrences of slightly overlapping or touching objects in previous experiments which will be impossible in this experiment with the increased center-to-center distance.

Procedure

Once given instructions, participants performed a short practice block of 18 trials with the experimenter observing. The practice trials included two trials with each combination of cued feature and cue presentation point (discussed further below) with array size selected randomly. Participants then completed five trials blocks with rest periods in between. Each trial block had identical instructions and within each block there were trials of each cue type at each array size.

The procedure for this experiment is presented graphically in Figure 3. The sequence of a single trial in this experiment differed from past experiments by the addition of textual cues that indicated which feature was allowed to change on that trial. The feature cues were a single word (e.g., "Color"). If the participant was not cued to a specific feature at a given point, they were shown a neutral cue, which was a series of dashes ("– – – – – – – – – –"). Cues (including neutral cues) were presented 4.65° below the center of the screen at both fixation and test on all trials. Participants were to interpret the cue words as a fragment of the phrase "The [cue word] of this object is ______ " and to fill in the blank by responding "the same" or "different" using the same keys as our previous experiments.

As Figure 3 shows, on fixation-cue trials, participants were presented with a feature-specific cue at fixation, which allowed participants have full knowledge of the feature that would later be tested while they were encoding the test array. These trials were similar to trials in the single-feature trial blocks of our previous experiments in that participants had full knowledge of the target feature throughout the trial. In order to ensure that the cue was not forgotten during the trial, on fixation-cue trials the same cue word that was presented at fixation was always presented again at test. On the test-cue trials, participants were given a neutral cue at fixation but a feature-specific cue at test. This condition, when compared to the fixation-cue condition, will allow us to determine if knowledge about the target feature at encoding causes an change in accuracy, a finding which would not be predicted if objects are the sole limiting factor of storage. Finally, on no-cue trials, participants were given a neutral cue at fixation and another neutral cue at test. This condition is similar to the trials in the multi-feature blocks in prior experiments due to the fact that the participant has no information about which feature might changed. Participants performed 540 total trials divided among five trial blocks of 108 trials each. Each trial block contained an equivalent distribution of trials: Within each trial block there were four trials of each trial type (nine types) at each array size. The nine trial types were the no-cue trials, test-cue trials for each of the four features, and fixation-cue trials for each of the four features.

Results

In this experiment, we have the ability to separate out the effect of relevant feature count at encoding (presumably meaningful in terms of memory storage) and relevant feature count at test (presumably related to errors in retrieval or decision making). Regardless of cuing condition, the number of objects was simply the array size. The number of relevant features at encoding was equal to the array size in the fixation-cue condition, and it was equal to the array size times four in the test-cue and no-cue conditions. The number of relevant features at test was one for both the fixation-cue and test-cue conditions, and it was four in the no-cue condition.

A full model with linear effects for object count, relevant features at encoding, and relevant features at test plus a random effect for participant was constructed. This full model was compared with three reduced models, each of which lacked one of the object or feature effects from the full model. The full model was preferred to all of the reduced models, with a BF_FR of 3.59 * 10¹¹ over the model lacking an object count effect, a BF_FR of 2.31 * 10³ over the model lacking a relevant features at encoding effect, and a BF_FR of 1.71 * 10⁴ versus the model lacking a relevant features at test effect. The slope of the object count effect was similar to previous experiments (−3.09%). The slopes for relevant features at encoding and relevant features at test were −0.39% and −1.87%, respectively. The slope that we are most interested in is the slope of relevant features at encoding, which shows the feature load effect in memory while controlling for feature load at test.

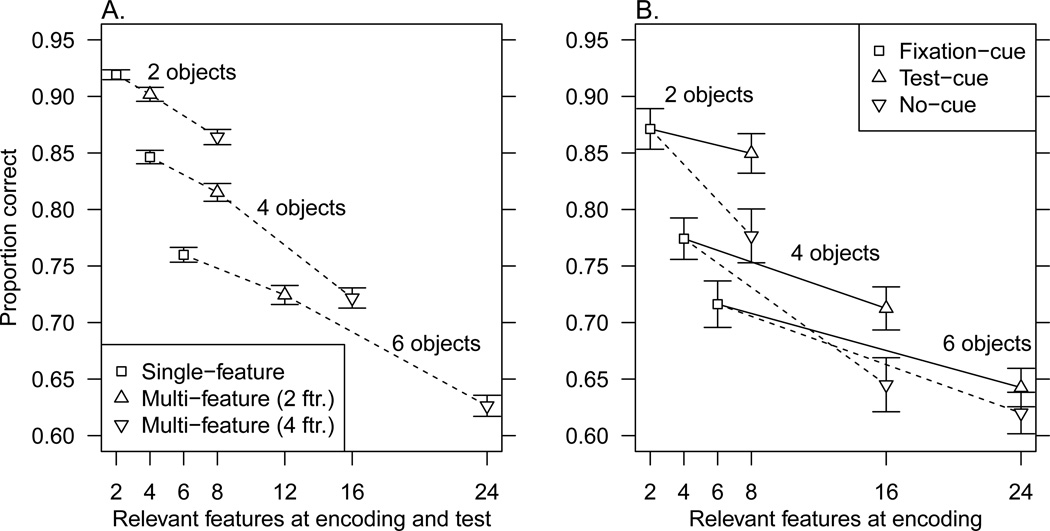
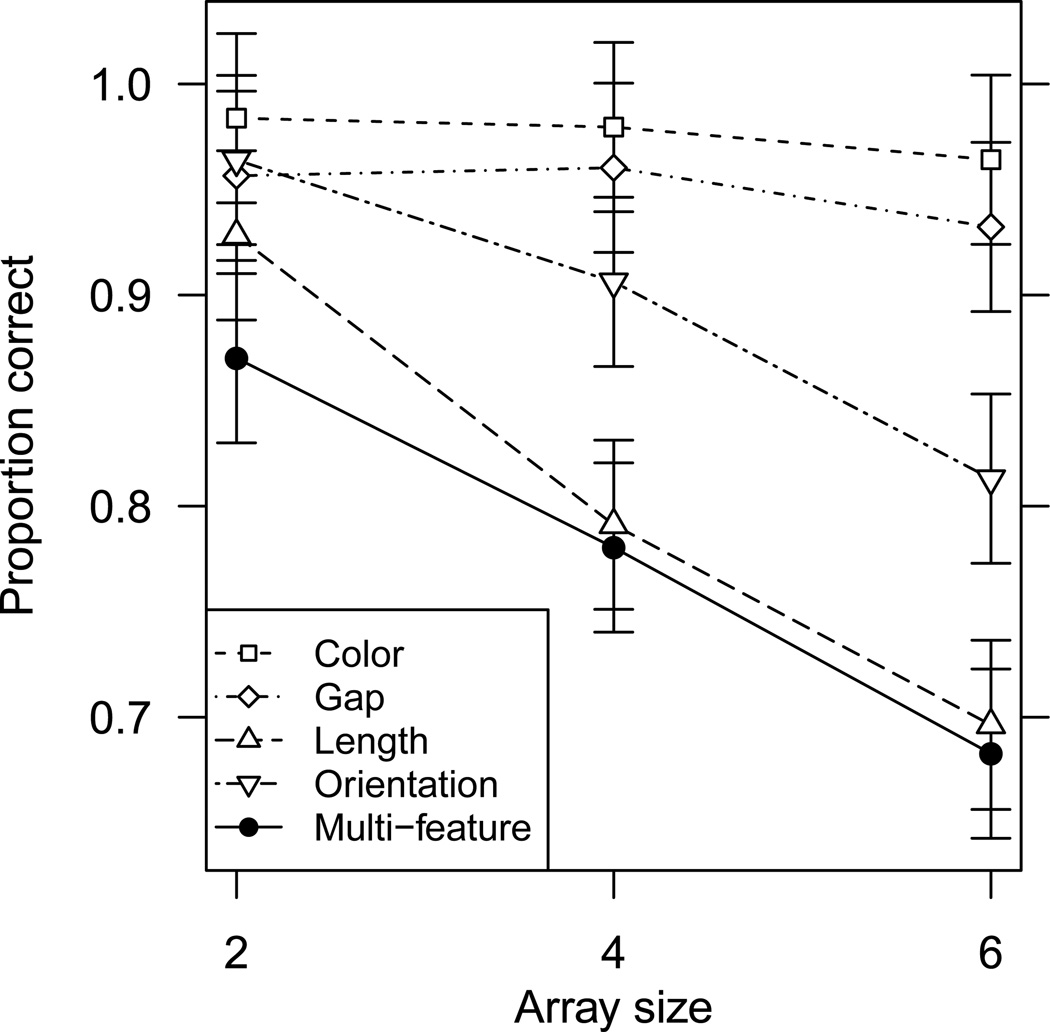
One way to compare this slope with the overall feature effect slopes from our previous experiments is by plotting the data with relevant features on the X-axis, which we did in Figure 4. An can be seen in Panel B of the figure, there is a clear decrease in accuracy between the fixation-cue condition and the test-cue condition at each array size. With this figure, it is possible to visually compare the features at encoding slope obtained in this experiment with the average of those obtained in our other experiments, which did not cue specific features at test. Panel A of Figure 4 shows the slopes obtained in our other experiments, which are steeper than the slope of relevant features at encoding shown with solid lines in Panel B. Clearly, the magnitude of the effect of relevant features at encoding obtained in this experiment is smaller than the overall feature effect from our previous experiments. This seems reasonable because this experiment controlled for the effect of relevant features at test, which was not done in previous experiments. In this experiment, the impact of increasing the number of relevant features at encoding is small relative to the cost adding additional objects: The ratio of the object count slope to the relevant features at encoding slope is approximately 8. However, in spite of the magnitude difference between these effects, there is still an effect of adding features to the memory load that improves model fit meaningfully. Although features have a smaller effect on accuracy than objects, feature load must be taken into effect in order to provide a complete account of the data.

Figure 4.

Plots of the data from all experiments, highlighting the effect of feature load. The y-axes show proportion correct responses. Error bars are standard error. Lines connect conditions matched in terms of array size, where the topmost group is array size 2 and the bottommost is array size 6. Solid lines in Panel B indicate loss in accuracy as the number of stored features increases, whereas dashed lines in both panels indicate loss in accuracy as both the number of stored features and tested features increases. A. Plot of data from experiments 1–5, 7 and 8, where the x-axis is the number of relevant features at both encoding at test. Square symbols indicate the single-feature conditions, upward pointing triangles indicate the multi-feature conditions for experiments with two features (experiments 7 and 8), and downward pointing triangles indicate multi-feature conditions for experiments with four features (experiment 1–5). B. Plot of data from Experiment 6, where the x-axis is the number of relevant features at encoding.

More standard representations of the data from this experiment, with array size on the X-axis, are shown in Figure 5. Panel A shows the same data plotted in Panel B of Figure 4, but as a function of array size and cuing condition, which provides a different perspective on the data showing the clear accuracy differences between cuing conditions. Panels B, C, and D present feature-specific results from each of the three different cuing conditions. Examination of these plots indicates that the relative difficulties of the individual features in the fixation-cue and test-cue conditions were similar to our previous experiments, with generally best performance for color and worst performance for length. This indicates that cuing specific features does not appear to change the relative difficulty of the features.

Figure 5.

Plots of data from Experiment 6. Results are collapsed across change and no-change trials in all but Panel D, which did not have no-change trials specific to each feature. A) Proportion of correct responses by cuing condition collapsed across features. B) Proportion correct in the fixation-cue condition. C) Proportion correct in the test-cue condition. D) Proportion of correct responses by changed feature within the no-cue condition. E) Difference in change discrimination between the test-cue (TC) and no-cue (NC) conditions. F) Difference in change discrimination between the fixation-cue (FC) and test-cue (TC) conditions. Error bars for Panels A, B, and C are 95% repeated measures confidence intervals (Hollands & Jarmasz, 2010), others are standard error because the structure of data made it impossible calculate the repeated measures confidence intervals.

For this experiment, change discrimination difference comparisons were made separately between the fixation-cue and test-cue conditions and between the test-cue and no-cue conditions. Between the fixation-cue and test-cue conditions, there was good evidence that the change discrimination difference the color and gap features was non-zero, but the evidence was equivocal for the length and orientation features. See Table 2 for the values of the Bayes factors. Between the test-cue and no cue conditions, there was again evidence that the color and gap features had a non-zero change-discrimination difference. However, for the orientation and length features, the evidence was weakly toward the null hypothesis of no difference. The change discrimination differences are plotted in panels E and F of Figure 5.

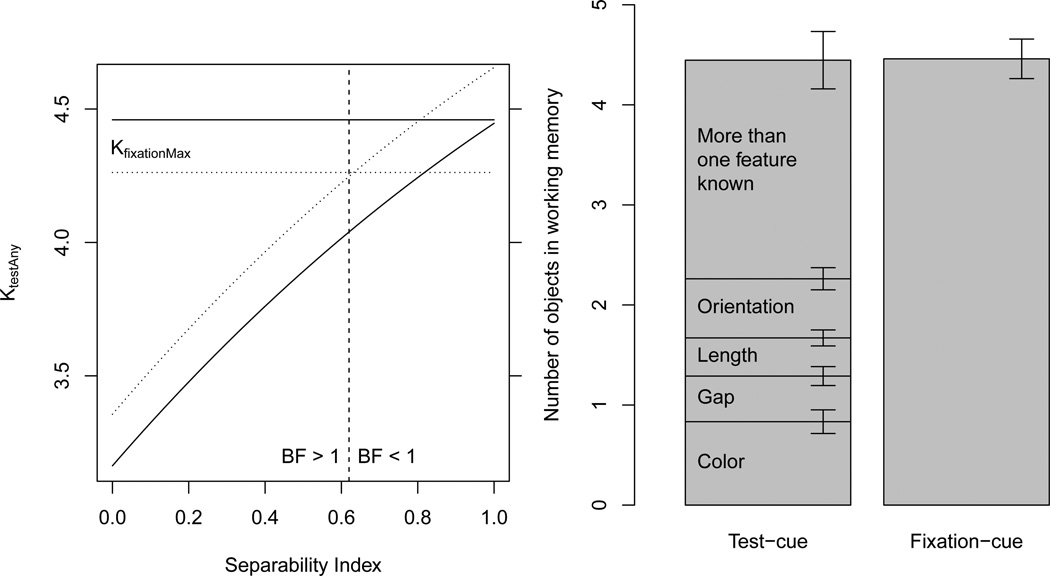
It is possible to obtain estimates of the number of features of different types that are in WM based on performance in different conditions. In both the fixation-cue and test-cue conditions, participants were cued to make a decision about a single feature of a single object, which means that we can use a single-probe model in order to get our capacity estimates (Cowan, 2001; Rouder et al., 2008). The capacity estimates for each feature were only estimated at array size 6 due to concerns about ceiling effects present at the smaller array sizes (see the Appendix for more information about the ceiling effect). In the fixation-cue condition at array size 6, participants knew an average of 4.0 colors, 3.0 gaps, 1.7 lengths, and 2.3 orientations. In the test-cue condition, participants knew an average of 2.4 colors, 1.8 gaps, 1.4 lengths, and 2.0 orientations. Unsurprisingly, participants knew more of the cued features in the fixation-cue condition, which parallels the accuracy results. What is more interesting is that in the test-cue condition, participants knew an average of 7.5 total features (rounding error is responsible for this value not matching the sum of the reported amounts above), which is 1.5 more than the number of objects in the array. To compare the amount of information known in different conditions, we should consider the average amount of information that is encoded in both conditions. For the fixation-cue condition, this is simply an average of the number of known features. However, for the test-cue condition, it is a sum of the number of known features because on each trial the participant was required to encode information about all of the features, so their performance is based on the average amounts of each feature that were encoded. A t-test comparing the average number of features known in the fixation-cue condition to the sum of the number of features known in the test-cue condition gave strong evidence for a difference, BF_FR = 5.74 * 10⁵, favoring the test-cue condition. This shows that when participants are made responsible for all of the features of the objects in the test-cue condition, they are able to remember a greater total amount of relevant information than in the fixation-cue condition. We cannot say that they are remembering more information without the "relevant" qualifier, because it may be that in the fixation-cue condition, participants remember irrelevant features that they have not been cued to remember. This result is interesting in part because worse performance in conditions in which multiple features are relevant can lead to the impression that participants are doing something badly in those conditions. However, this result shows that they are doing very well in terms of stored information and their poor accuracy is due to the high difficulty of the task relative to single-feature conditions, and not due to the amount of information they are remembering.

When only a single feature of the objects was relevant (fixation-cue condition), the number of features known of different types varied (BF_FR = 7.14 * 10⁶). This could be taken as evidence for the possibility of feature-specific capacity limits. Certainly, a limit to the number of known objects cannot account for the difference, because if WM was only limited by object capacity, participant would remember the same number of objects in each condition. However, an alternative explanation to feature-specific capacity limits is that the magnitudes of the changes may have differed from one feature to another. Perhaps the addition or removal of a gap is of a different magnitude than a change from red to green. If the magnitudes of the changes differ, then it is possible that the same number of features from each dimension are held with the same precision, but that some changes are harder to detect than others.

Discussion

The design used in this experiment allowed for a direct test of the hypothesis that feature load has no effect on accuracy. By comparing accuracy on fixation-cue and test-cue trials, it can be determined if participants can improve their accuracy by using information about the feature on which they will be tested. If participants have unlimited feature storage capacity, it would not matter whether they are cued before encoding or at test. However, as the results clearly show, it does matter when participants are cued. In particular, accuracy was worse when, at the time of encoding, participants did not know which feature of the objects they were to be tested on (see Panel A of Figure 5). This result is predicted very clearly if it is thought that feature storage is capacity-limited. If participants do not know which feature they will be tested on at the time of encoding, they have to be able to store information about every feature in order to perform optimally. If they are unable to store information about every feature, then performance will suffer. Given that accuracy in the test-cue condition is reduced relative to the fixation-cue condition, it is reasonable to think that feature storage is capacity-limited.

One possible explanation for the results of this experiment that still allows for high-or unlimited-capacity feature storage is an inherent inequality between the fixation-cue and test-cue conditions. In the fixation-cue condition, the cue word presented at test was always the same as the cue presented at fixation, so participants did not need to look at the cue word presented at test in order to perform the task. However, in the test-cue condition, participants have to determine which feature they must make a decision about at test. The additional time and/or cognitive load required in the test-cue condition to comprehend the feature cue could reduce accuracy for reasons unrelated to storage capacity. On the other hand, accuracy in the test-cue condition was reliably better than accuracy in the no-cue condition, showing that there was a distinct benefit of having a cue in the test-cue condition. Still, it is possible that accuracy in the test-cue condition was affected by processing of the cue and that we are overestimating the advantage that the fixation-cue condition has over the test-cue condition.

The finding that accuracy in the no-cue condition was worse than that in the test-cue condition indicates the importance of performing this experiment. The only difference between those two conditions was that the number of features which participants were tested on differed. This means that there is a factor which affects accuracy when participants are required to make decisions about multiple features of an object at once. One possibility is that participants scan each feature in serial order when making a decision, which would force some features to wait longer before they are scanned. This would allow the quality of the stored representation to degrade, causing errors on later features. Alternatively, there could be a component of decision error that results from the difficulty of integrating information about multiple features when making a decision. Whatever the factor that caused the difference between the no-cue and test-cue conditions is, it was likely also present in the multi-feature conditions of our previous experiments and may have led to an underestimate the ability of WM to store multi-feature objects in those experiments. This experiment helps to control for this problem and allows for a more clearly-interpretable result than our previous experiments.

Experiment 7

One limitation of the stimuli used in the four-feature experiments that we have performed so far is that each feature can only take on two states (for example, the orientation can be only vertical or horizontal.) It is possible that this impoverishment of feature states resulted in the use of storage strategies that would not generalize to richer stimuli. To begin to address this possibility, we tried to extend our results to a situation in which features were allowed to take on more states. In this experiment, we used the same long rectangular bars as in the four-feature experiments, but only the color or orientation of the bars was allowed to change. In order to increase featural richness, we allowed each of the feature dimensions to take on any of four values (see Figure 6 for an example of the stimuli). This experiment is based very closely on another experiment from Luck and Vogel (1997; numbered Experiment 11 in Vogel et al., 2001).

Figure 6.

Diagram of the task used in Experiment 7. This figure shows how the stimuli for this experiment can take on a greater range of feature values than stimuli in the earlier experiments while also reducing the feature load in terms of the number of feature dimensions per object.

Data from 21 participants (8 female, mean age 19.9 years) were used. One additional participant was not included in the analysis because they fell below the accuracy criterion. Three of the participants in this experiment were recruited from the community and were paid $15 for their participation. The materials used in this experiment differed from those of other experiments in that each object could possess any of four colors and orientations. The orientations were 0, 45, 90, and 135 degrees (because the bars were rotated around a central point, 0 degrees is equal to 180 degrees, 45 degrees is equal to 225, etc.). The rectangles were the same dimensions as the long rectangles used in the other experiments and did not have a gap. The colors used in this experiment were red (255,0,0), green (0,246,0), cyan (0, 254, 255), and magenta (255, 0, 255) for the objects and background (60, 60, 60). These were not the same colors used by Luck and Vogel (1997), who used red, green, blue, and black. Our stimuli were still easily discriminable, so we find it unlikely that the colors would have an effect of the results. The increased center-to-center spacing of objects of 2.25° introduced in Experiment 6 was used in this experiment as well. There was no secondary verbal load task in this experiment. See Figure 6 for a diagram of the method for this experiment and examples of the stimuli. In this experiment, there were two-single feature trial blocks (color and orientation) and one multi-feature trial block, each with 180 trials.

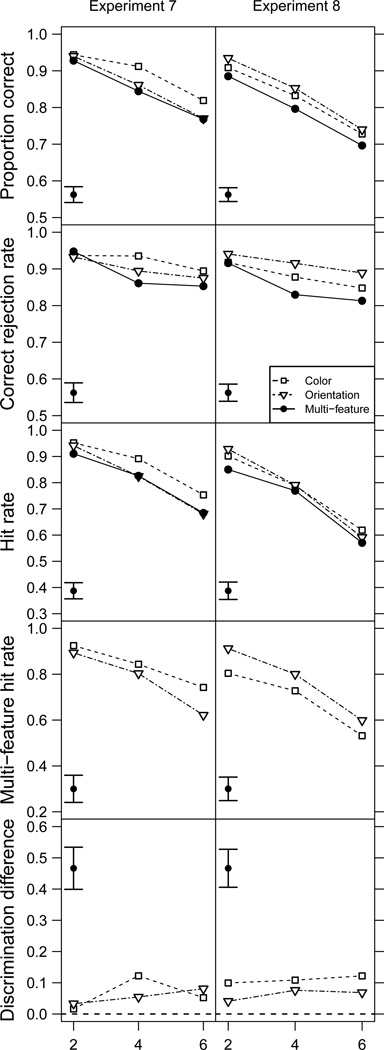
The data for this experiment are plotted in Figure 7. As shown in Table 1, the main results of this experiment are similar to the previous experiments that used four features with two possibles states per feature. When using two features with multiple possible states per feature, we still find similar accuracy slopes as a function of object and feature count. Unlike our other experiments, in this experiment we did not find very strong evidence that including the object effect in the model improved the fit of the model, suggesting that feature load alone provided a very good account of the data. The use of feature sets that included more than two possible feature values helps to reduce the likelihood that our previous results were solely caused by an artifact of using feature sets that possessed only two of the many possible values.

Figure 7.

Plots of data from Experiments 7 and 8. Array size is plotted on the X-axes and the labels shown on the Y-axes are the same as in Figure 2. Note that the scale of the Y-axis varies. In a corner of each panel is an error bar showing a 95% repeated measures confidence interval for the panel. The legend applies to all panels in the figure.

When the difference in change discrimination between the single- and multi-feature conditions was examined, the evidence did not provide clear support either for or against a difference. With a BF of 0.64 for color and a BF 0.88 for orientation, the evidence pointed toward the null, albeit weakly. It is not clear why the evidence points toward no change discrimination difference for both of the features in this experiment. In our other experiments there were always at least two features for which there was a non-zero change discrimination difference (see Table 2). It is possible that this difference between experiments is due to the differences in the stimuli, or it could be caused by the fact that the multi-feature condition accuracy is not very different from accuracy in the single-feature conditions, which would result in small and hard to detect change discrimination differences. Our inability to find a change discrimination difference in this experiment is one of the reasons why we performed Experiment 8, in which we controlled the difficulty of the stimuli more than in this experiment.

In this experiment it still appears by visual examination of Figure 7 that accuracy in the multi-feature condition was equivalent to that in the most difficult single-feature condition. This is notable because in this experiment orientation was the most difficult single feature, whereas length was the most difficult single feature in previous experiments. It was previously hypothesized that there was something about the length feature of the objects that was limiting accuracy on the multi-feature condition. However, we see here that accuracy in the multi-feature condition is generally limited by the most difficult single feature in the set of salient features, not by a specific feature dimension. In the next experiment, we focus on this finding in an attempt to determine if it is possible to eliminate the correspondence between the multi-feature condition and the most difficult single-feature condition.

Experiment 8

There seems to be a correspondence in proportion of correct responses between the multi-feature condition and the most difficult single-feature condition in our experiments. This finding evokes a sense that perhaps the most difficult feature is the weakest link and that it is what limits performance in the multi-feature condition, which goes against our interpretation of a general effect of feature load. We tested whether accuracy in the multi-feature condition was equivalent to the most difficult single-feature condition with a Bayesian t-test. In the first comparison, we collapsed across Experiments 1 to 5 and found a BF of 5.32 in favor of the hypothesis that there was no difference. Furthermore, in Experiment 7, we found a BF of 2.96 in favor of the same hypothesis. This shows that there is evidence that the visually-apparent correspondence is a real phenomenon. But does it mean that the most difficult feature is the weakest link? In this experiment, we will attempt an experimental manipulation to determine if the weakest link hypothesis is tenable.

Given that Luck and Vogel (1997) found equivalent accuracy for all single-feature conditions, it is possible that we have been unable to find the same result that they did because for some reason our stimuli are not equated in accuracy for the individual features of the objects. If we equate the single-feature conditions and, as we have been finding, accuracy in the multi-feature condition is equal to the most difficult single feature, we might find the exact result that Luck and Vogel found. To examine this possibility, we attempted to equate the difficultly of the color and orientation features. In Experiment 7, accuracy for color was better than accuracy for orientation, so in this experiment we changed the colors to be less discriminable in order to decrease accuracy for color.

In this experiment, data from 33 participants (25 female; mean age 18.5 years) were used. One additional participant was removed from the sample due to falling below the accuracy cutoff. The colors of the stimuli used in this experiment were dark pink (235, 76, 90), pale violet red (210, 94, 140), medium purple (165, 108, 214), and light slate blue (120, 116, 253). The method was otherwise identical to Experiment 7.

As can be seen in Table 1, the effects of object count and feature count were similar to previous experiments. When a between-experiments comparison was performed with Experiment 7, the reduced model without an object by experiment interaction term was preferred to the full between-experiments model (BF_RF = 8.64), as was the reduced model without a feature by experiment interaction term (BF_RF = 9.64). This supports the claim that the manipulation of stimulus colors had little meaningful effect on the main results. The data for this experiment are summarized in Figure 7.

We verified that the multi-feature condition of this experiment was as difficult as either single-feature condition by performing a t-test on proportion correct between the multi-feature condition and each single-feature condition. The BF was 116 for the comparison with the orientation condition and 2.08 for the comparison with the color condition, providing only a small amount of evidence that the color and multi-feature conditions showed different levels of performance. There was weak evidence that the color and orientation conditions were equated (BF = 0.61). These results suggest that with this experiment we were able to separate accuracy in the multi-feature condition from both single-feature conditions. This shows that our previous finding that the multi-feature condition is as difficult as the most difficult single feature does not hold in all cases. This provides evidence against the possibility that accuracy in the multi-feature condition could be explained by a weakest link hypothesis.

The other way that we can examine the weakest link hypothesis is through the change discrimination difference results. The change discrimination difference measure, discussed in the results section of Experiment 1, was able to extract information about change discrimination (hits minus false alarms) for each feature separately in the multi-feature condition. This was compared with the same hits minus false alarms measure from the corresponding single-feature condition. If the change discrimination difference is zero, then there is no loss for that feature. In this experiment, there was evidence that change discrimination differences were greater than zero (see Table 2 for the results). However, we can aggregate our change discrimination difference results across experiments in order to eliminate any experiment-specific effects and more clearly see the overall trends in the change discrimination difference results. For Experiments 1 – 5, the product of the Bayes factors resulting from t-tests on the change discrimination difference for each individual feature were 7.61 * 10¹8 for color, 2.53 * 10⁸ for gap, 1.01 * 10⁴ for length, and 7.66 * 10² for orientation (see Table 2). For Experiments 7 and 8, the product of the Bayes factors were 24.7 for color and 10.8 for orientation. This shows that although there may be some variability in certain experiments in the strength of evidence for the change discrimination difference being greater than zero, that overall there is strong evidence that for all features there is a loss in change discrimination when participants are required to attend to all of the features of the objects. Because there is a loss for every feature, including the most difficult feature, it seems very implausible that the most difficult single feature acts as a weakest link that defines the limit of multi-feature performance.

Based on the evidence from the proportion correct data from Experiment 8 and from the change discrimination difference results across all of our experiments, we believe that the finding that the multi-feature and most difficult single-feature conditions were equally difficult is a coincidence that does not reflect WM processes.

General Discussion

The initial purpose of this series of experiments was to determine if a commonly-cited result that showed that objects, but not features of the objects, were related to visual WM performance (Luck & Vogel, 1997) could be replicated under a variety of conditions – including a direct replication. We consistently found an effect of feature load in experiments using two or four features per object, whereas Luck and Vogel found no such effect. Our studies consist of eight experiments with a total of 165 participants. Given how consistently we have observed an effect of feature load across a number of experimental manipulations and different participant samples, we believe our results are reliable. When our results are combined with the results of two recent studies which used similar designs (Cowan et al., 2013; Oberauer & Eichenberger, 2013), it becomes clear that there are a number of studies which show an effect of feature load when objects possess multiple features drawn from different feature dimensions. This helps to show that prior studies which used objects with multiple features from the same feature dimension (Delvenne & Bruyer, 2004; Wheeler & Treisman, 2002) were not investigating a special case of feature load. Rather, it seems that feature load affects performance regardless of whether the features are drawn from the same dimension or different dimensions, although it is possible that the magnitude of the effects is different.

We are also interested in whether the magnitude of our feature load effect depends on the number of relevant features in the multi-feature condition. The visual comparison that can be made between Figures 2 and 7 seems to suggest that there is a large difference in feature effect size between the two- and four-feature experiments. It even appears that we are approximately replicating the effect size that Luck and Vogel (1997) observed in their two-feature experiment that used the same stimuli as we used in Experiment 7, suggesting that the only reason they found no effect was due to insufficient statistical power. Concerning the difference between the single-feature and multi-feature conditions, it should be noted that this difference would be expected to be depend on the number of features that are relevant in the multi-feature condition and, naturally, this value changes between our two- and four-feature experiments. Thus, one would expect a larger difference for the four-feature experiments than for the two-feature experiments. The interesting question is whether the effect of each relevant feature is different depending on whether two or four features are relevant. Based on the feature slopes presented in Table 1 (Experiments 7 and 8 vs. previous experiments), the answer appears to be that the per-feature load effect does not depend on the number of relevant features. Thus, we would argue that the visually small effect of feature load observed in Experiments 7 and 8 is in reality in line with the effect we found in our four-feature experiments.

At the least, we can say that feature load affects accuracy in procedures very similar to those used by Luck and Vogel (1997). It is possible that there is an as-yet-unknown boundary condition controlling feature storage that awaits discovery. Although our results and the results of others who attempted direct replications (Delvenne & Bruyer, 2004; Wheeler & Treisman, 2002) are inconsistent with the feature-conjunction results of Luck and Vogel, simply failing to replicate a result does not necessarily invalidate a theory supported by that result. One must seek to eliminate confounds in order to allow for unambiguous interpretation of results with respect to a theory. In particular, the theoretical issue we are interested in is storage in visual WM, so we should attempt to remove confounds related to the encoding and retrieval of stimuli in order to verify that our effects are due to visual WM storage.

Experiment 3 controlled for the possibility that participants’ ability to perform the task was limited by an encoding time bottleneck. Experiment 5 controlled for the number of objects about which a decision must be made at test, suggesting that our pattern of results observed in experiments with a full-array probe are not due to accumulated decision error across multiple objects. However, it is possible that accuracy in the multi-feature condition of Experiment 5 was limited by the fact that participants were required to make four decisions, one for each feature of the object. Experiment 6 extended the results of Experiment 5 by further controlling the number of decisions that participants were required to make. This showed that when participants are only required to make a single decision at test, there is an advantage if participants are able to selectively encode information about the feature of interest, just as they were able to do in the single-feature conditions of the other experiments. This confirms that the results of Experiments 1 – 5 were not entirely due to decision error. We also verified that precise stimulus characteristics do not much affect our results by using different stimulus and background colors in Experiments 4 and 5 than we used in Experiments 1 to 3. In Experiments 7 and 8, we further verified that we were able to find an effect of feature load in experiments in which only two features were allowed to vary between a greater number of feature values per feature dimension than were used in the four-feature experiments. When combined, these experiments clearly support the argument that feature load has an effect on WM performance.

We do not currently have the evidence to say what causes the effect of feature load. There are two obvious possibilities that should be considered, although they are not exhaustive. One is that WM can store some limited number of features in a general-purpose feature store for which the dimensions from which the features are drawn is irrelevant. The other is that each feature dimension has its own feature-specific storage mechanism and capacity limit. One of the results of Experiment 6 was that people appear to remember about 7.5 features when they are not cued to a specific feature at encoding, but are cued to a feature at test. When participants were cued to a feature at encoding, they remembered on average 4.0 features for the easiest feature (color). This suggests that there may not be a general feature storage mechanism, because otherwise participants should have been able to remember all of the colors when that feature was cued at encoding. However, it is also possible that when only a single feature was cued, participants failed to encode all of the colors because they hit an object limit before filling a general feature store. Still, an object limit cannot be the only explanation, because participants do not remember equal numbers of all of the features even when they are only cued to remember a single feature. For example, participants remembered on average 4.0 colors but only 1.7 lengths when cued to those features at encoding. This provides some evidence for feature-specific capacity limits. More work on the subject of feature capacity limits is necessary.

We do not argue that object load is unimportant, simply that it is not the sole factor contributing to WM performance. In seven out of eight experiments, we found strong evidence for effect of object load (see the "Object BF_FR" column in Table 1). Only in Experiment 7 did the Bayes factor for the object load effect not provide strong evidence for such an effect. The reason why the evidence was weak for the effect is not clear, although it is possible that the experiment simply lacked enough power to provide strong evidence for the effect (for which strong evidence was found in the very similar Experiment 8). It could be that the number of relevant features provided a very good predictor for performance in Experiment 7 and that the addition of an object effect did not improve the fit very much given that a feature effect was already present. Wheeler and Treisman (2002) reported a similar experiment in which the number of relevant features fully accounted for their results, without a need to use object load as a predictor. In contrast to that result, based on the evidence from our experiments it seems clear that we cannot ignore the importance of object load.

A result that might appear to conflict with ours is that of Awh, Barton, and Vogel (2007). They found that the reduction in accuracy that appears when complex stimuli are remembered could be attributed to difficulty comparing insufficiently-precise stimulus representations to test stimuli, not to a reduction in the number of stored representations. The stimuli they used possibly could be characterized as possessing multiple features, much like our stimuli. If their stimuli are similar to ours in terms of possessing multiple features, it is possible that what they say is an imprecise object representation we might say is an object for which only some of the features are known. As such, we see no necessary conflict between our results and those of Awh et al..

Analysis of high performers

One difference between our data and the data of Luck and Vogel (1997) was that our participants did not seem to perform as well as the participants of Luck and Vogel. Averaging across feature conditions at array size six, their participants achieved approximately 82% accuracy, whereas our participants in Experiment 1 only achieved 73% accuracy. It could be that many of the participants used by Luck and Vogel were at ceiling performance and that the pattern of results we observed only occurs when most participants are not at ceiling performance. To investigate this possibility, we chose to examine high performers from our three most similar experiments: Experiments 1, 2, and 4. These experiments were the same except for the use of a secondary verbal load task in Experiment 1 and a different set of display colors in Experiment 4. We collapsed across experiments in order to get a sample of high performers large enough to allow for statistical analysis.

We selected a group of participants (N = 7) with an average accuracy of 81.6% at array size six to be our group of high performers. In this group of participants, we observed a main effect of attended feature block (i.e. which feature or features participants were made responsible for), F(4, 24) = 23.61, MSE = 0.0067, p < .001, ${\eta }_p^2=.80$. The data used in this analysis are plotted in Figure 8, in which it can be observed that the pattern of relationships between conditions is very similar to our general population. These results show that even when we select a subsample of our participants who are matched in accuracy to the participants of Luck and Vogel (1997), we find an effect where Luck and Vogel did not. It appears that although the participants of Luck and Vogel performed better than our participants, it is unlikely that this is the reason that we did not find their result.

Figure 8.

Plot of accuracy for the top performing participants in Experiments 1, 2, and 4. The data are from the top seven participants whose average accuracy at array size six is matched to the same for the participants of Luck and Vogel (1997). Error bars are 95% repeated measures confidence intervals.

Potential chunking confound

It seems likely that participants were able to engage in a relatively large amount of chunking in our experiments due to the type of objects we used. In our four-feature experiments, features could take on only one of two values, meaning that feature value repetitions in multiple adjacent objects could lead participants to encode those features as a chunk that may exist separately from the underlying objects (Jiang, Chun, & Olson, 2004). For example, if a few objects in a small cluster were all the same color, participants might remember that spatial region as having that color. Since there were only two values available for each feature, it was fairly common that there were easily chunked sections of the array. Perhaps the most clear evidence for this chunking is in Experiment 3 where the color and gap features seemed to suffer very little performance decrement as array size increased. In fact, in a number of the four-feature experiments accuracy for color only decreased slightly as array size increased all the way to six. The major difference between Experiment 3 and the other experiments was that participants were given 500 ms to encode the sample array in Experiment 3 versus 100 ms in the other experiments. It is possible that participants were better able to chunk in Experiment 3 than in the other experiments because they had more time to actively form chunks while viewing the sample array.

If chunking is an active process that requires attention and participants were relying heavily on chunking, our finding that the multi-feature condition was more difficult than most single-feature conditions could be an artifact of the stimuli we used. To explain: In the multi-feature condition, in order to chunk well enough to "keep up" with the single-feature conditions, participants would have had to form chunks which contained information about all four features. They might have had to create separate chunks for each feature dimension, which except in unusual circumstances would be located in different spatial regions. This task is clearly much more difficult than creating chunks for only one feature dimension at once. That nearby objects would share most or all feature values is quite unlikely compared to the probability that nearby objects would share a feature value for just a single feature dimension, making chunking objects that shared multiple features a strategy that would only be effective on a small number of trials. It seems plausible that if participants were using an attention-demanding chunking strategy, they would be limited in their ability to form chunks in the multi-feature condition relative to the single-feature conditions due to the added attentional demands of attempting to chunk in multiple feature dimensions at once. Given this, the differences we found between the single- and multi-feature conditions may be due to difficulty creating chunks in the multi-feature condition, and not directly due to difficulties storing multi-feature objects.

One piece of evidence that suggests that chunking may not be the only explanation for our results comes from Experiments 7 and 8. In those experiments, each feature dimension was allowed to take on any of four values, which should reduce the ability of participants to chunk objects together relative to the four feature experiments. The reason for this is simply that when each feature is allowed to take on more values, the probability that there are multiple objects in the sample array with the same value goes down. When fewer objects have a feature with the same value, it is less effective to make a chunk out of those objects than if the chunk could contain more objects. In spite of reduced chunking potential in Experiments 7 and 8, we still found an effect of feature load of similar magnitude to that of the four-feature experiments, suggesting that chunking may not be entirely driving the effect. Additionally, stronger evidence that chunking is not the only explanation comes from the work of Oberauer and Eichenberger (2013). Those authors found lower change detection accuracy with increased feature load even when the values of the relevant features were not allowed to repeat in a given display, which should eliminate the ability to chunk. This shows that under conditions in which chunking objects with identical feature states was prevented, an effect of feature load was still found. Although it is possible that chunking played a role in our experiments, it is clearly not the only reason for our results.

Is it possible for a slot model to remain viable?

We were curious if it was possible to find support in our data for a slot model like the one proposed by Luck and Vogel (1997). In that model, participants have a fixed number of slots, each of which can hold one object. Originally, Luck and Vogel argued on the basis of their results that each object slot always held all of the features of the object held in that slot. Our finding of an effect of feature load casts doubt on the idea that each object slot always holds all of the features of the object. However, it is possible that the capacity of WM is limited in part by the number of objects which can be held, even if each stored object does not have full feature information intact. We wanted to discover if there was a set of plausible assumptions about how objects and features are stored in WM that would allow a fixed-capacity slot model to remain viable in spite of the importance of feature load. The question of whether constant capacity hold for multi-feature objects is important because in many of the experiments examining WM capacity, objects with only a single feature were used (e.g. Rouder et al., 2008). In experiments which only use a single relevant feature, the number of objects and the number of features are always the same, confounding object load and feature load. Our analysis, which we report in the Appendix, describes some evidence for a constant object capacity even when multiple features were relevant. Note, though, that the plausibility of the constant-slots model with an additional feature limit depends on some assumptions that have not yet been proven (as explained in the Appendix), providing a compelling motivation for further work to assess such models and their assumptions. At the very least, our analysis did not rule out such a model. Thus, we believe that a slot model with a fixed number of object slots remains viable even with our finding of an effect of feature load.

Future directions

Future work on this topic could focus further on separating the effect of the number of relevant features at encoding from the effect of the number of features at test. We used one method of doing so in Experiment 6, but there is a possible issue of the attention demands of cuing at encoding versus cuing at test (discussed in more detail in the discussion section of Experiment 6).

One important factor to investigate further is feature separability (Fougnie & Alvarez, 2011). It is possible that the result of Luck and Vogel (1997) could be correct for the special case when all of the features of an object are drawn from integral feature dimensions (e.g., brightness and color). There is some evidence that when the features of an object are from integral dimensions, precision does not change with set size (demonstrated for set sizes 1 and 2 by Bae & Flombaum, 2013). The features in our experiment are likely to be more separable, as we explain in the Appendix. With integral features, under the hypothesis of Luck and Vogel, one would expect the fixation-cue and test-cue results to produce equal K values with an assumed separability index of 0 (see the Appendix for more information).

Another important issue is how to quantify the number of stored features of each type. Across our experiments, we found that participants consistently performed better for some features than for others, even when only one feature of the objects was relevant. This suggests the possibility of separate capacity limits in WM for features from different feature dimensions, suggesting a model like that of Treisman (1988) in which features from different dimensions are stored separately, possibly in feature stores that have different capacity limits for different features. An alternative explanation could be that the magnitudes of the changes for the features we used differed from feature to feature. For example, a change from red to green might be a larger change than a change from vertical to horizontal. This explanation would suggest that the differences between features are not indicative of different storage mechanisms, but rather of a feature-general change-magnitude effect. More work should be done to examine the possibility of the existence of different WM capacities for different features.

Conclusions

Our results so far are strong evidence that storage in visual WM is limited by the number of objects and by the number of relevant features of those objects. We have consistently observed an effect of feature load, which goes against the belief that the number of objects which can be stored in visual WM is the sole determinant of accuracy. It is clear that features affect performance, although the mental mechanisms underlying the effect of feature load is not yet clear. We believe that claiming that either objects or features are the single facet of WM that mediates visual WM performance in all cases is untenable in light of the available data. We suggest that rather than attempting to specify the most important (or only) factor which mediates visual WM performance, we would be better served by improving our understanding of the contributions of all of the factors which meaningfully impact visual WM performance.

Appendix

Estimation of Number of Objects in Working Memory Under Varying Feature Load

Given that our results showed a clear effect of feature load, we were curious to see if it was possible for participants to be holding the same number of objects in WM regardless of the number of relevant features. It is an important prediction of an object-slot model of WM, such as that proposed by Luck and Vogel (1997), that the number of object slots available to participants does not depend on the featural content of the objects stored in those slots. This implies that it is possible that participants will be able to store the same number of objects in mind, regardless of the number of relevant features of those objects. Cowan et al. (2013) and Oberauer and Eichenberger (2013) found that such a constant capacity model held despite incomplete feature sets remembered for each object, but did not fully consider the consequences of different assumptions about feature dependence, which we will do here. There is evidence that knowledge of one feature of an object is neither fully dependent nor independent of knowledge of other features of the object (Bays, Wu, & Husain, 2011; Fougnie & Alvarez, 2011; Fougnie, Cormiea, & Alvarez, 2013).

In order to test this equality of the number of objects held in mind, we performed a further analysis of the data from Experiment 6. In Experiment 6, it is possible to get an estimate of the number of objects in WM for which the cued feature was known in both the fixation-cue and test-cue conditions by using Cowan’s K (Cowan, 2001). In one stage of the analysis, we obtain an estimate of the number of objects that participants hold in mind when only one feature is relevant (fixation-cue condition). We will then estimate the number of objects held in mind when all four features of the objects were relevant (test-cue condition) and compare these two estimates of objects held in mind. With this analysis applied to Experiment 6, we find that it is indeed plausible (though not proven) that a model may hold in which a constant number of objects is held in WM. With this overview in mind, we will continue with fleshing out the details.

This analysis is appropriate for Experiment 6 because the use of feature cues at test allows us to be confident about which feature the participant was making a decision about. Knowing this, we are able to infer that the participant made full use of their knowledge about that particular feature, which allows us to feel confident that the K estimates we get for the individual features are reliable. While this reason makes this experiment appropriate for this analysis, it also renders our other experiments ill-suited to the same analysis. In the multi-feature conditions of those experiments, we cannot be sure what information about features was used by participants in order to make their responses, so we cannot feel confident that the K estimates are a good indication of the amount of knowledge held about a specific feature.

Our model makes two assumptions about how stimuli are encoded into WM: 1) Information about stimulus objects is encoded into WM on a feature-by-feature basis and 2) the probability of encoding information about a given feature of an object can depend on whether any information about that object had already been encoded. To expand on the first assumption, our model assumes that the contents of WM are sequentially filled with stimulus data from a sample array. One way of thinking about the process would be to say that a participant begins by encoding a single feature from some number of objects. For example, a participant might begin by encoding the color of 3 objects. The participant then moves on to the subsequent feature, perhaps orientation, and encodes that feature from some other number of objects, and so on until they have sampled from all of the available stimulus dimensions. It is not necessary to assume that one feature dimension is sampled from all objects before the next feature dimension is sampled: the only requirement is that the probability of encoding a given feature of an object is dependent on knowledge of already known features of the object. We are treating the features of the objects as important handles with which participants track object representations, so we assume that objects are only stored if at least one of the features of that object has been encoded.

To expand on the second main assumption, a key factor is how knowledge of some features of an object leads to changes in the conditional probability of encoding subsequent features. We can estimate the unconditional probability of knowing a specific feature of an object based on task performance, but we are really interested in the conditional probability of knowing a feature given other knowledge about the object. We will assume that the probability of knowing a given feature of an object can be, but is not necessarily, dependent on prior knowledge about that object. In our color and orientation example, at the time the orientations are sampled, the colors of some objects are already known, so the probability of encoding the orientation of those objects is affected. We base our index of conditional encoding on a prior study. Fougnie and Alvarez (2011) used what they termed the separability index (SI) as a measure of the dependence between two features. The SI is 1 if the features are fully separable (which is the same as full independence) and 0 if the features are inseparable. Using a change-detection task, Fougnie and Alvarez found that the separability index was .80 for color and orientation and .28 for the width and height of rectangles, where width and height were treated as two features of the rectangles. We can use these observations of separability to inform our analysis of varying levels of independence. We propose that in our model when features after the first feature are encoded, for SI less than 1, subsequent features are more likely to be encoded for a given object if at least one other feature of that object has already been encoded. The likelihood of encoding features after the first to an object for which at least one feature is already known depends in part on the SI.

The mathematical model takes as variables the K estimates for each participant for each of the 4 features we used and an assumed SI. The following process is performed for each participant individually so that each participant receives an estimate for the number of objects held in mind when all of the features of the objects were relevant. To begin, each participant’s K estimates are sorted into descending order, which is required when the SI is small. Then the proportion of the sample array for which the first feature is not known is calculated with

$$p(U_1)=1-K_1/N.$$ (1)

where p(U₁) is the probability that the first feature is unknown for any given object in the sample array (or equivalently the proportion of the sample array for which the first feature is unknown), K₁ is the number of objects for which the first feature is known, and N is the number of objects in the sample array. Then, for each of the subsequent features, some part of the unknown proportion of the sample array is filled with feature knowledge by subtracting a newly-encoded area from the unknown proportion of the sample array. For example, assume that a participant begins by encoding the color of 4 objects out of a sample array of 6 objects. Assuming an SI of 1 (full feature independence), if they then encode the orientations of 3 objects, on average 2 of those orientations will be sampled from objects for which color is already known and 1 of those orientations will be sampled from an object for which color is not known. This one object for which orientation was encoded but color was not adds to the number of known objects, filling the unknown part of the sample array with partially known objects, taking away part of the unknown. Our mathematical instantiation of this process is

$$p(U_i)=p(U_{i-1})-((SI*K_i/N)*p(U_{i-1}))$$ (2)

where p(U_n) is the proportion of the sample array for which none of the 1 to n features is known and SI is the separability index. For the second feature, p(U_i–1) is equal to p(U₁) calculated in Equation 1. The right-hand side of the equation is the currently unknown proportion of the sample array (p(U_i–1)) minus the newly-encoded proportion of the sample array for which nothing else was known ((SI * K_i/N) * p(U_i–1)). Now that the broad stokes of the model have been given, the details will be filled in.

A full understanding of Equation 2 requires an understanding of the definition of SI, which we will give here. It would be used if one had enough information to calculate SI, though we simply show results for all values of SI from 0 to 1. Fougnie and Alvarez (2011) define SI as the ratio of the probability that feature 2 of an object is known given that feature 1 of the object is unknown to the probability that feature 2 is known, unconditional of feature 1. We are making the simplifying assumption that knowledge of feature i is conditioned on prior knowledge of any feature of the object, not a specific other feature. So for our purposes, SI is defined as p(f_i|U_i–i)/p(f_i), where f_i is the event that feature i is known for given object and U_i–1 is the event that all features from 1 to i – 1 are unknown for a given object. Given that K_i/N is equal to p(f_i), the expression SI * K_i/N reduces to p(f_i|U_i–1), i.e. the probability of knowing the i^th feature for some object given that nothing about that object was known. Now that we know that SI * K_i/N reduces to p(f_i|U_i–1), it becomes clear that the expression (SI * K_i/N) * p(U_i–1) becomes p(f_i|U_i–1) * P(U_i–1), which by basic results in probability is the intersection between the proportion of the sample array for which the i^th feature is known and the proportion of the sample array for which none of the prior features is known. In Equation 2, this intersection is then subtracted from the unknown proportion of the sample array prior to the current feature and the resulting proportion is equal to p(U_i).

The final step is the calculate the number of objects for which at least one feature was known with

$$K_{\mathit{\text{textAny}}}=(1-p(U_4))*N$$ (3)

where K_testAny is the number of objects in the test-cue condition for which at least one feature was known and p(U₄) is the proportion of the sample array for which none of the four features is known. Thus 1 – p(U₄) is the proportion of the sample array for which at least one feature was known, which, when multiplied by the array size, N, gives the number of objects for which at least one feature was known. We can perform the process in Equations 1,2, and 3 for different values of SI, giving us estimates for K_testAny for each participant.

In order to test a constant object capacity hypothesis, we need to compare K_testAny to a quantity representing the number of object slots used by participants when only a single feature of the objects was relevant. We took the K estimate from the feature in the fixation-cue condition for which each participant performed the best, which we will call K_fixationMax, and used it as our estimate of the number of object slots used by that participant when only one feature was relevant. Using the maximum of the fixation-cue K estimates as our estimate of object slots raises the question of why participants would not use all of their object slots for all of the features. One possibility is that, in addition to an object limit, there are also feature-specific capacity limits, which is supported by the fact that we consistently found better performance for some features even in single-feature conditions.

We compared our estimates of K_fixationMax and K_testAny in order to test if our participants appeared to be using the same number of object slots in both the fixation-cue and test-cue conditions of Experiment 6. Array sizes two and four were not analyzed because most participants seemed to be at ceiling performance on those trials. To put numbers to it, at array size six, 20 out of the 30 participants had a K_fixationMax greater than four, suggesting that most of the participants were at ceiling at array size four. Presumably even more would have been at ceiling at array size two. Given these problems with ceiling effects, only data from array size six is analyzed. At array size six, the mean value of K_fixationMax was 4.46 (SEM = 0.20). The K_testAny estimates resulting from values of SI from 0 to 1 are plotted in Figure A1. K_fixationMax and K_testAny are nearest to each other when SI is 1 and the BF for this comparison is 0.26, giving good support for the hypothesis that they are the same. At the other extreme, an SI of 0 provides clear evidence for a difference, with a BF_FR of 1.43 * 10⁴. At an SI of approximately .62, the BF is 1. Thus, there is a region of SI values above .62 for which there is evidence for the hypothesis that K_fixationMax and K_testAny have the same value.

Figure A1.

Results of the comparison between K_fixationMax and K_testAny. Left panel: Plot of K_testAny estimates (angled solid line) as a function of Separability Index (SI), with a standard error line drawn above it (angled dotted line). The horizontal solid line is K_fixationMax, which does not depend on SI, with standard error drawn below it (horizontal dotted line). The vertical dashed line represents the SI value for which the Bayes factor of a t-test comparing K_testAny to K_fixationMax is equal to 1. To the right of the vertical line, the Bayes factor is less than 1, giving evidence for there being no difference between K_testAny and K_fixationMax. We think it is plausible that the true SI for our features was near 0.8 (Fougnie & Alvarez, 2011). Right panel: Bargraph of K estimates in analysis of Experiment 6 showing the distribution of feature information across objects when an SI of 1 is assumed. Left bar: K estimate from the test-cue condition (K_testAny) broken down by the number of objects for which each feature was the only feature known and the number of objects for which more than one feature was known, which can be calculated if one assumes an SI of 1. Right bar: K estimate from the fixation-cue condition (K_fixationMax). Error bars are standard error.

Based on the features we used and the results of Fougnie and Alvarez (2011), it is plausible that the SI for our features falls into the range of SI values for which there is evidence for constant object capacity. The features we used were presumably all fairly separable from one another as none of the pairs of features combine together to form a specific percept. Indeed, in order for Luck and Vogel (1997) to claim that objects are stored with features strongly integrated, they needed to use separable features to avoid the interpretation that only integral features are stored in a strongly integrated way. Fougnie and Alvarez found that the SI for color and orientation was 0.80 using a change-detection task. If we assume that our features are all as separable as color and orientation, we can use the SI value Fougnie and Alvarez found for color and orientation to estimate K_testAny. When we use an SI of 0.8, we obtain a K_testAny of 4.24 (SEM = 0.21) which results in a BF_F R of 0.37 in the comparison with K_fixationMax, which suggests that constant object capacity is 2.68 times as likely as variable object capacity under our modeling assumptions. However, we do not know for sure what the true SI is for our features, so it is possible that an SI of 0.8 is not correct. Even if an SI of 0.80 is only approximately correct, there is a range of SI values around 0.80 for which there is still evidence for a constant object capacity. Thus, our conclusions are not fully dependent on a highly-specific value of SI.

A potentially problematic assumption is that K_fixationMax may not be an appropriate estimate of the number of slots that participants have available to them. It is likely that K_fixationMax is an overestimate of the number of object slots available to participants due to the fact that it is estimated based on the maximum of the four K estimates from each of the features in the fixation-cue condition. Using an estimator based on the maximum of a set of values is guaranteed to be biased high. However, if K_fixationMax were lower, it could still be near the values of K_testAny that we estimate, so even if K_fixationMax is biased high, we could still easily find support for a constant object capacity with an unbiased estimate of object slots when only one feature is relevant. A different potential problem is that it is possible that our estimates of K_fixationMax and K_testAny are underestimates of the number of objects that can be encoded into WM due to the fact that our design does not allow us to examine a number of possible ways in which information might be lost or not used. For example, if features are forgotten over the retention interval we used, then our K estimates, which are based on performance at test, will not fully capture the amount of information that was available to participants before some of that information was lost.

Even though although our analysis rests on a number of assumptions about the process underlying feature storage in WM, we believe that our results show that it is plausible that there is a constant object capacity in WM. This is in spite of our findings across experiments that there is an effect of feature load. Evidence for a constant object capacity when multiple features were relevant was also found by Cowan et al. (2013) in a design which used objects that had a color and a shape. Also, Oberauer and Eichenberger (2013) found a evidence for a constant object capacity when using stimuli that possessed multiple features. Thus, there is evidence that there is a constant capacity for objects that does not decrease as the number of relevant features increases. Our finding of a constant capacity for objects agrees with many additional prior studies (e.g. Cowan, 2001; Rouder et al., 2008; Zhang & Luck, 2011), although see Keshvari, van den Berg, and Ma (2013) for contradictory results obtained in a paradigm that considers precision of representations. That we are still able to find a constant object capacity even with multi-feature stimuli gives support to the idea of a fixed capacity limit, but it does not provide any evidence against models which hypothesize WM storage models that use flexible resources rather than object slots (e.g. Keshvari et al.). We believe that it is worthwhile to continue research in this direction to better understand how features are stored in WM and to pursue the questions of whether there is a constant object capacity in WM that is independent of feature load.

In order to help validate the relationship between K_fixationMax and K_testAny, it would be valuable to examine the correlation between the two K estimates. However, with our sample of only 30 participants with a small number of trials from which the K estimates are calculated, we do not have sufficient power to feel confident in the robustness of performing a correlational analysis with our data.