Zebrafish Ca_V2.1 Calcium Channels Are Tailored for Fast Synchronous Neuromuscular Transmission

Abstract

The Ca_V2.2 (N-type) and Ca_V2.1 (P/Q-type) voltage-dependent calcium channels are prevalent throughout the nervous system where they mediate synaptic transmission, but the basis for the selective presence at individual synapses still remains an open question. The Ca_V2.1 channels have been proposed to respond more effectively to brief action potentials (APs), an idea supported by computational modeling. However, the side-by-side comparison of Ca_V2.1 and Ca_V2.2 kinetics in intact neurons failed to reveal differences. As an alternative means for direct functional comparison we expressed zebrafish Ca_V2.1 and Ca_V2.2 α-subunits, along with their accessory subunits, in HEK293 cells. HEK cells lack calcium currents, thereby circumventing the need for pharmacological inhibition of mixed calcium channel isoforms present in neurons. HEK cells also have a simplified morphology compared to neurons, which improves voltage control. Our measurements revealed faster kinetics and shallower voltage-dependence of activation and deactivation for Ca_V2.1. Additionally, recordings of calcium current in response to a command waveform based on the motorneuron AP show, directly, more effective activation of Ca_V2.1. Analysis of calcium currents associated with the AP waveform indicate an approximately fourfold greater open probability (P_O) for Ca_V2.1. The efficient activation of Ca_V2.1 channels during APs may contribute to the highly reliable transmission at zebrafish neuromuscular junctions.

Introduction

At central synapses, the Ca_V2.1 and Ca_V2.2 calcium channels commonly co-mediate neurotransmission, but their contributions to release vary greatly, particularly among GABAergic and glutamatergic synapses (1). Evidence continues to accumulate in support of the idea that they play distinctly different roles in synaptic transmission.

For example, cholecystokinin-expressing interneurons in the rat dentate gyrus release GABA (γ-aminobutyric acid) in a highly asynchronous manner when compared to the parvalbumin interneurons. Cholecystokinin neurons rely principally on Ca_V2.2 whereas parvalbumin neurons utilize Ca_V2.1 (2), leading to the proposal that Ca_V2.2 may play a greater role in asynchronous release.

Weaker coupling to fast release on the part of the Ca_V2.2 is also reflected in the channel’s delayed recruitment, which was associated with action-potential (AP) broadening during repetitive stimulation (3). The stronger coupling of the Ca_V2.1 channel to release has been ascribed to a closer proximity to the release site (4), which might be expected to promote exocytosis by providing either greater access to calcium (2,5) or through physical interaction with the exocytotic machinery (6–10).

One more idea, however, arose from modeling studies, suggesting that functional advantages offered by Ca_V2.1 facilitated high-frequency signaling (3). As a test of this idea, we sought to compare the function of heterologously expressed zebrafish Ca_V2.2 and Ca_V2.1 isoforms under conditions of high-quality voltage-clamp wherein pharmacological inhibition of additional isoforms is not required. This avoids potential contribution by additional isoforms due to incomplete inhibition.

Finally, we also capitalized on the ability to use the AP waveform recorded from the zebrafish primary motor neuron in vivo, which mediates fast synchronous neuromuscular transmission solely through Ca_V2.1 calcium channels (11).

Materials and Methods

Human embryonic kidney cells (HEK293T) were transfected (Lipofectamine 2000; Invitrogen, Carlsbad, CA) with an equal molar cDNA ratio coding for the EGFP-tagged zebrafish α-subunit, rat α₂δ₁ subunit (addgene accession:AF286488; Addgene, https://www.addgene.org/), and zebrafish β_4b subunit (11). Within 24–48 h posttransfection the cells were mechanically lifted, replated, and given 1 h to reattach. Calcium currents were recorded in the whole-cell configuration with an EPC-9 amplifier under PATCHMASTER software control (HEKA Instruments, Darmstadt, Germany). Patch electrodes with resistances of 3–5 MΩ contained 115 mM Cs-methanesulfonate, 15 mM CsCl, 5 mM BAPTA, 4 mM Mg-ATP, and 10 mM Cs-HEPES, pH 7.2. The bath solution contained 134 mM NaCl, 2.9 mM KCl, 1.2 mM MgCl₂, 2.1 mM CaCl₂, 10 mM Glucose, and 10 mM Na-HEPES, pH 7.8. Whole-cell currents were sampled at 100 kHz except for the AP waveform that that was sampled at 50 kHz.

All signals were digitally filtered at 8 kHz (Bessel filter, −3 dB). The effective bandwidth, determined on the basis of 10–90% rise and delay, was consistent with a 5 kHz Bessel filter. Voltage pulse protocols typically used either P/8 or P/10 leakage subtraction, and traces generated by the AP waveform used P/8. Only recordings having series resistance <10 MΩ were accepted with compensation set to 80–94%. FITMASTER data (HEKA Instruments) were exported to the software IGOR PRO (WaveMetrics, Lake Oswego, OR) and then converted into PCLAMP format using the ABF File Utility, Ver. 2.1.76 (Synaptosoft, Decatur, GA). Current traces analysis and fits were done with CLAMPFIT 10.3 (Molecular Devices, Sunnyvale, CA). Results were presented as mean ± SE and either standard t-tests or Whitney-Mann tests were used for statistical comparisons.

Kinetic estimates for Ca_V2.1 and Ca_V2.2 were used to simulate calcium currents generated in response to either square or AP command waveforms using the software IonChannelLab, Ver. 1.0 (12). For this purpose, voltage protocols identical to those applied experimentally were created with the protocol editor. Simulated traces produced by 1000 calcium channels with a divalent Goldmann-Hodgkin-Katz (GHK) permeation regime were exported as text columns to the software CLAMPFIT 10.3 (Molecular Devices), filtered to 5 kHz, and compared to the experimental traces. For the simulated AP-elicited currents, the voltage protocol was set to mimic experimentally recorded AP. This was done with the protocol editor by splicing together 27 consecutive voltage ramps with different durations. Simulated APs lacking the capacitive discharge component were also generated in this manner.

Results

Macroscopic currents

The α-subunits cDNAs corresponding to zebrafish Ca_V2.2 and Ca_V2.1 calcium channels were coexpressed in HEK293 cells with cDNAs encoding accessory subunits. Both isoforms expressed voltage-activated calcium current within three days after transfection, but Ca_V2.2 currents were consistently larger (Fig. 1, A and G). Failure to include the accessory subunits resulted in greatly diminished calcium currents. Functional comparisons indicated a ∼6 mV negative shift for Ca_V2.2 that was reflected in both the voltage-dependence of peak steady-state current (Fig. 1 B) and peak tail current (Fig. 1 C).

Figure 1.

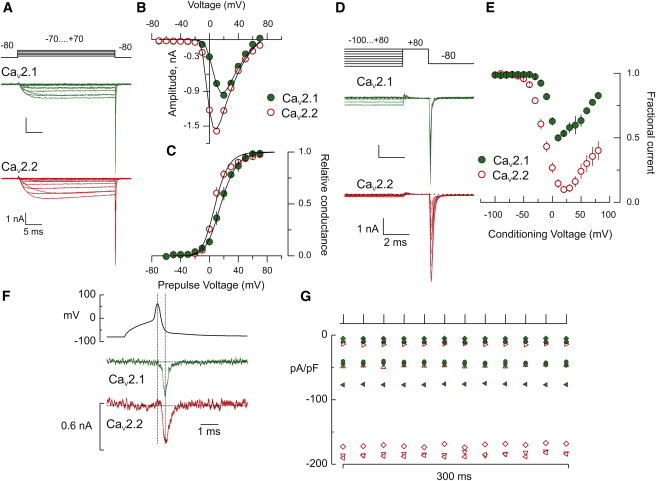
The voltage-dependent properties of Ca_V2.1 and Ca_V2.2 calcium channels. (A) Sample traces of voltage-activated Ca_V2.1 (upper) and Ca_V2.2 (lower) calcium currents. Currents were leak-subtracted using a P/10 protocol. (B) The peak current voltage relations for the recordings shown in (A). (C) The voltage-dependent activation derived from tail current measurements at −80 mV. Data were fit to a Boltzmann distribution with parameters corresponding to the voltage for half-activation (V_1/2) and the apparent electrical valence (z). For Ca_V2.2 channels V_1/2 = −1.3 ± 1.1 mV, z = 2.4 ± 0.2 (n = 14 cells); and for Ca_V2.1-type V_1/2 = 4.9 ± 0.5 mV, z = 2.0 ± 0.1 (n = 12 cells) (fit parameter ± SE of the fit). (D) Sample traces of the Ca_V2.1 (upper) and Ca_V2.2 (lower) calcium currents during protocols used to determine the extent of inactivation at the end of a 200-ms conditioning pulse. (E) Maximal channel availability was determined on the basis of the tail current amplitude elicited by a pulse to −80 mV after a 2-ms pulse to +80 mV (n = 15 recordings for Ca_V2.2 and n = 14 for Ca_V2.1). (F) Twelve superimposed Ca_V2.1 (upper green) and Ca_V2.2 (lower red) calcium current recordings in response to a train of AP waveform recorded from the CaP motor neuron in vivo. Each superimposed current was generated using the same p/8 subtraction trace. Hence, the noise in each of the 12 traces is similar but not identical. (Vertical lines) Peak of the AP and peak of calcium current. (G) The inward current density measured for each of 12 consecutive traces obtained during 38-Hz stimulation for six Ca_V2.2 (red open symbols) and six Ca_V2.1 whole cell recording (solid green symbols).

Additionally, Ca_V2.2 inactivation was nearly complete during a 200-ms depolarization whereas the Ca_V2.1 only partially inactivated (Fig. 1 D). Inactivation measured with tail currents was maximal near +10 mV for both isoforms, with increasing fractional availability seen as the conditioning pulse was made more positive (Fig. 1 E). This likely reflects a calcium-dependent component of inactivation. The extent to which inactivation could contribute to physiologically relevant synaptic responses was tested using 38-Hz trains of depolarization. The command waveform was based on the AP recorded from the zebrafish CaP motor neuron in vivo (Fig. 1 F). The transient calcium currents coincided with the repolarizing phase of the AP. Superimposing sample Ca_V2.1 and Ca_V2.2 currents associated with 12 consecutive depolarizations showed no change in peak amplitude during the train (Fig. 1 F).

Plotting of peak current density for individual recordings (Ca_V2.1, n = 6 and Ca_V2.2, n = 6) further confirmed the absence of inactivation during the stimulus train (Fig. 1 G). This suggests that the pronounced synaptic depression reported for zebrafish neuromuscular transmission was not a consequence of Ca_V2.1 calcium channel inactivation (13,14). There was a curious bimodal distribution of current densities recorded for Ca_V2.2. Comparisons of the low-and high-expressing calcium current showed no systematic differences in half-width so the differences are not a consequence of functional distinctions. This is consistent with the finding that the fitted decay was independent of current amplitude.

In response to voltage steps, the activation for both channel types followed a sigmoidal time course that was well described by an exponential raised to the second power (Fig. 2, A and B). This supports a transition between at least two closed states before opening. The relationship between activation time constants and membrane potential was bell-shaped for both channel types (Fig. 2 C). Additionally, the maximal time constants measured at 0 mV were approximately twofold faster for Ca_V2.1 (Fig. 2 C). Deactivation kinetics were determined by means of tail currents elicited by steps from +30 mV to potentials between −110 mV and +80 mV (Fig. 2, D and E). The current decays fit well to exponential curves over the −110 to +60 mV voltage range (Fig. 2, D and E). The time constants of deactivation also exhibited a bell-shaped relationship with voltage (Fig. 2 F). For both channel types, the voltage dependence of deactivation showed two components, with a distinctly steeper voltage dependence positive to −40 mV. This inflection was independent of current density, ruling out the possibility of inadequate voltage-clamp. At 0 mV, the average time constant for the Ca_V2.2 current was threefold larger than Ca_V2.1 values compared to only ∼30% larger at −110 mV. This difference reflected an overall steeper voltage dependence for Ca_V2.2.

Figure 2.

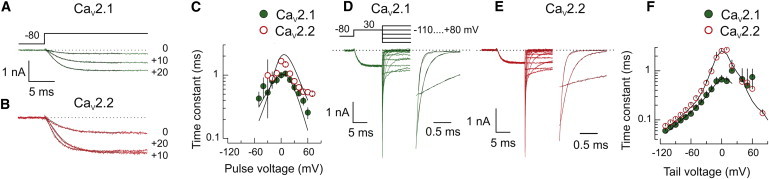
Time-dependent activation and deactivation of Ca_V2.1 and Ca_V2.2 currents. (A and B) Sample traces of Ca_V2.1 and Ca_V2.2 calcium currents showing the activation time course in response to three different voltage steps. The time course of each trace was fit using a single exponential raised to the second power (black line) and the time constants were determined for each potential (n = 10 and n = 8 for Ca_V2.2 and Ca_V2.1, respectively). (C) The time constants of activation for Ca_V2.1 (solid green symbols) and Ca_V2.2 (open red symbols) currents as a function of the voltage step. (Solid lines) Predictions from Scheme 1. (D and E) Tail currents associated with different voltages showing the voltage-dependence of the deactivation time course for the Ca_V2.1 and Ca_V2.2 tail currents, respectively. Expanded sample tail currents for both channel types that were fit to single exponential decay (in black) after ignoring the first 100 μs of the tail. The time constants correspond to 0.065, 0.15, and 0.65 ms for Ca_V2.1 and 0.09, 0.25, and 2.0 ms for Ca_V2.2 at −100, −50, and 0 mV, respectively. (F) The time constants of tail current deactivation as shown as a function of voltage for Ca_V2.1 (solid green symbols) and Ca_V2.2 (open red symbols). (Solid lines) Predictions based on Scheme 1. The parameters used to fit the relationships in panels C and F were α₁ = 400 s⁻¹, z = 1.8; β₁ = 765 s⁻¹, z = −0.7; α₂ = 251 s⁻¹, z = 1.4; β₂ = 1530 s⁻¹, z = −0.7 for Ca_V2.1 and α₁ = 130 s⁻¹, z = 1.16; β₁ = 490 s⁻¹, z = −1.85; α₂ = 4280 s⁻¹, z = 0.4; and β₂ = 1800 s⁻¹, z = −0.5 for Ca_V2.2.

These data were introduced into a minimal linear model (Scheme 1) in order to fit the voltage versus time constant relationships shown in Fig. 2, C and F:

$$\mathsf{C}\underset{{\beta }_1}{\overset{{\alpha }_1}{\rightleftarrows }}\mathsf{C}\underset{{\beta }_2}{\overset{{\alpha }_2}{\rightleftarrows }}\mathsf{O}$$ (Scheme 1)

The predictions were determined using the IChMascot environment (15). In this program, the characteristic differential equations of the models were solved by numerical integration and the Q-Matrix method. To initiate the fitting process, Hodgkin-Huxley-like rate constants were set to α₁ = 2α₂ and β₂ = 2β₁. At very negative voltages, the slope values from the voltage versus time constant relations (Fig. 2 F) were used to estimate β₂. On this basis, β₂ was fixed to 1800 s⁻¹ with the effective valence z = −0.5 for Ca_V2.2. From the activation time constants at voltages positive to −10 mV (Fig. 2 C), α₁ was fixed to 130 s⁻¹ with z = 1.16. With these constraints, the other four parameters were left free to converge for fitting. The same fitting strategy was used with the Ca_V2.1 with β₂ fixed to 1530 s⁻¹ with z = −0.7 and α₁ fixed to 400 s⁻¹ with z = 1.8.

Model-generated data that was filtered to 5 kHz, and fitted as the experimental data, predicted well the voltage-dependence of activation between −20 mV and +50 mV, the voltage range corresponding to the largest currents (Fig. 2 C). The model also predicted well the voltage-dependence of deactivation between −110 mV and +20 mV, describing the inflection in both channels’ voltage dependencies near −40 mV (Fig. 2 F).

Single channel conductance

Nonstationary noise analysis (16,17) was used to estimate the elementary channel current for Ca_V2.1 and Ca_V2.2 channels. The cell was stepped to either +80 or +40 mV, followed by a return to negative potentials and the variance associated with the current fluctuations was determined for all but the first 300 μs of the decay phase of the tail current (Fig. 3, A and B). For both channel types, the variance during the decay exhibited a parabolic relationship with the mean current amplitude (Fig. 3 C). Averaged maximal P_O values of 0.73 ± 0.14 and 0.78 ± 0.15 for Ca_V2.1 and Ca_V2.2, respectively, were not significantly different at P ≤ 0.05 (p-value = 0.337). Current-voltage relationships were constructed for both channel types and fitted to a divalent GHK permeation curve with zero current predicted near +80 mV (Fig. 3 D). The interpolated single channel amplitudes at 0 mV are 0.12 pA for Ca_V2.2 and 0.14 pA for Ca_V2.1, which agree with the estimated values obtained from hippocampal mossy fiber boutons (3).

Figure 3.

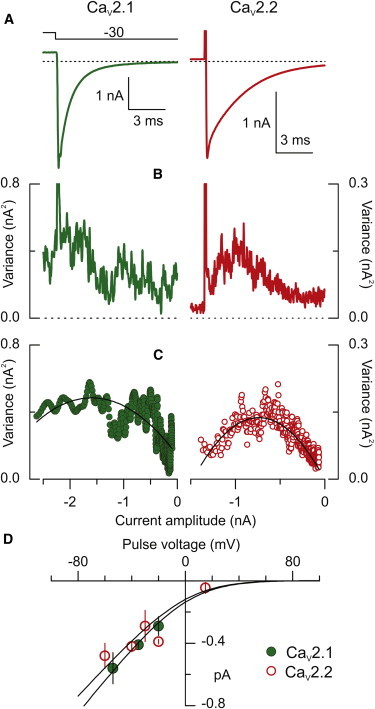
Single channel conductance of Ca_V2.1 and Ca_V2.2 channels. (A) Average tail currents for 79 Ca_V2.1 traces (green trace) from a prepulse to +40 mV and 45 Ca_V2.2 traces from a prepulse to +80 mV (red trace). (B) Variance associated with the decay phase between successive tail currents shown in (A). (C) Mean versus variance plots for Ca_V2.1 (solid green symbols) and Ca_V2.2 (open red symbols) from the traces in (B). The data corresponding to the first 300 μs after the voltage jump were discarded. The relationship in panel C was obtained from the subsequent 10 ms after the voltage jump. Data were fitted with the expression: ν = i^∗I−I²/n + ν_b, where ν is the variance, i is the single channel amplitude, I is the average current amplitude during the tail, n is the number of channels, and ν_b is the variance associated with the background noise. For these particular measurements, the fitting parameters were i = −0.42 ± 0.02 pA, n = 7747 ± 641, ν_b = 0.135 ± 0.08 nA² for Ca_V2.1; and i = −0.34 ± 0.01 pA, n = 4238 ± 138, and ν_b = 0.015 ± 0.002 nA² for Ca_V2.2. (D) The current voltage relationship from the estimated single channel currents for Ca_V2.1 (green solid symbols, 4 cells) and Ca_V2.2 currents (red open symbols, 7 cells). For Ca_V2.1, the data taken at −60 and −50 mV, and at −40 and −30 mV were pooled, thus each data point represents the average of at least four experiments. The continuous lines were generated using a GHK curve for a divalent cation assuming a reversal potential of +80 mV for both channels.

Ca_V2.1 versus Ca_V2.2 current during an AP

A simulated AP waveform, based on the motor neuron AP (Fig. 4 A), was used to predict both the time course and amplitude of inward calcium current using the kinetic model provided by Scheme 1 (see Materials and Methods). Calcium currents, associated with the AP waveform, were normalized to the maximal calcium tail currents in order to compare the modeled to the experimentally recorded calcium currents and between cells with different calcium current densities. The maximal tail current for each recording was determined by means of a voltage step from +70 mV to −80 mV. Open probabilities for modeled calcium channels that were associated with the simulated AP were calculated from the fractional conductance option in the software IonChannelLab (12), with a purely Ohmic permeation regime.

Figure 4.

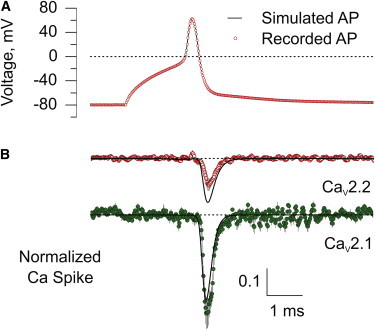
Calcium currents for both channel types in response to the motor neuron AP waveform. (A) Comparison of a recorded AP waveform from a CaP motor neuron in vivo (red open circles) with the one used to simulate calcium currents with Scheme 1 (solid line). The simulated AP waveform was constructed from 27 voltage ramps concatenated to match the recorded waveform. (Dashed line) 0 mV. (B) Experimentally measured average Ca_V2.2 (n = 8) and Ca_V2.1 (n = 7) calcium currents elicited in response to a neuronal AP. To obtain average values, each recording was normalized to the total available calcium current in that cell by using the peak tail current during a step from +70 mV to −80 mV. (Solid lines) Predicted calcium currents with the GHK permeation regime in response to the simulated AP based on Markov chain simulations using the software IonChannelLab (12). Parameters were based on Scheme 1 and extra- and intracellular Ca²⁺ concentrations were set to 2 mM and 4 μM, respectively, to yield a calcium reversal potential of ∼+80 mV. (Calibration bar) 0.1 normalized calcium current; (dashed traces) 0 current level.

The half-duration of the measured calcium current for Ca_V2.2 and Ca_V2.1 corresponded to 0.39 ± 0.09 ms (n = 8) and 0.30 ± 0.05 ms (n = 7), respectively, reflecting a ∼30% difference (p < 0.05). The predicted half-durations determined on the basis of Scheme 1 were 0.39 and 0.33 ms for Ca_V2.2 and Ca_V2.1, respectively. Estimates of P_O during the AP reached 0.5 for Ca_V2.1 versus 0.22 for Ca_V2.2, representing a 2.3-fold difference. However, correcting for differences in predicted/experimental peak current obtained in Fig. 4 B data, P_O values reached 0.15 and 0.59 for Ca_V2.2 and Ca_V2.1, respectively, yielding a P_O ratio of ∼4. The magnitude of the calcium current with an idealized AP lacking the capacitive charging component predicted a negligible decrease for the Ca_V2.1 and ∼10% for Ca_V2.2 (data not shown). We interpret the decrease to mean that the slower rise in the voltage due to the C-charging artifact for Ca_V2.2 leads to more activation because their P_O curve is shifted toward more negative voltages. P_O was also estimated for AP waveforms that were threefold and 10-fold longer in duration, thereby slowing the depolarizing phase of the AP. For an AP three-times longer, the predicted P_O values peaked at ∼0.9 and ∼0.6 for Ca_V2.1 and Ca_V2.2, respectively. For an AP 10-times longer in duration, the corresponding P_O values reached ∼0.95 and ∼0.9, respectively (data not shown).

Discussion

Investigation into the biophysical properties of the zebrafish Ca_V2.1 calcium channel was prompted by our unexpected discovery of its central involvement in neuromuscular transmission (11). Before this finding, it was widely assumed that Ca_V2.2 mediated neuromuscular transmission in lower vertebrates (18). However, this assignment was based solely on pharmacology rather than molecular sequence. Further fueling our interest were two physiological findings pointing to specific roles in fast transmission played by Ca_V2.1. First, at the zebrafish neuromuscular junction, Ca_V2.1 is the sole mediator of synchronous fast transmission and is not required for slow asynchronous release (14). Second, Ca_V2.1-mediated synchronous release in zebrafish places unusually high demand on the release of transmitter from the motor neuron.

Release in zebrafish CaP motor neurons is limited to a quantal content of only 8–15 (19). Despite this limitation, the synapse can follow frequencies in excess of 100 Hz without failures, even after a drop in release probability associated with depression. Our findings now indicate that Ca_V2.1 is well suited for this role in minimizing synaptic failure. Specifically, the P_O value during the fast AP for zebrafish Ca_V2.1 reaches ∼0.6 and is fourfold higher than the Ca_V2.2 counterpart. The high P_O ensures sufficient calcium entry for exocytosis and the fast kinetics, and absence of inactivation contributes to the ability to follow firing at high frequencies.

That Ca_V2.1 has a higher P_O measurement than Ca_V2.2 was first determined for calcium channels in mossy fiber terminals (3). In that study, as with ours, the P_O was based on computational estimates associated with an AP waveform. In our study, the higher P_O for Ca_V2.1 agreed well with the computational predictions using Scheme 1. The differences in P_O between channel types vanished, however, when the estimates were made after longer depolarizations. This observation may also account for the lack of difference found in side-by-side recordings of the two channel types from the Calyx of Held, where long-step depolarizations were used (20). Thus, it seems critical to obtain estimates of P_O using physiologically relevant command waveforms.

While both mossy fiber and our studies estimate a higher P_O for Ca_V2.1, our fourfold difference is considerably higher than that from the mossy fibers (3). This could arise from either differences in primary data and/or in the methods of analysis used to generate the model. Overall, the methods and approaches utilized were similar between studies with the sole distinction of models used to estimate P_O. For mossy fiber recordings, a six-state model for gating was used (3), whereas we found that a simpler three-state scheme was adequate for fitting the data. The greatest source of difference between studies lies in the data involving voltage dependence of channel kinetics. The only reported functional distinction for the two channel isoforms in mossy terminals was a 5-mV positive shift in the voltage dependence of activation for Ca_V2.2. We identified faster activation and deactivation along with a shallower voltage-dependence of activation for Ca_V2.1. This functional difference acts to promote more effective calcium channel activation during brief depolarizations. Consistent with the findings from Calyx of Held differences in P_O are minimized as the AP broadens (3). Thus, for brief depolarizations Ca_V2.1 open more efficiently, whereas longer depolarizations would be required to achieve equivalent opening by Ca_V2.2.

Why is there a higher P_O ratio for Ca_V2.1/Ca_V2.2 in zebrafish motor neurons when compared to mossy fiber terminals? First, the two studies may be comparing calcium channels with different subunit compositions. In the case of mossy fibers, isoform assignment rests solely on pharmacology, not molecular identification (3). As such, only the identity of the α-subunit is known. The pharmacology on the mossy fibers does not inform the overall subunit composition with regard to accessory subunits. We have assigned the Ca_V2.1 α-subunit as the principal isoform in zebrafish motor neuron terminals on the basis of the tb204a mutant line (11). Our assignment of zebrafish β4 was based on published expression patterns in zebrafish larvae. Seven genes have been identified in the zebrafish genome encoding voltage-dependent calcium channel β-subunits with distinct expression patterns during development (21). We chose to express β4 together with other calcium channel subunits in this study because it has been shown to express in spinal cord in a segmental fashion, consistent with the location of primary motor neurons. Both α- and β-cDNAs used in the study represent the most abundant splice variants in larval fish. Coexpression with α₂δ₁ subunits was based on the requirement for functional expression and their known role in stabilizing the core complex (22). While HEK cells do not express calcium current, it remains formally possible that they contribute some unidentified functional component to the expressed channel because this cell type does express a few neuron-specific genes (23). In light of the uncertainty as to molecular composition at mammalian nerve terminals, difference in composition between the two preparations remains a viable candidate.

Second, the differences between studies could reflect incomplete voltage control and limited speed provided by conventional patch-clamp recordings that vary with experimental context. The functional distinctions that we identified between channel types expressed in HEK cells placed the highest demands on voltage control. The functional distinctions reported for morphologically simplified HEK cells may be even further obscured in morphologically complex nerve terminals owing to compromised voltage control.

Third, the differences could reflect the evolutionary distance between fish and mammals or alternatively a difference in Ca_V2.1 function in the peripheral nervous system compared to the central nervous system. In sum, the answer to this question will have to await further comparative analyses.

Conclusions

Both mossy fiber and zebrafish studies support the prediction that Ca_V2.1 channels open more effectively during brief APs than the Ca_V2.2 counterpart. Our findings, as well as with those from mossy fiber terminals, show that prolongation of the AP reduces the difference in P_O for the two isoforms. This further points to a specific role of Ca_V2.1 in fast neuronal firing (3). This functional bias toward speed for Ca_V2.1 is in line with studies showing that Ca_V2.2 underlies slow release in chromaffin cells and asynchronous release in certain central neurons (1,2,24). The slow release process depends on calcium accumulation that is associated with repetitive firing (3,25).

Ca_V2.1 and Ca_V2.2 are the substrates for different modulation resulting in altered AP waveforms and associated changes in calcium entry (26,27). In addition to functional distinctions, there likely exist additional important differences between calcium channel isoforms, such as sensitivity to modulatory agents and physical coupling to release machinery for specific isoforms (6,27–29). Overall, evidence is mounting in support of very different functional roles played by these two channel types, perhaps answering, in part, the question as to why they are coexpressed at so many synapses.