Unconventional Mechanics of Lipid Membranes: A Potential Role for Mechanotransduction of Hair Cell Stereocilia

Abstract

A force-conveying role of the lipid membrane across various mechanoreceptors is now an accepted hypothesis. However, such a mechanism is still not fully understood for mechanotransduction in the hair bundle of auditory sensory hair cells. A major goal of this theoretical assessment was to investigate the role of the lipid membrane in auditory mechanotransduction, especially in generating nonlinear bundle force versus displacement measurements, one of the main features of auditory mechanotransduction. To this end, a hair bundle model that generates lipid membrane tented deformation in the stereocilia was developed. A computational analysis of the model not only reproduced nonlinear bundle force measurements but also generated membrane energy that is potentially sufficient to activate the mechanosensitive ion channel of the hair cell. In addition, the model provides biophysical insight into 1) the likelihood that the channel must be linked in some way to the tip link; 2) how the interplay of the bending and stretching of the lipid bilayer may be responsible for the nonlinear force versus displacement response; 3) how measurements of negative stiffness may be a function of the rotational stiffness of the rootlets; and 4) how the standing tension of the tip link is required to interpret migration of the nonlinear force versus displacement and activation curves. These are all features of hair cell mechanotransduction, but the underlying biophysical mechanism has proved elusive for the last three decades.

Introduction

Auditory mechanosensation starts when the sensory hair cells of the inner ear, a part of the organ of Corti within the cochlea, are mechanically stimulated in response to sound, creating pressure waves between the cochlea compartments. Each hair cell features an apically located bundle of stereocilia of varying lengths extending from its top side, forming an elaborate structure with linkages connecting the tips of adjacent stereocilia with one another—features known as tip links. When these bundles of stereocilia, or hair bundles, are deflected in response to sound in the cochlea, they generate electrical signals that can trigger a sensation of hearing once they reach the brain (1). When a hair bundle is deflected, tension is produced in the stereociliary tip links, which in turn release energy used for activation of the mechanosensitive (MS) transduction channel, which is presumed to be located within the tip complex of each stereocilium (2).

Consistent with studies on hair bundles in many different organ systems and animal species, the nonlinear force versus displacement relationship dictates that the minimum stiffness is generated with the intermediate displacement of bundles (3–5). As this nonlinear force versus displacement measurement is a central feature of hair bundle mechanics and mechanotransduction activation, elucidating the underlying molecular and biophysical components is crucial to our overall understanding of auditory neuroscience.

The traditional gating spring model suggests that hair bundle nonlinear force versus displacement measurement results from gate opening of the hair cell MS channel (3). However, a problem with this long-standing hypothesis is that the length estimates for the channel gating are quite large. Here, an alternative theory is proposed to determine whether deformation of the lipid membrane of the stereocilia induces this nonlinearity, and to elucidate the potential influence of the lipids in activation of the hair cell MS channel.

To this end, a biophysical hair bundle model based on the viscoelastic lipid membrane system of the stereocilia was developed. This model considers elastic and hydrodynamic responses of the lipid membrane under ciliary cytoskeleton interactions. Although the model reproduces the nonlinear force measurement from turtle auditory papilla hair cell bundles in this work, the theory can be applied to hair bundles in any system of any species with some alterations in geometry. Furthermore, the model provides biophysical insights into many important aspects of hair bundle mechanotransduction, including channel activation and its relation to bundle nonlinearity, negative stiffness, linearization, and migration components of the nonlinear bundle force measurement, the underlying mechanism of which has remained elusive during the past three decades.

Materials and Methods

Description of the biophysical hair bundle model

The model considers two basic components. The first is the rigid-body kinematic component of the bundle, which describes the motion of the side links, tip links, and rigid stereocilia, and the translation of their motion to the membrane deformation in the stereocilia. When the bundle is displaced, stereocilia bend about their base from the resting position by deflecting roots (Fig. 1 B). Here, the stiffness of the rootlet is parameterized with the rotational spring (k_i in Eq. 1). The stereocilia are rigid and increase in height toward a taller edge. Also, they are linked to each other by side and tip links (Fig. 1 A). The side links function to ensure that the hair bundle deflects coherently and is able to slide along the top edge of the stereocilia (6–8). Both side and tip links are considered to be inextensible (9).

Figure 1.

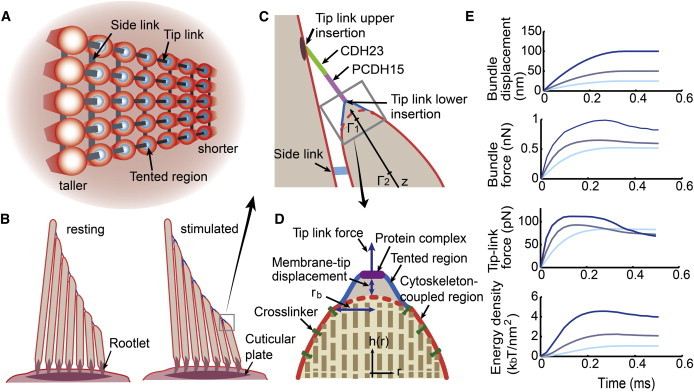
Description of the hair cell stereocilia bundle from turtle auditory papilla. (A) Top view of five rows and seven columns of stereocilia bundle interconnected by side and tip links. (B) Side view of the hair bundle provides the kinematic components in its resting (left) and stimulated (right) configuration. (C) Ciliary tip and tip-link complex. The tip link, composed of CDH23 and PCDH15, is inserted into the upper dense region, whereas the other end is tethered into the lipid membrane. Tension on the tip link separates the membrane from the cytoskeleton. (D) Partitioned lipid membrane for the stereocilia tip. The red region could be tightly coupled to the stereocilia cytoskeleton (i.e., a bundle of actin filaments) through a cross-linker; blue indicates the membrane tented region into which the tip link inserts. A possible stiff region for the channels and the other proteins with radius of 3 nm is shown in purple. (E) Model responses to different-size step functions (first row) are indicated by different intensities of blue. Bundle force (second row), single tip-link force (third row), and membrane free-energy density at a point 3.5 nm from tip-link lower insertion (fourth row) are plotted. See Table 1 for the parameters used. See Fig. S7 for results obtained without considering the stiff protein region. To see this figure in color, go online.

The second component is the lipid bilayer membrane of the stereocilia. The lipid membrane of a coarse-grained continuum, according to the theory originally introduced by Canham (10) and Helfrich (11), is presented as two regions in this model: a tented-tip region into which the tip link inserts and a cytoskeleton-coupled region where the membrane is more tightly associated with the cytoskeleton (Fig. 1, C and D). In the tented-tip region, the membrane is stretchable in the tangential direction of the membrane and flexible (i.e., bendable) to change the curvature of the surface, whereas in the cytoskeleton-coupled region, the membrane is not flexible (although it is still stretchable). Therefore, the tip region can separate from the underlying cytoskeleton when it is mechanically perturbed, whereas the cytoskeleton-coupled region maintains constant curvature of the cytoskeleton. In addition, the lipid mobility in the cytoskeleton-coupled region is parameterized with the diffusion constant but is considered quasi-statically in the tented-tip region. Since the tented region presumably does not interact with the cytoskeleton, it should have minimal lipid viscosity, whereas the cytoskeleton-coupled region might have significant lipid viscosity. In a cellular environment where the membrane interacts strongly with the cytoskeleton, viscous shear drag and the corresponding nonuniform stretching of the membrane can be significant. As denoted in Figs. 1 D and S4 B in the Supporting Material, the possible cross-linking proteins anchored to the cytoskeleton may serve as a barrier against the flow of lipids, and such interactions could potentially generate viscous drag force for lipid molecules within the membrane (12,13). Therefore, lipid molecules quickly reorganize their distribution to achieve a uniform lipid area density in the tented region, but a considerable lipid density gradient can be generated in the cytoskeleton-coupled region. At the tip-link lower insertion point, a small rigid disk (radial size ∼3 nm) is also assumed to represent a possible region for stiff membrane proteins, including the MS channels, three transmembrane insertion domains of the tip link (9), and tip-link-associated proteins such as TMIE and TMHS/LHFPL5 (14,15) (note that simulation results obtained without consideration of the stiff protein region are available in Figs. S7–S11). Finally, the radius of the interface of the two membrane regions is termed r_b and can be systematically varied.

The interaction of the membrane and cytoskeleton, which is central to this model, is not a heretical idea, since the possibility has already been biologically characterized for the stereocilia. First, the morphology suggests that the upper tip-link insertion is kept rigid by a plaque containing a variety of important molecules, such as harmonin and whirlin (1), whereas membrane tenting is often observed by electron microscopy on the lower insertion site (9,16–18). Second, electron microscopy studies have confirmed the membrane-cytoskeleton connection along the stereocilia, and more recent experiments even identified proteins such as radixin and myosin IIIa as potential cross-linker molecules for this connection (19,20). Thus, the assumption regarding the membrane-skeleton interaction in both the tented-tip region and the cytoskeleton-coupled region is well supported by existing morphological and functional data.

A flow diagram of the model components and their interactions is presented in Fig. S1. Briefly, a prescribed stimulus of the bundle is introduced and translated kinematically to the tip-link lower insertion point, which gives the magnitude of the membrane-tip displacement for each stereocilium. According to the kinematic component of the bundle, membrane-tip displacements for six stereocilia in a row are identical to the given stair-pattern geometry of the bundle (see Figs. S2 and S5); therefore, a single analysis of the membrane can be equally applied to all stereocilia. When the membrane is pulled, the tented-tip membrane undergoes elastic deformation associated with bending and stretching, whereas the viscoelastic property of the cytoskeleton-coupled region results in nonuniform stretching of that region, which ultimately modulates lipid flow to the tented region. Therefore, elastic deformations together with fluidic interactions between the two partitioned regions determine the tip-link force and free-energy density of the membrane. Finally, the bundle force is determined using the system equation (see Eqs. 1 and 2), which expresses the overall moment equilibrium of the bundle. From this model, the tip-link force, hair bundle force, and free-energy density at specific points in the lipid membrane in response to a hair bundle deflection can be determined. Movie S1 shows the bundle motion, deformed shape and free-energy density profile for the tented tip region, and lipid density profile for a single stereocilium in response to a hair bundle displacement of 50 nm. Table 1 summarizes the primary parameter values used in the model.

Table 1.

Summary of the parameters

Material properties	Selected values
ϕ0 (resting lipid areal density)	1000/629 × 1018/m2
σ0 (lipid bilayer surface tension with zero density strain)	exp(−7) mN/m
km (lipid bilayer bending modulus)	36 kBT
Kapp (lipid bilayer apparent area stretching modulus)	300 mN/m
krootlet (rootlet rotational stiffness of single stereocilium)	0.2 fN/rada
D (lipid diffusion constant)	5 μm2/s
ΔAchannel (hair cell MS channel area difference between open and closed states)	3 nm2
ΔG (hair cell MS channel internal energy difference between open and closed states)	7 kBT
rb (radial size of axisymmetric tented membrane)	22 nmb

For a discussion about how these parameters are selected, see Supporting Material.

^aThe value is varied from 0.2 to 0.05 fN/rad in Fig. 4A.

^bThe value is varied from 19 to 30 nm in Figs. 2, A and B, and 4B.

Kinematics and mechanics of the hair bundle

In the hair bundle model, the actin core, tip links, and side links are modeled as rigid bodies (see Fig. 1). The side links are allowed to slide freely along the surface of the taller stereocilium to constrain a fixed distance between two adjacent stereocilia (8). The model contains two deformable components: the rotational elastic spring of the rootlet and the lipid bilayer membrane of each stereocilium. These two elements interact with the rigid-body components to yield the following equilibrium equation (Eq. 1) for a hair bundle row composed of seven stereocilia (see Fig. S2 for the free-body diagram):

$$\begin{array}{c}\left[\begin{array}{cccc}{a}_1\text{cos}\left({\theta }_1\right)& -c_1& & \\ & a_2\text{cos}\left({\theta }_2-{\theta }_1\right)& \ddots & \\ & & \ddots & -c_6\\ & & & a_7\text{cos}\left({\theta }_7-{\theta }_6\right)\end{array}\right]\left[\begin{array}{c}F\\ F_{sl1}\\ ⋮\\ F_{sl6}\end{array}\right]=\\ \left[\begin{array}{cccc}{k}_1& & & \\ & \ddots & & \\ & & & \\ & & & k_7\end{array}\right]\left[\begin{array}{c}{\theta }_1-{\theta }_{1,init}\\ ⋮\\ \\ {\theta }_7-{\theta }_{7,init}\end{array}\right]-\\ \left[\begin{array}{cccc}0& -b_1\text{cos}\left(\frac{\pi }{2}-{\alpha }_1\right)& & \\ & a_2\text{cos}\left(\frac{\pi }{2}-{\alpha }_1+{\theta }_2-{\theta }_1\right)& \ddots & \\ & & \ddots & -b_6\text{cos}\left(\frac{\pi }{2}-{\alpha }_6\right)\\ & & & a_7\text{cos}\left(\frac{\pi }{2}-{\alpha }_6+{\theta }_7-{\theta }_6\right)\end{array}\right]\left[\begin{array}{c}0\\ f_{tl1}\\ ⋮\\ f_{tl6}\end{array}\right].\end{array}$$ (1)

Each stereocilium is identified with index i, with the shortest designated i = 1 and the tallest i = 7. The coefficients a_i, b_i, and c_i correspond to the total stereocilium height, the height to the tip-link upper insertion site, and the height to the side-link sliding insertion point, respectively; θ_i is the cuticular plate to rootlet angle; α_i is the angle between the tip link and the stereocilium; f_tli is the force in the tip link connecting the i and i + 1 stereocilia; F_sli is the force in the side link connecting the i and i + 1 stereocilia; and F is the force applied to the tallest stereocilium. Expressing Eq. 1 in matrix form,

$$\stackrel{\rightharpoonup }{\text{A}}\stackrel{\rightharpoonup }{F}=\stackrel{\rightharpoonup }{K}\stackrel{\rightharpoonup }{\theta }-\stackrel{\rightharpoonup }{\text{B}}{\stackrel{\rightharpoonup }{f}}_{TL}$$ (2)

the components k_i of the diagonal matrix $\stackrel{\rightharpoonup }{K}$ represent the linear torsional stiffness of the stereociliary rootlets. In prescribing the motion of the hair bundle temporally (Fig. 1 E, first panel), the arrays $\stackrel{\rightharpoonup }{\theta }$, $\stackrel{\rightharpoonup }{\text{A}}$, and $\stackrel{\rightharpoonup }{\text{B}}$ are determined from the kinematics of the bundle motion. Equation 2 can be solved for the vector $\overline{F}$, which includes the bundle row force F, as well as the internal forces F_sli in the six side links. Assuming five rows of stereocilia shown in Fig. 1 A, the total summed bundle force is then simply found from F_total = 5F.

Membrane deformation in the tented-tip region

With the given time-dependent membrane-tip displacements translated from the bundle displacement in Fig. 1 E (first panel), the force applied on the tip link and the shape of the membrane in the tented-tip region for each state at time t can be found by modeling the lipid membrane deformation over the tip region. Given the axisymmetric geometry of the stereociliary tip, shown in Fig. 1 D, the total energy functional of the tented-tip membrane for each state (i.e., at time t with the given membrane-tip displacement) is given by

$${\Pi }_{total}=E_{tented-tip}-W,$$ (3)

where E_tented-tip is the membrane energy and W is the external work. The membrane energy functional can be written in a Canham-Helfrich form (10,11,21):

$$E_{tented-tip}=\int \left(2k_m{\left(H-H_0\right)}^2+k_{g}K+{\sigma }_t\right)dA.$$ (4)

The constants k_m and k_g in Eq. 4 are the bending modulus and Gaussian curvature modulus, respectively. In this model, k_g = (1 − υ)k_m = 0.5 k_m is assumed (22), where υ is the Poisson ratio of the lipid membrane. The surface tension σ_t at time t is treated as a constant state variable in Eq. 4 by assuming grand canonical (i.e., open) systems. Using the Monge gauge, which employs the function h(r) to measure the height of the lipid membrane above a reference plane, and the radial coordinate r (Fig. 1 D), the mean curvature H and Gaussian curvature K appearing in Eq. 4 can be expressed as

$$H=0.5\left(\frac{h_{rr}}{{\sqrt{1+h_r^2}}^3}+\frac{h_r}{r\sqrt{1+h_r^2}}\right)$$ (5)

$$K=\frac{h_{rr}{h}_r}{r{\left(1+h_r^2\right)}^2}.$$ (6)

The first and second derivatives of the membrane height function h(r) are indicated by h_r and h_rr, respectively. In Eq. 4, H₀ denotes the spontaneous curvature of the membrane, which can be equivalent to the cytoskeleton curvature for the tip region, and $dA=2\pi r\sqrt{\left(1+h_r^2\right)}dr$ is the membrane axisymmetric area element. For all values of tip-link stimulus, changes in the Gaussian curvature energy integrated over the membrane surface are identically zero according to the Gauss-Bonet theorem (23).

The equilibrium configuration, free energy, and free-energy densities of the tented-tip membrane for each state can be obtained by finding the stationary of the total potential energy functional given by Eq. 3, such that $\delta {\Pi }_{total}=\delta E_{tented-tip}-\delta W=0$. With the prescribed membrane-tip displacement, this is equivalent to finding h(r) that satisfies $\delta E_{tented-tip}=0$ i.e., the minimum energy configuration of the membrane. For this purpose, the shape of the lipid membrane height h(r) is parameterized by using a Fourier series expansion, and the membrane energy is then minimized with respect to the Fourier coefficients. At the junction where the tented-tip region joins the cytoskeleton-coupled membrane, the radius is denoted by r = r_b and the tented-tip membrane height function h(r) is also constrained to be C¹ continuous with the cytoskeleton-coupled membrane. At the boundary of the stiff protein region, r = 3 nm, the height function is constrained to satisfy h_r = 0, which is required by symmetry.

To estimate the tip-link force for each state, the concept of virtual displacements can be used. Noting that h(0) in Eq. 7 defines the virtual membrane-tip displacement, the external work W of the tip-link force appearing in Eq. 3 is given by

$$W=f_{tl}h\left(0\right).$$ (7)

From Eq. 7 it follows that the tip-link force at time t is then given by $f_{tl}=\partial E_{tented-tip}/\partial h\left(0\right)$ with respect to the energy minimized membrane configuration by varying the virtual displacement h(0). The tip-link force may be decomposed into flexing and stretching contributions for the membrane deformation as $f_{tl}=f_{flexing}+f_{stretching}$ by using Eq. 4. Here, flexing and stretching forces can be defined by $f_{flexing}=\partial \left(\int 2k{\left(H-H_0\right)}^{2}dA\right)/\partial h\left(0\right)$ and $f_{stretching}=\partial \left({\sigma }_t\int dA\right)/\partial h\left(0\right)$, respectively (see Fig. 3 B for the tip-link force decomposition).

Figure 3.

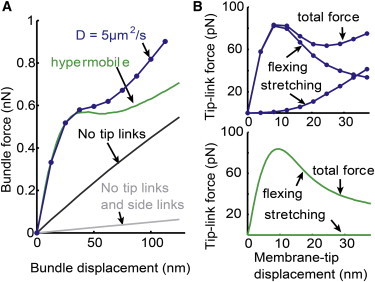
Bundle force versus displacement responses and the tip-link force decomposition. (A) Force versus displacement responses for the five rows of the seven-staircase-pattern stereocilia bundle shown in Fig. 1A. From the tip-link force versus membrane-tip displacement response in the middle panel of Fig. 2A (r_b = 22 nm), bundle force versus displacement responses are plotted. Two different mobilities of the lipid in the cytoskeleton-coupled region (blue for D = 5μm²/s and green for hypermobile lipid) are considered. Detaching the tip links from the membrane linearized the response (black), and disconnecting the side links as well further reduced the magnitude of the linear response (gray). (B) Membrane flexing and stretching components of the tip-link force. For each case of lipid mobility, the total single tip-link force is decomposed into two different force contributions (see Materials and Methods section for the mathematical definition of the forces). For the hypermobile case, the membrane stretching component of the tip-link force is negligible. See Table 1 for the parameters used. See Fig. S9 for results obtained without considering the stiff protein region. To see this figure in color, go online.

Since lipid molecules flow into the tented-tip region from the cytoskeleton-coupled region, the lipid concentration and the corresponding surface tension in the tented tip can be changed temporally for different states. Therefore, an expression for the membrane surface tension σ_t can be found from the vesicle in a pipet experiment as follows (24,25):

$$\begin{array}{l}{\sigma }_t={\sigma }_0\text{exp}\left(\frac{8\pi k_m}{k_{b}T}{\alpha }_t\right)for{\alpha }_t\le {\alpha }_{cross}\hfill \\ {\sigma }_t=K_{app}\left({\alpha }_t-{\alpha }_{cut}\right)for{\alpha }_t>{\alpha }_{cross}\hfill \end{array}.$$ (8)

Here, the cutoff strain α_cut and crossover strain α_cross can be selected to have smooth continuity for two surface tension equations in Eq. 8 at α_cross. σ₀ is surface tension with zero strain and K_app is the apparent area stretching modulus. The lipid density strain at time t, α_t is simply ${\alpha }_t={\varphi }_0/{\varphi }_t-1$, where ϕ_t and ϕ₀ are the lipid number density (number of lipid molecules / apparent, i.e., projected membrane area) at time t and the resting configuration (i.e., t₀), respectively. The bending rigidity k_m of the membrane might also be renormalized and vary for different states due to stretching of surface ripples (26,27). However, such an effect is assumed to be negligible for the main results of this work.

Theory for lipid flow in the stereocilia

The lipid flow in the cytoskeleton-coupled region modulates the lipid density in the tented-tip membrane, and the rate of transport depends on the mobility of lipids in the cytoskeleton-coupled region. Under the action of tip-link pulling, the movement of the continuous membrane from the viscous skeleton-coupled region to the minimally viscous tip region can be controlled by two different kinds of physical flow of the lipid molecules in the cytoskeleton-coupled compartment (see the illustration in Fig. S3 for the motion of lipids with different mobility).

First, the diffusive flow generated by Brownian motion of the lipid follows the lipid density gradient, and the diffusive flux of lipids can be modeled by using Fick’s law as follows:

$$J_{diffusion}\left(z,t\right)=-DL\left(z\right)\frac{\partial }{\partial s}\varphi \left(z,t\right).$$ (9)

Here, the z coordinate lies on the central axis of the cylindrically symmetric cytoskeleton-coupled region shown in Fig. 1 C. The arc-length element is given by $ds=\sqrt{d{z}^2+d{r}^2}$, where r(z) is the radius of the cylindrical stereocilia at z. The circumferential length of the cytoskeleton-coupled region at z is thus given by $L\left(z\right)=2\pi r\left(z\right)$. The diffusion constant for the lipids in this region is denoted by D and ϕ(z, t) is the lipid number density, which varies spatially with respect to z and temporally with respect to t.

The second component is the convectional flow of lipids. The term “convection” may remind us of the lipid movement due to the flow of the external media. In fact, most studies involving modeling of lipid convectional flow dealt with a velocity field directly applied to the lipid membrane (28–30). However, the convectional velocity formulated here is driven by the change in the potential energy interaction among lipid molecules. As denoted in Fig. S4 B, the cross-linking proteins anchored to the cytoskeleton may serve as flow barriers for the freely mobile lipid molecule in the membrane (12,13), and such viscous interactions potentially generate nonuniform stretching of the membrane when it is mechanically perturbed. The nonuniform stretching and corresponding surface tension gradient may result in spatial variation of the convective velocity $\upsilon \left(s,t\right)$ of the lipid molecules. In the cytoskeleton-coupled region, the convective flux of the lipid is formulated as follows (see Supporting Material for the detailed formulation of Eq. 10):

$$J_{convection}\left(z,t\right)=L\left(s\right)\varphi \left(s,t\right)\upsilon \left(s,t\right)=\frac{2D}{k_{b}T}L\left(z\right)\frac{\partial \sigma \left(z,t\right)}{\partial s},$$ (10)

where k_B is Boltzmann’s constant and T is the temperature in Kelvin. Here in the cytoskeleton-coupled region, the surface tension σ is also a function of ϕ given by Eq. 8, but the difference is that the lipid number density varies both temporally and spatially while the value is spatially uniform in the tented-tip region. Quantitative analysis of Eqs. 9 and 10 indicates that in most cases the lipid flux has a much greater contribution from the convection, whereas the contribution from the diffusion is minimal. Now, considering particle number conservation (i.e., balance law), the final equation for the lipid flow and the corresponding lipid density profile in the cytoskeleton-coupled region of the stereocilia can be found from

$$\frac{\partial }{\partial t}\left(L\left(z\right)\varphi \left(z,t\right)\right)=D\frac{\partial }{\partial s}\left(L\left(z\right)\frac{\partial \varphi \left(z,t\right)}{\partial s}-\frac{2}{k_{b}T}L\left(z\right)\frac{\partial \sigma \left(z,t\right)}{\partial s}\right).$$ (11)

The lower boundary of the membrane is defined by a plane with elevation given by z = Γ₂ (z = Γ₂ and z = Γ₁ are denoted in Fig. 1 C). The boundary condition imposed on ϕ at this plane corresponds to a constant resting lipid density:

$$\varphi \left({\Gamma }_2,t\right)={\varphi }_0.$$ (12)

This boundary condition corresponds to an infinite supply of lipid molecules at fixed number density. The upper coupled region boundary is located at the interface with the tented-tip region at z = Γ₁. The boundary condition imposed here describes a balance of lipid flux at the interface and the time rate of change of the total number of lipid molecules in the tented tip:

$$J_{diffusion}\left({\Gamma }_1,t\right)+J_{convection}\left({\Gamma }_1,t\right)=-\frac{\partial }{\partial t}\left({\varphi }_{tip}{A}_{tip}\right),$$ (13)

where A_tip is the area of the tented-tip membrane. This boundary condition implies that lipids supplied from the cytoskeleton-coupled region to the tip region instantaneously reorganize the lipid distribution to produce a uniform lipid density over the tip (see Fig. S3). When the membrane is not pulled, the resting lipid density is initially uniform (i.e., ϕ (z, t = 0) = ϕ₀). The lipid transport model presented in this study is implemented numerically by using a finite-difference scheme.

Probability of opening the channel

The possibility that the membrane free-energy density in the tip region can be used to determine the opening of the mechanotransduction channel is also explored. The total potential energy of a channel E, including the applied external work from the lipid membrane to the channel, $\tau$ΔA_channel, can be written as

$$E\left(\lambda ,\tau \right)=\left(1-\lambda \right)G_{closed}+\lambda G_{open}-\lambda \tau \Delta A_{channel}.$$ (14)

The free-energy density of the tip membrane $\tau$ can be expressed directly using the integrands in the Helfrich form of Eq. 4 when the membrane is equilibrated. Since two or three channels are expected to be located in the tip-link lower insertion site, an ∼3 nm² expansion for each of three channels may result in ∼1–1.5 nm radial expansion of the protein region under the tip-link lower insertion. Therefore, the average is taken from r = 3 to r = 4.5 nm for the free-energy density from $\tau =\left[\int \left(2k{\left(H-H_0\right)}^2+k_{g}K+{\sigma }_t\right)dA\right]/\left[\int dA\right]$. The two-state variable λ represents either the open (λ = 1) or closed (λ = 0) configuration of the channel. G_open and G_closed represent the internal energy of the channel for open and closed configurations, respectively. The energy required for the channel to open is calculated as the product of the membrane free-energy density and the area difference ΔA_channel between the open and closed configurations of the mechanotransduction channel, and is subtracted from the total potential energy when the channel is open. Given the total potential energy of the channel expressed in Eq. 14, the Boltzmann distribution can be defined to determine the probability of finding the system in a state with total channel energy E, which results in the following probability function for the channel opening (31):

$$p=\frac{1}{1+\text{exp}\left(\frac{1}{k_{b}T}\left(G_{open}-G_{closed}-\tau \Delta A_{channel}\right)\right)},$$ (15)

where G_open − G_closed = ΔG and ΔA_channel are treated as constant channel parameters.

Results

Time-dependent responses to step displacements

Temporal responses generated by the model to a series of displacement steps to the tallest stereocilium are presented in Fig. 1 E. Plotted against time are the bundle force (whose value is a function of the summed stereocilia response), the single tip-link force, and the membrane free-energy density calculated at a point 3.5 nm from the tip-link insertion site. Force applied both at the tip link and across the bundle has a rapid onset and is graded with intensity. Responses are complex temporally, with a decrease in force observed during a continued stimulation. Such force relaxation is generated by the lipid flow for the nonuniformly stretched membrane to homogenize the lipid area density. Since the focus is on the force versus displacement relationship, the temporal changes are less consequential; however, they do demonstrate that lipid energy is accumulated rapidly enough to be relevant to hair cell activation. Calculations are sampled at 0.5 ms from the onset of the stimulation to plot force and energy versus displacement relationships to mimic previous experimental data obtained in a turtle (4).

Mechanics of the stereocilia membrane deformation

The main variables associated with the membrane deformation are the radial size of the tented-tip region and the lipid mobility in the cytoskeleton-coupled region. To investigate the relative contribution of these variables, each variable is systematically varied. The radius of the tented-tip region r_b is stepped through 19, 22, and 30 nm, and the lipid mobility for the cytoskeleton-coupled region, parameterized by the diffusion constant D, is set to be hypermobile (i.e., D→∞) and D = 5 μm²/s (see Fig. S3 for a description of the lipid mobility). The hypermobile case can be solved without considering the time dependency, and the force versus displacement result is obtained with a quasi-static analysis. The cases with physiologically relevant diffusivity values, i.e., D = 5 μm²/s, are solved by sampling the calculation in the temporal step response, as depicted previously, and data between sample points are linearly interpolated. Plots of membrane-tip displacement versus tip-link force and membrane free-energy density at 3.5 nm from the tip-link insertion are presented in Fig. 2, A and B, respectively.

Figure 2.

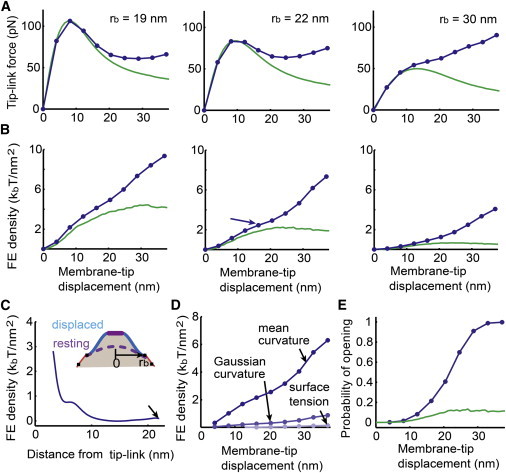
Effects of varying lipid mobility and r_b for the membrane. (A and B) Tip-link force (A) and membrane-free-energy density (B) at a point r = 3.5 nm with respect to membrane-tip displacement. Both responses are obtained at time = 0.5 ms from the step stimuli stimulation shown in Fig. 1E. Data are indicated with linearly interpolated dots for D = 5 μm²/s case (blue). Hypermobility (green) of the lipid in the cytoskeleton-coupled region is also considered in (A) and (B). The first, second, and third columns of (A) and (B) use r_b = 19 nm, 22 nm, and 30 nm, respectively. (C) Free-energy density profile of the tented-tip membrane corresponding to the arrowed data in (B), middle panel (r_b = 22 nm). Energy decays from the boundary of the stiff protein region. (D) Decomposed membrane free-energy density shown with a blue trace in (B), middle panel. (E) Open probability of the MS channel using the free-energy density averaged from r = 3 nm to r = 4.5 nm. Both D = 5 μm²/s (blue) and hypermobility (green) cases are plotted. See Table 1 for the parameters used. See Fig. S8 for results obtained without considering the stiff protein region. To see this figure in color, go online.

The characteristic nonlinearity of the tip-link force versus membrane-tip displacement relation can be altered by varying the values of both the radius of the tip region r_b and the lipid diffusion constant D. In Fig. 2 A, the negative stiffness in the regime where the force is reduced (around the membrane-tip displacement of 18 nm) is strongly dependent on the membrane radius, r_b, i.e., smaller values of r_b result in greater negative stiffness. On the other hand, the ability of the tip-link force to be increased with larger displacements is strongly dependent on the lipid mobility in the cytoskeleton-coupled region. For a given value of r_b, the tip-link force on the larger displacement increases with a reduction in the lipid mobility from hypermobile to the physiologically relevant value. In Fig. 2 A, with r_b = 22 nm and D = 5 μm²/s, the nonlinear characteristic showing minimum stiffness in the intermediate displacement is very similar to that of the measured hair bundle nonlinearity in previous studies (3–5).

In Fig. 2 B, the free-energy density of the membrane at 3.5 nm shows similar trends as the tip-link force, but monotonically increases when D = 5 μm²/s, whereas the tip-link force does not. It is unlikely that channel activation is directly following the tip-link force, because hair cell activation curves do not activate less with larger stimulation. From this perspective, it would be reasonable to assume that channel activation follows the membrane energy. To further explore the membrane free energy in channel activation, a plot of the free-energy density profile for the tented-tip region without consideration of stiff protein complex at center of the tented-tip region is first simulated and shown in Fig. S8 C (this energy profile is taken at 0.5 ms when the bundle is step displaced with 50 nm; r_b = 21 nm and D = 7 μm²/s are used for this plot). The free-energy density rapidly decays from the tip-link insertion point. The profile suggests that if the free energy associated with membrane deformation induced by the tip-link force is used to activate the MS channel, the channel should be located close to the tip-link insertion site for efficient energy transfer. This observation is consistent with the initial assumption for the channel complex located at tip-link lower insertion. A plot of the free-energy density profile with the stiff protein complex is presented in Fig. 2 C (the profile is taken at 0.5 ms when the bundle is step displaced with 50 nm, corresponding to the data indicated by the blue arrow in Fig. 2 B, middle panel). The trends are identical to Fig. S8 C in general, but the profile shows a steep gradient generated at the region away from the tip-link insertion site by the size of the stiff protein complex. One might also predict that the free energy would also increase minimally at the interface between two compartments due to increased curvature (see arrow in Fig. 2 C).

The free-energy density of the membrane surface associated with tip-link displacement consists of mean and Gaussian curvature energies and surface tension energy according to the Helfrich theory (see Eq. 4). These three energy densities that correspond to the data indicated by the blue trace in Fig. 2 B, middle panel, are shown separately in Fig. 2 D. As shown in Fig. 2 D, the two curvature energy densities are dominant and the surface tension energy density is negligible. The mean and Gaussian curvature energy densities have the same order of magnitude and separately or together could potentially be sufficient to activate the MS ion channel of the hair cell. Assuming the channel gating is sensitive to the membrane energy, with the energy difference between open and closed states being 7 k_BT, the membrane free-energy density averaged from r = 3 nm to r = 4.5 nm generates the activation curve in Fig. 2 E. Here, selection of the channel energy 7 k_BT might be arbitrary for the hair cell MS channel because the structural identity of the channel remains unknown. However, a typical MS channel has an internal energy difference of ∼10 k_BT between open and closed states (31), and the hair cell channel energy is also estimated as ∼10 k_BT, although the theoretical of our model is different (32). The channel open probability analysis presented here indicates that potentially enough energy for the channel to open is present, and that the channel needs to be close to the tip link to sense enough lipid membrane energy for effective activation. This proximity is consistent with the channel being linked in some manner to the tip link, considering the fluid nature of the lipid membrane. The recent hypothesis that the TMIE and TMHS/LHFPL5 proteins serve as a linker between the MS channel and the tip link may provide a molecular underpinning for this idea (14,15).

Nonlinear force versus displacement relationship for hair bundles

To determine whether deformation of the membrane could actually reproduce the nonlinear bundle force versus displacement response, the total bundle force is computed for the hypermobile and D = 5 μm²/s conditions in Fig. 3 A. Nonlinear responses are obtained with each condition. However, the results again reveal that using limited lipid mobility in the cytoskeleton-coupled region is the key to increasing the bundle force in the large displacement regime, and thus obtaining a more similar curve shape with nonlinear bundle force measurements. Similar to the experimental data, loss of the tip links linearizes and reduces the hair bundle force. Loss of the side links further reduces the linear force by terminating the coherent, coordinated movement of the bundle.

For conditions in which the lipid mobility of the cytoskeleton-coupled region is limited to the physiologically relevant value (Fig. 3 B, upper panel) or is hypermobile (Fig. 3 B, lower panel), the single tip-link force is decomposed into two different force contributions to better interpret the underlying physical mechanism of this nonlinearity. Here, two decomposed tip-link forces are termed the flexing force and stretching force. The flexing force component is responsible for changing the curvature of the tented membrane, and the stretching force component is responsible for the increased membrane area in the tented-tip region (see Materials and Methods for the mathematical definition of flexing and stretching forces). In both cases, the nonlinear flexing force increases sharply with the onset of displacement. For larger displacements, the flexing force is reduced after its peak value by showing a saturation characteristic. The stretching force is most sensitive to the lipid mobility in the cytoskeleton-coupled partition. When hypermobility is defined for the cytoskeleton-coupled region, the monotonically increasing stretching force is negligible, but a significant amount of stretching force exponentially increases when the physiologically relevant limited mobility of the lipid is used. This increased stretching force can be explained as follows: the increased membrane area must accompany a decrease of the lipid density (i.e., number of lipid / apparent surface area) when the membrane-to-skeleton viscosity is considered, whereas this is not necessary when the system is hypermobile. Therefore, defining the viscous membrane system is the key to generating a more complicated nonlinear force versus displacement response that is more similar to experimental measurements.

After seeing that the monotonic increase of the stretching force, understanding the behavior of the nonlinear flexing force in Fig. 3 B (upper and lower panels), which is decayed and saturated after its peak, appears to be critical to interpret the biophysical mechanism of the bundle nonlinearity. An analysis for such a nonlinear characteristic might be found in a model for tethers, in which the membrane is similarity point loaded. Based on the analysis for tethers described by Powers et al. (23), the applied point force f for the axisymmetric membrane can be calculated from the following force equilibrium relation: $f=2\pi r\sigma \text{sin}\theta =2\pi r\sigma /\sqrt{1+r_h^2}$ (see Fig. 1 D for r and h(r), where σ is the surface tension and θ is the angle between the membrane surface and the coordinate r). From this formula, the applied point force for each membrane-tip displacement can be computed by taking dr/dh, i.e., r_h at an arbitrary point on the coordinate r from the calculated tether shape. As shown in the formula, the force can be decreased when the r_h is increased; therefore, the membrane shape parameter r_h at an arbitrary point r can be evaluated to check the validity of the decreased flexing force in Fig. 3. Therefore, the calculated tented shape is checked and the result confirms that r_h is initially decreased but then increases and becomes saturated as the membrane tip is further displaced. Now, after determining that the decreased flexing force is followed by the increase of r_h, one might ask, why does the increase of r_h, (i.e., the decrease of h_r) reduce the flexing force? To answer this question, it is also determined that the decrease of h_r results in a decrease in the local curvature energy density of the membrane. Therefore, the rate of the curvature energy increase for the tented-tip membrane, i.e., the flexing force component of the tip-link force, can be decreased with the membrane-tip displacement.

In frog saccule hair bundles, force versus displacement measurements often have a negative slope (33). This negative stiffness potentially identifies a mechanical amplification mechanism, and thus understanding the underlying mechanism for its generation is relevant (33). The model results show that the magnitude of the nonlinearity observed in the force versus displacement plot is in part dictated by the choice of rootlet stiffness. As shown in Fig. 4 A, decreasing the rootlet stiffness generated a negative slope similar to that observed in the frog (33). Bundle stiffness versus displacement plots are also presented to further illustrate the negative stiffness. Single rootlet stiffness measurements for the frog are not available, but a comparison of the whole bundle stiffness calculation with k_rootlet = 0.05 fN/rad (Fig. 4 A) with the whole bundle frog measurement shows good agreement. Whether this is biologically relevant remains to be explored, but it does offer an alternative explanation for the negative stiffness and a rationale for why this phenomenon has only been observed in the frog saccule, where the rootlets are more compliant, and not in turtle or mammalian preparations.

Figure 4.

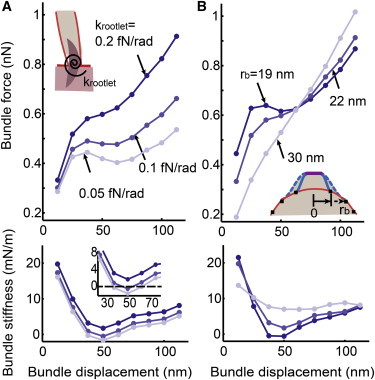
Possible mechanisms for the negative stiffness and the linearization component. Using the bundle force versus displacement response with D = 5 μm²/s in Fig. 3A, force (top) and stiffness (bottom) responses are calculated by varying the rotational stiffness of the rootlet and the parameter r_b. (A) Generation of the negative bundle stiffness by decreasing the stiffness of the rootlet (with fixed r_b = 22 nm). (B) Linearized bundle force responses by increasing r_b (with fixed k_rootlet= 0.2 fN/rad). See Table 1 for the parameters used. See Fig. S10 for results obtained without considering the stiff protein region. To see this figure in color, go online.

The nonlinearity in force versus displacement measurements can be abolished by treatment with a drug during the hair cell preparation. In this experiment, the drug treatment also results in blockage of the transduction current when a hair bundle is stimulated (3). In the original gating spring model, such observations provided a causal link between channel activation and the nonlinear bundle mechanics under the simple assumption that the drug bonds to the channel protein and prohibits the opening of the channel that generates nonlinearity (3). However, recent data regarding the use of aminoglycosides to block the transduction current and abolish nonlinear bundle mechanics demonstrated that aminoglycosides are permeable to this channel to the cytoplasm of the stereocilia tip, and thus it is unlikely that they can bind to a particular position of the channel (34,35). So how does blocking the mechanotransducer current then interfere with nonlinear mechanics? In the model presented here, the force versus displacement response is linearized by simply increasing r_b. That is, by increasing the radial size of the tented-tip region to 30 nm from 19 nm, the nonlinearity is lost (Fig. 4 B) and the channel open probability is also reduced by following the reduction of the membrane free-energy density. The results may suggest mechanisms by which the size of the tented lipid membrane can be controlled by a certain intracellular mechanism generated by drug treatments. The recent hypothesis regarding flexoelectricity of the stereocilia lipid membrane, which suggests that intracellular ionic transport can alter the cylindrical radius and thus the curvature of the ciliary membrane, may be relevant to these linearization and nonlinearization mechanisms (36,37). Although the validity of this model prediction remains to be tested, it nonetheless provides an alternative explanation for the mismatch between the classical hypothesis and the recently measured data.

Although a nonlinear calculation similar to the measurement is achieved in Fig. 3 A, as it stands, the model does not directly reproduce the biological nonlinearity measured in the turtle hair bundles. The nonlinear force versus displacement calculation (the 0 nm case in Fig. 5 B, which correspond to D = 5 μm²/s in Fig. 3 A) is shifted as compared with actual measurements (Ricci et al. (4) in Fig. 5 B). To align the model results with the measured data, it is necessary to apply a standing tip-link force in the resting configuration of the hair bundle. This standing force, as depicted in Fig. 5 A, is posited to be contributed by the forces exerted at the upper tip-link insertion, perhaps due to myosin motor proteins, as suggested for adaptation processes (38,39). A standing membrane-tip displacement of 5.9 nm, resulting in a standing force of ∼60–65 pN, is sufficient to reproduce the data obtained from turtle auditory hair cells (4). This standing tip-link force is similar to that observed in mammalian hair bundles (∼60 pN) but greater than that found in frog saccule hair bundles (40,41). With this standing tension in place, disruption of the tip link resulted in a hair bundle movement toward the tall edge, as was previously reported (42).

Figure 5.

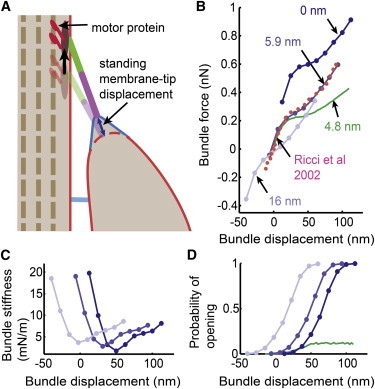
Standing membrane-tip displacement and corresponding migration of the bundle force versus displacement responses. (A) Schematic representing a possible mechanism for applying a standing force to the tip link using a motor protein at the upper insertion point. (B) Hair bundle force versus displacement plots with varying levels of the standing membrane-tip displacement (blue affiliation), using D = 5 μm²/s from Fig. 3A. The calculation that correlates best with experimental data (magenta; from Ricci et al. (4)) uses a standing membrane-tip displacement of 5.9 nm. The zero displacement corresponds to zero bundle force for all cases in (B). (C) Bundle stiffness calculated from (B). (D) Open probability of the MS channel calculated using the membrane free-energy density averaged from r = 3 nm to r = 4.5 nm. Here, the half-channel opening probability region (p = 0.5) in (D) covaries with the minimum stiffness region of the force versus displacement response in (B), in response to the different magnitude of the standing tip-link force. The hypermobile case (green) demonstrates that neither the nonlinear force versus displacement in (B) nor the open probability of the channel in (D) can be explained when the lipid mobility in the cytoskeleton-coupled region is not physiologically relevant. See Table 1 for the parameters used. See Fig. S11 for results obtained without considering the stiff protein region. The sensitivity of the lipid mobility in the cytoskeleton-coupled region for both the nonlinear bundle force and the activation curve are plotted in Fig. S6. To see this figure in color, go online.

To illustrate that the membrane energy can serve to activate the hair cell MS channel and that the channel activation follows the nonlinear force versus displacement plots, again the MS channels that are sensitive to the free energy of the membrane and the channel internal energy difference between the opened and closed state of 7 k_BT are assumed near the tip-link insertion site. Activation curves are generated and presented in Fig. 5 D. The plots are presented for different standing tip-link tensions to demonstrate that the channel activation shifts in parallel with the nonlinear force versus displacement plot overlap the minimum stiffness region in the force plot and the half-open probability region in the activation curve, as was previously shown experimentally (3,4). However, in contrast to previous interpretations, in this model the nonlinearity is not causally linked to channel activation, as the channel is passively following the membrane energy.

Discussion

The nonlinear force versus displacement relationship, which is prevalent in many end organs and species, can be seen in auditory hair bundles to activate the MS ion channels of sensory hair cells. However, the underlying biophysical mechanism of this nonlinearity and the channel activation has remained elusive (3–5,43). Here, a theoretical framework in which the lipid membrane deformation explains the bundle nonlinear force versus displacement measurement is presented. In this model, two partitioned lipid membranes—a small component that can be separated from the actin core (i.e., the tented-tip region) and a pool in which the curvature change is not considered (i.e., the cytoskeleton-coupled region)—define the stereocilia lipid membrane. Here, lipid mobility in the tented-tip region is fast enough to be quasi-static, but it is significantly limited in the cytoskeleton-coupled region. When the bundle is deflected, forces applied at the tip link generate a rapid membrane-flexing component of the tip-link force. Larger stimulations reduce the flexing force component but increase the stretching force due to the decreased lipid area density under viscoelastic interactions. When nonlinearity occurs, the stretching force does not compensate for the reduced flexing force, resulting in an overall reduction in the force, whereas the stretching force restores the total tip-link force at a still larger displacement.

The model suggests that the membrane curvature change near the tip-link point source can generate the energy needed to activate the MS channels of the hair cells. Although this ability of the lipid to convey force is less understood for hair cell mechanotransduction, it is a much more accepted phenomenon across other mechanoreceptors. For instance, the MscL and MscS channels use the energy created by the lipid to control the turgor pressure of bacterial (44–46). Many other MS ion channels, including TREK-1, TRAAK, PIEZO-1, and PIEZO-2, are all sensitive to lipid membrane stretching (47–53). The model suggests that the force applied to the channel may share a more common underpinning with other mechanosensory systems, and that the nonlinearity of the hair cell system might be generated by the cellular and molecular environments of the stereocilia effectively controlling this force transfer to the channel.

Recent modeling studies in which membrane tenting at the tiny tip of stereocilia was similarly investigated also supported the force-conveying role of the lipid for auditory mechanotransduction (54–56). However, the mechanism for the nonlinear force versus displacement measurements remained elusive. The model presented in this work extends those previous models by additionally parameterizing size of the tented lipid membrane. In addition, this work considers whole bundle deflection by providing realistic models for the bundle kinematics and viscous flows of the lipid on the surface of the stereocilia. The rootlet stiffness and the standing membrane-tip displacement (for the kinematics model) as well as the lipid mobility (for the lipid flow model) are parameterized. As a result, the model additionally explains the nonlinearity, linearization, and negative stiffness components of the bundle mechanics; channel activation curves; and in-parallel migration of the nonlinear bundle force and the activation curves. Overall, the data support the notion that the lipid bilayer plays a significant role in hair bundle mechanics and mechanotransduction.

A caveat in exploring how the lipid membrane stretches is the possibility that the membrane might be able to rupture. The rupture parameters estimated from vesicles indicate that a decrease of ∼3–5% in lipid density may lead to rupture of the lipid membrane. However, in this model simulation with consideration of the physiologically relevant diffusion constant, it turns out that the membrane density strain does not increase to a value above 3% with any tested rise time of the bundle in the step stimuli. For all of the data presented in this article, the maximum lipid density strains are <2%. Such a low-density strain despite the significant area generation can be achieved by the fast convective flow of the lipid followed by the membrane surface-tension gradient. Here, the low-density strain also indicates that the membrane area generated results largely from stretching of the surface undulation in the stereocilia tip membrane (including some part of the cytoskeleton coupled membrane) rather than from direct expansion of the interlipid distance (24). Of course, unreasonably fast stimulation of the bundle or assuming a critically limited lipid mobility in the cytoskeleton-coupled region can result in rupture of the lipid membrane, but in most cases of the bundle stimuli in real physiological conditions, stereocilia lipid membranes may not be stretched beyond the rupture point (14,57).

In summary, a theoretical framework that considers physical characteristics of the partitioned lipid membrane in the stereocilia is introduced. The model considers the membrane-cytoskeleton interaction and the corresponding viscous flow of the lipid and elastic deformation of the membrane under the action of tip-link pulling. The model reproduces biologically relevant hair bundle force versus displacement responses by interpreting how bending and stretching of the membrane generate a nonlinear tip-link force, and by demonstrating the need for a resting tip-link tension. In addition, the model reproduces and predicts a mechanism for the negative stiffness, and identifies a means by which nonlinearity could be lost (i.e., the linearization component). This model also provides an energetic rationale for why the channel must be very close to the tip link. Overall, the theoretical analysis presented here suggests that the auditory mechanotransduction also can be delineated by the force-conveying role of the lipid membrane, and thus provides a unifying hypothesis for cellular mechanotransduction.

Supporting Citations

References (58–64) appear in the Supporting Material.