Abstract
Kinetic measurements of the self-assembly of proteins into amyloid fibrils are often used to make inferences about molecular mechanisms. In particular, the lag time—the quiescent period before aggregates are detected—is often found to scale with the protein concentration as a power law, whose exponent has been used to infer the presence or absence of autocatalytic growth processes such as fibril fragmentation. Here we show that experimental data for lag time versus protein concentration can show signs of kinks: clear changes in scaling exponent, indicating changes in the dominant molecular mechanism determining the lag time. Classical models for the kinetics of fibril assembly suggest that at least two mechanisms are at play during the lag time: primary nucleation and autocatalytic growth. Using computer simulations and theoretical calculations, we investigate whether the competition between these two processes can account for the kinks which we observe in our and others’ experimental data. We derive theoretical conditions for the crossover between nucleation-dominated and growth-dominated regimes, and analyze their dependence on system volume and autocatalysis mechanism. Comparing these predictions to the data, we find that the experimentally observed kinks cannot be explained by a simple crossover between nucleation-dominated and autocatalytic growth regimes. Our results show that existing kinetic models fail to explain detailed features of lag time versus concentration curves, suggesting that new mechanistic understanding is needed. More broadly, our work demonstrates that care is needed in interpreting lag-time scaling exponents from protein assembly data.
Introduction
Amyloid fibrils are structured polymeric aggregates of protein molecules, which form when proteins misfold, such that they stack together in a cross-β-sheet conformation. Understanding the mechanisms involved in the self-assembly of these fibrils is of great importance, both because they are implicated in many degenerative diseases (1), and because they have potential applications in the design of new materials (2,3). The molecular processes involved in the very early stages of aggregation are of particular interest because increasing evidence suggests that early aggregates, rather than mature fibrils, may be the toxic species in fibril-linked diseases (4–6). In this article, we investigate the interplay between two competing processes, primary nucleation and autocatalytic growth, during the early stages of amyloid fibril aggregation, and assess whether this interplay can account for so-far unexplained features of our own and others’ experimental data.
Amyloid fibril formation is commonly studied by monitoring the kinetics of self-assembly in vitro. In these experiments, a protein sample is placed under conditions where fibril formation is favored, and measurements of fluorescence (with β-sheet binding fluorescent dyes) or absorbance are made as a function of time. The resulting kinetic curves typically show a sigmoidal shape, with an initial lag time in which little fibrillar material is detected, followed by a period of rapid growth, and finally saturation as the pool of available unaggregated protein is exhausted. Addition of preformed fibril seeds at the start of the experiment usually abolishes the lag phase, suggesting that aggregation is initiated by a nucleation process, in which a rare fluctuation leads to the energetically unfavorable formation of the smallest stable growth-competent aggregate (primary nucleus). Once a fibril has been formed, it is expected to grow by sequential addition of protein molecules at its ends (and possibly by end-joining with other fibrils (7)).
Fitting observed kinetic data to theoretical models provides a powerful tool for elucidating the molecular mechanisms involved in fibril self-assembly (8,9). This approach has shown that the sigmoidal shape of typical kinetic curves cannot be explained by models that only involve primary nucleation and fibril growth; it also requires autocatalytic formation of new fibrils from existing ones (8,10–13). The breaking of fibrils into shorter fragments (fragmentation) provides one such autocatalysis mechanism, because it increases the number of growth-competent ends. Alternatively, or additionally, autocatalysis could happen via the nucleation of new fibrils on the surfaces of existing ones (secondary nucleation) (11–13).
The results of in vitro kinetic experiments are often summarized by plotting the measured lag time τlag as a function of the protein concentration mtot, defining τlag as the time at which the concentration of aggregated protein reaches a predefined threshold (although other definitions are also used (11,14–16)). The lag time decreases as the protein concentration increases, and this relation is typically fitted to a power-law function τlag ∝ mtot−γ (i.e., one plots log(τlag) versus log(mtot), and obtains the exponent γ from the gradient). Explaining experimentally observed lag time versus concentration behavior is an important challenge for theoretical models, and different models make different predictions for the scaling exponent γ. In particular, if the lag time is dominated by the formation of a primary nucleus, we expect γ > 1, while for models where the lag time is dominated by autocatalytic growth by fragmentation, theory predicts that γ = 1/2 (8,11–13).
In this article, we show, using our own and others’ experimental datasets, that lag time versus concentration curves are not always well-fitted by a simple power law. In contrast, we observe clear kinks in these curves, where the lag-time scaling changes. These kinks may reflect changes in the dominant molecular mechanism at play during the lag time. We explore using theoretical arguments and computer simulations whether the kinks can be explained by the interplay between the two mechanisms identified in existing models as being important during the lag phase: primary nucleation and autocatalytic growth. Our results show that the position and shape of the kinks are not well explained by the competition between nucleation and growth, as represented in existing models. This suggests that new mechanistic insights are needed to fully understand kinetic data on amyloid fibril assembly.
Background
Theoretical models for amyloid fibril assembly
Theoretical models for the kinetics of amyloid fibril assembly often represent the key molecular processes as a set of chemical reactions. This reaction set typically includes primary nucleation, fibril elongation, and (possibly) fragmentation or secondary nucleation, and can be written as
| (1) |
| (2) |
| (3) |
| (4) |
Here, fi denotes a fibril of length i, m denotes a protein monomer, and it is implicitly assumed that concentrations of all components are spatially homogeneous, i.e., that the system is well-mixed.
Reaction 1 describes the spontaneous formation of a primary nucleus (), from nc monomers (i.e., we assume that the nucleus consists of the smallest stable growth-competent fibril which is of length nc). The total rate of this process is given by , where kn is a nucleation rate constant and m(t) is the time-dependent monomer concentration. This representation of nucleation as a single-step reaction whose rate depends on the ncth power of m arises from a classical nucleation picture in which prenuclear aggregates are in rapid equilibrium before formation of the nucleus (17). The factor of nc! in the nucleation rate, which is not used in some other work (8), arises from ignoring the order in which the nc monomers come together. This is equivalent to rescaling kn.
Reaction 2 describes fibril growth by monomer addition at the ends. This process occurs at rate 2k+m(t)fi, where k+ is the elongation rate constant and fi is the concentration of fibrils of length i. The factor of 2 arises because each fibril has two ends; omitting this amounts to a rescaling of k+.
Reaction 3 describes fragmentation, in which a fibril of length i breaks into two shorter fibrils of length j and i − j. The fibril is assumed to break with equal probability at all sites along its length, so that the total rate of this process is given by (i – 1)kf × fi, where kf is the fragmentation rate constant and the factor (i = 1) arises because there are i − 1 possible breakage sites in a fibril of length i. In the case that one of the fragments is shorter than the nucleus size nc, this fragment is assumed to split immediately into monomers—i.e., Reaction 3 should be replaced by fi → j m + fi−j or fi → fj + (i – j) m, as appropriate.
Reaction 4 describes the autocatalytic formation of new fibrils by secondary nucleation on the surface of existing ones. Here, ns monomers combine to form a fibril of length ns, catalyzed by the presence of a fibril of length i. The rate at which this process happens is assumed to be , where ks is the secondary nucleation rate; this form of the rate equation is analogous to that for primary nucleation except for the factor of i, which accounts for the fact that longer fibrils have more sites where secondary nucleation can take place.
In this article, we base our theoretical analysis on the model described by Reactions 1–4 (using either the fragmentation reaction (3) or the secondary nucleation reaction (4), but not both). It is important to note, however, that others have also considered models including fibril end-joining (18), inhomogeneous fragmentation (19), and spatial propagation of the fibrillation process (20).
Predictions for lag-time scaling with protein concentration
The model described by Reactions 1–4 leads to a number of analytical predictions for the scaling of the lag time with protein concentration, in different parameter regimes. As in many experimental studies, we define the lag time as the time taken for the total amount of aggregated protein to reach a predetermined threshold (typically 10% of full aggregation).
Lag-time scaling without autocatalysis
We first discuss the case where new fibrils form only by primary nucleation (Reaction 1) and grow by elongation (Reaction 2)—i.e., the autocatalytic mechanisms, Reactions 3 and 4, are absent. This case has two possible regimes depending on the relative rates of primary nucleation and fibril elongation.
If primary nucleation is slow relative to the rate of fibril growth once a nucleus has formed, then we expect the lag time to be dominated by the time to formation of the first primary nucleus. As discussed above, the primary nucleation rate is assumed to be proportional to . At early stages in the aggregation process, almost all protein is present as monomers and m(t) ≈ mtot. We therefore expect that the lag time is —i.e., in this regime the model predicts a lag-time versus concentration scaling exponent γ = nc.
If, on the other hand, primary nucleation occurs on a similar or faster timescale than fibril growth, so that the fibril growth process makes a significant contribution to the lag time, a different prediction holds. In classic work, Oosawa and Asakura (21) and Oosawa and Kasai (22) showed that in this scenario, the kinetic curves for fibril growth can be described by
| (5) |
where M(t) is the total concentration of fibrillar protein and defines a characteristic timescale. From Eq. 5, one can show that the lag-time scales with the protein concentration as —i.e., that in this regime the scaling exponent γ = nc/2 (11,21). (Some versions of this model have instead γ = (nc + 1)/2. This arises from a subtlety in the definition of the nucleus. Here we have assumed that the nucleus, of size nc, is a growth-competent fibril. One could alternatively assume that the nucleus only becomes growth-competent upon addition of a further monomer. The latter scenario results in γ = (nc + 1)/2.)
Lag-time scaling with autocatalysis
We now turn to the case where in addition to primary nucleation, and elongation, autocatalytic fibril formation can occur via fragmentation (Reaction 3) or secondary nucleation (Reaction 4). We assume that these mechanisms do not occur simultaneously—i.e., we have either Reaction 3 or Reaction 4 but not both. Knowles et al. (8) have presented an analytical solution to the deterministic differential equations corresponding to Reactions 1, 2, and either 3 or 4, under the assumptions that monomer depletion can be ignored at early times, and that kn ≪ k+. This solution can be written as follows:
| (6) |
Here, two timescales come into play. The first is given by δ−1, where δ is the same as in the Oosawa model (Eq. 5), and represents the characteristic timescale of fibril growth in the absence of autocatalysis. The second timescale is given by κ−1, where κ takes different forms for fragmentation and secondary nucleation:
and
respectively. This is the characteristic timescale for the autocatalytic growth process and depends on the rates of both growth and autocatalytic fibril formation. Finally, the constants C± are given by
where N0 and M0 are the initial numbers of fibrils, and total fibrillar protein, per unit volume.
Defining a threshold concentration of aggregated protein M∗, we can compute from Eq. 6 the lag time τlag as the time at which M(t) reaches M∗ (provided M0 ≪ M∗),
| (7) |
where D = δ2/κ2 and Φ = log(1 – M∗/mtot) (note that all logarithms are to base e). For unseeded aggregation, M0 = 0 and N0 = 0. If we further assume that the timescale of autocatalytic growth is faster than the Oosawa timescale, i.e., that δ ≪ κ, and that M∗ ≪ mtot, we obtain the simpler prediction
| (8) |
where Φ∗M = M∗/mtot. In Eq. 8, the dominant contribution to the lag-time scaling comes from the dependence of the prefactor κ−1 on the protein concentration mtot (while C+ also varies with mtot, the logarithm means that this contribution is weak). The value κ−1 scales differently with protein concentration for the two autocatalysis models. For fragmentation, κ−1 ∼ mtot−1/2, leading to a prediction for the lag-time scaling exponent γ = 1/2 (8,11–13). For secondary nucleation, , so that the model instead predicts γ = (ns + 1)/2 (12).
Materials and Methods
Experiments
Insulin sample preparation
Bovine insulin was obtained from Sigma-Aldrich, St. Louis, MO (I5,500, lot No. 0001434060) with zinc content ∼0.5% (w/w). The samples in this study were dissolved in 25 mM HCl (pH 1.6) immediately before the experiment. All solvents and solutions were filtered through a 0.22-mm filter (Millipore, Billerica, MA). Concentrations were checked via UV-vis absorption spectroscopy. ThT was added to each solution to a final concentration of 20 mM.
Lysozyme sample preparation
Lysozyme was obtained from Seikagaku, Tokyo, Japan (100940, lot No. E00 301), 6× crystallized. All samples in this study were dissolved in 20 mM HCl-KCl (pH2.0) buffer and 1 M NaCl, immediately before the experiment. All solvents and solutions were filtered through a 0.22 mm filter (Millipore). Concentrations were checked via UV-vis absorption spectroscopy. ThT was added to each solution to a final concentration of 55 μM.
ThT fluorescence kinetic measurements for bovine insulin and lysozyme
The ThT fluorescence measurements were conducted using a Fluostar plate reader (BMG Labtech, Life Technologies, Offenburg, Germany) and NBS 96-well plates (Cat. No. 3641; Corning, Corning, NY). Each well of the plate was filled with 100 μL of solution. Experiments for each protein concentration of bovine insulin were replicated across 2–3 whole plates, while those for lysozyme were replicated with several protein concentrations on the same plate. The final number of individual experiments for a given concentration of bovine insulin ranged from 140 to 200, and those of lysozyme ranged from 12 to 60. The plates were incubated at 60°C and fluorescence readings were taken from the bottom of the plate at wavelengths of 450 nm for excitation and 485 nm for emission. Readings were taken every 10 min in the case of bovine insulin, and 3 min for lysozyme.
Lag times for β2-microglobulin
The lag-time data for β2-microglobulin was kindly provided by Xue et al. (9). These data were obtained from ThT fluorescence kinetics at pH 2.0 and 37°C with 50 mM NaCl and 0.02% NaN3. The data set contains 20 different protein concentrations in the range 8–244 μM, totaling 235 measurements.
Computer simulations
Simulation algorithm
We carried out stochastic computer simulations of the model defined by the chemical reaction sets 1–4 (including either Reaction 3 or Reaction 4, but not both), using a kinetic Monte Carlo algorithm (23). As we have shown in previous work, these simulations can quantitatively reproduce experimental kinetic curves (14). Here, we extend the parameter range, allowing us to explore the full range of possible behaviors of the model. Because our simulations are stochastic and account for discrete numbers of molecules, we can resolve individual molecular events such as the formation of the first primary nucleus. Because we focus on the lag time, simulations were terminated once half of the total protein was aggregated. For each parameter combination, 150 replicate simulation runs were performed.
Baseline parameter set
Our baseline parameter set for these simulations was obtained as in our previous work (14), by fitting Eq. 6 to averaged experimental data for the aggregation kinetics of bovine insulin at concentrations of 0.1, 0.2, 0.4, and 0.75 mg mL−1, assuming fragmentation but not secondary nucleation, and a primary nucleus size nc = 2. This fitting resulted in parameter values for fibril elongation and fragmentation k+ = 5 × 104 M−1 s−1 and kf = 3 × 10−8 s−1. The primary nucleation rate kn was varied in our simulations as described in Results. All protein was assumed to start in the monomeric form. For computational convenience, in most of our simulations we chose a small simulation volume V = 0.83 pL, comparable with that of a human cell.
Determination of lag times and scaling exponent
For each simulation trajectory, the total amount of fibrillar protein was obtained as a function of time by summing over all fibril lengths. The lag time was then determined as the time at which 3% of the total protein had been incorporated into fibrils (however, our results do not depend strongly on the choice of threshold). The lag time was computed for each simulation run and then averaged over replicate runs. To obtain the lag-time scaling exponent γ, we repeated our simulations over a range of protein concentrations mtot, and using the Levenberg-Marquardt algorithm to fit our data to the functional form log(τlag) = log(A) – γlog(mtot), where A is a constant, mtot is the protein concentration and τlag denotes the lag time, averaged over replicate simulations, for a given protein concentration.
Results
Experimental data shows kinks in lag time versus concentration plots
Fig. 1 shows lag time versus protein concentration data, obtained from our own experiments with bovine insulin and lysozyme (Fig. 1, a and b, respectively), and experiments by Xue et al. (9) on β2 microglobulin Fig. 1 c). These experiments involved a large number of replicate experiments, and covered a wide range of protein concentrations (for details, see the caption of Fig. 1). These data show clear evidence for kinks: well-defined points in the lag-time versus concentration curves where the lag-time scaling changes. Because different lag-time scaling exponents are predicted to arise from different molecular mechanisms, this observation suggests that the dominant mechanism in early self-assembly kinetics changes with the protein concentration. Present-day theoretical models suggest that three mechanisms may be at play during the lag time: primary nucleation, sequential addition of monomers to existing fibrils, and autocatalytic growth via fragmentation or secondary nucleation. These mechanisms produce different lag-time scaling exponents (respectively, γ = nc, γ = nc/2, and γ = 1/2 or (ns + 1)/2). Our starting hypothesis is therefore that the kinks that we observe in Fig. 1 arise from a crossover between regimes in which one or other of these mechanisms is dominant. In the rest of the article, we test this hypothesis, by assessing whether our models indeed predict kinks similar to those seen in the experimental data, first from a qualitative and then from a quantitative point of view.
Figure 1.
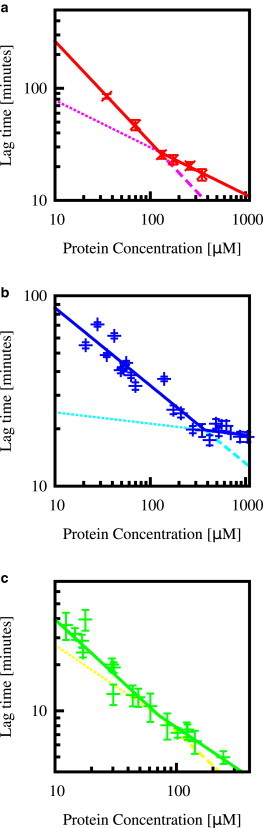
Lag time as a function of protein concentration for (a) bovine insulin, (b) lysozyme, and (c) β2 microglobulin, in all cases averaged over replicate experiments. The data in panel c was kindly provided by Xue et al. (9). The error bars indicate the standard deviation among replicate experiments at a given concentration, and the lines indicate the best fit of the power law τlag ∝ mtot−γ to data for a specified range of protein concentrations. (a) Two data sets for bovine insulin: (black) data fitted by the single power law over all protein concentrations (resulting in γ = 0.36) indicate experiments in the absence of NaCl; (red) data fitted by two power laws indicate self-assembly in the presence of 0.49 M NaCl. Each point corresponds to the mean and standard deviation of 140–200 kinetic traces at each of six protein concentrations (see Materials and Methods). Fitting the data for bovine insulin in the presence of NaCl in the range mtot ≤ 160 μM results in γ = 0.90(2) (dashed line). Fitting the data in the range mtot ≥ 160 μM results in γ = 0.42(10) (dotted line). (b) Data for lysozyme (for conditions, see Materials and Methods), where each point corresponds to the mean and standard deviation of 12–60 kinetic traces at each of 25 protein concentrations (see Materials and Methods). Fitting this data in the range mtot ≤ 300 μM results in γ = 0.41(6) (dashed line); while fitting the data in the range mtot ≥ 300 μM results in γ = 0.06(5) (dotted line). (c) Data for β2 microglobulin, where each point corresponds to the mean and standard deviation of 235 kinetic traces at 20 different protein concentrations (for conditions, see Materials and Methods and Xue et al. (9)). Fitting the data in the range mtot ≥ 30 μM gives γ = 0.77(14) (dashed line), while fitting the data in the range mtot ≥ 40 μM gives γ = 0.54(5) (dotted line). To see this figure in color, go online.
Model predicts kinks due to competition between primary nucleation and autocatalysis
Simulations reveal changes in lag-time scaling exponent due to interplay between nucleation and growth
We first explore, for present-day theoretical models, how the interplay between different molecular mechanisms leads to changes in the lag-time scaling exponent. We carried out stochastic simulations of the chemical reaction sets Reactions 1–3, i.e., of a model which includes primary nucleation, fibril growth by elongation, and fragmentation (for simulation details, see Methods). For now we neglect secondary nucleation, but this will be considered later. As a simple way to control the interplay between different molecular mechanisms, we systematically varied the primary nucleation rate constant kn over a wide range (15 orders of magnitude), keeping all other parameters fixed. Primary nucleation rates are poorly determined by fitting theoretical predictions such as Eq. 6 to experimental data (8), so reliable estimates of their true values are lacking, but the information that is available does suggest a wide range of possible nucleation rate constants: 10−4–10−14 s−1 (8,24,25) for various protein systems. For each value of the nucleation rate constant kn, we repeated our simulations for protein concentrations mtot in the range 1 × 10−5 ≤ mtot ≤ 7.5 × 10−4 M (commensurate with concentration ranges used in our own and others’ experiments (9,14)), and computed the lag-time scaling exponent γ using linear fits to our simulation data for log(τlag) versus log(mtot), as described in Materials and Methods.
Fig. 2 a shows plots of lag-time versus concentration obtained in our simulations, for increasing values of the primary nucleation rate constant (top to bottom; also color-coded purple to red). As expected, we see clear changes in lag-time scaling behavior as the nucleation rate constant changes, reflecting the shift in relative importance of primary nucleation and growth in determining the lag time. These changes in lag-time scaling can be seen in more detail in Fig. 2 b. Here, the black symbols (with error bars) show the scaling exponent γ, extracted from the gradients of the curves in Fig. 2 a, plotted as a function of the primary nucleation rate constant kn (note that, for clarity, Fig. 2 a shows only a subset of our simulated nucleation rates). Two features are immediately apparent.
-
1)
The limits of high and low nucleation rate constants are consistent with theoretical predictions. If nucleation is very slow, γ tends to 2; this is consistent with the prediction γ = nc (= 2 in this case), for the regime in which the lag time is dominated by the time to formation of the first primary nucleus. In contrast, if nucleation is very rapid, we obtain γ = 1, consistent with the Oosawa prediction γ = nc/2 of nucleation-dependent polymerization in the absence of autocatalysis.
-
2)
For intermediate values of the nucleation rate constant, the scaling exponent dips down toward the prediction of the fragmentation model, γ = 1/2, but never actually reaches this value.
Figure 2.
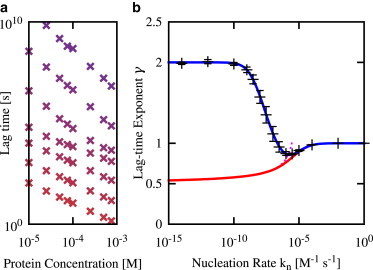
Lag-time scaling with protein concentration for the fragmentation model depends on the primary nucleation rate constant. (a) Lag-time versus concentration curves obtained from stochastic simulations, for several values of the nucleation rate constant kn: kn increases top to bottom in factors of 100, from 10−12 M−1 s−1 (purple) to 1 M−1 s−1 (red). (b) Lag-time scaling exponent γ as a function of primary nucleation rate constant kn. (Black symbols) Simulation results obtained by fitting the data shown in panel a to log(τlag) = log(A) – γlog(mtot). The error bars are dominated by the confidence in the fit, rather than the error in the lag-time measurements. (Red line) The value γ(kn) extracted from the full prediction of the fragmentation model, Eq. 7. (Magenta line) The value γ(kn) extracted from the approximate prediction of the fragmentation model, Eq. 8. (Blue line) The value γ(kn) extracted from the lag-time expression Eq. 9—i.e., the full fragmentation model solution augmented by an extra term to describe the first primary nucleation event. For all the data shown, the protein concentration range was 1 × 10−5 ≤ mtot ≤ 7.5 × 10−4 M and the parameters were nc = 2, k+ = 5 × 104 M−1 s−1, kf = 3 × 10−8 s−1, and the volume V = 0.83 pL. To see this figure in color, go online.
These results show clearly that changes in the dominant molecular mechanism can indeed produce shifts in the scaling exponent. Interestingly, they also show that the regime where autocatalysis (in the form of fibril fragmentation) is dominant can become masked by the effects of primary nucleation, leading to an apparent scaling exponent significantly larger than one-half, even for systems where fragmentation plays an important role.
Modification of standard theory is needed to reproduce simulation results
Fig. 2 b (red line) also shows the lag-time scaling exponents emerging from the analytical expression for the lag time, Eq. 7, derived for a model that includes nucleation, fibril elongation, and fragmentation, all treated deterministically. Lag-times derived from the limit of this expression in the case of rapid autocatalysis (Eq. 7; magenta line) produce similar results. These results were obtained by using the analytical expressions to plot log(τlag) versus log(mtot), from which predictions for γ were extracted numerically, for different values of the nucleation rate constant kn. The predictions of this deterministic model are in good agreement with our simulation results for higher nucleation rate constants, showing that the analytical solution to the fragmentation model does correctly capture the crossover to an Oosawa-like regime. (The crossover to the Oosawa-like regime can be seen in the analytical expression Eq. 7 by noting that at high values of kn, δ ≫ κ, and in this limit D in Eq. 7 becomes large, which gives τlag ≈ (2Φ)1/2 δ−1 and γ = 1.) However, the deterministic model does not capture the shift to the primary nucleation-dominated regime (γ = nc = 2) at low values of kn, instead tending toward the fragmentation-like value of γ = 1/2 as kn decreases.
Why does the analytical result fail to capture the simulation behavior at low nucleation rates? This discrepancy arises because the deterministic differential equations used to generate the theoretical prediction, Eq. 7, do not take account of the discrete nature of the primary nucleation process. In the deterministic differential equation representation, all concentrations are continuous variables that can be arbitrarily small—thus the concentration of nuclei increases continuously from time zero and initially corresponds to less than one nucleus in the corresponding simulated volume. In the continuous model, the autocatalytic growth processes are able to operate on this very low concentration of nuclei, leading to a lag time that is dominated by κ (the timescale of autocatalytic growth) rather than by slow primary nucleation. In contrast, in our stochastic simulations, as in reality, the autocatalytic growth processes cannot start until the first nucleus has been generated—thus the lag time is dominated by the formation of the first primary nucleus, leading to γ = nc = 2.
Fortunately, it turns out that this problem can easily be remedied. The formation of the first primary nucleus in the volume V occurs as a Poisson process, with mean waiting time , where V is the volume and NA is Avogadro’s number (this follows from our definition of the nucleation reaction, Reaction 1). In the regime where the nucleation rate is very low, we expect that a single nucleus forms, and grows autocatalytically until the threshold is reached (i.e., we do not expect to see multiple primary nucleation events). Once the nucleus has formed, its growth should be well described by the deterministic model prediction, Eq. 7. We can therefore simply add the predicted waiting time for formation of a single nucleus to Eq. 7 to obtain the new prediction
where, as before, D = δ2/κ2 and Φ = log(1 – M∗/mtot). Because we are considering the unseeded case, C± = ±δ2/κ2 = ±D/2, we can rewrite Eq. 7. Modification of standard theory is needed to reproduce simulation results, thus:
If kn is large such that δ ≫ κ, we expect the second term in Eq. 7. Modification of standard theory is needed to reproduce simulation results to become negligible, leading to the same scaling behavior as Eq. 8 (red line in Fig. 2 b).
If, on the other hand, kn is small such that δ ≪ κ, Eq. 9 can be simplified by neglecting small terms in the logarithm:
| (9) |
As kn → 0, the logarithmic term can be neglected completely, yielding τlag ≈ 2k+/(VNAδ2) and hence γ = nc as expected when primary nucleation is very slow. For large nucleation rates kn, the logarithmic term dominates, leading to the autocatalysis-dominated scaling regime with γ = 1/2.
The blue line in Fig. 2 b shows the lag-time scaling exponent extracted from the modified lag-time expression (9), as a function of the nucleation rate constant kn. This prediction is indeed in excellent agreement with our simulation results over the entire range of primary nucleation rates.
Theory predicts kinks in lag-time versus concentration plots
Using the modified analytical lag-time expression, Eq. 9, which correctly accounts for the stochasticity of primary nucleation, we now investigate whether present-day theoretical models can account for the kinks that we observe in experimental lag time versus concentration plots. Fig. 3 a shows lag-time versus concentration curves predicted by Eq. 9, plotted over a wide range of protein concentrations (nine orders of magnitude). Results are shown for various values of the nucleation rate constant kn, indicated by the colors; kn increases top-right to bottom-left. The symbols show our stochastic simulation results, which are in good agreement with the predictions of Eq. 9. It is immediately apparent from Fig. 3 a that the model does indeed predict kinks in the lag-time versus concentration curves. These kinks appear for intermediate values of the nucleation rate constant. In these curves, the lag-time scaling changes smoothly, over approximately an order of magnitude in protein concentration, between the fragmentation-dominated scaling γ = 1/2 and either the primary nucleation-dominated scaling γ = nc or the Oosawa (elongation-dominated) scaling γ = nc/2. For very low or very high values of the nucleation rate constant, the lag-time versus concentration curves in Fig. 3 a do not show kinks, showing instead either primary nucleation-dominated scaling, γ = nc = 2, or Oosawa scaling, γ = nc/2 = 1, respectively. Thus our analysis shows that present-day models are consistent with the occurrence of kinks in lag-time versus concentration curves. These curves may show no kinks, one kink, or two kinks, depending on the molecular parameters and the protein concentration range observed.
Figure 3.
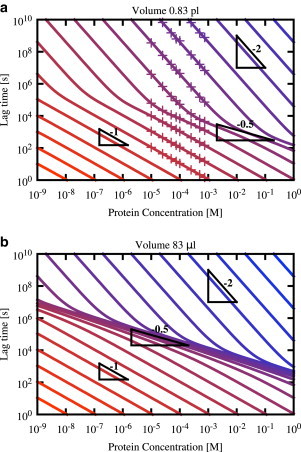
Transitions between different scaling regimes appear as kinks in lag-time versus concentration curves. Lag-time versus concentration curves predicted by Eq. 9 are plotted for a range of primary nucleation rates kn. The kn value increases top-right to bottom-left and is color-coded from kn = 10−30 M−1 s−1 (blue) to kn = 1010 M−1 s−1 (red), being increased by factors of 100. The two panels show results for different system volume V: (a) V = 0.83 pL, (approximately the size of a human cell). (b) The much larger volume V = 83 μL (a typical volume used in in vitro protein aggregation experiments). In panel a, the crosses correspond to the simulation data given in Fig. 2a. In all cases, k+ = 5 × 104 M−1 s−1, kf = 3 × 10−8 s−1, and nc = 2. To see this figure in color, go online.
Fragmentation-dominated scaling is more apparent at larger volumes
In vitro protein aggregation experiments are typically performed using system volumes of between 10 μL and 10 mL (10−5 to 10−2 L), while the typical volume of a human cell is ≤10–100 pL (10−11–10−10 L). To investigate the effect of sample volume, we repeated our analysis for a larger volume of 83 μL. For this volume, stochastic simulations are not practical, but the analytical result of Eq. 9 still holds. We expect that changing the sample volume will have a strong effect on the kinks in the lag-time versus concentration curves, because the time to formation of the first primary nucleus scales inversely with the volume (see Eq. 9). However, once a nucleus has been formed, the average time for the autocatalytic growth process to reach the threshold is independent of the volume (see, for example, Eq. 7). This implies that changing the system volume will shift the crossover points between the regimes in which the lag time is dominated by primary nucleation and by fragmentation—i.e., it will shift the kinks in the lag-time versus concentration curves. For larger systems, we expect the fragmentation-dominated regime to extend over a wider range of protein concentrations than for smaller systems.
Fig. 3 b shows lag-time versus concentration curves, computed using Eq. 9 for a volume of 83 μL, for the same parameter set as in Fig. 3 a. For the larger volume, we still see the two primary nucleation-dominated regimes γ = nc and γ = nc/2 at low and high nucleation rates, respectively. However, for intermediate nucleation rates, the fragmentation-dominated scaling regime γ = 1/2 typically extends over a wide range of concentrations (for some nucleation rates, we even see γ = 1/2 over the entire nine orders of magnitude of protein concentration).
Interestingly, these results suggest that lag-times for amyloid fibril formation are likely to scale quite differently with protein concentration in small volume samples than in in vitro experiments where the volume is large. While fragmentation-dominated lag-time scaling, with exponent γ = 1/2, may be a common feature of in vitro experiments, it is likely to be much less prevalent in smaller volumes on the scale of human cell, which are of clinical relevance.
Similar results are obtained for autocatalysis via secondary nucleation
Up to now, we have focused on the case where the autocatalytic growth mechanism is provided by fibril fragmentation. We now show that similar phenomena occur when autocatalysis instead occurs by secondary nucleation on the surface of existing fibrils. Fig. 4 a shows predicted lag-time versus concentration curves, for different values of the nucleation rate constant, for a model with primary nucleation, fibril elongation, and secondary nucleation (i.e., Reactions 1, 2, and 4). In this case, the same theoretical prediction for the lag time, Eq. 9, holds, but we use the alternative expression for the timescale of autocatalytic growth, . The predicted values of γ in the primary nucleation-dominated regimes are the same as for the fragmentation case: for very low nucleation rates (or low protein concentrations) we expect γ = nc = 2 while for high nucleation rates (or high protein concentrations) we expect γ = nc/2 = 1. However, the scaling in the intermediate, autocatalysis-dominated regime is now predicted to be γ = (ns + 1)/2, where ns is the size of the secondary nucleus (here assumed to be ns = 2 so that we predict γ = 3/2). These three regimes are indeed apparent in Fig. 4 a. As in the fragmentation case, increasing the system size increases the range of parameters (i.e., kn and protein concentration) for which autocatalysis dominates the lag time (Fig. 4 b).
Figure 4.
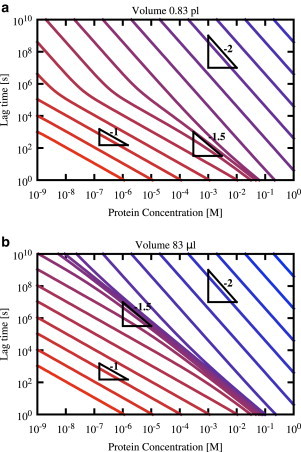
Kinks are also predicted in lag-time versus concentration curves for a model where the autocatalysis mechanism is provided by secondary nucleation. Lag-time versus concentration curves predicted by Eq. 9 are shown for a series of values of the primary nucleation rate kn (increasing top-right to bottom-left) from 10−30 M−1 s−1 (blue) to 106 M−1 s−1 (red), increasing by factors of 100. The two panels show results for different system volume V: (a) V = 0.83 pL (approximately the size of a human cell). (b) The much larger volume V = 83 μL (a typical volume used in in vitro protein aggregation experiments). The other parameters are k+ = 5 × 104 M−1 s−1, ks = 24 M−1 s−1, nc = 2, and ns = 2. To see this figure in color, go online.
Interestingly, the predicted lag-time scaling in the high concentration limit is somewhat different in the case of secondary nucleation, compared to fragmentation. In the fragmentation case, at very high protein concentrations, we expect to obtain the Oosawa-like scaling γ = nc/2 (see Fig. 3). In contrast, for secondary nucleation, some of our lag time versus concentration curves never reach the Oosawa-like scaling limit but instead converge to the secondary nucleation-dominated scaling exponent γ = (ns + 1)/2 = 3/2 in the high concentration limit (this is most apparent in Fig. 4 b). The crossover between the Oosawa-like and autocatalysis-dominated regimes occurs when δ = κ. These two parameters scale differently with protein concentration: δ scales as while κ scales as for secondary nucleation and mtot1/2 for fragmentation. For fragmentation, because nc/2 > 1/2, at high enough protein concentration there will always be a regime where δ > κ, leading to Oosawa-like scaling. For secondary nucleation, however, we may be in a situation where nc/2 < (ns + 1)/2 (this is indeed the case for our parameter set). In this case, for some parameter combinations, there may be no protein concentration range for which δ > κ; thus the Oosawa-like scaling regime may never be reached. In this case, we expect to see only a single kink in the lag time versus concentration curve, at the transition between the primary nucleation- and secondary nucleation-dominated regimes.
Are the kinks in experimental data explained by contemporary models?
We now assess quantitatively whether the kinks that we observe in the experimental data of Fig. 1 are consistent with the shifts among regimes dominated by primary nucleation, autocatalytic growth, and sequential monomer addition, as predicted by the model.
We first consider the values of the scaling exponent to the left and right of the kink, which we denote γL and γR. For insulin (Fig. 1 a), we obtain γL = 0.90(2) and γR = 0.42(10). These exponents are roughly consistent with a shift from a primary nucleation-dominated regime at low concentration, with γL = nc ≈ 1 to a fragmentation-dominated regime at higher concentration, with γR ≈ 1/2. Similarly, the exponents for β2 microglobulin (Fig. 1 c), γL = 0.77(14) and γR = 0.54(5), are roughly consistent with the same scenario. In contrast, for lysozyme (Fig. 1 b), we obtain quite different exponents, γL = 0.41(6) and γR = 0.06(5). In this case, while γL could conceivably correspond to a fragmentation-dominated regime (γ ≈ 1/2), the observed value of γR = 0.06(5) appears to be too small to correspond to any of the regimes predicted by the model. We also note that in the case where nc = 1, our model predicts that the Oosawa regime of nucleation-dependent polymerization will have a lag-time scaling exponent γ = 1/2 and thus not be distinguishable from the fragmentation-dominated regime. However, the shape of the growth curves at protein concentrations to the right of the kink (9,14) still appear strongly dominated by autocatalysis, and so it is unlikely that our range of data encompasses the second kink, i.e., a transition to the Oosawa regime.
We next consider the protein concentration at which the kink happens (the position of the kink) in the plots of Fig. 1. If the kinks do indeed signify a transition between primary nucleation- and fragmentation-dominated regimes (at least for insulin and β2 microglobulin), we can use our analytical model results to predict the concentration at which this should happen. Returning to our lag-time prediction, Eq. 9, the two terms inside the square brackets arise from autocatalytic growth and primary nucleation, respectively. The crossover in dominance between these mechanisms should happen when these two terms are equal in magnitude, i.e., when the following condition is satisfied:
| (10) |
Here, Φ = log(1 – M∗/mtot) is a constant relating to the lag-time threshold M∗, and D = δ2/κ2 measures the relative importance of the characteristic timescales for Oosawa-like growth and fragmentation-dominated growth κ−1 = (2k+kfmtot)−1/2. We now would like to determine whether Eq. 10 is satisfied for the kinks that we observe in the experimental data of Fig. 1.
A direct test of Eq. 10 requires knowledge of the kinetic parameters κ, k+, and kn, for each of the protein systems shown in Fig. 1. The value of κ can be extracted to a high degree of accuracy by fitting the predictions of the deterministic model, Eq. 6, to kinetic curves, and it can be reasonably assumed that the elongation rate k+ takes a similar value to that of insulin, for which it is known (14). Kinetic fits do not, however, accurately determine the nucleation rate constant kn, which is believed to vary widely among proteins (8,24,25). We are therefore obliged to take an indirect approach to testing Eq. 10. We ask what value of the nucleation rate constant kn would be required in order for Eq. 10 to be satisfied, for the data of Fig. 1. Then we ask whether this resulting prediction for kn is reasonable. If it is not reasonable, we can conclude that the kinks observed in the data of Fig. 1 cannot be explained by a transition between primary nucleation- and autocatalytic growth-dominated lag time regimes.
To this end, we extracted from the datasets of Fig. 1 the protein concentration (i.e., the value of mtot) at which the kink was observed. Using these values together with the known values of the sample volume V and lag-time threshold M∗, values of κ obtained by fitting kinetic curves (either in our own work (14) or that of Xue et al. (9)), and the value of k+ obtained by fitting the kinetic curves of insulin (14), we solved Eq. 10 numerically for D. From this, we obtained a value of the nucleation rate constant consistent with the position of the kink on the protein concentration axis, for each dataset. Based on our observations for the scaling exponents left of the kink, γL, we chose to use a nucleus size nc = 1, but we also repeated our calculations for larger values of nc. The parameters used in these calculations, together with the resulting values of kn, are presented in Table 1. Note that the predicted value of kn has different dimensionality depending on the assumed nucleus size.
Table 1.
Testing whether the condition from Eq. 10 is consistent with the kinks observed in the experimental data of Fig. 1
| Description | Insulin | Lysozyme | β2 microglobulin |
|---|---|---|---|
| mtot at kink (from Fig. 1) | 160 μM | 300 μM | 40 μM |
| κ from kinetic fit (9,14) | 1.3 × 10−4 s−1 | 1.2 × 10−3 s−1 | 7.2 × 10−5 s−1 |
| k+ from insulin kinetic fit (14) | 5 × 104 M−1 s−1 | 5 × 104 M−1 s−1 | 5 × 104 M−1 s−1 |
| V | 100 μL | 100 μL | 100 μL |
| M∗/mtot | 0.1 | 0.1 | 0.1 |
| Solution for kn for nc = 1 | 5.2 × 10−22 M−1 s−1 | 2.3 × 10−21 s−1 | 1.2 × 10−21 s−1 |
| Solution for kn for nc = 2 | 6.4 × 10−18 M−1 s−1 | 1.6 × 10−17 M−1 s−1 | 5.8 × 10−17 M−1 s−1 |
| Solution for kn for nc = 3 | 1.2 × 10−13 M−1 s−1 | 1.6 × 10−13 M−1 s−1 | 4.4 × 10−12 M−1 s−1 |
| Average time to nucleus | 56 h | 7 h | 98 h |
| Predicted lag time at kink | 112 h | 13 h | 197 h |
| Lag time at kink (from Fig. 1) | ∼25 h | ∼20 h | ∼10 h |
rows 2–6 show the parameter values used. Rows 7–9 show the resulting values of the nucleation rate constant kn from numerical solution of Eq. 10, for nc = 1, nc = 2, and nc = 3. Rows 10–12 show the implied predictions for the time to formation of the first nucleus and the lag time at the kink. The latter is compared to the experimental value extracted from Fig. 1. Values of κ were extracted from the gradient of the steepest part of the growth curves. Those shown here are the means, for each protein, at the protein concentration where the kink occurs.
To determine whether the resulting predictions for the nucleation rate constant kn were reasonable, we used them to calculate an estimated time to formation of the first nucleus, in a sample of the same volume and protein concentration as the experiment. This time is given by , and, due to a cancellation with the nc-dependence of kn, it is independent of the chosen value of nc. Table 1 lists the resulting times to formation of the first nucleus. For insulin and β2 microglobulin, it is immediately apparent that the predicted waiting times are not reasonable, because they are significantly longer than the observed lag time at the kink. We can also directly calculate the predicted lag time at the kink, by inputting our predicted value of kn (together with the other parameters) into Eq. 9. The results are presented in Table 1 and compared with the observed lag times at the kink, extracted from the data of Fig. 1 (again, these predictions are independent of nc).
Again, for insulin and β2 microglobulin, the predicted lag time is far longer than the observed lag time, suggesting that Eq. 10 is not satisfied for a reasonable choice of primary nucleation rate constant. Interestingly, for lysozyme, this procedure actually predicts a lag time that is within a factor of 2 of that observed experimentally (and is shorter rather than longer than the experimental value). While this might suggest that the kink observed for lysozyme could be explained by a transition between primary nucleation- and autocatalytic growth-dominated regimes, we note that for lysozyme, unlike the other proteins, the scaling exponents to the left and right of the kink do not seem to be consistent with such a transition.
To conclude, our analysis shows that the kinks we observe in the experimental lag-time versus concentration plots of Fig. 1 are not quantitatively consistent with a transition from primary nucleation- to growth-dominated lag-time regimes. For bovine insulin and β2 microglobulin, such a transition requires a primary nucleation rate constant that is too small to be consistent with the data, while for lysozyme the scaling exponents to the left and right of the kink are inconsistent with this transition. Understanding the origin of these kinks is likely to require new mechanistic understanding, beyond that provided by existing kinetic models.
Discussion
In experimental studies of amyloid fibril self-assembly kinetics, measurements of lag time as a function of protein concentration are often used to diagnose the underlying molecular mechanism (26). Based on predictions of theoretical models that include primary nucleation, elongation by monomer addition, and autocatalytic growth via fragmentation (or secondary nucleation), a scaling exponent γ < 1 is usually taken to imply a fragmentation-dominated mechanism, while an exponent γ > 1 suggests that fragmentation is not involved. In this article, we find that a more complex picture emerges from experimental lag-time versus concentration curves, when they are averaged over many replicates and measured over a wide range of protein concentrations. For three different protein systems (including both our own and others’ data), we observe kinks in the lag-time versus concentration curves, at which the scaling exponent γ changes. Other published datasets also show tantalizing hints of kinks, but with insufficient statistical certainty, or without a sufficiently wide concentration range to be sure (9,27–29).
The presence of a kink in the lag-time versus concentration curve apparently signifies a change in the dominant molecular mechanism at play during the lag phase of fibril assembly. To test whether these kinks are consistent with the existing theoretical picture, we carried out a detailed analysis of the lag-time scaling behavior of the standard model, including nucleation, elongation, and fragmentation (or secondary nucleation). Our analysis shows that indeed this model does predict changes in lag-time versus concentration scaling, and that these kinks in the lag-time versus concentration curve are due to crossovers among primary nucleation-dominated, autocatalysis-dominated, and elongation-dominated regimes. Capturing these kinks correctly requires us to modify the deterministic expression for the lag time to take account of stochastic primary nucleation events.
Importantly, however, an inconsistency is revealed upon quantitative comparison between the properties of the kinks that we observe in our and others’ experimental data, and the model predictions. For our data on bovine insulin (14) (Fig. 1 a) and the data of Xue et al. (9) on β2 microglobulin (Fig. 1 c), the scaling exponents to the left and right of the kink are broadly consistent with a transition from a primary nucleation-dominated regime at low protein concentration to a fragmentation-dominated regime at higher concentration. However, fitting the protein concentration at which this transition is observed to the prediction of the theoretical model requires us to assume a primary nucleation rate constant that is too low to account for the observed magnitude of the lag time. Thus for these protein systems, the theoretical model prediction is not quantitatively consistent with the data. For lysozyme (Fig. 1 b) the model also fails to account for the data, but in a different way: while the position of the kink is predicted correctly within a factor of 2, the scaling exponent to the right of the kink is inconsistent with any of the regimes predicted by the model. Thus, while the standard theoretical model generally does a good job of explaining kinetic curves for amyloid fibril formation, new mechanistic understanding is needed to explain detailed features of the lag-time concentration curves.
What mechanisms could account for the kinks that we see in the data of Fig. 1? The standard theoretical model investigated in this work is incomplete in that it does not include fibril end-joining (18) or length-dependent fragmentation; however, neither of these factors is expected to have a significant influence during the lag phase (30). Another factor not included in our model is spatial heterogeneity. For insulin fibril formation tracked microscopically in microdroplets, fibril formation has been shown to propagate out from an initial nucleation site as a spatial wave (20,31). It would be very interesting to investigate the consequences of this spatial propagation for the apparent lag-time scaling; however, it seems unlikely that it would affect the scaling in the apparent nucleation-dominated regime (left of the kink), where we obtain lower-than-expected scaling exponents for insulin and β2 microglobulin. It seems possible that our results may reflect the nature of the primary nucleation event itself. While this is often assumed to be a homogeneous, stochastic event occurring at a rate proportional to (i.e., involving the spontaneous union of nc monomers), fitting in vitro kinetic data is actually highly sensitive to the nature of the nucleation event. Factors such as nucleation on the surface of the sample chamber, the presence of preexisting nuclei, or slow conformational changes during the nucleation process could result in lag-time scaling with exponents lower than those predicted by the standard model. More generally, high-concentration saturation, either of the primary nucleation step (e.g., due to surface nucleation) or of the fibril elongation process, seems likely to lead to decreased lag-time scaling exponents. Indeed, lag-time scaling exponents smaller than one-half are quite frequently observed both in our own experimental work (14), and in that of others (8,16,32–36).
From an immediate practical point of view, our results demonstrate that great care is needed in interpreting lag-time scaling exponents from protein assembly data. More broadly, our work highlights a need to better understand the molecular mechanisms at play during the lag phase of amyloid fibril assembly. The lag phase of fibril assembly is of particular importance in the clinical context, both because lag-time variability may be associated with variable time of neurodegenerative disease onset (30) and because it has been suggested that toxicity of early-stage aggregates rather than fully assembled fibrils may be causative in disease (5,37,38). Detailed measurements of lag-time versus concentration scaling, combined with the development of new mechanistic models, may provide a way to probe what is going on during this crucial stage of the assembly process.
Acknowledgments
We thank Juraj Szavits-Nossan for useful discussions. The β2 microglobulin data was used in our analysis with kind permission of Xue et al. (9).
This work was supported by the Engineering and Physical Sciences Research Council under grant No. EP/J007404. K.E. was supported by an Engineering and Physical Sciences Research Council Doctoral Training Partnership endowment and R.J.A. was supported by a Royal Society University Research Fellowship.
References
- 1.Chiti F., Dobson C.M. Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 2006;75:333–366. doi: 10.1146/annurev.biochem.75.101304.123901. [DOI] [PubMed] [Google Scholar]
- 2.Knowles T.P.J., Buehler M.J. Nanomechanics of functional and pathological amyloid materials. Nat. Nanotechnol. 2011;6:469–479. doi: 10.1038/nnano.2011.102. [DOI] [PubMed] [Google Scholar]
- 3.Morris R.J., MacPhee C.E. Encyclopedia of Biophysics. Springer; New York: 2013. Amyloid protein biomaterials; pp. 76–81. [Google Scholar]
- 4.Kayed R., Head E., Glabe C.G. Common structure of soluble amyloid oligomers implies common mechanism of pathogenesis. Science. 2003;300:486–489. doi: 10.1126/science.1079469. [DOI] [PubMed] [Google Scholar]
- 5.Glabe C.G., Kayed R. Common structure and toxic function of amyloid oligomers implies a common mechanism of pathogenesis. Neurology. 2006;66:S74–S78. doi: 10.1212/01.wnl.0000192103.24796.42. [DOI] [PubMed] [Google Scholar]
- 6.Glabe C.G. Structural classification of toxic amyloid oligomers. J. Biol. Chem. 2008;283:29639–29643. doi: 10.1074/jbc.R800016200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Binger K.J., Pham C.L.L., Howlett G.J. Apolipoprotein C-II amyloid fibrils assemble via a reversible pathway that includes fibril breaking and rejoining. J. Mol. Biol. 2008;376:1116–1129. doi: 10.1016/j.jmb.2007.12.055. [DOI] [PubMed] [Google Scholar]
- 8.Knowles T.P.J., Waudby C.A., Dobson C.M. An analytical solution to the kinetics of breakable filament assembly. Science. 2009;326:1533–1537. doi: 10.1126/science.1178250. [DOI] [PubMed] [Google Scholar]
- 9.Xue W.-F., Homans S.W., Radford S.E. Systematic analysis of nucleation-dependent polymerization reveals new insights into the mechanism of amyloid self-assembly. Proc. Natl. Acad. Sci. USA. 2008;105:8926–8931. doi: 10.1073/pnas.0711664105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ferrone F.A. Analysis of protein aggregation kinetics. Methods Enzymol. 1999;309:256–274. doi: 10.1016/s0076-6879(99)09019-9. [DOI] [PubMed] [Google Scholar]
- 11.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J. Chem. Phys. 2011;135:065105. doi: 10.1063/1.3608916. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. II. Determination of self-consistent solutions to growth processes described by non-linear master equations. J. Chem. Phys. 2011;135:065106. doi: 10.1063/1.3608917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. Nucleated polymerization with secondary pathways. III. Equilibrium behavior and oligomer populations. J. Chem. Phys. 2011;135:065107. doi: 10.1063/1.3608918. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Morris R.J., Eden K., MacPhee C.E. Mechanistic and environmental control of the prevalence and lifetime of amyloid oligomers. Nat. Commun. 2013;4:1891. doi: 10.1038/ncomms2909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nielsen L., Khurana R., Fink A.L. Effect of environmental factors on the kinetics of insulin fibril formation: elucidation of the molecular mechanism. Biochemistry. 2001;40:6036–6046. doi: 10.1021/bi002555c. [DOI] [PubMed] [Google Scholar]
- 16.Padrick S.B., Miranker A.D. Islet amyloid: phase partitioning and secondary nucleation are central to the mechanism of fibrillogenesis. Biochemistry. 2002;41:4694–4703. doi: 10.1021/bi0160462. [DOI] [PubMed] [Google Scholar]
- 17.Gillam J.E., MacPhee C.E. Modeling amyloid fibril formation kinetics: mechanisms of nucleation and growth. J. Phys. Condens. Matter. 2013;25:373101. doi: 10.1088/0953-8984/25/37/373101. [DOI] [PubMed] [Google Scholar]
- 18.Michaels T.C.T., Knowles T.P.J. Role of filament annealing in the kinetics and thermodynamics of nucleated polymerization. J. Chem. Phys. 2014;140:214904. doi: 10.1063/1.4880121. [DOI] [PubMed] [Google Scholar]
- 19.Hill T.L. Length dependence of rate constants for end-to-end association and dissociation of equilibrium linear aggregates. Biophys. J. 1983;44:285–288. doi: 10.1016/S0006-3495(83)84301-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Knowles T.P.J., White D.A., Weitz D.A. Observation of spatial propagation of amyloid assembly from single nuclei. Proc. Natl. Acad. Sci. USA. 2011;108:14746–14751. doi: 10.1073/pnas.1105555108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Oosawa F., Asakura S. Academic Press; New York: 1975. Thermodynamics of the Polymerization of Protein. [Google Scholar]
- 22.Oosawa F., Kasai M. A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 1962;4:10–21. doi: 10.1016/s0022-2836(62)80112-0. [DOI] [PubMed] [Google Scholar]
- 23.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 24.Morris A.M., Watzky M.A., Finke R.G. Fitting neurological protein aggregation kinetic data via a 2-step, minimal/“Ockham’s razor” model: the Finke-Watzky mechanism of nucleation followed by autocatalytic surface growth. Biochemistry. 2008;47:2413–2427. doi: 10.1021/bi701899y. [DOI] [PubMed] [Google Scholar]
- 25.Watzky M.A., Morris A.M., Finke R.G. Fitting yeast and mammalian prion aggregation kinetic data with the Finke-Watzky two-step model of nucleation and autocatalytic growth. Biochemistry. 2008;47:10790–10800. doi: 10.1021/bi800726m. [DOI] [PubMed] [Google Scholar]
- 26.Cohen S.I.A., Vendruscolo M., Knowles T.P.J. The kinetics and mechanisms of amyloid formation. In: Otzen D.E., editor. Amyloid Fibrils and Prefibrillar Aggregates. Wiley-VCH; Weinheim, Germany: 2013. pp. 183–209. [Google Scholar]
- 27.Wright C.F., Teichmann S.A., Dobson C.M. The importance of sequence diversity in the aggregation and evolution of proteins. Nature. 2005;438:878–881. doi: 10.1038/nature04195. [DOI] [PubMed] [Google Scholar]
- 28.Hellstrand E., Boland B., Linse S. Amyloid β-protein aggregation produces highly reproducible kinetic data and occurs by a two-phase process. ACS Chem. Neurosci. 2010;1:13–18. doi: 10.1021/cn900015v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ramachandran G., Udgaonkar J.B. Evidence for the existence of a secondary pathway for fibril growth during the aggregation of tau. J. Mol. Biol. 2012;421:296–314. doi: 10.1016/j.jmb.2012.01.007. [DOI] [PubMed] [Google Scholar]
- 30.Szavits-Nossan J., Eden K., Allen R.J. Inherent variability in the kinetics of autocatalytic protein self-assembly. Phys. Rev. Lett. 2014;113:098101. doi: 10.1103/PhysRevLett.113.098101. [DOI] [PubMed] [Google Scholar]
- 31.Cohen S., Rajah L., Knowles T. Spatial propagation of protein polymerization. Phys. Rev. Lett. 2014;112:098101. doi: 10.1103/PhysRevLett.112.098101. [DOI] [PubMed] [Google Scholar]
- 32.Serio T.R., Cashikar A.G., Lindquist S.L. Nucleated conformational conversion and the replication of conformational information by a prion determinant. Science. 2000;289:1317–1321. doi: 10.1126/science.289.5483.1317. [DOI] [PubMed] [Google Scholar]
- 33.Kelly J.W. Mechanisms of amyloidogenesis. Nat. Struct. Biol. 2000;7:824–826. doi: 10.1038/82815. [DOI] [PubMed] [Google Scholar]
- 34.Collins S.R., Douglass A., Weissman J.S. Mechanism of prion propagation: amyloid growth occurs by monomer addition. PLoS Biol. 2004;2:e321. doi: 10.1371/journal.pbio.0020321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhu L., Zhang X.-J., Perrett S. Relationship between stability of folding intermediates and amyloid formation for the yeast prion Ure2p: a quantitative analysis of the effects of pH and buffer system. J. Mol. Biol. 2003;328:235–254. doi: 10.1016/s0022-2836(03)00249-3. [DOI] [PubMed] [Google Scholar]
- 36.Foderà V., Librizzi F., Leone M. Secondary nucleation and accessible surface in insulin amyloid fibril formation. J. Phys. Chem. B. 2008;112:3853–3858. doi: 10.1021/jp710131u. [DOI] [PubMed] [Google Scholar]
- 37.Bucciantini M., Calloni G., Stefani M. Prefibrillar amyloid protein aggregates share common features of cytotoxicity. J. Biol. Chem. 2004;279:31374–31382. doi: 10.1074/jbc.M400348200. [DOI] [PubMed] [Google Scholar]
- 38.Xue W.-F., Hellewell A.L., Radford S.E. Fibril fragmentation enhances amyloid cytotoxicity. J. Biol. Chem. 2009;284:34272–34282. doi: 10.1074/jbc.M109.049809. [DOI] [PMC free article] [PubMed] [Google Scholar]


