Abstract
Two alternative hypotheses attribute different benefits to codon-anticodon adaptation. The first assumes that protein production is rate limited by both initiation and elongation and that codon-anticodon adaptation would result in higher elongation efficiency and more efficient and accurate protein production, especially for highly expressed genes. The second claims that protein production is rate limited only by initiation efficiency but that improved codon adaptation and, consequently, increased elongation efficiency have the benefit of increasing ribosomal availability for global translation. To test these hypotheses, a recent study engineered a synthetic library of 154 genes, all encoding the same protein but differing in degrees of codon adaptation, to quantify the effect of differential codon adaptation on protein production in Escherichia coli. The surprising conclusion that “codon bias did not correlate with gene expression” and that “translation initiation, not elongation, is rate-limiting for gene expression” contradicts the conclusion reached by many other empirical studies. In this paper, I resolve the contradiction by reanalyzing the data from the 154 sequences. I demonstrate that translation elongation accounts for about 17% of total variation in protein production and that the previous conclusion is due to the use of a codon adaptation index (CAI) that does not account for the mutation bias in characterizing codon adaptation. The effect of translation elongation becomes undetectable only when translation initiation is unrealistically slow. A new index of translation elongation ITE is formulated to facilitate studies on the efficiency and evolution of the translation machinery.
Keywords: codon usage bias, codon-anticodon adaptation, translation elongation, translation efficiency, index of translation elongation
FOLLOWING empirical documentation of the correlation between codon usage and tRNA abundance (Ikemura 1981a,b, 1982, 1992), many studies have demonstrated a strong relationship not only between codon adaptation and gene expression (Coghlan and Wolfe 2000; Comeron and Aguade 1998; Duret and Mouchiroud 1999; Xia 2007) but also between experimentally modified codon usage and protein production (Haas et al. 1996; Ngumbela et al. 2008; Robinson et al. 1984; Sorensen et al. 1989). These results have led to the explicit formulation of codon-anticodon coevolution and adaptation theory (e.g., Akashi 1994; Moriyama and Powell 1997; Ran and Higgs 2012; Xia 1998, 2008), which states that (1) protein production is rate limited by both translation initiation and elongation efficiency, (2) codon usage and tRNA anticodons coevolve to adapt to each other, resulting in increased production of correctly translated proteins, and (3) the increased elongation efficiency and accuracy represent the driving force for the highly expressed genes to acquire a high degree of codon-anticodon adaptation. These studies not only advanced our understanding of the joint effect of mutation and selection on codon usage (Chithambaram et al. 2014a,b; Palidwor et al. 2010) but also resulted in improved computational tools for characterizing codon usage and codon-anticodon adaptation (Sun et al. 2013; Xia 2007).
Whether translation elongation is a rate-limiting process in protein production has been controversial. Early theoretical considerations (Andersson and Kurland 1983; Bulmer 1990, 1991; Liljenstrom and von Heijne 1987) tended to favor the argument that translation elongation is not rate limiting in protein production but that translation initiation is. This hypothesis states that codon-anticodon adaptation and increased elongation efficiency are not related to protein production. Instead, the benefit of codon adaptation and increased elongation efficiency is to increase ribosomal availability for global translation.
To test these two alternative hypotheses, Kudla et al. (2009) engineered a synthetic library of 154 genes, all encoding the same green fluorescent protein in Escherichia coli but differing in synonymous sites [and consequently the degree of codon adaptation, as measured by codon adaptation index (CAI)]. All sequences share an identical 5′-UTR that is 144 nt long, so there is no variation in the Shine-Dalgarno sequence. Because the engineered genes all encode the same protein, it is justifiable to use protein abundance as a proxy for protein production (assuming that protein molecules sharing the same amino acid sequence have the same degradation rate).
Kudla et al. (2009) interpreted minimum folding energy (MFE), computed from sites −4 to +37 (where ribosomes position themselves at the initiation codon), as a proxy for initiation efficiency. The rationale for using MFE as a measure of translation initiation is that an initiation codon would be inaccessible if it were embedded in a strong secondary structure and that accessibility of the initiation codon is a key determinant of translation initiation efficiency (Nakamoto 2006). A stable secondary structure in sequences flanking the start codon has been shown experimentally to inhibit translation initiation (Osterman et al. 2013). MFE can be computed by using DAMBE (Xia 2013), which implements the RNA folding library from the Vienna RNA package (Hofacker 2003).
Kudla et al. (2009) interpreted CAI as a proxy for translation elongation. If both translation initiation and translation elongation contribute to translation efficiency, then protein production is expected to depend on both MFE and CAI. If only translation initiation is important, then protein production will depend only on MFE. These authors found that MFE accounts for 44% of the variation in protein production but that CAI is essentially unrelated to protein production. They concluded, consequently, that “translation initiation, not elongation, is rate-limiting for gene expression” (Kudla et al. 2009, p. 258).
The conclusion by Kudla et al. (2009), however, is based on two critical assumptions: (1) that MFE and CAI are good proxies of translation initiation and elongation efficiencies, respectively, and (2) that the effect of translation elongation is independent of translation initiation. The problem with the second assumption has been pointed out recently (Supek and Smuc 2010); Tuller et al. (2010) reanalyzed the data in addition to providing an overwhelming amount of additional empirical evidence to demonstrate the joint effect of both translation initiation and translation elongation on protein production. In short, the protein production rate is expected to increase with elongation efficiency only when translation initiation is efficient. If translation initiation is slow, then an increasing elongation rate is not expected to increase protein production. Kudla et al. (2009) ignored the dependence of elongation effect on translation initiation.
However, the results reported by Tuller et al. (2010) are not much different from those of Kudla et al. (2009). The key finding from the reanalysis (Tuller et al. 2010) is that the effect of codon usage bias on protein production is only marginally significant when translation initiation (with MFE as proxy) is controlled for. The partial correlation between codon usage bias and protein production is only marginally significant (P = 0.04), accounting for less than 3% of the total variation in protein abundance. This finding simply reinforces the original conclusion of Kudla et al. (2009) that the effect of codon usage and translation elongation on protein production is negligible relative to that of translation initiation (with MFE as proxy), which accounts for 44% of the total variation in protein production.
CAI by Kudla et al. (2009) and translation adaptation index (tAI) by Tuller et al. (2010) as proxies for translation elongation efficiency are both problematic and can lead to serious bias, as will be illustrated in the next section. In this paper, I develop a new CAI that accommodates the background mutation bias. I found that translation elongation accounts for about 17% of total variation in protein production.
Necessity of a New Translation Elongation Index
Many gene-specific codon usage indices have already been formulated and improved, including CAI (Sharp and Li 1987; Xia 2007), tAI (dos Reis et al. 2004) and several indices that are based on coding sequences only, such as the effective number of codons (Wright 1990) and its improved versions (Novembre 2002; Sun et al. 2013) and the codon deviation coefficient (CDC) (Zhang et al. 2012). The first two have been used frequently as proxies for translation elongation efficiency, whereas the others are typically not related to translation rate. For example, in contrast to CAI and tAI, which are at least positively correlated with the protein production data in Kudla et al. (2009), CDC is negatively correlated with protein production, although the correlation is not significant (r = −0.1254, P = 0.1211).
The problem with tAI is that codon usage bias is not always inferable from tRNA gene copy numbers or experimentally measured tRNA abundance because codon and anticodon do not always pair as expected according to the wobble or extended wobble hypothesis (Crick 1966; Grosjean et al. 2007, 2010). For example, inosine is expected to pair best with C and U, less with A (partly because of the bulky I-/A pairing involving two purines), and not with G. However, tRNAVal/IAC from rabbit liver pairs better with the GUG codon than with other synonymous codons (Jank et al. 1977; Mitra et al. 1977). Similarly, the Bacillus subtilis genome codes a tRNAAla/GGC for decoding GCY codons, but the GCC codon that forms the Watson-Crick base pair with the anticodon is not used as frequently as the GCU codon, which wobble-pairs with the anticodon. One might argue that based on previous studies (Fiers and Grosjean 1979; Grantham et al. 1981; Grosjean et al. 1978; Ikemura 1981a), the intermediate binding strength between codon and anticodon is optimal, especially for highly expressed genes. A weak binding at the third codon position is preferred, with strong binding occurring at the first two codon positions, and a strong binding at the third codon position is preferred, with weak binding occurring at the first two codon positions. Thus, GCU is preferred by anticodon GGC because of the strong binding at the first two codon positions. However, this explanation does not work for Gly, where four tRNAGly/GCC genes are present for decoding GGY codons, and GGC is used more frequently than GGU (Sun et al. 2013). Furthermore, codon-anticodon base pairing is known to be context dependent (Lustig et al. 1989), for example, a wobble cmo5U in the anticodon of tRNAPro; tRNAAla and tRNAVal can read all four synonymous codons in the respective codon family, but the same cmo5U in tRNAThr cannot read C-ending codons (Nasvall et al. 2007). For this reason, the optimal codon usage is likely better approximated by the codon usage of highly expressed genes than by what we can infer based on codon-anticodon pairing. Consistent with this proposition, CAI, which is based on the codon usage of highly expressed genes (HEGs), performs better in predicting protein production or abundance than other indices based on tRNAs (Coghlan and Wolfe 2000; Comeron and Aguade 1998; Duret and Mouchiroud 1999).
CAI has its own problems, however. Other than those outlined previously (Xia 2007), it often leads to a wrong interpretation of tRNA-mediated selection. I illustrate this problem here with the Ala codon subfamily GCR (where R stands for either A or G). The frequencies of GCA and GCG in E. coli HEGs, as compiled and distributed with EMBOSS (Rice et al. 2000), are 1973 and 2654, respectively, which may lead one to think that the E. coli translation machinery prefers GCG over GCA. However, the codon frequencies of GCA and GCG for E. coli non-HEGs are 25,511 and 43,261, respectively. Thus, GCA is relatively more frequent in E. coli HEGs than in E. coli non-HEGs. This suggests that mutation bias favors GCG but that tRNA-mediated selection favors GCA, which is relatively more preferred by E. coli HEGs. This interpretation is corroborated by the E. coli genome encoding three tRNAArg genes for GCR codons, all with a UGC anticodon forming a perfect Watson-Crick base pair with codon GCA.
For the NNR or NNY codon family or subfamily, we first define Pi.HEG and Pi.non-HEG as the proportion of codon i within its R- or Y-ending family for E. coli HEGs and non-HEGs. For example, take data for codons GCA and GCG in Table 1
| (1) |
where SGCA and SGCG may be viewed as relative codon frequencies of HEGs corrected for the “background” non-HEGs. Codon i is considered selected for if Si > 1 and against if Si < 1. Thus, codon GCA is considered selected for because, according to Equation 1, SGCA > 0. This insight would be obscured if we were to use codon frequency data from only E. coli HEGs or only non-HEGs, which would have suggested that codon GCA is selected against. The Si values for the sense codons in E. coli are listed in Table 1.
Table 1. Codon frequency (CF) for E. coli highly expressed genes (HEGs) and non-HEGs, as well as the computed Si values according to Equation 1.
| AA | Codon | CFHEGa | CFnon-HEGb | Si |
|---|---|---|---|---|
| A | GCA | 1973 | 25,511 | 1.1495 |
| A | GCG | 2654 | 43,261 | 0.9118 |
| A | GCC | 1306 | 33,463 | 0.5646 |
| A | GCU | 2288 | 18,526 | 1.7865 |
| C | UGC | 475 | 8,397 | 1.1541 |
| C | UGU | 270 | 6,802 | 0.8098 |
| D | GAC | 2786 | 23,226 | 1.5125 |
| D | GAU | 2345 | 41,472 | 0.7130 |
| E | GAA | 4683 | 49,154 | 1.1180 |
| E | GAG | 1459 | 22,920 | 0.7470 |
| F | UUC | 2229 | 20,332 | 1.7637 |
| F | UUU | 872 | 29,556 | 0.4746 |
| G | GGA | 118 | 10,786 | 0.7282 |
| G | GGG | 267 | 14,842 | 1.1975 |
| G | GGC | 2987 | 37,418 | 0.8210 |
| G | GGU | 3583 | 30,154 | 1.2221 |
| H | CAC | 1160 | 12,144 | 1.7105 |
| H | CAU | 477 | 17,170 | 0.4975 |
| I | AUA | 22 | 5,926 | 0.0000 |
| I | AUC | 3488 | 30,787 | 1.5592 |
| I | AUU | 1640 | 39,788 | 0.5673 |
| K | AAA | 4129 | 41,696 | 1.0469 |
| K | AAG | 1050 | 13,057 | 0.8502 |
| L | CUA | 54 | 5,258 | 0.1275 |
| L | CUG | 5698 | 66,130 | 1.0694 |
| L | CUC | 541 | 14,591 | 1.2085 |
| L | CUU | 357 | 14,679 | 0.7927 |
| L | UUA | 210 | 18,739 | 0.7639 |
| L | UUG | 333 | 18,273 | 1.2422 |
| M | AUG | 2444 | 35,527 | 0.0000 |
| N | AAC | 2832 | 26,674 | 1.5850 |
| N | AAU | 539 | 23,652 | 0.3402 |
| P | CCA | 474 | 11,046 | 0.5779 |
| P | CCG | 2509 | 29,125 | 1.1601 |
| P | CCC | 38 | 7,443 | 0.2235 |
| P | CCU | 343 | 9,235 | 1.6258 |
| Q | CAA | 550 | 20,405 | 0.4975 |
| Q | CAG | 2548 | 36,780 | 1.2788 |
| R | AGA | 21 | 2,880 | 0.9782 |
| R | AGG | 13 | 1,681 | 1.0374 |
| R | CGA | 34 | 4,837 | 1.2807 |
| R | CGG | 33 | 7,370 | 0.8158 |
| R | CGC | 1530 | 28,473 | 0.6413 |
| R | CGU | 2995 | 25,528 | 1.4001 |
| S | AGC | 1015 | 20,868 | 1.3432 |
| S | AGU | 168 | 11,802 | 0.3931 |
| S | UCA | 189 | 9,614 | 0.9119 |
| S | UCG | 275 | 11,909 | 1.0711 |
| S | UCC | 1110 | 10,649 | 0.8950 |
| S | UCU | 1320 | 10,217 | 1.1094 |
| T | ACA | 181 | 9,527 | 0.7719 |
| T | ACG | 526 | 19,197 | 1.1132 |
| T | ACC | 2533 | 29,335 | 0.9108 |
| T | ACU | 1286 | 10,950 | 1.2389 |
| V | GUA | 1329 | 13,513 | 1.5053 |
| V | GUG | 1784 | 34,133 | 0.8000 |
| V | GUC | 824 | 19,972 | 0.4993 |
| V | GUU | 2669 | 22,297 | 1.4485 |
| W | UGG | 819 | 19,945 | 0.0000 |
| Y | UAC | 1569 | 15,094 | 1.5503 |
| Y | UAU | 865 | 21,207 | 0.6083 |
Taken from the Ecoli_high.cut file distributed with EMBOSS 6.4 (Rice et al. 2000) representing a compilation of codon usage from known highly expressed E. coli K12 genes.
The index of translation elongation ITE is then calculated in a way similar to CAI except that the computation is applied to NNR and NNY codon subfamilies:
| (2) |
| (3) |
where Fi is the frequency of codon i, and Ns is the number of sense codons (excluding those in single-codon families). For example, AUG for methionine, AUA for isoleucine, and UGG for tryptophan in the standard genetic code are excluded from computing ITE. Just like CAI, tAI, and , ITE is a gene-specific index of codon usage bias.
The main reason for dividing codons into the R- and Y-ending groups is that for genes encoded by the nuclear genome, the R-ending codons are typically decoded by two types of tRNA species (one with a wobble C and the other with a wobble U), whereas the Y-ending codons are decoded typically by a single type of tRNA species with either a wobble G or a wobble A modified to inosine, but never by both (Grosjean et al. 2007; Marck and Grosjean 2002). For this reason, the R- and Y-ending codons, even within a single fourfold codon family, are subject to different tRNA-mediated selection and therefore should be treated separately. However, for comparative purposes, I have chosen to include the other two alternative approaches for computing ITE, that is, one with compound six- and eightfold codon families broken into two- and fourfold codon families and the other lumping all synonymous codons into one codon family. A new version of DAMBE (Xia 2013) has been uploaded with all three approaches included. One may access the function by clicking on “Seq.Analysis|Codon usage|Index of translation elongation.”
One may note that CAI is a special case of ITE when there is absolutely no codon usage bias in non-HEGs in all codon subfamilies. That is, when NGCA.non-HEG = NGCG.non-HEG, NGCC.non-HEG = NGCU.non-HEG, and so on. The range of ITE is the same as CAI, that is, between 0 and 1. The reason for separating synonymous codons into R- and Y-ending codon subfamilies is that they are typically translated by different tRNAs and subject to different mutation bias. I have outlined the problems of lumping synonymous codons together and illustrated the benefit of treating R- and Y-ending codons separately elsewhere (Sun et al. 2013; Xia 2007).
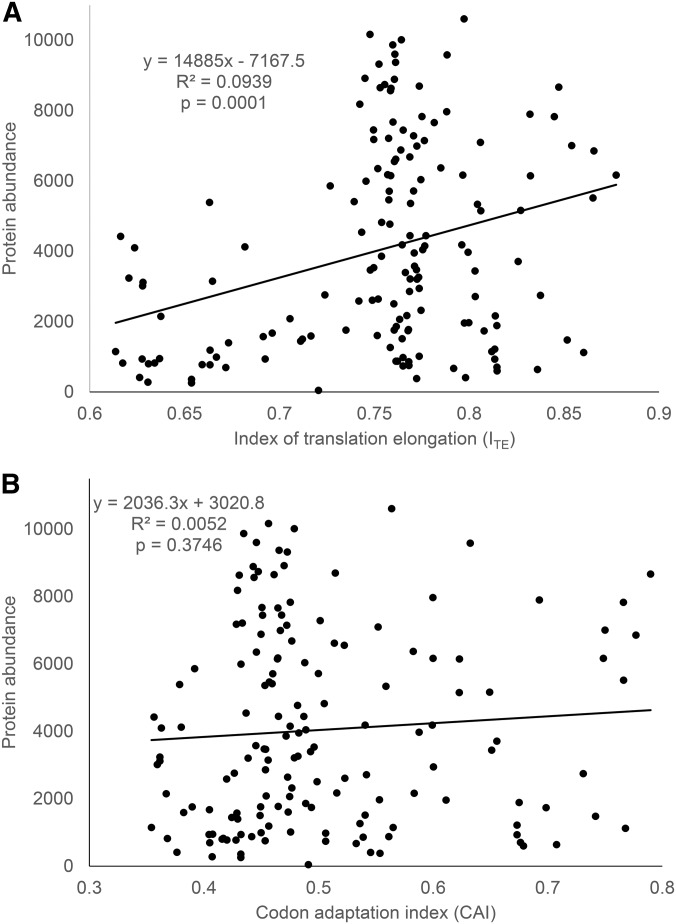
The relationship between protein abundance and ITE (Figure 1a) for the data from Kudla et al. (2009) is contrasted with that between protein abundance and CAI (Figure 1b). There are three points worth highlighting. First, a highly significant relationship between protein abundance and translation elongation is revealed by the new ITE, accounting for nearly 10% of the total variation in protein abundance (P = 0.0001) (Figure 1a). In contrast, no relationship exists between protein abundance and CAI (Figure 1b). Second, when ITE is small (e.g., ITE < 0), protein abundance is generally low, which suggests that translation elongation is limiting. Third, a large ITE (efficient translation elongation) does not imply high protein production because translation initiation is also limiting. A large ITE will lead to increased protein production only if translation initiation is also efficient.
Figure 1.
Relationship between protein abundance (measured by GFP normalized fluorescence; data kindly provided by Dr. Plotkin) and translation elongation efficiency ITE, contrasting with that between protein abundance and CAI (codon adaptation index).
One may argue that ITE should be computed without the first 36 bases because these sites have already been used in computing MFE. I have computed codon frequencies and ITE without the first 36 bases (designated ITE_shortCDS) and added this to Supporting Information, Table S1. ITE_shortCDS and ITE_full-lengthCDS (the original ITE with full-length CDS) are almost perfectly correlated (r = 0.9976).
Conceptual Framework for Evaluating the Effect of Translation Initiation and Elongation
It is only genes with efficient translation initiation that are expected to increase protein production with improved codon-anticodon adaptation. If we express the protein production rate Prot as a linear function of elongation efficiency ITE, that is,
| (4) |
we would expect the slope b to change with initiation efficiency. A low initiation efficiency implies little benefit for high ITE, and b should be close to 0. In contrast, elongation efficiency would become rate limiting with high translation initiation efficiency, and we would expect b to increase with translation initiation efficiency.
I tested these predictions by using the original data in Kudla et al. (2009) with the same proxies that they used for Prot and translation initiation; that is, Prot was measured by normalized GFP fluorescence level and translation initiation efficiency by MFE of the sequences flanking the initiation codon, from sites −4 to +37. I replaced their CAI by ITE as a proxy for translation elongation efficiency. I followed the practice of Tuller et al. (2010) by ranking Prot (designated as rProt in supporting information, Table S1, which contains all relevant data for the following analysis).
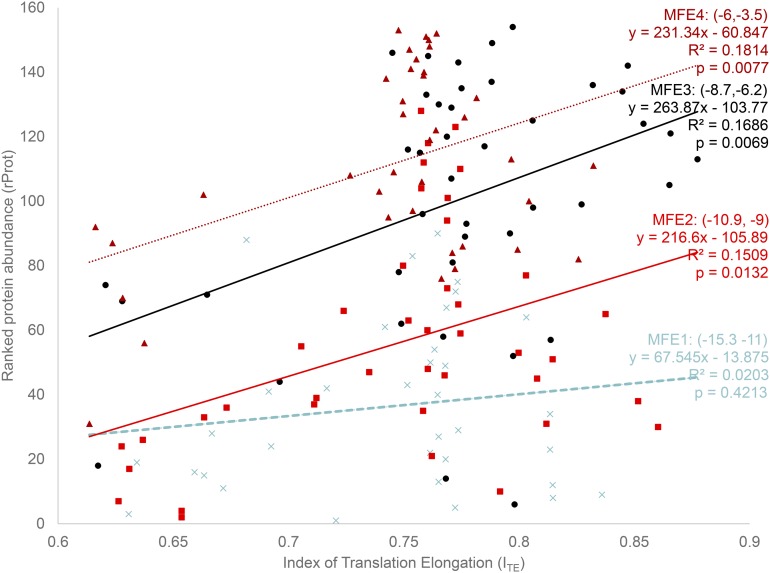
I binned the MFE into four categories, (−15.3, −11), (−10.9, −9), (−8.7, −6.2), and (−6, −3.5), representing translation initiation from the lowest to the highest and designated as MFE1–MFE4 (Figure 2). The intervals were chosen in such a way that all MFE values fall into four roughly equal-sized groups, with within-group MFE being as small as possible. The benefit of binning is that one can exclude the MFE variable so that the effect of ITE can be modeled more explicitly. If MFE is included as an independent variable, then it becomes difficult to isolate the effect of ITE because ITE and MFE may interact with each other in unexpected ways. It is for this same reason that Tuller et al. (2010) also used binned analysis for this data set.
Figure 2.
Ranked protein abundance rProt (protein abundance is measured by GFP normalized fluorescence; data kindly provided by Dr. Plotkin) increases with translation elongation efficiency ITE, except for the group with extraordinarily strong secondary structure at the 5′ end (the MFE1 group). rProt also increases with decreasing stability of secondary structure, with MFE1 having the most stable and MFE4 the weakest secondary structure. The range of MFE is indicated for each of the four MFE groups.
In the MFE1 group, translation initiation is the lowest, and we should expect little increase in protein production with translation elongation efficiency (ITE), that is, a weak relationship between ITE and rProt. This is consistent with the empirical result (Figure 2), where the relationship between ITE and rProt is not statistically significant in the MFE1 group (b = 67.545, P = 0.4213) (Figure 2), with ITE accounting for only 2% of total variation in ranked protein abundance (rProt). In contrast, when translation initiation is more efficient in groups MFE2–MFE4, rProt increases significantly with ITE, with the simple linear model consistently accounting for about 17% of the total variation in rProt (Figure 2, with b varying from 216.60 to 263.87). Thus, the contribution of translation elongation (ITE) to protein production is much greater than previously documented for this data set, that is, no (Kudla et al. 2009) or less than 3% of the total variation in protein production (Tuller et al. 2010).
Alternatively, one may rank MFE as an index of translation initiation (ITI) so that a more negative MFE (more stable secondary structure) will have a smaller ITI and fit the data to the following model:
| (5) |
The effect of ITE can be evaluated by testing the hypothesis that b2 = 0. Because protein abundance is measured by fluorescence levels (Kudla et al. 2009), b0 in Equation 5 represents the background fluorescence. The fitted model is
| (6) |
This model accounts for 56.0% of total variation in rProt. The P-value associated with b2 is 0.00000004. The fitted model in Equation 6 suggests that when elongation efficiency is low (e.g., ITE < 0.4822), increasing ITI would either have no effect or a negative effect on protein production. The negative effect could be generated when ribosomes collide/interfere with each other when initiation is efficient but elongation is not.
Discussion
Many codon optimizing and deoptimizing experiments have used both prokaryotic and eukaryotic translation systems and consistently have suggested an increased translation rate with optimized codon usage and a reduced translation rate with deoptimized codon usage (Haas et al. 1996; Ngumbela et al. 2008; Robinson et al. 1984; Sorensen et al. 1989). Kudla et al. (2009) are exceptional in claiming that translation efficiency is not limited by elongation rate or codon usage bias. However, as shown in this paper, the claim is false for two reasons. First, the authors ignore the interaction between translation initiation and translation elongation. Second, CAI is an inadequate proxy for measuring translation elongation.
While theoretical models can fail to capture the essence of reality, experimental models can fail the same way. Tuller et al. (2010) have pointed out that the average MFE in the sequences of Kudla et al. (2009) is extraordinarily low. The average MFE is only −8.87, with a range from −15.3 to −3.5. Among the 4320 annotated coding sequences in the E. coli K12 strain (NC_000913), the MFE for the segment between sites −4 and +37 has a mean of −5.23, with only 16 sequences with MFE values smaller than −15.3 but 1278 sequences with MFE values greater than −3.5. Thus, the MFE1 group in Figure 2 is not representative of the real data and should be excluded in interpreting the effect of elongation on protein production for most genes.
I also wish to point out that the data of Kudla et al. (2009) also suffer from unrealistically small variation in elongation efficiency. The CAIs for the experimental sequences are all smaller than 0.6 according to Figure 2A in Kudla et al. (2009). More than 1000 E. coli genes have CAIs greater than 0.6. This means that the experimental sequences in Kudla et al. (2009) all have relatively low elongation efficiency, and the data set therefore is inadequate for a fair assessment of the effect of elongation on protein production. The fact that even such a limited variation in translation elongation efficiency can still demonstrate a highly significant effect of elongation rate on protein production represents strong evidence that protein production depends heavily on elongation efficiency and codon adaptation.
It is also problematic to attribute the effect of MFE all to translation initiation, as did Kudla et al. (2009). While a stable secondary structure embedding the initiation codon will surely affect translation initiation, it may well hinder translation elongation as well. This would suggest that the effect of MFE on protein production could be due to both translation initiation and translation elongation. That is, translation elongation as characterized by ITE may well account for more than about the 17% shown in Figure 2.
In summary, the hypothesis that translation efficiency is limited by both translation initiation and translation elongation is strongly supported by the empirical evidence, with translation elongation accounting for about 17% of total variation in protein production. The new index of translation elongation ITE is far superior to the conventional CAI or tAI as a proxy for translation elongation efficiency. The original conclusion by Kudla et al. (2009) that translation elongation does not contribute to protein production is based on an inadequate analysis aggravated by as an inadequate index of codon usage bias.
Acknowledgments
I thank J. Plotkin for sharing the experimental sequence data and Paul Higgs, R. Prabhakaran, S. Chithambaram, M. Gilchrist, and Juan Wang for discussion and comments. This paper was substantially improved by two anonymous reviewers. This study was funded by the Natural Science and Engineering Research Council of Canada.
Footnotes
Supporting information is available online at http://www.genetics.org/lookup/suppl/doi:10.1534/genetics.114.172106/-/DC1.
Available freely online through the author-supported open access option.
Communicating editor: W. Stephan
Literature Cited
- Akashi H., 1994. Synonymous codon usage in Drosophila melanogaster: natural selection and translational accuracy. Genetics 136: 927–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson D. I., Kurland C. G., 1983. Ram ribosomes are defective proofreaders. Mol. Gen. Genet. 191: 378–381. [DOI] [PubMed] [Google Scholar]
- Bulmer M., 1990. The effect of context on synonymous codon usage in genes with low codon usage bias. Nucleic Acids Res. 18: 2869–2873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulmer M., 1991. The selection-mutation-drift theory of synonymous codon usage. Genetics 129: 897–907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chithambaram S., Prabhakaran R., Xia X., 2014a Differential codon adaptation between dsDNA and ssDNA phages in Escherichia coli. Mol. Biol. Evol. 31: 1606–1617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chithambaram S., Prabhakaran R., Xia X., 2014b The effect of mutation and selection on codon adaptation in Escherichia coli bacteriophage. Genetics 197: 301–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coghlan A., Wolfe K. H., 2000. Relationship of codon bias to mRNA concentration and protein length in Saccharomyces cerevisiae. Yeast 16: 1131–1145. [DOI] [PubMed] [Google Scholar]
- Comeron J. M., Aguade M., 1998. An evaluation of measures of synonymous codon usage bias. J. Mol. Evol. 47: 268–274. [DOI] [PubMed] [Google Scholar]
- Crick F. H., 1966. Codon–anticodon pairing: the wobble hypothesis. J. Mol. Biol. 19: 548–555. [DOI] [PubMed] [Google Scholar]
- dos Reis M., Savva R., Wernisch L., 2004. Solving the riddle of codon usage preferences: a test for translational selection. Nucleic Acids Res. 32: 5036–5044 Print 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duret L., Mouchiroud D., 1999. Expression pattern and, surprisingly, gene length shape codon usage in Caenorhabditis, Drosophila, and Arabidopsis. Proc. Natl. Acad. Sci. USA 96: 4482–4487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiers W., Grosjean H., 1979. On codon usage. Nature 277: 328. [DOI] [PubMed] [Google Scholar]
- Grantham R., Gautier C., Gouy M., Jacobzone M., Mercier R., 1981. Codon catalog usage is a genome strategy modulated for gene expressivity. Nucleic Acids Res. 9: r43–r79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosjean H., de Crecy-Lagard V., Marck C., 2010. Deciphering synonymous codons in the three domains of life: co-evolution with specific tRNA modification enzymes. FEBS Lett. 584: 252–264. [DOI] [PubMed] [Google Scholar]
- Grosjean H., Marck C., de Crecy-Lagard V., 2007. The various strategies of codon decoding in organisms of the three domains of life: evolutionary implications. Nucleic Acids Symp. Ser., No. 51: 15–16. [DOI] [PubMed]
- Grosjean H., Sankoff D., Jou W. M., Fiers W., Cedergren R. J., 1978. Bacteriophage MS2 RNA: a correlation between the stability of the codon:anticodon interaction and the choice of code words. J. Mol. Evol. 12: 113–119. [DOI] [PubMed] [Google Scholar]
- Haas J., Park E.-C., Seed B., 1996. Codon usage limitation in the expression of HIV-1 envelope glycoprotein. Curr. Biol. 6: 315–324. [DOI] [PubMed] [Google Scholar]
- Hofacker I. L., 2003. Vienna RNA secondary structure server. Nucleic Acids Res. 31: 3429–3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ikemura T., 1981a Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes. J. Mol. Biol. 146: 1–21. [DOI] [PubMed] [Google Scholar]
- Ikemura T., 1981b Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: a proposal for a synonymous codon choice that is optimal for the E. coli translational system. J. Mol. Biol. 151: 389–409. [DOI] [PubMed] [Google Scholar]
- Ikemura T., 1982. Correlation between the abundance of yeast transfer RNAs and the occurrence of the respective codons in protein genes: differences in synonymous codon choice patterns of yeast and Escherichia coli with reference to the abundance of isoaccepting transfer RNAs. J. Mol. Biol. 158: 573–597. [DOI] [PubMed] [Google Scholar]
- Ikemura T., 1992. Correlation between codon usage and tRNA content in microorganisms, pp. 87–111 in Transfer RNA in protein synthesis, edited by Hatfield D. L., Lee B. J., Pirtle R. M. CRC Press, Boca Raton, FL. [Google Scholar]
- Jank P., Shindo-Okada N., Nishimura S., Gross H. J., 1977. Rabbit liver tRNA1Val. I. Primary structure and unusual codon recognition. Nucleic Acids Res. 4: 1999–2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kudla G., Murray A. W., Tollervey D., Plotkin J. B., 2009. Coding-sequence determinants of gene expression in Escherichia coli. Science 324: 255–258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liljenstrom H., von Heijne G., 1987. Translation rate modification by preferential codon usage: intragenic position effects. J. Theor. Biol. 124: 43–55. [DOI] [PubMed] [Google Scholar]
- Lustig F., Boren T., Guindy Y. S., Elias P., Samuelsson T., et al. , 1989. Codon discrimination and anticodon structural context. Proc. Natl. Acad. Sci. USA 86: 6873–6877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marck C., Grosjean H., 2002. tRNomics: analysis of tRNA genes from 50 genomes of Eukarya, Archaea, and Bacteria reveals anticodon-sparing strategies and domain-specific features. RNA 8: 1189–1232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra S. K., Lustig F., Akesson B., Lagerkvist U., 1977. Codon-acticodon recognition in the valine codon family. J. Biol. Chem. 252: 471–478. [PubMed] [Google Scholar]
- Moriyama E. N., Powell J. R., 1997. Codon usage bias and tRNA abundance in Drosophila. J. Mol. Evol. 45: 514–523. [DOI] [PubMed] [Google Scholar]
- Nakamoto T., 2006. A unified view of the initiation of protein synthesis. Biochem. Biophys. Res. Commun. 341: 675–678. [DOI] [PubMed] [Google Scholar]
- Nasvall S. J., Chen P., Bjork G. R., 2007. The wobble hypothesis revisited: uridine-5-oxyacetic acid is critical for reading of G-ending codons. RNA 13: 2151–2164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ngumbela K. C., Ryan K. P., Sivamurthy R., Brockman M. A., Gandhi R. T., et al. , 2008. Quantitative effect of suboptimal codon usage on translational efficiency of mRNA encoding HIV-1 gag in intact T cells. PLoS One 3: e2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novembre J. A., 2002. Accounting for background nucleotide composition when measuring codon usage bias. Mol. Biol. Evol. 19: 1390–1394. [DOI] [PubMed] [Google Scholar]
- Osterman I. A., Evfratov S. A., Sergiev P. V., Dontsova O. A., 2013. Comparison of mRNA features affecting translation initiation and reinitiation. Nucleic Acids Res. 41: 474–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palidwor G. A., Perkins T. J., Xia X., 2010. A general model of codon bias due to GC mutational bias. PLoS One 5: e13431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ran W., Higgs P. G., 2012. Contributions of speed and accuracy to translational selection in bacteria. PLoS One 7: e51652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice P., Longden I., Bleasby A., 2000. EMBOSS: the European Molecular Biology Open Software Suite. Trends Genet. 16: 276–277. [DOI] [PubMed] [Google Scholar]
- Robinson M., Lilley R., Little S., Emtage J. S., Yarranton G., et al. , 1984. Codon usage can affect efficiency of translation of genes in Escherichia coli. Nucleic Acids Res. 12: 6663–6671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharp P. M., Li W. H., 1987. The codon adaptation index—a measure of directional synonymous codon usage bias, and its potential applications. Nucleic Acids Res. 15: 1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorensen M. A., Kurland C. G., Pedersen S., 1989. Codon usage determines translation rate in Escherichia coli. J. Mol. Biol. 207: 365–377. [DOI] [PubMed] [Google Scholar]
- Sun X. Y., Yang Q., Xia X., 2013. An improved implementation of effective number of codons (nc). Mol. Biol. Evol. 30: 191–196. [DOI] [PubMed] [Google Scholar]
- Supek F., Smuc T., 2010. On relevance of codon usage to expression of synthetic and natural genes in Escherichia coli. Genetics 185: 1129–1134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuller T., Waldman Y. Y., Kupiec M., Ruppin E., 2010. Translation efficiency is determined by both codon bias and folding energy. Proc. Natl. Acad. Sci. USA 107: 3645–3650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright F., 1990. The “effective number of codons” used in a gene. Gene 87: 23–29. [DOI] [PubMed] [Google Scholar]
- Xia X., 1998. How optimized is the translational machinery in Escherichia coli, Salmonella typhimurium, and Saccharomyces cerevisiae? Genetics 149: 37–44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia X., 2007. An improved implementation of codon adaptation index. Evol. Bioinform. 3: 53–58. [PMC free article] [PubMed] [Google Scholar]
- Xia X., 2008. The cost of wobble translation in fungal mitochondrial genomes: integration of two traditional hypotheses. BMC Evol. Biol. 8: 211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia X., 2013. DAMBE5: A comprehensive software package for data analysis in molecular biology and evolution. Mol. Biol. Evol. 30: 1720–1728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Z., Li J., Cui P., Ding F., Li A., et al. , 2012. Codon deviation coefficient: a novel measure for estimating codon usage bias and its statistical significance. BMC Bioinformatics 13: 43. [DOI] [PMC free article] [PubMed] [Google Scholar]