Efficiently Tracking Selection in a Multiparental Population: The Case of Earliness in Wheat

Abstract

Multiparental populations are innovative tools for fine mapping large numbers of loci. Here we explored the application of a wheat Multiparent Advanced Generation Inter-Cross (MAGIC) population for QTL mapping. This population was created by 12 generations of free recombination among 60 founder lines, following modification of the mating system from strict selfing to strict outcrossing using the ms1b nuclear male sterility gene. Available parents and a subset of 380 SSD lines of the resulting MAGIC population were phenotyped for earliness and genotyped with the 9K i-Select SNP array and additional markers in candidate genes controlling heading date. We demonstrated that 12 generations of strict outcrossing rapidly and drastically reduced linkage disequilibrium to very low levels even at short map distances and also greatly reduced the population structure exhibited among the parents. We developed a Bayesian method, based on allelic frequency, to estimate the contribution of each parent in the evolved population. To detect loci under selection and estimate selective pressure, we also developed a new method comparing shifts in allelic frequency between the initial and the evolved populations due to both selection and genetic drift with expectations under drift only. This evolutionary approach allowed us to identify 26 genomic areas under selection. Using association tests between flowering time and polymorphisms, 6 of these genomic areas appeared to carry flowering time QTL, 1 of which corresponds to Ppd-D1, a major gene involved in the photoperiod sensitivity. Frequency shifts at 4 of 6 areas were consistent with earlier flowering of the evolved population relative to the initial population. The use of this new outcrossing wheat population, mixing numerous initial parental lines through multiple generations of panmixia, is discussed in terms of power to detect genes under selection and association mapping. Furthermore we provide new statistical methods for use in future analyses of multiparental populations.

ALTHOUGH the recent development of genome sequencing in crop species has strongly increased capacity for gene discovery, the accurate mapping of genes controlling the genetic variation of complex traits (QTL) remains a key objective. The principal mapping methods rely on the detection of statistical association between polymorphisms at molecular markers and quantitative variation of phenotypic traits and were historically developed for progenies of biparental crosses with parents chosen for their extreme phenotypes at a trait of interest. These populations are powerful resources for QTL detection, but have low precision as few effective meioses (and thus subsequent recombinations) occur during their development. As a result, large parental haplotype blocks are preserved in the segregating population. In addition, the number of QTL segregating is limited by the use of only two parents (Cavanagh et al. 2008). Association genetics in a panel of diverse accessions can partly overcome these limits. These have higher numbers of loci segregating and exploit numerous historical recombinations leading, in theory, to finer mapping of multiple QTL. However, a major limit of association mapping is the unavoidable genetic structure within the panel, which can lead to increased rates of false-positive associations (Breseghello and Sorrells 2006). This can be accounted for in statistical models (Yu et al. 2006), but power to detect QTL that are correlated with that structure is lost.

Therefore, different kinds of multiparental populations have been developed to obtain greater precision in fine mapping with little or no genetic structure. One proposed option is to combine different biparental populations, for example, factorial crosses or diallels (Rebai and Goffinet 1993) or crosses with a common reference line (nested association mapping, NAM; Yu et al. 2008). For complete allele reshuffling, another option relies on optimized pyramidal or circular crosses between 4, 8, or 16 parents (Multiparent Advanced Generation Inter-Cross, MAGIC; Kimura and Crow 1963; Cavanagh et al. 2008; Huang et al. 2012).

When the number of parents increases, or when multiple generations of intercrossing are added (advanced intercrosses) to accumulate more meiosis per individual (Rockman and Kruglyak 2008), controlled crossing becomes too onerous and random crossing appears the best solution (see, for instance, the Arabidopsis thaliana MAGIC population obtained with a diallel cross followed by panmixia; Scarcelli et al. 2007). In finite populations, random advanced intercrosses may induce genetic drift and selection leading to evolution of allele frequencies. Although drift can be reduced through increasing the number of crosses (increasing effective size) and was shown to be limited in effect (Rockman and Kruglyak 2008), avoiding selection is a hard task. Nevertheless, shifts in allele frequency can be used to detect regions under selection and these provide another approach to QTL identification.

Various methods have been proposed to identify regions under selection by detecting selective sweeps (Maynard Smith and Haigh 1974), through either (i) shifts in allele frequency at some markers, which are large when compared to shifts in the rest of the genome (Goldringer and Bataillon 2004; Nielsen 2005) or (ii) directional temporal shift in frequency using genetic time series data (Bollback et al. 2008; Nishino 2013; Feder et al. 2014). These methods raise a number of statistical challenges. A major complication is that the actual population size is unknown (Feder et al. 2014).

The purpose of this study is to assess the impact of 12 generations of advanced random intercrosses on an evolved dynamic management population of wheat (Triticum aestivum) (Henry et al. 1991) and to demonstrate the value of this kind of population for gene discovery, using flowering time as an illustration. The studied population has been derived from a dynamic management program aiming at conserving adaptive potential of the crop through repeated cultivation of numerous populations in contrasted locations. These populations have three specific features: (i) a large number of founders (60); (ii) a mating system modified from predominantly selfing to strict outcrossing using genetic male sterility; and (iii) a middle-term evolution with 12 generations of open pollination. First we describe the evolution from the parents to the evolved population of (i) a phenotypic trait involved in climatic adaptation, flowering time, and (ii) the genetic diversity using the 9K i-Select SNP array. Then, as parental contributions can also evolve during the intercross generations, we develop a Bayesian method to estimate the parental contributions to the evolved population. Third, we estimate the effective size of the population and search for loci under selection using a novel method that allows detection of selection between only two temporal samples, providing both a test of significance and an estimation of the selection coefficient. The loci we detected as under selection were additionally tested for association with flowering time. Finally we discuss the use of panmictic multiparental populations to study the genetic bases of local adaptation.

Materials and Methods

Biological material: The INRA MAGIC population

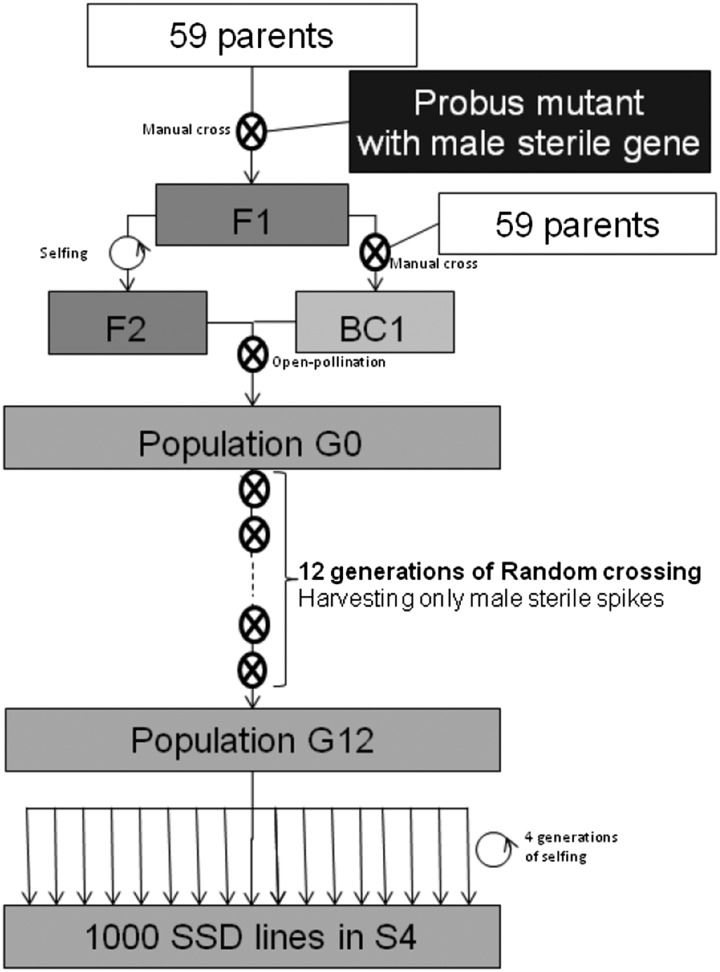
The material studied is referred to as a MAGIC population, in its broad sense, as it incorporates both multiple parents and advanced intercrossing. It is derived from a very diverse composite population created between 1976 and 1980 (Trottet 1988), by crossing 60 European and worldwide wheat breeding lines selected for their resistance to diseases and their good agronomic values (Supporting Information, Table S1). Each of the 59 parents was first crossed with male sterile segregants from the 60th, the variety “Probus” (Fossati and Ingold 1970), which is maintained as heterozygous for the recessive nuclear sterility gene ms1b (McIntosh 1988). Among the F1 plants (Ms1b/ms1b = fertile), some were selfed (F2) while others were backcrossed (BC1) with the 59 parents to reduce the proportion of Probus genome in the population. The bulked seeds of the two progenies (F2 and BC1) were then sown in a mixed row design, in an isolated field surrounded by rye (Secale cereal) (Figure 1). Male-sterile individuals (ms1b/ms1b) were tagged at flowering time, naturally wind pollinated by fertile plants, and harvested at maturity. Due to this open pollination, the relative contribution of F2 vs. BC1 plants was unknown, leading to uncertainty regarding the contribution of Probus relative to the other parents. The progeny of this first outcrossing cycle (G0 population) were resown in isolation and male-sterile plants harvested again. Such management stabilizes the proportion of male-sterile plants at 50% in the field. The Probus contribution is therefore expected to range between 50% (F2 only) and 25% (BC1 only), with 37.5% in the balanced case. Note that around the male-sterility gene the Probus contribution is either 100% for male-sterile (ms/ms) or 50% for male-fertile (Ms/ms) genotypes.

Figure 1.

INRA MAGIC population creation scheme. Intensity of shading represents the proportion of Probus in the population.

This population has been managed in Le Moulon (48.4°N, 21°E) for 12 generations, as part of the French dynamic management project (Henry et al. 1991), and has always been grown in isolation without artificial selection. Each generation, at least 10,000 seeds, was sown and ∼3000 spikes from tagged male-sterile plants were harvested and threshed as a bulk. At the 12th generation, 1000 “S4” lines were derived by single-seed descent (SSD) (Figure 1). Note that in total, these lines underwent 15 outcrossing cycles (three for the creation of the original population, G0 population, plus 12 at Le Moulon).

In this study, we analyzed 56 of the 60 parental lines including Probus (4 were no longer available; Table S1), as well as a subset of 380 out of 1000 S4 SSD lines. The SSD lines were chosen to represent the phenotypic diversity of the population on the basis of a principal component analysis (PCA) of all phenotypic traits scored the first year. These 380 lines (hereafter the “evolved population”) consist of all individuals with extreme phenotypes and a random sample of intermediate scoring lines. This selected set was not significantly different from 500 random samples of 380 individuals, both for SNP allelic frequencies and for mean flowering time (data not shown). In contrast, this sampling strategy increased the phenotypic variance and the subsequent ability to detect QTL.

Phenotyping

Flowering time was assessed in field trials at Le Moulon over two seasons (2010–2011 and 2011–2012), with a November sowing. Each genotype (S4 SSD lines + parents) was sown in two single-row (20 seeds) replicates in a randomized complete block design. For each line, flowering time was approximated using heading date score, when 50% of the plants had half of their main ears emerged from the flag leaf. Heading date was transformed into the sum of the mean temperatures per day (i.e., degree days or dd) from sowing to heading, based on data recorded by the meteorological station at Le Moulon.

Molecular analysis

Total DNA of each of the 436 lines (380 SSD lines + 56 parents) was extracted from 500 mg of leaf tissue. Extractions were performed using a modified procedure of Dellaporta et al. (1983) including a carbohydrate precipitation described in Michaels et al. (1994). Genotyping was performed by M. J. Hayden’s team at DPI Victoria in Bundoora, Australia, using a 9K i-Select SNP array (Cavanagh et al. 2013). SNP allele clustering was performed using GenomeStudio software (http://support.illumina.com/array/array_software/genomestudio.html). Errors in allele assignation by GenomeStudio were detected by visual inspection of SNP allele clusters and manually corrected. Only SNPs that could be unambiguously scored as biallelic were kept, i.e., SNPs exhibiting three clusters or less. Fourteen additional polymorphisms located in candidate genes involved in the earliness pathway (Table S2) were genotyped using the KASPar SNP genotyping system developed by KBioscience (http://www.kbioscience.co.uk/).

Population structure analysis

Population genetic structure was analyzed independently for the parental and the evolved populations with a discriminant analysis of principal components (DAPC; Jombart et al. 2010). The DAPC computation was made using the package “adegenet” v. 1.3–6 (Jombart and Ahmed 2011) and the statistical program R v. 2.15.3-1 (R Development Core Team 2013). Euclidian distance among genotypes was calculated using the procedure dist.gene in the package “ape” (Paradis 2010). An analysis of molecular variance (AMOVA; Excoffier et al. 1992) was performed to estimate the percentage of genetic variance explained by structure, as determined by the PCA k-means procedure included within the DAPC method, using the “pegas” R-package (Paradis 2010).

Estimation of parental contributions

As the contribution of parental lines to the evolved population is unknown due to the generations of open pollination, we developed a Bayesian approach for its estimation. We considered the SSD lines to be a finite sample of a theoretical infinite population (i.e., no genetic drift but sampling stochasticity) resulting from many cycles of free recombination of a set of 56 parental lines without selection pressure, mutation, migration, or linkage disequilibrium among markers. Under these assumptions, the likelihood of an observed data set is

$$\mathrm{ℒ}={\displaystyle \prod }_l^L\left(\begin{array}{c}380\times 2\\ n_l\end{array}\right)p_l^{n_l}{(1-p_l)}^{380\times 2-n_l},$$

with p_l the allelic frequency of allele A at the locus l in the evolved population, n_l the total count of allele A at locus l over all the sampled SSD lines, and L the total number of loci (the complete Bayesian model is fully described in the Appendix). This model is very similar to that used in the Structure software (Pritchard et al. 2000) when population of origin is known (i.e., the case with learning) except that we have focused on the origin of the whole population and not on individual assignments. Similarly we have assumed that loci were in Hardy–Weinberg equilibrium within the population. Thus we have assumed that allelic frequencies were fixed after the first round of random mating.

The probability p_l depends on the expected contribution of each parental line k, P(Par = k), and on the frequency of allele A at locus l in each parental line k, f(A)_lk,

$$p_{jl}={\displaystyle \sum }_k^{K}f{\left(A\right)}_{lk }P\left(\text{Par}=k\right),$$

with K the total number of parental lines. Genetic information is assumed to be available for all putative parental lines K; thus ${\displaystyle {\sum }_k^{K}P}\left(\text{Par}=k\right)=1$. Furthermore P(Par = k) is assumed to be the same for any part of the genome (no selection, no LD) and, therefore, the same for all loci studied.

We considered that no previous information is available on the putative contribution of each parental line k (even for Probus); thus, we chose a noninformative prior distribution using a flat Dirichlet distribution (i.e., an even contribution of all parental lines).

Bayesian estimations of the posterior distributions of P(Par = k) were performed considering the whole set of markers, P_gw(Par = k), or at the chromosome level considering subsets of markers for each chromosome c, P_c(Par = k). The posterior distributions were estimated for each of the 56 available parental wheat lines with a MCMC method using the Gibbs sampler (i.e., a particular case of the Metropolis–Hastings algorithm) implemented in JAGS (Plummer 2003). Note that the four unavailable parental lines were ignored since no genetic information was available. We used the 5590 markers polymorphic in the parental populations for the genome-wide estimations and the 5056 markers mapped for the chromosome level estimations. Three independent Markov chains ran for five million iterations for genome-wide estimates (56 parental lines × 3 chains × 5.10⁶ iterations) and ran for 1 million iterations for estimates at the chromosome level [56 parental lines × 21 chromosomes (for bread wheat) × 3 chains × 10⁶ iterations]. To reduce temporal correlation between successive elements within the Markov chain only one element over five was kept. Chain convergence was checked using a Gelman and Rubin (1992) test. Analyses were conducted using R (R Development Core Team 2013) and the “CODA” package (Plummer et al. 2006).

The 56 genome-wide estimates of parental contributions were considered as good proxies for the genetic composition of the initial population. Indeed, global variation in parental contributions can occur only in the very early intercrosses, as the high level of recombination accumulated over subsequent generations makes global selection against one parent very unlikely on a genome-wide scale. A theoretical initial population was therefore designed, composed of the 56 parental multilocus genotypes, weighted according to their contributions estimated on genome-wide data. This population will be referred hereafter as the “initial population.”

To validate this method we simulated a set of 50 SSD lines derived from the random mating of six parental genotypes. Full random reshuffling of 30 biallelic and independent SNP markers was simulated, using variable initial parental contributions including even contributions (100 simulated data sets for three scenarios). In all cases, the mean and the mode of the posterior distribution of P(Par = k) were always close to the real simulated contributions, which were all included in the highest posterior density interval (HPD).

To test the robustness of this method to the assumption of linkage equilibrium, we compared estimates using all the markers on chromosome 1A (442 markers) with estimates after removing markers in linkage disequilibrium, i.e., by removing marker pairs with a correlation above a 0.06 threshold (130 independent markers). Estimates of parental contributions with the two sets of markers differed on average only by 0.004 (max 0.02) showing the low impact of linked loci on estimates.

Finally we tested the robustness of the model to missing information, as four parental lines were missing from our panel of 60. Using the chromosome 1A data described above, we removed four randomly chosen parental lines from the analysis and recomputed the relative contributions of the 52 remaining parents. Probus was always retained in the selected set. We repeated these computations 12 times with three parallel chains each for five million iterations. We then compared the percentage of information lost (the sum of the contributions, from the analysis of all parents, of the four excluded parents) to the mean absolute error (estimated from the difference between estimates from all parents and from censured data). We found a near-perfect linear positive relationship between the percentage of information lost and the mean absolute error (Figure S1). Except for Probus, the observed and expected contributions difference of each parental line is ∼1% (from an expected contribution of 37.5% for Probus and a balanced contribution of the remaining parents). Thus the four missing parents should lead to a mean absolute error of ∼0.16% (Figure S1). This is very small and thus should not dramatically influence our analyses.

Comparison between chromosomal and genome-wide contribution estimates

The contributions of parental lines to the evolved population were computed genome-wide, $P_{\text{gw}}\left(\text{Par}=k\right)$, and at the chromosome level, $P_{\text{c}}\left(\text{Par}=k\right)$. In absence of evolutionary forces, contributions of parental line k at both levels should be similar. An upward or downward deviation of the contribution of a parental line at the single chromosome level relative to the genome-wide estimate, indicating that this contributor was favored or depreciated over the others, can result from selection acting on genes located within this chromosome. We defined a test based on the following statistic:

$${\Delta }_{kc}=P_{\text{c}}\left(\text{Par}=k\right)-P_{\text{gw}}\left(\text{Par}=k\right).$$

In the absence of selection and genetic drift the whole genome must behave similarly leading to ${\Delta }_{kc}=0$ (i.e., the null hypothesis), whereas it should differ significantly from 0 (positively or negatively) if parental line k is respectively over- or underrepresented in chromosome c relative to its genome-wide contribution (i.e., the alternative hypothesis). $P_{\text{c}} (\text{Par}=k)$ and $P_{\text{gw}} (\text{Par}=k)$ differed in their statistical power to estimate the contribution of parental lines due to differences in the number of markers considered. Furthermore the number of iterations used to reach the convergence of Markov chains also differed. Thus to test if ${\Delta }_{kc}$ differed from 0 we estimated its posterior distribution with 10,000 values of ${\Delta }_{kc}$ computed by randomly drawing within posterior distributions of $P_{\text{c}} (\text{Par}=k)$ and $P_{\text{gw}} (\text{Par}=k)$,respectively. This allowed nonsymmetric and/or multimodal posterior distributions of $P_{\text{c}} (\text{Par}=k)$ and $P_{\text{gw}} (\text{Par}=k)$, in contrast to simple tests of mean difference based on summary statistics (e.g., Student’s t-test). Significance was tested by computing ${\text{IC}}_{\alpha }\left({\Delta }_{kc}\right)$, the credible interval of the posterior distribution of ${\Delta }_{kc}$ at the $(1-\alpha )$ level. If $0\in {\text{IC}}_{\alpha }\left({\Delta }_{kc}\right)$ the null hypothesis was accepted, whereas if $0\notin {\text{IC}}_{\alpha }\left({\Delta }_{kc}\right)$ it was rejected with a risk α and ${\Delta }_{kc}$ was judged to differ significantly from 0. We computed this test for all combinations of each parental line k and each chromosome c. Because of multiple comparisons, to keep an overall $\alpha =0.05$ level we applied a conservative adjustment to ${\alpha }_{kc}$ for each single test with a Bonferroni correction resulting in ${\alpha }_{\text{kc}}=\alpha /\left(K\times C\right)=0.05/\left(56\times 22\right)=4.06\times {10}^{-5}$.

Temporal genetic evolution

To monitor the evolution of genetic diversity, we estimated the average minor allele frequencies (MAF), the average expected heterozygosity (H_e, Nei diversity), and the observed heterozygosity for the 56 parents, the initial and the evolved populations.

We estimated linkage disequilibrium as the square of the Pearson correlation coefficient (r²) between all pairs of loci (R Development Core Team 2013). The decay of LD with genetic distance was compared between the initial and the evolved populations using the map of the 9K i-Select SNPs (Cavanagh et al. 2013).

Temporal variance of allelic frequencies (F_c) was computed by the standardized variance at each biallelic locus (Nei and Tajima 1981),

$$F_{\text{c}}{}_{{}_l}=\frac{{(F_{{\text{i}}_l}-F_{{\text{e}}_l})}^2}{\left(F_{{\text{i}}_l}+F_{{\text{e}}_l}\right)/2-F_{{\text{i}}_l}\times F_{{\text{e}}_l}},$$

where $F_{{\text{i}}_l}$ and $F_{{\text{e}}_l}$ are the frequency at locus l in the initial and the evolved populations, respectively.

The multilocus F_c was calculated as the average of the single locus $F_{\text{c}}{}_{{}_l}$ estimated over all markers. Effective population size (N_e), assumed constant over time, was then estimated by the temporal Waples (1989) method,

$$N_{\mathrm{e}}=\frac{\Delta t}{2F_{\mathrm{c}}-1/2S_0-1/2S_t},$$

where ∆t is the number of generations of recombination between the theoretical “initial population” and the evolved populations (15 in our case), S₀ is the sample size of the initial population and S_t that of the population at generation t (respectively 56 and 380). Due to the high inbreeding level, the numbers of independent alleles sampled (2S₀ and 2S_t) could be approximated by the number of individuals (S₀ and S_t).

The demographic population size ($N_{{\text{e}}_{\text{d}}}$) was estimated as the harmonic mean of the minimum true number of plants of each gender grown in the population (>5000 male plants and 3000 harvested female plants per generation) (Charlesworth 2009).

Detection of traces of selection

To determine whether changes in SNP allele frequencies were possibly driven by selection and drift (as opposed to drift alone), we used a maximum-likelihood approach. Considering one of the alleles at a given SNP, let X₀ be the number of copies of this allele in the population at generation 0, and $X_{15}$ be the number of allele copies at generation 15. Let N_e be the effective population size. Here, N_e is assumed to be known. Finally, let s be the coefficient of selection of the allele, such that the fitness of the genotypes aa, aA, and AA is 1, 1 + s, and 1 + 2s, respectively (with $s\ge 0$). Here, A is the positively selected allele at the SNP $(s\ge 0)$. Assuming these parameters are known, one can compute $\text{Pr}(X_{15}|X_0, s, N_{\text{e}})$, the probability that the allele copy number at generation 15 is $X_{15}$, given that the allele copy number at generation 0 was X₀, with a selection coefficient s and an effective population size N_e. This probability was computed numerically by iterating a standard formulation of a Wright–Fisher model with genetic drift and selection, as described, for example, in Neuhauser (2004).

The effect of sampling of genotyped individuals was taken into account by setting N_e = n in the last generation when iterating the Wright-Fisher model, where n is the size of the sample of individuals genotyped at generation 15 (here n = 380). A similar sampling effect could also affect the estimate of initial allelic frequencies, but in our case we considered that the founders were extensively represented in the initial population.

Now, for a given locus, we know $(X_{0,}{X}_{15},N_{\text{e}})$, so the only parameter of the model is s, and $L\left(s\right)=\text{Pr}(X_{15}|X_0,s,N_{\text{e}})$ gives the likelihood of the model. In practice, L(s) was maximized numerically for positive values of s ranging from 0 to 1, and for “negative” values by symmetry. Negative selection was then implemented as

$$\begin{array}{cc}\mathrm{Pr}\left(X_{15}\text{|}{X}_0,s,N_{\text{e}}\right)=\mathrm{Pr}\left(2N-X_{15}\text{|}2N_{\text{e}}-X_0,-s,N_{\text{e}}\right)& \text{for} s<0\end{array}.$$

Now, for $\left\{X_0,X_{15}\right\}$, let s* be the value of s that maximizes L(s). A likelihood-ratio test (LRT) was computed as

$$\text{LRT}\left(X_0,X_{15}\right)=-2\ln \left[\frac{L(s=0)}{L(s=s*)}\right].$$

The significance of the test was assessed by assuming that the LRT follows a χ² distribution with one degree of freedom (Wilks’ theorem) under the null hypothesis of absence of selection (i.e., if $s=s*=0$). As we performed multiple tests, estimated P-values were transformed into Q-values, which are measures of significance in terms of false discovery rate (FDR) rather than the false-positive rate (Storey and Tibshirani 2003), using the “qvalue” R-package (Dabney and Storey 2004). Markers were tested with a threshold of 0.05 after a FDR correction.

When testing for selection in the MAGIC population, X₁₅ corresponded to the number of alleles observed in the evolved population (>380 individuals maximum), while X₀ was considered as a large gametic pool, where alleles were sampled according to their inferred frequencies (parental contributions) to produce a G1 of size $N_{\text{e}}$.

Phenotypic analysis, differentiation, and association tests

Broad-sense heritabilities of earliness traits in the evolved population were assessed for each year using an ANOVA model including only a replicate and a genotype effect. Heritability across years was estimated on adjusted replicate means data using an ANOVA including year and genotype effects. Experimental factor effects were then tested using the following linear model,

$$Y_{ijk}=\mu +y_j+r{(y)}_{jk}+G_i+{(G\times y)}_{ij}+{\epsilon }_{ijk},$$

where G_i is the effect of the genotype i, y_j is the effect of the year j (2010–2011 or 2011–2012), r(y)_jk is the effect of replicate k in year j, (G × y)_ij is the interaction between year and genotype, and ε_ijk is the residual error term. Genotype and genotype-by-year interaction effects were both declared as random effects. We estimated adjusted means over replicate and year effects for each genotype of the evolved population. Each marker’s association with flowering time was then tested successively, using adjusted means.

Results

Molecular diversity

The genotyping of the 436 wheat lines (56 parents + 380 SSD lines) with the 9K i-Select SNP assay provided a data set of 8632 SNPs. After removing SNPs failing to generate clear genotype clustering, 7270 (84.2%) high-quality SNPs were kept. Among these, 6476 (75.0% of the total) were polymorphic. This polymorphism rate is reasonably high, compared to the 100% rate observed with a worldwide panel on the same SNP array (Cavanagh et al. 2013). After removing monomorphic markers and pairs of cosegregating markers over the 436 wheat lines, the final data set consisted in 5621 unique polymorphic SNPs (65.1%) for the parental and the evolved populations.

Structure analyses

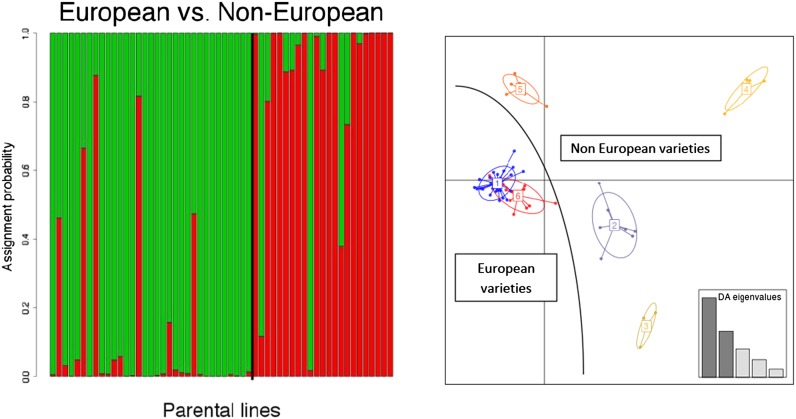
The first two axes of the PCA on the parental lines explained 17.1% of genetic variance. K-means clustering on principal components axes (the first step of the DAPC analysis) revealed that the optimal genetic structure of parental lines consisted of two groups, mainly separating European wheat lines (France, Bulgaria, Germany, Great Britain, Netherlands, Poland, and Switzerland), from non-European (United States, South America, Russia, Ukraine, Australia, Japan, and Brazil). This is in agreement with the clear division found between lines of European and Asian origin in a diverse collection of worldwide wheat varieties (Balfourier et al. 2007). This structure was confirmed by the assignment probabilities provided by the DAPC (Figure 2). AMOVA showed that these two groups explained 15% of the parental genetic diversity. Increasing the number of groups led to identification of six groups of lines related by pedigree, most notably a group of U.S. lines and another group related to the pre-breeding line VPM.

Figure 2.

Left: Estimated population structure in parental lines. Each individual is represented by a vertical line, which is partitioned into two colored segments that represent the individual’s estimated membership fractions in two clusters. Black vertical line separates European lines (mainly green) from non-European lines (mainly red). Right: Projection of individuals onto discriminant axes with groups represented by different colors: six groups related by pedigree.

Both AMOVA and DAPC results showed very low structure in the evolved population. The K-means clustering on PCA axes revealed two groups that explained only 4.2% of the variation according to an AMOVA and the first two axes of PCA explained only 5.09% of the genetic variance.

These results demonstrated that the population structure observed in the parents has been nearly completely eroded after 12 panmictic generations, leading to very low structure in the evolved population.

Parental contributions estimation

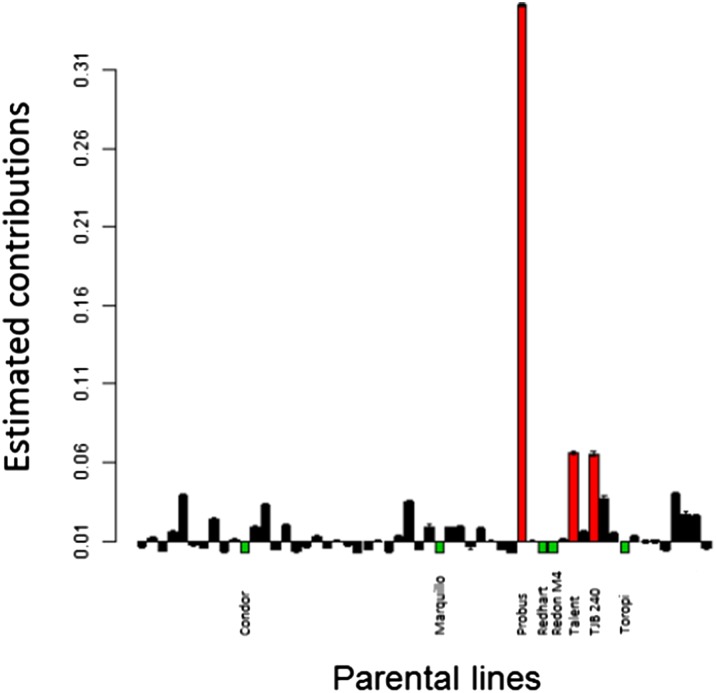
To infer the contribution of each parent to the evolved population, Bayesian estimates were conducted both at genome-wide and at chromosome levels (see Materials and Methods). The genome-wide estimates were precise, with a 95% credible interval of 0.1% around the mean, but varied widely between parents. The Probus parental line had the highest contribution (35%), followed by Talent and TJB 240 lines, with contributions close to 6%. The other parents had much lower contributions, ranging from 0.008 to 3.8% (Figure 3), with five lines contributing <0.01% (Condor, Marquillo, Redhart, Redon M4, and Toropi). The high contribution of Probus is in accordance with its weight in the initial crossing scheme, during ms1b sterility introduction, and confirms a balanced contribution between the selfed and backcrossed F1’s (Figure 1) for which we expected a 37.5% contribution to the initial population.

Figure 3.

Genome-wide estimates of contribution for each parent. Maximum credible interval 0.002. Above bars represent the contribution higher than the median contribution while below bars correspond to contributions lower than the median. Parents with the highest contribution are in red and those with the lowest in green.

Estimates of contribution at the single chromosome level showed little difference from the genome-wide ones, with a mean average difference of 1.4% (Figure S2). However, ∼40% of these slight variations were significantly different (Bonferroni correction, Table S3). However, as some estimated contributions were very low, significant variation can be due to very small differences. In these cases, the differences are most likely artifacts. D genome chromosomes exhibited a lower number of significant tests (18% of the comparisons, Table S3) despite their higher absolute differences. This apparent discrepancy reflects the lower precision of contribution estimates (i.e., larger credible intervals) due to the lower number of markers on the D genome: chromosomes covered with higher marker densities (1B, 2A, 2B, 3A, and 4B) exhibited more numerous significant differences between genome-wide and chromosome-level estimates (in 30–40 parental lines out of 56). The genome-wide results will be used in the following analyses.

Evolution between the initial and the evolved populations

Estimates of parental contributions allowed us to infer the allelic frequencies in the theoretical initial population. As expected, genetic diversities of initial and evolved population were very similar and lower than those found in the panel of the 56 parents (average MAF, 0.18, 0.17, 0.25 and $H_{\text{e}}$, 0.25, 0.24, 0.34). Furthermore 129 markers turned out to be monomorphic in the evolved population, this loss being due either to nondetection in the sample or to fixation. Conversely, 31 markers were polymorphic in the evolved population but not among the parents. This could be explained by (i) alleles specific of the four lines missing from our parental panel, (ii) alleles lost for some parental lines during the management procedure in genebanks (regeneration through selfing cycles; Esquinas-Alcazar 2005), as they could have presented initial residual heterozygosity, (iii) contamination (migration) despite the isolation of plots (Hucl and Matus-Cadiz 2001), and (iv) mutation, as found for SSR markers in another wheat experimental population (Raquin et al. 2008). The observed heterozygosity in the evolved population was 3.2%. This is significantly higher than predicted after four selfing generations starting from an initial H_e of 0.24 (1.6%). A possible explanation to this difference could be a fitness advantage of heterozygote individuals (heterosis). The $N_{\text{e}}$ estimated from F_c between the initial and the evolved populations was 310.97, much lower than the demographic population size ($N_{{\text{e}}_{\text{d}}}$ = 7500).

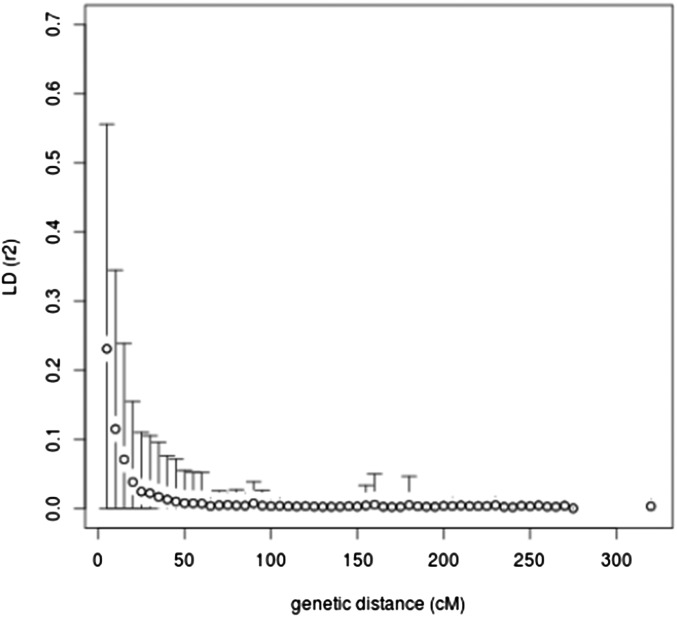
The evolved population presented a globally low linkage disequilibrium (LD) with a long-distance LD (between independent markers or between chromosomes) almost null (r² = 0.003, Figure 4). Short-distance LD peaked at 0.4 for completely linked loci and decreased with genetic distance to reach a plateau at a distance of ∼50 cM. LD was much higher at medium/long distances for the initial population (Figure S3).

Figure 4.

LD decay (mean and standard deviation every 5 cM) in the evolved population as a function of genetic distance. Interchromosome mean LD is set at an arbitrary distance of 320 cM.

Detection of traces of selection

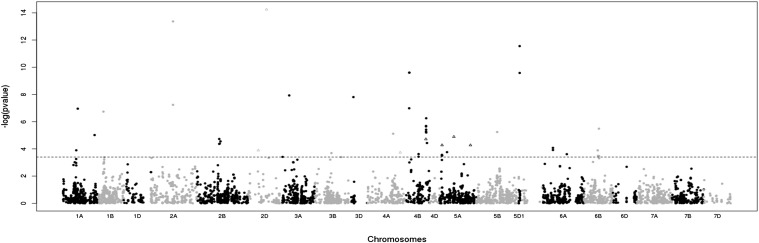
Among 5635 markers (5621 SNPs from the 9K i-Select array + 14 KASPar SNPs), 57 markers representing 26 independent genomic areas were detected as significantly under selection (i.e., behaving nonneutrally), with a likelihood ratio >12.45 (Table S4). The selection coefficients ranged from 0.07 to 0.7 (Table S4). The selected markers were located on multiple chromosomes (1A, 1B, 2A, 2B, 2D, 3A, 3B, 3D, 4A, 4B, 5A, 5B, 5D, 6A, 6B), but mainly on 2B, 4B, 5A, and 6B (Figure 5). Among the 14 KASPar markers located in flowering-time candidate genes, a single one matched with a genomic area under selection (Ppd-D1, Figure 5).

Figure 5.

Manhattan plot of the –log₁₀(P-value) of selection tests. The horizontal line represents the significance threshold (FDR correction = 4.2e-4). Markers under significant selection and associated with heading date are represented by triangles. Ppd-D1 is represented with a triangle on chromosome 2D (P-value < 1e-13).

Association of markers with heading date

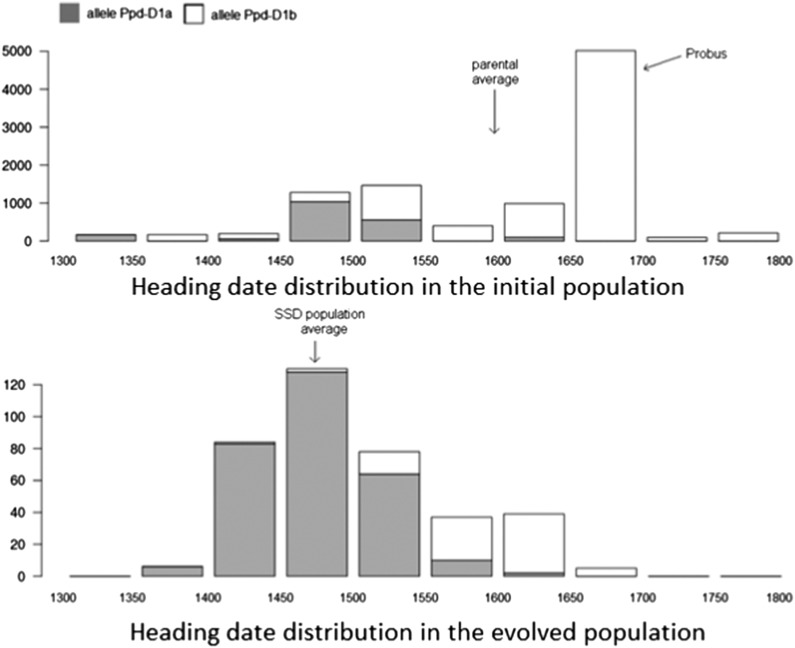
Heading date was highly heritable, at 0.95 and 0.96, respectively in the 2 years of experimentation and at 0.91 across years. Heading date variability was larger among the parents than in the evolved population, while mean heading date was 128 dd earlier in the evolved population (Figure 6).

Figure 6.

Distributions of heading date (in degree days) estimated by the Bayesian method. Top: Initial population. Bottom: Evolved population. Proportion of individuals in each class: shaded bars indicate photoperiod-insensitive allele (Ppd-D1a) and open bars indicate photoperiod-sensitive allele (Ppd-D1b).

The markers detected as significantly under selection were tested for their association with heading date. Seven markers, located on chromosomes 2D (two markers), 4A and 5A (three markers), were associated with heading date with a P-value <0.05. Two markers located on chromosome 2D were strongly associated with heading date: Ppd-D1 (P-value = 5.10⁻⁷⁰), and wsnp_CAP11_c3842_1829821 (P-value = 3.5 × 10⁻¹¹) (Figure 5 and Figure 6). Ppd-D1 explained 56% of the phenotypic variation in a single marker model (Figure 6). The frequency of the allele associated with earlier flowering at this locus (the photoperiod insensitive allele) increased from 0.19 to 0.77 between the initial and the evolved populations. With a 117 dd difference between the two Ppd-D1 alleles (Figure 6), this allelic frequency variation accounted for 53% of the total phenotypic evolution $\left(\left[0.58 \times 117\text{dd}\right]/128\text{dd}\right)$. wsnp_CAP11_c3842_1829821 explained 12% of phenotypic variation and its insensitive photoperiod allele frequency increased from 0.73 to 0.94 between the initial and the evolved populations. The difference between the effects of the two alleles being 103 dd, allelic frequency variation at this marker accounted for 17% of the total phenotypic evolution $\left(\left[0.21 \times 103\text{dd}\right]/128\text{dd}\right)$. However, a global model including both markers showed that the effect of wsnp_CAP11_c3842_1829821 was due only to its small but significant LD with Ppd-D1 (LD = 0.18, P-value = 0.002). Hence, Ppd-D1 is probably the only selected gene in this region.

Discussion

We analyzed an evolved population derived from an experimental population with a very broad genetic basis (60 diverse parents, Table S1). To our knowledge, this is the first long-term use of nuclear male sterility to modify a plant’s reproductive biology, i.e., turning wheat from selfing to outcrossing during 12 generations (even if genetic male sterility has often been used in recurrent selection programs to facilitate recombination; see, for example, Mackay and Gibson 1993 and Kannenberg and Falk 1995). The specific characteristics of the population and of its history led us to develop various methods to describe its evolution and the genetic basis of this evolution.

To assess selection and drift effects, we first performed a Bayesian inference of parental contributions to the putative ancestral population, using parental genotypes and observed allelic frequencies in the evolved population. Estimates highlighted the strong contribution of Probus, with a more balanced contribution from the remaining parents, in good agreement with the known crossing scheme. This confirmed the robustness and accuracy of our method of estimation as suitable to infer the allelic frequencies in our theoretical initial population. Note that methods based on haplotype reconstruction can be used to infer parental contributions (Huang et al. 2012), but would necessitate much higher marker density than currently available in this highly recombined population. A future comparison of these two approaches should bring additional information about which is most suitable in studies with differing crossing schemes and objectives, given tradeoffs in precision, robustness, and computing time.

To test for selection, we used the estimated parental contributions to infer the initial allelic frequencies, thus allowing the estimation of the effective population size for use in a likelihood-ratio selection test.

The estimated effective size of the population ($N_{\text{e}}$ = 311) was very low compared to its demographic size ($N_{{\text{e}}_{\text{d}}}$=7500). The ratio $N_{\text{e}}$/$N_{{\text{e}}_{\text{d}}}$ = 0.04 is low, but not far from the 1/10 ratio commonly found in other studies (Frankham 1995; Luikart et al. 2010). Note that this value is similar to that estimated by Goldringer et al. (2001) for selfing populations in dynamic management ($N_{\text{e}}$/$N_{{\text{e}}_{\text{d}}}$ = 0.03, with $N_{\text{e}}$ ranging from 40 to 150). Higher $N_{\text{e}}$ for an outcrossing population is expected, with a theoretical twofold difference due to the uncorrelated segregation of the two alleles present in each open-pollinated individual, as well as to the lower transmission of reproductive success to a recombinant progeny (Austerlitz and Heyer 1998). Despite uncertainty about initial allelic frequencies, the striking gap observed between genetic and demographic sizes is an indication of selective pressures on dynamic management populations even though they are managed to avoid bottlenecks. However, other factors can explain the low $N_{\text{e}}$/$N_{{\text{e}}_{\text{d}}}$ ratio; for example, the variance in output of male and female gametes per plant is probably higher than the theoretical Poisson distribution (Caballero 1994).

Based on this inferred effective size, we implemented a method determining the likelihood of observed allelic frequency shifts in the absence of selection, as well as estimating the most likely selection coefficient, thus allowing us to build a likelihood ratio test. $N_{\text{e}}$ is thus a key parameter and, as expected, in our test, the likelihood ratio increases with $N_{\text{e}}$: the lower the genetic drift, the higher the power to detect selection (simulations not shown). As reviewed by Feder et al. (2014), its estimation represents a major statistical challenge. Various methods to detect selection without estimating $N_{\text{e}}$ have been developed , but none were appropriate to the present study as they require more than two samplings in a time series (Bollback et al. 2008; Feder et al. 2014). Our test for nonneutral temporal variations in SNP allele frequencies detected 26 genomic areas, mainly located on chromosomes 2B, 4B, 5A, and 6B (Figure 5). We checked that the detected SNPs also yielded the lowest P-values with the method developed in Goldringer and Bataillon (2004) and therefore would also have been identified as the best candidates. Note that chromosomes 2B and 4B were among those for which many parental contributions estimated at the chromosome level diverged from their genome-wide estimations (Table S4). This highlights the complex interaction between parental contribution estimates and the selection test: strong selection might bias parental estimates and thus decrease the power of the selection detection test itself. Effectively, parental contribution estimates are those best fitting the allele frequencies in the evolved population, and therefore they minimize the genetic divergence between the initial and the evolved populations. This should minimize the apparent impact of selection on allele frequencies. The test for selection is therefore conservative. In our study, there is no global correlation (cor = −0.09, P-value = 0.69) over the 21 wheat chromosomes between the number of areas in which selection is detected and divergence in genome-wide vs. chromosomal-parental contribution estimates. This might be related to the low LD of the population, explaining that selection affects only small chromosomal areas and, reciprocally, that selection on a given area has little effect on the estimation of parental contribution at the chromosome level and even less at the genome-wide level. However, for chromosome 5A, the presence of strong selection with a hitchhiking effect on numerous SNPs resulted in a link between selection and local variations in estimates of parental contributions.

Within the 57 SNPs under selection, the highest P-value corresponded to Ppd-D1, which is a known candidate gene involved in photoperiod sensitivity (Beales et al. 2007) and a key earliness QTL in many genetic studies (Hanocq et al. 2007; Le Gouis et al. 2012). Using association tests on the evolved population, we confirmed the strong impact of this QTL on flowering time. In addition to Ppd-D1, five other markers were associated with heading date (two markers with P-value <0.05 and three markers with P-value <0.1, Table S4). Most were located on chromosome 5A. Assuming that allelic effects are additive, these five markers explained only 1% of the phenotypic shift in heading date. Hence, heading-date evolution is mainly explained by one gene (Ppd-D1) with the remainder due to numerous loci either with a strong effect on flowering time and a low allelic frequency shift or with a significant allelic frequency evolution and a low effect (Kremer and Le Corre 2012). One area was detected as under selection and associated with heading date (P-value < 0.1, Table S4) at the end of chromosome 4B (Figure 5). This area could match with the location of Vrn2B, a known gene involved in an integrative pathway of vernalization requirement and photoperiod sensitivity but not located in the available map. Three areas, one on chromosome 4A and two on chromosome 5A, could also match previously detected QTL for heading date (Hanocq et al. 2007; Le Gouis et al. 2012). Finally one additional area on chromosome 5A did not correspond to any reported QTL.

In the selfing populations of the dynamic management experiment (Rhoné et al. 2008, 2010), not only Ppd-D1 showed a strong effect on earliness, but a significant association was also found for candidate genes with major effects on flowering time, such as Vrn1, which were not detected here. Vrn1 is known for its epistatic control of vernalization (Rousset et al. 2011) and in these selfing populations different combinations of alleles made with each of the three copies of Vrn1 (Vrn-A1, Vrn-B1, and Vrn-D1) have been selected. One hypothesis explaining why Vrn1 is detected as under selection in these selfing populations but not here might be that in outcrossing populations, selection is less efficient in maintaining epistatic combinations, because they can be readily broken by recombination.

In agreement with previous studies (Allard 1988; Le Boulc’h et al. 1994; Goldringer et al. 2006), we found that earliness is a major target trait for selection, the evolved population flowering earlier than the initial one. A fast response to selection is expected given the large initial genetic variability and high heritability of earliness. Here, this clear phenologic evolution was used as a model when analyzing genomic areas under positive selection. The selective pressures might have at least three origins. First, the viability of pollen might decrease in late flowering plants (higher summer temperatures; Welsh and Klatt 1971). Second, earlier male flowering plants have a selective advantage as few females are already fertilized (Gérard et al. 2006), leading to less competition and higher reproductive success. Third, there might be a bias during the male sterile plants tagging phase, with a higher tagging intensity at the beginning of the season (sterile spikes are easier to identify).

Here, we checked only association with earliness and found it significant for 24% of the genomic areas detected under selection (six different areas, Table S4). The other markers found under selection but not associated with earliness could still be involved in its regulation, as they could have reached near fixation in the evolved population in response to selection and therefore escape detection in an association test (Luo 1998). Alternatively they could be involved in the regulation of other adaptive traits such as disease resistance and plant height.

One area under selection, on the short arm of chromosome 4B, corresponds to the location of the sterility gene ms1b (Driscoll 1975). In this area, one marker exhibited an allelic frequency change from 0.37 in the initial population (allele present in five parents including Probus, which contributed to 34% of the initial population) to 0.02 in the evolved population. In this area of chromosome 4B, the frequency of the Probus allele decreased dramatically for four markers, in contrast with markers in adjacent regions (mean of allelic frequency differences between the initial and the evolved populations: 0.37 vs. 0.04, data not shown). This is in full agreement with the expected evolution of male-sterility gene ms1b, which was under stabilizing selection during population evolution (75% of sterile allele; Doggett and Eberhart 1968) and then selected against during fixation generations as ms1b/ms1b genotypes are sterile.

The introduction of the nuclear male-sterility gene, ms1b, transformed the wheat self-pollinating habit to outcrossing. The 12 generations of panmixia broke both the initial population structure and long distance LD, resulting in a very low level of LD in the evolved population (r² = 0.003 at 100 cM). This is to be compared to a r² of 0.04 between independent markers in a 19-parent MAGIC population of A. thaliana (Kover et al. 2009) or of 0.004 in a four-parent MAGIC population of wheat (Huang et al. 2012). The LD in the INRA MAGIC experimental population is the lowest described so far for a wheat population, with r² = 0.28 at a 2.5-cM distance (Figure 4). As a comparison, r² was 0.8 at 5 cM for a four-parent MAGIC population (Huang et al. 2012), or between 0.25 and 0.5 at 5 cM for an association mapping panel (Cavanagh et al. 2013). The low value of short distance LD in the INRA MAGIC population is due mostly to the low initial LD within the set of 56 parents (r² = 0.3 at 2.5 cM). The importance of parental diversity at very short distances (close to 0 cM) is well illustrated in the 4-parent and 19-parent MAGIC populations, with LD values of 1.0 and 0.2, respectively (Kover et al. 2009; Huang et al. 2012). Thus the overall very low LD of the INRA MAGIC population is the result of both low initial LD due to the high number of parents (and their relatively low relatedness) and a high number of recombinations, breaking LD at medium to long genetic distances. This low LD, combined with the absence of structure and a large diversity, make this population of great value for fine mapping.

The INRA MAGIC population is similar in concept to other advanced intercross populations such as the mouse Collaborative Cross (Churchill et al. 2004), the Arabidopsis 19-parent MAGIC lines (Kover et al. 2009), the Arabidopsis multiple parent recombinant inbred lines (AMPRIL with eight parent lines;Huang et al. 2011), the Drosophila Synthetic Population Resource (DSPR) (King et al. 2012a), the rice eight-parent MAGIC lines (Bandillo et al. 2013), and the yeast four-parent MAGIC lines (Cubillos et al. 2013) (see Rakshit et al. 2012 for a complete review on multiparent intercross populations). Nevertheless, these designs differ by the number of combined parental genomes per individual. The power to detect QTL was found to be higher in multiparental than in biparental populations, and it increased with the number of combined parental genomes per individual (Klasen et al. 2012). This factor allows a finer mapping since the number of recombination breakpoints is increased. Moreover, all of these populations resulted from many generations of intercrossing, which allowed more precise detection of QTL. They were mainly analyzed using traditional association mapping methods directly on the phenotype and genotype of lines (Huang et al. 2011; Cubillos et al. 2013) or on reconstructed parental haplotypes (Kover et al. 2009; King et al. 2012b). Only Cubillos et al. (2013) complemented standard association mapping with an evolutionary approach, i.e., detection of temporal allelic shifts corresponding to population adaptation, which allowed them to detect and map precisely a gene involved in heat stress resistance.

With such an evolutionary approach, studying both at phenotypic and genetic levels, we successfully identified 26 genomic areas under selection. Among them, 6 were associated with earliness: one major gene, four areas already detected in previous QTL studies, and one new genomic area. As the population exhibited quite fast evolution in one environment, growing such diversified gene pools in different divergent environments could give access to more genetic areas associated with local adaptation. In dynamic management, experiments so far have been performed without gene flow between populations, although appropriate gene flow would add genetic variability and could strengthen the detection of selected areas, as it is expected to homogenize neutral genomic areas. In addition, the genetic basis of local adaptation could be analyzed through association genetics since the number of panmictic generations guarantees very low LD and absence of structure. Using more individuals (1000 SSD lines are available—seed samples are available on request) with a higher density of markers should confirm that these evolutionary mapping populations are an invaluable platform for trait discovery and validation in the future.

Appendix

The observations (Figure A1), n_il, were defined as the number of alleles A (arbitrarily chosen from the two alleles of each biallelic SNP) observed in the SSD lines for each individual i at each locus l. The random variable N_il, defined as the number of A alleles for individual i at locus l can take three possible values: 0 or 2 when homozygous for allele A or B, respectively, and 1 if heterozygous. We did not consider linkage disequilibrium; consequently the number of alleles A at each locus for each individual is independent. The likelihood function is thus defined as

$$\mathrm{ℒ}={\displaystyle \prod }_i^I{\displaystyle \prod }_l^{L}P(N_{il}=n_{il}),$$

with I the total number of individuals (i.e., the 380 SSD lines here) and L the total number of loci considered (i.e., the number of markers). The probability function of N_il follows a binomial distribution leading to

$$\mathrm{ℒ}={\displaystyle \prod }_i^I{\displaystyle \prod }_l^L\left(\begin{array}{c}2\\ n_{il}\end{array}\right)p_l^{n_{ij}}{(1-p_l)}^{2-n_{ij}},$$

with p_l the probability of an individual carrying allele A at locus l (i.e., the expected frequency of allele A at locus l in the evolved population). Given that individuals and loci are independent in the model above, the equation is exactly equivalent to

$$\mathrm{ℒ}={\displaystyle \prod }_l^L\left(\begin{array}{c}380 \times 2\\ n_{.l}\end{array}\right)p_l^{n_{.l}}{(1-p_l)}^{380\times 2-n_{.l}},$$

with n_.l the total number of alleles A at locus l over all individuals. In others terms this model relies only on allele frequencies in the evolved population and not on their associations (i.e., no LD). It is thus capable of coping with the numerous selfing events necessary to obtain SSD lines. The probability p_j depends on the expected contribution of each parental line k, $\mathit{P}(\text{Par}=k)$, and on the frequency of allele A in each parental line k, $f{\left(A\right)}_k$. We can thus formulate p_j as

$$p_j={\displaystyle \sum }_k^{K}f{\left(A\right)}_{k}P(\text{Par}=k),$$

with K the total number of parental lines (i.e., K = 56 in this study).Genetic information is available for all putative parental lines K thus:

$${\displaystyle \sum }_k^{K}P(\text{Par}=k)=1.$$

Furthermore $P(\text{Par}=k)$ is the same for all loci considered during estimation. Finally because no previous information was available on the virtual contribution of each putative parental line k, we considered a flat Dirichlet prior distribution,

$$P\left(\text{Par}=1\dots K\right)\sim \mathcal{D}\text{ir}\left(\alpha \right),$$

with ${\alpha }_k=1$ for each of the K elements of the vector α.

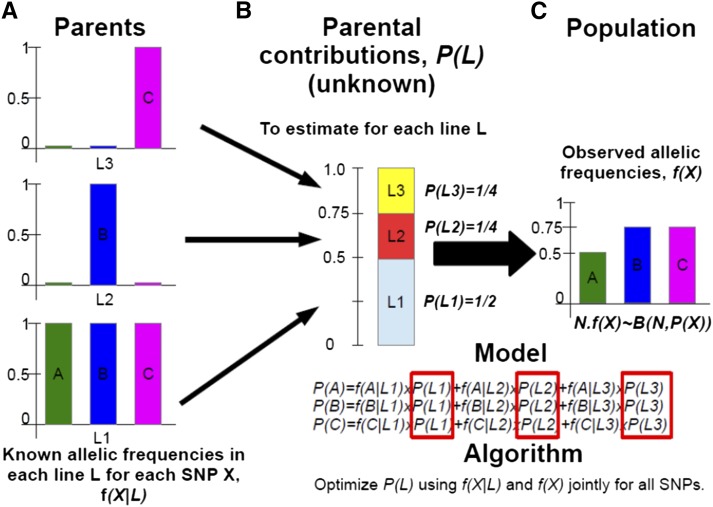
Figure A1.

Scheme of the method of parental contribution estimation. (A) The available data, f(X/L) i.e. the allele frequency at each locus X within each parental line L. (B) The unknown parameters to estimate, P(L) i.e. the probability of contribution to the observed population of each parent L. (C) The observations, f(X) i.e. the allele frequency at each locus. In this example we consider 3 parent lines (L1 in grey, L2 in red and L3 in yellow) genotyped at 3 SNPs (A, in green, B in blue and C in pink). We specify a binomial distribution of the allele frequencies with N the total number of individuals sampled in the observed population. Each locus is treated independently and the aim of the algorithm is estimation of genomic contribution of parents to the population.