Abstract
The magnetoelectric effects in multiferroic materials enable the mutual control of electric polarization by a magnetic field and magnetization by an electric field. Nonvolatile electric-field control of magnetization is extremely important for information storage applications, but has been rarely realized in single-phase multiferroic materials. Here we demonstrate the prominent direct and converse magnetoelectric effects in the Y-type hexaferrite BaSrCoZnFe11AlO22 single crystal. The electric polarization due to conical magnetic structure can be totally reversed by a small magnetic field, giving rise to large magnetoelectric coefficients of 6000 and 4000 ps/m at 100 and 200 K, respectively. The ab-plane magnetization can be controlled by electric fields with a large hysteresis, leading to nonvolatile change of magnetization. In addition, the reversal of magnetization by electric fields is also realized at 200 K. These diverse magnetoelectric effects with large coefficients highlight the promise of hexaferrites as potential multiferroic materials.
Electric-field (E) control of magnetism has aroused intense interests due to its potential to develop new spintronic and electronic devices1,2,3. Many schemes have been attempted in the past decade to achieve this goal. In heterostructures and thin films, magnetization can be electrically modified via strain from piezoelectric substrates4,5,6,7,8,9; via exchange bias from antiferromagnetic-ferroelectric (BiFeO3)10,11,12 or magnetoelectric (Cr2O3) substrates13,14 etc. For the case of single-phase materials, magnetoelectrics and magnetoelectic (ME) multiferroics are top candidates to achieve the direct E control of magnetizations (M) because of its intrinsic ME coupling15,16,17,18,19. However, such a converse ME effect usually requires a large external magnetic field (H) or low temperature, which is not practical for device application. Furthermore, nonvolatile E control of magnetization, which is important for information storage, poses more severe challenges for ME multiferroics.
Hexaferrites with conical magnetic structures are promising multiferroic materials which show direct ME effect (the manipulation of polarization P by H) up to room temperature20,21,22,23,24. The converse ME effect was also observed in several hexaferrites25,26,27,28. For instance, E control of M was realized in Ba0.5Sr1.5Zn2(Fe0.92Al0.08)12O22 single crystal below 170 K. Even at room temperature, converse ME effects were still observed in Y- and Z-type hexaferrites ceramics. Nevertheless, the reported converse ME effects are usually volatile - after removing E field, M restores the initial state. Although nonvolatile E control of M was recently reported in Y-type hexaferrite ceramics27, the hysteresis of the M-E curve is very small, with a tiny remanent magnetization in zero E field, which is unsuitable for nonvolatile applications. In this work, we performed a systematic study on both the direct and converse ME effects in the Y-type hexaferrite BaSrCoZnFe11AlO22 single crystal. The results demonstrate pronounced ME effects with the direct ME coefficients of 6000 and 4000 ps/m at 100 and 200 K, respectively. Moreover, the converse ME effect exhibits a large hysteresis in the M – E loop which enables a clear nonvolatile E control of M.
Results
Characterization of the Y-type hexaferrite BaSrCoZnFe11AlO22
As shown in Fig. 1a, the Y-type hexaferrite has a stacked layer structure with the space group R-3m. Our prepared single crystals of BaSrCoZnFe11AlO22 were characterized by single crystal x-ray diffraction (XRD), and the room-temperature XRD pattern (Fig. 1b) suggests that our specimen belongs to Y-type hexaferrite with c = 4.32 nm.
Figure 1. Characterization of the Y-type hexaferrite BaSrCoZnFe11AlO22.
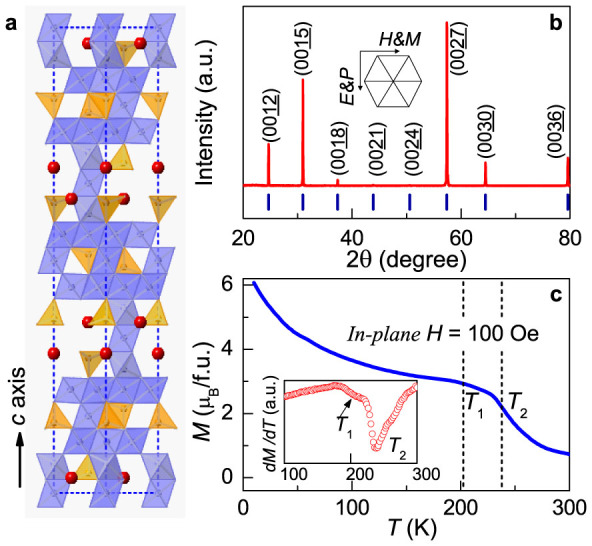
(a) The schematic crystal structure of Y-type hexaferrite. (b) The X-ray diffraction pattern of the Y-type hexaferrite single crystal sample along [001] direction. Inset of panel (b) shows the schematic experimental configuration. (c) Temperature dependent magnetization with H = 100 Oe along [100] axis. Before the measurements, H = 10 kOe was applied at 10 K to induce a metastable commensurate transverse cone state, then H was ramped down to 100 Oe. The Inset shows the derivative dM/dT as a function of temperature.
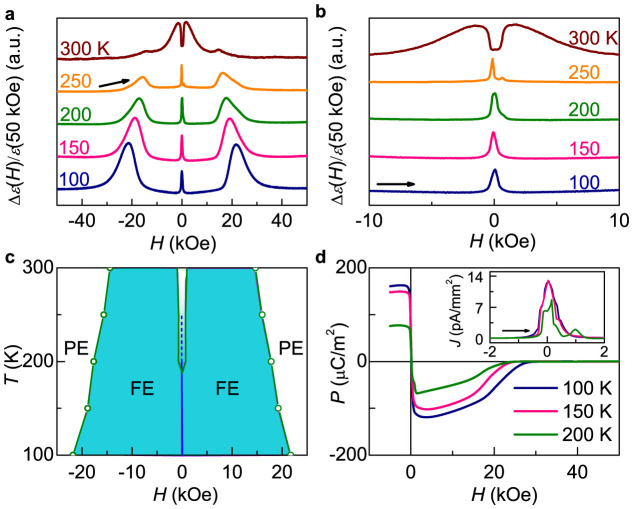
Fig. 1c shows the temperature (T) dependent magnetization curve with H = 100 Oe along the [100] direction. Before the measurement, an external magnetic field H = 10 kOe was first applied at 10 K to induce commensurate transverse cone state29, which is an intermediate ferroelectric (FE) phase according to the spin-current (KNB) or inverse Dzyaloshinskii-Moriya (DM) interaction models30,31; then H was ramped down to 100 Oe. The commensurate transverse cone would be kept under H = 100 Oe. Two critical temperatures T1 and T2 are observed in the M – T and dM/dT curves (Fig. 1c). At T1 ~ 200 K the magnetization starts to drop more abruptly, suggesting that the commensurate transverse cone is no longer stable near zero magnetic field. The magnetodielelectric and magnetoelectric current measurements, as discussed in next section, also suggest that the commensurate transverse cone is likely to change to the longitudinal cone above T1 due to the change of magnetic anisotropy. With further increasing temperature, there is another critical temperature T2 and it is likely to be the transition to proper screw due to its easy in-plane anisotropy at higher temperatures32.
Magnetic field control of electric polarization
To check the nature of magnetic-order-induced FE phase, we measured the in-plane (H // [100] and E // [120]) magnetodielectric properties at different temperatures. Fig. 2a shows the relative change of dielectric constant, Δε(H)/ε(50 kOe) = [ε(H)-ε(50 kOe)]/ε(50 kOe), at selected temperatures. At high fields, there are broad peaks at all temperatures, corresponding to the transitions from PE to FE or FE to PE phase. Fig. 2b shows the detailed magnetodielectric behaviors near zero field. Below 200 K, only one single dielectric constant peak appears at low magnetic field, indicating the switching of FE domain, which is also confirmed by the P – H curves in Fig. 2d. At 200 K, a slight shoulder feature starts appearing at finite H, signaling a new phase coexists with FE phase near zero field. This new phase is none other than PE phase mentioned above. With further rising temperature, the intensity of the shoulders increase gradually and the height of zero-field single peak decreases simultaneously. At 300 K, the zero-field single peak completely disappears and is replaced by the double peaks around H = ±2 kOe, which marks FE – PE – FE double phase transitions. All these magnetodielectric behaviors are in accordance with the M – T curve (Fig. 1c). Based on the magnetodielectric data, we obtain the magnetoelectric phase diagram shown in Fig. 2c. Below T1, only transverse cone (FE phase) exists around zero fields and the reversal of electric polarization by magnetic field can be attributed to direct in-plane reversal of the transverse cone state. Above T1, the PE phase would emerge and coexist with the FE phase near zero fields. With temperature further rising, the PE phase gradually dominates near zero fields at high temperatures.
Figure 2. Magnetic field control of electric polarization.
(a) The magnetodielectric ratio Δε(H)/ε(50 kOe) = [ε(H)-ε(5 kOe)]/ε(5 kOe) at selected temperatures. (b) The details of the magnetodielectric behavior around zero field. (c) The magnetoelectric phase diagram of BaSrCoZnFe11AlO22. (d) Magnetic field reversal of in-plane electric polarization at 100, 150, and 200 K. The inset shows the magnetoelectric current near zero magnetic field.
We also measured the magnetoelectric current (JME) below T1 and integrated it by time to obtain electric polarization (P), as displayed in Fig. 2d. The P can be reversed by a small H. The ME coefficients (αh = ∂P/∂H) calculated by the magnetoelectric current reach a maximum of ~6000 ps/m at 100 and 150 K, and ~4000 ps/m at 200 K. Above 200 K, because of the low resistivity of our crystal at high temperature, we are not able to pole the sample to obtain reliable ME current. The inset of Fig. 2d shows the JME around zero magnetic fields. At 200 K, besides the current peak at zero field like those at 100 K and 150 K,there is a small current peak around H = 1 kOe corresponding to the magnetodielectric shoulder. Therefore, we can attribute the weak current peak to the transition of PE to FE, which suggests chirality is unchanged during the transverse cone - longitudinal cone - transverse cone transitions, similar to that reported in Ba2Mg2Fe12O22 (Ref. 21). Moreover, the little current peak also verifies the existence of PE phase near zero magnetic field.
Nonvolatile electric control of magnetization
We then focus on the converse ME effect in the BaSrCoZnFe11AlO22 single crystal sample. For multiferroics, there usually exist four kinds of compound domains signified by magnetic and electric order parameters ±M and ±P33. In Y-type hexaferrite, the in-plane P is caused by long range transverse conical magnetic order with wave vector along c axis, which is in accordance with the spin-current (KNB) model. Therefore, the directions of P and M of compound domain are totally dependent on the electric field E and magnetic field H during poling process. To achieve the converse ME effect as large as possible, the converse ME effects were measured after a ME poling procedure in which H was decreased from 50 kOe to 5 kOe under application of E = 500 kV/m and then the E field was turned off. After that, H was set to zero or a low field for the converse ME effect measurement.
Fig. 3a shows the E dependence of M along [100] direction at 100 K. The maximum E for the converse ME effect measurement is limited under 1 MV/m for safety reason. The substantial hysteresis between the data obtained during increasing and decreasing E scan produces a well-defined M – E hysteresis loop. To estimate the converse ME coefficients in the M-E hysteresis case, the magnetizations of the increasing and decreasing E-scan data were averaged. A quadratic function: 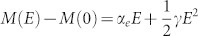 is used to approximate the E dependence of M, where it includes linear and quadratic E terms25. The linear coefficient αe = 3100 ps/m and quadratic coefficient γ = 80 ps/MV were obtained, indicating the converse ME effect at 100 K is mainly dominated by the linear term. The smaller difference between the values of αe and αh in single crystal than ceramic samples27 suggests that the contribution from trapped space charges is effectively suppressed.
is used to approximate the E dependence of M, where it includes linear and quadratic E terms25. The linear coefficient αe = 3100 ps/m and quadratic coefficient γ = 80 ps/MV were obtained, indicating the converse ME effect at 100 K is mainly dominated by the linear term. The smaller difference between the values of αe and αh in single crystal than ceramic samples27 suggests that the contribution from trapped space charges is effectively suppressed.
Figure 3. Nonvolatile electric control of magnetization.
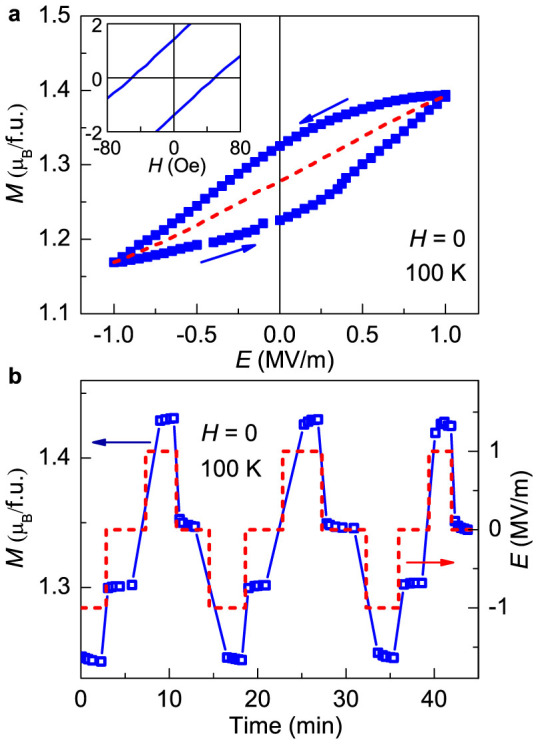
(a) Magnetization as a function of electric field at 100 K showing the M − E hysteresis loop. The inset shows the M–H hysteresis at low magnetic fields. (b) Four magnetization levels controlled by applying electric field in a repeated sequence of −1 MV/m → 0 → 1 MV/m → 0. No bias magnetic field is needed.
The large M – E hysteresis loop at 100 K indicates its potential for nonvolatile magnetization controlled by E, shown in Fig. 3b. After the poling procedure mentioned above, we measured M with applying E field in a sequence: −1 MV/m – 0 – 1 MV/m – 0 without a magnetic field bias. When applying a negative E, the magnetization is reduced owing to the clamped M & P orders. In contrast, the positive E leads to an increase in M. It clearly displays that two magnetization values at E = 0 are distinctively different after remove E = 1 MV/m and E = −1 MV/m, due to its large M – E hysteresis loop shown in Fig. 3a. Moreover, no obvious damping of magnetization was observed after several periods, though we did not apply large enough E to make the magnetization saturated.
The reversal of magnetization by electric field
Next, we performed similar measurements at 200 K. Fig. 4a displays the M – E curve showing a large hysteresis at 200 K with external H = −10 Oe along [100] direction. Compared with that at 100 K, the M – E curve at 200 K is more asymmetric and M almost remains constant with decreasing negative E-scan. With the same fitting method taken at 100 K, we got αe = 1100 ps/m and γ = 535 ps/MV at 200 K. Such a large quadratic coefficient γ is likely to be the reason for the asymmetric shape of the M – E curve at 200 K. This quadratic converse ME effect is possibly introduced by the new PE phase around zero magnetic field, as our magnetic and magnetodielectric measurements have suggested the existence of mixed phases at this temperature and the transverse cone is responsible for the linear converse ME effect, which has been evidenced by the results at 100 K. the substantial hysteresis at 200 K suggests its potential for nonvolatile magnetic states controlled by E, just like that at 100 K. A distinguished feature at 200 K is the reversal of M by E field. Fig. 4b demonstrates the repeated reversal of M by switching the polarity of electric field (E = ±1 MV/m) under a small bias H = −10 Oe at 200 K. The positive E causes an increase in M, while the negative E leads to polarity reversal of M.
Figure 4. The reversal of magnetization by electric field.
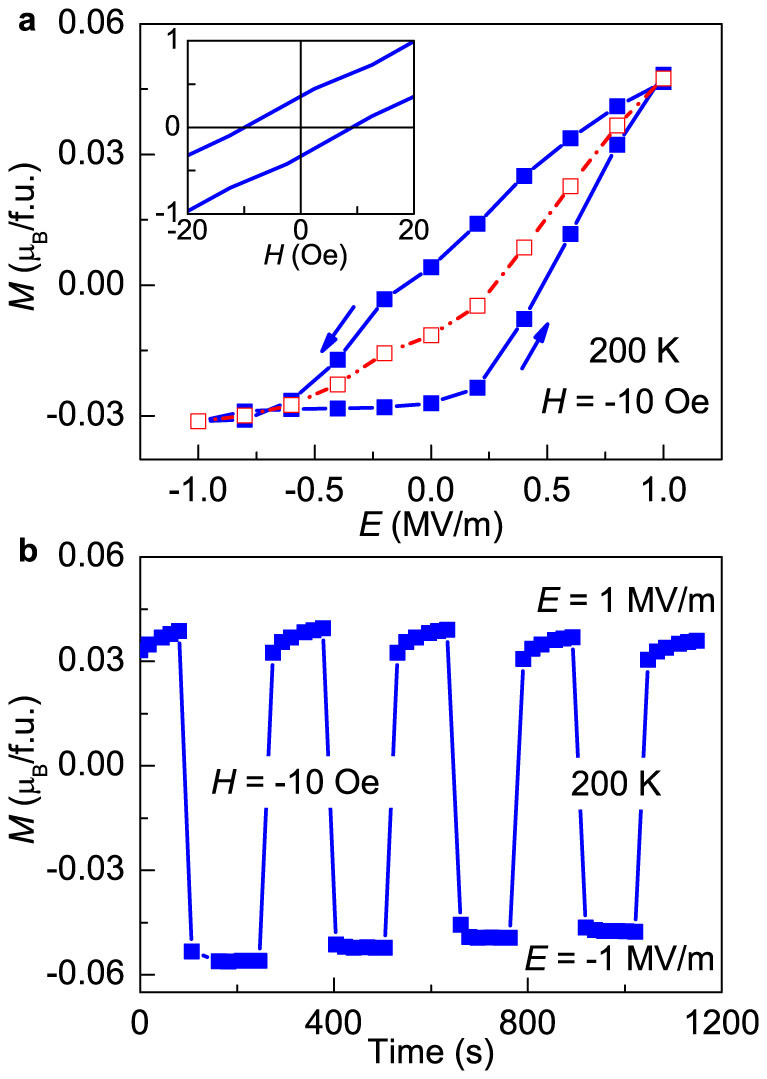
(a) Magnetization as a function of electric field measured with a bias magnetic field H = −10 Oe at 200 K. The inset shows the M – H hysteresis loop at low magnetic fields. (b) Electric-field reversal of magnetization under a small bias magnetic field H = −10 Oe.
Discussion
The electric polarization in Y-type hexaferrite can be well explained by the spin-current model P ∝k0 × (Si × Sj), where Si and Sj denote the neighbor spins at site i and j, k0 // [001] is the magnetic propagation vector. According to this model, the screw or longitudinal conical spin configurations cannot generate P due to spin chirality Σ(Si × Sj) // k0. However, the transverse cone is a FE phase. Below 200 K, the transverse cone (FE) still persists after we decrease H from high field to zero, which is responsible for the direct reversal of P by H and the linear converse ME effect. In benefit of the large converse ME susceptibility (αe = 3100 ps/m) and substantial M-E hysteresis loop, we achieve nonvolatile distinguished change of M by E, that is to say, the magnetizations differ even after removing +E and −E. This result provides the potential for future nonvolatile magnetic memory device controlled by E.
Due to the clamped M & P orders in multiferroic hexaferrites, there are only two kinds of compound domains: +M/+P and −M/−P since +E and +H are applied during poling process. The manipulation of M by E can be thought as the result of the compound domain wall movement. Like the hysteresis loop in the M – H loop, the hysteresis characteristics for M – E curves appear due to resistance of domain wall movement. The relatively large coercive field (Hc = 50 Oe) in the M – H loop is probably responsible for the substantial M – E hysteresis loop, which is the prerequisite for nonvolatile magnetization controlled by E.
Different from the case at 100 K where the linear converse ME effect dominates, the contribution of quadratic converse ME effect is no longer negligible at 200 K. Magnetodielectric and JME measurements at 200 K suggest that PE and FE phase coexist at zero field, that is to say, besides the transverse cone phase, there is a longitudinal cone or proper screw phase when we ramp from high-H down to zero. Thus, it could be the existence of the PE phase (proper screw or longitudinal cone) responsible for the quadratic converse ME effect.
In summary, we have demonstrated pronounced ME effects in the Y-type hexaferrite BaSrCoZnFe11AlO22 single crystal at different temperatures. Its direct ME susceptibility can reach as high as 6000 ps/m at 100 K, and 4000 ps/m at 200 K. In benefit of the large M – E hysteresis loop as well as the large converse ME coefficients (3100 and 1100 ps/m at 100 and 200 K, respectively) in single crystals, nonvolatile E control of magnetization can be realized. In addition, reversal of magnetization by E field was also demonstrated at 200 K. These excellent properties promise its potential for the future magnetoelectric functional devices. Further tailoring of the composition of Y-type hexaferrites may eventually realize these diverse ME effects at room temperature.
Methods
Sample preparation
Single-crystal samples of the Y-type hexaferrite BaSrCoZnFe11AlO22 were prepared by Na2O-Fe2O3 flux method in air as described elsewhere34. The as-grown samples were annealed at 900°C in O2 atmosphere to enhance the resistivity35.
Electric and magnetic measurements
For electrical measurements, the crystals were cut into thin plates with the widest faces perpendicular to the [120] direction in the hexagonal setting and then were painted with sliver paste on the widest faces. The JME and dielectric constant were measured by an electrometer (Keithley 6517B) and a LCR meter (Aglient, 4980A), respectively, in a Cryogen-free Superconducting Magnet System (Oxford Instruments, TeslatronPT). The converse ME effects were measured by using a magnetometer with a homemade sample holder (MPMS, Quantum Design). Before JME measurements, we need to carry out the following steps to pole our sample: (1) E = 500 kV/m was applied at H = 50 kOe along [100] direction where sample was in a high-field PE phase; (2) ramped down the H to 5 kOe, where the sample was driven to the intermediate field FE phase, then withdrew electric field and shortened two electrodes for 30 mins to release free charges; (3) swept magnetic field with 25 Oe/s to −50 kOe and measured the JME.
Author Contributions
Y.S. and S.S conceived the project. S.S prepared the samples and performed the experiments. Y.C. helped in experiments and analysis of the data. All authors contributed to writing the paper.
Acknowledgments
This work was supported by the National Key Basic Research Program of China under Grant No. 2011CB921801, the Natural Science Foundation of China under Grants Nos. 11227405 and 11374347, and the Strategic Priority Research Program of the Chinese Academy of Sciences under Grant No. XDB07030200.
References
- Spaldin N. A. & Fiebig M. The renaissance of magnetoelectric multiferroics. Science 309, 391–392 (2005). [DOI] [PubMed] [Google Scholar]
- Eerenstein W., Mathur N. D. & Scott J. F. Multiferroic and magnetoelectric magterials. Nature 442, 759–765 (2006). [DOI] [PubMed] [Google Scholar]
- Spaldin N. A., Cheong S. W. & Ramesh R. Multferroics: Past, present, and future. Phys. Today 63, No. 10, 38 (2010). [Google Scholar]
- Eerenstein W., Wiora M., Prieto J. L., Scott J. F. & Mathur N. D. Giant sharp and persistent converse magnetoelectric effects in multiferroic epitaxial heterostructures. Nat. Mater. 6, 348–351 (2007). [DOI] [PubMed] [Google Scholar]
- Sahoo S. et al. Ferroelectric control of magnetism in BaTiO3/Fe heterostructures via interface strain coupling. Phys. Rev. B 76, 092108 (2007). [Google Scholar]
- Thiele C., Dörr K., Bilani O., Rödel J. & Schultz L. Influence of strain on the magnetization and magnetoelectric effect in La0.7A0.3MnO3/PMN-PT(001) (A = Sr, Ca). Phys. Rev. B 75, 054408 (2007). [Google Scholar]
- Weiler M. et al. Voltage controlled inversion of magnetic anisotropy in a ferromagnetic thin film at room temperature. New J. Phys. 11, 013021 (2009). [Google Scholar]
- Ghidini M. et al. Non-volatile electrically driven repeatable magnetization reversal with no applied magnetic field. Nature comm. 4, 1453 (2012). [DOI] [PubMed] [Google Scholar]
- Zhang S. et al. Electric-Field control of nonvolatile magnetization in Co40Fe40B20/Pb (Mg1/3Nb2/3)0.7Ti0.3O3 structure at room temperature. Phys. Rev. Lett. 108, 137203 (2012). [DOI] [PubMed] [Google Scholar]
- Zhao T. et al. Electrical control of antiferromagnetic domains in multiferroic BiFeO3 films at room temperature. Nat. Mater. 5, 823–829 (2006). [DOI] [PubMed] [Google Scholar]
- Lebeugle D. et al. Electric field switching of the magnetic anisotropy of a ferromagnetic layer exchange coupled to the multiferroic compound BiFeO3. Phys Rev. Lett. 103, 257601 (2009). [DOI] [PubMed] [Google Scholar]
- Chu Y. H. et al. Electric-field control of local ferromagnetism using a magnetoelectric multiferroic. Nat. Mater. 7, 478–482 (2008). [DOI] [PubMed] [Google Scholar]
- Wu N. et al. Imaging and control of surface magnetization domains in a magnetoelectric antiferromagnet. Phys. Rev. Lett. 106, 087202 (2011). [DOI] [PubMed] [Google Scholar]
- He X. et al. Robust isothermal electric control of exchange bias at room temperature. Nat. Mater. 9, 579–585 (2010). [DOI] [PubMed] [Google Scholar]
- Iyama A. & Kimura T. Magnetoelectric hysteresis loop in Cr2O3 at room temperature. Phys. Rev. B 87, 180408(R) (2013). [Google Scholar]
- Lottermoser T. et al. Magnetic phase control by an electric field. Nature 430, 541–544 (2004). [DOI] [PubMed] [Google Scholar]
- Tokunaga Y., Taguchi Y., Arima T. & Tokura Y. Electric-field-induced generation and reversal of ferromagnetic moment in ferrites. Nature Phys. 8, 838–844 (2012). [Google Scholar]
- Tian Y. et al. Electric control of magnetism in a multiferroic metal–organic framework. Phys. Status Solidi RRL 8, 91–94 (2014). [Google Scholar]
- Tian Y. et al. Cross coupling between electric and magnetic orders in a multiferroic metal-organic framework. Sci. Rep. 4, 6062 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura T., Lawes G. & Ramirez A. P. Electric polarization rotation in a hexaferrite with long-wavelength magnetic structures. Phys. Rev. Lett. 94, 137201 (2005). [DOI] [PubMed] [Google Scholar]
- Ishiwata S. et al. Low-magnetic-field control of electric polarization vector in a helimagnet. Science 319, 1643–1646 (2008). [DOI] [PubMed] [Google Scholar]
- Chun S. H. et al. Realization of giant magnetoelectricity in helimagnets. Phys. Rev. Lett. 104, 037204 (2010). [DOI] [PubMed] [Google Scholar]
- Wang F., Zou T., Yan L. Q., Liu Y. & Sun Y. low magnetic field reversal of electric polarization in a Y-type hexaferrite. Appl. Phys. Lett. 100, 122901 (2012). [Google Scholar]
- Kitagawa Y. et al. Low-field magnetoelectric effect at room temperature. Nature Mater. 9, 797–802 (2010). [DOI] [PubMed] [Google Scholar]
- Chun S. H. et al. Electric field control of nonvolatile four-state magnetization at room temperature. Phys. Rev. Lett. 108, 177201 (2012). [DOI] [PubMed] [Google Scholar]
- Chai Y. S. et al. Electric control of large magnetization reversal in a helimagnet. Nature Comm. 5, 4208 (2014). [DOI] [PubMed] [Google Scholar]
- Hirose S., Haruki K., Ando A. & Kimura T. Mutual control of magnetization and electric polarization by electric and magnetic field at room temperature in Y-type BaSrCo2-x ZnxFe11AlO22 ceramics. Appl. Phys. Lett. 104, 022907 (2014). [Google Scholar]
- Okumura K. et al. Multilevel magnetization switching by electric field in c-axis oriented polycrystalline Z-type hexaferrite. Appl. Phys. Lett. 103, 032906 (2013). [Google Scholar]
- Shen S. P. et al. Magnetic field reversal of electric polarization and magnetoelectric phase diagram of the hexaferrite Ba1.3Sr0.7Co0.9Zn1.1Fe10.8Al1.2O22. Appl. Phys. Lett. 104, 032905 (2014). [Google Scholar]
- Katsura H., Nagaosa N. & Balatsky A. V. Spin current and magnetoelectric effect in noncollinear magnets. Phys. Rev. Lett. 95, 057205 (2005). [DOI] [PubMed] [Google Scholar]
- Sergienko I. A. & Dagotto E. Role of the Dzyaloshinskii-Moriya interaction in multiferroic perovskites. Phys. Rev. B 73, 094434 (2006). [Google Scholar]
- Smit J. & Wijn H. P. J. Ferrites (Phillips Technical Library, Eindhoven, 1959). [Google Scholar]
- Tokunaga Y. et al. Composite domain walls in a multiferroic perovskite ferrite. Nature Mater. 8, 558–562 (2009). [DOI] [PubMed] [Google Scholar]
- Momozawa N., Mita M. & Takei H. Single crystal growth of (Ba1-xSrx)2Zn2Fe12O22 from high temperature solution. J. Cryst. Growth 83, 403–409 (1987). [Google Scholar]
- Chai Y. S. et al. Low-magnetic-field control of dielectric constant at room temperature realized in Ba0.5Sr1.5Zn2Fe12O22. New J. Phys. 11, 073030 (2009). [Google Scholar]