Calibration of Multiple In Silico Tools for Predicting Pathogenicity of Mismatch Repair Gene Missense Substitutions

Abstract

Classification of rare missense substitutions observed during genetic testing for patient management is a considerable problem in clinical genetics. The Bayesian integrated evaluation of unclassified variants is a solution originally developed for BRCA1/2. Here, we take a step toward an analogous system for the mismatch repair (MMR) genes (MLH1, MSH2, MSH6, and PMS2) that confer colon cancer susceptibility in Lynch syndrome by calibrating in silico tools to estimate prior probabilities of pathogenicity for MMR gene missense substitutions. A qualitative five-class classification system was developed and applied to 143 MMR missense variants. This identified 74 missense substitutions suitable for calibration. These substitutions were scored using six different in silico tools (Align-Grantham Variation Grantham Deviation, multivariate analysis of protein polymorphisms [MAPP], Mut-Pred, PolyPhen-2.1, Sorting Intolerant From Tolerant, and Xvar), using curated MMR multiple sequence alignments where possible. The output from each tool was calibrated by regression against the classifications of the 74 missense substitutions; these calibrated outputs are interpretable as prior probabilities of pathogenicity. MAPP was the most accurate tool and MAPP + PolyPhen-2.1 provided the best-combined model (R² = 0.62 and area under receiver operating characteristic = 0.93). The MAPP + PolyPhen-2.1 output is sufficiently predictive to feed as a continuous variable into the quantitative Bayesian integrated evaluation for clinical classification of MMR gene missense substitutions.

Introduction

Missense variants that cause a single amino acid substitution in a protein sequence may or may not lead to altered protein function [Tavtigian et al., 2008c]. Many germline missense variants have unclear functional and medical consequences and cannot be easily classified as either pathogenic or neutral before they have been subjected to a detailed analysis. These variants of unknown clinical significance cannot be used to guide patient management, and are a source of anxiety for families [O'Neill et al., 2009]. Accurately placing them in a spectrum from neutral to clearly pathogenic through the development of robust classification systems would allow resources for screening, prevention, and treatment to be focused on individuals truly at elevated genetic risk and provide reassurance to those who are not at risk [Hicks et al., 2011; Miller et al., 2011; Tavtigian et al., 2008c].

The most common form of hereditary colorectal cancer (CRC) is Lynch syndrome (LS), which accounts for about 3% of all CRC [Lynch et al., 2009]. LS results from defects in DNA mismatch repair due to the inherited mutations in one of four mismatch repair (MMR) genes MLH1 (MIM# 120436), MSH2 (MIM# 609389), MSH6 (MIM# 600678), and PMS2 (MIM# 600259) [Viel et al., 1998; Wang et al., 1999]. Genetic testing for these four genes is routinely performed. Between 20% and 30% of genetic variants identified are missense variants, almost all of which are considered of unknown clinical significance [Woods et al., 2007].

A five-tiered classification system, with recommendations for clinical management of variants, was proposed by the IARC Working Group on Unclassified Genetic Variants, and is now under study in several areas of clinical cancer genetics. When possible, each class is associated with a probability that a variant is pathogenic derived from statistical studies [Plon et al., 2008] that incorporate data from various independent sources important to disease pathology. These include clinicopathologic and epidemiological studies, but also in vivo or in vitro functional assays, and computational (in silico) analyses [Couch et al., 2008; Tavtigian et al., 2008b].

Strategies to integrate these methods have been a topic of significant activity for researchers and clinicians working with MMR and other cancer susceptibility genes [Arnold et al., 2009; Barnetson et al., 2008; Easton et al., 2007; Goldgar et al., 2004; Miller et al., 2011; Pastrello et al., 2011]. An increasingly well-developed method for classifying variants (initially BRCA1 [MIM# 113705] and BRCA2 [MIM# 600185] variants) integrates different lines of genetic evidence using Bayesian analysis [Easton et al., 2007; Goldgar et al., 2004]: each variant starts with a “prior probability” of pathogenicity based on in silico algorithm outputs, ultimately calibrated against a reference set of variants that have been classified with confidence using other types of data [Easton et al., 2007; Tavtigian et al., 2008a]; a “posterior probability” of pathogenicity is derived by updating the prior probability with likelihood ratios (LR) or odds ratios for pathogenicity determined from statistical analyses of observational data such as segregation of the variant in families, pathological characteristics, and in vitro studies.

A wide variety of in silico tools using various implementations and combinations of features have now been developed [Tavtigian et al., 2008c; Thusberg et al., 2011]. These in silico tools are generally based on: (1) analyses of sequence conservation at the position of a missense substitution, which is measured from a protein multiple sequence alignment, (2) severity of a missense substitution with respect to the observed range of variation at its position in an alignment, and/or (3) structural features of the wild-type and variant proteins. This study focuses on comparing the accuracies and calibrating the outputs of in silico tools for MMR missense substitution analysis. We report (1) a list of 74 qualitatively classified MMR variants used in the calibration, (2) the creation of curated protein multiple sequence alignments for the four MMR genes associated with LS, (3) comparison of six in silico tools for predicting the pathogenicity of the list of variants, (4) comparison of pairwise combinations of these in silico tools, and (5) calibration of the output, expressed as a continuous variable, of the best paired combination in describing probability in favor of pathogenicity. This output variable can be used now as a tool for classification, feeding into the quantitative integrated evaluation of MMR gene missense substitutions (see the accompanying paper [Thompson et al., in press]).

Methods and Materials

Development of the Qualitative Classifier

An existing qualitative missense classifier originally developed for research classification of Colon Cancer Family Registry (CCFR) MMR gene variants [Thompson et al., 2012] was further developed with the coauthors, following suggestions from the InSiGHT Mutation Interpretation Committee. The classifier presents a five-class system as described for quantitative assessment of variant pathogenicity in [Plon et al., 2008]. However, instead of mathematically derived probabilities of pathogenicity, the classes reflect consensus opinion that a set of qualitative data correspond to a ≥99%, ≥95%, ≤5%, or ≤0.1% probability of pathogenicity. Two general types of data were combined: (1) association of the variant with clinical cases of LS cancers, such as segregation with disease in families, microsatellite instability-high (MSI-H) or loss of the appropriate protein by immunohistochemistry (IHC) in tumors of variant carriers; and (2) association of the variant with decreased function in an in vitro assay. The criteria used to classify the variants are shown in Table 1. Importantly, the standardized qualitative classifier excluded data from in silico tools.

Table 1.

Missense Classification Criteria

Class	Criteria used for qualitative classification
Class 5—Pathogenic	All of the following characteristics:
	– deficient protein function in in vitro/ex vivo functional assays in mammalian system (cannot be in yeast only)
	– cosegregation with disease in at least one AMS family with ≥4 affected carriers, or ≥2 familiesa with ≥3 affected nonproband carriers
	– not present in the general population (>160 individuals = 320 alleles)
	– MSI-H in ≥2 independent tumors with no contradictory IHC results or immunoloss of MMR protein(s) consistent with the variant location in ≥2 independent tumors for MLH1 or ≥1 tumor for MSH2, MSH6, and PMS2
Class 4—Likely pathogenic	Deficient protein function in one or more in vitro/ex vivo assays in any eukaryote, plus one of the following:
	– cosegregation with disease in at least one AMS family with ≥3 affected carriers
	– MSI-H in ≥2 independent tumors with no contradictory IHC results or immunoloss of MMR protein(s) consistent with the variant location in ≥2 independent tumors for MLH1 or ≥1 tumor for MSH2, MSH6, and PMS2
Class 3—Uncertain	Insufficient evidence to classify, that is, not class 1, 2, 4, or 5
Class 2–Likely not pathogenic	Variants reported to occur in a specific ethnic group at frequency ≥1%, and that have not yet been excluded as known founder mutations
	Or variants reported to occur in the general population at a frequency <1%, with normal protein function in in vitro/ex vivo functional assays in any eukaryote and no aberrant splicing
Class 1—Not pathogenic	Variants reported to occur in the general population at frequency ≥1%
	Or present in the general population at frequency 0.1%– 1% and determined by large case-control studies to be associated with estimated risk <1.5, with upper bound 95% CI <4

Note: These classification guidelines (froze in October 2011) are similar to criteria currently being developed and tested by the InSiGHT Mutation Interpretation Committee.

^aThe families used in variant classification fulfilled the Amsterdam Criteria.

AMS, revised Amsterdam criteria [Vasen et al., 1999]; MSI-H, microsatellite instability-high.

Generation of the List of Qualitatively Classified Missense Substitutions

An initial list of 143 MMR missense variants considered (likely) pathogenic or neutral was compiled from five sources for standardized classification using the qualitative criteria (Table 1). These sources were: a population-based study by Barnetson et al. (2008), two studies of in silico methods by Chan et al. (2007) and Chao et al. (2008), variants identified by the Australasian CCFR population and clinic-based recruitment arms [Arnold et al., 2009], common missense substitutions drawn from dbSNP, (http://www.ncbi.nlm.nih.gov/sites/entrez?db=snp). All the MMR variants assessed (classes 1–5) have been submitted to the InSiGHT locus-specific database (www.insight-group.org). Standardized classification used mostly information from the literature/databases, supplemented with some unpublished data on tumor characteristics collected from the clinicians listed in the acknowledgments. None of these sources reported using tumor prescreening criteria; overall only 56% of these variants were associated with MSI-H tumors and only 41% showed loss of IHC staining.

The 143 missense substitutions were classified independently by two investigators (BAT and MSG), and discrepancies resolved by consensus among four investigators (BAT, MSG, ABS, and SVT). Variants with reported evidence of a splice defect were excluded from further analysis to prevent the possibility of pathogenicity actually attributable to splice effects from confounding analyses of pathogenicity attributable to missense dysfunction. Calibration used all true missense variants that were ultimately classified as class 1, 2, 4, or 5 (but not class 3 variants).

Preparation of Protein Multiple Sequence Alignments

We constructed MLH1, MSH2, MSH6, and PMS2 protein multiple sequence alignments over a fixed phylogeny of species: human, Cercopithecidae (Macaca mulatta or Chlorocebus aethiops), Glires (Mus musculus), Laurasiatheria (Bos taurus or Canis lupus), Marsupialia (Monodelphis domestica), Aves (Gallus gallus), Amphibia (Xenopus laevis or Xenopus tropicalis), Teleostei (Danio rerio), Agnatha (Petromyzon marinus), Urochordata (Ciona intestinalis), Cephalochordata (Branchiostoma floridae), Echinodermata (Strongylocentrotus purpuratus), Cnidaria (Nematostella vectensis), and Placozoa (Trichoplax adhearens). Individual sequences were curated by hand, and in areas where exon predictions or splice junction predictions were unclear, peptide sequences were replaced with “X,” rather than “-” to allow distinction between ambiguous amino acids and true alignment gaps [Tavtigian et al., 2008c]. Sequences were aligned using M-Coffee [Wallace et al., 2006], followed by minor hand editing. The sequences and alignments satisfied three criteria: (1) the individual sequences are essentially full-length and encode clear orthologs of the relevant human protein, (2) the individual sequences are substantially free of cDNA (or gene model) structural errors, and (3) the concatenated alignment of all four genes contains an average of at least three amino acid substitutions per position and meets the missense substitution analysis program Sorting Intolerant From Tolerant (SIFT) “median sequence conservation” criterion for confident prediction of substitutions that should “affect protein function,” thus meeting criteria of sufficient sequence diversity to grade missense substitutions [Greenblatt et al., 2003; Ng and Henikoff, 2002; Tavtigian et al., 2008c]. These alignments, or updated versions thereof, are available at http://agvgd.iarc.fr/alignments.php.

Missense Substitution Scoring and Output Manipulation for Regression Analyses

Missense substitutions were scored using six distinct in silico tools.

1. Align Grantham Variation Grantham Deviation (Align-GVGD—http://agvgd.iarc.fr/) [Tavtigian et al., 2006, 2008a] was run at three depths of sequence alignment: through Strongylocentrotus (the shallowest alignment to reach the sequence diversity target of an average of three substitutions per position), through Nematostella, and through Trichoplax. For regressions, the standard output of seven grades was coded as 0 (for C0, the least likely functionally deleterious grade) through 6 (for C65, the most likely functionally deleterious grade). For some regressions, C0 was split into two grades: GD = 0 (least likely to be functionally deleterious) and GD > 0 (slightly more likely to be functionally deleterious).

2. Multivariate analysis of protein polymorphisms (MAPP—http://mendel.stanford.edu/SidowLab/downloads/MAPP/) [Stone and Sidow, 2005] was run at three depths of sequence alignment: through Strongylocentrotus, through Nematostella, and through Trichoplax. For regressions, we used the MAPP score as a continuous variable and also used ln(MAPP Score) as a continuous variable. MAPP-MMR (http://mappmmr.blueankh.com/), which is a modification of MAPP that focuses on the MMR genes MLH1 and MSH2, was also run [Chao et al., 2008].

3. PolyPhen-2.1 (http://genetics.bwh.harvard.edu/pph2/) [Adzhubei et al., 2010] was used in two modes: (1) default mode with native alignments, which is equivalent to the online version, and (2) a custom mode in which the program was retrained without MMR gene data. In the latter case, the native PolyPhen-2.1 MMR gene alignments were lightly edited to remove 5′ or 3′ protein sequence segments that bore little or no resemblance to the corresponding human gene, and internal insertions that were likely to be consequences of exon boundary prediction errors. From both modes, “HumVar” outputs were used for statistical analyses. For regressions, “Class” (deleterious/neutral) was used as a binary predictor. “Benign/possible damaging/probably damaging” was used as a trinary predictor with benign set to 0, “probably damaging” set to 2, and the value for “possible damaging” optimized; on this scale, the optimum value usually came out between 0.9 and 1.1. The output variable “pph2_prob” was used as a continuous variable.

4. MutPred (http://mutpred.mutdb.org/) [Li et al., 2009] was used in two modes: (1) default mode with native alignments, which is equivalent to the online version, and (2) a custom mode in which the program was retrained without MMR gene data. For regressions, we used the MutPred “RF score” with a threshold of 0.5 as a binary variable, MutPred “RF score” as a continuous variable, and ln(RF score) as a continuous variable.

5. SIFT (http://sift.jcvi.org/) [Kumar et al., 2009; Ng and Henikoff, 2002] was used in two modes: (1) SIFT BLINK, which uses native SIFT alignments, and (2) with our curated alignments. In the latter case, we checked the SIFT “median sequence conservation” score and found that only the complete alignments (through Trichoplax) were diverse enough for confident prediction of substitutions that should “affect protein function.” Consequently, these are the alignments that we used with SIFT. For regressions, we used the SIFT predictions of tolerated/affect protein function as a binary predictor. We also used the SIFT score and –log(SIFT + 0.01) as continuous variables.

6. Mutation Assessor (Xvar; http://mutationassessor.org/) [Reva et al., 2011] was used in default online mode. Qualitative functional impact (low/medium/high) was used as a trinary predictor with low set to 0, “high” set to 2, and the value for “medium” optimized; on this scale, the optimum value came out between 1.0 and 1.1. We used the output variable “Functional Impact Score” and ln(Functional Impact Score) as continuous variables.

Regression and Related Analyses

We performed three types of regression and related analyses: least squares regression, ordinal logistic regression, and receiver operating characteristic (ROC) area analysis. Statistical analyses were performed in STATA 11.0 (StataCorp, College Station, Texas, USA). For least squares regressions, the qualitative class of each sequence variant (pathogenic, likely pathogenic, likely not pathogenic, or not pathogenic) was treated as the dependent variable and assigned the minimum value for the threshold probability in favor of pathogenicity from the corresponding quantitative classification system (0.99, 0.95, 0.05, or 0.001, respectively) [Plon et al., 2008]. The scores generated by the in silico tools for each sequence variant were treated as independent variables. For analyses of the performance of individual in silico tools, we then performed least squares regressions on logit(probability in favor of pathogenicity) (logit[Pr]) versus program scores. For analyses of combined outputs from two in silico tools, we performed bivariate least squares regressions on logit(Pr) versus pairs of program scores. We note that using logit(Pr) as the dependent variable constrains the resulting regression equations to produce probabilities between 0.00 and 1.00, a feature normally associated with logistic regression. For ordinal logistic regressions, the qualitative class of each sequence variant was treated as the dependent variable and assigned the ordering pathogenic > likely pathogenic > likely not pathogenic > not pathogenic. Program scores generated were treated as independent variables. For analyses of the performance of individual in silico tools, we then performed ordinal logistic regressions of qualitative class versus program scores. For analyses of combined outputs from two in silico tools, we performed bivariate ordinal logistic regressions on qualitative class versus pairs of program scores. For ROC area under the curve (AUC) analyses, we collapsed the qualitative classifications “pathogenic” and “likely pathogenic”into“pathogenic”andcollapsed“likelynotpathogenic” and “not pathogenic” into “not pathogenic.” For analyses of the performance of individual in silico tools, this binary classification was used as the reference variable and program scores were used as the classification variable. For ROC area analyses of combined outputs from two in silico tools, we used the regression intercept and coefficients calculated for a given pair of tools from the least squares regression to calculate their combined score. The binary classification was then used as the reference variable and the combined program score was used as the classification variable.

A 10-fold cross-validation approach was used to estimate the goodness of fit of the combined models, reported as adjusted R² from bivariate least squares regressions. In each cross-validation cycle, the 74 missense substitutions were randomly split into 10 approximately equal partitions, and each partition was then used for testing the estimated linear regression equation learned from the remaining nine partitions. After all 10 partitions were tested, an adjusted R² between the predicted and observed probabilities of pathogenicity was calculated. This process was repeated independently 1,000 times to obtain the adjusted R² point estimates and 95% confidence intervals (CIs).

Results

Classification of 143 MMR Missense Variants Using a Qualitative Classifier

Of the 143 variants analyzed, 12 were excluded because of the evidence of aberrant splicing. Seventy-four (56.5%) of the remaining missense substitutions could be classified as class 1, 2, 4, or 5, which are clinically actionable. Of these, approximately 85% were easily classified by consensus, and approximately 15% were considered potentially ambiguous, usually because of the existence of discordant data combinations that were not explicitly included in the criteria. The distribution of classifications was: class 1 (n = 20), class 2 (n = 9), class 4 (n = 37), and class 5 (n = 8) (Table 2; Supp. Table S1). The remaining 57 variants remained class 3, uncertain.

Table 2.

Qualitative Classification of 143 Missense Substitutions Evaluated for Use in Calibration of In Silico Tools

Class 1—not pathogenic (n = 20)
MLH1 p.(Ile32Val)
MLH1 p.(Val213Met)
MLH1 p.(Ile219Val)
MLH1 p.(Ile219Leu)
MLH1 p.(Gln689Arg)
MLH1 p.(Val716Met)
MLH1 p.(His718Tyr)
MSH2 p.(Asn127Ser)
MSH2 p.(Gly322Asp)
MSH2 p.(Leu390Phe)
MSH2 p.(Ile735Val)
MSH6 p.(Gly39Glu)
MSH6 p.(Leu396Val)
MSH6 p.(Val878Ala)
MSH6 p.(Ile886Val)
PMS2 p.(Thr277Lys)
PMS2 p.(Pro470Ser)
PMS2 p.(Thr485Lys)
PMS2 p.(Thr597Ser)
PMS2 p.(Met622Ile)

Class 2—Likely not pathogenic (n = 9)
MLH1 p.(Val326Ala)
MLH1 p.(Val384Asp)
MLH1 p.(Ser406Asn)
MLH1 p.(Ile655Val)
MLH1 p.(Lys751Arg)
MSH2 p.(Asp167His)
MSH2 p.(Gln629Arg)
MSH2 p.(Met688Ile)
MSH6 p.(Val509Ala)

Class 3—Uncertain (n = 57)
MLH1 p.(Arg18Cys)
MLH1 p.(Gly22Ala)
MLH1 p.(Glu23Lys)
MLH1 p.(Ala29Ser)
MLH1 p.(Asn38Ser)
MLH1 p.(Glu89Gln)
MLH1 p.(Ser93Gly)
MLH1 p.(Thr117Arg)
MLH1 p.(Lys134Asn)
MLH1 p.(Arg217Cys)
MLH1 p.(Asp304Gly)
MLH1 p.(Arg325Gln)
MLH1 p.(Lys443Gln)
MLH1 p.(Thr452Ser)
MLH1 p.(Val506Ala)
MLH1 p.(Gly532Val)
MLH1 p.(Trp538Gly)
MLH1 p.(Leu549Pro)
MLH1 p.(Pro581Leu)
MLH1 p.(Asp601Gly)
MLH1 p.(Leu607His)
MLH1 p.(Lys618Ala)
MLH1 p.(Lys618Thr)
MLH1 p.(Tyr646Cys)
MLH1 p.(Arg659Gln)
MLH1 p.(Leu729Val)
MLH1 p.(Asp737Val)
MSH2 p.(Ala2Thr)
MSH2 p.(Val3Leu)
MSH2 p.(Phe19Leu)
MSH2 p.(Thr33Pro)
MSH2 p.(Leu93Phe)
MSH2 p.(Arg96His)
MSH2 p.(Tyr103Cys)
MSH2 p.(Arg106Lys)
MSH2 p.(Val163Asp)
MSH2 p.(Leu175Pro)
MSH2 p.(Glu188Gln)
MSH2 p.(Lys246Gln)
MSH2 p.(Lys248Glu)
MSH2 p.(Leu330Pro)
MSH2 p.(Leu341Pro)
MSH2 p.(Val342Ile)
MSH2 p.(Pro349Arg)
MSH2 p.(Phe447Val)
MSH2 p.(Gly548Asp)
MSH2 p.(Asn596Ser)
MSH2 p.(His639Leu)
MSH2 p.(Ile704Val)
MSH2 p.(Ala834Thr)
MSH2 p.(Asn835His)
MSH2 p.(Leu911Arg)
MSH2 p.(Val923Glu)
MSH6 p.(Pro623Ala)
MSH6 p.(Glu983Gln)
PMS2 p.(Arg20Gln)
PMS2 p.(Asn775Ser)

Class 4—Likely pathogenic (n = 37)
MLH1 p.(Pro28Leu)
MLH1 p.(Asp63Glu)
MLH1 p.(Gly67Trp)
MLH1 p.(Gly67Glu)
MLH1 p.(Cys77Arg)
MLH1 p.(Cys77Tyr)
MLH1 p.(Phe80Val)
MLH1 p.(Lys84Glu)
MLH1 p.(Ile107Arg)
MLH1 p.(Leu155Arg)
MLH1 p.(Val185Gly)
MLH1 p.(Gly244Asp)
MLH1 p.(Ser247Pro)
MLH1 p.(Leu550Pro)
MLH1 p.(Asn551Thr)
MLH1 p.(Leu559Arg)
MLH1 p.(Leu582Phe)
MLH1 p.(Ala589Asp)
MLH1 p.(Pro648Ser)
MLH1 p.(Pro648Leu)
MLH1 p.(Pro654Leu)
MLH1 p.(Arg687Trp)
MLH1 p.(Leu749Pro)
MLH1 p.(Arg755Ser)
MSH2 p.(Val161Asp)
MSH2 p.(Gly162Arg)
MSH2 p.(Gly164Arg)
MSH2 p.(Leu173Pro)
MSH2 p.(Leu187Pro)
MSH2 p.(Cys333Tyr)
MSH2 p.(Asp603Asn)
MSH2 p.(Gly692Arg)
MSH2 p.(Cys697Arg)
MSH2 p.(Cys697Phe)
MSH2 p.(Glu749Lys)
MSH2 p.(Gly751Arg)
PMS2 p.(Ser46Ile)

Class 5—Pathogenic (n = 8)
MLH1 p.(Met35Arg)
MLH1 p.(Asn38His)
MLH1 p.(Ser44Phe)
MLH1 p.(Gly67Arg)
MLH1 p.(Thr117Met)
MLH1 p.(Leu622His)
MSH2 p.(Pro622Leu)
MSH2 p.(Ala636Pro)

Splicing Defects (n = 12)
MLH1 p.(Asp41Gly)
MLH1 p.(Arg100Pro)
MLH1 p.(Arg182Gly)
MLH1 p.(Arg265Cys)
MLH1 p.(Ser295Asn)
MLH1 p.(His329Pro)
MLH1 p.(Arg659Leu)
MLH1 p.(Arg659Pro)
MLH1 p.(Glu663Asp)
MSH2 p.(Ala272Val)
MSH2 p.(Ser554Gly)
MSH2 p.(Ser554Asn)

Note: Variant nomenclature was derived from the GenBank reference sequences NM_000249.3 for MLH1, NM_000251.1 for MSH2, NM_000179.2 for MSH6, and NM_000535.5 for PMS2. Nucleotide numbering reflects cDNA numbering with +1 corresponding to the A of the ATG translation initiation codon in the reference sequence, with the initiation codon as codon 1.

In silico Tools

In silico tools were applied as described in the section “Materials and Methods.” In our initial analysis, MutPred, PolyPhen-2, and Xvar were used as trained in their standard online form. These programs plus SIFT were used with their internally generated protein alignments and all six programs were used under essentially default conditions. All single programs performed fairly well. Most produced least squares regression adjusted R² values >0.45 and P values <10^–10 (Table 3). The AUC of the ROC for all methods was >0.80 (data not shown). In these initial analyses, the two best performing in silico tools from this analysis were MutPred and PolyPhen-2. We explored whether evaluating output as a continuous rather than a binary or trinary function would affect results. The continuous variable approach yielded better correlation and lower P values for the three programs where it was possible to compare continuous output using least squares regression (Table 3) to binary output using ordinal logistic regression (data not shown). The correlation and P values differed little between continuous and trinary output (likely deleterious, intermediate, likely neutral) for the two programs where it was possible to compare least squares regression (Table 3) to trinary output using ordinal logistic regression (data not shown).

Table 3.

Least Squares Regression Results from Individual Analysis Programs Run under Essentially Default Conditions

	Binary classification		Trinary classification		Continuous variable
Analysis program	Adjusted R2	P value	Adjusted R2	P value	Adjusted R2	P value
MutPreda	0.550	2.39 × 10−14	N/A	N/A	0.600	3.41 × 10−16
PolyPhen2.1a	0.464	1.45 × 10−11	0.577	2.60 × 10−15	0.591	7.60 × 10−16
MAPPb	N/A	N/A	N/A	N/A	0.586	1.15 × 10−15
Align-GVGDc	N/A	N/A	N/A	N/A	0.452	3.35 × 10−11
Xvara	N/A	N/A	0.465	1.39 × 10−11	0.449	4.01 × 10−11
SIFTa	0.356	1.19 × 10−8	N/A	N/A	0.420	2.53 × 10−10

^aOnline, default running conditions.

^bHand-curated alignment through star anemone, using ln(MAPP score) as a continuous variable.

^cHand-curated alignment through sea urchin, using the default 7 grades.

N/A, not applicable.

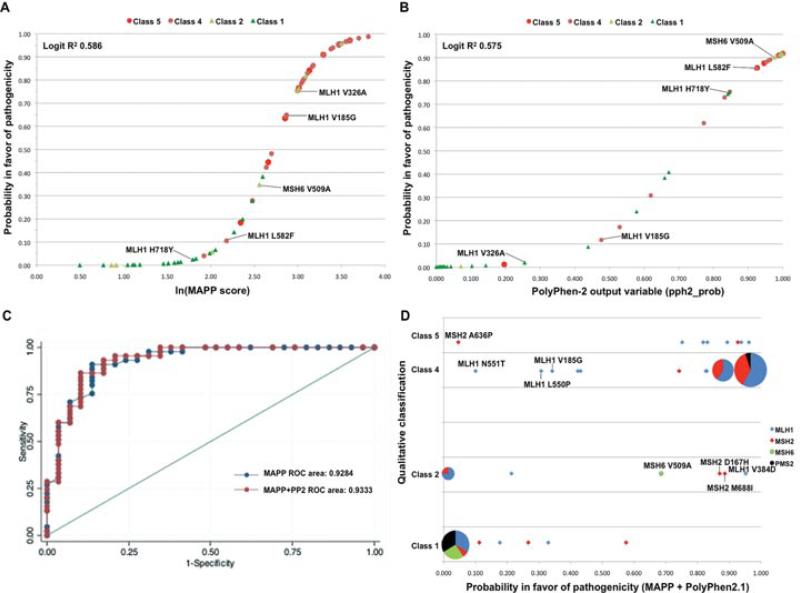
Because the MutPred and PolyPhen-2.1 training data included MMR gene missense substitutions that overlapped with our qualitatively classified set of substitutions, we conducted a second round of analyses in which MutPred and PolyPhen-2.1 were retrained with datasets that excluded all MMR gene missense substitutions. The multiple sequence alignments produced by PolyPhen-2.1 were also lightly curated, and SIFT was rerun using the same set of highly cu-rated alignments that were used with Align-GVGD and MAPP. All six in silico tools output a continuous variable that was appropriate for our analyses, so this second round of analyses focused on continuous variable outputs. Results, which we consider to have been produced under analytically appropriate conditions for each of the in silico tools tested, are summarized in Table 4. The performance of SIFT improved using the curated alignments (least squares regression R² increased from 0.420 to 0.541), there was a very slight degradation in the performance of PolyPhen-2.1 (R² decreased from 0.591 to 0.575) and there was a more notable decrease in MutPred's performance (R² decreased from 0.600 to 0.396). In this analysis, the program rankings obtained after least squares regression and after ordinal logistic regression were identical, and there was only one difference in the ordering obtained from the ROC area analysis. The best result was obtained for MAPP, with R² > 0.58 and AUC > 0.92; these results were only very slightly stronger than those obtained for PolyPhen-2.1 (Table 4). The distributions of the set of 74 missense variants on the sigmoid curves generated from the least squares regression equations for MAPP and PolyPhen-2.1 are shown in Figure 1A and B.

Table 4.

Results from Individual Analysis Programs Run Under Analytically Appropriate Conditions

	Logit regression		Ordered logistic regression
Analysis program	Adjusted R2	P value	Pseudo R2	P value	ROC area
MAPPa	0.586	1.15 × 10−15	0.253	2.26 × 10−11	0.928
PolyPhen-2.1b	0.575	3.15 × 10−15	0.250	2.83 × 10−11	0.925
SIFTc	0.541	5.07 × 10−14	0.250	2.76 × 10−11	0.878
Align-GVGDd	0.505	7.73 × 10−13	0.222	2.61 × 10−10	0.912
Xvare	0.449	4.01 × 10−11	0.191	5.83 × 10−9	0.872
MutPredf	0.396	1.12 × 10−9	0.163	7.78 × 10−8	0.867

^aHand-curated alignment through star anemone, using ln(MAPP score) as a continuous variable.

^bTrained excluding MMR genes, with lightly curated PolyPhen-generated alignments, using “probability pph2” as a continuous variable.

^cHand-curated alignment through Trichoplax, using -log(SIFT score +0.01) as a continuous variable.

^dHand-curated alignment through sea urchin, using 8 grades.

^eRun under default conditions using “Functional Impact Score” as a continuous variable.

^fTrained excluding MMR genes, using the “probability of a deleterious substitution” as a continuous variable.

Figure 1.

A: Distribution of the set of 74 class 1–2–4–5 missense variants on a sigmoid curve for MAPP outputs derived using the logit regression calibration equation—Logit(Pr) = −10.84 + 3.99(ln[MAPP score]), where Pr is the probability in favor of pathogenicity. The classifications of the variants are identified by colored symbols (defined in the legend). B: Sigmoid curve showing the outputs of the 74 missense variants from PolyPhen-2.1 using the logit regression calibration equation—Logit(Pr) = −6.04 + 8.45(pph2_prob). The missense variants with the largest differences (Δ) in probability of pathogenicity derived from MAPP versus PolyPhen-2.1 are identified in (A) and (B): MLH1 V185G (Δ = 0.528), MLH1 V326A (Δ = 0.733), MLH1 L582F (Δ = 0.748), MLH1 H718Y (Δ = 0.719), and MSH6 V509A (Δ = 0.553). C: Receiver operating characteristic (ROC) curves for MAPP and combined MAPP + PolyPhen-2.1 accuracy, using probabilities and scores associated with each program. D: Scatter diagram comparing the qualitatively assigned probability in favor of pathogenicity (class 1—not pathogenic, class 2—likely not pathogenic, class 4—likely pathogenic, and class 5—pathogenic) with the probability of pathogenicity as a continuous variable calculated from the MAPP + PolyPhen-2.1 outputs. The pie graphs are proportional representations of overlapping variants in the four mismatch repair genes (MLH1—blue, MSH2—red, MSH6—green, and PMS2—black). The variants with in silico scores predicting <0.40 probability of pathogenicity that were qualitatively classified as class 4 and class 5 are identified, as were variants that had in silico scores predicting >0.60 probability of pathogenicity with qualitative classifications of class 1 and class 2.

Under the conditions used to compare these six in silico tools, their outputs were highly correlated (Table 5). The strongest correlation was between PolyPhen-2.1 and SIFT (R² = 0.92). Seven of 15 pairs had R² ≥ 0.80. The weakest correlation was between Align-GVGD and MutPred (R² = 0.61). Using bivariate regressions, we then explored the consequence of combining the output from each of the three better performing in silico tools with the output of each of the other tools. By the criterion that both programs make a significant contribution to the least squares regression bivariate model, five pairs of programs gave stronger results than either member of the pair alone. In order of adjusted R², these were: MAPP + PolyPhen-2.1, Polyphen-2.1 + Align-GVGD, PolyPhen-2.1 + MutPred, SIFT + Align-GVGD, and SIFT + MutPred (Table 6). With the addition of the criteria that both programs also make a significant contribution to the bivariate ordinal logistic regression and increase the ROC area over that achieved by either program alone, only the combination MAPP + PolyPhen-2.1 outperformed its individual components. Backward selection arrived at the same result. Starting with all six in silico tools in a single model, removing the tool that made the weakest contribution to the combined model, and then repeating the process with five-tool, four-tool, and three-tool models, the order in which tools dropped out was: SIFT, Xvar, Align-GVGD, and MutPred. There were no models combining three or more in silico tools in which all of the tools made a significant contribution. The order in which the in silico tools dropped out was the same under least squares regression and ordinal logistic regression. Therefore, MAPP + PolyPhen-2.1 appears to be the best combination. This pair achieved an adjusted least squares regression R² of 0.62 (bootstrap 95% CI 0.46–0.80) and an ordinal logistic regression pseudo R² of 0.28 (bootstrap 95% CI 0.16–0.41). The ROC AUC (Fig. 1C) was 0.933 (95% CI 0.87–0.99). The lower bound of the 95% CIs for adjusted R², pseudo R², and AUC includes the performance point estimates from four of the individual algorithms and all of the pairs tested, but provides evidence against the argument that the two weaker in silico tools are actually equivalently effective predictors under the conditions used. To assess whether we have overestimated model performance, we used a cross-validation approach to reesti-mate adjusted R² for the bivariate least squares regression models. The cross-validation R² were only slightly decreased, by 0.03 to 0.04, from the directly estimated R² (Table 6).

Table 5.

Pairwise Correlation Matrix

	PP2.1a	SIFT	A-GVGDb	Xvar	MutPred
MAPP	0.86	0.89	0.82	0.78	0.69
PolyPhen-2.1		0.92	0.80	0.86	0.67
SIFT			0.79	0.84	0.67
Align-GVGD				0.73	0.61
Xvar					0.75

Computational tool use conditions are as in Table 4.

^aPP2.1 is PolyPhen-2.1.

^bA-GVGD is Align-GVGD.

Table 6.

Results from Regressions Using Pairs of Programs

Program combination		Least squares regression				Ordered logistic regression
First programa	Second programa	Adjusted R2(b)	Adjusted R2(c)	First program P value	Second program P value	Model P value	Pseudo R2	First program P value	Second program P value	Model P value	ROC aread
MAPP	PolyPhen-2.1	0.620	0.585	0.003	0.009	4.67 × 10−16	0.2753	0.038	0.048	2.57 × 10−11	0.933
MAPP	SIFT	0.595	0.553	0.002	0.116	4.30 × 10−15	0.2679	0.080	0.108	4.95 × 10−11
MAPP	Align-GVGD	0.603	0.570	<0.001	0.051	2.23 × 10−15	0.2665	0.009	0.119	5.63 × 10−11
MAPP	Xvar	0.595	0.562	<0.001	0.112	4.20 × 10−15	0.2622	0.001	0.194	8.19 × 10−11
MAPP	MutPred	0.602	0.566	<0.001	0.056	2.37 × 10−15	0.2656	<0.001	0.122	6.07 × 10−11
PolyPhen-2.1	SIFT	0.578	0.537	0.009	0.226	1.91 × 10−14	0.2635	0.123	0.132	7.34 × 10−11
PolyPhen-2.1	Align-GVGD	0.599	0.561	<0.001	0.024	3.07 × 10−15	0.2686	0.006	0.073	4.66 × 10−11	0.922
PolyPhen-2.1	Xvar	0.571	0.534	<0.001	0.598	3.47 × 10−14	0.2515	0.002	0.610	2.12 × 10−10
PolyPhen-2.1	MutPred	0.598	0.564	<0.001	0.026	3.31 × 10−15	0.2674	<0.001	0.078	5.17 × 10−11	0.923
SIFT	Align-GVGD	0.580	0.541	<0.001	0.007	1.53 × 10−14	0.2692	0.007	0.072	4.43 × 10−11	0.912
SIFT	Xvar	0.544	0.505	<0.001	0.238	3.00 × 10−13	0.2529	0.002	0.496	1.87 × 10−10
SIFT	MutPred	0.570	0.531	<0.001	0.018	3.62 × 10−14	0.2649	<0.001	0.103	6.45 × 10−11	0.914

^aComputational tool operating conditions were as defined in Table 4.

^bAdjusted R² directly from least squares regression.

^cAdjusted R² directly from cross-validation.

^dROC area calculated after application of the equation defined by the logit regression. Note that ROC area was only calculated for the combined computational tools where both tools contributed P < 0.05 to the least squares regression (in bold).

The least squares regression equation determined for the combination MAPP + PolyPhen-2.1 was: logit(Pr) = –9.20 + 2.27(ln[MAPP score]) + 4.26(“pph2_prob” output from retrained PolyPhen-2.1). The 95% CIs on the intercept, MAPP coefficient, and PolyPhen-2.1 coefficient were (–11.61 to –6.79), (0.80–3.75), and (1.11–7.41), respectively. Figure 1D shows the scatter plot of results comparing qualitatively assigned probability in favor of pathogenicity versus probability of pathogenicity as a continuous variable calculated from the MAPP + PolyPhen-2.1 output. Of the set of 74 variants, there were six class 4/5 variants with <50% prior probability of pathogenicity, and five class 1/2 variants with >50% probability of pathogenicity. No major patterns were noted among the 11 discordant predictions; however, two of the MLH1 pathogenic variants that were predicted to have <50% likelihood of pathogenicity were in adjacent codons within the interaction domain. In addition, there was existing in vitro evidence suggesting partial loss of MMR function or protein binding for three of the five variants considered “likely not pathogenic” (see Fig. 1D and Supp. Table S1). These three variants were classified on the basis of allele frequency in a control population, overriding functional assay results as per criteria stated in Table 1.

Results from the MAPP + PolyPhen-2.1 prior probability database/calculator are available through: http://hci-lovd.hci.utah.edu/. For the 57 variants that were assigned Class 3, 25% had in silico scores predicting >90% probability of pathogenicity, and 30% predicting >10% probability of pathogenicity (see Supp. Table S2).

Discussion

In several areas in cancer genetics, multiple data types are combined to assess the effects of genetic variants. Quantifying data types and applying integrated Bayesian analysis appears to be a robust approach to classifying variants [Arnold et al., 2009; Easton et al., 2007; Goldgar et al., 2004; Miller et al., 2011]. An important principle of classification, using this method, is that at least two different sources of data should be used for variant classification [Plon et al., 2008]. One approach to calibration of the individual components of the integrated evaluation of MMR gene unclassified missense substitutions would be to begin from a large series of securely classified missense substitutions. Ideally, these would be classified on the combined basis of segregation data (to show that the allele is associated with the syndrome) and functional assay data (to show that the identified variant, rather than a linked but unobserved variant, damages protein function) as a gold standard. However, because extensive segregation data on individual missense substitutions are scarce and functional assay data are often conflicting, very few MMR missense substitutions can actually be classified on this basis.

As an alternative first step, in silico tools can provide preliminary evidence on the effects of all missense variants. To develop this approach for clinical use in statistical variant classification models, we have qualitatively classified a set of MMR gene missense substitutions that were not preselected for IHC, MSI, or other clinicopathologic features, and then used class 1, 2, 4, and 5 variants to calibrate the output from a number of in silico missense substitution analysis tools as a probability in favor of pathogenicity. The performance of all classifiers that we tested was generally good, with 95% CIs overlapping considerably for many of them. Although we rank our preferences for the various methods, our study solidifies the concept that properly applied in silico methods carry sufficient power to be used clinically in models for variant classification. As an indication of the internal consistency of our study, it is encouraging that MAPP performed best in all regression and AUC of the ROC analyses, and that PolyPhen-2.1 functioned almost as well.

Three noteworthy factors emerged from our analyses of the individual in silico tools:

1. The importance of excluding MMR gene variants from a training set used to train the in silico tool. The generally accessible online versions of MutPred, PolyPhen-2, and Xvar were trained using data sets that included MMR variants. To eliminate overlap between training and calibration sets and thereby reduce the possibility of overfitting during our calibration exercise, the two more promising methods (MutPred and PolyPhen-2) were retrained by omitting all MMR variants from their training set. This resulted in significant degradation of performance for MutPred, but only a very small decrease for PolyPhen-2.1. This result calls into question a number of missense substitution in silico tool performance studies (e.g., Thusberg et al., 2011) reported over the last several years, in which variants in the gene of interest were part of the training set. Therefore, it is very important that this process is repeated for genes included in previous studies to investigate whether there is a similar degradation in program performance.

2. The performance of the in silico tools is sometimes influenced by the multiple sequence alignment with which they are run. All of the in silico tools except for Align-GVGD and MAPP have internally generated libraries of alignments. SIFT is unique in that it also gives users the option to supply their own alignment. In agreement with previous observations [Chan et al., 2007; Hicks et al., 2011], we found that SIFT performed markedly better with our hand-curated alignments than with its native alignments. PolyPhen-2.1 was run using two sets of alignments: native PolyPhen-2, and lightly hand-curated versions omitting grossly discordant sequences in conserved areas that were probably artifacts of either gene model assembly from genomic sequence or the automated alignment generating programs. Modest curation of the PolyPhen-2 alignment led to only modest changes in the results. Align-GVGD and MAPP were run with hand-curated alignments prepared at three different phylogenetic depths. Modest changes in depth of alignment produced only modest changes in performance.

3. Using in silico tool output as a continuous variable. Although, many methods generate data on a continuous scale, most algorithms apply a binary “cutoff point” and report results as likely pathogenic or likely not. The continuous output from our analysis showed that the predictive value for many variants was well over 90% and for other variants was between 25% and 75%. This degree of variation would be diluted if the output were categorized. We showed that considering data as a continuous variable provides better correlation with classification than does the binary output. There was no evidence for a difference in the utility of using the output as a trinary variable, but fitting trinary variables for each of the in silico tools would involve considerable multiple testing and increase risk of over-fitting. We encourage the use of continuous variable outputs for all results included in classification tools, to avoid the artificial dichotomy of binary categorization that may disregard useful subtleties in data, particularly for variants that are difficult to categorize using any individual tool. In the overall flow of the Bayesian integrated evaluation, the only point where we absolutely need to collapse from continuous variables to a limited set of qualitative classes is at the very end, when the output (posterior probability in favor of pathogenicity) is interpreted through the clinical five-class system described by Plon et al. (2008).

Many studies report the predicted effect of MMR gene missense substitutions on protein function determined from in silico tools, most commonly SIFT and PolyPhen. Those relevant to this study are discussed below. Chao et al. (2008) classified a set of MMR gene missense variants based on less rigorous clinical criteria than those incorporated in our qualitative classifier, and then used these classified variants to compare the accuracy of three in silico tools: MAPP, PolyPhen, and SIFT. As in this study, MAPP was the best performing in silico tool [for Chao et al., 2008]; however, it should be noted that use of the multiple sequence alignments with MAPP in the Chao et al. (2008) study was manipulated by varying the gap weight threshold across the alignments. Nonetheless, we note that the MAPP-MMR AUC of the ROC value reported by Chao et al. (2008) (0.945) was very near our point estimate and well within the 95% CI for our MAPP ROC value. Thus in a research area not noted for between-study consistency, the close correspondence between results obtained with MAPP in these two studies stands out as a welcome exception. On the contrary, both SIFT and PolyPhen performed somewhat better in our study than they had in Chao et al. (2008). For SIFT, we attribute the difference to our use of hand-curated alignments and use of the SIFT score as a continuous variable rather than as a binary classifier. For PolyPhen, there have been notable algorithm improvements in the intervening years, and these may account for the difference.

Ali et al. (2012) have recently published on a consensus-based predictor called PON-MMR that combines five in silico programs to derive a probability that a missense substitution will show loss of function in a functional assay. Although PON-MMR has a higher sensitivity (0.97) compared with the MAPP + PolyPhen-2.1 (0.933), we note some limitations of this study. Classification of the MMR variant calibration set was based on functional data alone, and the relationship between functional abrogation and pathogenicity as defined by clinical phenotype was not calibrated. The probability that a substitution will show dysfunction in a functional assay is a proxy for, rather than a direct measure of, the probability in favor of pathogenicity in humans. Furthermore, there is a risk that the model is overfit because there was no clean separation between the in silico program training sets and the sequence variant calibration set. We have seen evidence that this can be very important in the results of our own study. Additionally, the contribution of the in silico programs to the PON-MMR output was not addressed, which could also cause further overfitting. These concerns are explicitly addressed in the model we present here.

Two studies, Barnetson et al. (2008) and Pastrello et al. (2011), addressed classification of MMR variants by integrating in silico predictions with other lines of evidence. Barnetson et al. (2008) devised an arbitrary scoring system for variant classification that included SIFT and PolyPhen assessments as points of evidence, but there was no attempt to calibrate the in silico predictions per se. Pastrello et al. (2011) described a Bayesian approach to MMR missense variant classification that included a LR for missense substitutions based on in silico predictions using the tool Align-GVGD. However, the LRs assigned for MMR substitutions were actually based on those derived empirically for missense substitutions in BRCA1 and BRCA2 [Tavtigian et al., 2008a]. Because the LRs or probabilities associated with the individual grades generated by Align-GVGD depend on the depth of alignment and because the program's accuracy can degrade badly if it is not used with carefully curated alignments [Hicks et al., 2011; Tavtigian et al., 2008c], the approach taken by Pastrello et al. (2011) was suboptimal.

Here, we have advanced the field by combining (1) a set of reference variants that have been classified using carefully considered criteria vetted in the MMR variant community with (2) rigorously controlled analytic conditions for computational methods. We anticipate that a similar strategy applied to in vitro functional as-says (MMR and other) would similarly advance the field of variant classification. The probabilities in favor of pathogenicity that we have derived can be used as a prior probability of pathogenicity to feed into a multifactorial likelihood model for quantitative integrated evaluation of unclassified variants. However, we note that the clinical recommendations of the thresholds for “likely pathogenic” and “likely not pathogenic” are posterior probabilities in favor of pathogenicity of 0.95 and 0.05, respectively [Plon et al., 2008]. The MAPP + PolyPhen-2.1 output is able to produce prior probabilities that are more extreme than these thresholds. Because we view direct classification on the basis of the prior probability alone as a misuse of the Bayesian integrated evaluation model, we choose to truncate the dynamic range of the prior probability database/calculator to a maximum of 0.90 and a minimum of 0.10 so that additional sources of information are required to reach posterior probabilities that alter clinical management of patients with variants. The successful application of this method for classification of MMR gene variants in an integrated evaluation model that incorporates segregation and tumor pathology information is described in the accompanying manuscript humu-2012-0145.R1_001–010. Similarly, initial application of our in silico tool to the 57 class 3 variants in our study suggests that approximately 50% could be classified using Bayesian integrated analysis with additional supporting information of moderate strength from only one other data source.

There are several caveats to our findings. Clear discordance between prior probabilities and qualitative classifications for a minority of variants indicates that the in silico modeling does not adequately capture all alterations in protein function. In addition, the in silico tools assessed do not account for missense substitutions where the underlying sequence variant causes a splicing aberration. Important statistical caveats to the calibration equation must also be considered. First, the least squares regressions using logit(Pr) as the dependent variable, which constrains the resulting probabilities to fall between 0.00 and 1.00, assumes the probabilities assigned to the groups of variants in each of the four qualitative categories are reasonably accurate. The investigators who helped devise the qualitative classification were explicitly aware of the quantitative probability thresholds set for those categories in Plon et al. (2008) and genuinely attempted to craft the qualitative categories to correspond with the quantitative categories. But significant error, especially in the two extreme categories class 5 (pathogenic) and class 1 (not pathogenic), would alter the calibration. The main alternative would have been to use the ordered logistic regressions to generate the calibration, but two less obvious assumptions would have been required here. The first is the proportional odds assumption that underlies ordinal logistic regression, which is that the coefficients describing the relationship between the lowest versus all higher categories of the dependent variable are the same as those that describe the relationship between the next lowest category and all higher categories, and so on. The second is that converting the resulting calibration from LRs to probabilities assumes an underlying overall prior probability for the dataset. We prefer the least squares regression because the underlying assumptions are more transparent. Nonetheless, it is reassuring that least squares regression and ordered logistic regression gave the same ranking of the individual in silico tools, and that the combination of MAPP + PolyPhen-2.1 emerged as the best pair using either forward selection or backward selection with either regression method.

Finally, we specifically envision that the process of calibration will be iterative. When a similarly sized independent series of mis-sense substitutions have been classified qualitatively with reasonable certainty (e.g., through the efforts of the InSiGHT Mutation Interpretation Committee [Kohonen-Corish et al., 2011]), we will analyze those variants using the models presented here for replication and refinement of the in silico missense prior probabilities of pathogenicity. With the results of this work, all missense variants can now be assigned a prior probability, using in silico tools. Thus, any variants where another single source of reliable data exists (e.g., segregation, tumor histologic features) can now be assigned a posterior probability, and thus lead to significant improvement in variant classification.