Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2015 Mar 1.
Published in final edited form as: J Learn Disabil. 2014 Aug 5;48(2):115–119. doi: 10.1177/0022219414544544

Reconsidering the Simple View of Reading in an Intriguing Case of Equivalent Models: Commentary on Tunmer and Chapman (2012)

Richard K Wagner 1, Sarah K Herrera 1, Mercedes Spencer 1, Jamie M Quinn 1
PMCID: PMC4318790  NIHMSID: NIHMS621985  PMID: 25095787

Abstract

Recently, Tunmer and Chapman (2012) provided an alternative model of how decoding and listening comprehension affect reading comprehension that challenges the simple view of reading. They questioned the simple view’s fundamental assumption that oral language comprehension and decoding make independent contributions to reading comprehension by arguing that one component of oral language comprehension (vocabulary) affects decoding. They reported results from hierarchical regression analyses, exploratory factor analysis, and structural equation modeling to justify their conclusion. Their structural equation modeling results provided the strongest and most direct test of their alternative view. However, they incorrectly specified their simple view model. When correctly specified, the simple view of reading model and an alternative model in which listening comprehension affects decoding provide identically good fits to the data. This results from the fact that they are equivalent models. Although Tunmer and Chapman’s results do not support their assertion that a model in which oral language comprehension affects decoding provides a better fit to their data, the presence of equivalent models provides an ironic twist: The mountain of evidence that supports the simple view of reading provides equivalent support to their alternative interpretation. Additional studies are needed to differentiate these two theoretical accounts.

According to the simple view of reading, how well you comprehend a passage is the product of skill at word recognition and skill at oral language comprehension (Gough & Tunmer, 1986; Hoover & Gough, 1990). This simple yet powerful framework has served to generate considerable research over the years, the thrust of much of it being (a) whether the two key constructs of word recognition and oral language comprehension are sufficient to account for reading comprehension or whether additional constructs are required; (b) whether the constructs affect reading comprehension additively, interactively, or both; and (c) how best to conceptualize and assess word recognition and oral language comprehension (Catts, Adlof, & Weismer, 2006; Georgiou, Das, & Hayward, 2009; Gough, Hoover, & Peterson, 1996; Gustafson, Samuelsson, Johansson, & Wallman, 2013; Kendeou, Papadopoulos, & Kotzapoulou, 2013; Kendeou, Savage, & Van den Broek, 2009; Kershaw & Schatschneider, 2012; Kirby & Savage, 2008; Ouellette & Beers, 2010; Protopapas, Simos, Sideridis, & Mouzaki, 2012; Silverman, Speece, Harring, & Ritchey, 2013; Stuart, Stainthorp, & Snowling, 2008; Tilstra, McMaster, Van den Broek, Kendeou, & Rapp, 2009; Tunmer & Chapman, 2012).

Recently, Tunmer and Chapman (2012) provided an alternative account of relations among decoding, listening comprehension, and reading comprehension that refutes the simple view (see Note 1). They challenged the fundamental assumption that oral language comprehension and decoding make independent contributions to reading comprehension by arguing that one component of oral language comprehension (vocabulary) affects decoding. Using data obtained from a sample of 122 7-year-olds, they used three types of analyses (hierarchical regression, exploratory factor analysis, and structural equation modeling) to justify their assertion.

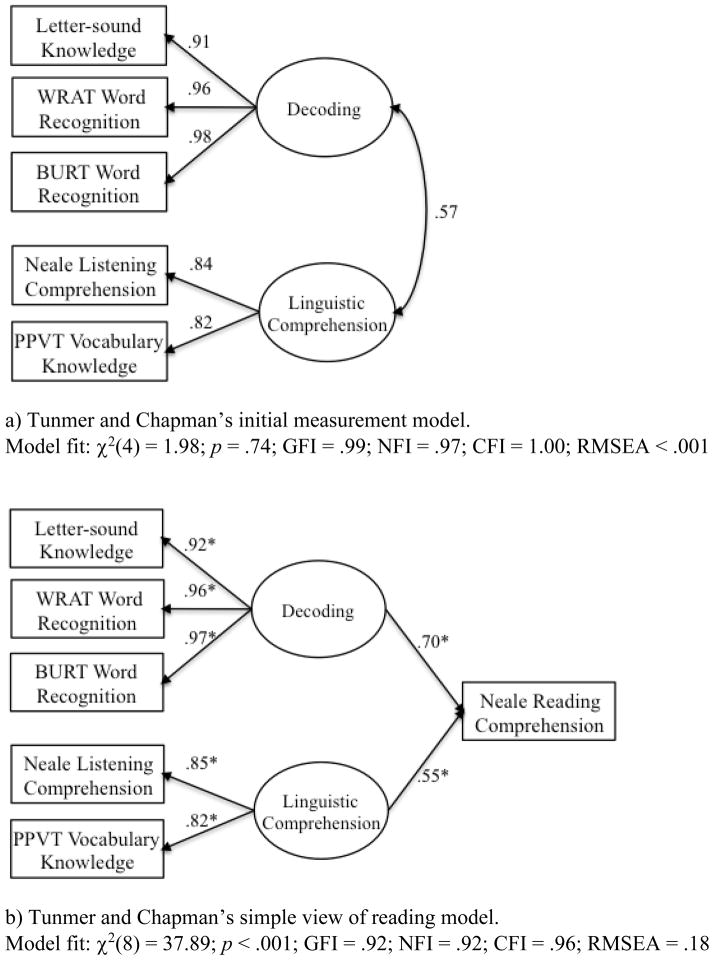
We focus on their structural equation modeling results because they provide the most direct and strongest test of their hypothesis. The models they tested also provide a helpful way to visualize how their proposed model differs from the simple view. They began by testing a measurement model to establish that the two latent constructs of decoding and linguistic comprehension (i.e., their version of an oral language comprehension construct) were well represented by the observed indicators of letter-sound knowledge and two measures of word recognition (for decoding) and listening comprehension and vocabulary knowledge (for linguistic comprehension). This model (Figure 1a) provided an excellent fit to the data. Testing the fit of a measurement model is an important first step because the results rule out measurement problems as the source of poor fit in subsequent models.

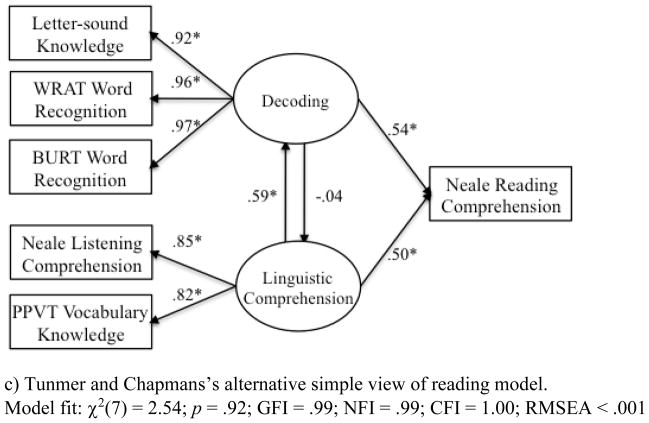
Figure 1.

Figure 1

Figure 1

Open in a new tab

Three models reported by Tunmer and Chapman (2012), including (a) an initial measurement model of decoding and linguistic comprehension, (b) the simple view of reading, and (c) a modified simple view of reading. Note. χ2 = Chi-square; GFI = Goodness of fit index; NFI = Normed fit index; CFI = Comparative fit index; RMSEA = Root mean square error of approximation.

Next, Tunmer and Chapman tested a structural equation model that represented the simple view of reading. This model (Figure 1b) provided a relatively poor fit to the data. Finally, they tested their alternative model that differed from the simple view by allowing linguistic comprehension to directly affect decoding and decoding to directly affect linguistic comprehension. These added direct effects are represented by the two single headed arrows between decoding and linguistic comprehension in Figure 1c. Their alternative model provided an excellent fit to the data. Only the direct path from linguistic comprehension to decoding (.59) was significant, supporting their claim that linguistic comprehension affects decoding.

One of us (Wagner) teaches courses on structural equation modeling and is on the lookout for articles such as these to have students read and analyze. The substantive problem is important and easy to convey. The models are relatively simple and can be used for basic exercises such as counting up the number of parameters to be estimated, determining the number of independent pieces of data that are provided by the covariance matrix, and verifying that the difference between the number of parameters to be estimated and the number of independent pieces of data in the covariance matrix equals the degrees of freedom for the χ2 test of model fit. We mention this context because the task of preparing some course exercises based on the models Tunmer and Chapman reported led us to recognize some facts that challenge their account of the results.

We initially were puzzled by the relatively poor fit of the simple view model relative to that of the initial measurement model. The only obvious differences between the two models are that the simple view model has decoding added and single-headed arrows were added from both decoding and linguistic comprehension to reading comprehension. Because reading comprehension was modeled as an observed variable as opposed to a latent variable (note the rectangle rather than oval in Figure 1b), adding the construct of reading comprehension as an observed variable could not have reduced model fit as could have been the case had reading comprehension been modeled as a latent variable that was poorly specified by its indicators. The inclusion of single-headed arrows from both decoding and linguistic comprehension to reading comprehension should also not have contributed substantially to a decrement in model fit because all paths are included (i.e., a fully saturated structural model). This is directly analogous to multiple regression. We do not need to worry about model fit when we do multiple regression because there are as many independent pieces of information in the correlation matrix as there are parameters to be estimated in a fully saturated structural model.

We discovered the source of the poor fit for their simple view model when we tried to create an assignment that would have required students verify the degrees of freedom for the χ2 test of model fit. We counted 14 parameters to be estimated, 21 independent pieces of information in the covariance matrix, and 7 degrees of freedom (the difference between 21 and 14) for the χ2 test of model fit (see Note 2). In contrast, Tunmer and Chapman reported 8 degrees of freedom.

The reason for the disparity in degrees of freedom and for the surprisingly poor fit of their simple view model is that Tunmer and Chapman left out a required covariance between the two latent variables of decoding and linguistic comprehension. In their model, decoding and linguistic comprehension are known as exogenous variables. By convention, exogenous variables are allowed to co-vary with one another. If you look at any SEM model with more than one exogenous variable, there will be double-headed arrows connecting them. This allows their covariance to be estimated. Exogenous variables presumably are related because they are jointly affected by constructs that are outside the scope of a given model. In the present case, decoding and linguistic comprehension are likely to be correlated because they both are affected by general language ability, socioeconomic status, or any number of factors. If the covariance is left out inadvertently, a restrictive constraint is added to the model that will almost always degrade model fit: The covariance (and correlation if the variables are standardized) between the exogenous variables is forced to be exactly 0 (see Note 3).

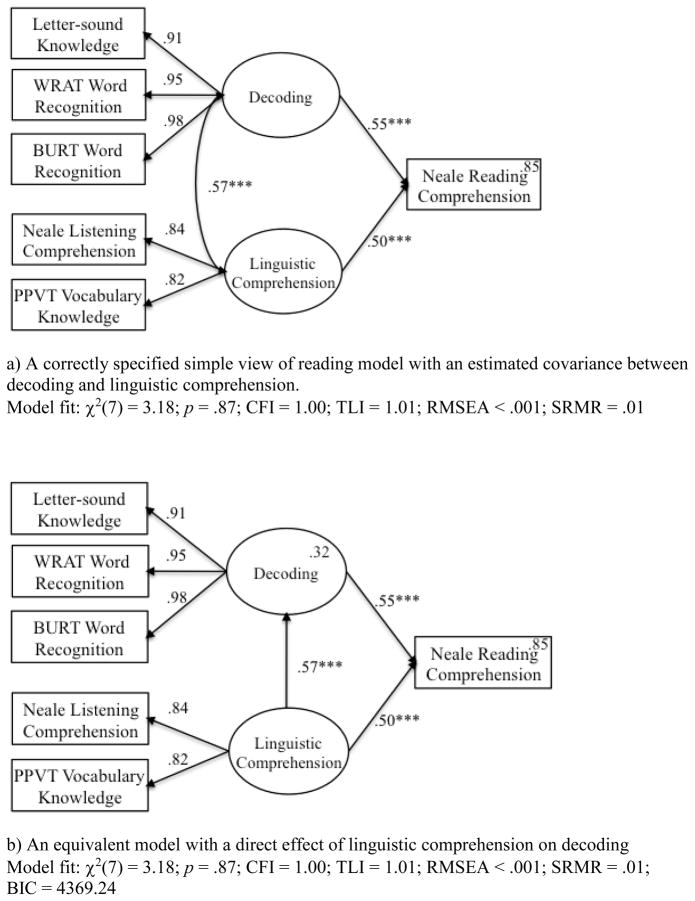
We reran their simple view model after including the missing covariance. This model (Figure 2a) provided an excellent fit to the data. Note that the correlation between decoding and listening comprehension of .57 is identical to what Tunmer and Chapman reported in their initial measurement model CFA. Intriguingly, it is remarkably close to the direct effect of .59 they reported from linguistic comprehension to decoding in their alternative model.

Figure 2.

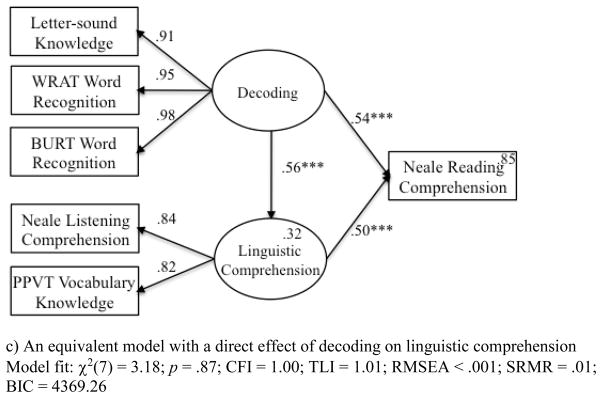
Figure 2

Figure 2

Open in a new tab

Three structural equation models of (a) a correctly specified simple view of reading model with an estimated covariance between decoding and linguistic comprehension, (b) an equivalent model with a direct effect of linguistic comprehension on decoding, and (c) an equivalent model with a direct effect of decoding on linguistic comprehension.

When models are fully saturated, meaning that all constructs in a model are connected by single or double-headed arrows, the problem of the existence of equivalent models is common (Lee & Hershberger, 1990; MacCallum, Wegener, Uchino, & Fabrigar, 1993; Stelzl, 1986). Equivalent models typically appear to be very different but in fact produce identical implied covariance matrices and consequently identical model fit statistics (Hershberger, 2006; Lee & Hershberger, 1990; Raykov & Marcoulides, 2001) (see Note 4). The only ways to distinguish equivalent models are by compelling theoretical frameworks or by using longitudinal designs that rule out equivalent models in which a variable at a subsequent time is specified as a cause of a variable at a preceding time-point.

Returning to the present case, it turns out that a correctly specified simple-view model (Figure 2a) is equivalent to a model that replaces the covariance with a direct effect from linguistic comprehension to decoding (Figure 2b), and these models are both equivalent to a model that replaces the covariance with a direct effect from decoding to linguistic comprehension (Figure 2c). Note that these three models provide identical estimates within rounding error of the respective covariance or direct effects between decoding and linguistic comprehension, and they also provide identical model fits.

The obvious conclusion to draw is that Tunmer and Chapman’s results do not support their assertion that a model with a direct effect from linguistic comprehension to decoding provides a better fit to their data than does the simple view model (see Note 5). A less obvious and more intriguing conclusion arises when we recognize that the simple view model and a model that specifies a direct effect of linguistic comprehension on decoding are equivalent models. As a result, the mountain of evidence that purportedly supports the simple view of reading model provides equivalent support to Tunmer and Chapman’s alterative view that linguistic comprehension affects decoding. If we assert that both models are motivated by reasonable theoretical rationales, more sophisticated designs including both longitudinal developmental studies and intervention studies will be required to differentiate them.

Acknowledgments

This research was supported by Grant P50 HD052120 from the Eunice Kennedy Shriver National Institute for Child Health and Human Development, and by Grants R305F100027 and R305F10005 from the Institute of Education Sciences.

Footnotes

Note 1

What makes this challenge even more remarkable and worthy of notice is that the lead author is the same individual who with Gough is credited with giving us the simple view (Gough & Tunmer, 1986).

Note 2

The 14 parameters to be estimated include 5 error variances for the indicators of the two latent constructs, 5 loadings (estimating all loadings requires fixing the variances of the two latent variables so they are not estimated), 1 covariance between the latent variables, 2 structure coefficients between the two latent variables and reading comprehension, and 1 disturbance for reading comprehension that represents variance in reading comprehension not accounted for by the two latent variable predictors. The 21 independent pieces of information in the covariance matrix include the 6 variances on the diagonal and the 15 non-redundant off-diagonal covariances. A handy way to determine the number of independent pieces of information in a covariance matrix is to multiply the number of observed variables times the number of observed variables plus 1, and divide the product by 2. Some SEM programs also estimate mean structures by default, a fact we can ignore for present purposes because the number of additional parameters to estimate equals the number of additional data points that are available. Consequently, χ2 and its degrees of freedom remain unchanged.

Note 3

Had Tunmer and Chapman happened to use Mplus to run their SEM models, they would not have left out the covariance because covariances among exogenous variables are estimated by default. But they used AMOS, a program that requires drawing models, making it possible to inadvertently leave out the double-headed arrow between decoding and linguistic comprehension.

Note 4

Model fit statistics reflect how closely the covariance matrix implied by the model’s parameters fits the observed covariance matrix.

Note 5

Technically speaking, Tunmer and Chapman’s modified model combined both a direct effect of linguistic comprehension on decoding and a direct effect of decoding on listening comprehension model into a single model, and this combined model is not an equivalent model of the simple view model. However, no support was provided for a direct effect from decoding to linguistic comprehension and their interpretation of the model is that it supports a direct effect from linguistic comprehension to decoding only. A model with only a direct effect from linguistic comprehension to decoding and the simple view model are equivalent models.

References

  1. Catts HW, Adlof SM, Weismer SE. Language deficits in poor comprehenders: A case for the simple view of reading. Journal of Speech, Language, and Hearing Research. 2006;49(2):278–293. doi: 10.1044/1092-4388(2006/023). [DOI] [PubMed] [Google Scholar]
  2. Georgiou GK, Das JP, Hayward D. Revisiting the “simple view of reading” in a group of children with poor reading comprehension. Journal of Learning Disabilities. 2009;42(1):76–84. doi: 10.1177/0022219408326210. [DOI] [PubMed] [Google Scholar]
  3. Gough PB, Hoover WA, Peterson CL. Some observations on a simple view of reading. Lawrence Erlbaum Associates Publishers; Mahwah, NJ: 1996. pp. 1–13. [Google Scholar]
  4. Gough PB, Tunmer WE. Decoding, reading, and reading disability. RASE: Remedial & Special Education. 1986;7:6–10. doi: 10.1177/074193258600700104. [DOI] [Google Scholar]
  5. Gustafson S, Samuelsson C, Johansson E, Wallmann J. How simple is the simple view of reading? Scandinavian Journal of Educational Research. 2013;57(3):292–308. doi: 10.1080/00313831.2012.656279. [DOI] [Google Scholar]
  6. Hershberger SL. The problem of equivalent structural models. In: Hancock GR, Mueller RO, editors. Structural equation modeling: A second course. Greenwich, CN: Information Age Publishing; 2006. pp. 13–41. [Google Scholar]
  7. Hoover WA, Gough PB. The simple view of reading. Reading and Writing. 1990;2(2):127–160. doi: 10.1007/BF00401799. [DOI] [Google Scholar]
  8. Kendeou P, Papadopoulos TC, Kotzapoulou M. Evidence for the early emergence of the simple view of reading in a transparent orthography. Reading and Writing. 2013;26(2):189–204. doi: 10.1007/s11145-012-9361-z. [DOI] [Google Scholar]
  9. Kendeou P, Savage R, Van den Broek P. Revisiting the simple view of reading. British Journal of Educational Psychology. 2009;79(2):353–370. doi: 10.1348/978185408X369020. [DOI] [PubMed] [Google Scholar]
  10. Kershaw S, Schatschneider C. A latent variable approach to the simple view of reading. Reading and Writing. 2012;25(2):433–464. doi: 10.1007/s11145-010-9278-3. [DOI] [Google Scholar]
  11. Kirby JR, Savage RS. Can the simple view deal with the complexities of reading? Literacy. 2008;42(2):75–82. doi: 10.1111/j.1741-4369.2008.00487.x. [DOI] [Google Scholar]
  12. Lee S, Hershberger S. A simple rule for generating equivalent models in covariance structure modeling. Multivariate Behavioral Research. 1990;25:313–334. doi: 10.1207/s15327906mbr2503_4. [DOI] [PubMed] [Google Scholar]
  13. MacCallum RC, Wegener DT, Uchino BN, Fabrigar LR. The problem of equivalent models in applications of covariance structure analysis. Psychological Bulletin. 1993;114:185–199. doi: 10.1037/0033-2909.114.1.185. [DOI] [PubMed] [Google Scholar]
  14. Ouellette G, Beers A. A not-so-simple view of reading: How oral vocabulary and visual-word recognition complicate the story? Reading and Writing. 2010;23(2):189–208. doi: 10.1007/s11145-008-9159-1. [DOI] [Google Scholar]
  15. Protopapas A, Simos PG, Sideridis GD, Mouzaki A. The components of the simple view of reading: A confirmatory factor analysis. Reading Psychology. 2012;33(3):217–240. doi: 10.1080/02702711.2010.507626. [DOI] [Google Scholar]
  16. Raykov T, Marcoulides GA. Can there be infinitely many models equivalent to a given covariance structure model? Structural Equation Modeling. 2001;8(1):142–149. doi: 10.1207/S15328007SEM0801_8. [DOI] [Google Scholar]
  17. Silverman RD, Speece DL, Harring JR, Ritchey KD. Fluency has a role in the simple view of reading. Scientific Studies of Reading. 2013;17(2):108–133. doi: 10.1080/10888438.2011.618153. [DOI] [Google Scholar]
  18. Stelzl I. Changing the causal hypothesis without changing the fit: Some rules for generating equivalent path models. Multivariate Behavioral Research. 1986;21:309–331. doi: 10.1207/s15327906mbr2103_3. [DOI] [PubMed] [Google Scholar]
  19. Stuart M, Stainthorp R, Snowling M. Literacy as a complex activity: Deconstructing the simple view of reading. Literacy. 2008;42(2):59–66. doi: 10.1111/j.1741-4369.2008.00490.x. [DOI] [Google Scholar]
  20. Tilstra J, McMaster K, Van den Broek P, Kendeou P, Rapp D. Simple but complex: Components of the simple view of reading across grade levels. Journal of Research in Reading. 2009;32(4):383–401. doi: 10.1111/j.1467-9817.2009.01401.x. [DOI] [Google Scholar]
  21. Tunmer WE, Chapman JW. The simple view of reading redux: Vocabulary knowledge and the independent components hypothesis. Journal of Learning Disabilities. 2012;45(5):453–466. doi: 10.1177/0022219411432685. [DOI] [PubMed] [Google Scholar]

RESOURCES