Merging of multi-string BWTs with applications

Abstract

Motivation: The throughput of genomic sequencing has increased to the point that is overrunning the rate of downstream analysis. This, along with the desire to revisit old data, has led to a situation where large quantities of raw, and nearly impenetrable, sequence data are rapidly filling the hard drives of modern biology labs. These datasets can be compressed via a multi-string variant of the Burrows–Wheeler Transform (BWT), which provides the side benefit of searches for arbitrary k-mers within the raw data as well as the ability to reconstitute arbitrary reads as needed. We propose a method for merging such datasets for both increased compression and downstream analysis.

Results: We present a novel algorithm that merges multi-string BWTs in $O(LCS\times N)$ time where LCS is the length of their longest common substring between any of the inputs, and N is the total length of all inputs combined (number of symbols) using $O(N\times lo{g}_2(F))$ bits where F is the number of multi-string BWTs merged. This merged multi-string BWT is also shown to have a higher compressibility compared with the input multi-string BWTs separately. Additionally, we explore some uses of a merged multi-string BWT for bioinformatics applications.

Availability and implementation: The MSBWT package is available through PyPI with source code located at https://code.google.com/p/msbwt/.

Contact: holtjma@cs.unc.edu

1 INTRODUCTION

The throughput of next-generation sequencing (NGS) technologies has increased at such a rate that it is now on the cusp of outpacing downstream computational and analysis pipelines (Kahn, 2011). The result is a bottleneck where huge datasets are held on secondary storage (disk) while awaiting processing. Raw sequence (e.g. FASTQ) files, composed of sequence and quality strings, are the most common intermediate piling up at this bottleneck. Moreover, the rapid development of new analysis tools has led to a culture of archiving raw sequence files for reanalysis in the future. This hoarding tradition reflects an entrenched notion that the costs of data generation far exceed the costs of analysis. The storage overhead of this bottleneck can be somewhat alleviated through the use of compression. However, decompression generally requires additional computational stages to decompress datasets before their use, which further impacts the throughput of subsequent analyses. This, in turn, has led to the need for algorithms that can operate directly on compressed data (Loh et al., 2012).

Others have previously proposed representing raw sequencing data in a form that is more compressible and indexed in a way that is suitable for direct queries by downstream tools (Bauer et al., 2011; Cox et al., 2012; Mantaci et al., 2005). Our primary contribution is a method for merging these indexable representations of NGS raw sequence data to increase compressibility and search through all merged datasets with one query. The entire collection of reads can be efficiently searched for specific k-mers and the associated reads recovered.

We leverage a Burrows–Wheeler Transform (BWT) variant that has been adapted to string collections by Bauer et al., 2011 for representing raw sequence data. Originally, the BWT was introduced as an algorithm for permuting a string to improve its compressibility (Burrows and Wheeler, 1994). The BWT of a string is closely related to a suffix array for the same string. In fact, it is merely the concatenation of the symbols preceding each suffix after those suffixes have been sorted. A special ‘end of string’ symbol (commonly ‘$’) is used as the predecessor of the string’s first symbol. The BWT increases string compressibility because it tends to group similar substrings together, which creates long runs of identical predecessor symbols. The BWT was exploited by Ferragina and Manzini (2001) who proposed an FM-index data structure that allows for searches of the BWT’s implicit suffix array to be performed. Additionally, these searches were shown to run in O(k) time where k is the query length, meaning that the BWT’s length does not affect the query time. Moreover, they showed that the FM-index can be constructed ‘on-the-fly’ in a single pass over a string’s BWT. The combination of the BWT and the FM-index allows large strings to be compressed into a smaller searchable form. A basic example of the BWT and the associated FM-index is shown in Table 1.

Table 1.

A sample BWT for the string ‘ACACAC$’

Index	Rotations	Sorted rotations	BWT	Counts
				$	A	C
0	ACACAC$	$ACACAC	C	0	0	0
1	CACAC$A	AC$ACAC	C	0	0	1
2	ACAC$AC	ACAC$AC	C	0	0	2
3	CAC$ACA	ACACAC $	$	0	0	3
4	AC$ACAC	C$ACACA	A	1	0	3
5	C$ACACA	CAC$ACA	A	1	1	3
6	$ACACAC	CACAC$A	A	1	2	3
Total	—	—	—	1	3	3

Notes: The ‘$’ represents the ‘end-of-string’ symbol, which is lexicographically smaller than all other symbols. All rotations of the string are shown on the left most column. These rotations are then sorted in the second column. Finally, the BWT is the concatenation of the predecessor symbols from each sorted rotation (the last column of the sorted rotations), ‘CCC$AAA’. The occurrence counts of the FM-index are also shown on the right side of this table. This is a count of the occurrences of each symbol before (but not including) that index. Given that the suffixes starting with ‘$’, ‘A’ and ‘C’ start at 0, 1 and 4, respectively (offsets into the BWT), the FM-index can be used to identify the index of the suffix that starts with the predecessor symbol for another suffix. For example, the first entry in the BWT is a ‘C’. The corresponding position in the BWT of that ‘C’ is found by taking the offset of ‘C’, which is 4, and adding the value of the FM-index at 0 for ‘C’, which is 0. The suffix at 0 is ‘$ACACAC’ and the suffix at 4 is ‘C$ACACA’, which is the suffix starting with the predecessor symbol for the suffix starting at index 0. Bold indicates that the final symbol (character) of the suffixes is equivalent to the BWT.

In bioinformatics, the BWT has proven to be a useful tool for aligning short reads. The fundamental problem of short-read alignment is to take small strings and place them along a larger string such that the edit distance between corresponding letters is minimized. The BWT is most often used to represent a reference genome so that it can be searched for smaller substrings. Two prominent aligners, BWA (Li and Durbin, 2009) and Bowtie (Langmead et al., 2009), take advantage of the BWT for alignment.

As sequencing and alignment rises in prominence, storing billions of reads on disk has become a common problem. Recently, several researchers have worked to apply the compression of the BWT to these large short-read sets. The BWT can be trivially constructed with multiple strings by simply concatenating them with a distinguishing breaking symbol as was done by Mantaci et al. (2005). Multi-string BWTs constructed this way generate suffixes that combine adjacent strings. Bauer et al. (2011) proposed a different multi-string BWT structure where component strings were both lexicographically ordered and would cycle on themselves, rather than transition to an adjacent string, when repeated FM-index searches were applied. Both versions allow reads to be compressed and indexed to perform searches. The Bauer et al. (2011) version was modified further by Cox et al. (2012) to increase the compression by modifying the order of the component strings. Both multi-string BWT construction methods require a preprocessing of the entire uncompressed string collection before assembling the BWT. In Bauer et al. (2011), the string dataset must first be sorted. On large datasets, this might require an ‘out-of-core’ or external sorting algorithm. The Cox et al. (2012) approach uses heuristics to choose a string ordering that maximizes the compression benefits of the BWT; this also requires an examination of the entire corpus.

In this article, we address the problem of merging two or more multi-string BWTs such that the result is a multi-string BWT containing the combined strings from each constituent multi-string BWT. Additionally, we require the strings in the resulting BWT to be annotated such that the origin of each string (in terms of which input it came from) can be identified later. The reasons for merging include adding new information to an existing dataset (more data from a sequencer), combining different datasets for comparative analysis and improving the compression. Others have addressed problems related to merging BWTs, and three of these are of particular interest.

The first is a BWT construction algorithm, which incrementally constructs a BWT in blocks and then merges those blocks together (Ferragina et al., 2012). The algorithm creates partial BWTs in memory. These partial BWTs are not true independent BWTs because they reference suffixes that are not included in the partial BWT (they either were processed previously or will be processed later). The partial BWTs are then merged into a final BWT on disk by comparing the suffixes either implicitly or explicitly depending on the location of the suffixes. Their algorithm is primarily applicable to constructing a BWT of long strings. However, it could be adapted by inserting one string at a time almost as if the string set were one long string. The memory overhead of the modified algorithm would require reconstituting the string collections for all but one of the inputs (the one used as the starting point), and then iteratively going through each string one at a time until the merged result was constructed.

The second algorithm, proposed by Bauer et al. (2011, 2013), is also a BWT construct algorithm that creates a multi-string BWT by incrementally inserting a symbol from each string ‘columnwise’ until all symbols are added to the multi-string BWT. Given a finished BWT, they also describe how to add new strings to the BWT using this algorithm. This algorithm could be adapted to solve the proposed BWT merging problem by keeping one input in the BWT format and decoding all of the other inputs into their original string collections. Then, their construction algorithm would merge each collection into the BWT. As with the first algorithm, the main issue with this approach is storage overhead of decoding each BWT into its original string collection.

The third algorithm is a suffix array merge algorithm proposed by Sirén (2009), which computes the combined suffix array for two inputs. These suffix arrays are actually represented as two multi-string BWTs. The algorithm searches for the strings of one collection in the other BWT to determine a proper interleaving of the first suffix array into the second. Once the interleaving is calculated, the merged BWT is trivially assembled. The algorithm requires an additional auxiliary index (such as the FM-index) to support searching. The memory overhead of an unsampled FM-index is O(n), where n is length of the BWT. Sampling of the FM-index impacts search performance. Moreover, this algorithm is ill-suited to multiple datasets (more than two) to merge. In this case, the algorithm performs multiple merges until only one dataset remains.

Our algorithm merges two or more multi-string BWTs directly without any search index or the need to reconstitute any string or suffix of the input BWTs. The only auxiliary data structures required are two interleave arrays, which identify the input source of each symbol in the final result, so the only auxiliary data structures used by the algorithm are stored as part of the result. The merging is accomplished by permuting the interleaves of the input BWTs, which we prove is equivalent to a radix sort over the suffixes of the string collections.

2 APPROACH

As with the approaches of Bauer et al., 2011, 2013; Ferragina et al., 2012; Sirén, 2009, our approach also takes advantage of the fact that a BWT and the suffix array are two related data structures. Intuitively, when BWTs are merged, the relative order of the suffixes within each original BWT do not change because they maintain a stable sort order, as discussed by both Sirén, 2009 and Ferragina et al., 2012. This means that the merged BWT can be defined as an interleaving of the original input BWTs (Sirén, 2009).

The proposed BWT merging algorithm is an iterative method that converges to the correct interleaving of BWTs. It starts by assuming that the interleaving is just a concatenation of one BWT onto the other. Then, in each iteration, it adjusts the current interleaving during a pass through the multi-string BWT inputs. Each iteration acts as an implicit radix sort to correct the interleaving (Knuth, 1973). After the first iteration, the first symbols of each suffix (‘A’, ‘C’, ‘G’, etc.) are grouped. After the second iteration, all identical dimer suffixes (‘AA’, ‘AC’, ‘AG’, etc.) are grouped. Eventually, the interleaving converges to the correct solution, which is detected by two consecutive iterations resulting in identical interleavings (in other words, the interleaving did not change). Finally, the two BWTs are merged based on the converged interleaving, and the result is stored as a single BWT. Additionally, we demonstrate that this method can be extended to merge any number of BWTs simultaneously in $O(LCS\times N)$ time where LCS is the longest common substring (LCS) between any two BWTs and N is the total combined length of the merged output.

3 METHODS

A multi-string BWT is defined over a finite alphabet, Σ, with lexicographically ordered symbols $\$<c_1<c_2<\mathrm{\dots }<c_{\alpha }$. We define a string as a series of k symbols from this alphabet terminated with a special end-of-string symbol, ‘$’. Let S be a collection of such strings, $S=\{s_1,s_2,\mathrm{\dots },s_m\}$. We construct our original multi-string BWTs using the technique as described by Bauer et al., 2011 such that a string can be reconstituted by prepending the predecessors repeatedly until the starting index is reached (each string forms a loop in the BWT). In a single pass through all input BWTs, we count the number of occurrences for each symbol, and determine a list of offsets into the final BWT for the first suffix starting with each symbol. These counts and offsets are a tiny subset of the FM-index, but for the unknown output BWT, rather than for the given input BWTs.

Overall, the goal of the algorithm is to construct an interleaving of the two input BWTs such that their implicit suffix arrays are in sorted order. It begins by constructing an initial interleave of the input BWTs that is simply a concatenation of the inputs. Then, a series of iterations are performed on the interleave. Each of these iterations functions like one pass of a most significant symbol radix sort over the implicit suffix array represented by the interleaved BWTs. After one iteration, the interleaving will be such that all suffixes are lexicographically sorted by their first symbol. After two iterations, the interleaving will be such that all suffixes are lexicographically sorted by their first two symbols. The third is the first three symbols. These iterations will continue until there is no change in the interleaving, indicating that the implicit suffix array has converged to a correct interleaving.

Given two BWTs, $B_0=msbwt(S_0)$ and $B_1=msbwt(S_1)$, of length m and n, respectively, we note that the target result, $B_2=msbwt(\{S_0,S_1\})$, can be trivially constructed if the interleave of B₀ and B₁ is known. As such, the primary goal of our proposed method is to calculate this interleave. We define an auxiliary array called the interleave, I, which is a series of zeroes and ones of length $(m+n)$ such that a zero corresponds to a symbol in B₂ originating in B₀ and a one corresponds to a symbol originating in B₁. There are exactly m zeroes and exactly n ones in I. As the merge algorithm progresses, this interleave will be corrected until it converges to the final interleave. This I array is similar to the interleave array in Sirén, 2009.

Let totals be a list of numbers such that for each symbol c in Σ, $totals[c]=count(c,B_0)+count(c,B_1)$. In short, totals is a combined count of each symbol in the two BWTs. Additionally, let $offsets$ be defined for each symbol c such that $offsets[c]$ is the position of the first suffix in the merged BWT, B₂, that starts with c, which can be calculated by adding the totals for all symbols lexicographically before c. This is equivalent to the offsets component of the FM-index for the final merged BWT.

Finally, we will define our iteration function mergeIter as follows:

//I - the current interleave of B₀ and B₁

//B₀ - the first BWT to merge

//B₁ - the second BWT to merge

//$offsets$ - for each symbol in Σ, $offsets$ contains a value indicating the

//position of the first suffix starting with that symbol in the merged BWT

function mergeIter(I, B₀, B₁, $offsets$)

 //initial conditions

 $INext=[null]\times len(I)$

 $currentPos0=0$

 $currentPos1=0$

 $tempIndex=offsets$

 //iterate through each bit value in I

 for all b in I do

  //b is a bit representing the input BWT

  if b == 0 then

   $c=B_0[currentPos0]$

   $currentPos0=currentPos0+1$

  else

   $c=B_1[currentPos1]$

   $currentPos1=currentPos1+1$

  end if

  //copy b into the next position for symbol c

  $INextPos=tempIndex[c]$

  $INext[INextPos]=b$

  //update the tempIndex to match the FM-index

  $tempIndex[c]=tempIndex[c]+1$

 end for

 return INext

end function

Repeated calls to this procedure converge to the correct interleaving of B₀ and B₁ resulting in B₂. To prove this claim, we first show that a correct interleaving will not change as a result of this function.

Lemma 3.1 —

Given a correct interleaving, I, of two BWTs, B₀ and B₁, into a single BWT, B₂, and the offsets for each symbol, c in Σ, into B₂, then $mergeIter(I,B_0,B_1,offsets)$ will return the same interleaving, I, as was passed into it.

This lemma follows from the properties of a BWT. The lemma assumes that the ordering I results in a correct BWT, B₂, for a collection of strings, $S_2=\{S_0,S_1\}$. In the initial condition, the current positions are both 0, and the tempIndex value corresponds to the offsets into the merged BWT array. First, it is easily noted that after each iteration, $i=\mathrm{1..}(m+n),currentPos0+currentPos1=i$. This is because as i increments, one of the currentPos values is also incremented at the end of the loop. Additionally, given an FM-index for the BWT represented by I, we note that $tempIndex=$FM-index$[i]$ after each iteration. At position 0, we started with only the offsets, and at each iteration, we add 1 to the $tempIndex[c]$ for the symbol c in that position to keep our tempIndex identical to the FM-index. Finally, after each iteration, one value of INext is changed corresponding to the current $tempIndex[c]$. As the value changed is based on the FM-index, it is effectively setting $INext[tempIndex[c]]=I[tempIndex[c]]$. After doing this for all values b in I, it will have set every value in INext to its corresponding value in I. Alternatively, if there exists a position, j, such that $INext[j]\ne I[j]$, then the original assumption that I is a correct ordering must be false because there is at least one position where the FM-index caused a string originating from B₀ to think it has a previous symbol originating from B₁ (or vice versa), which cannot happen in a correct multi-string BWT.

So given a correct interleaving, its correctness can be verified by executing this function once and comparing the resulting I_i with the input interleave $I_{i-1}$.

The function, $mergeIter(\mathrm{...})$, performs one iteration of the merge of two BWTs. To apply this function for a full merge requires simple setup and an outer loop to test for convergence. The following pseudocode for bwtMerge operation is presented below:

//B₀ - the first BWT to merge

//B₁ - the second BWT to merge

//Σ - lexicographically ordered valid symbols in the BWTs

function bwtMerge(B₀, B₁, Σ)

 //initial pass to calculate $offsets$

 off = 0

 for all c in Σ do

  $totals[c]=\text{count}(c,B_0)+\text{count}(c,B_{\text{1}})$

  offsets[c] = off

  $off=off+totals[c]$

 end for

 //initialize the ret array to zeroes followed by ones

 I = null

 $ret=[0]*\text{len}(B_0)+[1]*\text{len}(B_1)$

 while $I\ne ret$ do

  //copy the old interleaving and re-iterate

  I = ret

  ret = mergeIter(I, B₀, B₁, $offsets$)

 end while

 return ret

end function

As mentioned earlier, the BWT implicitly represents a sorted suffix array. The BWT can be used to generate partial suffixes as well, which is the first i symbols (i-mer prefix) of the suffix. We will refer to these as i-suffixes. Given a BWT string, it can be sorted using a radix sort to recover all 1-suffixes in lexicographic order. Then, if the BWT is prepended to the sorted 1-suffixes and sorted again using only the prepended BWT characters, all 2-suffixes in the BWT are recovered in lexicographic ordering. If this process is repeated for i iterations, all i-suffixes in the BWT can be recovered. This is fundamentally equivalent of doing a least significant symbol radix sort of all i-suffixes in the suffix array. As the algorithm is sorting the prefixes of the suffixes by increasing the prefix length, it is really performing a most significant symbol radix sort on the full suffixes.

The iterations of the while loop in bwtMerge are equivalent to performing this radix sort. The I array indicates the current interleaving of symbols at the start of an iteration. Then, the bits are placed into the next available location for their corresponding symbol using the tempIndex. With each iteration in the loop, the sorting of suffixes is extended by one symbol until I converges to a correct interleaving. The actual suffixes are never explicitly reconstructed or stored. In the example executions in Tables 2 and 3, the suffixes are shown after each iteration for illustration only. The final merged BWT is created trivially using the interleave from bwtMerge.

Lemma 3.2 —

Given an initial interleaving, I, of two BWTs, B₀ and B₁, such that all zeroes come before all ones, after k executions of mergeIter, all corresponding suffixes are stably sorted up to their first k symbols.

Table 2.

The above table shows the state after each iteration, i, for merging two BWTs each containing one string, ‘ACCA$’ and ‘CAAA$’, respectively

Iteration 0			Iteration 1			Iteration 2			Iteration 3
I	S	B	I	S	B	I	S	B	I	S	B
0		A	0	$	A	0	$A	A	0	$AC	A
0		C	1	$	A	1	$C	A	1	$CA	A
0		$	0	A	C	0	A$	C	0	A$A	C
0		C	0	A	$	1	A$	A	1	A$C	A
0		A	1	A	A	1	AA	A	1	AA$	A
1		A	1	A	A	1	AA	C	1	AAA	C
1		A	1	A	C	0	AC	$	0	ACC	$
1		A	0	C	C	0	CA	C	0	CA$	C
1		C	0	C	A	1	CA	$	1	CAA	$
1		$	1	C	$	0	CC	A	0	CCA	A

Notes: Their respective starting BWT strings are ‘AC$CA’ and ‘AAAC$’. At each iteration, the table shows the interleaving, I, the i-suffixes, S, and what the merged BWT, B, is with that interleaving. After the first iteration, there are three bins of zeroes followed by ones representing the three i-suffixes of length one: ‘$’, ‘A’ and ‘C’. The second iteration puts all 2-suffixes in their correct bins, and at this point it happened to converge to the correct solution early. Iteration three will detect no change in the interleaving, and the merged BWT in bold is stored as the final solution. Note that in each iteration the i-suffixes are in sorted order and i-suffix group containing both zeroes and ones have all zeros before all ones.

Table 3.

The above table shows the state after each iteration, i, for merging three BWTs, each containing one string: ‘ACAC$’, ‘CAAC$’ and ‘ACCA$’ respectively

Iteration 0				Iteration 1				Iteration 2				Iteration 3				Iteration 4
I	S	B		I	S	B		I	S	B		I	S	B		I
0		C		0	$	C		0	$A	C		0	$AC	C		0
0		C		1	$	C		2	$A	A		2	$AC	A		2
0		$		2	$	A		1	$C	C		1	$CA	C		1
0		A		0	A	C		2	A$	C		2	A$A	C		2
0		A		0	A	$		1	AA	C		1	AAC	C		1
1		C		1	A	C		0	AC	C		0	AC$	C		0
1		C		1	A	A		0	AC	$		1	AC$	A		1
1		A		2	A	C		1	AC	A		0	ACA	$		0
1		A		2	A	$		2	AC	$		2	ACC	$		2
1		$		0	C	A		0	C$	A		0	C$A	A		0
2		A		0	C	A		1	C$	A		1	C$C	A		1
2		C		1	C	A		0	CA	A		2	CA$	C		2
2		$		1	C	$		1	CA	$		1	CAA	$		1
2		C		2	C	C		2	CA	C		0	CAC	A		0
2		A		2	C	A		2	CC	A		2	CCA	A		2

Notes: Their respective starting BWT strings are ‘CC$AA’, ‘CCAA$’ and ‘AC$CA’. At each iteration, the table shows the interleaving, I, the i-suffix, S, and what the merged BWT, B, is with that interleaving. Each iteration corrects the suffix interleave by one symbol, which can be seen in the S columns of each iteration. After three iterations, the ordering is correct. The I of iteration 4 is shown on the far right simply to show the termination detection when the interleave stops changing. Bold text was to indicate that the final symbol (character) of the suffixes is equivalent to the BWT.

Using induction, consider the initial condition, k = 0. In this base case, all 0-suffixes are identical (empty string) and the ordering is all zeros followed by all ones. Now, consider iteration k = i where the interleaving, I, is a stable sort of the first i symbols of the suffixes of the corresponding BWTs. In the next iteration, the algorithm performs a passover I retrieving the corresponding predecessor symbol for each bit in I. If two suffixes have different start symbols, then those suffixes are automatically ordered correctly because each will be placed into the appropriate bin for that symbol. As a property of the radix sort, all $(i+1)$-suffixes starting with the same symbol, c, are placed sequentially in the output in lexicographical ordering. Given that the i-suffixes are already stably sorted, if the symbol c is found at two indices, x and y where x < y, then the corresponding $(i+1)$-suffixes must be of the form cX and cY where X is an i-suffix that lexicographically precedes the other i-suffix Y. This implies that the corresponding $(i+1)$-suffixes are also in sorted order.

Theorem 3.3 —

Given that the LCS of two BWTs, B₀ and B₁, is of length k, and that the initial ordering, I, is a single series of zeros followed by ones, then the bwtMerge algorithm will converge in k + 1 or fewer iterations. Additionally, this convergence can be detected by iterating until I stops changing.

Using Lemma 3.2, it is known that after k + 1 iterations, all $(k+1)$-suffixes will be lexicographically sorted. If the LCS is of length k, then it follows that after k + 1 iterations the suffixes will be sorted up to their first $(k+1)$ symbols. This means that further iterations should not change the sort order of the suffixes, and the interleaving has converged. Additionally, we know from Lemma 3.1 that convergence can be detected through an additional iteration.

In terms of memory, this algorithm uses O(N) bits of memory owing to the creation of I and INext. Assuming a fixed alphabet, all other variables are constant sized. For practical purposes, all large arrays (B₀, B₁) are actually stored on disk because of their size.

The algorithm will detect convergence after at most LCS + 1 iterations. If all strings are of length L, the algorithm will converge after at most L + 1 iterations. This algorithm does allow for variable length strings. In fact, it is completely unaware of the string lengths present in either BWT. However, the one caveat to Theorem 3.3 is the determination of LCS when the input strings are of variable length. In some instances, there are string collections that can result in iterations up to $2*L+1$ iterations because of the contents of the strings. The reason for this is the cyclic nature of strings in the BWT and the similarity between two BWTs. Consider two strings ‘AA$’ and ‘AAA$’. At first glance, the LCS = 3, ‘AA$’. However, because of the cyclic nature of the strings when represented in a BWT, the true LCS = 5, ‘AA$AA’, which can be generated by starting from the first symbol in the first string and the second symbol in the second string and cycling back through when there are no more symbols. For the real-data experiments presented in this article, all strings were of identical length, so this caveat was not an issue even in the presence of identical strings in each input BWT.

An example of an entire execution of bwtMerge is shown in Table 2. For this basic example, only two single-string BWTs were used in the merge. Iteration 0 represents the initial condition, and all subsequent iterations are the result from executing the mergeIter function once. After three iterations, the algorithm has converged and verified the convergence.

Until now, the algorithm has only been discussed and demonstrated using exactly two input BWTs and a bit-vector to distinguish the originating BWT for each position in the merged BWT. A basic extension of this technique repeatedly merges F input BWTs according to any binary tree resulting in a single merged BWT at the tree’s root. This requires F – 1 merges. However, the faster way is to extend the I array to multiple bits allowing for multiple BWTs to be merged simultaneously. For example, a byte array supports the merging of up to 256 multi-string BWTs simultaneously. Given F input BWTs, the above proofs can be extended by starting with an initial I consisted of a series of 0s, series of 1s, … , series of (F – 1)s as the initial condition and an initial offsets calculated in a pass over each input. Additionally, variables corresponding to a specific BWT (such as B₀, currentPos1, etc.) can be condensed into arrays of length F that can be indexed by the interleave value, b, at each position. Then, the algorithm can iterate as before until convergence is reached. This extension of the algorithm allows for an arbitrary number of multi-string BWTs to be merged simultaneously by using $O(N\times log(F))$ bits of storage for I. An example execution of this extension is shown in Table 3.

The merged BWT is a complete interleaving of the multiple BWTs into a single dataset. As distinguishing the source of a particular BWT symbol is important, the I array is stored as an auxiliary component to the merged BWT. Alternatively, if only the source of a particular string is required, the length of the I array can be truncated as described in Section 4.3. This allows for a merged dataset to differentiate the source BWT for a particular string in later analyses.

We summarize the algorithm complexities for merging two BWTs in Table 4. The performance of this algorithm is not directly affected by string length or the number of strings. For a constant N, increasing string length and decreasing the number of strings will not effect runtime unless there is also an increase in the LCS between the two BWTs. Furthermore, the memory and disk requirements for this algorithm are relatively low. In memory, the algorithm requires only O(N) bits for each interleave. The algorithm also requires $O(LCS\times N\times log(\alpha ))$ bits input from disk, but as the final merged BWT is only written once, it only writes $O(N\times log(\alpha ))$ bits to disk.

Table 4.

The asymptotic runtime, maximum memory use and disk I/O for the merge algorithm of two BWTs

CPU time	$O(LCS\times N)$
Max memory bits	O(N) − two interleaves
Disk I/O bits	$O(LCS\times N\times log(\alpha ))$ − Input BWTs
	$O(N\times log(\alpha ))$ − Output merged BWT
	O(N) − Output final interleave

Notes: LCS is the longest common substring between the two input BWTs, N is the total number of symbols, and α is the number of symbols in the alphabet (including ‘$’).

An alternative to BWT merging is to construct the BWT directly from the raw strings. For comparison purposes, we assume the construction uses the technique as described by Bauer et al., 2011. This method requires as input the full string collection in sorted order. Therefore, we need either the original strings or to decode them from the input BWTs. In either case, the strings would then need to be sorted before the start of the construction. For a collection of m strings with a maximum string length of k, they report the CPU time for their algorithm as $O(k\times m)$. However, the disk I/O is $O(m\times k^2\times log(\alpha ))$ bits because a partial BWT is written to disk at each iteration. As a result, one large string in the collection causes disk I/O to rapidly increase because of the k² term. In contrast, the merge algorithm will be less affected by long strings simply because the LCS typically does not grow at the same rate as k. In summary, when disk output speed is a limiting factor and/or LCS < k, the merge algorithm can be faster than constructing the combined BWT from the strings.

4 RESULTS

4.1 Merge times

As reported earlier, the runtime for this algorithm is $O(LCS\times N)$. To demonstrate this, we performed an experiment using real reads from mouse data provided by Sanger (ftp://ftp-mouse.sanger.ac.uk/REL-1302-BAM-GRCm38).

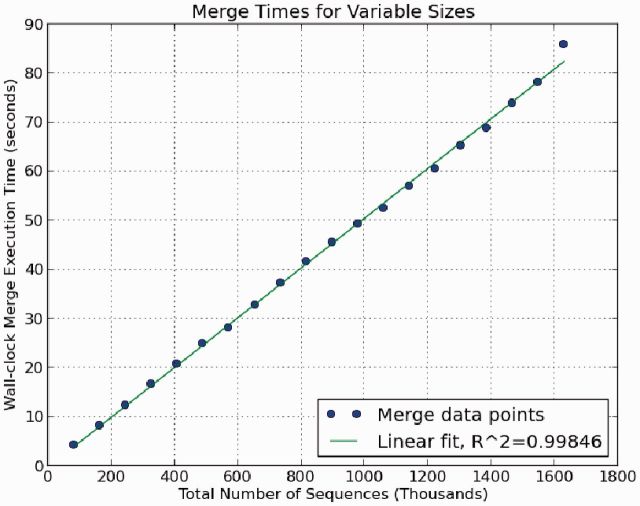
We chose two samples, WSB/EiJ and CAST/EiJ, to use for the merge. From these samples, we extracted all reads from each dataset that were aligned to the mitochondria (the reason for this choice becomes apparent in Section 4.2). The annotated mouse mitochondria is ∼16 299 bp long, and between the two samples, there were >1.6 million reads with each read being 100 bp long (over 10 000× coverage combined). We sampled reads from each set proportionally, created separate BWTs (one for WSB/EiJ, one for CAST/EiJ) and performed a merge of the two BWTs. The results of the merge execution times with respect to the total number of input sequences are shown in Figure 1.

Fig. 1.

This plot shows the relationship between the size of the data being merged and the wall-clock time to execute the merge. Each data point is a merge between two multi-string BWTs (CAST/EiJ and WSB/EiJ) where each BWT contains a randomly sampled collection of read sequences of length 100 bp aligned to the mouse mitochondria. In general, the time for completion follows a linear trend with the combined size of the inputs

4.2 Compression

One motivation for merging BWTs is to improve the compression. The redundancy of genomic data results from two factors. The datasets themselves are over-sampled, and the genomes of distinct organisms tend to share genomic features reflecting a common origin. Originally, the BWT was proposed as a method for data compression because it tends to create long runs of repeated symbols that can be used by many compression schemes (Burrows and Wheeler, 1994). If the two BWTs contain similar substrings, the potential for compression should increase. To measure compressibility, an average run-length (RL) metric is used. RL is defined as $\frac{S}{R}$ where S is the number of symbols in the BWT and R is the contiguous symbol runs in that BWT (including runs of length 1). This metric basically represents the compression potential of a BWT where it is better to have a larger average run length. This metric emphasizes the impact of merging rather than any subsequent compression methods used (e.g. move-to-front transforms, variable-length coding, Lempel-Ziv, etc.).

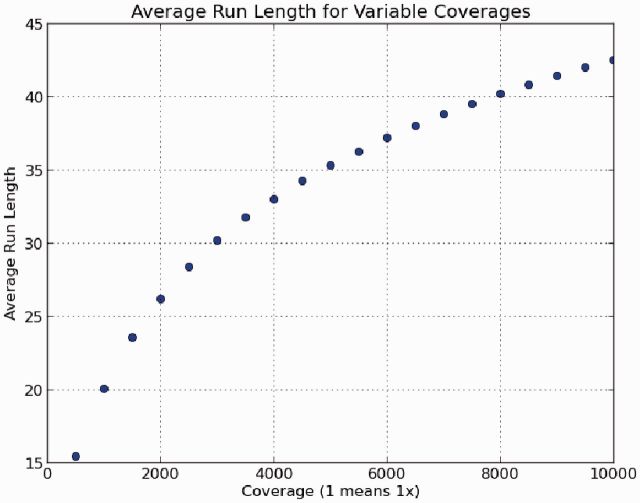
To demonstrate compressibility, we used the high-coverage mitochondria data described in Merge Times. We sampled each dataset at lower coverages to track how it impacted the average RL (see Fig. 2). In this experiment, we see faster growth at lower coverages before leveling off into linear growth at higher coverages.

Fig. 2.

This plot shows the average length of runs used for RL encoding at different levels of coverage. Note that as the coverage is increasing, the average RL increases with it. This effectively means greater compressibility with respect to the original data size. Note that there is faster growth at lower coverages before it eventually settles into a linear growth at high coverages

We also performed three other merge experiments using full RNA-seq datasets from different biological samples. The first combined two mouse biological replicates, which were both WSB/EiJ (HH) inbred samples. The second was performed on two samples from diverse mouse subspecies CAST/EiJ (FF) inbred and PWK/PhJ (GG) inbred mouse samples. The final experiment merged eight biological replicates, all of type CAST/EiJ (FF). In all three experiments, the strings were 100 bp paired-end reads.

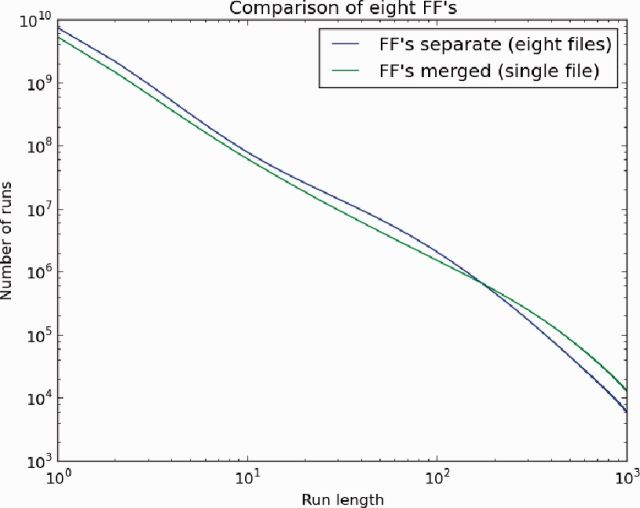
Each BWT file was analyzed both separately and as a merged BWT file as shown in Table 5. In all three scenarios, the compressibility was improved. Even GG1240, which had a relatively high average run length, showed improvement when merged with FF0683, a divergent mouse sample. The main reason for this is the lengthening of preexisting runs as more data are added. To show this, the distributions of RLs for the eight-way merge both before and after the merge are plotted in Figure 3. In this plot, we see a decrease in the number of short runs accompanied by an increase in longer runs after the merge.

Table 5.

Table showing the RL encoding metrics for RNA samples before and after merging

BWT(s)	Symbols	RLE Entries	Average RL
HH1361 individual	$6.68\times {10}^9$	$1.13\times {10}^9$	5.902
HH1380 individual	$6.32\times {10}^9$	$0.926\times {10}^9$	6.825
HH1361 + HH1380	$13.00\times {10}^9$	$2.05\times {10}^9$	6.317
HH’s Merged	$13.00\times {10}^9$	$1.83\times {10}^9$	7.086
FF0683 individual	$8.94\times {10}^9$	$1.11\times {10}^9$	8.000
GG1240 individual	$14.20\times {10}^9$	$1.36\times {10}^9$	10.401
FF0683 + GG1240	$23.14\times {10}^9$	$2.48\times {10}^9$	9.320
FF merged with GG	$23.14\times {10}^9$	$2.20\times {10}^9$	10.475
FF0683 individual	$8.94\times {10}^9$	$1.11\times {10}^9$	8.000
FF0684 individual	$7.97\times {10}^9$	$1.48\times {10}^9$	5.361
FF0685 individual	$13.11\times {10}^9$	$1.47\times {10}^9$	8.890
FF0727 individual	$7.98\times {10}^9$	$1.58\times {10}^9$	5.019
FF0728 individual	$13.64\times {10}^9$	$1.65\times {10}^9$	8.267
FF0754 individual	$18.36\times {10}^9$	$2.04\times {10}^9$	8.957
FF0758 individual	$13.13\times {10}^9$	$1.92\times {10}^9$	6.816
FF6136 individual	$10.34\times {10}^9$	$2.00\times {10}^9$	5.146
FF total individuals	$93.46\times {10}^9$	$13.3\times {10}^9$	7.026
FF’s Merged	$93.46\times {10}^9$	$9.47\times {10}^9$	9.865

Notes: Experiments are grouped into blocks. Each experiment compares the merged results (in bold) to the totals for separate files. Note that in all experiments there is a decrease in the number of RL entries and increase in average RL when moving from individual files to a single merged file indicating that the merged version is more compressible than separate files.

Fig. 3.

Plot showing the distribution of RLs for eight separate FF sample files (higher first, then lower) and a merged file containing all eight samples (lower first, then higher). Note that for the merged file, there are more runs of longer length and fewer runs of shorter length. This is because the merged BWT has brought the similar components of each BWT together leading to longer runs

4.3 Interleave storage

Thus far, we have ignored the storage requirements for the interleave vector. The interleave can be stored as the I array from the merging algorithm that requires $O(N\times lo{g}_2(F))$ bits of space, where N is the number of symbols and F the number of input BWTs.

After the merge finishes, the portion of the interleave array corresponding to suffixes starting with the ‘$’ is the only thing necessary to associate every read with its origin. In other words, you only need one interleave value per string. A particular symbol’s origin can be recovered by tracing backward through the BWT until the ‘$’ symbol is found, so the trade-off to reduce the I size is runtime speed. Using this smaller index means that the space for the I array will be $O(R\times lo{g}_2(F))$ where R is the number of strings. Finding the origin of a symbol will take O(L) time instead of O(1) where L is the length of the string. Compressing the interleave without increasing lookup times is the subject of ongoing research.

5 DISCUSSION

One motivation for merging BWTs is to improve on the compression achieved by separate BWTs. Depending on the types of data being merged, the merged BWT and its associated interleave are also useful for asking certain biological questions. The most basic benefit is performing a single query in place of multiple queries to separate datasets. For example, the comparison algorithm proposed by Cox et al., 2012, performs two queries to separate BWTs to find splice junctions. In their method, one dataset contained DNA and the other contained RNA for the same sample. As the sequences in each dataset are naturally similar, the combined version should compress well. Furthermore, as separate files, the algorithm needs $O(F\times k)$ time to search F BWTs for a given k-mer, which is reduced to O(k) when a merged BWT is used instead. In this regard, the merging provides a speedup in downstream analyses in addition to the compression.

BWTs in general can also be applied to de novo sequence assembly. In fact, some existing assemblers use the BWT as the underlying data structure (Simpson and Durbin, 2010, 2012). Several de novo assembly techniques currently use the De Bruijn graph as the underlying data structure (Butler et al., 2008; Pevzner et al., 2001; Salikhov et al., 2013; Simpson et al., 2009; Zerbino and Birney, 2008). BWTs can be used as efficient and compact De Bruijn graph representations with enhanced functionality. The presence, count and sample origin of individual k-mers are determined using the BWT’s FM-index. The k-mer size can be varied without any modifications to the BWT, and the surrounding context (i.e. the containing read fragment) of each k-mer is accessible. A De Bruijn graph constructed from a merged BWT for a species would include separate paths for haplotypes, thus representing a pan genome of the merged population (Rasko et al., 2008).

Merged multi-string datasets constructed from biological replicates can be used to increase statistical power in de novo assembly and other analyses as well. Such datasets can also be used to examine the consistency between replicates as well as the variants between diverse samples without the overhead of aligning. Robasky et al. (2014) discuss the advantages of using replicates to help reduce errors and biases in experiments. With the eight-way merge of biological replicates from Table 5, the merged BWT and the corresponding interleave can be used to calculate the abundance and variance of a given k-mer for all replicates simultaneously. Robasky et al. (2014) also mention how using replicates from different platforms can be useful to reduce bias. In addition to this benefit, we think that combining different datasets in de novo assembly is useful for extending contigs. For example, a BWT consisting of short reads (such as Illumina) could be merged with long reads (such as PacBio) to produce a merged BWT with the ability to query both datasets.

Alignment is another common use for reads. Given a reference genome, a BWT can be used to search for evidence of the genome in the reads. In this situation, the counts from the query would be similar to pileup heights from an alignment. Regions with lower than expected counts can be reexamined by selecting reads from nearby regions and generating a consensus, and thereby detecting variants including SNPs and indels, as if we were aligning the genome to the reads instead of the reads to the genome. Additionally, there is potential for algorithms that merge BWTs from raw sequencing files with a BWT of the reference genome. Ideally, this would lead to a merged BWT where strings from the genome are located near similar strings from the sequenced read fragments, making interleave the basis for alignment.

In some situations, researchers are only interested in a specific local effect instead of global analysis. A classic example is designing primers for targeted sequencing. Both BLAST (Altschul et al., 1990) and BLAT (Kent, 2002) search for k-mers within a database of strings allowing for small errors. Similar algorithms could be executed using the merged multi-dataset BWT as the database of strings. This would allow for queries for k-mer evidence among all of the datasets in a merged BWT simultaneously.

Thus, replacing raw sequencing files (i.e. FASTA) with BWTs has several advantages beyond improving compression. The indexing capabilities of the BWT increase the inherent utility of the data by allowing it to be searched and quantified. Furthermore, the interleave vector generated by merging BWTs enables finding both sequence similarities and differences between datasets without needing to align. Finally, as the BWTs are purely data driven, they are unaffected by new genome builds.

6 CONCLUSION

Multi-string BWTs improve on raw genomic read storage by reformatting the data such that it is searchable and more compressible. In this article, we presented a novel algorithm to merge multiple BWTs into a single BWT in $O(LCS\times N)$ time. The benefits of merging include a further increase in compressibility over the separate files accompanied by the ability to simultaneously search all merged datasets for a given k-mer. With the merge algorithm, new data can be merged into preexisting data as it becomes available. This is naturally useful for combining lanes from a sequencer, but it can also be extended to using replicates. Once these datasets are merged, one can then perform queries over all of the datasets simultaneously to look for common and/or differentiating signals in the read strings.

In our results, we showed that the improvement in compressibility extends to both biological replicates and to samples that are diverse subspecies. Additionally, we showed that as the coverage increases, the compressibility increases as well. We also discussed how the merged BWT and its associated interleave array can be used for de novo assembly, alignment and other analyses.

Currently, we have a publicly available Cython package that includes our implementation of the merge algorithm along with supporting query functions. Future improvements to this package will improve on the compression of both the BWT and the interleave. We currently do not address the quality strings associated with each read. We are aware of some work to compress quality strings such as that of Janin et al., 2014, but we have not yet explored the impact of quality string compression with respect to merging. Other ongoing research with this package includes developing applications such as de novo assembly and alignment techniques.