Abstract
Theory and simulations show that variables affecting the outcome only through exposure, known as instrumental variables (IVs), should be excluded from propensity score (PS) models. In pharmacoepidemiologic studies based on automated healthcare databases, researchers will sometimes use a single PS model to control for confounding when evaluating the effect of a treatment on multiple outcomes. Because these “full” models are not constructed with a specific outcome in mind, they will usually contain a large number of IVs for any individual study or outcome. If researchers subsequently decide to evaluate a subset of the outcomes in more detail, they can construct reduced “outcome-specific” models that exclude IVs for the particular study. Accurate estimates of PSs that do not condition on IVs, however, can be compromised when simply excluding instruments from the full PS model. This misspecification may have a negligible impact on effect estimates in many settings, but is likely to be more pronounced for situations where instruments modify the effects of covariates on treatment (instrument-confounder interactions). In studies evaluating drugs during early dissemination, the effects of covariates on treatment are likely modified over calendar time and IV-confounder interaction effects on treatment are likely to exist. In these settings, refitting more flexible PS models after excluding IVs and IV-confounder interactions can work well. The authors propose an alternative method based on the concept of marginalization that can be used to remove the negative effects of controlling for IVs and IV-confounder interactions without having to refit the full PS model. This method fits the full PS model, including IVs and IV-confounder interactions, but marginalizes over values of the instruments. Fitting more flexible PS models after excluding IVs or using the full model to marginalize over IVs can prevent model misspecification along with the negative effects of balancing instruments in certain settings.
1 Introduction
1.1 Instrumental variables in studies of multiple outcomes
The propensity score (PS), defined as the conditional probability of treatment or exposure given a set of observed covariates, has become a standard tool used to control for confounding in epidemiologic research (Rosenbaum and Rubin, 1983; D’Agostino, 1998; Stürmer et al., 2006). Variable selection for the PS model influences the efficiency and validity of effect estimates. Previous studies have shown that controlling for variables that affect treatment and are unassociated with the outcome except through treatment (instrumental variables or IVs) increases the variability of effect estimates (Brookhart et al., 2006; Myers et al., 2011). Studies have further shown that in the presence of unmeasured confounding, controlling for IVs can increase bias (Bhattacharya and Vogt, 2007; Wooldridge, 2009; Pearl, 2010; Myers et al., 2011).
In pharmacoepidemiologic studies based on automated healthcare databases, researchers will sometimes use a single PS model to control for confounding in multiple studies. For example, in studies focusing on drug safety and monitoring health events, researchers will often evaluate the effect of a treatment on multiple outcomes (Platt et al., 2009; Stang et al., 2010; Schneeweiss 2010). In these settings, it is often preferred to simplify the analysis by using a single PS model to simultaneously control for confounding for each of the outcomes (LoCasale et al., 2011;Wyss et al., 2013). Because these models are not constructed with a specific outcome in mind, researchers will generally be conservative and construct a model that includes a large number of covariates (a full model) to ensure the inclusion of all relevant risk factors for each of the outcomes. While using a single PS model for multiple outcomes can increase computational efficiency, these models are also prone to include IVs for any individual outcome since a covariate can act as a confounder for one outcome and an instrument for another. If researchers subsequently decide to evaluate a subset of the outcomes in more detail, they can construct reduced outcome-specific models that exclude IVs for the particular outcome(s) to improve the precision and validity of those estimates.
Reduced models that exclude IVs can be constructed by refitting a more flexible model as a function of the reduced set of covariates using an iterative process of fitting the model and checking covariate balance until an acceptable degree of balance is achieved (Imai et al., 2008). When using parametric regression models (e.g., logistic regression), however, this iterative process can be computationally inefficient and time-consuming when the number of reduced models is large. More flexible non- or semi-parametric methods can be used to model complex non-linear relationships between the reduced set of covariates and treatment (Lee et al., 2009; Harder et al., 2010; McCaffrey et al., 2004; Setoguchi et al., 2008). However, medical researchers often prefer parametric models (e.g., logistic regression), as these models are easy to implement and provide explicit information regarding the effects of covariates on treatment that is easy to interpret (Glynn et al., 2006).
In this study we explore ways of using parametric regression models to estimate PS functions that do not condition on IVs in settings where researchers initially fit a conservative (full) PS model (e.g., single PS model for multiple studies). In Section 1.2, we first discuss why the exclusion of IVs from non-linear parametric PS models (e.g., logistic regression) can result in misspecified PSs. We discuss how refitting the model as a more complex function of a reduced set of covariates after excluding IVs can improve model specification. Because refitting multiple reduced PS models can be tedious when the number of studies/outcomes is large, we then propose an alternative method that does not require researchers to refit the initial (full) PS model. This method simply extends conventional logistic regression by estimating the full PS model, with main effects and interactions, and then simultaneously marginalizing (averaging) over the empirical distribution of the assumed set of IVs. In Section 1.3 we discuss practical situations involving calendar time-modified PSs where model misspecification can result from excluding IVs. In Section 2 we use simulations to illustrate the discussed concepts. In Sections 3.1 through 3.3 we use the National Ambulatory Medical Care Survey (NAMCS) data to compare the performance of the discussed methods in their ability to accurately estimate the probability of statin use without controlling for the instrument calendar time. In Sections 4.1 and 4.2 we conclude and discuss limitations.
1.2 Exclusion of IVs from non-linear PS models and PS model misspecification
The PS, formally denoted as E[T|X|, where T is a binary treatment and X a set of measured baseline covariates, can be thought of as a balancing function that changes depending on the set of covariates on which it is conditioned. Rosenbaum and Rubin (1983) formalized PS methods and showed that a PS function conditioned on a set of measured covariates is sufficient to balance the distributions of those covariates across treatment groups through the implementation of PS matching or stratification. Robins (1998, 1999) extended the application of PSs through the development of inverse probability of treatment weighting (IPTW). He showed that weighting observations by the inverse of the probability of treatment actually received is also sufficient to balance treatment groups on the marginal distributions of the covariates upon which the PS function is conditioned.
When modeling the PS, it is necessary to specify the correct functional form of the associations between the variables included in the PS model and treatment. One of the benefits of PS methods is the ability to explicitly check the validity of the functional form of the specified PS model by observing the balance of covariates across treatment groups after matching, stratifying, or weighting on the estimated PS (Rosenbaum and Rubin, 1984; Glynn et al., 2006; Austin, 2009).
In medical studies utilizing large medical databases, researchers will sometimes fit an initial PS model that is a function of a large set of covariates to control for confounding in analyses of multiple outcomes. If the initial (or full) PS model successfully balances covariates across treatment groups, then it can reasonably be assumed that this specified model is a good approximation for the true PS function that conditions on the same set of variables as the specified full model. As discussed previously, researchers may subsequently decide to exclude variables that are thought to act as IVs when evaluating a subset of the outcomes in more detail. If the full PS model is correctly specified and follows a non-linear parametric model (e.g., logistic regression), however, simply excluding instruments (or any set of variables) from this initial model can result in misspecified relationships between the covariates and treatment.
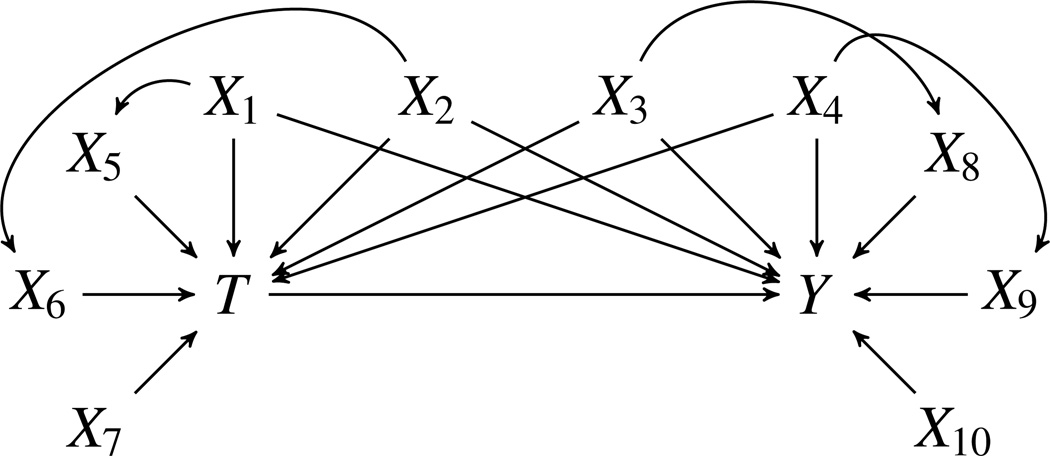
To illustrate, consider the causal structure shown in Figure 1. According to Pearl, an IV is associated with treatment and conditionally independent of the outcome, except through treatment, after conditioning on a set of covariates that are unaffected by treatment (Pearl, 2009). In pharmacoepidemiologic studies, however, researchers will usually consider a more strict definition of IVs described by Pearl (2009) and assume that instruments are associated with treatment and independent of both the outcome and all variables that have an influence on the outcome that are not mediated by the treatment (Rassen et al., 2009; Brookhart et al., 2010). The reason for using a more strict definition is that unmeasured confounding is a fundamental obstacle in studies using automated healthcare databases. If a variable is associated with measured confounders, it is likely that the variable is also associated with unmeasured confounders and, therefore, should not be treated as an IV since it is not possible to condition on the unmeasured set of covariates.
Figure 1.
Causal structure originally constructed by Setoguchi et al. (2008)
Under this stricter definition, only the variable X7 in Figure 1 would be considered an IV since it affects treatment and is associated with the outcome only through treatment. Let E[T|x1, …,x7] represent the full PS model as a function of X1 through X7 and E[T|x1, …,x6] the reduced PS model as a function of X1 through X6. The reduced PS function can be expressed as
| (1) |
In other words, the reduced model that does not condition on the IV, X7, is equal to the full model averaged (or marginalized) over the instrument. If E[T|x1, …,x7] follows a non-linear parametric function such as a logistic model, then E[T|x1, …,x6] will generally not follow the same functional form as E[T|x1, …,x7] (e.g., logistic model) since averaging over X7 changes the functional form of the model. The idea that averaging (or marginalizing) over variables in non-linear regression models can change the form of the model is well known and, in the case of logistic regression, is related to the non-collapsibility of the odds ratio. A more detailed and formal discussion on this topic is given by Whittemore (1978).
The reduced model E[T|X1, …,X6], described in Equation 1, can be approximated by refitting the logistic model as a more complex function of the reduced set of covariates (X1 through X6). Another approach that does not require researchers to refit the initial full model is to use the fitted model for E[T|X1, …X7] to marginalize (or average) over the empirical distribution of the excluded IV, X7.
For example, assume that the full model follows a logistic function that is linear on the logit scale. If the full model is correctly specified, the marginalized PS (described in Equation 1) for a given individual can be estimated by simply using the fitted model to sum over all of the observed values of X7 in the dataset while holding the other covariates in the model constant at the observed values for that individual. Dividing this sum by the total number of observations in the dataset will give the PS that is averaged over the instrument for that individual. This process, which is described in Equation 2, can then be repeated for each individual within the dataset. A simple example is provided in the Appendix.
| (2) |
1.3 Excluding instruments from calendar time-modified propensity scores
Misspecification that results from excluding IVs from parametric PS models is likely to have a negligible impact on effect estimates in many settings (e.g., the settings studied by Brookhart et al., 2006 and Myers et al., 2011). In situations where instrumental variables modify the effects of covariates on treatment, however, model misspecification will likely be more severe. In these settings, confounding factors will have non-linear relationships with treatment assignment due to the interactive effects between instruments and confounders on treatment. These non-linearities in the PS model can be difficult to capture with reduced models that exclude the IVs and IV-confounder interactions.
This issue of model misspecification is particularly relevant in pharmacoepidemiologic studies where there is rapid change over time in drug prescribing patterns or in the use of a treatment (Glynn et al., 2012; Mack et al., 2013). In these settings, calendar time is often associated with the dissemination (or restricted use) of the treatment of interest (Dusetzina et al., 2013). Examples include a newly approved treatment quickly diffusing through the market and the issuance of black box warnings (Dilokthornsakul et al., 2014). During these periods, the effects of covariates on treatment often change, or are modified over time (Mack et al., 2013, Dusetzina et al., 2013). For example, physicians becoming more familiar with a new treatment may take into account new considerations or drop previous ones when prescribing the treatment to patients (Schneeweiss et al. 2011). In studying the use of oxaliplatin for stage III colon cancer between the years 2003 and 2006, Mack et al. (2013) found diabetes to have no association with initiating oxaliplatin during these periods considered in the study, but found that diabetes steered people away from oxaliplatin use in later years (likely because of peripheral neuropathy).
If either variable involved in an interaction effect on treatment can be treated as an IV (instrument-confounder interaction), then it is unnecessary to include this interaction term when modeling the non-linear relationship between the confounder and treatment. After excluding IVs, researchers can include a complex function of the confounder to capture, or approximate, the non-linear relationship between the confounder and treatment that is due to instrument-confounder interaction. When using a single PS model to simultaneously control for confounding for multiple outcomes, however, it may not always be possible to exclude IVs prior to fitting the full model as discussed previously. Further, previous studies have discussed how calendar time itself can sometimes be treated as an IV when it is unassociated with risk factors for the outcome (Cain et al., 2009; Chen and Briesacher, 2011; Zeliadt et al., 2014). When conducting multiple studies over different time periods, however, it is unlikely that calendar time satisfies the conditions for an instrument over each of the study periods. It may therefore be necessary to incorporate heterogeneous effects for calendar time when using a single PS model to simultaneously control for confounding for multiple outcomes and over multiple study periods.
One approach is to fit a complex model that includes interaction terms involving calendar time within the PS model (Mack et al., 2013, Dilokthornsakul et al., 2014). Changes over time in the treatment assignment mechanism can also be addressed by estimating the PS within given time periods (Seeger et al., 2005; Mack et al., 2013). For the subset of studies where calendar time can be viewed as an IV, however, controlling for calendar time is prone to introduce the negative effects that balancing IVs can have on effect estimates. If a full PS model that includes calendar time is correctly specified, then researchers can use this full model to control for confounding within subgroups of the population (Rassen et al., 2012). This implies that this model can be used to marginalize (average) over calendar time for study periods where calendar time acts as an IV and control for calendar time in periods where it acts as a confounder (or a proxy for confounders). When evaluating multiple outcomes, this model can further be used to marginalize over other variables that act as instruments when researchers want to subsequently consider a subset of the outcomes in more detail. Using a single model to marginalize over IVs can allow researchers to avoid controlling for IVs without having to fit multiple reduced models in settings where it can be difficult to accurately model the relationship between covariates with treatment over time.
2 Simulation: a simple illustrative example
2.1 Simulation setup
To illustrate, we chose a simulation structure that was originally constructed by Setoguchi et al. (2008) and has been used in a number of previous studies (Lee et al., 2009; Austin 2012; Leacy & Stuart 2013). Simulations consisted of a dichotomous treatment (T), six binary covariates (X1, X3, X5, X6, X8, X9) and four standard-normal covariates (X2, X4, X7, X10). This simulation structure includes correlations between some of the covariates to reflect the complexities of treatment assignment that are likely to occur in practice. Lee et al. (2011) provide a description and code for this simulation structure. The associations among the variables are illustrated in Figure 1.
We simulated the conditional probability of treatment as a function of X1 through X7 according to Equation 3. Following the example of Lee et al. (2009) we simulated a normally distributed outcome according to Equation 4. We used the same parameter values for β1 through β7 and α1 through α7 as used by Setoguchi et al. (2008) and Lee et al. (2009). These values are based on the coefficients from actual claims data modeling the propensity of statin use (Setoguchi et al., 2008). We varied the strength of the interaction effect between X7 and X4 on treatment (β8). We simulated 1,000 studies for each scenario with a sample size of N = 5,000 for each simulated study.
| (3) |
| (4) |
We estimated the PSs using the following models:
PS Model 1: Logistic regression was used to estimate E[T|x1, …,x7] by fitting the full logistic model defined in Equation 3.
PS Model 2: Logistic regression was used to approximate E[T|x1, …,x6] by excluding terms involving the instrument from the full model (PS Model 1). After excluding these terms, this model included only main effects in the reduced set of covariates X1 through X6.
PS Model 3: Logistic regression was used to approximate E[T|x1, …,x6] by refitting the logistic model as a more complex function of the reduced set of covariates (X1 through X6). This model excludes the IV and IV-confounder interaction but allows for non-linear relationships between the confounders and the log-odds of treatment. We fitted this model by adding non-linear terms for X4, checking covariate balance, and then refitting the model in an iterative process to improve balance. The final model included main effects for the covariates X1 through X6 and all two-way interaction terms between the confounder X4 and the confounders X1, X2, and X3. The purpose of PS Model 3 is not to describe an algorithm for fitting reduced models, but to simply illustrate that more flexible reduced models can be fitted in an iterative process to improve covariate balance and the specification of the model.
-
PS Model 4: Using a more conservative definition of IVs discussed previously, it is straightforward to estimate E[T|X1, …,X6] by averaging over the empirical distribution of the instrument as described previously in Section 1.2. This was done by fitting the full model for E[T|X1, …,X7] and then using this model to marginalize over values of the instrument, X7, according to Equation 5.
(5) For simplicity and illustrative purposes we conducted simulations for only one instrument. In practice, X7 could be replaced with a set of IVs and the joint distribution of the IVs could be simultaneously marginalized over, using a similar process with the same assumptions.
Following the example of Lee et al (2009), we estimated the treatment effect in the treated using standardized mortality ratio (SMR) weighting. We evaluated the percent bias in the estimated treatment effect along with the standard error. We estimated the standard error using the empirical standard deviation of the distribution of the treatment effect estimates across all simulation runs.
Since the identification of IVs can be difficult in practice, it is likely that in some situations variables that are thought to act as instruments are correlated with variables that affect the outcome (Myers et al., 2011). Therefore, we repeated the simulations while treating the variables X5, X6 and X7 as instruments. The variables X5 and X6 do not causally affect the outcome (other than through treatment), but are correlated with the outcome through X1 and X2. Therefore, these variables should not be treated as IVs according to the stricter definition of instruments discussed previously.
2.2 Simulation results
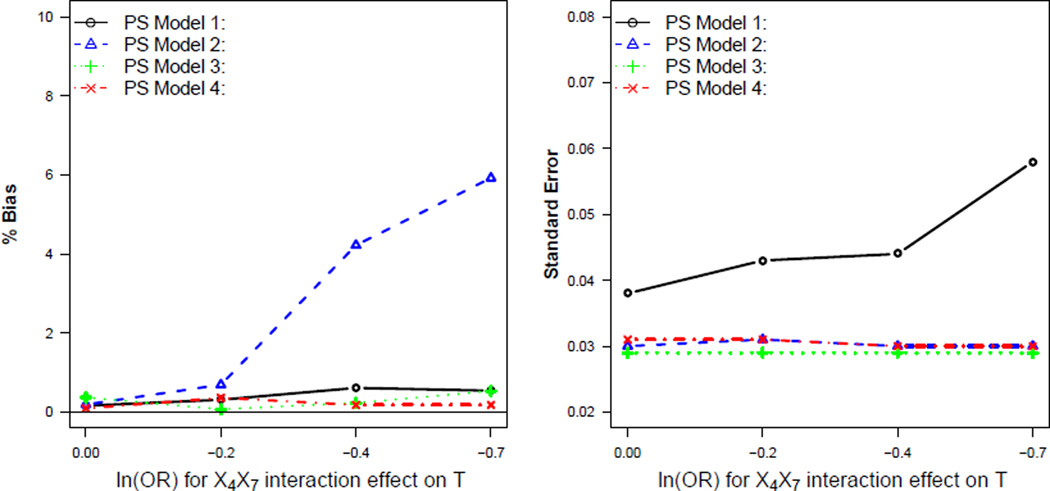
Figure 2 shows results when only X7 was treated as an IV. Figure 2 illustrates that when the instrument, X7, had no interaction effect on treatment (β8 = 0), each of the PS models resulted in approximately unbiased effect estimates. Excluding X7 from the full PS model (PS Model 2) in this case had a negligible effect on the functional form of the PS model. When X7 interacted with a confounder to affect treatment, simply excluding terms that involved the IV from the full model (PS Model 2) resulted in an increase in bias compared to the other PS models. This bias increased as the strength of the instrument-confounder interaction effect on treatment increased (Figure 2).
Figure 2.
Comparison of PS models when only X7 is treated as an instrumental variable
Fitting a more flexible logistic model (PS Model 3) or fitting the full logistic model and then marginalizing over the IV (PS Model 4) resulted in reduced bias compared to PS Model 2 when there existed an instrument-confounder interaction effect on treatment. These models also resulted in reduced standard error compared to PS Model 1 for all scenarios (Figure 2).
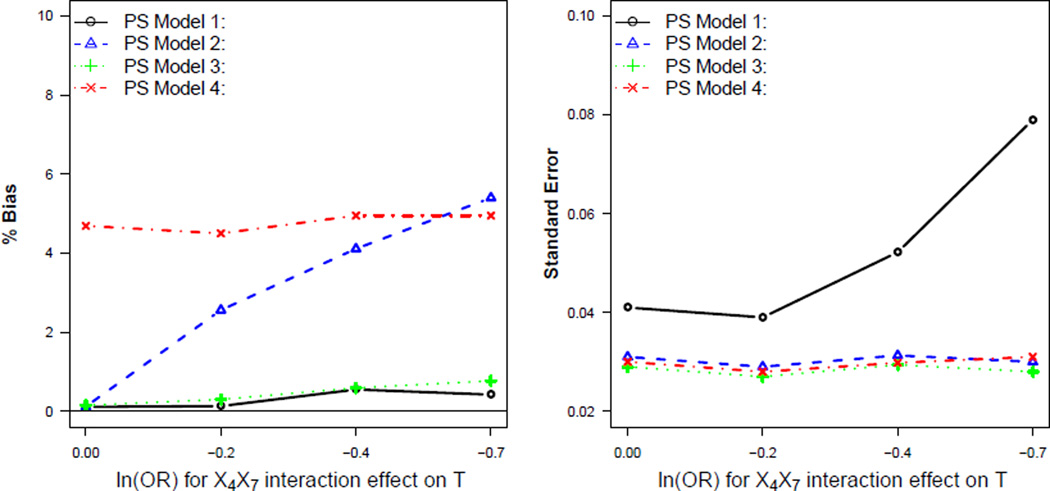
Figure 3 illustrates that fitting the full logistic model and then marginalizing over variables that are correlated with predictors of the outcome can produce substantial bias in the effect estimates. In these settings, refitting a more flexible logistic model (PS Model 3) as a function of the reduced set of covariates (X1,…,X4) resulted in reduced bias and standard error compared to PS Models 2 and 4.
Figure 3.
Comparison of PS models when X5 and X6 are incorrectly treated as instrumental variables
3 Empirical example using the National Ambulatory Medical Care Survey (NAMCS) data
3.1 Data source
To examine the relative performance of the discussed PS estimation strategies in data reflecting the complexities of real-world settings, we used data obtained from the National Ambulatory Medical Care Survey (NAMCS). The NAMCS data consist of medical information collected from a national probability sample survey of visits to office-based physicians. The data were collected by the National Center for Health Statistics, Centers for Disease Control and Prevention. The survey includes patient demographics, comorbidities, diagnosis history, diagnostic screening services, treatments received (including medications), and reasons for the visit.
We identified a cohort of statin users within the NAMCS data between the years 2005–2009. With no follow-up, the NAMCS files do not include outcome data. We therefore simulated an arbitrary, normally-distributed continuous outcome (representing, for example, serum cholesterol) as a linear combination of statin medication use and selected covariates that are known to be predictive of statin use (Table 1). We simulated a normally distributed outcome for simplicity and to avoid issues with the non-collapsibility of the odds ratio (Greenland et al., 1999; Whittemore, 1978).
Table 1.
Description of covariates (N=80,693)
| Variable | Description | % |
|---|---|---|
| statin (treatment) | statin user | 1.5 |
| male | individual is male | 41.7 |
| smoking | uses tobacco | 11.25 |
| CHF | congestive heart failure | 2.34 |
| circulatory | reason for visit circulatory | 3.55 |
| IHD | ischemic heart disease | 5.36 |
| CeVD | cerebrovascular disease | 2.6 |
| obesity | diagnosed as obese | 7.3 |
| hyperlipidemia | diagnosed hyperlipidemia | 14.74 |
| age | age in years | 61.3 (mean) |
Because the outcome was simulated, all confounding factors are known by design and can be included in each of the estimated PS models. Although the true outcome model and true treatment effect are known, the true PS function is unknown and a function of real data. By simulating the outcome as a function of real data, we are able to maintain some of the advantages of simulation studies while incorporating the complexities that often exist in practical settings when estimating the PS.
3.2 Calendar time as an instrumental variable
We modeled the probability of statin use as a function of the covariates described in Table 1 and calendar year. As discussed in Section 1.3, calendar time is often associated with the dissemination (or restricted use) of the treatment of interest (Mack et al., 2013). Setoguchi et al. (2007) and Mann et al. (2008) have reported trends of increased statin use over time. In the NAMCS data, we observed a significant correlation between calendar year and statin use over the entire study period 2005–2009 (Table 2).
Table 2.
Distribution of covaritaes over time (%)
| Variable | 2005 | 2006 | 2007 | 2008 | 2009 | p-valuea | p-valueb |
|---|---|---|---|---|---|---|---|
| statin | 1.1 | 1.5 | 1.5 | 1.6 | 1.8 | < 0.01 | 0.01 |
| male | 41.9 | 40.8 | 41.9 | 41.6 | 42.4 | 0.09 | 0.35 |
| tobacco | 10.7 | 11.9 | 11.1 | 10.9 | 11.5 | 0.47 | 0.19 |
| CHF | 2.3 | 2.2 | 2.4 | 2.0 | 2.7 | 0.05 | 0.43 |
| circulatory | 3.5 | 2.9 | 3.8 | 3.3 | 4.2 | < 0.01 | 0.07 |
| IHD | 5.5 | 5.4 | 5.6 | 5.1 | 5.4 | 0.70 | 0.46 |
| CeVD | 2.9 | 2.4 | 2.5 | 2.7 | 2.5 | 0.45 | 0.04 |
| obesity | 7.2 | 6.9 | 6.7 | 6.8 | 8.8 | < 0.01 | 0.07 |
| hyplipid | 13.1 | 13.2 | 13.5 | 15.9 | 17.9 | < 0.01 | 0.32 |
| mean age | 61.5 | 61.1 | 61.7 | 61.0 | 61.3 | 0.08 | 0.07 |
Somers’ D test of association between the years 2005–2009.
Somers’ D test of association between the years 2005–2007.
The associations between the covariates with calendar time were attenuated over this shorter time period
When evaluating a treatment effect over long time periods, calendar time is likely to be associated with biological factors. For example, studies have reported increased prevalence of many predictors of cardiovascular disease over time, including diabetes and hypertension (Hajjar et al., 2006, Danaei et al., 2011). Table 2 shows that calendar time was correlated with some of the selected covariates over the years 2005–2009. In these settings, calendar time should not be treated as an instrument since it is associated with the outcome through variables other than treatment.
Over short time intervals, however, it is less likely that there are significant changes in biological factors over time. Correlations between calendar time and biological characteristics in these settings are more likely to be small. As discussed in Section 1.3, calendar time has been viewed as an instrument over periods where calendar time is associated with treatment assignment, but not strongly correlated with predictors of the outcome (Cain et al., 2009; Chen and Briesacher, 2011; Zeliadt et al., 2014). While calendar time was associated with predictors of the outcome over the years 2005–2009, Table 2 also shows that these correlations were attenuated over the shorter period 2005–2007.
3.3 PS models and results
We initially fit a full PS model that included only first order terms (main effects of the covariates) over the entire study period (2005–2009). We evaluated the validity of the specified PS model by calculating the average standardized absolute mean difference (ASAMD) of the covariates across treatment groups. After including all two-way interactions in the PS model, the covariates were approximately balanced across treatment groups with an ASAMD of 0.01 (Table 3). This improved balance corresponded with reduced bias in the estimated treatment effect (Table 3). The improved balance that resulted after including interaction terms indicates that covariates likely have a complex non-linear relationship with statin use and that the propensity for statin use is modified over time. This modification is captured in the PS by modeling interaction terms between calendar time and the confounders described in Table 1.
Table 3.
Results for study period between 2005–2009
| PS Model | ASAMD | % bias | st. error | |
|---|---|---|---|---|
| Full model | Main effect only | 0.10 | 54.2 | 0.06 |
| Interaction termsa | 0.01 | 2.0 | 0.08 |
included all two-way interactions terms
Assuming the full PS model is correctly specified, we can then use this model to control for confounding when conducting multiple studies in different time periods. Because the full PS model with interaction terms successfully balances covariates across treatment groups, we make the assumption that this model is a close approximation to the true PS model that conditions on the same set of covariates.
In addition to estimating the treatment effect over the entire study period, we conducted an analysis over the period 2005–2007 where we treated calendar time as an IV.We used three methods to not control for calendar time within this period. First, we simply excluded terms involving calendar time from the full PS model, similar to PS Model 2 described in Section 2.1. We then refit a more flexible PS model within the years 2005–2007 without controlling calendar time. This model was fit using a process similar to that described for PS Model 3 in Section 2.1. We added higher-order terms in the confounders (interactions and quadratic terms) using an iterative process of adding terms and checking covariate balance until covariates were approximately balanced across treatment groups. For this model we included main effects along with all two-way interactions in the reduced set of covariates. We also included a quadratic term for age. Finally, we used the full model that was fit over the entire study period (2005–2009) to average (or marginalize) over calendar time within the period from 2005–2007. This process is described in Section 1.2 and is similar to PS Model 4 described in Section 2.1.
Among the models that did not control for calendar time during the years 2005–2007 (Reduced models in Table 4), refitting a more flexible model resulted in the greatest balance in covariates and least bias in the estimated treatment effect. The reduced models that did not control for calendar time did not substantially improve the precision of the effect estimate (Table 4). In practical settings where instruments have a modest effect on treatment assignment, potential gains that are achieved when excluding an instrument may be small (Myers et al., 2011). Overall the results were fairly similar across each of the methods.
Table 4.
Results for study period between 2005–2007
| PS Model | ASAMD | % bias | st. error | |
|---|---|---|---|---|
| Full model | Interaction termsa | 0.02 | 2.3 | 0.09 |
| Reduced models | Excluding IV termsb | 0.03 | 2.6 | 0.08 |
| Flexible modelc | 0.01 | 1.9 | 0.09 | |
| Marginalizing over IV d | 0.03 | 2.7 | 0.09 |
Full model that was fit to the entire study period (2005–2009).
Excluding all terms from the full model that involve calendar time
After excluding calendar time, fitting a flexible model by including interactions and higher order terms in the confounders in an iterative process of adding terms and checking covariate balance.
Using the full model to marginalize over calendar time.
4 Discussion, limitations, and conclusions
4.1 Discussion
In this study, we used both simulations and empirical data to examine various ways to exclude instrumental variables from a full PS model that is initially fit to simultaneously control for confounding in multiple studies. The simulation results illustrated that when there did not exist an IV-confounder interaction effect on treatment, simply excluding the IV from the full logistic model (PS Model 2) resulted in a negligible amount of bias in the estimated PSs for the scenarios evaluated. However, when instruments interacted with confounders to affect treatment, simply excluding terms involving the instrument from the full logistic model (PS Model 2) resulted in biased effect estimates. We also demonstrated that if researchers initially fit a full model that is correctly specified, then IVs can be excluded through a simple process of using the full model to average over the instruments (PS Model 4). With an incorrectly specified full model, or when variables thought to be IVs are actually correlated with predictors of the outcome, this marginalization method can result in substantial bias, and more valid results are likely to be obtained by refitting more flexible reduced models (PS Model 3).
In practice, the true functional form of the PS and relations between covariates with treatment are unknown. To address this, we used empirical data to model the probability of treatment (statin use) while treating calendar time as an instrumental variable. In this example, each of the estimation strategies for excluding the instrument calendar time produced similar results. While excluding instruments from full logistic PS models can, in theory, result in misspecified PSs, this example illustrated that the misspecification may cause only slight bias in practical scenarios that primarily involve dichotomous predictors of treatment. When predictors of treatment are dichotomous, model misspecification resulting from excluding IVs from the full model can be modest and the relative gains obtained by refitting a more flexible logistic model (PS Model 3) or fitting a full logistic model and then marginalizing over IVs (PS Model 4) will likely be small.
The proposed method of marginalizing over IVs and the alternative method of adding non-linear terms to fit more flexible logistic models are not the only ways to accurately estimate PSs that do not condition on IVs. Other examples include non- or semi-parametric models that do not require strong a priori assumptions regarding the functional relations between covariates with treatment (e.g. machine learning methods, generalized additive models and fractional polynomial models) (Lee et al., 2009; Hastie and Tibshirani, 1986; Royston and Altman, 1994). For situations where model misspecification can potentially be severe due to very little or no prior information regarding the functional form of the PS model, more flexible non- or semi-parametric methods may result in more accurate PS estimates (Lee et al., 2009, Westreich et al., 2010).
The example we presented in Section 1.3 and empirical example (i.e., calendar time as an IV that influences how risk factors for the outcome affect treatment) is likely to be common in pharmacoepidemiology and, more generally, comparative effectiveness research. Examples include, but are not limited to, cancer treatments (Sheets et al., 2012; Zeliadt et al., 2014). However, whether calendar time is an instrument is not always known, and incorrectly characterizing a variable as an instrument (and thus not controlling for the variable) when in fact it is a confounder leads to unmeasured confounding. With variables strongly affecting treatment, unmeasured confounding may be substantial, even with small effects on the outcome (Myers et al., 2011). In many practical situations it may therefore be necessary to present analyses treating calendar time both as a confounder and, separately, as an IV.
4.2 Limitations and conclusion
Certain other caveats and limitations should be kept in mind. As with any simulation or empirical study, the results observed here are specific to the causal structure and parameter values assessed. Further, the practical implementation of marginalizing over IVs requires a strict definition of instruments, as previously discussed. Also, neither marginalizing over IVs nor fitting more flexible models solves the practical issue of defining which variables are instruments and which variables are not. As with any method of PS estimation, the validity of the PS estimates depends on the validity of the assumptions regarding the causal structure between the covariates, treatment, and outcome. Therefore, we stress the importance of using study design and subject matter expertise to gain an understanding of the underlying causal structure when performing PS analysis (Robins, 2001). When the causal structure is not well understood, the specified full PS model may not be a good approximation for the true PS function, and therefore the proposed strategy of marginalizing over instruments should be avoided.
In conclusion, when interactions between IVs and confounders affect treatment, simply excluding all terms that involve IVs from an initial (full) logistic PS model can result in misspecified PSs and potentially invalid causal estimates. Instead, PSs that do not condition on IVs can be estimated accurately by refitting the PS model as a function of the reduced set of covariates, using a flexible model that allows for non-linear relations between the confounders and treatment. When it is reasonable to assume that the specified full PS model is a close approximation to the true PS function and when there is confidence about which variables are instruments in the strict sense, using the full (conservative) logistic PS model to marginalize over a set of instruments can avoid model misspecification and the negative effects of controlling IVs without having to refit the initial full logistic PS model. This strategy provides an easy way for researchers to avoid both controlling IVs and refitting multiple reduced models in situations where a single PS model is initially fit to simultaneously control for confounding across multiple studies.
Acknowledgments
This work was funded by a grant (R01 AG023178) from the National Institute on Aging.
Appendix
Marginalizing over Instrumental Variables when Estimating Propensity Scores
Step 1: For simplicity, consider a causal structure consisting of one instrument, X1, and one confounder, X2. Fit the full PS model (i.e., the PS model that includes all terms that affect treatment including interactions and higher order terms). Assuming that the fitted model is correctly specified for the true full PS model, then we can marginalize (average) over instruments using a simple process described in steps 2 and 3.
Step 2: Using the fitted model from Step 1, calculate N predicted values (where N is equal to the study size) for the first observation by holding the value of the variable that is not an instrument (X2) constant at the observed value for the first observation and inserting the observed values of the instrument (X1) for all N observations in the study. This will result in N predicted values for the first observation or individual. Take the mean of the resulting N predicted values to be the estimate of the conditional probability of treatment marginalized over the instrumental variable (X1) for this first observation.
Step 3: Repeat Step 2 for all of the remaining N − 1 observations in the dataset. This described process is a relatively simple computational procedure to marginalize over variables under the assumption that the full model is correctly specified and instruments are not correlated with predictors of the outcome.
References
- Austin PC. The relative ability of different propensity score methods to balance measured covariates between treated and untreated subjects in observational studies. Medical Decision Making. 2009;29:661–667. doi: 10.1177/0272989X09341755. [DOI] [PubMed] [Google Scholar]
- Austin PC. Using ensemble based methods for directly estimating causal effects: an investigation of tree-based G-computation. Multivariate Behavioral Research. 2012;47:115–135. doi: 10.1080/00273171.2012.640600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhattacharya J, Vogt WB. Do Instrumental Variables Belong in Propensity scores? Cambridge, MA: National Bureau of Economic Research; 2007. pp. 41–55. (NBER Technical Working Paper no. 343). [Google Scholar]
- Brookhart MA, Schneeweiss S, Rothman KJ, et al. Variable selection for propensity score models. American Journal of Epidemiology. 2006;163(12):1149–1156. doi: 10.1093/aje/kwj149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookhart MA, Rassen JA, Schneeweiss S. Instrumental variable methods in comparative safety and effectiveness research. Pharmacoepidemiology and Drug Safety. 2010;19(6):537–554. doi: 10.1002/pds.1908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cain LE, Cole SR, Greenland S, et al. Effect of highly active antiretroviral therapy on incident AIDS using calendar period as an instrumental variable. American Journal of Epidemiology. 2009;169(9):1124–1132. doi: 10.1093/aje/kwp002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Briesacher BA. Use of instrumental variable in prescription drug research with observational data: a systematic review. Journal of Clinical Epidemiology. 2011;64:687–700. doi: 10.1016/j.jclinepi.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DAgostino RB. Tutorial in biostatistics: propensity score methods for bias reduction in the comparison of a treatment to a non-randomized control group. Statistics in Medicine. 1998;17:2265–2281. doi: 10.1002/(sici)1097-0258(19981015)17:19<2265::aid-sim918>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- Danaei G, Finucane MM, Lu Y, et al. National, regional, and global trends in fasting plasma glucose and diabetes prevalence since 1980: systematic analysis of health examinations surveys and epidemiological studies with 370 country-years and 2.7 million participants. Lancet. 2011;378:31–40. doi: 10.1016/S0140-6736(11)60679-X. [DOI] [PubMed] [Google Scholar]
- Dilokthornsakul P, Chaiyakunapruk N, Schumock GT, Lee TA. Calendar time-specific propensity score analysis for observational data: a case study estimating the effectiveness of inhaled long-acting beta-agonist on asthma exacerbations. Pharmacoepidemiology and Drug Safety. 2014;23:152–164. doi: 10.1002/pds.3540. [DOI] [PubMed] [Google Scholar]
- Dusetzina SB, Mack CD, Stürmer T. Propensity score estimation to address calendar time-specific channeling in comparative effectiveness research of second generation antipsychotics. PLoS One. 2013;8(5) doi: 10.1371/journal.pone.0063973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glynn RJ, Schneeweiss S, Stürmer T. Indications for propensity scores and review of their use in pharmacoepidemiology. Clinical Pharmacology & Toxicology. 2006;98:253–259. doi: 10.1111/j.1742-7843.2006.pto_293.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glynn RJ, Gagne JJ, Schneeweiss S. Role of disease risk scores in comparative effectiveness research with emerging therapies. Pharmacoepidemiology and Drug Safety. 2012;21(S2):138–147. doi: 10.1002/pds.3231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greenland S, Pearl J, Robins JM. Confounding and collapsibility in causal inference. Statistal Science. 1999;14(1):29–46. [Google Scholar]
- Hajjar I, Kotchen JM, Kotchen TA. Hypertension: trends in prevalence, incidence, and control. Annual Review of Public Health. 2006;27:465–490. doi: 10.1146/annurev.publhealth.27.021405.102132. [DOI] [PubMed] [Google Scholar]
- Harder BS, Stuart EA, Anthony J. Propensity score techniques and the assessment of measured covariate balance to test causal association in psychological research. Psychological Methods. 2010;15(3):234–249. doi: 10.1037/a0019623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hastie T, Tibshirani R. Generalized additive models. Statistical Science. 1986;1(3):297–318. doi: 10.1177/096228029500400302. [DOI] [PubMed] [Google Scholar]
- Imai K, King G, Stuart EA. Misunderstandings among experimentalists and observationalists about causal inference. Journal of the Royal Statistical Society, Series A (Statistics in Society) 2008;171(2):481–502. [Google Scholar]
- Leacy FP, Stuart EA. On the joint use of propensity and prognostic scores in estimation of the average treatment effect on the treated: a simulation study. Statistics in Medicine. 2013 doi: 10.1002/sim.6030. [Epub ahead of print]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee BK, Lessler J, Stuart EA. Improving propensity score weighting using machine learning. Statistics in Medicine. 2009;29:337–346. doi: 10.1002/sim.3782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee BK, Lessler J, Stuart EA. Weight trimming and propensity score weighting. PLoS ONE. 2011;6(3) doi: 10.1371/journal.pone.0018174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LoCasale RJ, Girman CJ, Bortnichak EA, et al. A comparison of covariate selection approaches for propensity score derivation. Pharmacoepidemiology and Drug Safety. 2011;20(Suppl. 1):S312. [Google Scholar]
- Mack CD, Glynn RJ, Brookhart MA, et al. Calendar time-specific propensity scores and comparative effectiveness research for stage III colon cancer chemotherapy. Pharmacoepidemiology and Drug Safety. 2013;22(8):810–118. doi: 10.1002/pds.3386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mann D, Reynolds K, Smith D, Muntner P. Trends in statin use and low-density lipoprotein cholesterol levels among US adults: Impact of the 2001 national cholesterol education program guidelines. The Annals of Pharmacotherapy. 2008;42:1208–1215. doi: 10.1345/aph.1L181. [DOI] [PubMed] [Google Scholar]
- McCaffrey DF, Ridgeway G, Morral AR. Propensity Score Estimation with Boosted Regression for Evaluating Causal Effects in Observational Studies. Psychological Methods. 2004;9(4):403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- Myers JA, Rassen JA, Gagne JJ, et al. Effects of adjusting for instrumental variables on bias and precision of effect estimates. American Journal of Epidemiology. 2011;174(11):1213–1222. doi: 10.1093/aje/kwr364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patrick AR, Schneeweiss S, Brookhart MA, et al. The implications of propensity score variable selection strategies in pharmacoepidemiology: an empirical illustration. Pharmacoepidemiology and Drug Safety. 2011;20(6):551–559. doi: 10.1002/pds.2098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearl J. Causality. 2nd ed. New York, NY: Cambridge University Press; 2009. pp. 247–248. [Google Scholar]
- Pearl J. On a class of bias-amplifying covariates that endanger effect estimates. In: Grünwald P, Spirtes P, editors. Proceedings of the Twenty-Sixth Conference on Uncertainty in Artificial Intelligence. Corvallis, OR: Association for Uncertainty in Artificial Intelligence; 2010. pp. 425–432. [Google Scholar]
- Platt R, Wilson M, Chan KA, et al. The new sentinel network-improving the evidence of medical product safety. New England Journal of Medicine. 2009;361(7):645–647. doi: 10.1056/NEJMp0905338. [DOI] [PubMed] [Google Scholar]
- Rassen JA, Brookhart MA, Glynn RJ, et al. Instrumental variables I: instrumental variables exploit natural variation in nonexperimental data to estimate causal relationships. Journal of Clinical Epidemiology. 2009;62:1226–1232. doi: 10.1016/j.jclinepi.2008.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rassen JA, Glynn RJ, Rothman KJ, et al. Applying propensity score estimates in a full cohort to adjust for confounding in subgroup analyses. Pharmacoepidemiology and Drug Safety. 2012;21:697–709. doi: 10.1002/pds.2256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robins JM. Proceedings of the Section on Bayesian Statistical Science. Alexandria, VA: American Statistical Association; 1998. Marginal structural models; pp. 1–10. [Google Scholar]
- Robins JM. Marginal structural models versus structural nested models as tools for causal inference. In: Halloran E, Berry D, editors. Statistical Models in Epidemiology: The Environment and Clinical Trials. New York: Springer-Verlag; 1999. pp. 95–134. [Google Scholar]
- Robins JM. Data, Design, and Background Knowledge in Etiologic Inference. Epidemiology. 2001;12(3):313–320. doi: 10.1097/00001648-200105000-00011. [DOI] [PubMed] [Google Scholar]
- Rosenbaum PR, Rubin DB. The central role of the propensity score in observational studies for causal effects. Biometrika. 1983;70(1):41–55. [Google Scholar]
- Rosenbaum PR, Rubin DB. Reducing bias in observational studies using subclassification on the propensity score. Journal of the American Statistical Association. 1984;79(387):516–624. [Google Scholar]
- Royston P, Altman DG. Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling. Journal of the Royal Statistical Society: Series C. 1994;43(3):429–467. [Google Scholar]
- Schneeweiss S. A basic study design for expedited safety signal evaluation based on electronic healthcare data. Pharmacoepidemiology and Drug Safety. 2010;2010(19):858–868. doi: 10.1002/pds.1926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneeweiss S, Gagne JJ, Glynn RJ, et al. Assessing the comparative effectiveness of newly marketed medications: methodological challenges and implications for drug development. Clinical Pharmacology and Therapeutics. 2011;90:777–790. doi: 10.1038/clpt.2011.235. [DOI] [PubMed] [Google Scholar]
- Seeger JD, Paige WL, Walker AM. An application of propensity score matching using claims data. Pharmacoepidemiology and Drug Safety. 2005;14:465–476. doi: 10.1002/pds.1062. [DOI] [PubMed] [Google Scholar]
- Setoguchi S, Glynn RJ, Avorn J, et al. Ten-year trends of cardiovascular drug use after mycardial infarction among community-dwelling persons ≥ 65 years of age. The American Journal of Cardiology. 2007;100:1061–1067. doi: 10.1016/j.amjcard.2007.04.052. [DOI] [PubMed] [Google Scholar]
- Setoguchi S, Schneeweiss S, Brookhart MA, et al. Evaluating uses of data mining techniques in propensity score estimation: a simulation study. Pharmacoepidemiology and Drug Safety. 2008;17:546–555. doi: 10.1002/pds.1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheets NC, Goldin GH, Meyer AM, et al. Association of intensity modeulated radiation therapy, proton therapy, or conformal radiation therapy with morbidity and disease control in localized prostate cancer. JAMA. 2012;307(15):1611–1620. doi: 10.1001/jama.2012.460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stang PE, Patrick RB, Racoosin JA, et al. Advancing the science for active surveillance: rationale and design for observational medical outcomes partnership. Annals of Internal Medicine. 2010;153:600–606. doi: 10.7326/0003-4819-153-9-201011020-00010. [DOI] [PubMed] [Google Scholar]
- Stürmer T, Joshi M, Glynn RJ, et al. A review of the application of propensity score methods yielded increasing use, advantages in specific settings, but not substantially different estimates compared with conventional multivariate methods. Journal of Clinical Epidemiology. 2006;59(5):437–447. [Google Scholar]
- Westreich D, Lessler J, Jonsson-Funk M. Propensity score estimation: neural networks, support vector machines, decision trees (CART), and meta-classifiers as alternatives to logistic regression. Journal of Clinical Epidemiology. 2010;63:826–833. doi: 10.1016/j.jclinepi.2009.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittemore AS. Collapsibility of multidimensional contingency tables. Journal of the Royal Statistical Society: Series B. 1978;40(3):328–340. [Google Scholar]
- Wooldridge J. Should Instrumental Variables Be Used As Matching Variables? (Technical Working Paper) East Lansing, MI: Michigan State University; 2009. [Google Scholar]
- Wyss R, Girman CJ, LoCasale RJ, et al. Variable selection for propensity score models when estimating treatment effects on multiple outcomes: a simulation study. Pharmacoepidemiology and Drug Safety. 2013;22:77–85. doi: 10.1002/pds.3356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeliadt SB, Loggers ET, Slatore CG, et al. Preoperative PET and the reduction of unnecessary surgery among newly diagnosed lung cancer patients in a community setting. Journal of Nuclear Medicine. 2014;55:1–7. doi: 10.2967/jnumed.113.124230. [DOI] [PubMed] [Google Scholar]