Myocardial Infarct Segmentation and Reconstruction from 2D Late-Gadolinium Enhanced Magnetic Resonance Images

Abstract

In this paper, we propose a convex optimization-based algorithm for segmenting myocardial infarct from clinical 2D late-gadolinium enhanced magnetic resonance (LGE-MR) images. Previously segmented left ventricular (LV) myocardium was used to define a region of interest for the infarct segmentation. The infarct segmentation problem was formulated as a continuous min-cut problem, which was solved using its dual formulation, the continuous max-flow (CMF). Bhattacharyya intensity distribution matching was used as the data term, where the prior intensity distributions were computed based on a training data set LGE-MR images from seven patients. The algorithm was parallelized and implemented in a graphics processing unit for reduced computation time. Three-dimensional (3D) volumes of the infarcts were then reconstructed using an interpolation technique we developed based on logarithm of odds. The algorithm was validated using LGE-MR images from 47 patients (309 slices) by comparing computed 2D segmentations and 3D reconstructions to manually generated ones. In addition, the developed algorithm was compared to several previously reported segmentation techniques. The CMF algorithm outperformed the previously reported methods in terms of Dice similarity coefficient.

1 Introduction

Myocardial infarction, a condition characterized by reduced viability of cardiac muscle tissue due to insufficient blood supply, is a leading cause of mortality and morbidity worldwide [1]. It is important to accurately segment and reconstruct the geometry of infarct region from clinical images, as the volume and spatial distribution of the infarct zone are shown to predict prognosis and clinical outcomes [2,3]. Moreover, accurate 3D reconstructions of infarct regions are needed in patient-specific computational modeling of the heart for optimal therapeutic guidance, such as in prediction of ablation targets [4].

Among the various imaging techniques used to acquire infarct structure, late-gadolinium enhanced magnetic resonance imaging (LGE-MRI) is considered the most accurate. Indeed, numerous recent studies have focused on the segmentation of the infarct regions from 2D LGE-MR images [5]. Most of the approaches apply a form of image thresholding on the extracted myocardium, such as in full width at half maximum (FWHM) [2] and signal threshold to reference mean (STRM) [6], to delineate infarct regions from previously segmented myocardium region. Other methods have used classification techniques, including support vector machines, region growing, and watershed segmentation [5]. These segmentation methods are highly influenced by image noise, as they do not incorporate spatial consistency or a smoothness constraint in the segmentation. Incorporation of regional intensity statistics of the infarct and normal myocardium, and a smoothness constraint may improve the robustness of infarct segmentation.

To this end, we developed an infarct segmentation algorithm for 2D LGE-MR images using a continuous max-flow (CMF) based method, and this is our main contribution. The segmented regions are then reconstructed as a 3D volume using a logarithm of odds (LogOdds) framework. The results of the proposed method were compared with those of several previously reported ones in clinical studies, using both 2D and 3D metrics.

2 Methods

The processing pipeline of our method is shown in Fig. 1. The operator initially delineates the epi- and endo-cardium boundaries of the left ventricle (LV) on short-axis (SAX) 2D LGE-MR slices. Optionally, an algorithm may be used to segment the myocardium directly from LGE-MR images or from spatially registered cine MR images. We then use the CMF algorithm to segment the infarct from the extracted myocardial region which was used as the initialization of the algorithm. The LogOdds-based interpolation method is then used to reconstruct the 3D infarct volumes from the 2D segmentations.

Fig. 1.

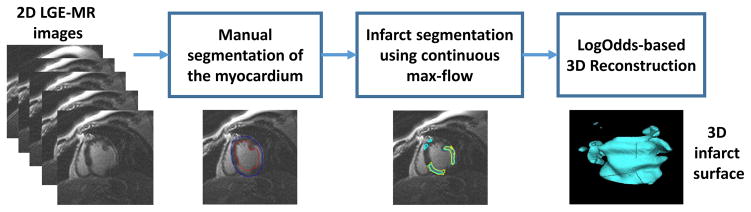
Block diagram of our image processing pipeline

Variational Formulation

The CMF algorithm iteratively evolves a contour over time. The current contour at time t is propagated to its new position 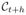at time t + h such that 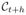minimizes the energy [7] (see Fig. 2(a)):

$$\underset{\mathcal{C}}{min}\left\{{\int }_{{\mathcal{C}}_f^{+}}{c}_f^{+}(x)dx+{\int }_{{\mathcal{C}}_b^{+}}{c}_b^{+}(x)dx+{\int }_{\partial \mathcal{C}}g(s)ds\right\}$$ (1)

where ${\mathcal{C}}_f^{+}$ and ${\mathcal{C}}_b^{+}$ are the expansion regions with respect to 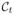, and $c_f^{+}(x)$ and $c_b^{+}(x)$ are the corresponding cost functions. g(s) is a boundary smoothness term [7]. Let u(x) ∈ {0, 1} be the labeling function of the enclosed region of 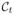such that u(x) = 1 when x is inside C_t and u(x) = 0 when x is outside C_t.

Fig. 2.

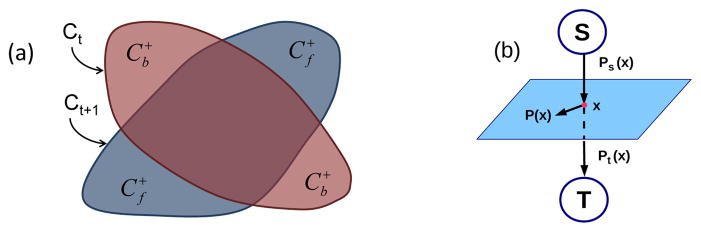
(a) Foreground (f) and background (b) region changes arising from evolution of segmentation contour (b) max-flow configuration

Let I(x) ∈ 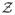be the given image, where z ∈ is the set of image intensities. In this work, the contour is propagated by minimizing the Bhattacharyya distance E_Bh(u) [8] between the estimated intensity probability density functions (PDFs) h_f,b(z), of the infarct and the normal myocardium and their respective PDF models ĥ_f,b(z):

$$E_{\text{Bh}}(u)=-\sum _{i=f,b}\sum _{z\in \mathcal{Z}}\sqrt{h_i(z){\widehat{h}}_i(z)}.$$ (2)

The intensity PDF models ĥ_f,b(z) of the regions are calculated from manual delineations of seven training images using the Parzen method [9]. The region fidelity costs $c_f^{+}(x)$ and c⁺b(x) are given by the first-order derivatives of E(u) w.r.t. u_t(x), i.e.

$$c_i^{+}(x)=\frac{1}{2A_i}\sum _{z\in \mathcal{Z}}\left\{\sqrt{h_i(z){\widehat{h}}_i(z)}-\sqrt{\frac{{\widehat{h}}_i(z)}{h_i(z)}}K(z-I(x))\right\},i=f,b$$ (3)

where A_i = ∫_Ω u_i dx, is the area of the foreground and background and K(.) is the Gaussian kernel function [9]. The cost functions (3) guide the evolution of the contours towards the minimization of the intensity PDF matching function (2). An additional distance term dist (x, ∂C_t), which is the distance from x to the current segmentation boundary, is added to the costs $c_{i=f,b}^{+}(x)$ to constrain the contour movements during each time step [7].

Let D₁(x) and D₂(x) be label assignment functions defined as follows:

$$D_1(x):=\{\begin{array}{ll}{c}_b^{+}(x),\hfill & \text{where}x\in {\mathcal{C}}_t\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}{D}_2(x):=\{\begin{array}{ll}{c}_f^{+}(x),\hfill & \text{where}x\notin {\mathcal{C}}_t\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}.$$ (4)

The optimization problem (1) for contour evolution can be equally reformulated as the continuous min-cut formulation [7] such that:

$$\underset{u(x)\in \{0,1\}}{min}\langle 1-u,D_1\rangle +\langle u,D_2\rangle +{\int }_{\mathit{\Omega }}g(x)\mid \nabla u\mid dx,$$ (5)

where binary constraint u(x) ∈ {0, 1}. g(x) = λ₁ + λ₂ exp(−λ₃ |∇I(x)|), is the gradient-weighted smoothness term, where parameters λ_1,2,3 > 0.

It is challenging to solve the combinatorial optimization problem (5), because it is highly non-linear and non-convex. However, it can be proven that using the CMF theory [7], the combinatorial optimization problem (5) can be solved globally and exactly via convex relaxation such that

$$\underset{u(x)\in [0,1]}{min}\langle 1-u,D_1\rangle +\langle u,D_2\rangle +{\int }_{\mathit{\Omega }}g(x)\mid \nabla u\mid dx,$$ (6)

where u(x) ∈ {0, 1} is now relaxed to u(x) ∈ [0, 1]. According to the convex max-flow theory, thresholding the result of the convex relaxation of (6) provides the exact and global optimum of (1). In other words, the continuous min-cut problem (1) can be solved globally, thus the contour can be propagated to its globally optimal position at each time-frame.

Continuous Max-Flow (CMF) Model

We used a CMF formulation et al. [7], as shown in Fig. 2(b). Let p_s(x) and p_t(x) be source and sink flows to and from pixel x to the source and sink terminals. The spatial flow p(x) exists around the neighborhood of pixel x. Then, the CMF model that maximizes the flow can be formulated as follows:

$$\underset{p_s,p_t,p}{max}{\int }_{\mathit{\Omega }}{p}_s(x)dx$$ (7)

subject to the following flow constraints:

$$\begin{array}{c}{p}_s(x)\le D_1(x),p_t(x)\le D_2(x),\forall \in \mathit{\Omega }\\ \mid p(x)\mid \le g(x),\text{div}(p(x)-p_s(x)+p_t(x))=0,\forall \in \mathit{\Omega }\end{array}$$

In has been proven that the CMF model (7) is equivalent to the convex relaxation problem (6) [7], which in turn is equivalent to (1). The continuous max-flow model (7) is then formulated and solved using the classical augmented Lagrangian method [10], the details of which can be found in Yuan et al. [7]. We fully parallelized the developed CMF algorithm, and implemented it on a graphics processing units (GPU) to achieve high computational performance.

Interpolation Based on Logarithm of Odds (LogOdds)

We also developed a novel method to obtain 3D reconstructions of infarct regions from 2D segmentations using logarithm of odds (LogOdds) [11] based interpolation approach. LogOdds are a type of functions that map the space of binary/discrete label maps to Euclidean vector space. In comparison to the discrete space, which permits only convex combinations, broader class of linear combinations are allowed in the LogOdds space.

Let p ∈ 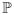be the probability that a voxel is assigned to a particular anatomical structure. The LogOdds of p is the logarithm of the odds between p and its complement. $\mathit{logit}(p)=\mathit{log}\frac{p}{(1-p)}$. The LogOdds space is defined as 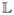= {logit(p)|p ∈ 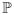}. The inverse of the LogOdds function logit(.) is the generalized logistic function $P(t)=\frac{1}{1+e^{-t}}$, P(.) maps each element t ∈ 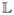to a unique probability p ∈ 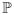, thus, the function logit(.) and its inverse comprise a structure-preserving map between 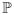and 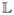[11]. LogOdds maps define boundary of a shape as a zero-level set. We used smoothing by spatial Gaussians, with standard deviation σ of 3 voxels, to map binary space to LogOdds space. The LogOdds maps of binary images were then created using logit(.) function, and the cubic spline method was used to interpolate the LogOdds maps. The interpolation results were finally mapped back to the binary space via the logistic function.

2.1 Performance Evaluation

Study Subjects and Imaging

The data set comprised of LGE-MR images of 54 subjects with ischemic cardiomyopathy. All subjects had LV ejection fraction (LVEF) ≤ 35%, and were recruited by the CMR arm of the PROSE-ICD study [2]. Patients were scanned with a 1.5T scanner (Signa CV/I, GE Healthcare, Milwaukee, WI). Standard steady-state free precession and post-gadolinium inversion-recovery fast gradient-echo sequences were used. In-plane voxel size of the data set was 0.6–1 mm, and slice thickness was 8 mm with 0 or 2 mm gap.

We evaluated the proposed algorithm using the acquired data (54 LGE-MR images, with a total of 344 2D slices). Seven of the images consisting of 35 slices were used as training data, for optimizing the parameters of the algorithm, and rest were used for testing. The testing was done in two stages. In the first stage, we compared the 2D contours generated by the algorithm to 2D manually delineations from the observer. The metrics for this comparisons were Dice similarity coefficient (DSC), root mean square error of boundary-distance (RMSE), and percentage absolute area difference (δA). In the second stage, we validated 3D reconstructions using LogOdds with DSCs, volumetric-, surface area-, and topological-based metrics. We also used percentage absolute volume difference (δV) and percentage surface area difference (δSA). The percentage absolute differences were reported as a ratio of the measurement differences and manual measurements. To assess the topological accuracy of reconstructions, absolute difference in Euler characteristic (χ) of the surfaces of the computed reconstructions were contrasted with those of generated reconstructions (δχ). Statistical analyses were performed using GraphPad Prism 6.2, and an α of 0.05 was considered as the level of significance. Wilcoxon signed rank sum tests were performed to analyze the statistical significance for DSCs, whereas paired t-tests were performed on the on the log-transformed volumes. The CMF algorithm was compared to several widely used techniques in clinical studies including FWHM, STRM method with standard deviations (SDs) one (STRM1), two (STRM2) and three (STRM3) from the reference mean, and region growing method (RG).

The experiments were performed using a Windows PC of Intel Core i7 CPU with 2.3 GHz with 12 GB RAM. The CMF algorithm was parallelized and implemented in CUDA (NVIDIA Corp., Santa Clara, CA), and the experiments were performed using Matlab (Mathworks Inc., Natick, MA). To maximize testing set size, we used a small training set of seven LGE-MR images. The training data set was used to generate the intensity PDFs as well as to optimize the parameters (i.e., λ_1,2,3 = 0.3, 0.1, 10) of the algorithm. Expanding the training set to 10 images did not change the parameters substantially (≤ 3%).

3 Results

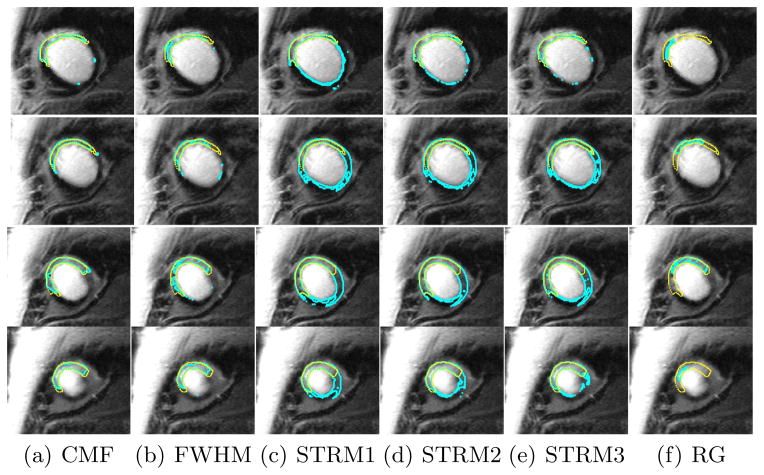
The algorithm converged within two iterations for a single slice. The computational time was 0.8 ±0.3 s for a single slice, and was 4.3±1.3 s on average for a single LGE-MR image. Example results of our algorithm segmentations are shown in Fig. 3 for a single LGE-MR image. Visually, the results of the CMF algorithm is the most similar to the manual contours. The performance results of the algorithm, and its comparison with other methods are shown in Table 1 for the testing dataset of 47 LGE-MR images comprising of 309 2D slices. The CMF algorithm yielded the highest DSC. Similarly, the CMF algorithm also reported the smallest RMSE error and smallest δA.

Fig. 3.

Segmentation results of each method for an example patient. Rows correspond to the 2D LGE-MR slices of the patient heart. Manual contours are shown in yellow whereas algorithm contours are shown in cyan.

Table 1.

Results of the algorithm for 47 2D LGE-MR images comprising of 309 2D slices. Statistical testing was performed for DSC, and a significance between the CMF and the corresponding method is indicated by an asterisk at the beginning of the value.

Method	DSC (%)	RMSE (mm)	δA (%)
CMF	75.58±6.45	8.60±10.5	20.03±13.60
FWHM	*62.72±10.78	23.82±16.1	42.41±23.14
STRM1	*64.45±9.65	15.03±9.90	68.87±55.00
STRM2	*67.00±11.0	13.10±11.5	38.74±34.92
STRM3	*66.22±13.18	11.70±12.2	27.36±23.69
RG	*40.92±15.93	12.81±5.62	98.87±117.4

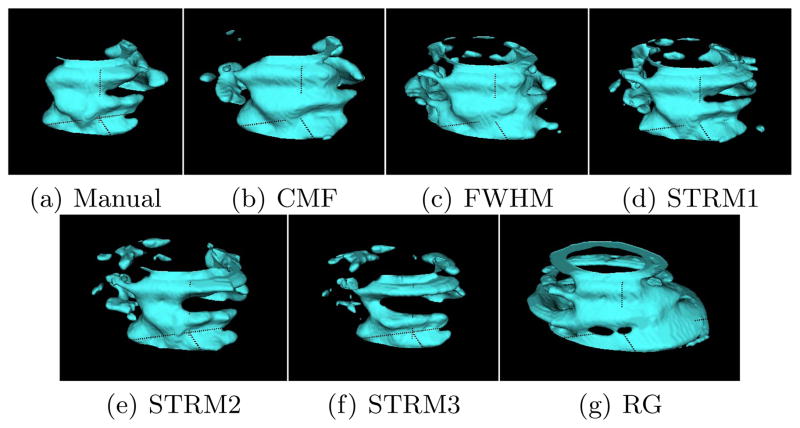
Volumes reconstructed using the LogOdds interpolation method for an example patient are visualized as surfaces in Fig. 4. Comparison of the 3D reconstructions between the different methods is shown in Table 2. Similar to the 2D comparison, the CMF algorithm provided significantly higher DSCs and significantly lower volume errors than the other methods. For the topological measure, the algorithm yielded smaller δχ, which indicates that volumes generated from CMF method are the closest in topology to the manually generated surfaces.

Fig. 4.

Comparison of the infarct surfaces generated using each method for one 2D LGE-MR image

Table 2.

Results of the algorithm for reconstructing the LV infarct from 47 2D LGEC-MR images comprising of 309 2D slices. Statistical analyses were performed for DSC and volumes, and a significance between the CMF and the corresponding method is indicated by an asterisk at the beginning of the value.

Method	DSC (%)	δV (%)	RMSE (mm)	δSA (%)	Euler δχ
CMF	73.0±11.5	20.2±10.9	3.16±2.89	16.5±11.7	5.1±3.99
FWHM	*61.7±13.3	*58.0±18.3	3.63±3.25	30.3±18.4	8.3±7.07
STRM1	*66.15±11.7	*46.7±39.11	4.63±5.14	29.4±24.7	8.9±6.2
STRM2	*68.8±12.6	*25.2±20.0	7.22±3.65	31.4±25.6	12.4±8.6
STRM3	*67.6±12.6	*24.04±16.6	5.35±2.99	22.3±20.7	10.8±7.3
RG	*39.8±15.8	*84.34±104.8	7.22±3.65	57.3±43.9	3.9±4.25

4 Discussion and Conclusion

The developed CMF method for segmenting infarct regions from clinical LGE-MR images outperformed all the other methods in terms of accuracy. In addition, the proposed method yielded significantly smaller volume errors in comparison with other methods. Since the myocardial infarct may comprise of both the gray zone and the hyper intensity core regions [2], segmentation based on energy minimization has several advantages over image threshold-based techniques. Also, incorporation of intensity distributions of the infarct and normal myocardial tissue into the segmentation provided more robustness to segmentation across different LGE-MR sequences. Since we constrained the boundaries to be smooth, the CMF algorithm generated fewer isolated regions, and therefore a smaller δχ. Unlike the other methods, the CMF method does not require further user interactions to identify normal myocardial region, such as the case in STRM methods apart from manual segmentation of the LV epi- and endo-cardium.