Structure Function for High-Concentration Biophantoms of Polydisperse Scatterer Sizes

Abstract

Ultrasonic backscattering coefficient (BSC) has been used extensively to characterize tissue. In most cases, sparse scatterer concentrations are assumed. However, many types of tissues have dense scattering media. This study addresses the problem of dense media scattering by taking into account the correlation among scatterers using the structure functions. The effect of scatterer polydispersity on the structure functions is investigated. Structure function models based on polydisperse scatterers are theoretically developed and experimentally evaluated against the structure functions obtained from cell pellet biophantoms. The biophantoms were constructed by placing live cells of known concentration in coagulation media to form a clot. The BSCs of the biophantoms were estimated using single-element transducers over the frequency range from 11 to 105 MHz. Experimental structure functions were obtained by comparing the BSCs of two cell concentrations. The structure functions predicted by the models agreed with the experimental structure functions. Fitting the models yielded cell radius estimates that were consistent with direct light microscope measures. The results demonstrate the role of scatterer position correlation on dense media scattering, and the significance of scatterer polydispersity on structure functions. This work may lead to more accurate modeling of ultrasonic scattering in dense medium for improved tissue characterization.

I. Introduction

Quantitative ultrasound (QUS) imaging is a model-based approach for identifying and classifying disease and monitoring treatments. It has been used in the characterization of the eye [1], [2], prostate [3], kidney [4], heart [5], [6], blood [7], [8], breast [9]–[11], liver [12], [13], cancerous lymph nodes [14], and apoptotic cells [15], [16], and in evaluating disease treatment [17]. Unlike conventional B-mode imaging that provides primarily qualitative images of tissue, QUS attempts to use the frequency-dependent information of the RF echo data to yield quantitative estimates of tissue properties such as scatterer size, shape, number density, and acoustic impedance. Typically, a model-based approach is applied which requires the development of ultrasonic scattering models that match the anatomic geometry of the investigated tissue. However, tissue is complex as an acoustic scattering media and to date there has not been an adequate scattering model that fits it well, which could limit further successes of QUS techniques. One major limitation of current scattering models used in QUS is that the models are often oversimplified such that they could only serve the differentiation purpose but cannot provide accurate tissue property estimates. For instance, the widely used Gaussian form factor model [18] yields an average scatterer size estimate which could be used to differentiate two diseases but does not reveal the absolute cell/nucleus size of the tissue.

We proposed a step-wise approach [19] to accurate tissue scattering modeling: to dissect the scattering by analyzing at one time each factor that may significantly contribute to scattering. To that end, we proposed to compare the strengths and weaknesses of simple models (individual cells), moderately complex models (groupings of cells at various concentrations), and significantly complex models (actual tissue/tumors). The study of individual cells or low-concentration cells may give insight into the effect of cell geometry and acoustic impedance distribution on scattering, the comparison of various concentrations may give insight into the effect of the spatial distribution of cell positions, and the comparison between cells and actual tissue/tumors may demonstrate what is unique in a specific tissue that contributes to scattering. A previous study [20] demonstrated that a model termed the concentric-sphere model that matches the geometry of a eukaryotic cell is accurate for low-concentration cell pellet biophantoms that consist of live cells embedded in a plasma-thrombin supportive background. The study [20] also showed that the ultrasonic backscatter coefficient (BSC) increases linearly with cell concentration. The follow-up study [21] showed that the linear relationship between BSC and cell concentration does not hold when the concentration is high. These results lead to the attempts to isolate the scattering contributed by the spatial distribution of cell positions, because the cells are presumably more randomly distributed at lower concentrations than at higher concentrations. It is of theoretical interest to design experiments to isolate and demonstrate the scattering contributed by the spatial distribution of cell positions. Also, it is of practical importance to develop theories to model such a scattering component, because the cell concentration is high in real tissues such as mammary tumors. In fact, it has been found that the BSC of a homogeneous tumor (minimum extracellular matrix and no necrosis) is similar to that of the dense cell pellet of the same cell type [22]. This suggests that a model applicable to the high-concentration cell pellet biophantom might be applicable to the homogeneous tumor of the same cell type.

In this paper, we propose to dissect the BSC of high-concentration cell pellet biophantoms into two components: the scattering from individual cells (incoherent scattering, determined by the geometry and acoustic impedance profile of the cells), and the scattering caused by correlation among cell positions. The former component (incoherent scattering) can be described by form factor models and has been extensively studied. Many form factor models exist: the spherical Gaussian model [18], [23], the fluid-filled sphere model [23], the spherical shell [23] and two concentric spheres models [10], [20], etc. The focus of this paper is on the latter component: we propose to experimentally measure the additional scattering caused by the correlation among cell positions, and model the additional scattering using the concept of structure function that was originally developed in statistical mechanics [24], [25] to describe the contribution to scattering caused by the pattern of the spatial arrangement of the scatterers. To best demonstrate and model the additional scattering caused by correlation among cell positions, it is desirable to separate the effect of the form factor. Therefore, instead of modeling the BSC that is affected by both the structure function and the form factor, we focus only on modeling the structure function.

The structure function has been applied in several areas of ultrasonic scattering. The concept of structure function was introduced for the first time by Twersky [26], [27] to model ultrasonic scattering. The structure function was used to model the differential cross section per unit volume for a random distribution of identical scatterers [26] and for a mixture of similarly shaped but differently sized particles [27]. In the field of QUS techniques for tissue characterization, Franceschini and Guillermin [28] recommended modeling the scattering from densely packed cells in tumors using BSC models that take into account the structure function. They performed experiments on concentrated tissue-mimicking phantoms and showed the superiority of the BSC models that take into account the structure function in comparison with other classical BSC models that do not account for the structure function. Vlad et al. [29] performed two-dimensional simulations to study the difference in the BSC between the particle distribution with uniform and heterogeneous sizes. They also made a comparison with the Percus–yevick packing factor—the low-frequency limit of a specific structure function. In [29] and [30], particle size variance was shown to be affecting the structure function and BSC behavior in the case of a highly concentrated scattering medium. Moreover, the structure function has been applied in the field of ultrasonic characterization of blood to address the difficulty of modeling aggregated cells [31], [32].

In this paper, we will develop analytical structure function models for randomly distributed scatterers that are polydisperse in size, and evaluate the models against the cell pellet biophantoms both forwardly and inversely. More specifically, we will estimate the BSCs of cell pellet biophantoms at two concentrations, a very low concentration for which the cells are randomly distributed, and a very high concentration for which the cells are closely packed to mimic the condition of a tumor. The structure function that is related to the spatial distribution of cell positions will be isolated by comparing the BSCs of the two concentrations. The theoretical structure function will be calculated from three models and compared with the experimentally estimated values. The inverse problem will also be explored to generate cell size estimates. Three distinct cell lines will be studied to demonstrate repeatability.

Several advantages exist in the models developed and the approach used in this study: 1) By studying only the structure function rather than the entire BSC, the effect of spatial scatterer position correlation on scattering is separated and thus can be better studied. 2) The structure function models can elucidate the effects of scatterer size distribution on scattering. For instance, the polydisperse structure function models suggest that the size distribution could affect the BSC by affecting not only the incoherent scattering component (which is well established), but also the structure function. 3) The models have minimal dependence on the form factor, which is a significant advantage because identifying the best form factor for a tissue is challenging. 4) The models are in analytical forms and have limited numbers of variables, which makes the inverse problem easier to solve. 5) The study is strengthened by evaluating the models in a forward manner using high-frequency (the center of the frequency band is around ka = 2) experimental data from biophantoms that mimic tumors.

II. STRUCTURE FUNCTION MODELS

A. Definition of Structure Function

Consider a plane wave of unit amplitude incident on a scattering volume V that contains N polydisperse scatterers. If the scatterers have acoustic property values (density, ρ, and compressibility, κ) very close to those of the background medium, the total scattered field far from the scattering volume behaves as a spherical wave ([23, Eq. (4)]):

$$p_s\left(\mathrm{r}\right)=\frac{e^{ikr}}{R}\sum _{j=1}^N{\Phi }_j\left(\mathbf{K}\right)e^{i\mathrm{K}\cdot {\mathrm{r}}_j},$$ (1)

where r is the observation position with respect to the origin, R = |r|, r_j is the position of the jth scatterer, k is the propagation constant (k = ω/c, where ω is the angular frequency and c is the propagation speed). The factor Φ_j(K) is the scattering amplitude of the jth scatterer and describes the spatial frequency dependence of the scattered pressure; Φ_j is a function of the scattering vector K whose magnitude is given by |K| = 2ksin (θ/2), where θ is the scattering angle (θ = π for backscattering). Φ_j is dependent on the scatterer size, shape, and acoustic properties.

The differential cross section per unit volume σ_d (i.e., the power scattered into a unit solid angle observed far from the scattering volume divided by the product of the incident intensity and the scattering volume) may be expressed as

$${\sigma }_{\mathrm{d}}\left(\mathbf{K}\right)=\frac{R^2{I}_S}{V{I}_0}=\frac{1}{V}{\mid \sum _{j=1}^N{\Phi }_j\left(\mathrm{K}\right)e^{i\mathrm{K}\cdot {\mathrm{r}}_j}\mid }^2,$$ (2)

where I_s and I₀ denote the scattering intensity and incident intensity, respectively, and | |² represents the squared modulus of the quantity.

If the scattering volume contains a sparse concentration of scatterers that are spatially randomly distributed, the phase terms e^iK·rj may be assumed to be uncorrelated. The differential cross section per unit volume for this case is denoted as σ_d,incoherent, and may be expressed as

$${\sigma }_{\mathrm{d},\mathrm{incoherent}}\left(\mathrm{K}\right)=\frac{1}{V}\sum _{j=1}^N{\mid {\Phi }_j\left(\mathrm{K}\right)\mid }^2.$$ (3)

The structure function in this paper is defined as

$$S\left(\mathrm{K}\right)=\frac{{\sigma }_{\mathrm{d}}\left(\mathrm{K}\right)}{{\sigma }_{\mathrm{d},\mathrm{incoherent}}\left(\mathrm{K}\right)}.$$ (4)

For backscattering (|K| = 2k), the quantity σ_d is denoted as BSC, and (4) becomes

$$S\left(2k\right)=\frac{\mathrm{BSC}\left(2k\right)}{{\mathrm{BSC}}_{\mathrm{incoherent}\left(2k\right)}}.$$ (5)

The structure function defined in (4) or (5) is a quantity describing the effect on scattering caused by the pattern of the spatial arrangement of the scatterers. In practice, the spatial arrangement of the cells in a biophantom or tumor can be assumed to be related to the cell concentration. For low cell concentration, the positions of the cells are assumed to be perfectly random, resulting in a structure function of unity. As the cell concentration increases, the positions of the cells become correlated. The higher the cell concentration is, the higher the correlation is. Therefore, the structure function in some sense describes how the shape of BSC versus frequency curve changes with concentration. With the structure function, the BSC for high-concentration media can be modeled more accurately. More importantly, the structure function per se is an independent quantity from which tissue properties such as scatterer size and concentration can be extracted.

B. Three Structure Function Models

This subsection deals with theoretically calculating the structure function. Three structure function models are presented, with each model representing a different degree of approximation to the polydisperse system.

1) Monodisperse Model: In this model, the scatterers are assumed to be identical non-overlapping spheres. The scattering amplitudes Φ_j(K) are identical for all the scatterers. Therefore, (2) may be simplified as

$${\sigma }_{\mathrm{d}}\left(\mathrm{K}\right)=\stackrel{‒}{n}\mid {\Phi }_j\left(\mathrm{K}\right){\mid }^2\frac{1}{N}\left(\sum _{j=1}^N{e}^{i\mathrm{K}\cdot {\mathrm{r}}_j}\right)\left(\sum _{j=1}^N{e}^{-i\mathrm{K}\cdot {\mathrm{r}}_j}\right),$$ (6)

where n̄ = N/V is the number density of the scatterers. By substituting (3) and (6) into (4) and making appropriate simplifications, the structure function may be expressed as

$$S\left(\mathrm{K}\right)=\frac{1}{N}\left(\sum _{j=1}^N{e}^{i\mathrm{K}\cdot {\mathrm{r}}_j}\right)\left(\sum _{j=1}^N{e}^{-i\mathrm{K}\cdot {\mathrm{r}}_j}\right),$$ (7)

where the structure function is determined by the scatterer positions, and is not dependent on the scattering amplitude Φ_j(K). Eq. (7) is directly applicable when the exact position of each scatterer is known. If the exact positions of the scatterers are unknown, the structure function can be determined statistically from the statistical distribution (e.g., pair correlation function) of the scatterer positions. Eq. (7) is mathematically equivalent to [26]

$$S\left(\mathrm{K}\right)=1+\stackrel{‒}{n}\int [g\left(\mathrm{r}\right)-1]e^{-i\mathrm{K}\cdot \mathrm{r}}\mathrm{dr},$$ (8)

where the structure function is expressed in terms of the pair correlation function g(r), which is a quantity related to the probability of finding two scatterers separated by the distance r. With (8), the structure function can be interpreted as the 3-d Fourier transform of the total correlation function h(r) = g(r) − 1. The total correlation may be obtained by solving the set of equations formed by the ornstein–Zernike (OZ) integral equation [33] and a closure relation. The OZ equation splits the total correlation h(r) into the direct correlation c(r) and the indirect correlation by the equation $h\left(r\right)=c\left(r\right)+\stackrel{‒}{n}{\int }_0^{\infty }h\left(\mid r-r^{\prime }\mid \right)c\left(\mid r^{\prime }\mid \right)\mathrm{d}{r}^{\prime }$. The closure relation couples the same quantities h and r. The Percus–yevick (Py) approximation [34] is a commonly used closure valid for non-overlapping spheres. With Py closure, an analytical expression of the structure function has been obtained for backscattering [24], [28], [35], which leads to the monodisperse model:

$$S\left(2k\right)=\frac{1}{1-\stackrel{‒}{n}C\left(2k\right)}$$ (9a)

$$C\left(2k\right)=-30\pi a^3{\int }_0^1{s}^2\frac{\sin \left(4kas\right)}{4kas}(\alpha +\beta s+\gamma s^3)\mathrm{ds}$$ (9b)

$$\eta =\frac{4\pi a^3}{3}\stackrel{‒}{n},\alpha =\frac{{(1+2\eta )}^2}{{(1-\eta )}^4},\beta =-\frac{6\eta {(1+\eta ∕2)}^2}{{(1-\eta )}^4},\gamma =\frac{\eta {(1+2\eta )}^2}{2{(1-\eta )}^4},$$ (9c)

where a is the sphere radius, s is a dummy variable of integration, and η is the sphere volume fraction.

For the monodisperse model described in (9), a comparison among structure functions at various volume fractions is shown in Fig. 1 (similar results can be found in [24] and [28]). It is observed from Fig. 1 that a sharp peak starts to appear in the structure function curve as the concentration becomes considerably large. This sharp peak cannot be observed from tissue data because the monodisperse model is physically unrealistic for tissues—the scatterers are polydisperse in nature.

Fig. 1.

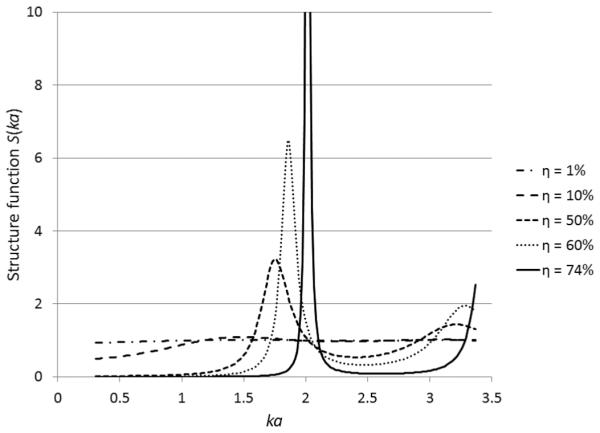
Comparison among structure functions at five different volume fractions: 1%, 10%, 50%, 60%, and 74%, computed by the monodisperse model defined in (9).

2) Polydisperse Model I: In this model, the scatterers are assumed to be non-overlapping spheres that are polydisperse in size but monodisperse in scattering amplitudes Φ_j(K). note that the assumption of monodisperse scattering amplitude is unrealistic if the system is polydisperse in size, because the scattering amplitude is a function of scatterer size. We make the monodisperse scattering amplitude assumption simply as a mathematical approximation such that (7) and (8) will still hold and the structure function will be determined solely by the pair correlation function. as such, the structure function may be written in terms of partial structure functions H_ij(2k) as given by blum and stell [36] using Py closure as in [25]

$$S\left(2k\right)=1+\stackrel{‒}{n}{\int }_0^{\infty }{\int }_0^{\infty }{H}_{ij}\left(2k\right)f{x}_{i}f\left(x_j\right)\mathrm{d}{x}_i\mathrm{d}{x}_j,$$ (10)

where f(x) is the probability density function of the sphere radius, x.

The structure function has an analytical expression following (10) if the sphere size follows a Γ (Schulz) distribution with a probability density function [25]

$$f_z\left(x\right)=\frac{1}{z!}{\left(\frac{z+1}{a}\right)}^{z+1}{x}^z{e}^{-(z+1)x∕a},z=0,1,2,\cdots ,$$ (11)

where a is the mean of the radius, and z is the Schulz width factor which measures the width of the distribution (a greater z representing a narrower distribution). The Γ distribution has been widely used to model polydisperse systems, and the cell radius in this study closely fits the Γ distribution.

The analytical expression of the structure function for polydisperse model I is listed in Appendix A. The structure function is expressed as a function of the mean sphere radius a, Schulz width factor z, wave number k, and sphere volume fraction η. The structure functions at various Schulz width factors are shown in Fig. 2. When z → ∞, the polydisperse model I yields the same result as that of the monodisperse model, which could serve as a code sanity check. as the polydispersity of sphere radius increases (i.e., z decreases), the peak of the structure function curve reduces accordingly.

Fig. 2.

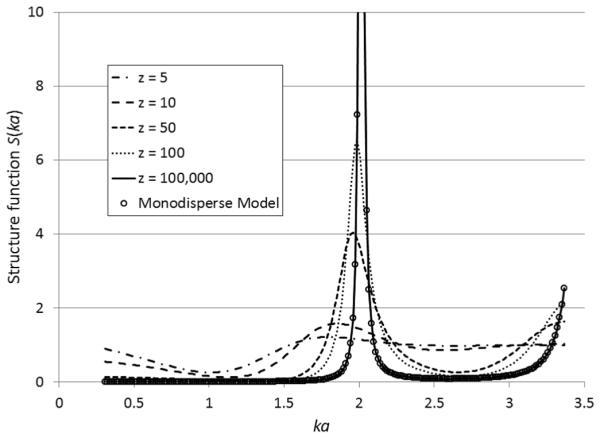
Comparison among structure functions at five different Schulz width factor values: 5, 10, 50, 100, and 10⁵, computed by polydisperse model I. The structure function at z = 10⁵ computed by polydisperse model I (solid line) is identical to that computed by the monodisperse model (circles). The volume fraction is assumed to be 74% for all the curves.

3) Polydisperse Model II: In this model, the scatterers are assumed to be non-overlapping spheres that are polydisperse in both size and scattering amplitude, and the sphere size is assumed to follow a Γ distribution. as a result of the polydispersity in scattering amplitude, the scattering amplitude cannot be factored out in (2). Therefore, (7) and (8) are no longer valid. To derive the structure function expression for this case, we first express the BSC as

$$\begin{array}{cc}\hfill \mathrm{BSC}\left(2k\right)=& \stackrel{‒}{n}{\int }_0^{\infty }\mid {\Phi }_j\left(2k\right){\mid }^{2}f\left(x_j\right)\mathrm{d}{x}_j\hfill \\ \hfill & \stackrel{‒}{n}{\int }_0^{\infty }{\int }_0^{\infty }{\Phi }_i\left(2k\right){\Phi }_j\left(2k\right)H_{ij}\left(2k\right)f\left(x_i\right)f\left(x_j\right)\mathrm{d}{x}_i\mathrm{d}{x}_j.\hfill \end{array}$$ (12)

Eq. (12) is a modification of [37, Eq. (1)]. Similar expressions may also be found in [27]. The first integral $\stackrel{‒}{n}{\int }_0^{\infty }{\mid {\Phi }_j\left(2k\right)\mid }^{2}f\left(x_j\right)\mathrm{d}{x}_j$ in (12) represents the quantity BSC_incoherent(2k). The second integral in (12) represents the excess scattering caused by the spatial correlation in scatterer positions. Substituting (12) into (5) yields the structure function for polydisperse model II:

$$S\left(2k\right)=1+\frac{{\int }_0^{\infty }{\int }_0^{\infty }\Phi \left(2k\right){\Phi }_j\left(2k\right)H_{ij}\left(2k\right)f\left(x_i\right)f\left(x_j\right)\mathrm{d}{x}_i\mathrm{d}{x}_j}{{\int }_0^{\infty }\mid {\Phi }_j\left(2k\right){\mid }^{2}f\left(x_j\right)\mathrm{d}{x}_j}.$$ (13)

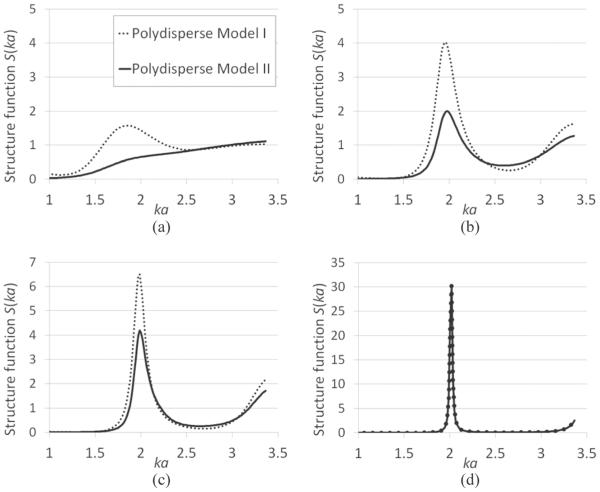
This structure function is dependent on the scattering amplitude Φ_j(2k). Therefore, a specific form of scattering amplitude is needed to evaluate (13). The scattering amplitude that is used in this paper is derived from the fluid-filled sphere form factor [23] for which the integrals in (13) have analytical expressions. The resulting expression for the structure function is listed in Appendix B. The structure function is expressed as a function of the mean sphere radius a, Schulz width factor z, wave number k, and sphere volume fraction η. The structure functions for polydisperse model I and polydisperse model II are compared at various degrees of polydispersity (Fig. 3). The peak at around ka = 2 in the structure function curve is lower for polydisperse model II than for polydisperse model I when the scatterers are polydisperse [Figs. 3(a)–3(c)]. As a code sanity check, polydisperse model I and polydisperse model II generate identical results when the scatterers are essentially monodisperse [Fig. 3(d)].

Fig. 3.

Comparison between structure functions of polydisperse model I (dotted line) and polydisperse model II (solid line) at (a) z = 10, (b) z = 50, (c) z = 100, and (d) z = 10⁷. The volume fraction is assumed to be 74% for all the curves.

III. Methods

A. Biophantom Construction

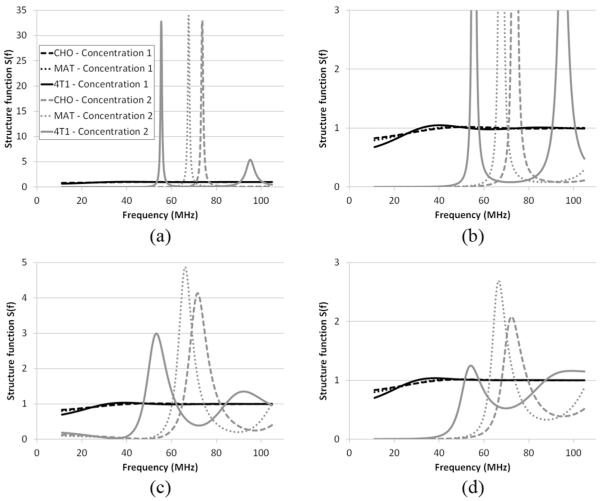
The cell pellet biophantoms were composed of a known number of cells clotted in a mixture of bovine plasma (Sigma-Aldrich, St. Louis, MO) and bovine thrombin (Sigma-Aldrich). Three cell lines, Chinese hamster ovary [CHO; American Type Culture Collection (ATCC) #CCL-61, Manassas, VA], 13762 MAT B III (MAT; ATCC #CRL-1666), and 4T1 (ATCC #CRL-2539), were used to create the cell pellet biophantoms. The three cell lines were chosen because: 1) they have been used in our previous studies [20]–[22]; 2) they represent normal and tumor cell lines (normal cells: CHO, tumor cells: MAT and 4T1); and 3) they represent different cell sizes (see Fig. 4 for measured cell radius histograms and corresponding Schulz distribution fit). Two cell concentrations (Table I) were realized for each cell line, with each concentration having two to three independent replicates of biophantoms. The cell concentration was calculated using the method described in [21, Section IV-A].

Fig. 4.

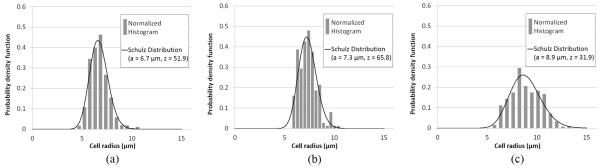
Measured cell radius distribution and Schulz distribution fit for (a) CHO cells, (b) MAT cells, and (c) 4T1 cells. The size of live cells was measured by light microscope using a procedure detailed in [20]. The normalized histograms were generated from results of 500 CHO, 200 MAT, and 200 4T1 cell size measurements. The mean radius is 6.7, 7.3, and 8.9 μm for CHO, MAT, and 4T1 cells, respectively. The fitted Schulz width factor z is 51.9, 65.8, and 31.9 for CHO, MAT, and 4T1 cells, respectively.

TABLE I.

Summary of the Cell Concentrations for Cell Pellet Biophantoms of the Three Cell Lines.

	Concentration 1		Concentration 2
Cell line	Number density (Mcell/mL)	Volume fraction (%)	Number density (Mcell/mL)	Volume fraction (%)
CHO	20	2.7	556	74
MAT	20	3.4	442	74
4T1	20	6.1	244	74

The cell concentration is represented by number density in million cells/mL (Mcell/mL) and volume fraction (%).

The detailed procedure of constructing cell pellet biophantoms is as follows. The cells were cultured in an ATCC-recommended medium along with 8.98% of fetal bovine or calf serum (Hyclone laboratories, Logan, UT) and 1.26% of antibiotic (Hyclone Laboratories). A reichert bright-line hemacytometer (Hausser Scientific, Buffalo, NY) was used to count viable cells to yield the number of cells per known volume. Equal volumes of the dye Trypan blue (Hyclone Laboratories) and cell suspension were gently mixed by pipetting and then added to the counting chambers of the hemacytometer. Trypan blue was used to differentiate nonviable cells (stained as blue cells) from viable cells (displayed as bright cells). At this point, the cells had an average of over 90% viability. a known number of cells was placed in a 50-ml conical centrifuge tube (Corning Inc., Corning, NY), and spun in a 4°C centrifuge at 2500 rpm for 10 min, and the supernatant was removed. Then 90 μL of bovine plasma were added to the cell sediment in the centrifuge tube, which was then vortexed. next, 60 μL of bovine thrombin were added, and the mixture was lightly agitated to coagulate and form a biophantom. The biophantom was transferred onto a planar poly(methyl methacrylate) (PMMA) plate, and submerged in Dulbecco’s phosphate buffered saline (DPBS; Sigma-Aldrich) for ultrasonic scanning.

B. Experimental Setup and BSC Estimation Method

The biophantoms were ultrasonically scanned using three single-element, weakly focused transducers [20-MHz transducer IS2002HR, from Valpey Fisher Corp., Hopkinton, MA; 40- and 80-MHz transducers from the national Institutes of Health (NIH) High-Frequency Transducer Resource Center, University of Southern California, Los Angeles, CA; see Table II]. The total frequency range covered was from 11 to 105 MHz.

TABLE II.

Transducer Information and Characteristics.

Center frequency (MHz)	−10-dB bandwidth (MHz)	Wavelength at center frequency (μm)	f-number	−6-dB depth of field (mm)	−6-dB beam width (μm)
20	11–33	75.0	3.0	4.0	230
40	26–65	37.5	3.0	2.4	113
80	49–105	18.8	3.0	1.2	56.4

The transducers were interfaced with a UTEX UT340 pulser/receiver (UTEX scientific Instruments Inc., Mississauga, ON, Canada) that operated in the pitch-catch mode. A 50DR-001 BNC attenuator (JFW Industries Inc., Indianapolis, IN) was connected to the pulser to attenuate the driving pulse to avoid transducer saturation. An RDX-6 diplexer (Ritec Inc., Warwick, RI) was used to separate the transmitted and received signals because only the transmitted signal needed to be attenuated. The received RF signals were acquired using a 10-bit agilent U1065a-002 A/D card (Agilent Technologies Inc., Santa Clara, CA) set to sample at 1 GHz. The transducers were moved using a precision motions control system (Daedal Parker Hannifin Corp., Irwin, PA) that has a linear spatial accuracy of 1 μm. The biophantoms were placed on the PMMA plate during ultrasound scans. The scans were performed in a small tank filled with DPBS at room temperature (Fig. 5).

Fig. 5.

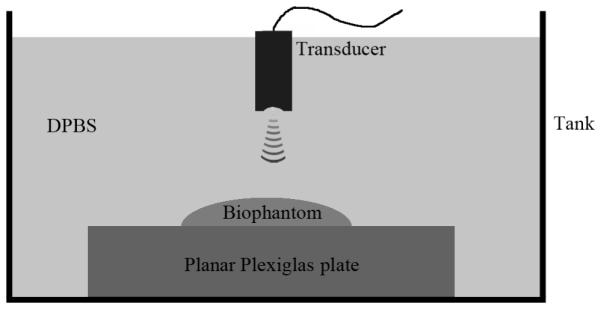
Diagram of the experimental setup for attenuation and BSC measurements.

Attenuation and BSC measurements were performed for each sample. The attenuation was determined to allow for attenuation compensation during the BSC estimation process. an insertion-loss broadband technique [38] was used to estimate the attenuation. The insertion loss was determined by comparing the power spectra of the echoes reflected off the top surface of the PMMa with and without the sample being inserted in the ultrasound path. The transducer focus was positioned at the PMMA surface when the signal was being recorded. The effect of dPbs attenuation was compensated for when the biophantom attenuation was estimated from the insertion loss. The attenuation (in decibel per centimeter) of a sample was generated by averaging the attenuation obtained from 36 independent locations laterally across the sample.

The BSC scanning procedure started with acquiring the reference signals from the DPBS–PMMA interface whose pressure reflection coefficient at room temperature is known (= 0.37). The reference signals were acquired at the set of axial positions that covered the −6-db depth of focus with a step size of a half wavelength. next, a raster scan on the biophantom sample was performed with a lateral step size of one beam width. The transducer focus was positioned in the sample during the scan. The scan covered a sufficient length both axially and laterally to make sure that a sufficient number of regions of interest (ROIs) could be acquired and processed. Eleven equally spaced slices were imaged for each sample, and the number of A-lines per sample varied depending on the transducer frequency and sample size. The BSC was estimated from the RF data using a planar reference method [39] to remove equipment-dependent effects. To generate a BSC versus frequency curve for a sample scanned by a single transducer, 1) a BSC estimate was made for each ROI based on the gated RF echo data from that ROI; 2) a mean BSC was estimated for each of the 11 slices by averaging the BSCs from all the ROIs within that slice; and 3) the 11 mean BSCs were averaged.

C. B-Spline Fit and Structure Function Estimation

Two concentrations (Table I) were studied for each cell line: the higher concentration was chosen to be as high as possible to mimic the cell concentration in tumors, and the lower concentration was chosen to be sufficiently low such that the structure function can be assumed to be unity, while still high enough to ensure sufficient signal-to-noise ratio in the backscatter data. based on these conditions, the structure function for the higher concentration may be obtained experimentally by

$$S\left(f\right)=\frac{{\stackrel{‒}{n}}_{\mathrm{L}}{\mathrm{BSC}}_{\mathrm{H}}\left(f\right)}{{\stackrel{‒}{n}}_{\mathrm{H}}{\mathrm{BSC}}_{\mathrm{L}}\left(f\right)},$$ (14)

where n̄_L and n̄_H represent the number density for the lower and the higher concentrations, respectively, BSC_L(f) and BSC_H(f) represent the BSC for the lower and the higher concentrations, respectively.

There were several BSC versus frequency curves obtained from multiple transducers and multiple realizations for each concentration of each cell line. A B-spline fit was performed on these curves to generate a single fitted curve that covered the entire frequency range (from 11 to 105 MHz) for a concentration of a cell line. The fitted BSC values were used for structure function estimation using (14).

The B-spline is a commonly used smoothing spline for large data sets. The advantage of a smoothing spline is that the resulting curve is not required to pass through each data point. The resulting B-spline curve is a linear combination of M B-spline basis functions, where M is the degrees of freedom, and the B-spline basis functions are spaced at different locations to provide local shape control. In this study, we fit cubic b-splines with five degrees of freedom, giving us five B-spline basis curves at five equally spaced locations in the frequency range. The best-fit B-spline is then a linear combination of five B-spline basis functions:

$$\mathrm{bs}\left(f\right)=\sum _{i=1}^5{\beta }_i{b}_i\left(f\right),$$ (15)

where b_i(f) is the ith B-spline basis function, and β_i is the corresponding coefficient of each basis function to control the shape locally. The calculation of b_i(f) and the least square estimation of β_i are performed using custom programs developed in Matlab (The MathWorks Inc., Natick, MA).

IV. Results and Discussion

A. BSC Estimates and B-Spline Fit

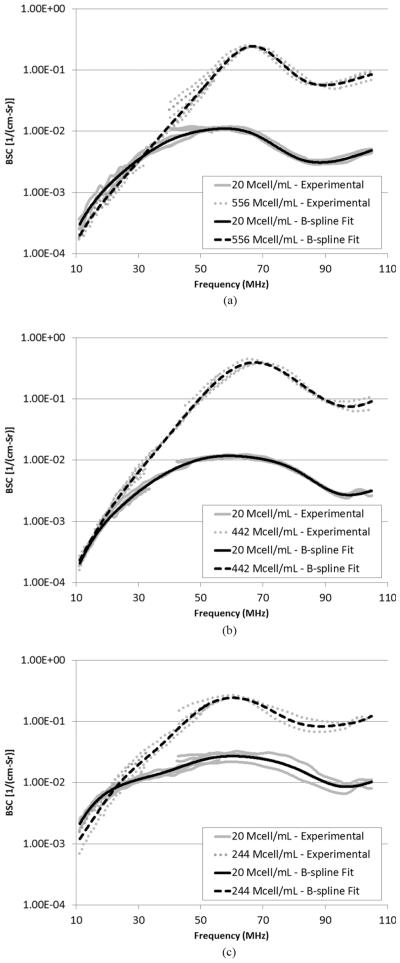
The attenuation-compensated BSC estimates for the biophantoms are shown in Fig. 6 for each cell line. The BSC curves of all realizations were plotted to show the degree of measurement uncertainty and/or the uncertainty in concentration control. overall, multiple realizations had consistent BSC results.

Fig. 6.

BSC versus frequency for (a) CHO, (b) MAT, and (c) 4T1 cell pellet biophantoms measured using three transducers with center frequencies at 20, 40, and 80 MHz, respectively. The B-spline curve is also displayed for each concentration.

The BSC behaviors in Fig. 6 reveal significant information about the structure function. The BSC shape is significantly different between the lower and higher concentrations for all three cell lines. This observation confirms that it is necessary to consider the structure function for the higher concentration condition. The BSC magnitude appears to be similar between the lower and higher concentrations at lower frequencies (f < 30 MHz), whereas the difference in BSC magnitudes of the two concentrations start to increase at higher frequencies (f ~ 60 MHz). a physical interpretation of this behavior is that the effect of cell position correlation on scattering for the high-concentration case is destructive at frequencies lower than 30 MHz, and is constructive (or less destructive) at around 60 MHz. This interpretation is consistent with the shape of the theoretical structure functions presented in Figs. 1–3: the structure functions are lower than unity at lower ka values, and are peaking at around ka = 2. Furthermore, a peak at around 60 MHz, and a dip at around 90 MHz are observed for every BSC curve. The peak and dip behavior for the lower-concentration case is explained by form factors (e.g., fluid-filled sphere, concentric spheres) that match the geometry and acoustic impedance distribution of individual cells. The peak for the higher concentration is sharper compared with the lower concentration. none of the commonly used form factors could yield such a sharp peak [22], indicating that other factors such as the structure function might contribute to the sharp peak.

B. Experimental and Theoretical Structure Functions

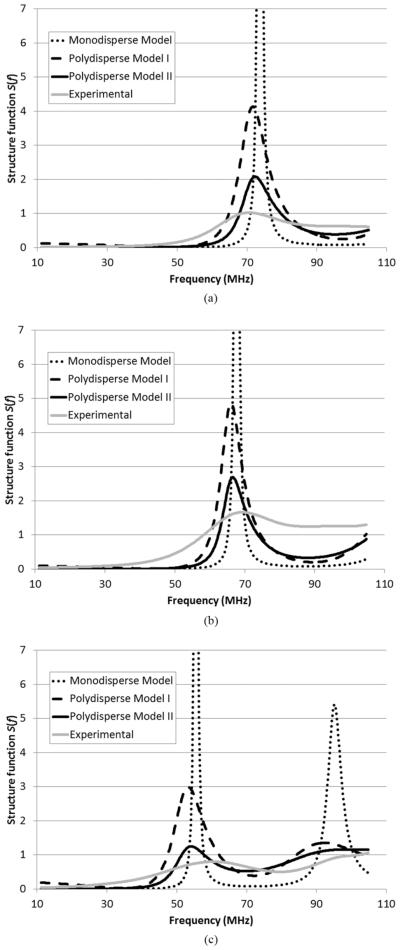
The experimental structure function (Fig. 7) for concentration 2 (see Table I) was determined using (14) assuming the structure function was unity for concentration 1 as discussed in details in Section IV-E. The theoretical structure functions (Fig. 7) for concentration 2 were calculated using the three structure function models. For the theoretical calculation, the volume fraction was assumed to be 74% for concentration 2. The values of parameters a and z used for theoretical calculation were the same as the Schulz distribution fit results presented in Fig. 4. To convert from k to f, a propagation speed of 1540 m/s was assumed throughout this paper.

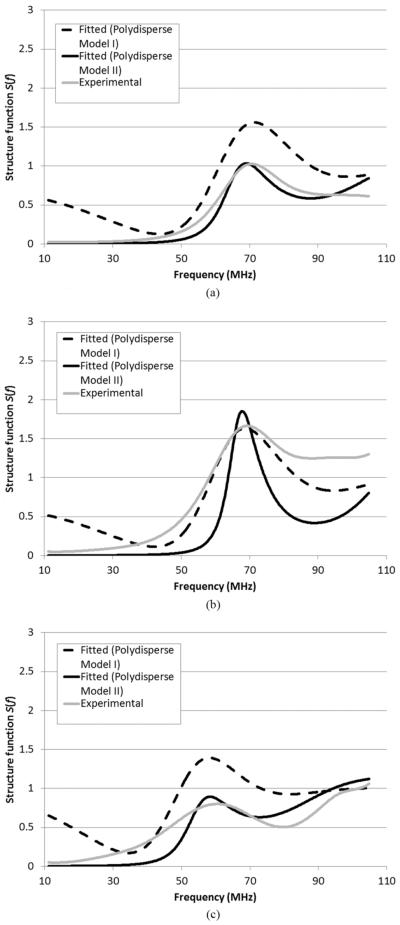
Fig. 7.

Comparison between experimental structure functions (solid gray lines) and theoretical structure functions (dotted lines: monodisperse model, dashed lines: polydisperse model I, solid dark lines: polydisperse model II) for high-concentration (a) CHO, (b) MAT, and (c) 4T1 cell pellet biophantoms.

Fig. 7 shows that the theoretical structure functions from the three models have a peak-dip pattern consistent with that of the experimental structure function. The positions of the peaks and dips are well aligned between the theoretical and experimental curves. However, the exact magnitude of the major peak varies among the theoretical and experimental curves. The monodisperse model shows the highest peak, which extends well above 7 and is clipped in Fig. 7. Polydisperse model I shows a lower peak, and polydisperse model II shows the lowest peak among all three models. relative to the magnitude of the peak, polydisperse model II has the best agreement to the experimental curve, and therefore seems to be the most accurate model out of the three.

Although the theoretical curves of the two polydisperse models show agreement with the experimental curves, the agreement is not perfect. a perfect agreement is not expected because the scattering of cells is so complex that many factors could contribute to scattering. The structure function only models one factor, the spatial correlation of cell positions, and shows that this factor is important. other factors, such as multiple scattering, might explain in general why the polydisperse models do not perfectly agree with experimental data. That being said, we try herein to explain, within the framework of structure function, several observed discrepancies between the model and the experimental data. The polydisperse models seem to work better for CHO and MAT than for 4T1. This observation might be attributed to the fact that 4T1 has the highest degree of polydispersity among all the three cell lines. a higher degree of polydispersity leads to a smoother peak in the structure function. a smooth peak is easier to be shifted as a result of measurement errors than a sharp peak. another noticeable difference between the theoretical and experimental curves is that the peak of the theoretical curves is higher than that of the experimental curves. There could be several explanations for this difference. We might have underestimated the polydispersity of cells. We have considered only the polydispersity in cell size, but not the polydispersity in cell shape. Experimental errors might as well contribute to the difference. For instance, if the attenuation was underestimated for the higher concentration, then the BSC might be underestimated consequently, resulting in an underestimated experimental structure function. also, the volume fraction of 74% might have uncertainty. If the actual volume fraction was slightly deviated from 74%, then the theoretical structure functions in Fig. 7 would be slightly different as well.

C. Inverse Problem

The usefulness of polydisperse models I and II is demonstrated herein via solving the inverse problem: estimating the mean radius from experimental structure functions. The monodisperse model is not evaluated for the inverse problem because it has been shown in Section IV-B to be less accurate than polydisperse models I and II.

The mean radius a and the Schulz width factor z were the unknowns in the inverse problem. The volume fraction was assumed to be known a priori (η = 74%). The two unknowns were estimated by fitting the theoretical structure function SF_theo to the experimental structure function SF_exp(f). Specifically, we perform an exhaustive search procedure for values of (a, z) ∈ [4 μm, 12 μm] × [5, 100] to minimize the cost function

$$C(a,z)=\sum _i\mid \mid {\mathrm{SF}}_{\mathrm{theo}}\left(f_i\right)-{\mathrm{SF}}_{\exp }\left(f_i\right)\mid {\mid }^2,$$ (16)

over the frequency range from 11 to 105 MHz.

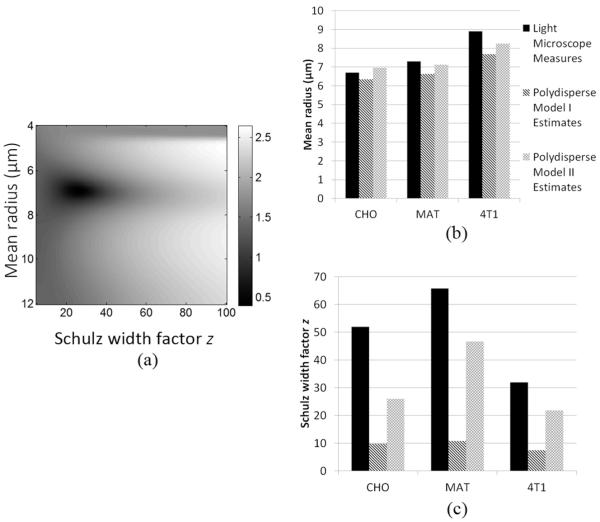
The results of the search show that a unique global minimum always exists for the CHO, MAT, and 4T1 cell pellets for polydisperse model I and polydisperse model II. A typical logarithm of the cost function C(a, z) is shown in Fig. 8(a). The mean radius estimates and the Schulz width factor estimates are shown in Figs. 8(b) and 8(c), respectively. Overall polydisperse models I and II yield relatively accurate mean radius estimates, with a maximum percentage error of 13.5% for polydisperse model I and 6.7% for polydisperse model II for all three cell lines evaluated. as expected, polydisperse model II provides slightly better size estimates than does polydisperse model I. The Schulz width factor estimates are not as accurate as the mean radius estimates. Both polydisperse models underestimate the Schulz width factor, i.e., overestimate the degree of polydispersity in cell size, possibly because the polydispersity in cell shape might also contribute to scattering and could decrease the estimated Schulz width factor value. It is not surprising that polydisperse model II yields a better Schulz width factor estimate than does polydisperse model I, because polydisperse model II takes into account the polydispersity in scattering amplitude to some extent, whereas polydisperse model I does not. Although the Schulz width factor z is underestimated by the models, the estimated z values are accurate in relative terms: 4T1 has the lowest z values, both measured and estimated, and MAT has the highest z values, both measured and estimated.

Fig. 8.

(a) A representative 2-D cost function map: the logarithm of the cost function C(a, z) for polydisperse model II obtained from experimental structure function for CHO. (b) a comparison between the mean radii estimated by polydisperse model I and II and direct light microscope measures. (c) A comparison between the estimated and directly measured parameter z. The legends in (c) are the same as in (b).

The fitted structure function curves (Fig. 9) show good agreement with the experimental curves in terms of peak positions. This observation is consistent with the relatively good accuracy in size estimates, because the position of the peak is mainly determined by the cell size. Polydisperse model II appears to have better fitted curves than polydisperse model I in terms of agreement in the peak magnitude (Fig. 9). This observation might explain why polydisperse model II has better Schulz width factor estimates, because the peak magnitude is presumably related to the Schulz width factor more than to the mean radius.

Fig. 9.

A comparison between experimental and best-fit structure function curves for (a) CHO, (b) MAT, and (c) 4T1.

D. Comparison With Gaussian and Fluid-Filled Sphere BSC Models

To test whether fitting the structure function curves could yield better mean cell radius than fitting BSC curves, we fit two commonly used BSC models, the spherical Gaussian and the fluid-filled sphere model, to the high-concentration BSC curves presented in Fig. 6. both BSC models take into account only the geometry and acoustic impedance profile of the cells, but not the spatial correlation of cell positions. The detailed estimation procedure can be found in [10]. The estimated effective scatterer radius from the two BSC models is compared with the estimated mean cell radius from the two polydisperse structure function models (Fig. 10). The two polydisperse structure function models show advantage in terms of estimating the cell radius. They yield relatively accurate mean cell radius estimates, whereas the two BSC models do not. one might argue that the effective scatterer size estimates from the two BSC models might correspond to the size of cell nucleus. In fact, this argument pointed out a significant disadvantage of the two BSC models: it is difficult to relate the effective scatterer size estimates to real tissue anatomy. It is not clear if the effective scatterer size estimates relate to the cell radius, the nucleus radius, or anything else. This ambiguity does not exist in the polydisperse structure function models. The estimated mean scatterer radius from the polydisperse structure function models can only be related to the cell radius, because the models describe the spatial correlation of scatterer positions, which is affected by the cells as opposed to the nuclei.

Fig. 10.

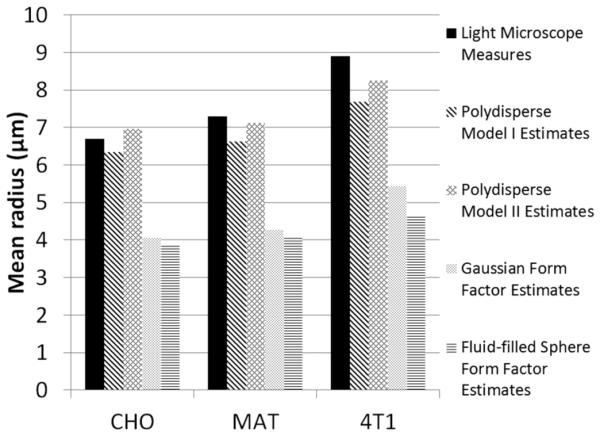
A comparison between the estimated effective scatterer radius from two BSC models (the spherical Gaussian and the fluid-filled sphere model) and the estimated mean cell radius from the two polydisperse structure functions models presented in this paper.

E. The Theoretical Structure Function for Concentration 1

A basic assumption for the experimental structure function curves presented in Fig. 7 is that the structure function is unity for concentration 1. This subsection investigates if the assumption is reasonable.

We start with calculating the theoretical structure function curves for concentration 1 predicted by monodisperse model, polydisperse model I, and polydisperse model II (Fig. 11), and compare them to unity. The volume fraction values in Table I (2.7% for CHO, 3.4% for MAT, and 6.1% for 4T1) and the size distribution parameters in Fig. 4 are used for theoretical structure function calculation. at frequencies above 40 MHz, Fig. 11 shows no noticeable difference between unity and the theoretical structure function curves for concentration 1. slight (compared with concentration 2) but noticeable difference appears at the lower frequency end. overall, the unity assumption of structure function for concentration 1 appears to be reasonable, which may be further demonstrated by comparing the difference between size parameters estimated with and without the unity assumption.

Fig. 11.

Theoretical structure function curves for concentration 1 predicted by [(a) and (b)] monodisperse model, (c) polydisperse model I, and (d) polydisperse model II, along with the curves for concentration 2 for comparison. (b) is a zoomed-in version of (a).

Size parameters were estimated in Section IV-C by fitting the theoretical structure function curves to the experimental curves, under the unity assumption. If the unity assumption does not hold, then the accurate way of fitting the data to an equation would be to fit the ratio of the theoretical structure function of concentration 2 to concentration 1, to the experimental structure function curves presented in Fig. 7. Eq. (16) should be revised as

$$C(a,z)=\sum _i{\Vert \frac{{\mathrm{SF}}_{\mathrm{theo},\mathrm{conc}2}\left(f_i\right)}{{\mathrm{SF}}_{\mathrm{theo},\mathrm{conc}1\left(f_i\right)}}-{\mathrm{SF}}_{exp}\left(f_i\right)\Vert }^2,$$ (17)

where the subscripts conc1 and conc2 represent concentration 1 and concentration 2, respectively. The cell size parameters (a and z) estimated using this approach (17) appear to be sufficiently close to those estimated using the unity assumption (Table III), suggesting that the unity assumption is reasonable.

TABLE III.

Comparison Between Cell Size Parameters Estimated With and Without the Assumption That the Structure Function Curve for Concentration 1 is Unity.

	Estimated mean radius a (μm)		Estimated Schulz width factor z
Cell line	Polydisperse model I	Polydisperse model II	Polydisperse model I	Polydisperse model II
CHO	6.4 (6.4)	7.0 (7.0)	9.8 (10.4)	26.0 (26.1)
MAT	6.6 (6.7)	7.1 (7.1)	10.8 (11.0)	46.6 (46.8)
4T1	7.7 (7.9)	8.3 (8.3)	7.5 (8.5)	21.8 (22.0)

The numbers in parentheses represents estimated values without the unity assumption.

The preceding analysis also suggests that the frequency matters for determining at what concentration levels the structure function can be assumed to be unity. a previous study [28] at lower frequencies (ka < 0.5) showed that the structure function cannot be assumed to be unity for concentrations greater than 2.5%. The frequency range of our study extends up to ka = 3. For such a broad frequency range, a volume fraction of around 6.1% still seems to be sufficiently low for assuming a unity structure function. For high concentrations such as 74% volume fraction, however, the structure function is significant for both lower and higher frequencies.

F. Theoretical Implications of the Structure Function Models

The central problem we are trying to address is to elucidate the mechanism(s) of ultrasonic scattering at high concentrations and to model the scattering. Our results seem to support the hypothesis that the scattering at high concentrations is determined by both the scattering from individual scatterers [Φ_i(2k)] and the correlation of scatterer positions (the structure function). Without taking into account the contributions from the correlation of scatterer positions, it proves extremely difficult to interpret the BSC data for high-concentration media. The sharp peak in the BSC of high-concentration biophantoms (Fig. 6) cannot be explained alone by the fluid-filled sphere model or the more complex concentric spheres model that has worked well for the low-concentration case. neither the fluid-filled sphere model nor the concentric spheres model provides a satisfactory fit to the high-concentration BSC data ([22, Figs. 5 and 6]). Force-fitting those models to the data does not yield reasonable size estimates either ([22] and Section IV-D of the present paper). On the other hand, the structure function models could explain the data better and yields relatively accurate size estimates. This fact indicates the possible important role of correlation of scatterer positions on scattering.

This study also demonstrates the significant role of polydispersity on structure function. The monodisperse model, which does not take into account the polydispersity of scatterers, does not fit the data very well, although it could qualitatively explain the peaks in the experimental structure functions. Two types of treatment to the polydispersity issue have been considered: Polydisperse model I assumes polydispersity in scatterer size and monodispersity in individual scattering amplitudes Φ_i(2k), whereas polydisperse model II assumes polydispersity in both scatterer sizes and scattering amplitudes. Polydisperse model II has been shown to be better than polydisperse model I based on the biophantom data. This suggests that to achieve the best result, the scattering amplitude function Φ_i(2k) may not be decoupled from the structure function.

G. Practical Usefulness of the Structure Function Models

The structure function provides additional new information about tissue structure, independent of the information provided by BSC and attenuation. From the structure function, we may be able to estimate tissue properties such as the mean scatterer radius and the Schulz width factor. In the future, parameters such as the Schulz width factor could potentially be explored for tissue characterization. For instance, the Schulz width factor could be used for detecting cell death, because an earlier work [29] has shown that the cellular size variance increases after cell death.

The structure functions expressed in the models have a limited number of parameters. The structure function is not dependent on the acoustic property contrast between the scatterer and the background. For instance, the acoustic impedance contrast between the scatterer and the background is not affecting the structure function. nor is mass density an issue to be considered in the models. The limited number of parameters makes it more likely to find a unique global minimum in the inverse problem.

The experimental setup in this paper requires the measurement of biophantoms of two concentrations, with the lower concentration serving the reference purpose. This was designed primarily for dissecting the BSC, demonstrating the role of scattering position correlation on scattering, and quantifying that role in terms of structure function. It is difficult to directly implement this setup in clinical settings. However, with the models developed through this setup, we are progressing toward accurately modeling the BSC from high-concentration scattering media by combining the structure functions with appropriate form factors. If that were successful, then the requirement of measuring a low-concentration biophantom as a reference would be eliminated.

V. Conclusion

The correlation of scatterer positions has significant contributions to the scattering of dense media. This contribution could be modeled by the structure functions. The polydispersity of the scatterer size has a significant effect on the structure functions, and should be taken into account in structure function models. Polydisperse structure function models could lead to improved modeling of scattering from dense media.

Biographies

Aiguo Han was born in Jiangsu, China, in 1986. He graduated from nanjing University, Nanjing, China, in 2008 with a B.S. degree in acoustics. after graduation, he began his graduate studies at the University of Illinois at Urbana-Champaign, Urbana, IL. In August 2009, he joined the Bioacoustics Research Laboratory, where he completed his M.S. thesis in electrical and computer engineering in 2011, and is now pursuing a Ph.D. degree in the same field. His research interests include ultrasonic wave propagation in heterogeneous media, quantitative ultrasound imaging, tissue characterization, and computational methods. He is a student member of IEEE and the Acoustical Society of America.

William D. O’Brien, Jr. (S’64–M’70–SM’79–F’89–LF’08) received the B.S., M.S., and Ph.D. degrees from the University of Illinois at Urbana-Champaign. From 1971 to 1975, he worked with the bureau of radiological Health (currently the Center For Devices and Radiological Health) of the U.S. Food and Drug Administration. In 1975, he joined the faculty at the University of Illinois. He is currently research Professor of Electrical and Computer Engineering and director of the Bioacoustics Research Laboratory. Prior to becoming a research Professor, he was the donald biggar Willet Professor of Engineering. His research interests involve the many areas of ultrasound–tissue interaction, including biological effects and quantitative ultrasound imaging, for which he has published 390 papers. dr. o’brien is a life Fellow of IEEE, a Fellow of the acoustical society of america, and a Fellow of the american Institute of Ultrasound in Medicine, and is a Founding Fellow of the american Institute of Medical and biological Engineering. He was recipient of the IEEE centennial Medal in 1984, the AIUM Presidential recognition awards in 1985 and 1992, the AIUM/WFUMB Pioneer award in 1988, the IEEE outstanding student branch counselor award for region 4 in 1989, the AIUM Joseph H. Holmes basic science Pioneer award in 1993, the IEEE Ultrasonics, Ferroelectrics, and Frequency control society distinguished lecturer for 1997–1998, the IEEE Ultrasonics, Ferroelectrics, and Frequency control society’s achievement award in 1998, the IEEE Millennium Medal in 2000, the IEEE Ultrasonics, Ferroelectrics, and Frequency control society’s distinguished service award in 2003, the AIUM William J. Fry Memorial lecture award in 2007, and the IEEE Ultrasonics, Ferroelectrics, and Frequency control society’s rayleigh award in 2008. He has served as President (from 1982 to 1983) of the IEEE sonics and Ultrasonics Group (currently the IEEE Ultrasonics, Ferroelectrics, and Frequency control society), Editor-in-chief (from 1984 to 2001) of the IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, and President (from 1988 to 1991) of the american Institute of Ultrasound in Medicine.

Appendix A Analytical Expression of the Structure Function for Polydisperse Model I

The structure function expressed in (10) is a double integral, where the probability density function f(x) was given in (11), and the partial structure functions H_ij was given by blum and stell [36]. The analytical expression of (10) has been derived in [25, Eq. (2)]. For backscattering, [25, Eq. (2)] may be modified as (A1), see above, where

$$\begin{array}{cc}\hfill & S\left(2k\right)=1-\frac{\stackrel{‒}{n}}{4k^3({\Xi }^2+{{\rm Y}}^2)}\times \lambda [\lambda ({\rm Y}{\delta }_1-\Xi {\delta }_6)+{\lambda }^{\prime }({\rm Y}{\delta }_2-\Xi {\delta }_4)+\mu (\Xi {\delta }_1+{\rm Y}{\delta }_6)+{\mu }^{\prime }(\Xi {\delta }_2+{\rm Y}{\delta }_4)]\hfill \\ \hfill & +{\lambda }^{\prime }[\lambda ({\rm Y}{\delta }_2-\Xi {\delta }_4)+{\lambda }^{\prime }({\rm Y}{\delta }_3-\Xi {\delta }_5)+\mu (\Xi {\delta }_2+{\rm Y}{\delta }_4)+{\mu }^{\prime }(\Xi {\delta }_3+{\rm Y}{\delta }_5)]\hfill \\ \hfill & +\mu [\lambda (\Xi {\delta }_1+{\rm Y}{\delta }_6)+{\lambda }^{\prime }(\Xi {\delta }_2+{\rm Y}{\delta }_4)+\mu (\Xi {\delta }_6-{\rm Y}{\delta }_1)+{\mu }^{\prime }(\Xi {\delta }_4-{\rm Y}{\delta }_2)]\hfill \\ \hfill & +{\mu }^{\prime }[\lambda (\Xi {\delta }_2+{\rm Y}{\delta }_4)+{\lambda }^{\prime }(\Xi {\delta }_3+{\rm Y}{\delta }_5)+\mu (\Xi {\delta }_4-{\rm Y}{\delta }_2)+{\mu }^{\prime }(\Xi {\delta }_5-{\rm Y}{\delta }_3)]\hfill \end{array}$$ (A1)

$$\begin{array}{cc}\hfill \Xi =& 1-(2\pi ∕\Delta )\left(1+\frac{1}{2}\pi {\xi }_3∕\Delta \right)\stackrel{‒}{n}{\left(2k\right)}^{-3}(2k{\zeta }^{\prime }-\psi )\hfill \\ \hfill & -(2\pi ∕\Delta )\stackrel{‒}{n}{\left(2k\right)}^{-2}\left[({\chi }^{\prime }-{\zeta }^{\prime })+\left(\frac{1}{4}\pi {\xi }_2∕\Delta \right)({\chi }^{\prime \prime }-{\zeta }^{\prime \prime })\right]\hfill \\ \hfill & -{(\pi ∕\Delta )}^2\left(\frac{\stackrel{‒}{n}}{4k^2}\right)(\chi -1)({\chi }^{\prime \prime }-{\zeta }^{\prime \prime })-{({\chi }^{\prime }-{\zeta }^{\prime })}^2\hfill \\ \hfill & -(2k{\zeta }^{\prime }-\psi )(2k{\zeta }^{\prime \prime \prime }-{\psi }^{\prime \prime })+{(2k{\zeta }^{\prime \prime }-{\psi }^{\prime })}^2,\hfill \end{array}$$ A2a

$$\begin{array}{cc}\hfill {\rm Y}=& (2\pi ∕\Delta )\left(1+\frac{1}{2}\pi {\xi }_3∕\Delta \right)\stackrel{‒}{n}{\left(2k\right)}^{-3}(\chi +2k^2{\zeta }^{\prime \prime }-1)\hfill \\ \hfill & -(2\pi ∕\Delta )\stackrel{‒}{n}{\left(2k\right)}^{-2}\left[(2k{\zeta }^{\prime \prime }-{\psi }^{\prime })+\left(\frac{1}{4}\pi {\xi }_2∕\Delta \right)(2k{\chi }^{\prime \prime \prime }-{\zeta }^{\prime \prime })\right]\hfill \\ \hfill & -{(\pi ∕\Delta )}^2{\left(\frac{\stackrel{‒}{n}}{4k^2}\right)}^2(2k{\zeta }^{\prime }-\psi )({\chi }^{\prime \prime }-{\zeta }^{\prime \prime })\hfill \\ \hfill & -2(2k{\zeta }^{\prime \prime }-{\psi }^{\prime })({\chi }^{\prime }-{\zeta }^{\prime })+(2k{\zeta }^{\prime \prime \prime }-{\psi }^{\prime \prime })+(\chi -1),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\delta }_1=(\pi ∕\Delta )\left\{2+(\pi ∕\Delta )\left[{\xi }_3-\frac{\stackrel{‒}{n}}{2k}(2k{\zeta }^{\prime \prime \prime }-{\psi }^{\prime \prime })\right]\right\},\hfill \\ \hfill & {\delta }_2={(\pi ∕\Delta )}^2\frac{\stackrel{‒}{n}}{2k}(2k{\zeta }^{\prime \prime }-{\psi }^{\prime }),\hfill \\ \hfill & {\delta }_3=-{(\pi ∕\Delta )}^2\frac{\stackrel{‒}{n}}{2k}(2k{\zeta }^{\prime }-\psi ),\hfill \\ \hfill & {\delta }_4=(\pi ∕\Delta )\left[2k-(\pi ∕\Delta )\frac{\stackrel{‒}{n}}{2k}({\chi }^{\prime }-{\zeta }^{\prime })\right],\hfill \\ \hfill & {\delta }_5={(\pi ∕\Delta )}^2\left[\frac{\stackrel{‒}{n}}{2k}(\chi -1)+k{\xi }_2\right],\hfill \\ \hfill & {\delta }_6={(\pi ∕\Delta )}^2\frac{\stackrel{‒}{n}}{2k}({\chi }^{\prime \prime }-{\zeta }^{\prime \prime }),\hfill \end{array}$$ A3

and

$$\begin{array}{cc}\hfill & {\zeta }^{\prime }=bc,\hfill \\ \hfill & {\zeta }^{\prime \prime }=b^{2}c(c+1),\hfill \\ \hfill & {\zeta }^{\prime \prime \prime }=b^{3}c(c+1)(c+2),\hfill \\ \hfill & \psi =v_1^{c∕2}\sin \left[c{\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & {\psi }^{\prime }=bc{v}_1^{(c+1)∕2}\sin \left[(c+1){\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & {\psi }^{\prime \prime }=b^{2}c(c+1)v_1^{(c+2)∕2}\sin \left[(c+2){\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & \mu =2^c{v}_2^{c∕2}\sin \left[c{\tan }^{-1}\left(bk\right)\right]\hfill \\ \hfill & {\mu }^{\prime }=2^{c+1}bc{v}_2^{(c+1)∕2}\sin \left[(c+1){\tan }^{-1}\left(bk\right)\right],\hfill \\ \hfill & \chi =v_1^{c∕2}\cos \left[(c+1){\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & \chi {=}^{\prime }bc{v}_1^{(c+1)∕2}\cos \left[(c+1){\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & \chi {=}^{\prime \prime }{b}^{2}c(c+1)v_1^{(c+2)∕2}\cos \left[(c+2){\tan }^{-1}\left(2bk\right)\right],\hfill \\ \hfill & \lambda =2^c{v}_2^{c∕2}\cos \left[c{\tan }^{-1}\left(bk\right)\right],\hfill \\ \hfill & {\lambda }^{\prime }=2^{(c+1)}bc{v}_2^{(c+1)∕2}\cos \left[(c+1){\tan }^{-1}\left(bk\right)\right],\hfill \\ \hfill & v_1={[1+{\left(2bk\right)}^2]}^{-1},v_2={[4+{\left(2bk\right)}^2]}^{-1},\hfill \end{array}$$ (A4)

and

$$\begin{array}{cc}\hfill & {\xi }_2=\stackrel{‒}{n}{b}^{2}c(c+1),{\xi }_3=\stackrel{‒}{n}{b}^{3}c(c+1)(c+2),\hfill \\ \hfill & \Delta =1-\pi {\xi }_3∕6,b=2a∕(z+1),c=z+1.\hfill \end{array}$$

We point out two typographic errors in the expression for Θ in [25, Eq. (2)]. The expression for Θ is correctly printed in (A2a). We also point out that (A4) was modified from [37, Table I] for backscattering.

Appendix B Analytical Expression of the Structure Function for Polydisperse Model II

We start from (13) to derive the analytical expression of the structure function for polydisperse model II derived from the fluid-filled sphere form factor. The probability density function f(x) and the partial structure functions H_ij in (13) were the same as those in (10). The scattering amplitude Φ_i(2k) in (13) takes the following form derived from the fluid-filled sphere form factor:

$${\Phi }_i\left(2k\right)=\frac{{\gamma }_z}{8k}[\sin \left(2k{x}_i\right)-2k{x}_i\cos \left(2k{x}_i\right)]$$ (A5)

where Γ_z= (2(Z₀ − Z))/Z, which describes the acoustic impedance contrast between the sphere (Z) and the background (Z₀). However, the acoustic impedance contrast is irrelevant to polydisperse model II because Γ_z/(8k) is a common factor between the numerator and denominator of the fraction in (13), and is cancelled out.

Calculating the double integral in (13) gives the analytical expression of S(2k) for polydisperse model II as

$$S\left(2k\right)=1+\frac{I_N\left(2k\right)}{I_D\left(2k\right)},$$ (A6)

where

$$I_N\left(2k\right)=(M-k{\Lambda }^{\prime })∕\stackrel{‒}{n},$$

$$\begin{array}{cc}\hfill I_D\left(2k\right)=& -\frac{1}{8k^3({\Xi }^2+{{\rm Y}}^2)}\hfill \\ \hfill & \times \Lambda [\lambda ({\rm Y}{\delta }_1-\Xi {\delta }_6)+{\Lambda }^{\prime }({\rm Y}{\delta }_2-\Xi {\delta }_4)]\hfill \\ \hfill & +\mathrm{M}(\Xi {\delta }_1+{\rm Y}{\delta }_6)+{\mathrm{M}}^{\prime }(\Xi {\delta }_2+{\rm Y}{\delta }_4)\hfill \\ \hfill & +{\Lambda }^{\prime }\lambda ({\rm Y}{\delta }_2-\Xi {\delta }_4)+{\Lambda }^{\prime }({\rm Y}{\delta }_3-\Xi {\delta }_5)\hfill \\ \hfill & +\mathrm{M}(\Xi {\delta }_2+{\rm Y}{\delta }_4)+{\mathrm{M}}^{\prime }(\Xi {\delta }_3+{\rm Y}{\delta }_5)\hfill \\ \hfill & +\mathrm{M}\lambda (\Xi {\delta }_1+{\rm Y}{\delta }_6)+{\Lambda }^{\prime }(\Xi {\delta }_2+{\rm Y}{\delta }_4)\hfill \\ \hfill & +\mathrm{M}\left(\right(\Xi {\delta }_6-{\rm Y}{\delta }_1)+{\mathrm{M}}^{\prime }(\Xi {\delta }_4-{\rm Y}{\delta }_2)\hfill \\ \hfill & +{\mathrm{M}}^{\prime }\lambda (\Xi {\delta }_2+{\rm Y}{\delta }_4)+{\Lambda }^{\prime }(\Xi {\delta }_3+{\rm Y}{\delta }_5)\hfill \\ \hfill & +\mathrm{M}(\Xi {\delta }_4-{\rm Y}{\delta }_2)+{\mathrm{M}}^{\prime }(\Xi {\delta }_5-{\rm Y}{\delta }_3),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \Lambda =\psi -k({\zeta }^{\prime }+{\chi }^{\prime }),\hfill \\ \hfill & {\Lambda }^{\prime }={\psi }^{\prime }-k({\zeta }^{\prime \prime }+{{\chi }^{\prime }}^{\prime }),\hfill \\ \hfill & \mathrm{M}=1-\chi -k{\psi }^{\prime },\hfill \\ \hfill & {\mathrm{M}}^{\prime }={\zeta }^{\prime }-{\chi }^{\prime }-k{{\psi }^{\prime }}^{\prime }.\hfill \end{array}$$