Abstract
The unique hues—blue, green, yellow, red—form the fundamental dimensions of opponent-color theories, are considered universal across languages, and provide useful mental representations for structuring color percepts. However, there is no neural evidence for them from neurophysiology or low-level psychophysics. Tapping a higher prelinguistic perceptual level, we tested whether unique hues are particularly salient in search tasks. We found no advantage for unique hues over their nonunique complementary colors. However, yellowish targets were detected faster, more accurately, and with fewer saccades than their complementary bluish targets (including unique blue), while reddish-greenish pairs were not significantly different in salience. Similarly, local field potentials in primate V1 exhibited larger amplitudes and shorter latencies for yellowish versus bluish stimuli, whereas this effect was weaker for reddish versus greenish stimuli. Consequently, color salience is affected more by early neural response asymmetries than by any possible mental or neural representation of unique hues.
Keywords: unique hues, salience, color perception, color psychophysics, color electrophysiology, visual search, response asymmetry
Introduction
The unique hues—blue, green, yellow, red—first described by Leonardo da Vinci with reference to the elements water, air, earth, and fire (da Vinci, 1540), have posed a long-standing conundrum across visual perception, neurophysiology, and cross-cultural linguistics. Unique hues are linguistically salient and provide useful mental representations for organizing and using color percepts, but no direct psychophysical evidence exists for a privileged role, nor is there physiological evidence for a neural substrate. In this study, our aim was to see if we could show enhanced perceptual salience for the unique hues compared to nonunique hues, as could be expected from a privileged neural representation.
Hering (1878; Jameson & Hurvich, 1955) claimed that the phenomenological experience of color can be described in terms of a combination of red–green and blue–yellow color-opponent sensations, as only one sensation of a pair can be evoked by a spatially uniform stimulus. The two pairs thereby constitute a two-dimensional space in which every hue can be located in terms of its redness–greenness combined with its blueness–yellowness (Schrödinger, 1925). In language, unique hues comprise the set of focal colors used most consistently as categories in color-naming tasks (Boynton & Olson, 1990), and are claimed to show demonstrable significance and consistency as color categories across languages and cultures (Berlin & Kay, 1969; Lindsey & Brown, 2009; Regier, Kay, & Cook, 2005). On the other hand, there are no published psychophysical data that support a privileged role for these hues, especially for low-level tasks such as detection, discrimination, adaptation, or induction. For example, unique hues do not correspond to the minima of wavelength-discrimination curves (Holtsmark & Valberg, 1969) or of hue-discrimination thresholds around the color circle (Bachy, Dias, Alleysson, & Bonnardel, 2012), and color induction along different color axes cannot be deduced from color induction along any two privileged axes; that is, it cannot be represented in any two-dimensional linear space (Krauskopf, Zaidi, & Mandler, 1986).
Hering (1878) and others (Abney, 1895) proposed that the unique hues' perceptual primacy was the result of early cone-opponent combinations. To reconcile trichromacy with opponency, Schrödinger (1925) expressed color-opponent mechanisms as linear combinations of cone signals by representing them as straight lines joining opponent unique hues in a chromaticity diagram. Evidence against such a representation was provided by Dimmick and Hubbard's (1939) results that unique-hue pairs are not collinear with neutral white—a nonlinearity that was confirmed with other methods (Ikeda & Ayama, 1980; Larimer, Krantz, & Cicerone, 1974, 1975). These quantitative measurements are consistent with what has long been known to artists: “blue is the complementary of orange, yellow is the complementary of violet” (Vincent van Gogh quoting Eugéne Delacroix, in a letter to his brother Theo van Gogh, April 18, 1885).
A neural substrate for unique hues has also eluded investigators. The receptive fields of retinal ganglion cells (Sun, Smithson, Zaidi, & Lee, 2006) and lateral geniculate nucleus (LGN) cells (Derrington, Krauskopf, & Lennie, 1984) combine L-, M-, and S-cone outputs to correspond to the cardinal axes (L–M) and (S) (Krauskopf, Williams, & Heeley, 1982), but not to unique-hue axes (Webster, Miyahara, Malkoc, & Raker, 2000). Recordings from neurons in macaque striate cortex (Lennie, Krauskopf, & Sclar, 1990) and extrastriate cortex (Kiper, Fenstemaker, & Gegenfurtner, 1997) complicate the picture by revealing cells preferentially tuned to many other colors beyond those characteristic of LGN cells. Cells with narrow hue sensitivities spread over the color circle have also been reported in anterior and posterior inferotemporal (PIT) cortex (Conway, Moeller, & Tsao, 2007; Komatsu, Ideura, Kaji, & Yamane, 1992). This indicates a high-dimensional neural substrate for color percepts, far beyond the two dimensions of Hering's color-opponent mechanisms. Stoughton and Conway (2008) made a case for an overrepresentation of cells tuned to the unique hues in posterior inferior temporal cortex, but this inference was challenged by Mollon (2009).
In spite of these psychophysical and physiological caveats, unique hues remain extremely useful in psychophysical tasks. Mental representations of the two opponent dimensions are invaluable for systematically categorizing object colors (Smithson & Zaidi, 2004), and providing an affine geometry for perceptual color space (Ennis & Zaidi, 2013). The importance of unique hues could also arise from their usefulness in distinguishing between naturally occurring lights and surfaces (Broackes, 2011; Mollon, 2006; Schrödinger, 1925), corresponding to a more complex neural substrate.
Experiment 1: Relative salience of complementary hues
In an attempt to resolve the paradox, we explored whether a search task could reveal a privileged status for unique hues at a higher yet prelinguistic perceptual level. We used a chromatic analog of the search-based subitizing task used by Komban, Alonso, and Zaidi (2011) to show that dark targets are more salient than light targets when presented on equally dark and light binary-noise backgrounds: observers' response times (RTs) were significantly shorter and accuracy higher for detecting the number of dark than light targets. By pitting observers' unique hues against their complementary colors, we compared the salience of unique hues to nonunique colors.
Method
In the initialization task, observers (n = 7) were instructed to select four unique hues (i.e., a red and green that were neither bluish nor yellowish, and a blue and yellow that were neither reddish nor greenish). The unique hues were selected by navigating a gradated patch of hues forming a circle around neutral white, in the isoluminant plane of cardinal color space (Derrington et al., 1984; Krauskopf et al., 1982). With respect to neutral white, unique red was not found to be the complementary of unique green (nor unique yellow the complementary of unique blue), so we paired each observer's four unique hues with their complementary hues from across the color circle. Each color pair was thus equated for cone contrast from neutral white. In addition to the four axes created using unique hues, two pairs were formed from the extrema of the cone-opponent cardinal axes (S and L–M); these were the same for all observers. Figure 1 shows the polar coordinates of unique-hue choices for each observer in the isoluminant color plane formed by the cardinal axes.
Figure 1.
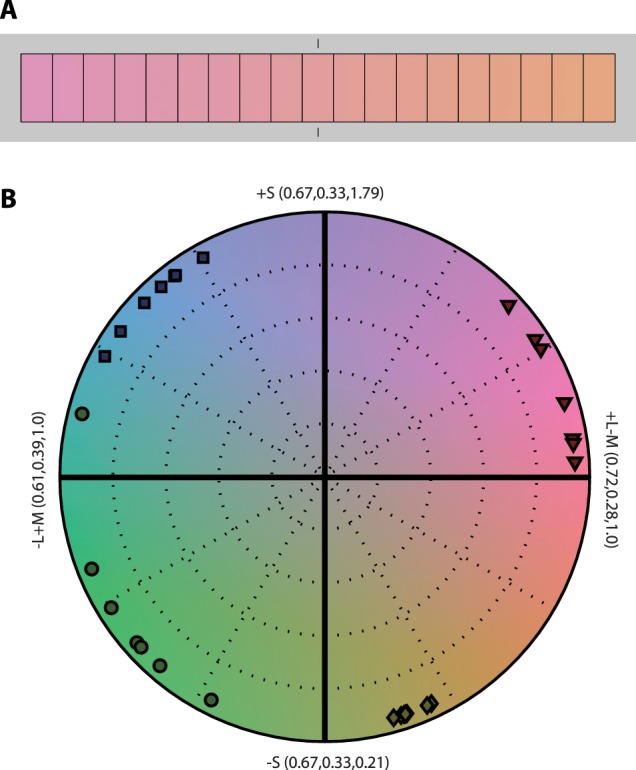
Stimulus color space. Observers were instructed to select four unique hues: a red and green that were neither bluish nor yellowish, and a blue and yellow that were neither reddish nor greenish. (A) Hues were selected by navigating a gradated patch of hues with a keyboard. (B) Candidate hues fell along a circle around neutral white in the isoluminant plane of cardinal color space; numbers indicate the cone coordinates (L, M, S) at axis extrema. Unique hues for seven observers are shown: red (▽), blue (□), green (○), and yellow (⋄).
In the visual search task, observers were instructed to report, as quickly and accurately as possible, the number of targets (1, 2, or 3) presented against a full-screen binary noise background (21.76° × 16.30°). Target locations were randomly assigned within a 10.37° × 7.64° central viewing area. Figure 2 shows a series of task stimuli for the two cardinal axes. Within a single color-pair condition, the random noise background comprised equal numbers of texels of both colors, and all targets in a trial were presented in one of the two colors chosen randomly. The target (0.509° × 0.509°) was equal to 6 × 6 background texels (0.085° × 0.085°), so the probability of a false target formed by a random grouping of texels was negligible (p < 0.02). Observers initially adapted to mean gray for 120 s. A foveal cue signaling stimulus onset was provided 7 s before the end of the adaptation period; stimuli were presented concurrently with an auditory tone and subsequent presentations were initiated automatically, following the observer's keypad response.
Figure 2.
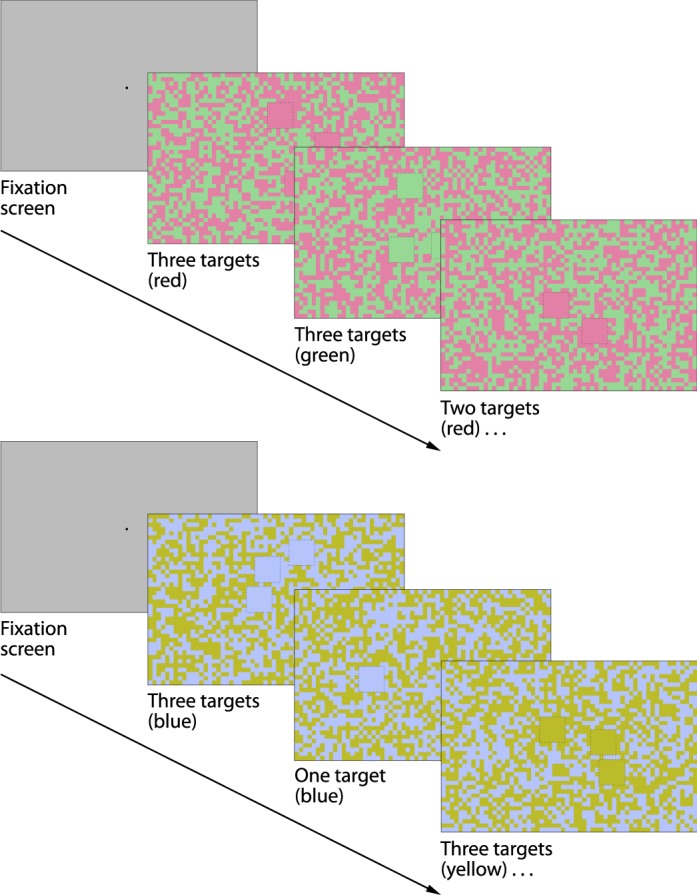
Subitizing-search task. After a 7-s fixation screen, each pairwise color condition was displayed in blocks of 36 trials, each trial consisting of 1, 2, or 3 targets in either color presented randomly on binary color noise. New trials were initiated by observer input into a number pad. Condition blocks (n = 6) were randomly interleaved, with each repeated a total of six times over the course of one session. Observers sat for a total of three sessions after a training session. An example series of trials for the cardinal red-green (top) and blue-yellow (bottom) conditions are shown. Dashed lines are illustrative and were not present during the task.
All visual stimuli were presented using MATLAB (MathWorks, Natick, MA) and a VSG graphics card (Cambridge Research Systems, Rochester, UK) on a SONY GDM-F500R monitor running at 100 Hz, gamma-corrected for linearity. The screen subtended 21.7° × 16.3° of visual angle at a distance of 1.0 m, with each pixel subtending 0.02° × 0.02°. The mean luminance of the monitor was 50 cd/m2. Experiments were conducted in a dark room, and observers used a keyboard to respond. Observers with normal or corrected 20/20 vision participated in all experiments. All human experiments were approved by the institutional review board at the State University of New York College of Optometry.
Each observer completed 4,536 trials over the course of three sessions, after completing one session of training (∼1,500 trials). Incorrect trials were discarded and outliers minimized by eliminating the longest correct RTs (top 1 percentile) in each color-pair condition (Ratcliff, 1993). RT distributions for the correct trials in each condition were fitted with maximum-likelihood estimation to an ex-Gaussian distribution (Lacouture & Cousineau, 2008; Luce, 1986; Ratcliff, 1979). An ex-Gaussian random variable is the sum of a Gaussian random variable (ϕ) with mean (μ) and standard deviation (σ), and an exponential random variable (exp) with mean (τ). The ex-Gaussian distribution results from the convolution of the Gaussian distribution with the exponential:
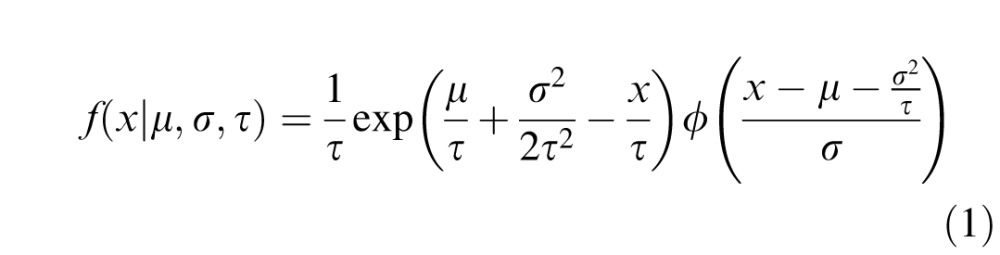 |
Goodness of fit was tested with a χ2 statistic.
Results
Cumulative RT distributions for each condition are shown for one observer in Figure 3, along with the ex-Gaussian fits. For this observer, RTs of unique hues were not shorter than their complementary colors. However, RTs were faster for all yellows compared to their complementary blues, whereas RTs for reds and greens were not significantly different.
Figure 3.
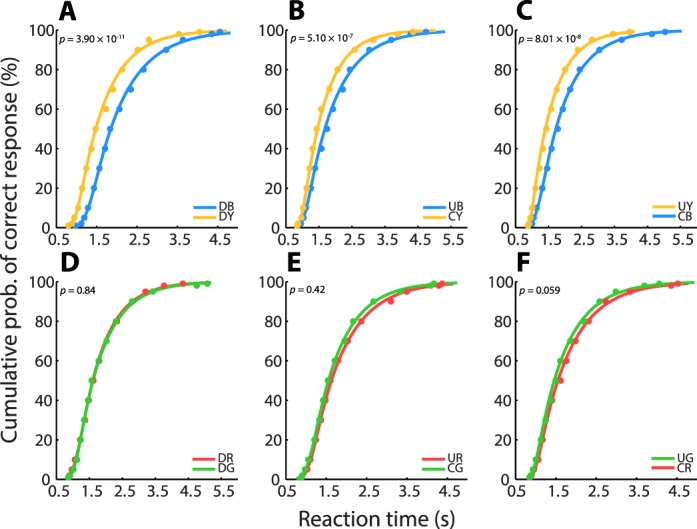
Reaction-time data for observer ET. Ex-Gaussian functions fitted to RT data plotted cumulatively for each of six color conditions: (A) cardinal blue (DB) and cardinal yellow (DY), (B) unique blue (UB) and complementary yellow (CY), (C) unique yellow (UY) and complementary blue (CB), (D) cardinal red (DR) and cardinal green (DG), (E) unique red (UR) and complementary green (CR), and (F) unique green (UR) and complementary red (CR). Inset p-values are the results of Kolmogorov-Smirnov (K–S) tests for significant differences between paired RT distributions.
RT distributions and their respective ex-Gaussian fits for all seven observers for all conditions can be found in the Supplemental Material available online (Supplementary Figures S1 through S6). The median RT was used for salience and statistical analyses. We compared the RT distributions of each color pair for each observer using a Kolmogorov-Smirnov (K–S) test. Across all observers, RTs for unique hues were not significantly faster than RTs for their complementaries, demonstrating that unique hues do not provide any salience advantage in this search task. However, for all three blue–yellow conditions (cardinal blue vs. cardinal yellow, unique blue vs. complementary yellow, and unique yellow vs. complementary blue), both the median salience (1/RT) and accuracy were greater for yellow targets than for complementary blue targets for all seven observers (Figure 4; p < 10−6 in 20 of 21 cases, and p < 0.05 for the 21st). Only 10 out of 21 red–green comparisons showed a significant difference, with red more salient in four instances and green more salient in six. To summarize, unique hues are not more salient than their complementary colors, but the method reveals that yellows are more salient than blues.
Figure 4.
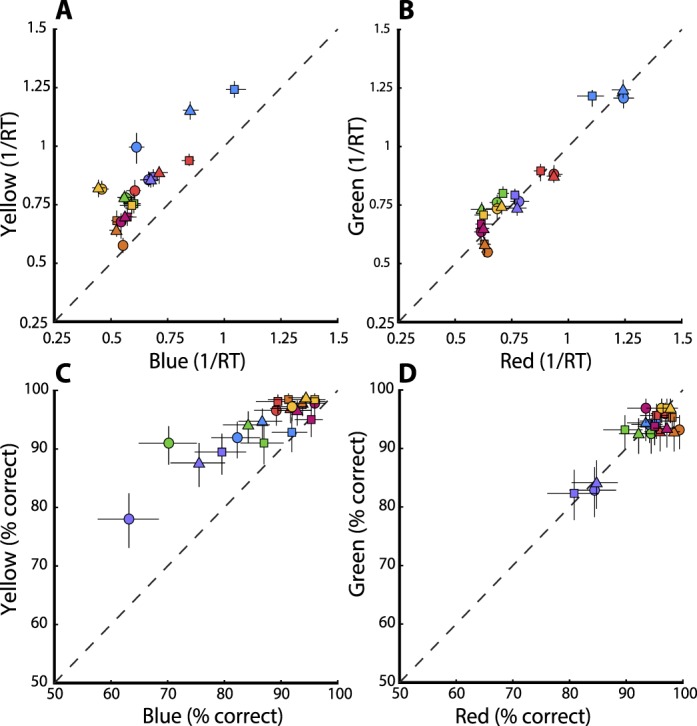
Salience comparisons of yellow versus blue and green versus red. (A, B) A salience index was calculated as the median of (1/RT) for all (A) blue-yellow and (B) red-green conditions across seven observers. (A) Yellow targets were detected significantly faster than their complementary blue targets; ○ = cardinal blue versus yellow; □ = unique yellow versus complementary blue; △ = unique blue versus complementary yellow. (B) Significant differences within red–green pairs were not reliably found; ○ = cardinal red versus green; □ = unique green versus complementary red; △ = unique red versus complementary green. Each color represents a single observer. Error bars denote 95% confidence intervals for the median. (C, D) Performance accuracy was calculated for all blue–yellow (C) and red–green (D) pairs. (C) Yellow targets were more accurately detected than their complementary blue targets. Symbols are the same as in (A). (D) Significant differences within red–green pairs were not reliably found. Symbols are the same as in (B). Each color represents a single observer. Error bars denote Clopper-Pearson 95% confidence intervals.
Perceptual isoluminance varies across the visual field, especially as the density of preretinal macular pigment decreases from the fovea, thus admitting progressively more short-wavelength light to the retina (Zaidi, Pokorny, & Smith, 1989). Since our targets were placed up to an eccentricity of 10° and observers were free to scan, it was not possible to use one equiluminant setting for the whole image. To examine whether the yellow versus blue RT differences were due to a luminance artifact (as would happen if the luminance of the blues was inadvertently higher than luminance for the yellows), we compared RTs of the cardinal blue–yellow condition to the RTs from a 10% contrast dark–light condition. All observers exhibited reliably faster RT distributions for darks than lights in the dark–light condition (K–S test, p < 0.01), extending Komban and colleagues' (2011) results to low contrasts. We predicted that if the blue–yellow salience bias were due only to a difference in luminance between the yellow and the blue stimuli, we would expect RT differences to approximate those observed in the achromatic condition. In five out of seven observers, the RT difference between yellow and blue was much greater than the RT difference between darks and lights (Figure 5). RT differences therefore cannot be entirely attributed to a luminance artifact, and the observed salience difference between yellow and blue is a chromatic effect.
Figure 5.
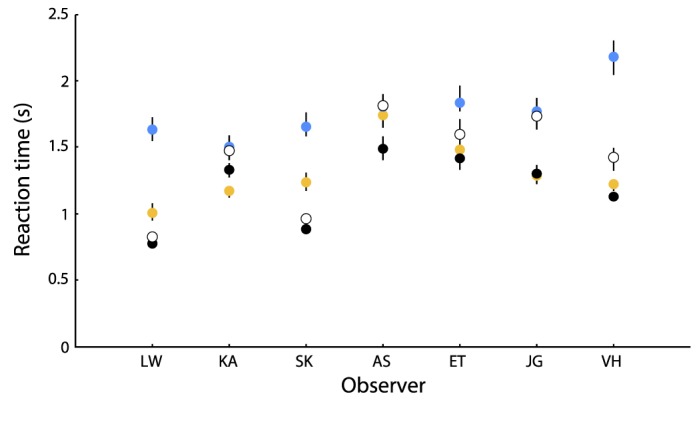
Color versus luminance RT differences. Median RT for the cardinal blue–yellow condition (blue, yellow points) and 10% contrast dark–light condition (black, white) are plotted for seven subjects. Error bars denote 95% confidence intervals for the median.
Experiment 2: Eye movements and salience
To examine observers' search strategies in the subitizing task, and to verify our inference that 1/RT reflected salience, we repeated our visual-search task while tracking eye movements.
Method
Two observers repeated the task for the cardinal red–green and blue–yellow isoluminant pairs, as well as a 100% contrast achromatic pair, for a total of 1,296 trials. A high-speed infrared video eye-tracker (Cambridge Research Systems) was used to track saccades during visual search on each trial. Eye positions were sampled at 250 Hz and filtered with a low-pass Butterworth filter. Saccades were defined as movements with velocity > 40°/s with an endpoint fixation ≥ 100 ms. Mean saccades per trial and median RT were calculated for each condition. Stimuli were presented as described in Experiment 1.
Results
Both observers detected dark targets faster than light targets, and also made significantly fewer saccades to darks than to lights (2.05 vs. 2.70 and 1.47 vs. 1.83; both p < 0.0001, Wilcoxon rank-sum test). For the blue–yellow condition, trials with yellow targets also exhibited significantly fewer saccades than those with blue targets (3.67 vs. 4.48 and 2.67 vs. 3.92; both p < 10−9, Wilcoxon rank-sum test). In contrast, the number of saccades made for red versus green targets was not significantly different if the RTs did not significantly differ. Observer 2 showed no significant difference in RTs or saccade counts between red and green target conditions (2.59 vs. 2.60), whereas Observer 1 showed shorter RTs and fewer saccades for red targets than for green (3.67 vs. 4.13, p = 0.01, Wilcoxon rank-sum test; Figure 6).
Figure 6.
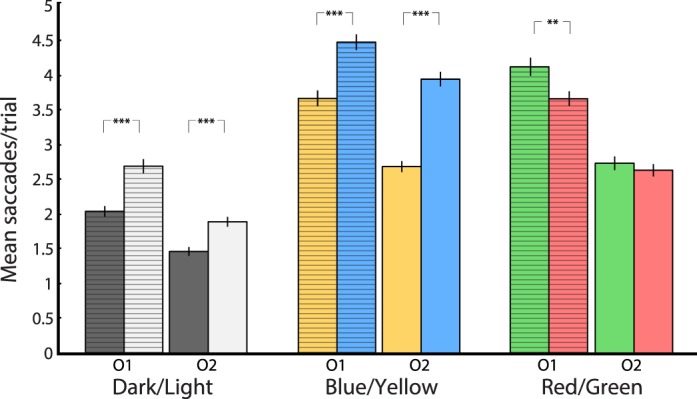
Role of eye movements in salience. Eye tracking revealed that significant differences in mean saccades corresponded to significant differences in RTs. O1 = observer 1; O2 = observer 2. **p < 0.01; ***p < 0.0001. Error bars denote SEM.
The eye-movement results suggest that observers employ search strategies in the subitizing task that highlight differentially activated salience. Less salient stimuli require observers to deploy saccade-dependent serial search (Sternberg, 1969; Treisman & Gelade, 1980), reflected in the increased number of saccades made in such trials. On the other hand, salient stimuli seem to pop out in multiples, reducing the number of serial-search eye movements required (Wolfe, 1994). The number of saccades per trial is thus a coarser alternative metric for quantifying salience.
Experiment 3: Irradiation illusion
Komban et al. (2011) noticed that binary noise comprising equal numbers of light and dark texels appeared to have more light area than dark. This illusion is similar to Helmholtz's irradiation illusion (von Helmholtz, 1886), in which a white square on a black background appears to be larger than the same size black square on a white background. When they corrected the background for the irradiation illusion by increasing the number of dark texels, the difference in RTs between dark and light targets was eliminated. To test whether yellow salience is due to a chromatic irradiation illusion, we asked observers to judge whether blue squares on yellow background patches appeared smaller or larger than yellow squares on blue background patches.
Method
There were two sets of stimuli. In the first set, a cardinal yellow test square was varied in width (0.298°–0.721°) on a cardinal blue background patch (5.1° × 5.1°), while a cardinal blue reference square had a fixed width (0.509°) on a cardinal yellow background patch (5.1° × 5.1°); the situation was reversed in the second set. Test-reference pairs were presented simultaneously 2.8° to the left and right of the screen's center, on a full-field background of the gray midpoint (mean luminance 50 cd/m2). Two seconds of full-field mid-gray was added between trials to minimize adaptation effects. Observers were instructed to choose the larger of the two squares in a two-alternative forced-choice task. Five subjects sat for 2,520 trials. Size, color, and location of the test stimulus were randomly interleaved, and results were fitted to a Naka-Rushton function using maximum log-likelihood estimation. The fit parameter ω (the test width at which 50% performance was observed) was used to determine the relative magnitude of irradiation illusion between the perceptual area of yellow and blue targets for each observer, and to estimate the ratio of yellow:blue noise required to achieve perceptual equivalency (computed as:
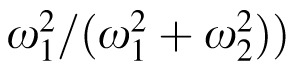 .
.
Results
Four observers judged blue targets as slightly larger than yellow, with perceptual equivalency at a yellow:blue ratio of ∼52:48. For one observer, the effect was reversed, ∼45:55 (see all results in Figure S7, Table S1, in the Supplemental Material available online). This result is markedly less pronounced than the 60:40 ratio of dark to light area reported in Komban et al. (2011), suggesting that, unlike luminance stimuli, there is only a meager irradiation-illusion effect for chromatic stimuli, which would not account for the salience results. Such a diminished effect is understandable, as any compressive nonlinearity (Kremkow et al., 2014) would involve only the S-driven subset of cones, which have by far the sparsest distribution. This minor effect could also be due to the wavelength-dependent characteristics of the point-spread function of the eye, or interobserver differences in macula and lens pigmentation that slightly shift equiluminance.
Experiment 4: Early neural substrate
“Salience” is a broad term, and yellows could be more salient than blues because of differences in low-level processing or because of high-level considerations. Kremkow et al. (2014) showed that the greater salience of darks over lights is due to an early luminance nonlinearity that is more compressive for increments than decrements, as predicted by Komban et al. (2014). To test for a similar early cause for yellow salience, we recorded from local field potentials (LFPs) in the primary visual cortex of rhesus macaques and measured the LFP responses to color changes along the three cardinal directions of color space.
The LFP is a measurement of the electrical activity from local populations of neurons recorded extracellularly and is thought to sample neuronal signals within a few hundred microns from the electrode tip (Jin et al., 2008; Katzner et al., 2009; Lindén et al., 2011; Liu, 2006; Xing, Yeh, & Shapley, 2009). In primary visual cortex (V1), LFPs can show selectivity for spatial position, orientation, and eye dominance (Berens, Keliris, Ecker, Logothetis, & Tolias, 2008; Katzner et al., 2009; Xing et al., 2009), and share similar stimulus preferences with single-unit activity recorded at the same location (Lashgari et al., 2012). LFPs are a powerful tool to study population responses to chromatic stimuli (Jansen et al., 2014), overcoming the difficulties of single-unit recordings caused by the paucity of color-preferring single neurons (Sincich & Horton, 2005).
Method
LFPs from striate cortex were recorded from V1 in awake rhesus macaque (n = 1) with a chronically implanted array of 3–7 ultrathin electrodes (1-μm tip, 15-μm shaft, 100–200 μm2 exposed metal area), each ∼150 μm apart, and all corresponding to visual-field eccentricities of 10–15°. The electrodes were made of platinum-alloy core (90% platinum and 10% tungsten) covered with quartz (40 μm in diameter) and had impedances of 1–3 MΩ. The electrodes were independently moved with individual microdrives (Lashgari et al., 2012; Swadlow, Bereshpolova, Bezdudnaya, Cano, & Stoelzel, 2005); LFPs were collected, amplified (×5,000), digitized, sampled at 5 kHz (Plexon) and low-pass filtered (<200 Hz) with a fourth-order Butterworth filter. Eye movements were sampled at 5 kHz. Visual stimuli were generated with a computer running MATLAB (MathWorks) and presented on a GDM-F520 monitor (Sony Electronics; refresh rate, 160 Hz; mean luminance, 60 cd/m2; resolution, 640 × 480 pixels) at a distance of 57 cm. Spatiotemporal receptive fields were mapped as described by Lashgari et al. (2012) and Kremkow et al. (2014). The animal grasped a bar and a fixation target appeared, after which chromatic patches (full contrast along a single axis, randomly interleaved, size ranging 1.75°–5° of visual angle, duration 200 ms) were presented in the RF (eccentricities of 10°–15°) on a full-field background of the gray midpoint. Amplitude and latency of LFP responses were measured as the maximum-to-minimum amplitude after stimulus onset and the time-of-maximum, respectively. All procedures were performed in accordance to the guidelines of the US Department of Agriculture and approved by the Institutional Animal Care and Use Committee at the State University of New York College of Optometry.
Results
LFP response signatures differed in both amplitude and latency for yellow versus blue stimuli compared to red versus green stimuli (Figure 7). We found that flashed −ΔS (cardinal yellow) stimuli produced significantly larger response amplitudes than +ΔS (cardinal blue) stimuli (0.14 μV and 0.08 μV; p = 0.0006, K–S test, n = 14); response amplitudes to −Δ(L–M) (cardinal green) and +Δ(L–M) (cardinal red) stimuli were not significantly different (0.11 μV and 0.09 μV; p = 0.54, K–S test, n = 14). Yellow/blue amplitude ratio (1.88) was significantly greater than green/red amplitude ratio (1.19; p = 0.0006, K–S test, n = 14; Figure 8A). Mean latencies of the peak response were significantly longer for blue stimuli than for yellow stimuli (blue = 92 ms, yellow = 70 ms, p = 2.85 × 10−7, K–S test, n = 14; Figure 8B). Mean latency difference between green and red stimuli was smaller and significant only at a much lower level (green = 90 ms, red = 83 ms; p = 0.036, K–S test, n = 14). Furthermore, the mean latency difference between blue and yellow stimuli (22 ms) compared with green versus red stimuli (7 ms) was significant (p = 1.87 × 10−5, K–S test, n = 14). These results, in particular the longer peak latencies of LFPs to blue stimuli compared to yellow, provide evidence for an early neural substrate for the color salience results.
Figure 7.
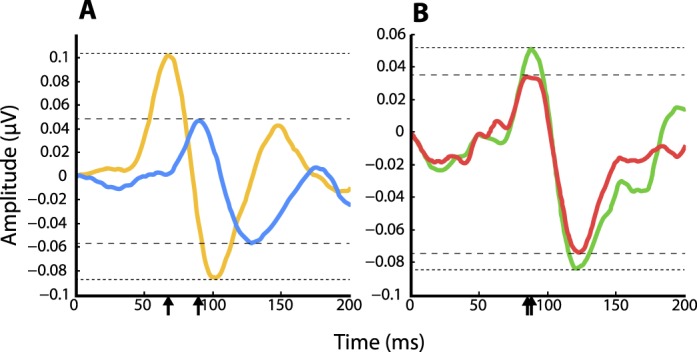
LFPs from recording site 130,605_2. Typical LFP responses to maximum-contrast cardinal yellow/blue (A) and green/red (B) stimuli. Magnitude of response is indicated by dashed lines; stimulus response latencies are indicated by arrows on the x axis.
Figure 8.
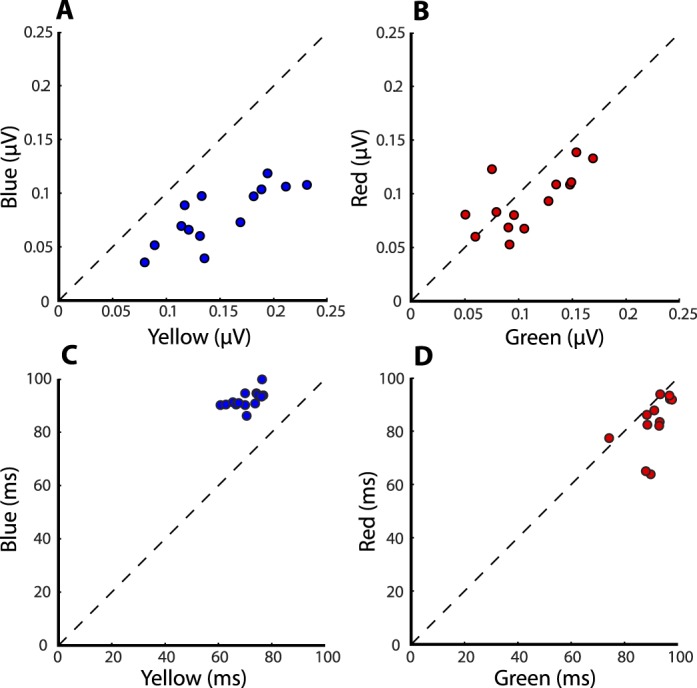
LFP amplitudes and peak latencies. LFP amplitudes and latencies for full-contrast yellow versus blue stimuli (A, C) and green versus red stimuli (B, D) for 14 recording sites. Amplitudes were measured as the magnitude of difference between the maximum and minimum response after stimulus onset; latency was measured as the time of maximum response.
Discussion
Our primary aim in this study was to quantify the salience of unique hues compared with other isoluminant colors. The RT distributions of observers in our target-subitizing task show that unique hues do not have enhanced salience compared with their nonunique complementary colors. This lack of salience refutes the notion of a privileged role for these hues in visual search tasks. If a population dominance of OFF cells is responsible for the enhanced salience of darks (Jin et al., 2008; Komban et al., 2011; Yeh, Xing, & Shapley, 2009), then our results challenge the idea that unique hues could be overrepresented in the cortex.
In cultural linguistics too, the primacy of red, green, blue, and yellow has recently been challenged as inaccurate and Anglocentric (Saunders & Van Brakel, 1997), with previous findings attributed to the use of artifactual abstraction created by the use of Munsell chips. In addition, Saunders and van Brakel point out that, in fact, cross-cultural research does not validate the universality of the four hues (e.g., some languages do not distinguish between green and yellow, and others split blue into pale and dark shades). In terms of opponency, Hering's argument seems inherently tied to modern language use: one may consider that it is as impossible to discern the simultaneous presence of any pair of complementary hues as it is to see a color as reddish-green or bluish-yellow. In addition, Bosten and Boehm (2014) have shown that hue scaling can be done just as well with intermediate colors as with unique hues.
While our results refute the perceptual primacy of unique hues on a psychophysical level, our method did reveal a previously unreported salience advantage for a wide range of yellowish colors compared to their complementary bluish colors: observer responses for yellow targets were faster, more accurate, and required fewer saccadic eye movements. Response asymmetries in visual search have been studied extensively (Wolfe, 2001). Treisman and Gormican (1988) reported search asymmetries using color stimuli, but whether such asymmetries are due to hue differences is debated (D'Zmura, 1991; Nagy & Cone, 1996; Nagy & Sanchez, 1990), especially since the effect of background color is known to influence asymmetries in the detection of colored targets among distractors in visual search (Rosenholtz, Nagy, & Bell, 2004). Our use of a random-noise background consisting of only target and distractor colors is an important simplification over classical target-distractor-background designs, because it rules out asymmetric experimental design as a cause for asymmetric search responses (Rosenholtz, 2001). It is worth pointing out that the greater nonlinear compression towards the bluish +S pole of the S–(L+M) mechanism, used in a model to explain psychophysical thresholds by Zaidi, Shapiro, and Hood (1992), could explain the salience difference in the same way that the greater compression in the ON channel explains the greater salience of darks than lights (Komban et al., 2011; Kremkow et al., 2014). Nissen and colleagues (Nissen, 1977; Nissen, Pokorny, & Smith, 1979) showed that duration thresholds, simple reaction times, and discriminative reaction times were longer for detecting single desaturated than single saturated chromatic stimuli. Though the yellow–blue pairs in our stimuli are physically equated for cone excursions from neutral white, this does not guarantee perceptually equal saturation. It is difficult to judge whether blues or yellows in our backgrounds are perceived as more saturated, since the yellows are more salient and dominate the percept. It is possible that the greater response compression toward blue correlates with lower perceived saturation; if this is the case, it would explain why our results are in agreement with Nissen and colleagues.
The greater amplitude and faster latency of LFPs for yellow targets suggests a low-level cause for the enhanced salience of yellows. Corroborating this possibility is Tailby, Solomon, and Lennie's (2008) finding of asymmetric S-ON and S-OFF neuron populations in macaque LGN. In primate retina, it has been suggested that S-ON and S-OFF signals have anatomically distinct pathways in bistratified S-ON and midget S-OFF ganglion cells, respectively (Dacey, Crook, & Packer, 2013).
We have demonstrated that unique hues are not especially salient colors, whereas early neural response differences strongly affect color salience. Consequently, if there is a salience effect due to a unique hue-based mental representation of color, this effect is much smaller than that produced in early-vision pathways. Unless purely perceptual evidence can be provided for a privileged role of unique hues, their putative primacy remains linguistic and unique hue-dependent color theories must be revised. Extant physiology suggests that cone-photoreceptor signals are combined into cone-opponent and cone-summation signals for efficiency of transmission to the cortex (Buchsbaum & Gottschalk, 1983; Zaidi, 1997). These signals are combined in striate cortex to give myriad color sensitivities that are progressively refined at subsequent stages toward inferior-temporal (IT) cortex. Recent simulations have shown that colors can be successfully decoded from the population responses of IT cells with a winner-take-all rule without invoking any privileged dimensions (Zaidi, Marshall, Thoen, & Conway, 2014). It remains to be seen whether the distribution of neural sensitivities in IT cortex reflects the distribution of colors in the world, or frequency of color-language use.
Acknowledgments
We thank Robert McPeek for helpful discussions on eye-movement analysis. The work was supported by National Institutes of Health (NIH) EY02067901 and EY05253 (to J. M. A.), and EY007556 and EY0133312 (to Q. Z.), and a DFG Research Fellowship (KR 4062/1-1) (to J. K.). The authors declare no competing interests. Author contributions: L. E. W., Q. Z., and J. M. A. conceived of the study; L. E. W., S. J. K., J. K., Q. Z., and J. M. A. designed the experiments; L. E. W. performed human research; L. E. W., J. K., X. L., and M. J. performed primate research; L. E. W. analyzed data; S. J. K. and J. K. contributed analytic tools; and L. E. W., Q. Z., and J. M. A. wrote the paper.
Commercial relationships: none.
Corresponding author: Lauren E. Wool.
Email: lwool@sunyopt.edu.
Address: College of Optometry, State University of New York, New York, NY, USA.
Contributor Information
Lauren E. Wool, Email: lwool@sunyopt.edu.
Stanley J. Komban, Email: stanley.kj@gmail.com.
Jens Kremkow, Email: jens@kremkow.de.
Michael Jansen, Email: mjansen@sunyopt.edu.
Xiaobing Li, Email: xli@sunyopt.edu.
Jose-Manuel Alonso, Email: jalonso@sunyopt.edu.
Qasim Zaidi, Email: qz@sunyopt.edu.
References
- Abney W. (1895). Colour vision: Being the Tyndall Lectures delivered in 1894 at the Royal Institution. New York: William Wood & Company. [Google Scholar]
- Bachy R., Dias J., Alleysson D., Bonnardel V. (2012). Hue discrimination, unique hues and naming. Journal of the Optical Society of America A, 29 (2), A60–A68. [DOI] [PubMed] [Google Scholar]
- Berens P., Keliris G. A., Ecker A. S., Logothetis N. K., Tolias A. S. (2008). Feature selectivity of the gamma-band of the local field potential in primate primary visual cortex. Frontiers in Neuroscience, 2 (2), 199–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berlin B., Kay P. (1969). Basic colour terms: Their universality and evolution. Berkeley, CA: University of California Press. [Google Scholar]
- Bosten J. M., Boehm A. E. (2014). Empirical evidence for unique hues? Journal of the Optical Society of America A, 31 (4), A385–393. [DOI] [PubMed] [Google Scholar]
- Boynton R. M., Olson C. X. (1990). Salience of chromatic basic color terms confirmed by three measures. Vision Research, 30 (9), 1311–1317. [DOI] [PubMed] [Google Scholar]
- Broackes J. (2011). Where do the unique hues come from? Review of Philosophy and Psychology, 2, 601–628. [Google Scholar]
- Buchsbaum G., Gottschalk A. (1983). Trichromacy, opponent colours coding and optimum colour information transmission in the retina. Proceedings of the Royal Society of London. Series B . 220 (1218), 89–113. [DOI] [PubMed] [Google Scholar]
- Conway B. R., Moeller S., Tsao D. Y. (2007). Specialized color modules in macaque extrastriate cortex. Neuron, 56 (3), 560–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- da Vinci L. (1540). Libro di Pittura (F. Melzi) [Translation: A treatise on painting]. Vatican City, Italy: Biblioteca Apostolica Vaticana. [Google Scholar]
- Dacey D. M., Crook J. D., Packer O. S. (2013). Distinct synaptic mechanisms create parallel S-ON and S-OFF color opponent pathways in the primate retina. Visual Neuroscience, 31 (2), 139–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Derrington A. M., Krauskopf J., Lennie P. (1984). Chromatic mechanisms in lateral geniculate nucleus of macaque. The Journal of Physiology, 357 (1), 241–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dimmick F. L., Hubbard M. R. (1939). The spectral location of psychologically unique yellow, green, and blue. The American Journal of Psychology, 52 (2), 242–254. [Google Scholar]
- D'Zmura M. (1991). Color in visual search. Vision Research, 31 (6), 951–966. [DOI] [PubMed] [Google Scholar]
- Ennis R., Zaidi Q. (2013). Geometrical structure of perceptual color space is affine. Journal of Vision, 13 (9): 10 000–000, http://www.journalofvision.org/content/13/9/295, doi:10.1167/13.9.295. [Abstract] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hering E. (1878). Zur Lehre vom Lichtsinn [Translation: Outlines of a theory of the light sense]. Vienna, Austria: C. von Gerold's Sohn. [Google Scholar]
- Holtsmark T., Valberg A. (1969). Colour discrimination and hue. Nature, 224 (5217), 366–367. [DOI] [PubMed] [Google Scholar]
- Ikeda M., Ayama M. (1980). Additivity of opponent chromatic valence. Vision Research, 20 (11), 995–999. [DOI] [PubMed] [Google Scholar]
- Jameson D., Hurvich L. M. (1955). Some quantitative aspects of an opponent-colors theory. I. Chromatic responses and spectral saturation. Journal of the Optical Society of America, 45 (7), 546–552. [DOI] [PubMed] [Google Scholar]
- Jansen M., Li X., Lashgari R., Kremkow J., Bereshpolova Y., Swadlow H. A., Alonso J.-M. (2014). Chromatic and achromatic spatial resolution of local field potentials in awake cortex. Cerebral Cortex , E-pub ahead of print. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J. Z., Weng C., Yeh C.-I., Gordon J. A., Ruthazer E. S., Stryker M. P., Alonso J.-M. (2008). On and off domains of geniculate afferents in cat primary visual cortex. Nature Neuroscience, 11 (1), 88–94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katzner S., Nauhaus I., Benucci A., Bonin V., Ringach D. L., Carandini M. (2009). Local origin of field potentials in visual cortex. Neuron, 61 (1), 35–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiper D. C., Fenstemaker S. B., Gegenfurtner K. R. (1997). Chromatic properties of neurons in macaque area V2. Visual Neuroscience, 14 (6), 1061–1072. [DOI] [PubMed] [Google Scholar]
- Komatsu H., Ideura Y., Kaji S., Yamane S. (1992). Color selectivity of neurons in the inferior temporal cortex of the awake macaque monkey. The Journal of Neuroscience, 12 (2), 408–424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komban S. J., Alonso J.-M. M., Zaidi Q. (2011). Darks are processed faster than lights. The Journal of Neuroscience, 31 (23), 8654–8658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komban S. J., Kremkow J., Jin J., Wang Y., Lashgari R., Li X., Alonso J.-M. (2014). Neuronal and perceptual differences in the temporal processing of darks and lights. Neuron, 82 (1), 224–234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krauskopf J., Williams D. R., Heeley D. W. (1982). Cardinal directions of color space. Vision Research, 22 (9), 1123–1131. [DOI] [PubMed] [Google Scholar]
- Krauskopf J., Zaidi Q., Mandler M. B. (1986). Mechanisms of simultaneous color induction. Journal of the Optical Society of America A, 3 (10), 1752–1757. [DOI] [PubMed] [Google Scholar]
- Kremkow J., Jin J., Komban S. J., Wang Y., Lashgari R., Li X., Alonso J.-M. (2014). Neuronal nonlinearity explains greater visual spatial resolution for darks than lights. Proceedings of the National Academy of Sciences, USA, 111, 3170–3175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacouture Y., Cousineau D. (2008). How to use MATLAB to fit the ex-Gaussian and other probability functions to a distribution of response times. Tutorials in Quantitative Methods for Psychology, 4 (1), 35–45. [Google Scholar]
- Larimer J., Krantz D. H., Cicerone C. M. (1974). Opponent-process additivity—I: Red/green equilibria. Vision Research, 14 (11), 1127–1140. [DOI] [PubMed] [Google Scholar]
- Larimer J., Krantz D. H., Cicerone C. M. (1975). Opponent process additivity—II. Yellow/blue equilibria and nonlinear models. Vision Research, 15 (6), 723–731. [DOI] [PubMed] [Google Scholar]
- Lashgari R., Li X., Chen Y., Kremkow J., Bereshpolova Y., Swadlow H. A., Alonso J.-M. (2012). Response properties of local field potentials and neighboring single neurons in awake primary visual cortex. The Journal of Neuroscience, 32 (33), 11396–11413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lennie P., Krauskopf J., Sclar G. (1990). Chromatic mechanisms in striate cortex of macaque. The Journal of Neuroscience, 10 (2), 649–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindén H., Tetzlaff T., Potjans T. C., Pettersen K. H., Grün S., Diesmann M., Einevoll G. T. (2011). How local is the local field potential? BMC Neuroscience, 12 (Suppl 1), O8. [Google Scholar]
- Lindsey D. T., Brown A. M. (2009). World Color Survey color naming reveals universal motifs and their within-language diversity. Proceedings of the National Academy of Sciences, USA, 106 (47), 19785–19790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J. (2006). Local field potential in cortical area MT: Stimulus tuning and behavioral correlations. Journal of Neuroscience, 26 (30), 7779–7790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luce R. D. (1986). Response times: Their role in inferring elementary mental organization. New York: Oxford University Press. [Google Scholar]
- Mollon J. D. (2006). Monge: The Verriest lecture, Lyon, July 2005. Visual Neuroscience, 23 (3–4), 297–309. [DOI] [PubMed] [Google Scholar]
- Mollon J. D. (2009). A neural basis for unique hues? Current Biology, 19 (11), R441–R442. [DOI] [PubMed] [Google Scholar]
- Nagy A., Cone S. M. (1996). Asymmetries in simple feature searches for color. Vision Research, 36 (18), 2837–2847. [DOI] [PubMed] [Google Scholar]
- Nagy A. L., Sanchez R. R. (1990). Critical color differences determined with a visual search task. Journal of the Optical Society of America A, 7 (7), 1209–1217. [DOI] [PubMed] [Google Scholar]
- Nissen M. J. (1977). Stimulus intensity and information processing. Perception & Psychophysics, 22 (4), 338–352. [Google Scholar]
- Nissen M. J., Pokorny J., Smith V. C. (1979). Chromatic information processing. Journal of Experimental Psychology: Human Perception and Performance, 5 (3), 406–419. [DOI] [PubMed] [Google Scholar]
- Ratcliff R. (1979). Group reaction time distributions and an analysis of distribution statistics. Psychological Bulletin, 86 (3), 446–461. [PubMed] [Google Scholar]
- Ratcliff R. (1993). Methods for dealing with reaction time outliers. Psychological Bulletin, 114 (3), 510–532. [DOI] [PubMed] [Google Scholar]
- Regier T., Kay P., Cook R. S. (2005). Focal colors are universal after all. Proceedings of the National Academy of Sciences, USA, 102 (23), 8386–8391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenholtz R. (2001). Search asymmetries? What search asymmetries? Perception & Psychophysics, 63 (3), 476–489. [DOI] [PubMed] [Google Scholar]
- Rosenholtz R., Nagy A. L., Bell N. R. (2004). The effect of background color on asymmetries in color search. Journal of Vision, 4 (3): 10 224–240, http://www.journalofvision.org/content/4/3/9, doi:10.1167/4.3.9. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Saunders B. A., Van Brakel J. (1997). Are there nontrivial constraints on colour categorization? Behavioral and Brain Sciences, 20 (2), 167–228. [PubMed] [Google Scholar]
- Schrödinger E. (1925). Über das Verhältnis der Vierfarben- zur Dreifarbentheorie [Translation: On the relationship of four-color theory to three-color theory]. Sitzungsberichte der Akademie der Wissenschaften, 134, 471–490. [Google Scholar]
- Sincich L. C., Horton J. C. (2005). The circuitry of V1 and V2: Integration of color, form, and motion. Annual Review of Neuroscience, 28, 303–326. [DOI] [PubMed] [Google Scholar]
- Smithson H., Zaidi Q. (2004). Colour constancy in context: Roles for local adaptation and levels of reference. Journal of Vision, 4 (9): 10 693–710, http://www.journalofvision.org/content/4/9/3, doi:10.1167/4.9.3. [PubMed] [Article] [DOI] [PubMed] [Google Scholar]
- Sternberg S. (1969). Memory-scanning: Mental processes revealed by reaction-time experiments. American Scientist, 57 (4), 421–457. [PubMed] [Google Scholar]
- Stoughton C. M., Conway B. R. (2008). Neural basis for unique hues. Current Biology, 18 (16), R698–R699. [DOI] [PubMed] [Google Scholar]
- Sun H., Smithson H. E., Zaidi Q., Lee B. B. (2006). Specificity of cone inputs to macaque retinal ganglion cells. Journal of Neurophysiology, 95 (2), 837–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Swadlow H. A., Bereshpolova Y., Bezdudnaya T., Cano M., Stoelzel C. R. (2005). A multi-channel, implantable microdrive system for use with sharp, ultra-fine “Reitboeck” microelectrodes. Journal of Neurophysiology, 93 (5), 2959–2965. [DOI] [PubMed] [Google Scholar]
- Tailby C., Solomon S. G., Lennie P. (2008). Functional asymmetries in visual pathways carrying S-cone signals in macaque. The Journal of Neuroscience, 28 (15), 4078–4087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treisman A. M., Gelade G. (1980). A feature-integration theory of attention. Cognitive Psychology, 12 (1), 97–136. [DOI] [PubMed] [Google Scholar]
- Treisman A., Gormican S. (1988). Feature analysis in early vision: Evidence from search asymmetries. Psychological Review, 95 (1), 15–48. [DOI] [PubMed] [Google Scholar]
- van Gogh V. (1885, April 18) [Letter to Theo van Gogh on Eugene Delacroix and color theory]. Van Gogh Museum, Amsterdam. [Google Scholar]
- von Helmholtz H. (1866). Handbuch der physiologischen Optik [Translation: Treatise on physiological optics]. Leipzig: Voss. [Google Scholar]
- Webster M. A., Miyahara E., Malkoc G., Raker V. E. (2000). Variations in normal color vision. II. Unique hues. Journal of the Optical Society of America A, 17 (9), 1545–1555. [DOI] [PubMed] [Google Scholar]
- Wolfe J. M. (1994). Guided search 2.0: A revised model of visual search. Psychonomic Bulletin & Review, 1 (2), 202–238. [DOI] [PubMed] [Google Scholar]
- Wolfe J. M. (2001). Asymmetries in visual search: An introduction. Perception & Psychophysics, 63 (3), 381–389. [DOI] [PubMed] [Google Scholar]
- Xing D., Yeh C.-I., Shapley R. M. (2009). Spatial spread of the local field potential and its laminar variation in visual cortex. The Journal of Neuroscience, 29 (37), 11540–11549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeh C.-I., Xing D., Shapley R. M. (2009). “Black” responses dominate macaque primary visual cortex V1. The Journal of Neuroscience, 29 (38), 11753–11760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaidi Q. (1997). Decorrelation of L- and M-cone signals. Journal of the Optical Society of America A, 14 (12), 3430–3431. [DOI] [PubMed] [Google Scholar]
- Zaidi Q., Marshall J., Thoen H., Conway B. R. (2014). Evolution of neural computations: Mantis shrimp and human color decoding. i-Perception, 5, 492–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaidi Q., Pokorny J., Smith V. C. (1989). Sources of individual differences in anomaloscope equations for tritan defects. Clinical Vision Sciences, 4 (1), 89–94. [Google Scholar]
- Zaidi Q., Shapiro A. G., Hood D. (1992). The effect of adaptation on the differential sensitivity of the S-cone color system. Vision Research, 32 (7), 1297–1318. [DOI] [PubMed] [Google Scholar]


