Bayesian hierarchical modeling of patient subpopulations: Efficient designs of Phase II oncology clinical trials

Abstract

Background

In oncology, the treatment paradigm is shifting toward personalized medicine, where the goal is to match patients to the treatments most likely to deliver benefit. Treatment effects in various subpopulations may provide some information about treatment effects in other subpopulations.

Purpose

We compare different approaches to Phase II trial design where a new treatment is being investigated in several groups of patients. We compare considering each group in an independent trial to a single trial with hierarchical modeling of the patient groups.

Methods

We assume four patient groups with different background response rates and simulate operating characteristics of three trial designs, Simon’s Optimal Two-Stage design, a Bayesian adaptive design with frequent interim analyses, and a Bayesian adaptive design with frequent interim analyses and hierarchical modeling across patient groups.

Results

Simon’s designs are based on 10% Type I and Type II error rates. The independent Bayesian designs are tuned to have similar error rates, but may have a slightly smaller mean sample size due to more frequent interim analyses. Under the null, the mean sample size is 2–4 patients smaller. A hierarchical model across patient groups can provide additional power and a further reduction in mean sample size. Under the null, the addition of the hierarchical model decreases the mean sample size an additional 4–7 patients in each group. Under the alternative hypothesis, power is increased to at least 98% in all groups.

Limitations

Hierarchical borrowing can make finding a single group in which the treatment is promising, if there is only one, more difficult. In a scenario where the treatment is uninteresting in all but one group, power for that one group is reduced to 65%. When the drug appears promising in some groups and not in others, there is potential for borrowing to inflate the Type I error rate.

Conclusions

The Bayesian hierarchical design is more likely to correctly conclude efficacy or futility than the other two designs in many scenarios. The Bayesian hierarchical design is a strong design for addressing possibly differential effects in different groups.

Introduction

The treatment paradigm in oncology is shifting toward personalized medicine, where the goal is to match patients based on their prognostic characteristics to a treatment most likely to deliver benefit [1,2]. The ability to personalize treatment has the potential for huge advantages for patients, but also for drug development.

A first step in evaluating a novel treatment for a particular group of patients is determining whether there is a desired level of efficacy in early Phase II trials. One approach common in oncology is to conduct a series of small screening trials in specific patient subgroups, perhaps based on histology or on biomarker signature. These trials are typically run in parallel, independent of each other. This approach does not consider the possibility that some of the patient subpopulations respond similarly to therapy. Treatment effects in the various subpopulation trials may provide some information about treatment effects in other subpopulations.

We apply Bayesian hierarchical models in Phase II oncology trials where a new treatment is being investigated in several groups of patients. Hierarchical modeling allows information about the treatment effect in one group to be ‘borrowed’ when estimating the treatment effect in another group [3]. In effect, the estimate of treatment effect in each group is shrunk toward the overall mean [4]. The amount of shrinkage depends on the results, including the relative precision of estimates in the various groups.

There are advantages to hierarchical modeling. One is that it provides a formal mechanism for adjusting for the regression effect, also called ‘regression to the mean’. The results in some groups will be unusually large or small, especially for modest sample sizes. Additional data usually correct fluke observations, pulling them back toward the mean; hierarchical modeling explicitly corrects for these by modeling the effect in all groups. Intuitively, shrinking mitigates some of the effects of randomness across groups. A consequence is that estimates tend to be more accurate, closer to the true values.

Shrinkage estimators have a long history in statistics. Making the assumption of normality in the 1950s, Charles Stein demonstrated that shrinkage decreased mean squared error [5,6]. He showed that shrinkage improved the naïve approach of no borrowing regardless of the state of nature. In particular, when there are at least three groups, the usual (no shrinkage) least squares estimator of means of the groups is ‘inadmissible’ in the sense that the total mean squared error is reduced uniformly, regardless of the true values of the group means. The James–Stein estimator and other similar shrinkage estimators dominate the no-borrowing estimates in this very strong sense. Perhaps most surprisingly, the groups need not be related. Borrowing measurements between entities that bear no relationship is better than letting them stand alone. Many other authors have since contributed to a rich body of literature on Bayesian hierarchical models and relationships with empirical Bayesian methods [7–21].

When borrowing hierarchically, groups that are extreme and those with greater uncertainty (i.e., those with smaller sample sizes) tend to experience greater shrinkage. The amount of borrowing is not specified in advance but is determined by the data. If results across groups are very similar, there will be more borrowing. If results differ, there is less borrowing and hence greater uncertainty associated with the estimates.

We assume four groups of patients for illustration, but our qualitative conclusions apply more generally. The four groups of patients may be defined by disease site, tumor type, histology (such as in Thall et al. [22] and Chugh et al. [23]), sets of biomarkers, or other distinguishing characteristics. For example, the trial or trials may enroll patients with tumors positive for a particular biomarker, but at various sites such as breast, prostate, ovary, and colon.

We compare three different design strategies. The first two approaches employ four separate trials, one for each patient group. The first approach uses Simon’s Optimal Two-Stage design [24]. The second is Bayesian and adaptive, with the results updated frequently for possibly stopping accrual early for futility. In effect, each trial involves many stages. Comparing the two approaches addresses the advantage of frequent monitoring versus having a single interim analysis. The third approach is a modification of the second in that the four groups are included in a single trial, one that employs Bayesian hierarchical modeling across the four groups in addition to frequent monitoring. Comparing the latter two approaches addresses the advantages of hierarchical modeling.

In this article, we consider a nonrandomized single-arm trial with an endpoint of tumor response. The same general approach applies to two-armed randomized trials and to trials with other types of endpoints, including time-to-event endpoints [3,13].

Trial designs

Simon’s Optimal Two-Stage

As described by Simon [24], this design is based on testing the null hypothesis that the rate of tumor response, p, is less than that considered uninteresting, p₀

$$H0:p\le p_0$$

versus an alternative hypothesis that the rate of tumor response is at least at a targeted level, p₁

$$H1:p\ge p_1$$

Simon’s design specifies four design parameters: the number of patients enrolled in the two stages, n₁ and n₂, and the maximum number of responses that will lead to rejection of the drug in the first and second stages, r₁ and r, respectively. If the total number of observed responses in the first stage is less than or equal to r₁, the trial will stop. Otherwise, the trial will continue and will enroll an additional n₂ patients. If there are r or fewer responses at the end of the trial among the N = n₁ + n₂ patients, the trial will reject the drug at the end of the second stage. Otherwise, the treatment will be considered efficacious and warrant consideration for further study.

Simon’s Optimal Two-Stage design finds the values of n₁, n₂, r₁, and r that minimize the expected sample size when the response probability is p₀ for all two-stage designs that have the specified Type I and Type II error probabilities. We set both Type I and Type II error rates to 0.10.

Patient groups may have known background differences that reflect in the group-specific historical response rates. For example, some tumor types may be known to be less sensitive to chemotherapy. Therefore, we will consider the three designs for four groups of patients that are expected to have different background response rates, which means p₀ and p₁ vary by group. Table 1 shows the values of p₀ and p₁ we use for each group and the corresponding Simon’s Optimal Two-Stage designs.

Table 1.

Simon’s Optimal Two-Stage design for each of the four patient groups

Group	p0	p1	Stage 1 r1/n1	Stage 2 r/N
1	5%	20%	0/12	3/37
2	5%	20%	0/12	3/37
3	10%	30%	1/12	5/35
4	20%	40%	3/17	10/37

Bayesian adaptive design

We model the log-odds of response, including an adjustment for the targeted p₁ rates

$$\theta =log\left(\frac{p}{1-p}\right)-log\left(\frac{p_1}{1-p_1}\right)$$

and use a subscript to indicate patient group: θ₁, θ₂, θ₃, and θ₄. This allows the change in log-odds from the targeted rates to be modeled, and hence similar values of θ across the groups reflect similar treatment effects relative to the targeted values. While the modeling is done on the log-odds scale, all inference of futility or efficacy is done on the probability scale, which is more clinically interpretable.

First, we present a Bayesian model with no borrowing. To accomplish this, we model the θ_i with independent normal distributions, with weak priors

$${\theta }_1~\mathrm{N}(-1.34,{10}^2),i=1,2,3,4$$

The mean of −1.34 reflects a prior mean consistent with the null hypothesis for the parameter θ, but a very large standard deviation, creating a nearly non-informative prior.

For this design, interim analyses are planned after the first 10 patients are enrolled, and each subsequent interim analysis occurs after every 5 additional patients. The updated posterior distributions are used to decide whether to stop accrual or to continue. The same early futility rule is applied to all four groups at each interim analysis. Early stopping for futility is based on the current posterior probability that p is greater than p_mid

$$Pr(p>p_{\mathit{mid}}\mid \text{Data})$$

where p_mid = (p₀ + p₁)/2, is halfway between p₀ and p₁. If this probability is less than 5% at any interim analysis then accrual stops for futility. Otherwise accrual will continue to the maximum sample size.

At the final analysis of the trial, the treatment will be declared efficacious and of interest for further study based on the posterior probability of being greater than p₀. In our example, this final evaluation criteria varies by group

$$\begin{array}{l}\text{Group}1:Pr(p>p_0\mid \text{Data})>82\%\\ \text{Group}2:Pr(p>p_0\mid \text{Data})>82\%\\ \text{Group}3:Pr(p>p_0\mid \text{Data})>85\%\\ \text{Group}4:Pr(p>p_0\mid \text{Data})>90\%\end{array}$$

Additionally, we will consider the operating characteristics of this design if we include the ability to stop for efficacy at each interim analysis. In this extension of the design, at any interim analysis, the trial will stop early for efficacy if the probability that the response rate, p, is greater than p_mid is greater than 90%

$$Pr(p>p_{\mathit{mid}}\mid \text{Data})>90\%$$

The Bayesian design parameters were chosen to make a direct comparison with Simon’s design. We assume the same maximum sample size within each group as in the corresponding Simon’s design (Table 1). The goal of the Simon’s design is to distinguish between p₀ and p₁, and so, we use p_mid for early stopping to emulate this behavior. If there is a low probability that p > p_mid, then there is confidence that p is close to p₀, and we stop early for futility. If there is high probability that p > p_mid, then there is confidence that p is close to p₁, and we stop early for efficacy. The final efficacy criteria were chosen to make both Type I and Type II error rates in each group approximately 10%, as in the Simon’s design. Differing numbers of interim analyses because of the varying sample sizes and differing null and alternative response rates in each group necessitated different final efficacy criteria across the four groups to achieve the stated error rates.

Bayesian hierarchical adaptive design

In this design, the four patient groups are considered together in a single, integrated trial, and a Bayesian hierarchical model borrows information across the groups. To accomplish this, we model the θ_i with a normal distribution with unknown mean μ and variance σ²

$${\theta }_i~\mathrm{N}(\mu ,{\sigma }^2),i=1,2,3,4$$

A second-level of the distribution (hierarchy) is used to model the unknown mean and variance. The data across the groups will shape the posterior distribution for the mean and variance across groups, thus creating a dynamic amount of borrowing, depending on the similarity across groups. The following prior distributions of μ and σ² are

$$\mu ~\mathrm{N}(-1.34,{10}^2),{\sigma }^2~\text{Inverse}-\text{Gamma}(0.0005,0.000005)$$

The parameter σ² represents the degree of heterogeneity between the patient groups. At one extreme, when σ² is 0, there is complete pooling, with adjustment for the targeted p₁ rates in each group, of the results across the patient groups. At the other extreme, when σ² is near infinity, then there is no borrowing across the groups. For values between these two extremes, there is an amount of borrowing consistent with the variability across groups. Because the model is powerful enough to capture such extremes, the model results are sensitive to the prior selection for σ². Our selection reflects a small amount of heterogeneity across the four groups. The prior for σ² is equivalent to assuming a prior estimate of σ = 0.1, but with very little weight, 0.1% of one observation. Given the four patient groups to be observed in the trial, the posterior distribution contributes very little information to the posterior. The prior distribution of μ is essentially noninformative, with a weak prior mean close to the null hypothesis.

The model enables learning about μ and σ² as the trial unfolds. However, the information about σ² is limited when there are only four patient groups, even if their sample sizes are large. Therefore, the prior distribution for σ² can affect the amount of borrowing across groups, and careful assessment of this prior distribution is important. Sensitivity to the prior for σ² is discussed below.

The adaptive algorithm (interim analyses, early stopping rules, and the final efficacy criteria) are as described above for the independent-group Bayesian design. For the hierarchical model analysis, we apply the same early stopping rules and final evaluation criteria separately for each group. For example, group 2 may stop early for futility, while groups 1, 3, and 4 continue to the maximum sample size. And at the conclusion of the trial, the efficacy criteria may be satisfied for group 1, but not for groups 3 and 4. This allows us to explore the effect of borrowing on the error rates and mean sample size.

For ease of presentation, we assume equal accrual to all groups. In practice, accrual to the groups will vary, with some accruing more rapidly and others more slowly. Attempts can be made to make accrual more balanced, such as opening additional sites for more slowly accruing groups.

Examples of Bayesian hierarchical modeling

In this section, we show two single simulated trials as examples to illustrate the Bayesian hierarchical modeling. These examples are a simplification of the design described above. In these examples, p₀ = 10% and p₁ = 30% in all four patient groups, whereas for the design described above and for the operating characteristics presented later, we assume a more complicated case, that p₀ and p₁ vary by group. In these examples, the interim analyses and the adaptive algorithm are as described above. The first example is a scenario in which responses are simulated assuming p = 30% in all four groups. This example illustrates the effect of borrowing across groups when all groups are similar, such as the smoothing of the observed response rates and a reduction in uncertainty. The second example is from a scenario in which responses are simulated assuming p = 10% in two groups and p = 30% in two groups. This example illustrates the effect of borrowing, and that the harm is not great, when groups are dissimilar.

Example 1: treatment is of interest in all groups

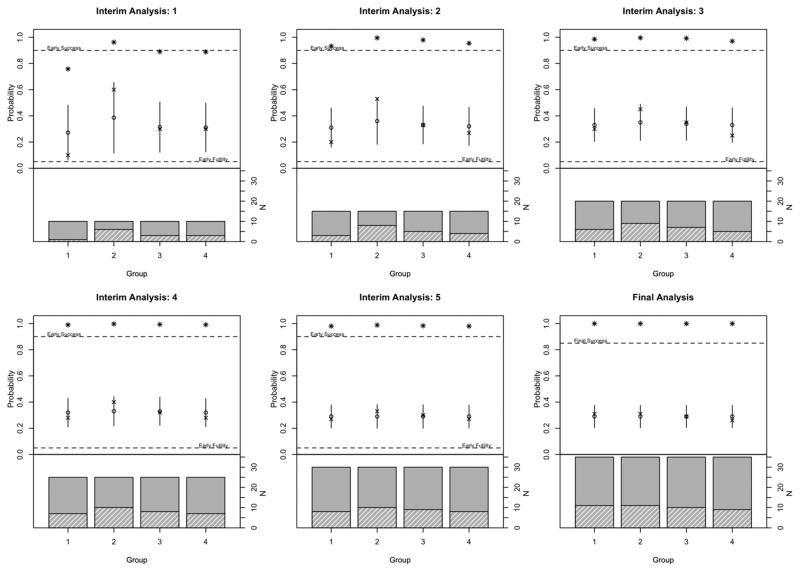
Figure 1 shows each of the interim analyses for this example. The first interim analysis occurs when 10 patients in each group have been assessed for response. We have observed one response in group 1, six responses in group 2, and three responses each in groups 3 and 4. The small sample sizes in each group result in strong borrowing, and the Bayesian hierarchical model shrinks the two most extreme groups, groups 1 and 2, more than 15% toward the overall mean. All groups have a high probability of being greater than p_mid, and so accrual continues in all groups to the next interim analysis.

Figure 1.

Example 1. Barplot shows sample size in each group where the height of the solid bar shows number of patients enrolled and height of the hashed bar shows number of patients who achieved a response. Upper part of the plot shows observed response (‘x’), fitted response (‘o’) and 2 times the standard deviation (line). Asterisks indicate Pr(p > pmid) for the interim analyses and Pr(p > p₀) at the final analysis.

The next interim analysis occurs when an additional five patients have been accrued in each group. We now observe 3, 8, 5, and 4 responses across the groups. The Bayesian hierarchical model pulls the highest observed response rate, 53%, down to a posterior mean estimate of 36%. Groups closer to the overall mean are shrunk less, such as group 3, in which the observed and model estimated response rates are the equal. With 15 patients in each group, there is a greater than 90% probability that p > p_mid in all groups.

Additional interim analyses occur after 20, 25, and 30 patients have been accrued in each group. The final analysis occurs when 35 patients have been accrued in each group. At the completion of the trial, we observe similar response rates across the groups – from 26% in group 4 to 31% in groups 1 and 2. The Bayesian hierarchical model estimates response rates as 29% in all four groups. The strong borrowing across the groups also results in a reduction in the uncertainty around these estimates. The 95% credible interval for the response rate in each group is 21%–37%. If each group had been considered in a separate trial and there was no borrowing between the groups, the 95% confidence intervals would be wider – (17%, 49%) for groups 1 and 2, (15%, 46%) for group 3, and (12%, 43%) for group 4. There is a high probability in each group that the response rate is greater than p₀, and so the treatment is considered efficacious and of interest for further investigation in all groups.

Example 2: treatment is of interest in only two groups

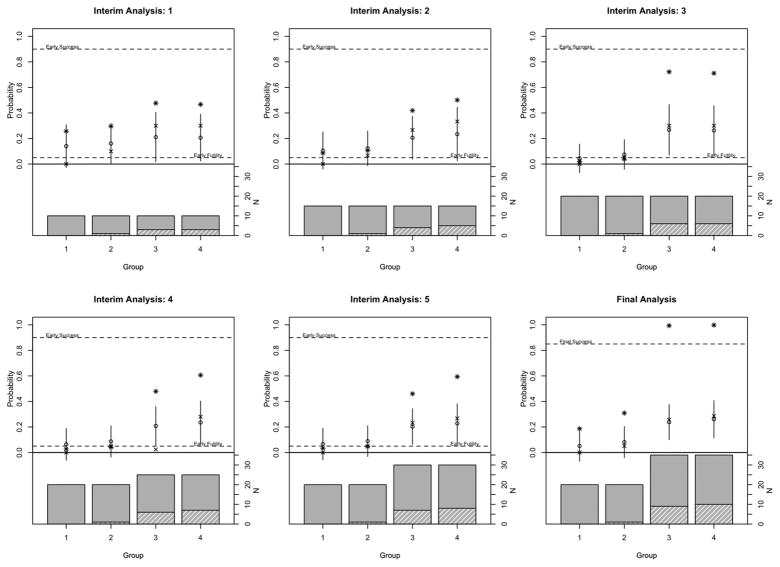
Figure 2 shows each of the interim analyses for this example trial. As above, the first interim analysis is conducted when 10 patients have been enrolled in each group. We observe zero responses in group 1 and three responses each in groups 3 and 4. There is a small sample size in each group at this first look, and so, there is substantial shrinkage from the Bayesian hierarchical model, with the posterior mean being 14% larger than the observed rate in group 1 and 9% smaller in groups 3 and 4.

Figure 2.

Example 2. Barplot shows sample size in each group where the height of the solid bar shows number of patients enrolled and height of the hashed bar shows number of patients who achieved a response. Upper part of the plot shows observed response (‘x’), fitted response (‘o’) and 2 times the standard deviation (line). Asterisks indicate Pr(p > pmid) for the interim analyses and Pr(p > p₀) at the final analysis.

The next interim look occurs when 15 patients have been enrolled in each group. We have observed zero responses in group 1 and only one response in group 2. With more patients and growing heterogeneity, there is now less shrinkage in groups 1 and 2, but the positive data in groups 3 and 4 keep the probability of being greater than p_mid greater than 5%, and thus, all groups continue to enroll to the next interim analysis.

The next interim analysis occurs when 20 patients have been enrolled in each of the groups. We have observed no additional responses in groups 1 and 2. The probability of being greater than p_mid is now less than 5%, and these groups stop for futility. Accrual to groups 3 and 4 continues.

Additional interim analyses occur when 25 and 30 patients have been enrolled. Groups 1 and 2 remain in the model for the purposes of estimation even though accrual to these groups has stopped. The final analysis occurs with 20 patients enrolled in groups 1 and 2 and the maximum accrual of 35 patients for groups 3 and 4. At the final analysis, the treatment would be considered efficacious and of interest for further investigation in groups 3 and 4 but not in groups 1 and 2. The 95% credible intervals for the response rate in each group are (0%, 17%) for group 1, (0%, 20%) for group 2, and (10%, 37%) for group 3, and (12%, 40%) for group 4. If each group had been considered in a separate trial, the 95% confidence intervals would be of similar width – (0.0%, 17%) for group 1, (0%, 25%) for group 2, (12%, 43%) for group 3, and (15%, 46%) for group 4. This example trial demonstrates that the algorithm can adjust to heterogeneous data and learn to shrink less.

Operating characteristics

To evaluate the performance of the three designs, we simulate each under varying assumptions of the true response rates in each group. In each scenario, 10,000 simulated trials are used. For the hierarchical design, we assumed equal numbers of patients in each group at each analysis. We report the proportion of simulated trials that concluded efficacy, the mean sample sizes, and describe the point estimation and the number of correct decisions (correctly rejecting or accepting the null) for each design.

The true response rates assumed for each scenario are shown in Table 2. The p₀ and p₁ for each group determining the design, reflecting the different background response rates across groups, are shown in Table 1. In Table 2, the first two scenarios are tailor-made for hierarchical borrowing because the treatment effect is similar in each group. In scenarios 3 and 4, there is a similar direction in the effect, but more heterogeneity, while in scenarios 5 and 6, there are stark differences in the effects for each group.

Table 2.

Response scenarios

Scenario	Response rate p
	Group 1	Group 2	Group 3	Group 4
1. Null	5%	5%	10%	20%
2. Alternative	20%	20%	30%	40%
3. One in the Middle	20%	20%	20%	50%
4. All in the Middle	15%	15%	20%	30%
5. One Nugget	5%	5%	10%	40%
6. 2 Null, 2 Alternative	5%	5%	30%	40%

Type I error

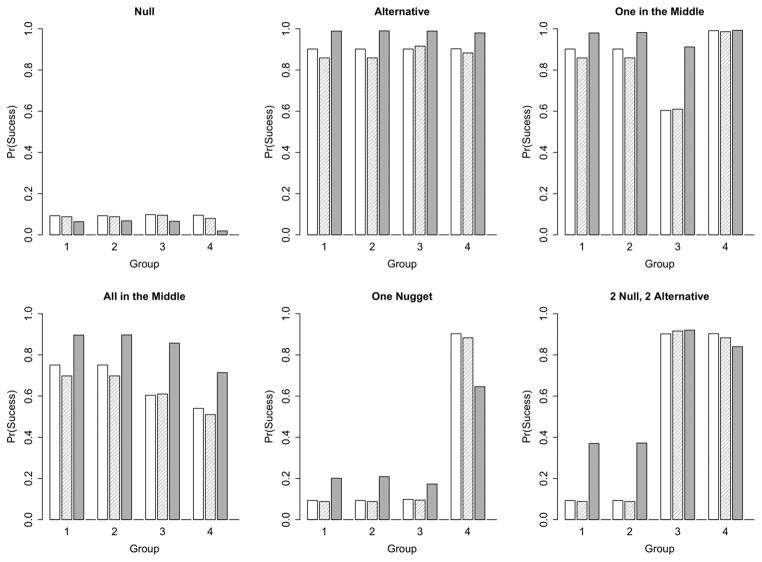
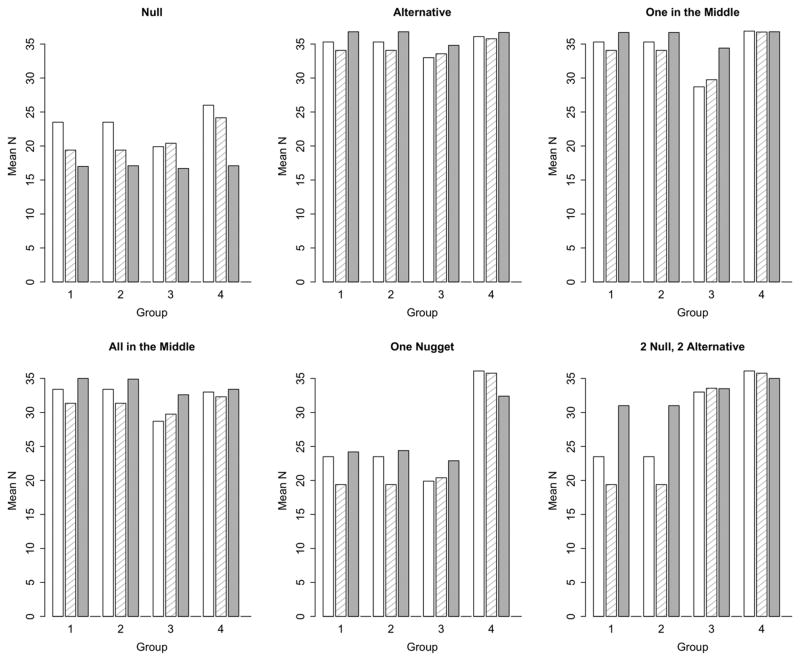
Type 1 error is the probability of claiming efficacy (i.e., reject H0) in scenarios where p = p₀. Probabilities of claiming efficacy by group are shown in Figure 3. The specification of the Simon’s design requires that Type I error be no more than 10%; actual Type I error rates are 9.3%, 9.3%, 9.8%, and 9.5%, for groups 1–4, respectively. As indicated above, we tuned the independent Bayesian design to have a Type I error of approximately 10%. For the particular null hypothesis that we assumed, scenario 1, when p = p₀, the Type I error rates are 8.8%, 8.8%, 9.5%, and 8.0% for groups 1, 2, 3, and 4, respectively. The Bayesian hierarchical design has Type I error of 6.4%, 6.8%, 6.6%, and 1.9% for groups 1, 2, 3, and 4, respectively. The hierarchical model reduces the Type I error rate in all groups, but the biggest reduction is in group 4. This is due to differing null and alternative response rates across the groups and the log-odds parameterization of the model. The borrowing in the Bayesian hierarchical model prevents Type I errors compared to the designs that ignore the data in the other groups.

Figure 3.

Probability of claiming efficacy by group in each scenario. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and the solid bar is Bayesian hierarchical.

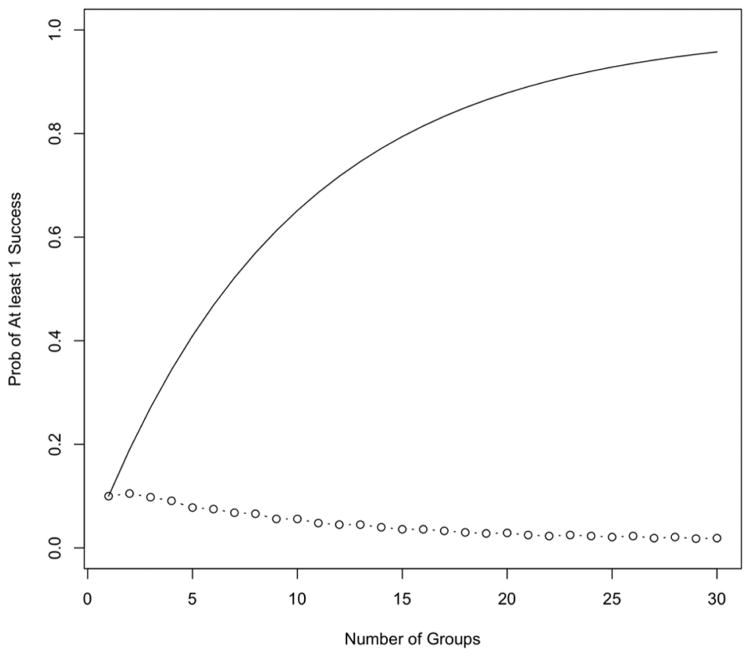
This reduction in Type I error has huge benefits when more groups are studied. Figure 4 shows the overall Type I error rate, the probability of claiming efficacy in at least one group under the null hypothesis for Simon’s design and the Bayesian hierarchical design for an increasing number of groups. We assume p₀ = 10% and p₁ = 30% for all groups. As the number of groups increases, the overall Type I error rate for parallel Simon’s designs increases – meaning that a Type I error is highly likely. The overall Type I error rate with 4 groups is 34.4% and with 10 groups is 65.1%. The Bayesian hierarchical design inherently adjusts for the multiplicities. As the number of groups increases, there is increasing shrinkage to the null and decreasing Type I error rates. The overall Type I error rate is 9.1% for 4 groups and 5.6% for 10 groups. The likelihood of a Type I error in multiple Simon’s designs goes to 1 as the number of groups increase, yet goes to 0 for the Bayesian hierarchical design. There are similar benefits of the Bayesian hierarchical design when the alternatives are true.

Figure 4.

Overall Type I error rate, probability of claiming efficacy in at least one group under the null hypothesis by the number of groups. Simon’s design is shown as a solid line and the Bayesian hierarchical design is shown as the dotted line. We assume p₀ = 10% and p₁ = 30% for all groups.

We consider two scenarios where the response rates are mixed between null and alternative across the four groups. Where there is ‘One Nugget’, the treatment would be considered of interest in only one group, p = p₀ in groups 1, 2, and 3 and p = p₁ in group 4. This is the most challenging scenario for the hierarchical model. In the Bayesian hierarchical design, the borrowing is weighted toward futility, but the single promising response rate in group 4 inflates the Type I error in groups 1, 2, and 3 to 17%–20%.

In the scenario, ‘2 Null, 2 Alternative’, p = p₀ in groups 1 and 2, and p = p₁ in groups 3 and 4. The Bayesian hierarchical design is able to recognize that groups 1 and 2 differ from groups 3 and 4. The probabilities of claiming efficacy in groups 1 and 2 are 37% compared with 92% and 84% in groups 3 and 4. Shrinkage toward the overall mean in this case makes the response rates for groups 1 and 2 appear more promising and the Type I error rate is inflated for these groups.

Power

Power is the probability of claiming efficacy in scenarios where p > p₀. Simon’s design requires that power be at least 90% when p = p₁; actual power is 90.2%, 90.2%, 90.2%, and 90.3%, for groups 1–4, respectively. Similarly, when p = p₁, the independent Bayesian designs have power of 86%, 86%, 92%, and 88% for groups 1, 2, 3, and 4, respectively. In the ‘Alternative’ scenario where p = p₁ for all groups, the addition of borrowing with the Bayesian hierarchical design increases power for all four groups. The similarity of treatment effects allows for strong borrowing, increasing precision, and boosting power to 98%–99% in each of the groups.

We consider two other scenarios for the demonstration of power. In the scenario ‘One in the Middle’, p = p₁ for groups 1 and 2, p = p_mid for group 3, and p > p₁ for group 4. Simon’s design has the specified power of 90% for groups 1 and 2, 60% power for the p_mid response rate in group 3, and 99% power to detect the large treatment effect in group 4. The independent Bayesian design has similar power. In the Bayesian hierarchical design, the promising treatment effects across the groups increase power for each group. The Bayesian hierarchical design has 91% power in group 3, compared to the 60% for Simon’s design and the independent Bayesian design.

In the scenario ‘All in the Middle’, the response rate is intermediate between p₀ and p₁ in all four groups. The true response rates in groups 1 and 2 are 15% and so slightly higher than p_mid. Simon’s design has 75% power, and the independent Bayesian design has 70% power for these groups. The true response rate in groups 3 and 4 are equal to p_mid. Simon’s design has power of 60% and 54%, and the independent Bayesian design has power of 61% and 51% in groups 3 and 4, respectively. The Bayesian hierarchical design has increased power. This design has powers of 90% in groups 1 and 2, 86% in group 3, and 71% in group 4.

The last two scenarios are a mixture of null and alternative response rates. In the ‘One Nugget’ scenario, borrowing is weighted toward futility as p = p₀ in three groups. Power in the Bayesian hierarchical design is reduced to 65%. Similarly, in the ‘2 Null, 2 Alternative’ borrowing reduces power in the Bayesian hierarchical design slightly to 92% and 84% in groups 3 and 4, respectively.

Mean sample size

We have first considered each Bayesian design with early stopping for futility only. Thus, the goal is to stop the trial early if the treatment appears not promising, but to enroll to the maximum sample size and gain more experience with the treatment if it appears promising. Simon’s design has a single early stopping analysis. The two Bayesian designs may have 5–6 early stopping analyses, depending on the maximum sample size.

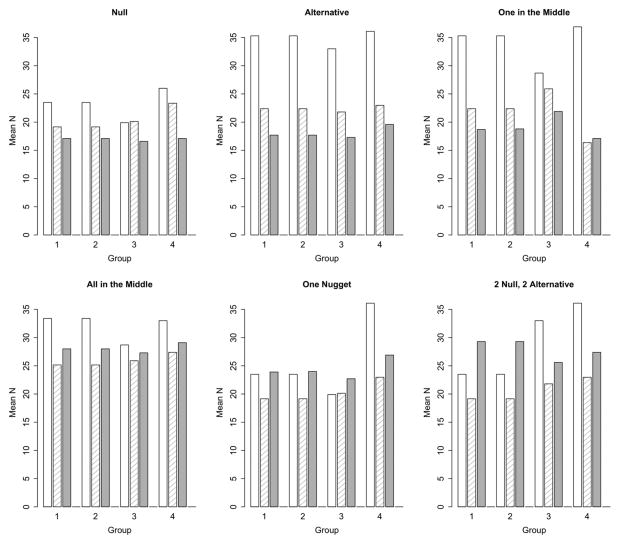
More interim analyses means the Bayesian designs are more likely to stop early when p = p₀ compared to Simon’s design. Mean sample sizes are shown in Figure 5. When p = p₀, Simon’s design has mean sample size of 23.5, 23.5, 19.9, and 26.0 in groups 1, 2, 3, and 4, respectively, while the independent Bayesian design has mean sample sizes of 19.3, 19.5, 20.5, and 24.2, respectively. The Simon’s design enrolls to the maximum sample size with 46% probability in groups 1 and 2, 34% probability in group 3, and 45% probability in group 4. The Bayesian hierarchical design enrolls to the maximum sample size with 20% probability in groups 1 and 2, 28% probability in group 3, and 37% probability in group 4.

Figure 5.

Mean sample size by group in each scenario. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and solid bar is Bayesian hierarchical.

Mean sample size is reduced again with the Bayesian hierarchical design, in correspondence with the lower Type I error (17.0, 17.1, 16.7, and 17.1 for groups 1 through 4, respectively). The Bayesian hierarchical design enrolls to the maximum sample size with 8% probability in groups 1 and 2 and 11% probability in groups 3 and 4. Therefore, under the null hypotheses, the mean sample size is smaller, and Type I error is smaller with the Bayesian hierarchical design.

In scenarios where p = p₁, early stopping for futility occurs rarely in each of the designs. Thus, most trials have the desired outcome of continuing to the maximum sample size. When p = p₁, Simon’s design has mean sample sizes of 35.3, 35.3, 33, and 36.1 in groups 1, 2, 3, and 4, respectively. Results are similar for the independent Bayesian design.

For the Bayesian hierarchical design, the increased probability of claiming efficacy in many scenarios corresponds to a larger mean sample size, such as in the ‘Alternative’, ‘One in the Middle’, and ‘All in the Middle’ scenario. In the ‘One Nugget’ and ‘2 Null, 2 Alternative’ scenario, the Bayesian hierarchical design has inflated Type I error for the groups where p = p₀, and a correspondingly larger average sample size in these groups.

Estimation

Table 3 shows the estimated means and standard deviations for the probabilities of response in each group. For Simon’s Optimal Two-Stage designs, we have calculated the average observed probability and average standard errors for each group and scenario. For the independent Bayesian designs, we have calculated the average posterior probability and average standard errors for each group and scenario. Point estimates are very similar between Simon’s design and the independent Bayesian design.

Table 3.

Estimated probability of response and standard errors

	Group 1	Group 2	Group 3	Group 4
Null
Truth	0.05	0.05	0.1	0.2
Simon	0.05 (0.05)	0.05 (0.05)	0.09 (0.06)	0.18 (0.08)
Independent Bayes	0.04 (0.04)	0.04 (0.04)	0.08 (0.06)	0.16 (0.09)
Hierarchical Bayes	0.05 (0.02)	0.05 (0.02)	0.09 (0.04)	0.14 (0.06)
Alternative
Truth	0.2	0.2	0.3	0.4
Simon	0.18 (0.08)	0.18 (0.08)	0.28 (0.09)	0.39 (0.09)
Independent Bayes	0.19 (0.08)	0.19 (0.08)	0.29 (0.10)	0.39 (0.10)
Hierarchical Bayes	0.20 (0.04)	0.20 (0.04)	0.30 (0.05)	0.40 (0.05)
One in the Middle
Truth	0.2	0.2	0.2	0.5
Simon	0.18 (0.08)	0.18 (0.08)	0.18 (0.08)	0.50 (0.09)
Independent Bayes	0.19 (0.08)	0.19 (0.08)	0.18 (0.09)	0.50 (0.09)
Hierarchical Bayes	0.20 (0.04)	0.20 (0.04)	0.26 (0.06)	0.44 (0.07)
All in the Middle
Truth	0.15	0.15	0.2	0.3
Simon	0.13 (0.07)	0.13 (0.07)	0.18 (0.08)	0.28 (0.09)
Independent Bayes	0.13 (0.08)	0.13 (0.08)	0.18 (0.09)	0.28 (0.11)
Hierarchical Bayes	0.14 (0.04)	0.14 (0.04)	0.21 (0.05)	0.29 (0.07)
One Nugget
Truth	0.05	0.05	0.1	0.4
Simon	0.05 (0.05)	0.05 (0.05)	0.09 (0.06)	0.39 (0.09)
Independent Bayes	0.04 (0.04)	0.04 (0.04)	0.08 (0.06)	0.39 (0.10)
Hierarchical Bayes	0.06 (0.03)	0.06 (0.03)	0.11 (0.05)	0.32 (0.12)
2 Null, 2 Alternative
Truth	0.05	0.05	0.3	0.4
Simon	0.05 (0.05)	0.05 (0.05)	0.28 (0.09)	0.39 (0.09)
Independent Bayes	0.04 (0.04)	0.04 (0.04)	0.29 (0.09)	0.39 (0.10)
Hierarchical Bayes	0.08 (0.04)	0.08 (0.04)	0.26 (0.08)	0.35 (0.09)

We indicated that the amount of borrowing in the Bayesian hierarchical approach is determined by the data: the more similar the groups, the greater the borrowing. The ‘Null’ and ‘Alternative’ scenarios illustrate that similarity across the groups results in strong borrowing and reduced uncertainty. The standard deviations for the Bayesian hierarchical design are smaller in this scenario as compared to the other two designs. The response rate for group 4 in the null scenario is 20%, but the Bayesian hierarchical model has a mean estimate of 14%. There is little to no bias for the other groups. As indicated above, there is a relatively larger amount of shrinkage for group 4 in this scenario, resulting in a particularly low Type I error rate.

Additionally, the ‘One in the Middle’ and the ‘2 Null, 2 Alternative’ scenarios illustrate shrinkage toward the overall mean in the Bayesian hierarchical design. In ‘One in the Middle’, the estimated probability of response for group 3 is more promising than truth, and the estimated probability of response for group 4 is less promising than truth. In the ‘2 Null, 2 Alternative’ scenarios, the estimated probability of response is pulled up for the two groups, where p = p₀ and pulled down for the two groups where p = p₁.

In the ‘One Nugget’ scenario, p = p₀ in the first three groups. The Bayesian hierarchical design borrows across these three groups such that point estimates are only slightly higher, and the standard deviations are smaller as compared to the other two designs. Group 4 is dissimilar, p = p₁, and so, the point estimate is shrunk toward the null response rate, but the heterogeneity of the groups results in a larger amount of uncertainty around the estimated probabilities of response.

Mean proportion of correct decisions

In the setting of simultaneously evaluating four groups, the interest is not only in evaluating each group individually but also in correctly evaluating all four groups – and thus evaluating the treatment overall. We define a correct decision as concluding futility where p = p₀ and concluding efficacy where p > p₀. Table 4 shows the proportion of correct decisions for each design across the scenarios.

Table 4.

Mean proportion of correct decisions

Scenario	Simon	Independent Bayes	Hierarchical Bayes
1. Null	0.905	0.913	0.946
2. Alternative	0.903	0.880	0.987
3. One in the Middle	0.850	0.828	0.967
4. All in the Middle	0.663	0.630	0.841
5. One Nugget	0.905	0.900	0.766
6. 2 Null, 2 Alternative	0.905	0.903	0.755

Generally, all three approaches are likely to make at least three out of four correct decisions. The Bayesian hierarchical design has a higher proportion of correct decisions, in all scenarios, except for the ‘One Nugget’, where it is more likely to conclude futility in the group where p > p₀ and in the ‘2 Null 2 Alternative’ scenario where the Bayesian hierarchical design has a higher probability of concluding efficacy in the groups where p = p₀.

Sensitivity analysis

The amount of borrowing depends on the prior distribution for the σ² parameter. This parameter allows the model to span from assuming all treatments are the same to assuming there is no borrowing. We have specified a prior that places approximately a weight of 0.001 on an estimated value of 0.1 for σ. This is a weak prior, allowing the data to shape the amount of borrowing. To understand the sensitivity of the results to the selected prior, we show, for the null and alternative scenarios, the probability of claiming efficacy and the estimated response rate across a range of prior distributions (Table 5). We show results for our same mean (0.1) with more weight (0.01) and with less weight (0.0001) and results for our same weight (0.001) with a larger mean (1) and a smaller mean (0.01). Each prior still allows the data to shape the amount of borrowing. Thus, the probability of claiming efficacy is consistent across the priors and the mean estimated probability of response varies little. Therefore, while the prior on σ² is important, we have selected priors that are robust to changes of an order of magnitude.

Table 5.

Sensitivity to the prior distribution of σ²

		Weight = 0.001 Mean = 0.1	Weight = 0.01 Mean = 0.1	Weight = 0.0001 Mean = 0.1	Weight = 0.001 Mean = 1	Weight = 0.001 Mean = 0.01
Null
Group 1	Efficacy	0.064	0.082	0.059	0.097	0.044
	Response	0.054	0.053	0.055	0.052	0.056
Group 2	Efficacy	0.068	0.080	0.058	0.098	0.045
	Response	0.054	0.054	0.055	0.052	0.056
Group 3	Efficacy	0.066	0.071	0.058	0.074	0.050
	Response	0.090	0.089	0.092	0.088	0.092
Group 4	Efficacy	0.019	0.021	0.021	0.024	0.015
	Response	0.143	0.144	0.143	0.146	0.143
Alternative
Group 1	Efficacy	0.989	0.991	0.988	0.992	0.981
	Response	0.200	0.200	0.200	0.200	0.200
Group 2	Efficacy	0.990	0.990	0.987	0.990	0.982
	Response	0.200	0.200	0.200	0.200	0.200
Group 3	Efficacy	0.989	0.989	0.987	0.991	0.982
	Response	0.299	0.299	0.298	0.298	0.298
Group 4	Efficacy	0.980	0.982	0.975	0.979	0.965
	Response	0.398	0.397	0.396	0.397	0.396

With early efficacy stopping

Early stopping with a claim of efficacy is not a characteristic of Simon’s design. It may be desirable to stop early for efficacy, saving time and patient resources, and moving the treatment to the next phase of development more rapidly. In other cases, one may want more information about an apparently effective treatment, but single-arm evidence with tumor response as an endpoint is of limited utility in addressing whether to move to Phase III. Consider again the examples of the Bayesian hierarchical trial. In Example 1, group 2 could have stopped early for efficacy at the first interim analysis with 10 patients, and the remainder of the groups could have stopped early for efficacy at the second interim analysis. Inference did not change with the additional patients enrolled. With an early efficacy stopping rule, this trial could have stopped early, with the correct answer, and saved most of the allotted patient resources. In this section, we compare the operating characteristics of the three designs when the Bayesian designs incorporate early stopping for both futility and efficacy.

Early stopping for a claim of efficacy typically does not change the overall probability of trial success, but does impact the mean sample size. Figure 6 shows the mean sample sizes for Simon’s design and the two Bayesian designs with early efficacy stopping. The addition of early efficacy stopping for the Bayesian designs tends to reduce the mean sample size in each group. Where the Bayesian hierarchical design has a greater probability of trial success, there is a further reduction in sample size.

Figure 6.

Mean sample size by group in each scenario with early efficacy stopping for the two Bayesian designs. The open bar is Simon’s design, the crosshatched bar is independent Bayesian, and solid bar is Bayesian hierarchical.

In the ‘Null’ scenario, mean sample size results are similar to those with no early efficacy stopping because in these scenarios, efficacy stopping is appropriately rare. In the ‘Alternative’ scenario, early efficacy stopping reduces the mean sample size in both Bayesian designs. The independent Bayesian design stops early for efficacy with 60%–64% probability across the groups and continues to the maximum sample size with 27% probability in groups 1 and 2, 30% probability in group 3, and 25% probability in group 4. The Bayesian hierarchical design has the greatest power in this scenario and correspondingly, the smallest mean sample sizes. The Bayesian hierarchical design stops early for efficacy with 82%–90% probability across the groups and continues to the maximum sample size with 10% probability in groups 1 and 2, 12% probability in group 3, and 16% probability in group 4. Results are similar for the ‘One in the Middle’ scenario.

In the ‘All in the Middle’ scenario, the Bayesian hierarchical design has a greater mean sample size as compared to the Independent Bayesian design as a result of continuing to the maximum sample size more frequently before being able to declare efficacy. With shrinkage in this scenario toward p_mid for all groups and early stopping criteria being based on p_mid, shrinkage in this scenario makes early efficacy stopping appropriately more difficult.

In the ‘One Nugget’ scenario, early efficacy stopping has little impact on the groups where p = p₀ as early efficacy stopping would be rare for these groups, but does reduce the mean sample size for group 4. The effect of early efficacy stopping is similar in the ‘2 Null, 2 Alternative’ scenario.

Discussion

We have compared two Bayesian adaptive approaches to the commonly used Simon’s Optimal Two-Stage design in the setting of Phase II trials in multiple patient groups. Bayesian adaptive designs can be tuned to have similar operating characteristics to Simon’s design in terms of Type I error and power. The resulting design will often have a lower sample size because of more frequent interim analyses and the possibility of stopping early for efficacy. Using a Bayesian hierarchical model to borrow across patient groups can provide a reduction in Type I error, increased power, and a further reduction in mean sample size. Bayesian hierarchical modeling makes personalized medicine tractable. Several different pharmaceutical companies have successfully implemented the Bayesian hierarchical design. Sometimes called tumor agnostic, the settings are frequently focused on patients who have a tumor positive for a particular biomarker irrespective of the tumor site.

The advantages of borrowing are pronounced when the treatment effects are similar in some of the groups, but they retain reasonably good properties more generally. With the model used, the null hypothesis response rates need not be similar across groups. When the drug appears promising in some groups and not in others, there is more potential for borrowing to inflate the Type I error rate. Hierarchical modeling adjusts for the regression effect. It is possible that such an adjustment is too great. But our experience with actual therapies is that the much greater problem is underadjustment or no adjustment at all. Hierarchical modeling partially accounts for the random highs and lows that occur in experiment results. The Bayesian hierarchical design inherently considers multiplicities and tends to make a higher number of correct decisions. If parallel Simon’s designs or independent Bayesian designs were conducted, the multiplicity of considering the same treatment in numerous patient groups would typically be ignored, allowing many ineffective treatments to advance through drug development.

Deciding whether and how to borrow across groups depends in part on whether similar treatment effects are a reasonable possibility. For example, would knowing there is positive treatment effect in one group make a positive treatment effect in another group more likely? The amount of borrowing in our model is determined by an inverse gamma hyperprior on the variance term for the log-odds of response rate. Other parametric forms for this prior could also be chosen, including uniform or half-cauchy [25]. There may be no optimal choice for the parametric form; however, our choice of the inverse gamma distribution performs well and creates desirable borrowing behavior in our examples. The appropriate amount of borrowing for a particular trial must be judged clinically at the time of trial design. For example, during trial design, the sponsor might consider example final results and the associated analyses across a range of models, and then use the model with which they are most comfortable.

For the purposes of comparing with Simon’s design, we tuned the independent Bayesian design to have the same Type I error rate, maximum sample size, and Type II error rate. The resulting operating characteristics of both Bayesian designs are a function of these choices. The purpose was to isolate the effect of borrowing, the unique feature of the Bayesian hierarchical design, by controlling as many design parameters as possible across the three strategies. However, in practice, alternative trial designs may be considered and need not be constrained by such correspondence to a traditional design.

The choice of futility and efficacy thresholds can be selected through examination of the simulation results. When p = p₀, if futility stopping is rare, the futility threshold can be increased to allow for increased futility stopping. This should be balanced by results when p > p₀. If groups stop for futility but efficacy would have been declared had enrollment been allowed to continue, the criterion can be decreased to lessen futility stopping. The final efficacy criterion can be selected by examining the overall Type I and Type II error rates and adjusted the threshold to achieve strong results. Fixed and Adaptive Clinical Trial Simulator (FACTS; Berry Consultants LLC and Tessella) is commercially available software that allows simulation of the Bayesian hierarchical design.

In our example, the Bayesian hierarchical design could be considered overpowered. With more stringent efficacy criteria, this design could be refined to have lower power in each group when p = p₁, 80%–90%, for example. This would lower the overall Type I error rate. The definitions of p₀, p_mid, and p₁ for the Bayesian designs are also in part an artifact of the comparison with Simon’s design. It may be more natural for these designs to have a single target response rate, p_goal, and to declare futility if the probability of p > p_goal is sufficiently small and to declare efficacy if it is sufficiently large.

In sum, with the ability to have greater power and lower Type I error with a lower mean sample size, the Bayesian hierarchical design is an important alternative in this Phase II setting.