Mathematical Modeling of the Insulin Signal Transduction Pathway for Prediction of Insulin Sensitivity from Expression Data

Abstract

Mathematical models of biological pathways facilitate a systems biology approach to medicine. However, these models need to be updated to reflect the latest available knowledge of the underlying pathways. We developed a mathematical model of the insulin signal transduction pathway by expanding the last major previously reported model and incorporating pathway components elucidated since the original model was reported. Furthermore, we show that inputting gene expression data of key components of the insulin signal transduction pathway leads to sensible predictions of glucose clearance rates in agreement with reported clinical measurements. In one set of simulations, our model predicted that glycerol kinase knockout mice have reduced GLUT4 translocation, and consequently, reduced glucose uptake. Additionally, a comparison of our extended model with the original model showed that the added pathway components improve simulations of glucose clearance rates. We anticipate this expanded model to be a useful tool for predicting insulin sensitivity in a mammalian tissues with altered expression protein phosphorylation or mRNA levels of insulin signal transduction pathway components.

Introduction

Insulin mediates glucose clearance from blood into tissues by triggering a cascade of interactions collectively known as the insulin signal transduction pathway [1]. Given the widespread, epidemic nature of obesity and type II diabetes mellitus (T2DM) [2], understanding and monitoring insulin sensitivity is critical to providing early and accurate diagnosis and treatment. Therefore, there is currently immense motivation in developing a comprehensive mathematical model of the insulin pathway. A few mathematical models have been developed that simulate mechanisms in this pathway [3, 4]. The highly cited model reported by Sedaghat et al. (Sedaghat's model) was one of the first comprehensive models of the insulin signal transduction pathway [3]. However, not all components of the insulin signal transduction pathway were known at the time of publication of Sedaghat's model. Since then, researchers have made significant progress toward elucidating components in this pathway. More recent models emphasize on the insulin-insulin receptor dynamics and whole body glucose homeostasis of the pathway [5,6,7,8], but took significantly different mathematical approaches from Sedaghat's model. We, however, chose to develop a comprehensive model based on Sedaghat's model that incorporates elements of the pathway that have been elucidated since 2002. The proposed model of this study is therefore a modification of Sedaghat's model.

In the insulin signal transduction pathway, the activation of insulin receptors leads to phosphorylation events of many, if not all, downstream components [9,10]. The insulin-stimulated phosphorylation of phosphatidyl inositol-3-kinase (PI3K) stimulates the phosphorylation of two downstream proteins – protein kinase C (PKC)- ζ and protein kinase B (Akt) [11,12]. Phosphorylated PKC-ζ and Akt initiate two separate pathway branches, both of which ultimately lead to the translocation of glucose transporter 4 (GLUT4) from the cytoplasm to the plasma membrane. Once at the plasma membrane, GLUT4 facilitates the uptake of glucose into skeletal muscle and adipose cells. The pathway steps elucidated since the introduction of Sedaghat's model in 2002 include crucial downstream signaling steps between PKC-ζ /Akt and GLUT4 translocation [13,14,15]. These downstream steps have been implicated in insulin resistance and T2DM. For example, AS160, which is an intermediate between Akt and GLUT4, is overexpressed or phosphorylated during exercise [16]. Because of the significance of these newly elucidated pathway steps, we developed an extension of Sedaghat's model incorporating these steps. Our model is also able to simulate both GLUT4 translocation and (clinically relevant) glucose clearance. We validated our expanded model using gene expression data from our knockout mouse model.

Glycerol kinase and insulin sensitivity

We used our expanded model to predict insulin sensitivity from gene expression data using a glycerol kinase (GK in humans, Gyk in mice) knockout mouse model in our lab. Glycerol kinase deficiency (GKD; MIM 307030) is an inherited inborn error of metabolism caused by mutations, deletions, or insertions in the glycerol kinase gene on Xp21 [17]. The association between the GKD and insulin sensitivity has been observed in several studies [18,19,20,21]. For example, Gaudet et al. [18] reported that 12 out of 18 individuals carrying a particular GKD missense mutation, N288D, met the criteria for either impaired glucose tolerance or diabetes mellitus. Such results suggest the hypothesis that the underexpression or deletion of GK may decrease insulin sensitivity.

We used our expanded model to simulate the translocation of GLUT4 to the plasma membrane and subsequently predict glucose uptake rates, in response to a given dose of insulin. The extent of this translocation is a measure of insulin sensitivity. We evaluated our expanded model by inputting differential gene expression levels in mice [22]. Our model simulations aimed to show the significance of adding new key components of the insulin signal transduction into the previous model.

Methods

Insulin Signaling Pathway and Mathematical Model

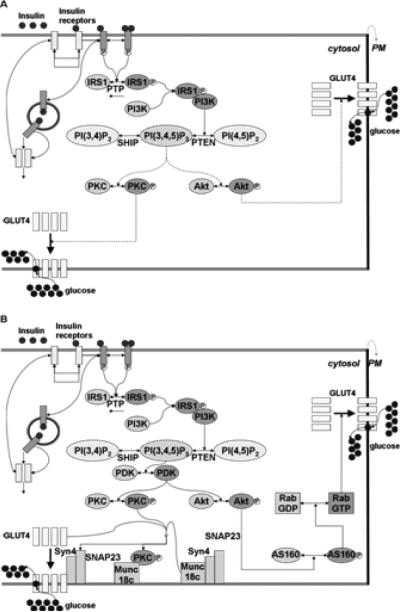
In the insulin signal transduction pathway, insulin binds to the insulin receptor and initiates a complex signal transduction cascade, ultimately leading to the transport of the glucose transporter GLUT4 to the plasma membrane and subsequent glucose uptake into the cell [3,10]. Figure 1A depicts Sedaghat's model and the dotted lines shown in the figure symbolizes mechanisms that were poorly understood at that time. Figure 1B depicts our expanded model that incorporates the additional pathway steps elucidated and characterized since the publication of Sedaghat's model. All signaling steps used in Sedaghat's model are included in our expanded model. To improve the level of uncertainty in Sedaghat's model, we have added steps downstream of PKC/ AKT components crucial for GLUT4 translocation events.

Figure 1.

Insulin signal transduction pathway. Unphosphorylated proteins and inactive molecules are shown in light gray, and phosphorylated proteins and active molecules are shown in dark gray.

A. Insulin signal transduction pathway modeled by Sedaghat et al. (2002). Incompletely elucidated pathway steps are shown as dashed lines.

B. Our expanded insulin signaling pathway that is simulated in this study. AS160, RabGDP, and Munc18c-Syn4-SNAP23 complex are the new components introduced to this model.

Our current mathematical model of the insulin signal transduction pathway comprises a set of ordinary differential equations (ODEs) describing all known events in this signal transduction pathway. Each step is modeled as a chemical reaction, whose rate is first order with respect to each reactant. Additionally, each reaction rate is dependent on the extent of a previous reaction (see Table 1). Table 1 lists the signal transduction events and rate constants in the original model by Sedaghat et al. (Equations 1-12) [3], and those that were added in this work (Equations 13-19). We added newly elucidated steps that accounts for the connections between both the PKC- ζ phosphorylation event and the GLUT4 translocation as well as between Akt phosphorylation and GLUT4 translocation. We modeled the steps downstream of PKC based on published studies that confirmed that phosphorylated PKC displaces munc18c from the plasma membrane, thereby facilitating increased GLUT4 translocation to the plasma membrane [13]. We modeled the steps downstream of Akt on the basis of recent investigations, that have shown that Akt phosphorylates AS160, which in turn activates the GTP activity of Rab, triggering movements of GLUT4-containing vesicles to the plasma membrane [14,15].

Table 1.

Signal transduction events, state variables, and model parameters in the insulin signal transduction pathway.

Reaction	Remarks	Rate constants Forward reactions.	Rate constants Reverse reactions.
1	IR + I ↔ IR-I	k1	km1
2	IR-I + I ↔ IR-I2	k2	km2
3	IR-I, IR-I2 → IR-I-P, IR-I2-P	k3	km3 [PTP]
4	IR-I-P + I ↔ IR-I2-P	k2	km2
5	IR ↔ IRintracellular	k4	km4
6	→ IRintracellular →	k5	km5
7	IR-I, IR-I2 → IRintracellular	k4’
8	IR-I-P, IR-I2-P ↔ IR-I-P intracellular, IR-I2-P intracellular	k4’	km4’
9	IRS 1 ↔> IRS 1-P	k7	km7[PTP]
10	IRS1-P + PI3K ↔ IRS1-P-PI3K	k8	km8
11	PI(4,5)P2 ↔ PI(3,4,5)P3	k9	km9[PTEN]
12	PI(3,4)P2 ↔ PI(3,4,5)P3	k10	km10[SHIP]
13	IRS 1 ↔ IRS1-P’	k113	km113
14	Akt <-> Akt-P	k113	km11
15	Akt-P + AS160 <-> AS160-P	k14a	km14a
16	AS160P + RabGDP<-> RabGTP	k15	km15
17	PKC-P + Munc18c-Syn4-SNAP <-> PKC-P –Munc18c + Syn4-SNAP	k16	km16
18	RabGTP +Glut4 -> Glut4 Translocation	k13p	km13
19	PKC-P-Munc18c + Glut4-> Glut4 Translocation	k13pp	km13

Reactions 1-12 are original equations included in Sedaghat's model (3). Reaction 13—19 are new events incorporated into this expanded model.

We modified some of the mathematical equations in Sedaghat's model, including the differential equations of Akt and PKC, due to the addition of new downstream components (e.g. AS160, Munc18c). To incorporate the new components into our model, we re-formulated the first order differential equations that simulate the formation and depletion of each component using new rate constants. For example, the transfer of a phosphoate group from phosphorylated Akt to AS160 subsequently triggering RabGTP formation, from RabGDP, can be represented by:

$$\begin{array}{cc}\hfill & \frac{\mathrm{d}\left[\mathrm{AS}160\right]}{\mathrm{dt}}=-{\mathrm{k}}_{\mathrm{AS}160}[\mathrm{Akt}-\mathrm{P}]\left[\mathrm{AS}160\right]+{\mathrm{k}}_{\mathrm{mAS}160}[\mathrm{AS}160-\mathrm{P}]\hfill \\ \hfill & \frac{\mathrm{d}[\mathrm{AS}160-\mathrm{P}]}{\mathrm{dt}}={\mathrm{k}}_{\mathrm{AS}160}[\mathrm{Akt}-\mathrm{P}]\left[\mathrm{AS}160\right]-{\mathrm{k}}_{\mathrm{bmAS}160}[\mathrm{AS}160-\mathrm{P}]-\hfill \\ \hfill & -{\mathrm{k}}_{\mathrm{fRabGTP}}[\mathrm{AS}160-\mathrm{P}]\left[\mathrm{RabGTP}\right]+{\mathrm{k}}_{\mathrm{bmAS}160}\left[\mathrm{RabGDP}\right]\left[\mathrm{AS}160\right]\hfill \end{array}$$

Supplementary Table 1 lists values of rate constants and boundary conditions. The set of ODEs representing the entire model (30 ODEs, including forward and reverse reactions of each step) was solved by using a ode15s ODE solver in MATLAB (The Mathworks, Natick, MA). We have retained all variable and parameter names common to both models. Our newly added pathway components downstream of the PKC/Akt replaced Eq. 25 of Sedaghat's model [3], which empirically models all the metabolic effects that take place between the PKC/Akt subsystem and the translocation event. Particularly, our expanded model assumes that the formations of RabGTP and the PKC-Munc18c complex are the last reactions of the pathway that directly activate the translocation of GLUT4 to the plasma membrane. In order to account for the metabolic effects of the Sedaghat's model, we created new rate constants, k13p and k13pp, which are designated for the translocation of GLUT4 in response to the RabGTP component and the PKC-Munc18c complex, respectively.

Determination of the new rate constants and initial conditions

We estimated the rate constants and initial conditions corresponding to the newly added model components by fitting our expanded model to data from the literature. We determined a limited range for each rate constant, tested different combinations of the rate constant values corresponding to the new model components, and ultimately chose the optimal set of parameters that would best fit published in-vivo data, e.g. Baus et al. [23]. The ranges of each rate constant were selected to match the scaling factors of the published data. For experimental data from the literature, see Results.

Output conversion to glucose uptake rate

Instead of using the percentage of Glut4 translocated to plasma membrane, we have simulated the more clinically relevant glucose uptake rate as the ultimate output of our expanded model. We employed Michaelis-Menten kinetics model in this output conversion. Important parameters of the kinetics model, such as Km and Vmax, are from Chew et al. [4]..

Experimental animals and animal care

Gyk deficient mice were courtesy of W. J. Craigen (Baylor College of Medicine) [24] and our breeding strategy is as previously described [22]. All mice were kept on a normal diet (Harlan Tekland) and all procedures and experiments were performed as per a protocol approved by the UCLA Chancellor's Animal Research Committee. RNA isolation, cDNA hybridization, and microarray analysis are as previously described [22]. The fold differences in selected genes, including PTP, PKC, and PI3K, between wild type mice and knock out mice, reported in Rahib et al. [22], were inserted into the appropriate boundary equations to generate the simulated response curves.

Statistical analysis

Statistical analysis on the predicted insulin responses was performed by employing a Bootstrap Monte Carlo algorithm [25] to transform the errors illustrated in published data to standard deviations or confidence intervals of the predicted GLUT4 translocation and glucose uptake rate. The statistical significance of the predictions (‘p’ values) were determined by using the Student's t test.

Results

Our model of the insulin signal transduction pathway extends the previously published Sedaghat model by capturing mechanisms that have been elucidated since its publication (Figs. 1A, B) [3]. In our model, PKC-ζ is mechanistically linked to the GLUT4 translocation event through the reaction of PKC-P with Munc18c, which is a component of the Munc18c-Syn4-SNAP23 complex. A second route leading to GLUT4 translocation involves Akt, in which Akt phosphorylates AS160, triggers activation of Rab GTP, and subsequently affects GLUT4 movement to the plasma membrane.

We took care to ensure that the changes made in our expanded model did not cause significant deviations in the dynamics of GLUT4 translocation and glucose uptake response in the physiological systems. To test our expanded model, we compared how closely our simulations compared with the simulations from Sedaghat's model. The time response curves of the GLUT4 translocation and the glucose uptake response of our expanded compared to original Sedaghat's model upon administration of an insulin dose of 0.1 nM for 60 min (t = 0 to 60 min) are seen in Figures 2A and 2B. The GLUT4 translocation and glucose uptake dynamics simulated by our expanded model qualitatively agrees with those simulated by Sedaghat's model (Figs. 2A, 2B).

Figure 2.

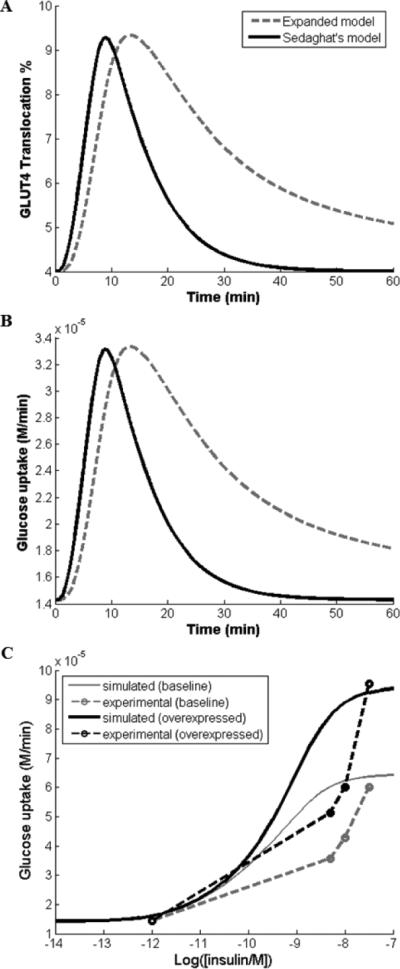
Comparison of our expanded model (dashed line) and Sedaghat's original model (solid line).

A. GLUT4 translocation time response curve comparing the two models with a single insulin dose input of 0.1nM and run time of 60 min

B. Glucose uptake rates with a single insulin dose of 0.1nM and run time of 60 min

C. Insulin dosage response curve showing expected glucose uptake rates from an insulin dose of 10⁻¹² M to 10⁻⁶ M. Comparison of simulated glucose uptake (solid lines) and experimental glucose uptake (dotted lines) as a result of AS160 overexpression. Experimental results were based on data from Baus et al. study and data points were presented as hollow circles in the figure.

To determine the rate constants of the newly added components, we gathered experimental data from published literature that implicates the components’ chemical kinetics. For example, we used data presented in Baus et al. to determine the rate constants k14a, which corresponds to the kinetics of the AS160 phosphorylation reaction [23]. In their study, Baus et al. examined insulin-stimulated glucose uptake of skeletal muscle cells expressing the AS160 splice variant, in which the expression of the AS160 transcript variant expression was approximately five fold less than that of the full length AS160 (Fig. 1B of Baus et al.). They showed that cells expressing the variant have increased glucose uptake, approximately 2.3 fold higher than the control, when stimulated with 50nM insulin. We revised their bar plot results (Fig. 3A of Baus et al.) into scatterplot format to facilitate our determination of the proper rate constant value k14a [23]. By using the chosen rate constant values, we simulated the AS160-glucose uptake fold change relationship observed in the scatterplot (Fig. 2C). Insulin dosage response curves were simulated in the insulin dose range of 10⁻¹⁴ to 10⁻⁷ M (exposure time of 60 min) for two concentrations (e.g. one with baseline expression of AS160 and one with 5-fold increase in expression of AS160. The basal glucose uptake rate under minimum insulin stimulation was approximately 15uM/min.The dosage response curves matched reasonably well, particularly at low insulin concentrations (0.1 nM) and high concentrations at 50nM. There was slight deviation at the hillslope of the response curve. Based on the comparison, we concluded that our current model was optimized for the input insulin dose of 0.1nM. All single dose simulations for the remainder of this study were done using that particular dose.

Figure 3.

Simulation of the effect of overexpression of PTP (2.8-fold) and PKC (3.0-fold), and underexpression of PI3K ( 2.8-fold). Recorded from our previous microarray data of Gyk KO with respect to Gyk WT mice.

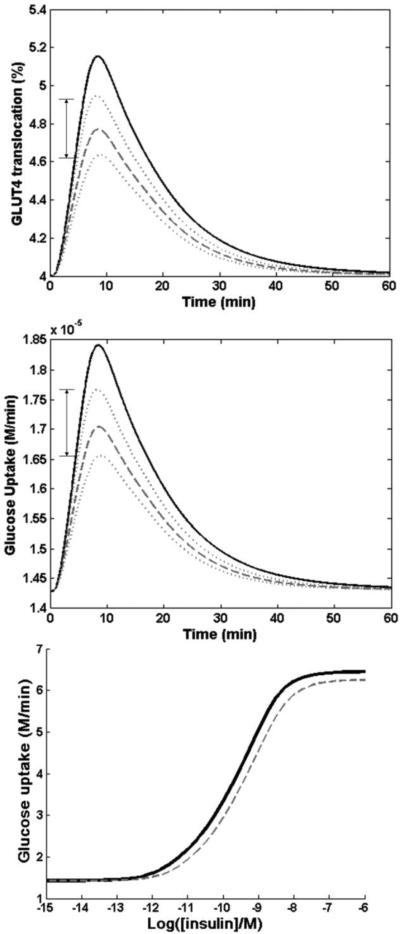
A. GLUT4 translocation time response curves, Gyk KO (dashed and dotted lines) vs WT (solid line), with a single insulin dose input of 0.1nM and run time of 60 min. (p<0.05). Dotted lines represent the range of outputs for GLUT4 translocation % of Gyk KO, accounting for the standard error of the data reported in Rahib et al. (2007)

B. Glucose uptake level, Gyk KO (dashed and dotted lines) vs WT solid line), with a single insulin dose of 0.1nM and run time of 60 min. (p<0.05). Dotted lines represent the range of outputs for GLUT4 translocation % of Gyk KO, accounting for the standard error of the data reported in Rahib et al. (2007) C. Insulin dosage response curves (Gyk KO vs WT) showing expected glucose uptake levels from insulin dose inputs from 10⁻¹² M to 10⁻⁶ M. (p<0.05)

Model predicts decreased insulin sensitivity in brown fat of Gyk knockout mice

Microarray analysis of brown fat from Gyk knockout (KO) mice revealed that a number of genes in the insulin signal transduction pathway were under- or over- expressed relative to wild type (WT) mice (Table 3 of Rahib et al.) [22]. Two principal genes in the pathway: PTP (protein tyrosine phosphatase, 1.51-fold) and PKC (protein kinase C, 1.42-fold) were overexpressed in the Gyk KO mice. Whereas, PI3K was underexpressed 1.48-fold. Other insulin-related genes that were differentially expressed in the Gyk knockout mice, but were not in the insulin signal transduction pathway, include c-Jun N-terminal kinase (overexpressed 1.45-fold), insulin growth factor 1 (overexpressed 2.1-fold), and insulin growth factor binding protein (underexpressed 3.7-fold) [22].

Using our expanded mathematical model of the insulin signal transduction pathway, we simulated the effect of these altered gene expressions on glucose uptake rates using the dataset from Rahib et al. [22]. The translocation of GLUT4 to the plasma membrane for an insulin dose of 0.1 nM for 60 min, was used as a measure of insulin sensitivity. The raw data of all GLUT4 simulations can be found in Supplementary Table 2. Figure 3 depicts the comparison of GLUT 4 translocation (Fig. 3A) and glucose uptake rates (Fig. 3B) in the Gyk KO (dotted line) and WT mice (solid line) due to PI3K underexpression accompanied with PTP and PKC overexpression. The reduction of GLUT4 translocation in Gyk KO mice, compared to WT, is 7.4 % (p<0.05), and the glucose clearance, the total amount of glucose uptake into cell, is 2.2% less than that of Gyk WT mice. We also simulated the responses of the Gyk WT and KO mice to various doses of insulin from 10⁻¹² M to 10⁻⁷ M (Figs. 3B, C). The WT mice exhibit a higher glucose uptake throughout the entire insulin dosage range, with the most pronounced difference at the highest insulin concentration.

Discussion

We successfully modified a previously published mathmatical model of the insulin signaling pathway (Sedaghat's model) by incorporating recently elucidated pathway components. Our expanded model is able to analyze the effect of insulin sensitivity from altered gene expression of the new components. We used this model to assess insulin sensitivity comparing WT and Gyk KO mice. Our results are consistent with the hypothesis that knockout Gyk mice have reduced insulin sensitivity.

Although we observed minor differences in the shape of the insulin-stimulated time response curves of our model compared to that of Sedaghat's model (Fig. 2), we believe that our model better suits the physiological system than the original, in terms of the insulin-stimulated GLUT4 translocation response. A recent in-vivo project studying differentiated myotubes showed that the GLUT4 translocation level was peaked at 10 minutes after stimulation and continued to degrade past 60 minutes, Fig. 4C of Yuasa et al (2009)[26], further supporting the trend of our model. We noted that the GLUT4 translocation response returns to basal level when simulation time goes passes 150 minutes. Our expanded model reflects that the amount of GLUT4 translocation and glucose uptake, the outputs of our design, are dependent on the amount of insulin input, the level of gene expressions of key players, and the rate of each reversible reactions.

The analysis using Gyk KO mice microarray data further strengthens GKD's association insulin sensitivity. Our model predicted that Gyk KO mice were insulin resistant compared to WT mice. Subsequently, our current Gyk KO mice model become growth retarded soon after birth and do not survive past day three of life, which does not allow for proper insulin sensitivity accessment [24]. However, the model prediction of insulin resistance in Gyk KO mice is consistent with the symptoms of isolated GKD in humans [18]. The model simulation results using Gyk microarray data also show the trend that GK underexpression accompanied by differential expressions of other genes result in a reduction of insulin sensitivity. We suggest two possible reasons why GK underexpression is likely contributing to reduced insulin sensitivity. Firstly, GK lies at the interface of carbohydrate and lipid metabolism [27]. In addition, it was reported that the thiazolidinediones, which are agonist for peroxisome proliferator-activated receptor γ (PPARγ) and a common drug to treat T2DM, increase GK expression in adipocytes [20,21]. GK maintains futile cycling between lipids and carbohydrates, thus perhaps preventing free fatty acid accumulation and insulin desensitization. It is logical to advocate that its deficiency can be expected to have an impact on insulin sensitivity.

Secondly, GK is a ‘moonlighting enzyme’, which has alternative non-enzymatic functions, having at least four functions apart from its enzymatic function[28, 29]. Of particular importance is its role as ATP-stimulated translocation factor (ASTP). ASTP is an ATP-stimulated factor that enhances the nuclear binding of the activated glucocorticoid-receptor (GR) complex, an important transcription factor. In fact, GR complex activation is known to activate genes related to obesity/T2DM. A particular study confirmed that white adipose tissues of mice treated with synthetic glucocorticoid have increased triglyceride synthesis[30]. GK may be indirectly responsible for the activation or suppression of other genes, some of which may be involved in insulin response. Therefore, GK deficiency is expected to reduce insulin sensitivity.

Our extended model has shown great potential in simulating GLUT4 translocation and glucose uptake in other applications as well. For example, we can potentially apply the model to an existing study of glucose sensitivity in human patients with obesity or T2DM in response to exercising. Exercise has been shown to prevent or improve obesity and insulin sensitivity in T2DM [16, 31, 32, 33]. Short-term exercise increases the concentration of active insulin receptors as well as insulin receptor substrate-1 (IRS1) phosphorylation in both obese and T2DM patients [31]. Exercise training has also been shown to increase overall insulin signaling transduction and glucose uptake rates in skeletal muscles of rodents [32]. We will make small changes to the current model by determining a new set of model parameters to fit expression data of human subjects and apply the model with obesity and T2DM data sets.

In order to test our expanded model with data sets of gene expression, we emphasize the subsets of reactions where the forward and reverse kinetic constants are not dependent on each other. If the enzyme product of the differentially expressed gene catalyzes both directions of a reversible reaction, we need to alter both forward and reverse kinetic constants. Some of these reactions are catalyzed irreversibly. For example, PTP dephosphorylates IRS1-P into IRS1, but it does not participate in the forward reaction. In this case, the forward kinetic constant is independent of the reverse reaction. Another subset of reactions includes differentially expressed genes or proteins that undergo post-translational modification in the insulin signal transduction pathway. The phosphorylation of the protein AS160 are reversible. When the gene or protein expression level of AS160 equals to the sum of the unphosphorylated and phosphorylated moieties, we can assume that an increase in the gene expression level will result in increased total availability of the protein. To test whether gene expression data and protein activity data can be used interchangeably, we found published data by Yu et al. [34], showing both gene expression and protein activity level of key insulin signaling gene, PTEN, in diabetic mice. Using their data, we performed our model simulations, generated by using either the published mRNA or protein data, and confirmed that the difference in using gene or protein data is insignificant (Supplementary Figure 1).

A potential weakness of simulating such a complex signaling system, such as the insulin signal transduction pathway, using a mathematical model is that the selection of appropriate rate constants and boundary conditions can be somewhat arbitrary. Our attempts to strengthen the power of our model include adapting strategies and model parameters that were presented in the established Sedaghat's model and similar models based on Sedaghat's model. We incorporated some key components between the insulin signaling pathway and GLUT4 trafficking to lower the degree of uncertainty in the model. We also validated our complete model by comparing dosage and time response curves to the selected study (e.g. Rahib et al.). This model could be applied to other datasets [16, 35, 36, 37] that emphasize exploring the relationship of exercising and key components in the insulin signal transduction pathway to strengthen our current model.

We could also incorporate the current model with elements from other recently developed models that cover other aspects of the insulin signal transduction pathway, such as Dalla Man's model of whole-body glucose homeostasis and Brannmark's dynamic model of receptor mechanisms [7, 8]. However, those models took significantly different approaches from the original Sedaghat's model, therefore did not fit into the comparisons performed in this study.

Conclusions

In this study, we developed an expanded mathematical model of the insulin signal transduction pathway based on Sedaghat's model, which allows for prediction of insulin sensitivity and glucose uptake from microarray data. Our expanded model can simulate the translocation events of the insulin signal transduction pathway more comprehensively with the added key components and present a more clinically relevant model output, glucose uptake. Our model predictions are consistent with our published results that the differential gene expression shown in Gyk KO mice contribute to decreased insulin sensitivity. Such predictions, in turn, will be valuable in investigating the relationship between GKD and insulin resistance. The expanded mathematical model developed here can be applied to many biological systems with minimal changes, and will be a useful tool to study insulin resistance for the insulin signal transduction and diabetes research community.

Highlights.

• The proposed mathematical model gives a sensible prediction of glucose clearance and insulin sensitivity in mouse

• This model is a modification of the published model by Sedaghat et al., with additions of newly elucidated components of the insulin signal transduction pathway and output of glucose uptake.

• Our model predicts reduced insulin sensitivity in Glycerol kinase knock out mice.

List of Abbreviations

T2DM

Type II Diabetes Mellitus

PI3K

Phosphatidyl inositol-3-kinase

(PKC)- ζ

Protein kinase C zeta

Akt

Protein kinase B

GLUT4

Glucose transporter 4

GK/Gyk

Glycerol kinase (GK in humans and Gyk in mice)

WT

Wildtype

KO

Knockout

PTP

Protein tyrosine phosphatase

[i]

The concentration of species i

$\frac{\mathrm{d}\left[\mathrm{i}\right]}{\mathrm{dt}}$

The change in concentration of species i over time

k_A

rate constant of the forward reaction including reacting species A

k_MB

rate constant of the reverse reaction including reacting species B