Brain hyper-connectivity and operation-specific deficits during arithmetic problem solving in children with developmental dyscalculia

Abstract

Developmental dyscalculia (DD) is marked by specific deficits in processing numerical and mathematical information despite normal intelligence (IQ) and reading ability. We examined how brain circuits used by young children with DD to solve simple addition and subtraction problems differ from those used by typically developing (TD) children who were matched on age, IQ, reading ability, and working memory. Children with DD were slower and less accurate during problem solving than TD children, and were especially impaired on their ability to solve subtraction problems. Children with DD showed significantly greater activity in multiple parietal, occipito-temporal and prefrontal cortex regions while solving addition and subtraction problems. Despite poorer performance during subtraction, children with DD showed greater activity in multiple intra-parietal sulcus (IPS) and superior parietal lobule subdivisions in the dorsal posterior parietal cortex as well as fusiform gyrus in the ventral occipito-temporal cortex. Critically, effective connectivity analyses revealed hyper-connectivity, rather than reduced connectivity, between the IPS and multiple brain systems including the lateral fronto-parietal and default mode networks in children with DD during both addition and subtraction. These findings suggest the IPS and its functional circuits are a major locus of dysfunction during both addition and subtraction problem solving in DD, and that inappropriate task modulation and hyper-connectivity, rather than under-engagement and under-connectivity, are the neural mechanisms underlying problem solving difficulties in children with DD. We discuss our findings in the broader context of multiple levels of analysis and performance issues inherent in neuroimaging studies of typical and atypical development.

Introduction

Nationally representative studies of young adults’ quantitative abilities, including basic arithmetic, indicate that nearly one in four have not mastered the mathematics expected of an 8th grader, making them functionally innumerate (e.g. unable to interpret quantitative information in a news story) (Bynner, 1997; Hudson, Price & Gross, 2009; NCES, 2007). The result is that independent of sex, race, intelligence, and reading ability, adults in the bottom quartile of mathematical competencies have reduced employment prospects, lower wages once employed, and difficulty with many routine quantitative activities (Parsons & Bynner, 1997; Rivera-Batiz, 1992). Individual differences in children’s mathematical achievement are highly consistent throughout schooling (Duncan, Claessens, Huston, Pagani, Engel, Sexton, Japel, Dowsett, Magnuson, Klebanov, Feinstein, Brooks-Gunn & Duckworth, 2007). Children who start school with a poor understanding of numerals and poor arithmetic skills are four times more likely than their peers to score in the bottom quartile on employment-relevant quantitative tests by adolescence, controlling for other factors (Geary, Hoard, Nugent & Bailey, 2013). Children within this at-risk group, with otherwise typical intelligence and reading achievement, are considered to have developmental dyscalculia (DD). These children have persistent difficulties in committing basic arithmetic facts to long-term memory, understanding or accessing magnitudes associated with number words and Arabic numerals, as well as delays in the learning of arithmetical procedures (Butterworth, Varma & Laurillard, 2011; Geary, 1993; Geary, Hoard, Nugent & Bailey, 2012b; Jordan, Hanich & Kaplan, 2003; Mazzocco, Feigenson & Halberda, 2011; Rousselle & Noel, 2007).

Despite much progress in our understanding of arithmetic problem solving deficits in children with DD, very little is currently known about the way in which different, but inter-related, arithmetic operations are processed in the brain. Most behavioral and brain imaging studies of arithmetic processing in children with DD have focused on tasks involving addition problems (Davis, Cannistraci, Rogers, Gatenby, Fuchs, Anderson & Gore, 2009; Geary, Bailey, Littlefield, Wood, Hoard & Nugent, 2009; Geary, Hoard & Bailey, 2012a; Jordan et al., 2003; Kucian, Loenneker, Dietrich, Dosch, Martin & von Aster, 2006). Behavioral studies have shown that children with DD use immature strategies to solve addition problems, relying more on counting than their typically developing (TD) peers. Moreover, when memory retrieval strategies are used, they tend to be error-prone (Geary, Hoard, Byrd-Craven & DeSoto, 2004; Geary, Hoard, Byrd-Craven, Nugent & Numtee, 2007). Relative to addition, subtraction is thought to draw more on an internal representation of quantity (Dehaene, Piazza, Pinel & Cohen, 2003) and the execution of calculation procedures (Campbell & Xue, 2001), two aspects of numerical cognition in which children with DD are thought to be particularly weak (Geary et al., 2009; Wilson, Dehaene, Pinel, Revkin, Cohen & Cohen, 2006).

Despite this, little is known about the cognitive profile of subtraction problem solving deficits in children with DD. Only one study to date has examined subtraction strategy use in children with DD (Ostad, 1999). Ostad (1999) reported that whereas TD children progressed to more sophisticated verbal counting and retrieval strategies, children with persistent difficulties in mathematics continued to rely almost exclusively on finger counting for subtraction problems, even in the 7th grade. In contrast, most children with DD eventually abandon finger counting for addition problems (Geary et al., 2004). This pattern suggests that the focus on solving addition problems in this literature may have underestimated the difficulties children with DD have in learning arithmetic, and contrasting their competencies when solving addition and subtraction problems will provide a more complete assessment of their deficits. In the current study, we compare the behavior, brain responses, and brain connectivity during addition and subtraction problem solving in a well-characterized set of children with DD and their TD peers.

Functional neuroimaging studies have consistently implicated the intraparietal sulcus (IPS) region of the dorsal parietal cortex as a key locus of numerical and arithmetic information processing deficits in adults and children with mathematical difficulties (Kesler, Haberecht, Menon, Warsofsky, Dyer-Friedman, Neely & Reiss, 2004; Kucian, Grond, Rotzer, Henzi, Schonmann, Plangger, Galli, Martin & von Aster, 2011a; Molko, Cachia, Riviere, Mangin, Bruandet, Le Bihan, Cohen & Dehaene, 2003; Mussolin, De Volder, Grandin, Schlogel, Nassogne & Noel, 2010; Price, Holloway, Rasanen, Vesterinen & Ansari, 2007). Previous studies have shown that IPS activity is modulated by numerical distance during both symbolic (e.g. determine which is more ‘3 2’) and non-symbolic (e.g. ‘••• ••’) numerical comparison tasks (Ansari & Dhital, 2006; Ansari, Garcia, Lucas, Hamon & Dhital, 2005; Pinel, Dehaene, Riviere & LeBihan, 2001). IPS activity is also modulated by the complexity of arithmetic problem solving (Jost, Khader, Burke, Bien & Rosler, 2011; Menon, Rivera, White, Glover & Reiss, 2000; Rosenberg-Lee, Barth & Menon, 2011a). Studies using these paradigms have been used to probe numerical problem solving deficits in children with DD. Price and colleagues (Price et al., 2007) found that children with DD have reduced activity in the IPS during a non-symbolic comparison task and, unlike TD children, they fail to demonstrate numerical-distance-related modulation of IPS activity. In the case of arithmetic problem solving, evidence to date using addition has been mixed with some studies pointing to modest reductions in task-related activation in the IPS in 3rd and 6th graders with DD (Kucian et al., 2006) and others finding differences primarily outside the IPS in 3rd graders with DD (Davis et al., 2009). These discrepancies may be related to differences in the criteria used to define DD, the age ranges studied, as well as the control tasks used.

Very few studies to date have directly compared brain responses to addition and subtraction problem solving (De Smedt, Holloway & Ansari, 2011; Kawashima, Taira, Okita, Inoue, Tajima, Yoshida, Sasaki, Sugiura, Watanabe & Fukuda, 2004; Rosenberg-Lee, Chang, Young, Wu & Menon, 2011b). In adults, using precise cyto-architectonic mapping Rosenberg-Lee (2011b) and colleagues found significantly greater activation of the IPS during single-digit subtraction when compared to single-digit addition. In a developmental study, contrasting a sample of eight 40–49-year-old adults and eight 9–14 year-old children, Kawashima and colleagues found no group differences in brain response between the two operations (Kawashima et al., 2004), perhaps because of the small sample size. In children with math difficulties, only one study to date has contrasted brain responses to addition and subtraction problem solving (De Smedt et al., 2011). De Smedt and colleagues examined the effects of problem size, operation and mathematical ability in 10–12-year-olds. Children were divided into two groups based on their performance on the Mathematical Fluency subtest of the Woodcock Johnson – III (Woodcock, McGrew & Mather, 2001): children who were at least one standard deviation below the mean comprised a low arithmetical fluency group (n = 8), whereas children scoring within one standard deviation of the mean comprised the typical arithmetical fluency group (n = 10). Consistent with findings for adults (Rosenberg-Lee et al., 2011b), they found greater IPS responses during subtraction than addition. Surprisingly, however, no differences were found in brain response between children with low and typical arithmetic fluency, perhaps because the typical achieving group had relatively low untimed calculation ability and because of the small sample size. We overcome these limitations here by using a larger sample of children and a more appropriate TD group, with whole-brain and cytoarchitectonic mapping as well as novel brain connectivity analyses.

The first goal of our study was to investigate whether addition and subtraction, two related mathematical operations, are processed differently in young children with DD. We focused on children in the 2nd and 3rd grades (7–9 years) because they are at an important stage for the acquisition and mastery of basic arithmetic (Jordan et al., 2003; Meyer, Salimpoor, Wu, Geary & Menon, 2010). Critically, we acquired data from a well-characterized sample of children with DD that was matched to a sample of TD children on IQ, reading ability as well as multiple working memory measures. Based on previous imaging literature suggesting IPS under-activation in DD, we predicted that, even after matching on IQ and reading ability, children with DD would show weaker responses in the IPS as well as the prefrontal cortex (PFC) while solving both addition and subtraction problems. Further, we predicted that this under-activation should be more pronounced for subtraction than addition, because subtraction relies to a greater extent on quantity-based calculation procedures that are particularly weak in children with DD (Geary et al., 2004; Wilson & Dehaene, 2007).

The second goal of our study was to examine the organization of key brain circuits underlying arithmetic problem solving in children with DD. To our knowledge, no previous studies have investigated arithmetic task-related deficits in brain connectivity in children with DD. Critically, recent studies have highlighted the important role of functional interactions among multiple brain areas in cognitive skill development (Fair, Dosenbach, Church, Cohen, Brahmbhatt, Miezin, Barch, Raichle, Petersen & Schlaggar, 2007; Supekar, Uddin, Prater, Amin, Greicius & Menon, 2010; Uddin, Supekar & Menon, 2010). Recently, Supekar and Menon (2012) investigated functional connectivity and causal interactions within fronto-parietal circuits important for arithmetic processing. They found that the maturation of prefrontal cortex control signals was crucial for the development of arithmetic problem solving skills. Use of this approach has the potential to substantially enhance our understanding of the brain systems and mechanisms underlying problem solving difficulties in children with DD.

Here, for the first time, we examine functional brain circuits associated with the IPS during arithmetic problem solving in children with DD. We used a new generalized form (McLaren, Ries, Xu & Johnson, 2012) of the well-established psycho-physiological interaction (PPI) method (Friston, Buechel, Fink, Morris, Rolls & Dolan, 1997) to examine task-related changes in connectivity of the IPS to other brain regions. PPI uses the general linear model to examine the temporal relation between a seed region (in this case the IPS) and all other voxels in the brain after accounting for overall task-related activation and common driving influences from other brain regions. We tested the hypothesis that in addition to localized processing deficits in multiple frontal and parietal areas, children with DD would also show aberrant task-related modulation of parietal circuits important for numerical problem solving. Based on previous findings of increases in long-range connectivity with development (Fair et al., 2007; Kelly, Di Martino, Uddin, Shehzad, Gee, Reiss, Margulies, Castellanos & Milham, 2009; Rosenberg-Lee et al., 2011a; Supekar, Musen & Menon, 2009) and stronger fronto-parietal connectivity during a free-viewing paradigm related to better math ability (Emerson & Cantlon, 2012), we hypothesized that children with DD would display weaker patterns of connectivity of the IPS with multiple brain regions, notably the PFC, when compared to their TD peers, and that these aberrations would be more pronounced during subtraction compared to addition.

Methods

Participants

Participants were recruited from a wide range of schools in the San Francisco Bay Area using mailings to schools and postings at libraries and community groups. Participants were selected from an ongoing longitudinal study of mathematical development, which recruited children between the ages of 7 and 9 years with no history of psychiatric illness and full-scale IQ above 80 (as assessed using the Wechsler Abbreviated Scale of Intelligence; Wechsler, 1999). Children who scored at or below the 25th percentile on the Numerical Operations subtest of the Wechsler Individual Achievement Test – Second Edition; WIAT-II, Wechsler, 2001) were classified as DD; the lowest scoring participant was at the 6th percentile, with the median level at the 14th percentile. The 25th percentile was used because the lowest quartile of adults on tests of basic mathematics are functionally innumerate (Bynner, 1997) and children scoring below this cutoff on tests that assess basic mathematical competencies are at heightened risk for poor long-term outcomes in mathematics learning (Geary et al., 2007; Geary et al., 2012b; Geary et al., 2013; Murphy, Mazzocco, Hanich & Early, 2007) and later functional innumeracy (Geary et al., 2013). The TD group was defined using symmetrical criteria, scoring between the 75th and the 94th percentile, inclusive, on the Numerical Operations subtest. Participants in both groups scored above the 25th percentile on the Word Reading subtest of the WIAT-II, to ensure that there were no reading disabilities in either group. These criteria identified 19 children with DD and 21 TD children from the larger study sample. Three children with DD and one TD child were excluded because of excessive movement during fMRI scanning; the final groups therefore consisted of 16 children with DD (10 girls, 6 boys; M = 8.34 years; SD = .65) and 20 TD children (11 girls, 9 boys; M = 8.44 years; SD = .57).

Standardized cognitive assessments

Mathematical abilities

Mathematical abilities were assessed using the Numerical Operations and Mathematical Reasoning subtests of the WIAT-II (Wechsler, 2001). For the age range assessed here, the Numerical Operations test includes items that assess number writing and identification, rote counting, number production and, using pencil-and-paper, accuracy when solving simple single-digit (e.g. 4 − 2 = ) and more complex double-digit (e.g. 37 + 54 presented vertically) addition, subtraction, multiplication, and division problems. The Mathematical Reasoning subtest requires verbal problem solving in areas such as geometric shape identification, and single- and multistep word problems involving time, money, and measurement with both verbal and visual prompts. The child is required to solve problems with whole numbers, fractions or decimals, interpret graphs, identify mathematical patterns, and solve problems involving statistics and probability. For example, a dime is presented and the child is asked: ‘How many pennies does it take to equal the value of one dime?’ A probability problem asks: ‘If you flipped a coin ten times, how many times would the coin be most likely to land on heads?’

Reading abilities

The WIAT-II was also used to assess reading abilities. The Word Reading subtest involves reading individual words presented visually to the child, whereas the Reading Comprehension subtest requires them to match words to pictures and answer questions about sentences and passages they have read.

Working memory

Four subtests of the Working Memory Test Battery for Children (Pickering & Gathercole, 2001) were used to assess the three core components of working memory (Baddeley, 1996). The Central Executive was assessed by the Counting Recall and Backward Digit Recall tests. Phonological capacity was assessed by the Digit Recall test and visuo-spatial sketchpad capacity was assessed by the Block Recall test, as described elsewhere (Meyer et al., 2010).

Brain imaging

Experimental procedures

The fMRI experiment consisted of one run of addition and one run of subtraction. Within each run there were four task conditions: (1) Complex arithmetic, (2) Simple arithmetic, (3) Number identification and (4) Passive fixation. In the Complex addition task, participants were presented with an equation involving two addends and asked to indicate, via a button box, whether the answer shown was correct or incorrect (e.g. ‘3 + 4 = 8’). The first operand ranged from 2 to 9, the second from 2 to 5 (tie problems, such as ‘5 + 5 = 10’, were excluded), and answers were correct in 50% of the trials. Incorrect answers deviated by ±1 or ±2 from the correct sum (Ashcraft & Battaglia, 1978). The Simple addition task was identical except that one of the operands was always ‘1’ (e.g. ‘3 + 1 = 4’). In the Complex subtraction task, the first operand ranged from 3 to 14 and the second operand from 2 to 5. In the Simple subtraction task, the first operand ranged from 2 to 14 and the second operand was always ‘1’. As in the addition task, incorrect answers deviated by ±1 or ±2 from the actual difference, with the additional constraint that the actual and presented difference was always greater than zero. A verification, rather than verbal production, task format was used in the scanner because overt verbal responses can result in significant head movement and unusable fMRI data. In the number identification task, arithmetic symbols were replaced by alternative keyboard symbols (e.g. ‘4 o 5 @ 7’) and participants were asked to assess if ‘5’ was among the presented digits. This task was intended to control for basic visual number processing and motor response. Finally, in the Passive fixation task, the symbol ‘*’ appeared at the center of the screen and participants were asked to focus their attention on it. To aid children’s performance, specific task instructions appeared below each problem. During the Complex and Simple arithmetic tasks, the word ‘Solve’ appeared below the problem. In the number identification task, the word ‘Find’ appeared on the screen, and during the passive fixation trials, the word ‘Look’ appeared on the screen.

Stimuli were presented in a block fMRI design in order to optimize signal detection and task-related functional connectivity analysis (Friston, Zarahn, Josephs, Henson & Dale, 1999). Within each run, there were four blocks of each of the four conditions and the order of the blocks was randomized across participants with the following constraints: in every set of four blocks, all conditions were presented and the Complex and Simple arithmetic task blocks were always separated by either a Number identification or Passive fixation block. All orders of arithmetic and non-arithmetic task conditions were equally likely. Each trial lasted 5.5 seconds with an inter-trial interval of 500 milliseconds followed by the stimuli displayed for 5 seconds. Trials were grouped together in sets of four or five trials resulting in 22- or 27.5-second blocks. With 18 trials per condition and four conditions, the total length of each experimental run was 6 minutes and 36 seconds and the addition run always preceded the subtraction run.

fMRI data acquisition

Images were acquired on a 3T GE Signa scanner (General Electric, Milwaukee, WI) using a custom-built head coil at the Stanford University Lucas Center. Head movement was minimized during the scan by cushions placed around the participant’s head. A total of 29 axial slices (4.0 mm thickness, 0.5 mm skip) parallel to the AC-PC line and covering the whole brain were imaged using a T2* weighted gradient echo spiral in-out pulse sequence (Glover & Lai, 1998) with the following parameters: TR = 2 s, TE = 30 msec, flip angle = 80°, 1 interleave. The field of view was 20 cm, and the matrix size was 64 × 64, providing an in-plane spatial resolution of 3.125 mm. To reduce blurring and signal loss from field inhomogeneity, an automated high-order shimming method based on spiral acquisitions was used before acquiring functional MRI scans (Kim, Adalsteinsson, Glover & Spielman, 2002).

fMRI preprocessing

Functional MRI data were analyzed using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). The first 5 volumes were not analyzed to allow for T1 equilibration. A linear shim correction was applied separately for each slice during reconstruction (Glover & Lai, 1998). Images were realigned to the first scan to correct for motion and slice acquisition timing. Following procedures similar to those used in AFNI 3dDespike (Cox, 1996), deviant volumes resulting from spikes in movement greater than 0.5 voxels or spikes in the global signal greater than 5% were then interpolated using the two adjacent scans. All participants had less than 10% of volumes interpolated from spikes due to movement and less than 15% total volumes interpolated. Four children (three DD and one TD) were excluded because of excessive movement. The DD and TD groups did not differ on total movement, scan-to-scan movement, or the number of volumes interpolated due to movement (all ps > .28, Table S1 in Supplementary Materials). Images were then spatially normalized to standard MNI space using the echo-planar imaging template provided with SPM8, resampled every 2 mm using trilinear sinc interpolation, and smoothed with a 6-mm full-width half-maximum Gaussian kernel to decrease spatial noise prior to statistical analysis.

Individual participant and group analyses – block design

Task-related brain activation was identified using the general linear model implemented in SPM8. In the individual participant analyses, interpolated volumes flagged at the preprocessing stage were de-weighted and did not contribute to calculating the model fit. Brain activity related to each task condition was modeled using boxcar functions corresponding to the block length and convolved with a canonical hemodynamic response function and a temporal dispersion derivative to account for voxel-wise latency differences in hemodynamic response. In addition, the six movement parameters generated from the realignment procedure were included as regressors of no interest. Low-frequency drifts at each voxel were removed using a high-pass filter (.5 cycles/min). Serial correlations were accounted for by modeling the fMRI time series as a first-degree autoregressive process. Voxel-wise t-statistics maps contrasting Complex addition and Complex subtraction were generated for each participant and used for all subsequent analyses. Because Simple problems can be solved with reference to the counting sequence, our analysis focused on Complex problems as they provide a purer measure of arithmetic performance.

At the group level, we first conducted an omnibus test of task activation using the individual contrast addition + subtraction in a random effects model. For this contrast, against a resting baseline, significant activation clusters were identified using a stringent height threshold of p < .001, corrected for multiple comparisons at p < .01 using a Monte Carlo determined cluster extent of 41 voxels after gray matter masking. Next we computed several group-level analyses contrasting brain response to addition and subtraction. Because the addition and subtraction tasks are well matched on visual and motor processing demands and because they differ only in arithmetic processing demands, we compared them directly: (i) a one-way t-test on pooled data from all participants was first used to identify areas of significantly greater activity for addition relative to subtraction and for subtraction relative to addition, (ii) a between-group t-test was used to compare activation between DD and TD children on the combined responses to addition and subtraction, (iii) a between-group t-test was used to directly compare activation between DD and TD children on the contrast of addition vs. subtraction, and (iv) additional analyses were conducted to examine whether differences in brain activation in the comparison between addition and subtraction arose because of potential behavioral differences between the groups. We first examined three ANCOVA models to test for group differences in the presence of the behavioral covariates of accuracy, reaction time and number of missed trials. We then examined the relation between these behavioral measures and brain activity.

Significant activation clusters for these contrasts between conditions and groups were identified using a height threshold of p < .01, corrected for multiple comparisons at p < .01 using a Monte Carlo determined cluster extent of 128 voxels after gray matter masking. Functional clusters were labeled based on the Harvard-Oxford Cortical and Subcortical Structural Atlases provided in FSLview (Smith, Jenkinson, Woolrich, Beckmann, Behrens, Johansen-Berg, Bannister, De Luca, Drobnjak, Flitney, Niazy, Saunders, Vickers, Zhang, De Stefano, Brady & Matthews, 2004), using a probability threshold of 25%. As the IPS is not a distinct region in the Harvard-Oxford Atlas, we used the Juelich Histological Atlas provided in FSLview (Smith et al., 2004) to identify peaks falling within the three cyto-architectonic subdivisions of the IPS (see Region of interest analyses).

Individual participant and group analyses – event-related design

In order to disentangle the relative contributions of correct and incorrect trials to brain responses in children with DD, we performed a ‘quasi-event-related’ analysis, in which each trial was treated as a separate event. We created separate event types for incorrect and correct Complex trials, but grouped incorrect Simple and Find trials together as they are not of specific interest here. To assess the validity of this quasi-event-related design, we examined the orthogonality between GLM regressors corresponding to incorrect and correct trials after hemodynamic-convolution of event time series corresponding to each trial type (Liu, 2004).

Region of interest analyses

Beta values were extracted in each functional cluster identified by the interaction of Group and Operation for each individual. Beta values were also extracted from unbiased anatomical regions of interest (ROI) based on the cyto-architectonic divisions of the IPS (Eickhoff, Stephan, Mohlberg, Grefkes, Fink, Amunts & Zilles, 2005). The IPS has been divided into three distinct subdivisions: hIP2 on the anterior lateral bank, hIP1 which is posterior to hIP2 (Choi, Zilles, Mohlberg, Schleicher, Fink, Armstrong & Amunts, 2006), and the hIP3 which is posterior and medial to both regions (Scheperjans, Hermann, Eickhoff, Amunts, Schleicher & Zilles, 2008).

Connectivity analysis

Psychophysiological interaction (PPI) was used to examine the connectivity of the IPS with the rest of the brain during addition and subtraction in DD and TD children. PPI measures the temporal relation between a given seed region and all other brain voxels after accounting for the common driving influence of task activity on both the seed and target voxel (Friston et al., 1997). Here we used a generalized form of PPI (gPPI) as implemented in the ‘Generalized Form of Context-Dependent Psychophysiological Interactions’ SPM toolbox (McLaren et al., 2012). This newly developed method has the flexibility of estimating task-dependent functional connectivity within each task condition, for experiments with multiple conditions. Simulation and empirical studies have shown that gPPI is more powerful than the standard PPI implementation in SPM, and is especially well suited to assessing functional connectivity in block design experiments (Cisler, Bush & Steele, 2014).

At the individual participant level we included: (1) three regressors for the psychological variables (i.e. the three task conditions, Complex, Simple and Find); (2) one regressor for the physiological variable (i.e. the time course in the seed region); and (3) three regressors for the psychophysiological interaction term (i.e. the cross-product of each psychological variable with the seed region time course). Movement parameters and a constant term were also included in the model. The regional seeds were 6 mm spheres centered on the left and right IPS peaks identified from the omnibus analysis (left: −28 −64 42, right: 32 −60 44). Time series for the IPS seeds were obtained by extracting the first eigenvariate of the raw voxel time series in the ROI, separately for each individual.

The parameter estimates from the PPI term for each seed and operation were entered into a 2 × 2 × 2 ANOVA with between-participant factor Group (DD, TD) and within-participant factors Operation (Addition, Subtraction) and Hemisphere (Left IPS, Right IPS). We first examined the pattern of connectivity within each group, which we present for illustration purposes at an uncorrected height threshold of p < .001. We next considered the main effect of Group as well as the two- and three-way interactions with Group. We extracted mean t-scores for each individual in order to visualize the direction of the group effects. Finally, we computed three ANCOVA models to test for group differences in the presence of the behavioral covariates of accuracy, reaction time and number of missed trials, and then examined the relationship of these measures with IPS connectivity. Significant activation clusters were again determined using a height threshold of p < .01 and cluster extent of 128 voxels after gray matter masking, similar to the procedures used in the brain activation analysis.

Results

Standardized cognitive assessments

Children in the DD and TD groups did not differ on full-scale, verbal, or performance IQ (ps >.39), or on the Word Reading and Reading Comprehension sub-tests (ps > .14) (Table 1). The groups did not differ on the Digit, Counting, and Backward Digit Recall (ps > .21) measures of working memory. However, children with DD had significantly lower scores on Block Recall (p = .008). By design, children with DD scored lower on the Numerical Operations subtest (p < .001). They also differed significantly on the Mathematical Reasoning subtest (p = .006), but this difference was not significant when Numerical Operations was used as a covariate (p = .257), indicating that the deficits of the DD children involve very basic numerical/arithmetic processes.

Table 1.

Demographic and cognitive measures

	DD		TD		t	p
	M	SD	M	SD
Age (years)	8.34	0.65	8.44	0.57	−0.51	.614
IQ – WASI
Verbal	106.9	12.40	109.2	13.46	−0.52	.605
Performance	109.3	16.36	111.8	12.45	−0.52	.606
Full scale	108.6	11.84	111.8	10.42	−0.86	.399
Achievement – WIAT-II
Word Reading	106.3	9.60	111.5	11.03	−1.49	.146
Reading comprehension	105.9	8.16	110.0	9.73	−1.34	.191
Numerical operations	84.6	3.69	115.8	3.55	−25.74	<.001
Mathematical reasoning	101.3	13.80	114.3	12.47	−2.95	.006
Working Memory – WMTB-C
Digit recall1	105.3	17.68	106.3	12.62	−0.19	.851
Block recall1	91.0	11.74	101.2	9.76	−2.80	.008
Counting recall	85.8	20.42	94.2	20.62	−1.22	.231
Backward digit recall	94.5	18.92	101.5	13.87	−1.27	.212

¹One participant in the DD group was excluded because their raw score was too low to be standardized. DD = Developmental Dyscalculia, TD = Typically Developing, WASI = Wechsler Abbreviated Scales of Intelligence, WIAT-II = Wechsler Individual Achievement Test –Second Edition, WMTB-C = Working Memory Test Battery for Children.

Brain imaging

Behavioral differences between DD and TD groups

Accuracy

We conducted a two-way ANOVA with Operation (Addition, Subtraction) as a within-participants factor and Group (TD, DD) as a between-participants factor. The significant main effects for Operation (F(34, 1) = 10.10, p = .003) and Group (F(34, 1) = 9.87, p = .003) were qualified by a significant Group × Operation interaction (F(34, 1) = 5.37, p = .027), as shown in Figure 1. The interaction emerged because children with DD showed greater impairments on subtraction (DD = 49.7% vs. TD = 73.9%, t(34) = −3.62, p = .001) than on addition (DD = 65.6% vs. TD = 76.4%, t(34) = 1.84, p = .074). Because children with DD had low accuracy on the subtraction task we examined the behavioral profile further. Children with DD failed to respond to 33.3% (SD = 19.7%) of subtraction problems, compared to only 14.4% (SD = 18.5%) missed trials in TD children (t(34) = 2.96, p = .006). However, accuracy on trials in which children with DD made a response was 75.4% (SD = 19.2%), which is significantly higher than chance (one-sample t(15) = 5.03, p < .001). This pattern suggests that children with DD were engaged in the task, but were often unable to produce responses in the allotted time.

Figure 1. Behavioral performance in DD and TD children on addition and subtraction problems.

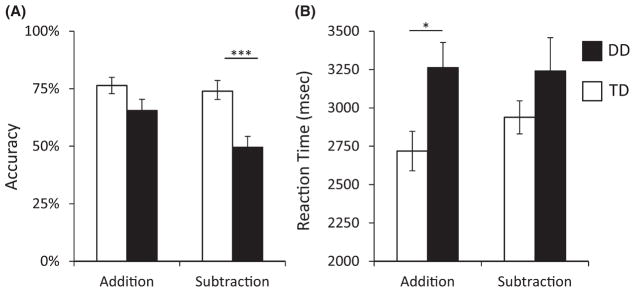
(A) Children with developmental dyscalculia (DD) were significantly less accurate than typically developing (TD) children during subtraction problem solving (p = .001), but this difference was marginally significant for addition problems (p = .074). (B) On correctly performed trials, children with DD were significantly slower than TD children for addition (p = .012), but did not differ on subtraction (p = .191), although the interaction did not reach significance (p = .217). *p < .05; ***p < .001.

Reaction times

A two-way ANOVA revealed that reaction times were significantly longer for children with DD than for TD children (F(34, 1) = 4.76, p = .036). Neither the main effect for Operation (F(34, 1) = 1.07, p = .308), nor the Group by Operation interaction (F(34, 1) = 1.58, p = .217) were significant (Figure 1).

Differential brain activation while solving addition and subtraction problems

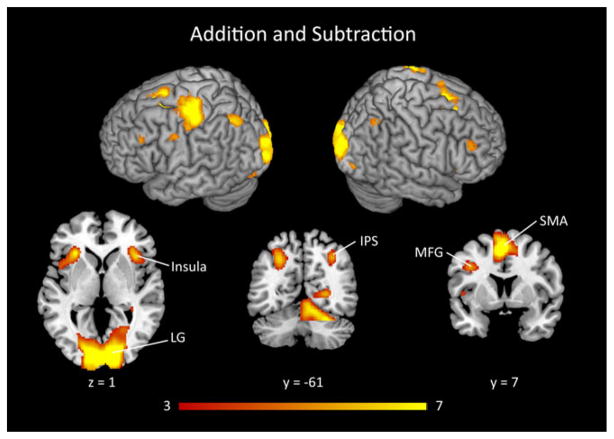
We first identified brain areas activated during the solving of both addition and subtraction problems in the pooled group of DD and TD children. This analysis revealed significant activation in bilateral posterior IPS, bilateral lingual gyrus, primary visual cortex, left motor cortex, pre-supplementary motor area, bilateral middle frontal gyrus, bilateral insula, left thalamus and right caudate (Figure 2 and Table 2).

Figure 2. Brain responses to addition and subtraction problems in combined data from DD and TD children.

The combined group of children with developmental dyscalculia (DD) and typically developing (TD) children showed strong activation during addition and subtraction problem solving in bilateral intraparietal sulcus (IPS), lingual gyrus (LG), bilateral insula, supplementary motor area (SMA) and middle frontal gyrus (MFG). Threshold as in Table 2, color bar indicates t-score.

Table 2.

Brain areas that showed significant activation during the solving of addition and subtraction problems in the combined group of DD and TD children

Peak z-score	Cluster size (voxels)	Peak z-score	Peak MNI coordinates
			x	y	Z
Addition & Subtraction
Bilateral visual cortex/lingual gyrus/ cerebellum	9467	7.59	16	−84	4
Pre-SMA	2742	7.43	−4	10	52
Left precentral/ postcentral gyrus	2876	6.65	−36	−26	54
Left insula	694	6.61	−30	24	6
Right insula	592	5.59	36	20	4
Left IPS	677	5.31	−28	−64	42
Left thalamus	286	5.21	−12	−20	12
Right IPS	263	4.93	32	−60	44
Left MFG	97	4.65	−50	30	34
Right MFG	271	4.51	48	38	26

DD = Developmental Dyscalculia, TD = Typically Developing, SMA = Supplementary Motor Area, IPS = IntraParietal Sulcus, MFG = Middle Frontal Gyrus. Regions significant at height threshold of p < .001, corrected for multiple spatial comparisons at p < .01. Voxel size is 2 mm³.

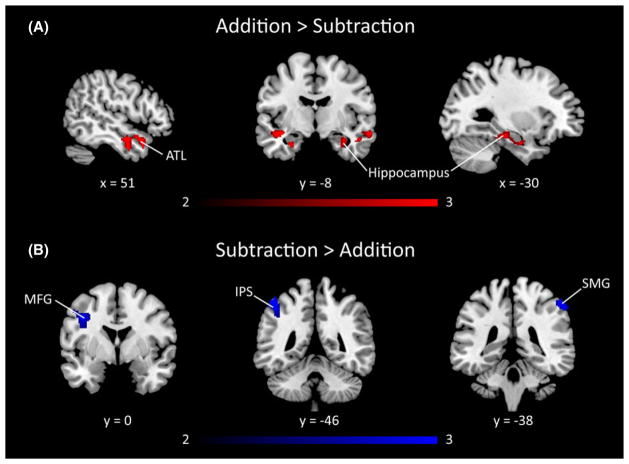
We next examined differential brain responses during the solving of addition and subtraction problems in the pooled sample of DD and TD children. Compared to subtraction, addition problems elicited greater activation in the bilateral hippocampus, left superior temporal gyrus, and right anterior middle temporal gyrus, as shown in Figure 3A and Table 3. Compared to addition, subtraction elicited greater activity in left anterior IPS, bilateral supramarginal gyrus, and left middle frontal gyrus (Figure 3B and Table 3).

Figure 3. Comparison of brain responses to addition and subtraction problems in combined data from DD and TD children.

(A) The combined group of children with developmental dyscalculia (DD) and typically developing (TD) children showed greater brain activation for addition than subtraction in bilateral hippocampus and anterior temporal lobe (ATL). (B) Greater brain activation for subtraction than addition was observed in the left MFG, left intraparietal sulcus (IPS), and right supramarginal gyrus (SMG). Threshold as in Table 3, color bar indicates t-score.

Table 3.

Differential brain activation to addition versus subtraction problems in DD and TD children

Region	Cluster size (voxels)	Peak z-score	Peak MNI coordinates
			x	y	z
Addition > Subtraction
Right STG/MTG/ hippocampus	715	3.64	50	−4	−20
Left STG	145	3.21	−44	−6	−14
Left hippocampus	242	3.10	−34	−18	−18
Subtraction > Addition
Right SMG	143	3.40	58	−36	54
Left SMG/IPS	157	3.07	−48	−46	58
Left MFG	240	3.01	−40	4	36

DD = Developmental Dyscalculia, TD = Typically Developing, STG = Superior Temporal Gyrus, MTG = Middle Frontal Gyrus, SMG = SupraMarginal Gyrus, IPS = IntraParietal Sulcus, MFG = Middle Frontal Gyrus. Regions significant at height threshold of p < .01, corrected for multiple comparisons at p < .01 which corresponds to cluster extent of 128 voxels after gray matter masking. Voxel size is 2 mm³.

Aberrant brain activation during addition and subtraction in children with DD

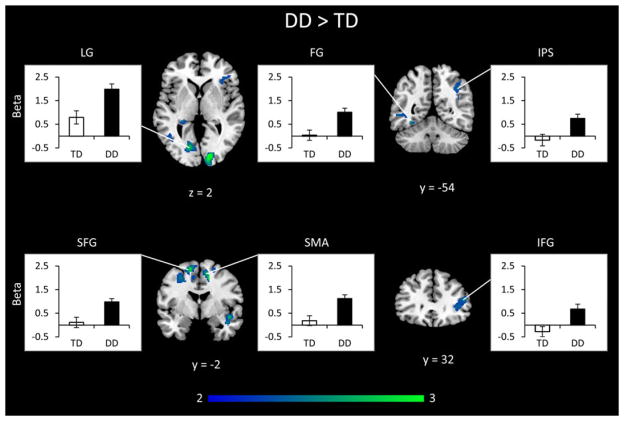
To investigate how children with DD process addition and subtraction problems, we conducted a two-way ANOVA with factors of Group (DD, TD) and Operation (Addition, Subtraction). We first examined the main effect of Group – brain areas that showed common differences in brain response to both operations. Children with DD had greater activity across operations in the right IPS, the bilateral fusiform gyrus, left lingual gyrus and right visual cortex. In prefrontal cortex, children with DD had greater activity in the right anterior insula and inferior frontal gyrus, bilateral superior frontal gyrus, and right supplementary motor area (Table 4 and Figure 4).

Table 4.

Differences in brain activation between DD and TD groups. Brain areas that showed significant group differences in activation during addition and subtraction problem solving. Both the main effect of Group and the interaction between Group and Operation are shown

Region	Cluster size (voxels)	Peak z-score	Peak MNI coordinates
			x	y	z
DD > TD (Addition + Subtraction)
Right visual cortex	392	4.07	16	−88	2
Right posterior insula	243	3.62	46	0	−12
Left lingual gyrus	191	3.56	−16	−76	4
Left SFG	664	3.56	−14	0	62
Right SMA/SFG	750	3.40	14	−2	50
Right fusiform gyrus	167	3.26	32	−74	14
Right ventricle/thalamus	189	2.94	22	−32	14
Right IPS	242	2.91	40	−58	30
Left fusiform gyrus	163	2.87	−40	50	−6
Right IFG/anterior insula	216	2.85	50	32	16
Right cuneal cortex	195	2.80	12	−72	30
Left ventricle/hippocampus/PHG	179	2.75	−26	−34	4
TD > DD (Addition + Subtraction)
No significant voxels
DD > TD (Subtraction − Addition)
Left IPS/SMG/AG	837	3.34	−42	−42	50
Left ITG/fusiform gyrus	129	3.11	−50	−50	−14
Right anterior IPS	343	3.07	30	−34	40
Right SPL/precuneus/posterior IPS/AG	1371	3.03	28	−60	58
TD > DD (Subtraction − Addition)
No significant voxels

DD = Developmental Dyscalculia, TD = Typically Developing, SFG = Superior Frontal Gyrus, SMA = Supplementary Motor Area, IPS = Intraparietal Sulcus, IFG = Inferior Frontal Gyrus, PHG = ParaHippocampal Gyrus, SMG = SupraMarginal Gyrus, AG = Angular Gyrus, ITG = Inferior Temporal Gyrus, SPL = Superior Parietal Lobule. Other details as in Table 3.

Figure 4. Differences in brain activation between DD and TD groups in combined addition and subtraction data.

Combining data across addition and subtraction problems revealed that children with developmental dyscalculia (DD) had significantly greater activity than typically developing (TD) children in left lingual gyrus (LG), fusiform gyrus (FG), right intraparietal sulcus (IPS), right anterior insula, interior frontal gyrus (IFG), superior frontal gyrus (SFG) bilaterally, and right supplementary motor area (SMA). Threshold as in Table 3, color bar indicates t-score.

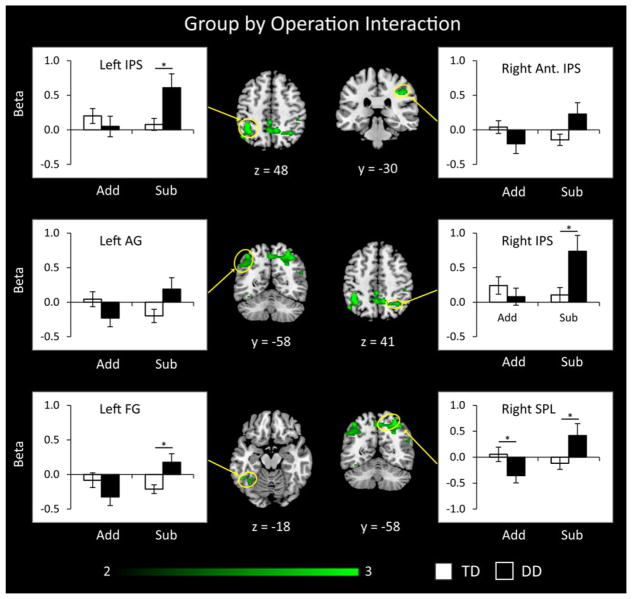
We then examined brain areas that showed a significant Group by Operation interaction. This analysis revealed significant differences specifically in dorsal posterior parietal areas and the inferior occipito-temporal cortex (Figure 5). Compared to TD children, children with DD showed greater activation in the bilateral IPS, right superior parietal lobule, and left fusiform gyrus during subtraction, compared to addition. To better understand this result, we examined the profile of activation and deactivation in each cluster that showed group differences (Figure 5). This analysis confirmed that compared to TD children, children with DD showed greater activation during subtraction in the bilateral IPS, right SPL and left fusiform gyrus but only the right SPL showed differences during addition. Children with DD also showed an aberrant pattern of greater deactivation during addition than subtraction in the left angular gyrus and right SPL.

Figure 5. Brain areas that showed significant group differences in activation to addition versus subtraction problems.

Analysis of interactions between Group (DD, TD) and Operation (addition, subtraction) revealed that, compared to typically developing (TD) children, children with developmental dyscalculia (DD) showed greater activation in several posterior brain regions for subtraction (Sub), compared to addition (Add). These regions included bilateral posterior intraparietal sulcus (IPS), right anterior IPS, right superior parietal lobe (SPL), left angular gyrus (AG) and left fusiform gyrus (FG). Threshold as in Table 3, color bar indicates t-score *p < .05.

We conducted several additional analyses to examine whether the aberrant brain activations observed in children with DD arose because of behavioral differences between the groups. Specifically, children with DD had significantly lower accuracy on subtraction problems, an effect driven largely by failing to respond in the limited allotted time to many subtraction problems, as well as slower reaction times on addition problems. We therefore constructed three ANCOVA models, with accuracy, reaction time and number of missed trials as covariates (Table S2). On the key contrast of subtraction relative to addition, including accuracy and reaction time as covariates revealed largely the same areas of greater activation in the DD group compared to the TD group (Figure S1 and Table S2) as did number of missed trials as a covariate (Table S2).

To further address potential confounding effects of performance on task activation, we examined whether activity in any of the brain regions that showed Group differences were associated with behavioral performance (Table S3). Among all the brain regions showing an interaction between Group and Operation in the whole-brain analysis, only the right anterior IPS overlapped with areas showing a positive correlation with accuracy. Follow-up, ROI-based correlation analyses (on the beta values) revealed that there were no significant relations between activity and any of the behavioral measures (all ps > .06), although the right anterior IPS approached significance (r = .298, p = .077) for accuracy during the addition task (Figure S2) with better performance related to greater activity. No other brain regions identified in the original analysis showed a relationship with reaction time or number of missed trials. Interestingly, for both accuracy and number of missed trials, better performance was associated with activity in the hippocampus. Taken together, these results show that aberrant brain activation patterns observed in children with DD remain significant even after controlling for behavioral differences between the groups.

Brain responses to incorrect and correct trials during subtraction

Overall accuracy on subtraction problems was low in the DD group, raising the question of whether differences in cognitive activities unrelated to numerical cognition are responsible for highly aberrant brain activation patterns seen in this group. To directly investigate the effects of incorrect trials on brain responses in children with DD, we re-analysed the data using a quasi-event-related design where each trial was treated as an event. Notably, because of low overall performance in the DD group, we had a comparable number of incorrect and correct trials in this analysis. One participant’s design matrix was degenerate, so singular value decomposition could not be computed. In the 15 remaining participants, we computed the orthogonality between the correct and incorrect canonical regressors (M = .120, SD = .07). This level of orthogonality was comparable to the mean orthogonality for all the task regressors in original block design (M = .102, SD = .02), and did not differ significantly from it (t(14) = .85, p = .408). The low orthogonality between HRF-convolved responses to correct and incorrect trials suggests that we can meaningfully separate brain activity associated with each trial type.

Using this approach, we found that both correct and incorrect trials produced robust activity in the bilateral IPS, visual cortex, cerebellum, SMA, insula, left IFG, left pre-motor cortex, motor and somatosensory cortex, and middle frontal gyrus (Figure 6A, Table S4). Direct comparison between the trial-types revealed greater activity for incorrect trials in the right ventral occipito-temporal cortex, bilateral cerebellum, left thalamus and brainstem. Crucially, none of these regions showed operation-specific differences in activation between the DD and TD groups in the block-design analysis (Figure 6b, Table S4). Together, these results demonstrate that similar patterns of brain response on correct and incorrect trials contribute to the highly aberrant brain activation observed in children with DD during subtraction problem solving.

Figure 6. Brain regions showing activity for correct and incorrect subtraction trials in children with DD.

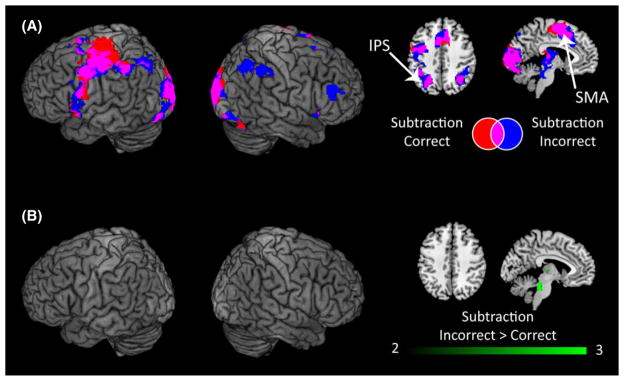
(A) When children with DD solved subtraction problems, both correct and incorrect trials activated bilateral intraparietal sulcus (IPS), supplementary motor area (SMA), visual cortex, left premotor cortex, and left inferior frontal gyrus. (B) Direct comparison between correct and incorrect trials revealed no differences in the IPS or other task-relevant cortical regions. Incorrect trials produced greater activity in the right ventral occipito-temporal cortex, cerebellum, brain stem and thalamus. Threshold as in Table 3, color bar indicates t-score.

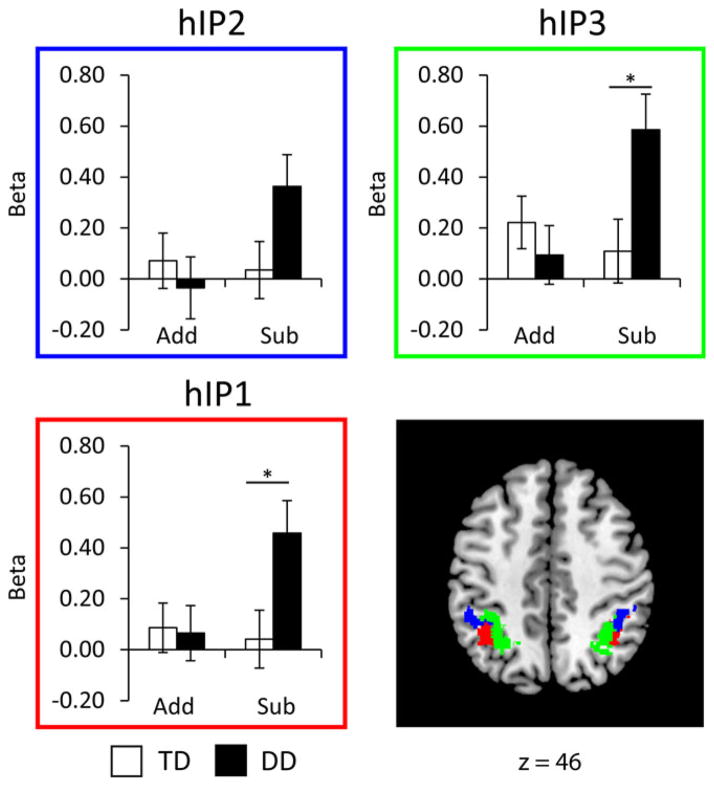
Analysis of group differences in structurally defined IPS ROIs

To further quantify the pattern of aberrant responses in the IPS, our primary region of interest, we used unbiased observer-independent cyto-architectonically defined probability maps encompassing the three subdivisions of the IPS (hIP2, hIP1, hIP3, Figure 7). We conducted a four-way ANOVA with Operation (Addition, Subtraction), Hemisphere (Left, Right) and ROIs (hIP1, hIP2, hIP3) as within-participant factors and Group (DD, TD) as a between-participant factor. There was an interaction between Group and Operation (F(34, 1) = 6.20, p = .018), as well as main effects of ROI (F(68, 2) = 10.38, p < .001), and a marginally significant effect of Operation (F(34, 1) = 3.37, p = .075), but no other effects or interactions (all ps < .17). Follow-up ANOVAs for each operation separately revealed that children with DD did not differ from TD children in their IPS response during addition problem solving (F(34, 1) = .33, p = .569), but did show significantly greater activation during subtraction problem solving (F(34, 1) = 5.95, p = .020).

Figure 7. Group differences in activation within cytoarchitectonically defined subdivisions of the intraparietal sulcus (IPS) in the DD and TD groups.

Children with developmental dyscalculia (DD) showed significantly greater activation during subtraction than typically developing (TD) children in the two posterior subdivisions, hIP3 (p = .016) and hIP1 (p = .020), and a trend towards significance was observed in the anterior-most subdivision hIP2 (p = .060). No such differences were seen in the addition task. *p < .05.

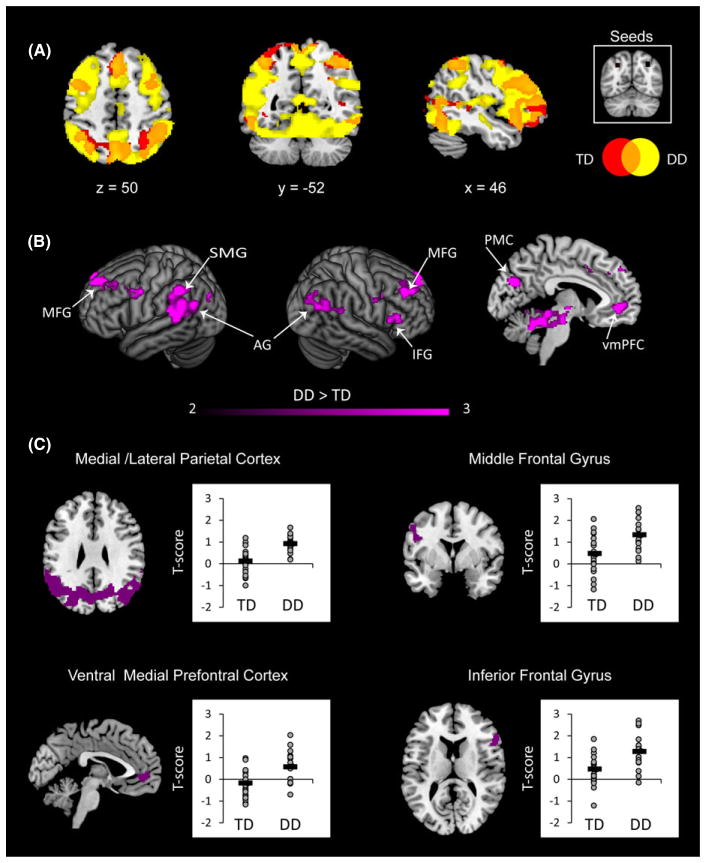
Aberrant IPS connectivity in children with DD

To examine differences in connectivity of the IPS between the groups, we conducted a gPPI analysis at the individual level and then entered the beta maps as dependent measures into a 2 × 2 × 2 repeated measures ANOVA with a between-participant factor of Group (DD, TD) and within-participant factors Operation (Addition, Subtraction) and Hemisphere (Left IPS, Right IPS). We first examined the connectivity of each group separately and then compared them directly. Both groups showed significant connectivity between bilateral IPS and multiple frontal, parietal and occipital cortical areas (Figure 8A). However, children with DD displayed significantly greater connectivity than TD children. Analysis of the main effect of Group revealed that children with DD had greater connectivity of the IPS with bilateral middle, superior and left inferior frontal gyri and bilateral supramarginal and angular gyri. The ventral medial prefrontal cortex, and anterior and posterior cingulate cortex also showed greater effective connectivity in the DD, compared to the TD group (Table 5, Figure 8B). Visualizing the connectivity strength in these clusters revealed that these effects were all driven by positive connectivity in the DD group, rather than reduced negative connectivity (i.e. anti-correlation) in the DD group (Figure 8C). Analysis of Group by Operation interaction revealed that during subtraction, relative to addition, children with DD showed greater IPS connectivity with the brain stem (Table 5).

Figure 8. Brain regions that showed differences in bilateral IPS connectivity for addition and subtraction problems between DD and TD groups.

(A) For both groups the bilateral intraparietal sulcus (IPS) was connected to multiple frontal, parietal and occipital regions (shown in orange). However, children with developmental dyscalculia (DD, yellow) showed greater extent of connectivity than typically developing children (TD, red). Threshold used for illustration: p < .001. (B) Compared to TD children, children with DD have greater IPS connectivity with bilateral angular gyrus (AG), left supramarginal gyrus (SMG), right middle frontal gyrus (MFG), right inferior frontal gyrus (IFG), posteriomedial cortex (PMC) and ventral medial prefrontal cortex (vmPFC). Threshold as in Table 3, color bar indicates t-score. (C) ROI profiles revealed that connectivity differences where driven by positive connectivity in the DD group.

Table 5.

Differences in IPS effective connectivity between DD and TD groups. Brain areas that showed significant group differences in IPS connectivity to addition and subtraction problems. Both the main effect of Group and the interactions between Group and Operation are shown

Region	Cluster size (voxels)	Peak z-score	Peak MNI coordinates
			x	y	z
DD > TD (Addition + Subtraction)
Medial cerebellum/brain stem	3564	4.59	0	−40	−14
Left SFG/frontal pole	468	4.15	−12	50	42
Right precentral gyrus	319	3.90	48	−2	34
Left SMG/AG/PMC/Right SMG/AG	3596	3.89	−58	−48	46
Right MFG	427	3.63	36	34	36
Left MFG	269	3.50	−54	10	44
Right SFG/frontal pole	160	3.48	8	52	42
Medial ventral PFC	776	3.47	−6	46	−4
Right IFG	153	3.03	60	26	14
Medial ACC	189	2.28	2	10	40
TD > DD (Addition + Subtraction)
No significant voxels
DD > TD (Subtraction − Addition)
Brain stem/cerebellum	880	3.77	−4	−18	−14
TD > DD (Subtraction − Addition)
No significant voxels

DD = Developmental Dyscalculia, TD = Typically Developing, SFG = Superior Frontal Gyrus, MFG = Middle Frontal Gyrus, SMG = SupraMarginal Gyrus, AG = Angular Gyrus, PMC = Posterior Medial Cortex, PFC = PreFrontal Cortex, IFG = Inferior Frontal Gyrus, PHG = ParaHippocampal Gyrus. ACC = Anterior Cingulate Cortex. Other details as in Table 3.

To examine the effects of performance differences between the groups on IPS connectivity, we again computed three ANCOVA models using accuracy, reaction time and number of missed trials as covariates, with the whole-brain beta maps from the gPPI as the outcome measure. On the key contrast comparing the groups across operations, including accuracy (Figure S3 and Table S5) and number of missed trials (Table S5) as covariates revealed largely the same areas of greater connectivity in the DD group. However, when controlling for reaction time many of the lateral prefrontal areas were not present, while the medial areas and lateral parietal areas remained significant (Figure S3 and Table S5).

Finally, we examined whether greater IPS connectivity for both groups was related to behavioral performance (Table S6). The brain areas identified by this analysis were almost entirely distinct from the original analysis with some small overlap in the right inferior frontal gyrus and anterior cingulate when controlling for reaction time (Figure S4). Follow-up, ROI-based correlation analyses on the t-scores (averaged across seeds) revealed that there were significant correlations between connectivity and reaction time during the addition task in the left supramarginal gyrus (r = .414, p = .012), anterior cingulate (r = .408, p = .013), right middle frontal (r = .366, p = .028) and inferior frontal gyri (IFG, r = .406, p = .014), with worse performance related to greater connectivity (Figure S4). There were no significant correlations in the subtraction task (all ps > .05). Taken together, these results show that aberrant IPS connectivity patterns observed in children with DD are partly dependent on performance during the addition task, and entirely independent of performance during the subtraction task.

Discussion

In this study, we examined behavioral performance, brain activation and connectivity in children with DD relative to TD peers who were matched on age, gender, IQ, reading ability and multiple working memory measures. We contrasted two inverse arithmetic operations, addition and subtraction, that differ in problem solving difficulty (Campbell & Xue, 2001; Dehaene et al., 2003; Rosenberg-Lee et al., 2011b). Behaviorally, children with DD were slower and less accurate than their TD peers when solving both problem types but were particularly impaired on accuracy during subtraction problem solving. Despite weaker performance on subtraction, children with DD showed greater activation in dorsal parietal cortex, ventral occipito-temporal cortex and prefrontal cortex regions that are typically engaged during numerical problem solving (Arsalidou & Taylor, 2011; Kaufmann, Wood, Rubinsten & Henik, 2011). Furthermore, a significant interaction between group and operation revealed that children with DD showed aberrant responses in multiple posterior brain areas encompassing both the dorsal parietal cortex and ventral occipito-temporal cortex. Critically, effective connectivity analysis revealed for the first time an unexpected pattern of parietal hyper-connectivity in children with DD across both addition and subtraction problems. In the following sections, we discuss these results and their implications for understanding dysfunctional parietal circuits underlying arithmetic problem solving deficits in young children with DD.

Operation-specific behavioral deficits in children with DD

In contrast to addition, surprisingly little research, either behavioral or neuroimaging, has focused on subtraction in children with DD, and even fewer studies have directly contrasted their competence at solving addition and subtraction problems. In the addition task, children with DD performed just as accurately as their TD peers, albeit more slowly. Children with DD were significantly impaired relative to TD children with subtraction problems. Additional analyses revealed that children with DD failed to respond in the allotted time in a large proportion of trials during the subtraction task. However, for trials in which they made a response, accuracy in the DD participants was relatively high at 75.4%, suggesting that DD participants were actively engaged in the task but were unable to solve many of the problems with the same fluency as their TD peers. In line with this interpretation, as discussed in detail below, children with DD showed robust brain activity during the subtraction task.

Together, our results suggest that timed trials exacerbate the difficulties children with DD have when solving subtraction problems consistent with their difficulties on timed number fact and story problems (Jordan & Montani, 1997). The latter are typically due to use of slower and more effortful counting strategies to solve the problems, as contrasted with direct retrieval of the answer in children without mathematical difficulties. This pattern may be exacerbated with subtraction because, unlike addition, subtraction problems are not commutative (e.g. 4 − 3 ≠ 3 − 4), which makes memorization of answers more difficult and thus results in less fluent problem solving for all students. This feature of subtraction (and division) and our current findings are consistent with the argument that focusing on addition skills in the study of mathematical disability may underestimate the severity of learning deficits and delays.

Operation-specific brain activation differences in children with DD

Analysis of brain imaging data revealed a significant interaction between group and arithmetic operation in multiple subdivisions of the posterior parietal cortex with significantly more aberrant activity on the subtraction task. Notably, children with DD showed significantly greater activation than TD children during subtraction problem solving in the IPS, fusiform gyrus and lingual gyrus. Direct examination of brain responses to correct and incorrect subtraction trials among children with DD revealed that both trial types produced robust and similar levels of activity in bilateral IPS as well as other cortical regions that showed hyper-activity in children with DD. These results demonstrate that similar cognitive processes during correct and incorrect trials contribute to the highly aberrant brain activation observed in children with DD during subtraction problem solving.

During the solving of addition problems, by contrast, children with DD showed a trend towards the expected pattern of lower brain activity compared to TD children, although this under-activation reached significance only in the right SPL (Figure 5). Together with the behavioral findings noted above (Ostad, 1999), these results suggest that children with DD find the subtraction task much harder than their TD peers. Our results suggest that the prevalent view that DD stems from inability to activate the IPS may not extend to all arithmetic operations, but rather point to aberrations in the way children with DD modulate key dorsal parietal cortex regions depending on task complexity and operation (Ashkenazi, Rosenberg-Lee, Tenison & Menon, 2012). Crucially, these effects remained even after controlling for behavioral differences between the groups.

In contrast to the present findings, the only previous neuroimaging study of children’s solving of addition and subtraction problems did not find an interaction between operation and mathematical ability (De Smedt et al., 2011). However, consistent with our study, De Smedt and colleagues reported greater parietal cortex engagement for subtraction and greater medial temporal lobe activity for addition when data from low and typical achievers were pooled together. This pattern of convergent and divergent results between the two studies may be due to differences in sample characteristics. The relatively small samples in the low fluency (n = 8) and typical fluency (n = 10) groups used in the previous study may have made it difficult to detect group differences relative to the larger samples (DD = 16 and TD = 20) used in our study. One further crucial difference is that the study by De Smedt and colleagues used a typically achieving group with relatively low-average mathematical abilities on the Woodcock-Johnson Calculation subtest (score 91.20, 27th percentile); some of these children may have fallen into a group with mathematical difficulties (Geary et al., 2012b; Murphy et al., 2007). In contrast, TD children in our study had high-average mathematics scores (115.75, 85th percentile) and they showed similar levels of performance (Figure 1) and IPS activation (Figure 7) on addition and subtraction problems. Children with DD, on the other hand, showed poorer performance and engaged the IPS to a greater extent on the subtraction task.

Apart from the dorsal posterior parietal cortex, the only other brain region that showed an interaction of group and operation was the left fusiform gyrus (MNI: −50, −50, −14) in the ventral occipito-temporal cortex. As with the IPS, this interaction was driven by greater activity during subtraction in the DD group as compared to their TD peers and no group differences during addition. The localization of processing deficits in similar regions of the left fusiform gyrus has been reported in two previous studies of children with DD. One study of non-symbolic number comparison found weaker numerical distance effects in children with DD (Talairach coordinates: −36, −54, −13; MNI: −38, −53, −20; Price et al., 2007), while another found stronger effects in children with DD (MNI: −45, −57, −21; Kucian, Loenneker, Martin & von Aster, 2011b). While the direction of effects varies depending on the control tasks used, these results collectively point to aberrant information processing not only in the dorsal visual stream but also the ventral visual stream. These findings are also noteworthy because this fusiform gyrus region overlaps with the putative visual word form area (Talairach coordinates: −43, −54, −12; MNI: −46, −53, −19; McCandliss, Cohen & Dehaene, 2003). While there is controversy surrounding the precise functions of this area (Price & Devlin, 2003), it likely plays a general role in attending to and processing basic symbolic information (Vogel, Miezin, Petersen & Schlaggar, 2012). Together, these findings suggest that deficits in ventral occipito-temporal areas associated with processing symbolic strings may contribute to arithmetic problem solving deficits observed in children with DD. These deficits are particularly acute for subtraction problems that place greater demands on mapping numerical symbols onto associated magnitude representations, consistent with the view that this mapping is a particular source of vulnerability in children with DD (Rousselle & Noel, 2007).

Hyper-connectivity in children with DD

Understanding cognitive deficits requires knowledge not only about aberrations in localized patterns of brain responses but also distributed functional circuits that might be impaired or organized in unusual ways (Uddin et al., 2010). This is particularly true for tasks that require the coordinated interaction of multiple brain regions, which includes children’s arithmetical problem solving (Rosenberg-Lee et al., 2011a; Varma & Schwartz, 2008). To our knowledge, no previous study has examined brain functional connectivity in children with DD. Because of its critical role in numerical processing (Dehaene et al., 2003), and its specific role in arithmetic deficits in children with DD (Price et al., 2007), our connectivity analysis focused on the IPS. We used an effective connectivity analysis to assess operation-specific interactions of the IPS with all other voxels in the brain after accounting for the effects of common task inputs and regional responses (Friston et al., 1997). To avoid circularity in choice of the precise seed region for the effective connectivity analysis we used the left and right IPS peaks that showed significant arithmetic task-related activation in the combined TD and DD groups. Based on previous developmental studies suggesting increases in long-range connectivity with development (Rosenberg-Lee et al., 2011a; Supekar et al., 2010; Uddin et al., 2010) and greater connectivity relating to better math ability during a passive movie viewing task (Emerson & Cantlon, 2012), we predicted that children with DD would display an immature pattern of connectivity characterized by prominent deficits in fronto-parietal coupling. Contrary to our prediction, children with DD showed hyper-connectivity of the IPS, rather than reduced connectivity, with several brain areas. Surprisingly, there were no brain areas that showed greater connectivity in TD children. Brain regions that showed hyper-connectivity in children with DD included two large-scale brain systems that have been consistently identified in both children and adults (Supekar et al., 2010; Uddin, Supekar, Ryali & Menon, 2011). These include the task-positive lateral fronto-parietal central executive network and the task-negative default mode network (DMN) (Fox, Snyder, Vincent, Corbetta, Van Essen & Raichle, 2005; Greicius, Krasnow, Reiss & Menon, 2003). Our finding of IPS hyper-connectivity points to a fundamental difference in parietal organization in children with DD, rather than developmentally delayed maturation of parietal circuits.

Children with DD showed prominent hyper-connectivity of the IPS with bilateral angular gyrus, posterior cingulate cortex and ventromedial prefrontal cortex. Collectively, these areas form core parts of the DMN, a network of brain areas which are tightly coupled at rest and which are typically deactivated during cognitively demanding tasks (Greicius et al., 2003; Raichle, MacLeod, Snyder, Powers, Gusnard & Shulman, 2001). Furthermore, this pattern of hyper-connectivity remained significant in these areas even after controlling for behavioral differences between the TD and DD groups (Figure S4, Table S5). Consistent with this finding, children with DD also showed reduced levels of deactivation during the subtraction, compared to the addition task, in the precuneus within the posterior medial cortex node of the DMN (Figure 5). Similar to our findings, Davis and colleagues found that while TD children showed deactivation of the posterior medial cortex and the ventromedial prefrontal cortex, children with math disability had above baseline activation in these regions (Davis et al., 2009). This pattern of aberrant coupling suggests that children with DD are unable to successfully disengage the DMN from task-positive IPS regions. Further studies are needed to investigate whether a failure to disengage the DMN during more difficult mathematical tasks broadly contributes to the poor math performance and learning in children with DD.

Compared to TD children, children with DD also showed hyper-connectivity of the IPS with multiple regions in lateral PFC and PPC. These regions included the bilateral ventrolateral and dorsolateral PFC and the supramarginal gyrus within the PPC. These differences were common to both addition and subtraction tasks. Unlike the DMN, these regions form part of the task-positive, central executive network that plays an important role in attention and working memory processes required for problem solving. Across operations children with DD also had greater activity in the right ventrolateral PFC, suggesting potential prefrontal compensatory mechanisms. However, connectivity to these regions was mediated by reaction time on the addition task (Figures S4, S5, Tables S5, S6), suggesting that engagement of this network may represent a common compensatory mechanism across ability levels.

Together, these results show for the first time that children with DD engage multiple fronto-parietal circuits differently from TD children. Children with DD may require greater engagement of these circuits, even while achieving only weaker levels of performance. Alternatively, greater engagement of these circuits may result in the activation of problem-irrelevant information that in turn disrupts problem solving. The latter view is consistent with behavioral studies that show the intrusion of problem-irrelevant information into working memory when children with DD attempt to retrieve arithmetic answers from long-term memory (Barrouillet, Fayol & Lathuliere, 1997; Geary, Hamson & Hoard, 2000; Geary et al., 2012a). The combination of hyper-connectivity with both task-positive and DMN networks suggests that parietal circuits may not be as well segregated in children with DD. Further studies are needed to disentangle the relation between compensatory processes and intrusive behaviors and aberrant brain connectivity in these children.

Taken together, our results highlight a network of brain regions that show aberrant responses during arithmetic and emphasize that, despite the focus on the IPS, arithmetic deficits in DD are unlikely to be localized to a single brain region. Rather, both localized processing deficits in multiple brain areas as well as the coordination between multiple brain circuits are impaired in DD. These conclusions are consistent with the proposal that most neurodevelopmental disorders and learning disabilities arise from diffuse disruptions and aberrant connectivity between regions rather than focal lesions (Johnson, Halit, Grice & Karmiloff-Smith, 2002).

Multiple levels of analysis, performance burden and the Task ‘B’ problem

Several aspects of our general approach here are noteworthy in the broader context of neuroimaging studies of typical and atypical development. First, our study addresses processing bottlenecks in children with DD from the perspective of multiple levels of analysis and performance by employing tasks that this group of children have significant performance deficits in, as well as tasks that they do not (Johnson et al., 2002). A particular challenge in developmental functional neuroimaging and learning disabilities research is interpreting the effects of performance differences which can impact brain responses, especially at higher levels of task complexity. In the context of DD, it is clearly important to characterize brain response and connectivity in problem domains such as addition where children with the disorder can perform moderately well, but also in operations such as subtraction where, as our findings reveal, they fail dramatically. Our use of addition and subtraction tasks which involved different levels of performance deficits in children with DD allowed us to examine atypical brain systems at multiple levels of performance.

Second, as noted by Church and colleagues (Church, Petersen & Schlaggar, 2010), discrepancy in performance on the task of interest, as well as any comparison task (‘the Task B Problem’), creates a potential confound in between-group analyses. Our study addresses this issue in two ways. First, we directly examined brain response to Complex addition and subtraction problems in the two groups without using a contrasting control task. Thus, we can be sure that differences between the groups resulted from brain responses to the task of interest, and not the control task. Second, quasi-event-related analysis in the subtraction task, in which children with DD performed poorly, allowed us to examine brain activity for correct and incorrect trials separately. An oversimplified subtraction task that was within the abilities of children with DD may have enabled us to equate performance, but it would not have captured core deficits in the disorder. Further studies are needed using stimuli which sample a range of complexity and characterize both correct and incorrect problem solving (Menon, Mackenzie, Rivera & Reiss, 2002) in typical and atypical development.

Conclusions

Children with DD show prominent impairments when attempting to solve both addition and subtraction problems, relative to a well-matched group of TD children. Contrary to our prediction, children with DD showed greater activation of the IPS during the solving of subtraction problems, compared to addition problems. Furthermore, the IPS showed prominent hyper-connectivity with both the task-negative DMN and task-positive lateral fronto-parietal cortex. Together, these results add further support to claims of the IPS as a major locus of dysfunction in dyscalculia, but suggest that inappropriate operation-specific response and hyper-connectivity, rather than gross under-activation, are the primary neural sources of problem solving difficulties in children with DD. Understanding the functions of the fronto-parietal circuits identified here will be important for remediating weaker arithmetic problem solving skills in children with DD.

Supplementary Material

Suppl. 1

Table S1. Movement statistics during addition and subtraction problem solving.

Table S2. Brain areas that showed significant group differences in activation to addition versus subtraction, after controlling for accuracy, reaction time and number of missed trials.

Table S3. Brain areas that showed significant correlations with accuracy, reaction time and number of missed trials in the brain activity analyses.

Table S4. Areas of activity for correct and incorrect subtraction trials in 15 children with DD.

Table S5. Differences in IPS connectivity between groups after controlling for the effects of accuracy, reaction time and number of missed trials.

Table S6. Brain areas that showed significant correlations with accuracy, reaction time and number of missed trials in IPS connectivity analyses.

Figure S1. Brain regions showing group differences in activation to addition and subtraction problems, after controlling for accuracy and reaction time.

Figure S2. Brain regions where activation was significantly correlated with behavioral measures.

Figure S3. Brain regions showing differences in IPS connectivity between DD and TD groups, after controlling for performance combining across addition and subtraction.

Figure S4. Brain regions where IPS connectivity was significantly correlated with behavioral measures.

Research highlights.

• Arithmetic operation-specific brain activity, connectivity and behavioral profiles were examined in children with developmental dyscalculia (DD). Children with DD were particularly impaired at solving subtraction, compared to addition, problems.

• Children with DD showed hyper-activation on both addition and subtraction problems in multiple frontal, parietal and visual areas. Children with DD showed especially high levels of hyper-activation in parietal cortex for both correctly and incorrectly solved subtraction problems.

• Children with DD showed hyper-connectivity of the IPS to prefrontal and parietal cortices.

• Inappropriate task modulation and hyper-connectivity, rather than under-engagement and under-connectivity, are key neural mechanisms underlying problem solving difficulties in children with DD.