Emerging landscape of oncogenic signatures across human cancers

Abstract

Cancer therapy is challenged by the diversity of molecular implementations of oncogenic processes and by the resulting variation in therapeutic responses. Projects such as The Cancer Genome Atlas (TCGA) provide molecular tumor maps in unprecedented detail. The interpretation of these maps remains a major challenge. Here we distilled thousands of genetic and epigenetic features altered in cancers to ~500 selected functional events (SFEs). Using this simplified description, we derived a hierarchical classification of 3,299 TCGA tumors from 12 cancer types. The top classes are dominated by either mutations (M class) or copy number changes (C class). This distinction is clearest at the extremes of genomic instability, indicating the presence of different oncogenic processes. The full hierarchy shows functional event patterns characteristic of multiple cross-tissue groups of tumors, termed oncogenic signature classes. Targetable functional events in a tumor class are suggestive of class-specific combination therapy. These results may assist in the definition of clinical trials to match actionable oncogenic signatures with personalized therapies.

In the past decade, advances in high-throughput techniques have allowed a systematic and comprehensive exploration of the genetic and epigenetic basis of cancer. Genomic studies of multiple tumor types have begun to reshape the understanding of cancer genomes and their complexity^1,2. The TCGA project was started in 2006 with the goal of collecting and profiling over 10,000 tumor samples from at least 20 tumor types. Half of these studies have been completed so far (Table 1). The globally coordinated International Cancer Genome Consortium (ICGC), of which TCGA is a member, will add thousands more samples and additional tumor types³. This vast collection of samples, profiled on multiple technical platforms, is yielding data for an increasingly complete atlas of molecular alterations in human cancer.

Table 1.

TCGA pan-cancer data set

Tumor type	TCGA ID	Number of cases	Subtypes
Bladder urothelial carcinoma	BLCA	97
Breast invasive carcinoma4	BRCA	488	Basal-like, Her2 enriched, luminal B, luminal A
Colon and rectum adenocarcinoma11	COADREADa	491	Microsatellite stable (MSS), microsatellite instability (MSI), ultramutators (ultra)
Glioblastoma multiformae9	GBM	218
Head and neck squamous cell carcinoma	HNSC	302
Kidney renal clear-cell carcinoma	KIRC	420
Acute myeloid leukemia13	LAML	184
Lung adenocarcinoma	LUAD	229
Lung squamous cell carcinoma12	LUSC	182
Ovarian serous cystadenocarcinoma10	OV	446
Uterine corpus endometrioid carcinoma5	UCEC	242	Serous-like, endometrioid (low CNA), MSI, ultramutators (ultra)

^aColon and rectum tumors were treated as a single sample set by the TCGA.

So far, analyses of genomic alterations in multiple tumor types have led to two fundamental observations: (i) tumors originating in the same organ or tissue vary substantially in genomic alterations⁴, and (ii) similar patterns of genomic alteration are observed in tumors from different tissues of origin⁵. These phenomena of intracancer heterogeneity and cross-cancer similarity represent both a clinical challenge and an opportunity to design new therapeutic protocols based on the genomic traits of tumors^6,7.

The wealth of genomic data available today provides an unprecedented opportunity to systematically analyze differences and similarities between tumors on the basis of their genetic and epigenetic traits. The complex landscapes of somatic modifications observed in tumors are typically the result of a relatively small number of functional oncogenic alterations (sometimes called driver events), which are outnumbered by non-functional alterations (passenger events) that do not substantially contribute to oncogenesis and progression⁸. The low signal to noise ratio (ratio of the number of functional to non-functional events) presents a major challenge for data mining or data analysis.

Here we developed a novel algorithmic approach that uses a reduced set of candidate functional events to hierarchically stratify more than 3,000 tumors from 12 tumor types. Our approach integrates multiple alteration types and is independent of tumor tissue of origin. The analysis identifies a striking inverse relationship, averaged over the 12 tumor types, between the number of recurrent copy number alterations and the number of somatic mutations. This trend subdivides tumors into two major classes, one primarily with somatic mutations and the other primarily with copy number alterations. Specific patterns of selected events—oncogenic signatures—characterize about 30 largely tissue-independent subclasses of tumors. These signatures are associated with distinct oncogenic pathways and can be used to nominate therapeutically actionable targets across tumor types and the fraction of patients that may benefit from target-specific agents.

RESULTS

In this study, we integrated genomic data from 12 cancer types from TCGA^4,5,9–13 with 3,299 tumor samples (Table 1 and Supplementary Table 1). Breast, colorectal and endometrioid tumors were separated into the molecular subtypes defined in their respective TCGA studies^4,5,11.

First, we reduced the thousands of genomic and epigenetic changes observed in these tumors to a selected list of candidate functional alterations (Fig. 1 and Supplementary Table 2). We integrated copy number alterations, somatic mutations from whole-exome sequencing and gene DNA methylation events identified in each cancer study. Recurrent regions of copy number change (Fig. 1a) were determined using the algorithm GISTIC¹⁴, and recurrently mutated genes (Fig. 1b) were identified using the algorithms MuSiC¹⁵ and MutSig¹⁶. A selected panel of genes with previous evidence of epigenetic silencing in cancer¹⁷ was inspected for DNA hypermethylation in our data set (Fig. 1c). To filter out events that were likely non-functional, genes with copy number alteration and DNA hypermethylation were required to have concordant changes in mRNA expression levels when compared to wild-type cases. In total, we selected 479 candidate functional alterations, including 116 copy number gains, 151 copy number losses, 199 recurrently mutated genes and 13 epigenetically silenced genes. Selected alterations were associated with tumor samples in a binary fashion, such that an alteration either occurred or did not occur in a given tumor (alteration event). The resulting set of SFEs provides a concise description of tumors, with immediate biological and clinical interpretations.

Figure 1.

From global profiles of genomic alterations to selected functional events. (a–c) Genomic alterations considered included copy number alterations (a), somatic mutations (b) and changes in DNA methylation (c). For the discovery of oncogenic signatures, we first reduced thousands of genomic alterations (heatmaps to the left) to a few hundred candidate functional events (heatmaps to the right). Copy number alterations (losses in blue, gains in red), somatic mutations (mutations in green) and DNA methylation status (high level of methylation in black) define the genetic and epigenetic landscapes of 3,299 samples from 12 tumors types (arranged from left to right with groups of columns labeled by tumor type). Altered genes are arranged vertically and sorted by genomic locus, with chromosome 1 at the top of each rectangular panel and chromosome 22 at the bottom. Candidate functional alterations were selected (Online Methods) for each data type (pie charts show the proportion selected). The most recurrent selected alterations (histograms) tend to involve well-known oncogenes and tumor suppressors. Tumor types abbreviated as in Table 1.

Second, we developed a novel algorithmic approach based on the concept of network modularity¹⁸ to identify tumor subclasses in our data set that are characterized by specific combinations (signatures) of SFEs. Our approach provides a hierarchical stratification that allows the exploration of tumor subclasses at different levels of granularity.

The cancer genome hyperbola

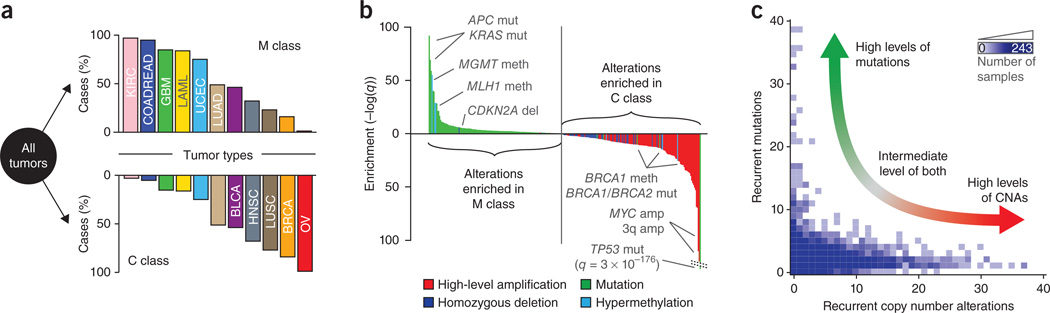
At the top of this hierarchical classification, we identified two main tumor classes of similar size, each characterized by distinct sets of SFEs (Fig. 2a). Unexpectedly, although the distinction between copy number alterations and mutations was not used as a feature in our classification, these characteristic events were predominantly somatic mutations in one class and copy number alterations in the other (Fig. 2b). To reflect this trend, we named these two classes the M class (primarily with mutations) and the C class (primarily with copy number alterations), respectively. Notably, TP53 mutations were an exception to this trend, as they were strongly enriched in the C class (q = 3 × 10⁻¹⁷⁶), consistent with early mutations in TP53 causing copy number genomic instability (Supplementary Fig. 1). This division into two main tumor classes indicates that recurrent copy number alterations and mutations are predominant in different subsets of tumors.

Figure 2.

The first partition of the pan-cancer data set identifies two main classes primarily characterized by either recurrent mutations (M class) or recurrent copy number alterations (C class). (a) Each class is composed of multiple tumor types in different proportions. (b) SFEs were tested for significant enrichment (more frequent than expected in a random distribution) in each class (events along the x axis, log-scaled q values on the y axis). Highly enriched events are primarily mutations in the M class and copy number alterations in the C class. Mut, mutation; meth, methylation change; amp, amplification; del, deletion. (c) The distribution of SFEs in tumors indicates that the number of copy number alterations in a sample (x axis) is approximately anticorrelated with the number of somatic mutations in a sample (y axis). The number of samples for a given (x,y) position range from 0 (white) to 243 (dark blue). CNAs, copy number alterations. Tumor types abbreviated as in Table 1.

Closer inspection of the distribution of selected functional events showed a striking inverse relationship between copy number alterations and somatic mutations at the extremes of genomic instability, particularly in highly altered tumors (Fig. 2c). Such tumors had either a large number of somatic mutations or a large number of copy number alterations, never both. We refer to this trend as the cancer genome hyperbola.

Tumors in the C class and M class were positioned along the two axes of this hyperbola (Supplementary Fig. 2). Whereas individual tumor types (defined by tissue of origin) had varying proportions of copy number alterations and mutations (Supplementary Fig. 3), none had high numbers of both.

We verified this approximately inverse relationship by adding 907 tumor samples from 6 additional tumor types to the pan-cancer set of 3,299 samples (Supplementary Fig. 4). In this larger data set, we also identified two major classes, one primarily dominated by mutations and the other primarily dominated by copy number alterations (Supplementary Fig. 4), with a remarkably similar set of characteristic functional events (Supplementary Fig. 4).

Starting from this first major subdivision, we applied the network modularity algorithm recursively to the C class and M class tumors and to their subclasses. The result was hierarchical division into several levels of subclasses characterized by distinct patterns of functional alteration at each level of granularity (Fig. 3, Supplementary Fig. 5 and Supplementary Table 3). We found that sample assignment to each subclass was robust in that it varied little upon systematic subsampling (Supplementary Fig. 6).

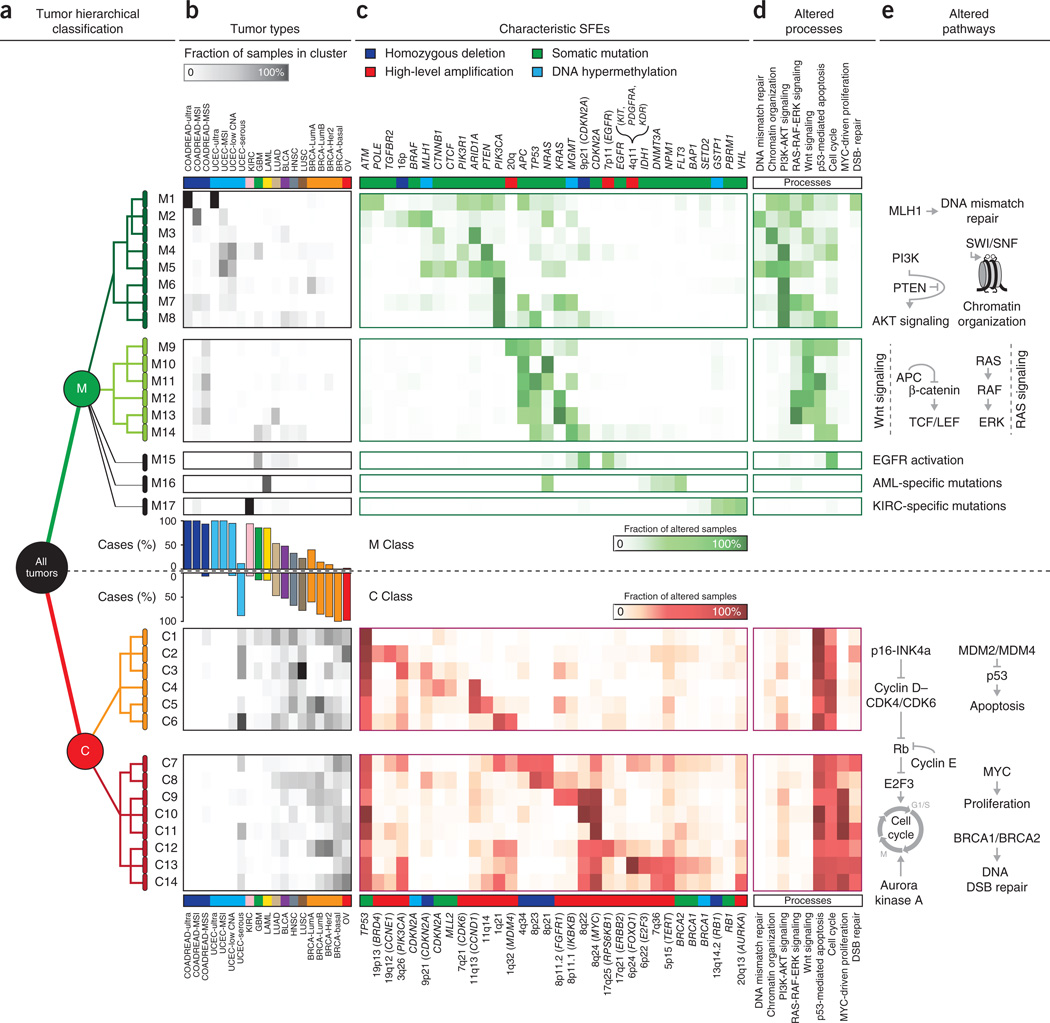
Figure 3.

Characteristic patterns of functional alterations and distinct oncogenic processes as determinants of oncogenic signature classes (OSCs). (a) The first partition of the tree-like stratification (starting with ‘all tumors’ on the left) identifies two main classes: the M class (green) and the C class (red). We identify 17 oncogenic signature subclasses for the M class (M1–M17) and 14 oncogenic signature subclasses for the C class (C1–C14) (one row per subclass). (b) Each subclass includes subsets of tumors from several cancer types (grayscale heatmap; gray intensity represents the fraction of samples in a particular tumor type (column) and a particular subclass (row)). (c) Tree classification is determined at each level by sets of characteristic functional events (color intensity represents the fraction of samples in a subclass (row) affected by a particular functional event (column)). For functional copy number alterations, we indicate, if present, known oncogenes and tumor suppressors in parentheses, for example, 8q24 (MYC). (d,e) Subclass characteristic events reflect particular cellular processes (color intensity represents the fraction of samples in a subclass (row) affected by alterations to a particular process (column)) (d) and altered pathways involved in each of the processes (e). RTK, receptor tyrosine kinase; DSB, double-strand break. Tumor types abbreviated as in Table 1.

This classification highlights distinct mechanisms of oncogenesis as determinants of tumor subclasses, unexpected similarities between tumors originating in different tissues and new insights into alterations shared by multiple tumor types. Additionally, it provides a framework to explore therapeutic protocols on the basis of the genetic and epigenetic traits of tumors.

The M class

The M class of tumors included almost all the samples in kidney clear-cell carcinoma (KIRC), glioblastoma multiformae (GBM), acute myeloid leukemia (LAML), colorectal carcinoma (COADREAD) and uterine carcinoma (UCEC), with the exception of the serous-like subtype of UCEC. We identified 17 subclasses (M1–M17).

The first partition of the M class contained two main subclasses of mixed tumor type, which were characterized by distinct mutational events (Fig. 3a, Supplementary Fig. 5 and Supplementary Table 4). These subclasses had alterations in distinct oncogenic pathways, with alterations of phosphatidylinositol 3-kinase (PI3K)-AKT signaling characterizing the first main subclass (M1–M8) and with APC, TP53 and KRAS mutations most prominent in the second subclass (M9–M14).

Within the M class, we discovered recurrently mutated amino acids (hotspots) in the chromatin modifiers ARID1A and CTCF (Supplementary Fig. 7). ARID1A (Supplementary Fig. 7) is a member of the chromatin-remodeling complex SWI/SNF¹⁹ and, although truncating mutations in this gene have been reported in several tumor types²⁰, no recurrent hotspot had previously been identified.

CTCF encodes a chromatin-binding factor that acts as both a repressor and an activator of multiple genes, including known oncogenes and tumor suppressor genes (MYC, PLK, PIM1, CDKN2A and IGF2)²¹. CTCF achieves sequence-selective DNA binding by using different combinations of 11 zinc-finger domains (ZF1–ZF11)²². Mutations in CTCF were characteristic of subclass M5, which included several endometrioid tumors with microsatellite instability (MSI) and a small fraction of luminal A breast cancers (Supplementary Fig. 7). Mutations of CTCF affecting Arg448 have previously been reported^22,23 and occurred in multiple endometrioid tumors in subclass M5. Here we also identified seven mutations affecting residues upstream of ZF5 (Arg377 and Pro378), four mutations affecting ZF2 (His312 and Asn314), one of which targets one of the zinc-binding histidine residues (His312), and seven mutations affecting ZF1 (Gly261, Arg283 and His284), three of which affected the zinc-binding histidine residue His284 (Supplementary Fig. 7). Mutations observed in luminal A breast tumors specifically targeted ZF1, implying selective inactivation. We identified three splice-site mutations just upstream of exon 4, which encodes ZF1 and ZF2. One of these mutations caused an in-frame exon-skipping event (Supplementary Figs. 7 and 8). Even though the functional role of impaired CTCF activity in tumorigenesis is still unexplored, these mutations indicate that there is selection for specific zinc-finger loss and altered DNA-binding specificity that is not tumor type specific but broadly defines a subset of breast and endometrioid tumors.

Although most recurrent patterns of alteration characterize tissue-independent tumor subsets, subclasses M15–M17 were characterized by tumor type–specific mutational events (Supplementary Fig. 4); for example, EGFR amplification in GBM (M15), NPM1 mutation in LAML (M16) and VHL mutation in KIRC (M17). Our approach is therefore sensitive for reclassification both within and between tumor types.

The C class

The second major class was characterized primarily by TP53 mutations and multiple recurrent chromosomal gains and losses and is therefore called the C class. This class included almost all serous ovarian (OV) and breast (BRCA) carcinoma samples, as well as a large fraction of lung (LUSC) and head and neck (HNSC) squamous cell carcinomas and endometrioid tumors of the serous subtype (UCEC-serous).

Overall hierarchical subdivision of the C class led to a first major partition into two groups, primarily determined by the absence (subclasses C1–C6) or presence (subclasses C7–C14) of gains and losses on chromosome 8 (Fig. 3, Supplementary Fig. 4 and Supplementary Table 5).

Subclasses C3 and C4, which included a large fraction of LUSC and HNSC tumors, provided an interesting example of cross-cancer similarity, in which genomic alterations are shared by subsets of tumors of different origin. Subclass C3 was characterized by mutation of TP53 (92%), amplification of 3q26 (64%) and deletion of CDKN2A (32%); in contrast, subclass C4 had recurrent focal amplification of 11q13 (82%) where CCND1 is located. Some of these genomic differences actually converged on the same pathway, as loss of CDKN2A (C3) and gain of CCND1 (C4) both impair Rb-mediated cell cycle control.

Amplification of the 3q26 locus spans multiple genes, including PIK3CA and TERC. To identify candidate functional targets of this copy number alteration, we analyzed the mRNA levels of all genes in the 3q26 peak in amplified and diploid samples across all tumor types. Combined differential expression analysis identified ZNF639 as the most upregulated gene in the region (Supplementary Fig. 9). The zinc-finger protein ZNF639, also known as ZASC1 (zinc-finger protein amplified in squamous cancer 1), has previously been associated with the pathogenesis of oral and esophageal squamous cell carcinomas^24,25. PIK3CA was also found to be upregulated when amplified, whereas no correlation between mRNA levels and copy number was found for TERC.

The second major set of subclasses, C7–C14, had the highest degree of copy number alteration and was strongly characterized by recurrent gains and losses on chromosome 8, including amplification of 8q24 where the MYC oncogene is located. Amplification of MYC and somatic mutations in TP53 were the most frequent events in this subclass.

Cell cycle regulation and the DNA damage response were additional pathways affected by copy number alterations in subclasses C7–C14. The G1/S checkpoint was compromised by CCNE1 amplification in subclasses C7 and C11 and was bypassed by E2F3 amplification in subclass C13. Subclass C13 also appeared to have defective cell cycle arrest in response to DNA damage owing to inactivation of BRCA1 and BRCA2, which is recurrent in basal breast and ovarian tumors^4,10. Finally, subclass C14 had recurrent amplification and overexpression of the regulator of mitosis AURKA (encoding Aurora kinase A). Notably, these alterations were not specific for a single tumor type but rather characterized distinct subsets of tumors across multiple cancer types.

In summary, we found inactivation of TP53, MYC-driven proliferation and dysregulated cell cycle checkpoints as the hallmarks of the C class of tumors, which is dominated by recurrent copy number changes (Supplementary Table 6).

From oncogenesis to therapy

Specific combinations of functional events observed in particular sets of tumors, even when they were derived from different tissues, point to distinct mechanisms of oncogenesis. However, the clinical impact of these signatures depends on the ability to selectively block the oncogenic action of these molecular alterations.

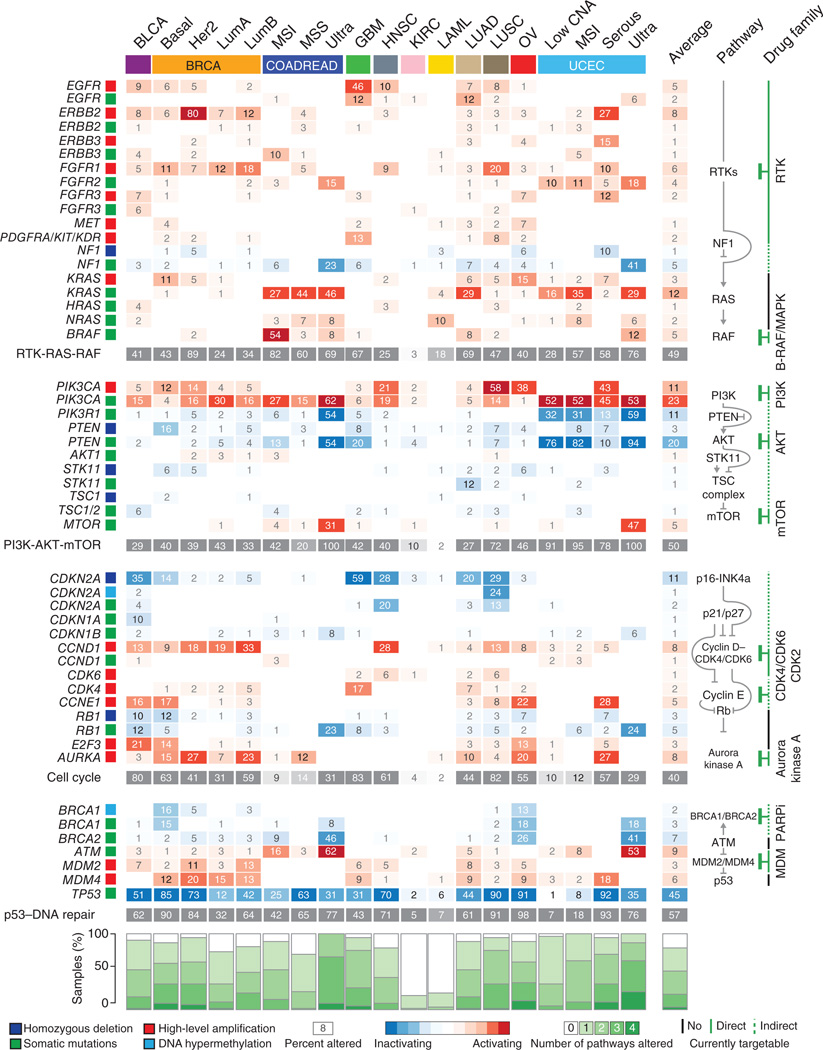
To explore the relationship between functional alterations and therapeutic interventions in more detail, we first assessed the distribution of potentially actionable alterations in different tissue-specific tumor types, focusing on a subset of the ~500 SFEs with well-characterized roles in pathways (Fig. 4). As is well known, such alterations are typically not exclusive to one tumor type, nor are they, with few exceptions, present in 100% of samples in a particular tumor type.

Figure 4.

Map of functional and actionable alterations across 12 tumor types. Genes (rows) encoding components of four major oncogenic pathways (RTK-RAS-RAF, PI3K-AKT-mTOR, cell cycle and p53–DNA repair; shown schematically in the pathway column) are affected by selected functional events (percent of samples altered and types of alteration are represented by colored squares) across tissue-specific tumor types (columns). Alterations to at least one of these pathways are observed in almost all samples of almost all tumor types (stacked green bar plots at bottom), except in KIRC and LAML. A sizable fraction of these alterations are directly or indirectly therapeutically actionable given the current availability of anticancer drugs (the column with drug family information shows the targets of specific inhibitors). Tumor types abbreviated as in Table 1.

Instead, a substantial number of targetable alterations were present in different tumor types. Examples included hotspot mutations and copy number amplifications of PIK3CA (Fig. 4 and Supplementary Fig. 10), directly targetable by specific inhibitors²⁶, and of CCND1 (Fig. 4 and Supplementary Fig. 10), indirectly targetable by selective inhibition of its regulating protein kinases CDK4 and CDK6 (refs. 27,28) (Supplementary Table 7). The observed cross-cancer distribution of targetable alterations presents an opportunity to design tumor treatment strategies tailored to subsets of tumors characterized by particular sets of functional events.

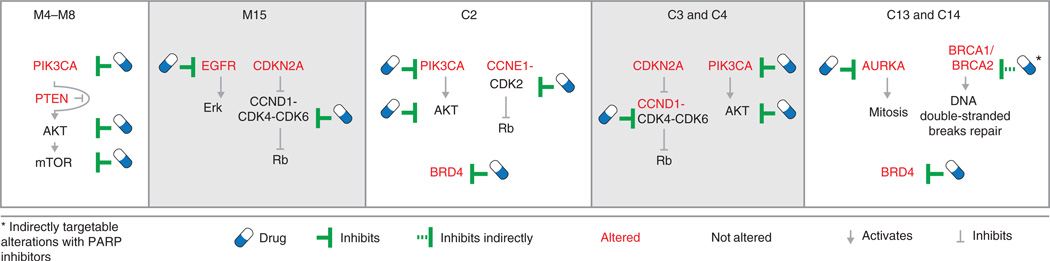
The systematic identification of genomic subclasses presented here is intended as a step toward this goal across a larger number of tumor types than was previously possible. With more than 3,000 tumors analyzed, genomic subclasses were found to be characterized not only by single oncogenic events but also by specific combinations of events (Fig. 5 and Supplementary Fig. 11). Such concurrent alterations may be targetable by combination therapies (Fig. 5). For example, subsets of lung and head and neck squamous cell carcinomas may benefit from concurrent blockade of the cell cycle and PI3K-AKT signaling (Fig. 5, subclasses C3 and C4), whereas inhibition of PARP and Aurora kinase A may be beneficial for subsets of BRCA1- or BRCA2-mutant ovarian and basal breast tumors (Fig. 5, subclasses C13 and C14).

Figure 5.

Combination of therapeutically actionable alterations in oncogenic signature classes. In these examples of oncogenic signature subclasses, functional events distinctive for a tumor subclass nominate potential combination therapy when these alterations are either directly or indirectly targetable (Supplementary Table 7). Other combinations of targeted compounds apply to the full set of subclasses in Figure 3.

A systematic stratification of tumors on the basis of therapeutically actionable alterations may therefore serve as a point of departure for designing ‘basket’ trials in which actionable oncogenic signatures are matched with targeted combination therapy for patients with diverse tumor types. The further accumulation of cancer genomics data sets as well as cancer genomics profiling in ongoing clinical trials, for example, as promoted in Stand Up to Cancer (see URLs) projects, will serve to increase the accuracy of matching patients with therapies.

DISCUSSION

The wealth of genomic data generated in the past decade from analyses of thousands of tumor samples has highlighted dramatic heterogeneity between and within single tumor types. Understanding of this diversity and especially of its impact on cancer treatment is still limited.

Here we propose a tissue-independent classification of tumors on the basis of genetic and epigenetic alterations. Our approach relies on two key steps: reducing the complexity of thousands of molecular alterations to a few hundred plausibly functional events and stratifying tumors on the basis of distinct patterns of these selected genomic features. We implemented these approaches in a new method combining biological knowledge with algorithmic invention and derived a hierarchical classification of thousands of tumors from 12 tumor types in terms of oncogenic signatures. The resulting classification identified unexpected relationships between copy number alterations and somatic mutations at the top level of the hierarchy (i.e., the M and C classes). More granular patterns of alteration at lower levels of the hierarchy, i.e., subclasses of the M and C classes, are characteristic of oncogenic signature subclasses and may provide insight into the mechanisms of oncogenesis and therapeutically actionable alterations.

The proposed stratification is a useful yet incomplete description of human tumors. The current set of results is based on molecular profiles from only 12 tumor types, which are represented by sample numbers varying from 97 to 488. Of these tumor types, only one (LAML) was not a solid cancer; therefore, alterations more frequently observed in hematological diseases are likely underrepresented. The selection of candidate functional events depends on the quantity and quality of the available data. The analysis will benefit from further refinement of criteria for the selection of likely functional events, especially for non-focal copy number changes. The available data are expected to triple in size over the next 2 years as a result of global efforts coordinated by the ICGC of which TCGA is a member. This increase in available data will allow refinement and expansion of the list of selected functional events to more comprehensively account for DNA methylation and other alteration types not fully covered in the TCGA data sets analyzed here, such as chromosomal translocations that create functionally altered fusion genes.

Despite the limitations intrinsic to the current data, this study provides a systematic approach for integrating large amounts of molecular data in a way that reduces its complexity (noise) and increases its biological and clinical interpretability (signal). The power of this strategy is likely to improve as it is applied to more complete data sets. We believe that an understanding of tumor biology in terms of systematically derived signatures of functional alterations will provide an informative resource to explore in the laboratory and in the clinic, serving the development of personalized cancer therapies.

ONLINE METHODS

Data

GISTIC¹⁴ analysis of copy number data from Affymetrix SNP 6.0 arrays was obtained for the set of samples in each TCGA study (Table 1), as generated with the Firehose analysis pipeline. All GISTIC peaks from different studies were taken into account. Overlapping or proximal peaks were merged if the number of events called in our data set was concordant in over 80% of the cases. Whole-exome sequencing data for each study were obtained from the cBioPortal for Cancer Genomics²⁹. Genes identified as recurrently mutated by either MuSiC¹⁵ or MutSig¹⁶ were used in this study. DNA methylation data from Illumina Infinium 27K and 450K arrays were obtained from the Firehose analysis pipeline. We looked for DNA hypermethylation events for a selected panel of genes with previous evidence of epigenetic silencing in cancer. For each of these genes, we selected the corresponding promoter probes and median centered their values. The combination of recurrently mutated genes determined by MuSiC and MutSig, GISTIC regions of recurrent copy number gain and loss, and epigenetically silenced genes represent the set of selected alterations used in this study.

To assign genomic alterations to tumor samples, we used the abstraction of binary event calls. A genomic event either occurred (1) or did not occur (0) in a given sample. Using this abstraction, somatic mutations of different types (missense, truncating, etc.) were treated equally (except for filtered missense mutations), and multiple mutations targeting the same gene in the same sample were treated as one event.

To determine copy number alteration events, we used the set of discrete copy number calls provided by GISTIC¹⁴: −2, homozygous deletion; −1, heterozygous loss; 0, diploid; 1, one copy gain; 2, high-level amplification or multiple-copy gain. We considered as altered only samples with either homozygous loss (−2) or high-level amplification (2) of genes located in regions with recurrent copy number alterations.

DNA methylation levels were measured in terms of β values ranging from 0 to 1, with 0 corresponding to the minimal level of DNA methylation and 1 to the maximal level of DNA methylation. DNA hypermethylation events were assigned to samples with β values greater than 0.1 and were only used if candidate altered samples had concordant downregulation of mRNA levels when hypermethylated.

The final selected set of binary calls for genomic alterations provides a simple but effective description of the genetic landscape observed in single tumors in terms of a few hundred plausibly functional alterations instead of thousands of molecular changes. We refer to these called events derived from selected functional genomic alterations as SFEs.

Filtered calls

The M class of tumors included several MSI and POLE-mutant cases, both of which have been associated with an unexpectedly high mutation rate^5,11. These types of tumors, therefore, have a large number of mutations that are probably not functional. To limit the number of likely non-functional events, we restricted our set of mutations in this class to all truncating mutations and to only nonsynonymous, single-residue substitutions that occurred at specific residues (hotspots). Hotspot residues were defined as recurrently mutated amino acids (represented by at least three mutations) or amino acids directly adjacent to a recurrently mutated one.

Similarly, the C class had a large number of copy number events that frequently spanned large chromosomal regions. The non-focal nature and high numbers of these alterations in the C class are likely to generate false positive assignments. To reduce this effect in the C class, assignment of copy number events in the GISTIC peaks was conditional on concordant mRNA expression changes.

Bipartite network modularity for recurrent genomic alterations

The SFEs naturally identify a network of relationships between samples and alterations. This network is a binary graph G = [(S,A), E], where nodes are either samples (S) or alterations (A) and edges (E) only connect samples to alterations. The problem of clustering tumors according to recurrent alterations can therefore be formulated as a graph clustering problem.

We addressed this problem using the notion of network modularity, originally introduced by Girvan and Newman³⁰. Given a partition of a graph G into distinct modules—subsets of nodes—the modularity associated with this partition is given by

$$Q=\sum _i(e_{ii}-r_i^2)$$

where i is a module, e_ii is the fraction of edges with both ends in i, e_ij is the fraction of edges with one end in i and the other in j and r_i = Σ_je_ij is the expected fraction given the degree of the nodes in i.

This concept can be translated from a simple graph to a bipartite network. Recall that we defined our graph as composed of two sets of nodes: a set of samples S and a set of alterations A. Edges in our graph were defined as E = ((s,a) | s ∈ S, a ∈ A). Given a partition of the set of samples S, its modularity is the difference between the number of alterations shared by samples in the same module and the expected value of alterations. We defined the degree of each alteration a as d(a), equal to the number of samples connected to alteration a. Given a module m, d_m(a) is the degree of alteration a restricted to samples in module m. The e_ij term of the Girvan-Newman modularity can then be formulated as

$$e_{ij}=\frac{1}{Z}\sum _a{d}_i(a)d_j(a)$$

where Z is a normalization factor. As with the Girvan-Newman modularity, given a partition of the set of samples S, the modularity measure defined above tells us how good this partition is in grouping together samples characterized by similar SFEs.

Modularity optimization by greedy partitioning

We adopted a greedy search procedure¹⁸ to optimize the modularity measure defined for our network of samples-to-alterations associations. This procedure starts by assigning each node or sample to a separate module and iteratively joining the pair of modules that produces the greatest increase in modularity. The approach is therefore similar to standard hierarchical agglomerative clustering. Although each step requires all (m²) pairs of modules to be scanned, the efficiency of this approach is derived from its requirement to compute, for each joined candidate pair, only the increase in modularity ΔQ. Note that ΔQ is given by

$$\mathrm{\Delta }Q=\mathrm{\Delta }e-\mathrm{\Delta }r-e_{t+1}-e_t-(r_{t+1}^2-r_t^2)$$

where e and r are intended to represent the corresponding sums over the set of modules and t is the iteration step.

In our network, upon joining modules m₁ and m₂ to form module m, we define e_m and r_m as

$$e_m=\sum _a{d}_m{(a)}^2=\sum _a{(d_{m_1}(a)+d_{m_2}(a))}^2\Rightarrow \mathrm{\Delta }e=\sum _{a}2d_{m_1}(a)d_{m_2}(a)r_m=r_{m_1}+r_{m_2}\Rightarrow \mathrm{\Delta }r=r_m^2-r_{m_1}^2-r_{m_2}^2=2r_{m_1}{r}_{m_2}$$

Therefore,

$$\mathrm{\Delta }Q=2(\sum _a{d}_{m_1}(a)d_{m_2}(a)-r_{m_1}{r}_{m_2})$$

The algorithm stops when all nodes are grouped within the same module. The optimal partition is selected as the one with the highest modularity value among the ones generated through the optimization process. We used this optimization strategy to identify the optimal partition of our data set.

Hierarchical stratification of tumors by recursive modularity optimization

Community detection by network modularity optimization is limited by the size of modules³¹, and greedy partitioning tends to prefer incremental inclusions of single nodes in big modules rather than growing multiple modules simultaneously³². Moreover, the heterogeneous nature of our data set leads modularity optimization to be dominated by major differences between the main subclasses. The combination of these factors, although not affecting the optimal partition, limits the ability of this approach to capture the submodular structure of our data set at different levels of granularity. To address these issues, we recursively applied the greedy partition method. The algorithm proceeds as follows:

• Step 0: Determine the optimal partition P₀ of the whole data set.

• Step n: Determine the optimal partition $P_n^{(m)}$ for each module m contained in the partition $P_{n-1}^{(m*)}$, where m^* is the supermodule containing m.

At each step, the method subdivides a given module m by determining its optimal partition, i.e., the partition with maximal modularity. A module is no longer partitioned if (i) the modularity value of its optimal partition is below a limiting threshold Q_min and/or (ii) the module contains less than S_min samples. For this work, we set Q_min = 0.05 and S_min = 30. At each step, few small modules may be generated if the network contains isolated nodes or nodes with very few connections. In our data set, a minority of samples had few or no recurrent alterations. Small modules (with fewer than S_min samples), including samples with no or few uncharacteristic alterations, were ignored in the analysis. At each step, alterations were selected if they occurred in at least 1% of samples. The resulting set of partitions provides a hierarchical tree decomposition of the original data set, where the root is the whole set of samples and the leaves are modules that could no longer be partitioned.

In the analysis of oncogenic signature classes (OSCs) in Figure 3, we selected subclasses respecting conditions (i) and (ii) up to the third step of stratification. Exceptions included M1–M3 (fourth step), selected because of the marked and biologically relevant differences between these subclasses, and M15–M17 (second step), selected because each subclass was dominated by samples from a single tumor type.

Validation of the modularity optimization method

We tested our approach on two well-characterized data sets frequently used as benchmarks for network modularity detection. The first network is known as the Southern Women Event Participation network³³. It represents women’s attendance of social events in the Deep South, using data collected by Davis and colleagues in the 1930s to study social stratification. For this network, our approach was able to identify the two-module structure of the network (Supplementary Fig. 12) that coincides with the solution proposed by Guimera and colleagues³⁴ and, except for one woman, with the subjective solution proposed by the ethnographers that conducted the study.

The second test network is derived from data on corporate interlocks in Scotland in the twentieth century³⁵. The largest connected component of this network is composed of 131 directors and 86 firms. Our approach identified a nine-module solution with modularity value Q = 0.65 (Supplementary Table 8). The same component was analyzed by Barber³⁶ using an approach based on the eigenspectrum of the adjacency matrix of the network. In this work, the best solution obtained with the standard approach had Q = 0.566. A solution with Q = 0.66 was found using a modified version of their method that performed a search to optimize the number of modules rather than letting this number emerge from the modularity optimization procedure.

Enrichment analysis of genomic alterations

Each node of the tree, except for the leaves, represents a partition of a set of samples into separate modules or clusters. At each step, we identified the determinants (particular SFEs) of the partition by testing for statistically significant enrichment of each SFE in each class. For each SFE, we first tested for significant deviation from the expected distribution of its occurrences using a χ² test. Second, we selected the cluster with the highest fraction of samples altered by the particular SFE and tested for statistical enrichment by Fisher’s exact test. All P values were corrected for the false discovery rate (q value). SFEs listed in Figure 3 (middle) were selected as the most significantly enriched in each subclass at each branching of the tree decomposition (q < 0.001) or as the most frequent in each subclass.

Robustness of the subclasses

The robustness of the subclasses was assessed by removal of different percentages of samples and reclassification of the reduced data sets. During each run, hierarchical stratification obtained with the reduced data set was mapped to the original one by mapping each module from the reduced classification to the module from the original classification that maximizes the overlap (Jaccard) coefficient (J) associated with the two sets³⁷. Given a module m₁ and a module m₂, the J coefficient of m₁ and m₂ is defined as

$$\mathbf{J}(m_1,m_2)=m_1\cap m_2/m_1\cup m_2$$

with J = 1 if the two sets are identical and J = 0 if they are completely disjoint. Each mapping was scored with the average J obtained by the mapped modules. For each classification derived from a reduced data set, we derived a corresponding randomized version with the same hierarchical structure but permuted class memberships. Robust solutions were those with high average J values, averaged over repeated removal runs.

Reduced data sets were generated randomly by removing 5%, 20% and 50% of the samples (15 instances for each reduction), with the set with 50% fewer samples only used to evaluate the robustness of the M and C classes. We evaluated the robustness of subclasses separately at different levels of the hierarchical stratification and, for each evaluation, by estimating the expected J value using the randomized classifications.

Testing for concordant mRNA and copy number changes

We tested genes located in regions of recurrent copy number gain and loss for concordant mRNA expression changes for each tumor type separately. For each region, we identified the sets of altered samples (+2 or −2) and diploid samples (0) and the corresponding distributions of mRNA levels for each gene in the region. mRNA levels were assayed by RNA sequencing. Given the non-normal distribution of RNA sequencing read counts, distributions of each gene in the two groups (altered and diploid) were compared using the Mann-Whitney test. Implementation of the Mann-Whitney test was provided in the Java Statistical Classes (JSC) library. Individual q values were then combined using Fisher’s method (product of the single-test q values), and genes within the same peak were scored using the corresponding combined q values.