Joint Analysis of Psychiatric Disorders Increases Accuracy of Risk Prediction for Schizophrenia, Bipolar Disorder, and Major Depressive Disorder

Abstract

Genetic risk prediction has several potential applications in medical research and clinical practice and could be used, for example, to stratify a heterogeneous population of patients by their predicted genetic risk. However, for polygenic traits, such as psychiatric disorders, the accuracy of risk prediction is low. Here we use a multivariate linear mixed model and apply multi-trait genomic best linear unbiased prediction for genetic risk prediction. This method exploits correlations between disorders and simultaneously evaluates individual risk for each disorder. We show that the multivariate approach significantly increases the prediction accuracy for schizophrenia, bipolar disorder, and major depressive disorder in the discovery as well as in independent validation datasets. By grouping SNPs based on genome annotation and fitting multiple random effects, we show that the prediction accuracy could be further improved. The gain in prediction accuracy of the multivariate approach is equivalent to an increase in sample size of 34% for schizophrenia, 68% for bipolar disorder, and 76% for major depressive disorders using single trait models. Because our approach can be readily applied to any number of GWAS datasets of correlated traits, it is a flexible and powerful tool to maximize prediction accuracy. With current sample size, risk predictors are not useful in a clinical setting but already are a valuable research tool, for example in experimental designs comparing cases with high and low polygenic risk.

Main Text

Genome-wide association studies (GWASs) have been highly successful in identifying variants associated with a wide range of complex human diseases.^1,2 However, most common diseases are highly polygenic and each variant explains only a tiny proportion of the genetic variation. Even when associated SNPs are considered jointly in polygenic approaches such as polygenic risk scores³ or genomic best linear unbiased prediction (GBLUP),^4,5 the accuracy of risk prediction is low. The use of more advanced methods^4–8 improved prediction accuracy for traits where a small number of relatively strong associations have been identified, such as type 1 diabetes, ankylosing spondylitis, and rheumatoid arthritis, but not for other traits characterized by small effect size variants, including psychiatric disorders.^4,5,9

A major factor determining how well a polygenic model can predict a trait value in an independent sample is the sample size of the discovery data.^10,11 Using more individuals will provide more information and hence increase the accuracy of the estimated effect size of a specific SNP. Sample size can also be effectively increased through datasets measured for correlated traits. Recently, we estimated the genetic relationships among five psychiatric disorders from the Psychiatric Genomics Consortium (PGC) by using a bivariate linear mixed model demonstrating that there are significant shared genetic risk factors across the disorders and that measurement of one trait provides information on other genetically correlated traits.¹² Here we extend our bivariate approach to a multivariate linear mixed model and apply multi-trait genomic best linear unbiased prediction (MTGBLUP)^13,14 for genetic risk prediction of disease. MTGBLUP is expected to be more powerful because it uses correlations between disorders and jointly evaluates individual risk across disorders. To date, the information from other correlated traits has been little exploited in the context of risk prediction although recently Li et al.⁹ applied bivariate ridge regression to two genetically correlated diseases to improve risk prediction.

An important advantage of the MTGBLUP approach is that it does not require multiple phenotypes to be measured on the same individuals and therefore can be readily applied to any number of existing datasets of genetically related traits. This is particularly beneficial for disease studies that are limited to a single phenotype but typically aim for large sample sizes. Moreover, it is not necessary for the datasets to be genotyped with the same SNP array because SNPs can be imputed to a common set of SNPs, such as those available from the HapMap or 1000 Genomes reference panels.^15,16 Prediction accuracy can be expected to improve as more data from phenotypes with shared etiology are utilized.

In this report, we apply the MTGBLUP approach to the cross-disorder PGC GWAS data and show a significant increase in risk prediction accuracy in independent cohorts of schizophrenia, bipolar disorder, and major depressive disorder. MTGBLUP increased the discriminant power between the top and bottom 10% of individuals ranked on their risk predictor, implying that this approach might be useful for stratified medicine in a research setting, to develop tailored interventions or treatments for individuals having different risks.^17–19 We further demonstrate a relationship between functionally annotated SNPs and increased prediction accuracy of schizophrenia and bipolar disorder.

As the main method, we use a multivariate linear mixed model for the analyses of GWAS data that estimates the total genetic values of individuals directly by utilizing genomic relationships based on SNP information. In the model, a vector of phenotypic observations for each trait is written as a linear function of fixed effects, random genetic effects, and residuals. For simplicity, we constrain the description to a single component for the random genetic effects, but the model can be readily extended to multiple components of random genetic effects:

$$\begin{array}{l}{\mathbf{y}}_1={\mathbf{X}}_1{\mathbf{b}}_1+{\mathbf{Z}}_1{\mathbf{g}}_1+{\mathbf{e}}_1\text{for}\text{trait}1\hfill \\ {\mathbf{y}}_2={\mathbf{X}}_2{\mathbf{b}}_2+{\mathbf{Z}}_2{\mathbf{g}}_2+{\mathbf{e}}_2\text{for}\text{trait}2\hfill \\ ⋮\hfill \\ {\mathbf{y}}_n={\mathbf{X}}_n{\mathbf{b}}_n+{\mathbf{Z}}_n{\mathbf{g}}_n+{\mathbf{e}}_n\text{for}\text{trait}\text{n}\hfill \end{array}$$

where y is a vector of trait phenotypes, b is a vector of fixed effects, g is a vector of total genetic value for each individual, and e are residuals. The random effects (g and e) are assumed to be normally distributed with mean zero. X and Z are incidence matrices for the effects b and g, respectively. Subscript 1,…, n represents trait 1 to trait n. The variance covariance matrix is defined as

$$\mathbf{V}=\left[\begin{array}{ccc}\mathbf{Z}\mathbf{A}{\sigma }_{g_1}^2\mathbf{Z}\text{'}+\mathbf{I}{\sigma }_{e_1}^2& \dots & \mathbf{Z}\mathbf{A}{\sigma }_{g_{1n}}\mathbf{Z}\text{'}+\mathbf{I}{\sigma }_{e_{1n}}\\ ⋮& \ddots & ⋮\\ \mathbf{Z}\mathbf{A}{\sigma }_{g_{n1}}\mathbf{Z}\text{'}+\mathbf{I}{\sigma }_{e_{n1}}& \cdots & \mathbf{Z}\mathbf{A}{\sigma }_{g_n}^2\mathbf{Z}\text{'}+\mathbf{I}{\sigma }_{e_n}^2\end{array}\right]$$

where A is the genomic similarity matrix based on SNP information and I is an identity matrix. The terms ${\sigma }_{g_i}^2$ and ${\sigma }_{e_i}^2$ denote the genetic and residual variance of trait i, respectively, and ${\sigma }_{g_{ij}}$ and ${\sigma }_{e_{ij}}$ the genetic and residual covariance between traits i and j. Multi-trait genomic residual maximum likelihood (MTGREML) estimates (see Appendix A) are obtained with the average information algorithm.^20–22

Next we show that SNP risk predictors can be easily transformed from individual risk predictors with a simplified BLUP model that uses individual risk predictors as the dependent variable and fits a covariance structure without residual variance (i.e., heritability is 1). Individual risk predictors are the best linear unbiased predictors (BLUPs) of total genetic value of individual subjects contributed by genome-wide SNPs, i.e., g in the previous section. Analogously, SNP risk predictors are defined as the BLUPs of SNP effects estimated jointly with a linear mixed model that intrinsically accounts for linkage disequilibrium between SNPs. The SNP-BLUP model is computationally more demanding for a large number of SNPs. Therefore, it is desirable to estimate genetic values (GBLUP) for efficiency and to transform them to SNP-BLUP. The SNP-BLUP can be projected to predict genetic risk for independent validation sample without the need to have access to the training individuals. The SNP-BLUP estimates can be applied to independent datasets as the SNP weights used to create a risk profile score, for example using the PLINK-score command. The individual BLUP model is

$$\left[\begin{array}{c}{\mathbf{g}}_1\\ ⋮\\ {\mathbf{g}}_n\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_{g_1}^2& \cdots & {\sigma }_{g_{1n}}\\ ⋮& \ddots & ⋮\\ {\sigma }_{g_{n1}}& \cdots & {\sigma }_{g_n}^2\end{array}\right]\otimes \mathbf{A}\cdot {\left[\begin{array}{ccc}{\mathbf{Z}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{Z}}_n\end{array}\right]}^{\prime }\cdot {\mathbf{V}}^{-1}\left[\begin{array}{c}{\mathbf{y}}_1-{\mathbf{X}}_1{\mathbf{b}}_1\\ ⋮\\ {\mathbf{y}}_n-{\mathbf{X}}_n{\mathbf{b}}_n\end{array}\right].$$ (Equation 1)

SNP-BLUP model is

$$\left[\begin{array}{c}{\mathbf{u}}_1\\ ⋮\\ {\mathbf{u}}_n\end{array}\right]=\left[\begin{array}{ccc}{\sigma }_{u_1}^2& \cdots & {\sigma }_{u_{1n}}\\ ⋮& \ddots & ⋮\\ {\sigma }_{u_{n1}}& \cdots & {\sigma }_{u_n}^2\end{array}\right]\otimes \mathbf{I}\cdot {\left[\begin{array}{ccc}{\mathbf{W}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{W}}_n\end{array}\right]}^{\prime }\cdot {\mathbf{\Omega }}^{-1}\left[\begin{array}{c}{\mathbf{y}}_1-{\mathbf{X}}_1{\mathbf{b}}_1\\ ⋮\\ {\mathbf{y}}_n-{\mathbf{X}}_n{\mathbf{b}}_n\end{array}\right]$$

where W_i is a N × M matrix of standardized SNP coefficients with N being the number of individuals and M the number of SNPs, ⊗ is the Kronecker product function, and the variance covariance matrix for SNP-BLUP mode is defined as

$$\mathbf{\Omega }=\left[\begin{array}{ccc}\mathbf{W}\mathbf{I}{\sigma }_{u_1}^2\mathbf{W}\text{'}+\mathbf{I}{\sigma }_{e_1}^2& \dots & \mathbf{W}\mathbf{I}{\sigma }_{u_{1n}}\mathbf{W}\text{'}+\mathbf{I}{\sigma }_{e_{1n}}\\ ⋮& \ddots & ⋮\\ \mathbf{W}\mathbf{I}{\sigma }_{u_{n1}}\mathbf{W}\text{'}+\mathbf{I}{\sigma }_{e_{n1}}& \cdots & \mathbf{W}\mathbf{I}{\sigma }_{g_n}^2\mathbf{W}\text{'}+\mathbf{I}{\sigma }_{e_n}^2\end{array}\right].$$

Replacing y with g (individual BLUP) and setting residual (co)variances as zero (because individual BLUP is already adjusted for residuals), the variance covariance matrix can be simplified as

$$\mathbf{\Omega }=\left[\begin{array}{ccc}{\sigma }_{u_1}^2& \cdots & {\sigma }_{u_{1n}}\\ ⋮& \ddots & ⋮\\ {\sigma }_{u_{n1}}& \cdots & {\sigma }_{u_n}^2\end{array}\right]\otimes \mathbf{W}\mathbf{W}\text{'}=\left[\begin{array}{ccc}{\sigma }_{u_1}^2& \cdots & {\sigma }_{u_{1n}}\\ ⋮& \ddots & ⋮\\ {\sigma }_{u_{n1}}& \cdots & {\sigma }_{u_n}^2\end{array}\right]\otimes \mathbf{A}\cdot M.$$

Therefore, SNP-BLUP can be written as

$$\left[\begin{array}{c}{\mathbf{u}}_1\\ ⋮\\ {\mathbf{u}}_n\end{array}\right]={\left[\begin{array}{ccc}{\mathbf{W}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{W}}_n\end{array}\right]}^{\prime }\otimes {\mathbf{A}}^{-1}\left[\begin{array}{c}{\mathbf{g}}_1\\ ⋮\\ {\mathbf{g}}_n\end{array}\right]\cdot M^{-1},$$ (Equation 2)

and this can be rewritten as

$$\left[\begin{array}{ccc}{\mathbf{W}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{W}}_n\end{array}\right]\left[\begin{array}{c}{\mathbf{u}}_1\\ ⋮\\ {\mathbf{u}}_n\end{array}\right]=\left[\begin{array}{c}{\mathbf{g}}_1\\ ⋮\\ {\mathbf{g}}_n\end{array}\right].$$

This agrees with Hayes et al.²³ and Yang et al.²² when it reduces to a univariate model. Equation 2, after replacing [g₁, …, g_n]’ with the right-hand side in Equation 1, can be rewritten as

$$\left[\begin{array}{c}{\mathbf{u}}_1\\ ⋮\\ {\mathbf{u}}_n\end{array}\right]={\left[\begin{array}{ccc}{\mathbf{W}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{W}}_n\end{array}\right]}^{\prime }\cdot \left[\begin{array}{ccc}{\sigma }_{g_1}^2& \cdots & {\sigma }_{g_{1n}}\\ ⋮& \ddots & ⋮\\ {\sigma }_{g_{n1}}& \cdots & {\sigma }_{g_n}^2\end{array}\right]\otimes \mathbf{I}\cdot {\left[\begin{array}{ccc}{\mathbf{Z}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{Z}}_n\end{array}\right]}^{\prime }\cdot {\mathbf{V}}^{-1}\left[\begin{array}{c}{\mathbf{y}}_1-{\mathbf{X}}_1{b}_1\\ ⋮\\ {\mathbf{y}}_n-{\mathbf{X}}_n{b}_n\end{array}\right]M^{-1}.$$ (Equation 3)

This agrees with VanRaden²⁴ and Strandén and Garrick²⁵ derived from a matrix inversion theory when it reduces to a univariate model.

We extended our approach to genomic partitions according to gene annotation. An enrichment analysis based on gene annotation categories has shown that SNPs located within genes identified as being differentially expressed in the central nervous system (CNS) explain a significantly larger proportion of phenotypic variance than expected by chance for schizophrenia and bipolar disorder.^12,26 It is of interest to determine whether the gene/functional annotation information can further increase the prediction accuracy. In the annotation analysis, we grouped SNPs that were located within ±50 kb from the 5′ and 3′ UTRs of 2,725 genes differentially expressed in the CNS^26,27 together, and 21% of the SNPs belonged to this category. We then estimated SNP effects from a two-component model fitting relationship matrices of SNPs in CNS genes and SNPs localized elsewhere. The model is

$$\begin{array}{l}{\mathbf{y}}_1={\mathbf{X}}_1{\mathbf{b}}_1+{\mathbf{Z}}_1{\mathbf{g}}_{1_{CNS}}+{\mathbf{Z}}_1{\mathbf{g}}_{1_{non-CNS}}+{\mathbf{e}}_1\text{for}\text{trait}1\hfill \\ ⋮\hfill \\ {\mathbf{y}}_n={\mathbf{X}}_n{\mathbf{b}}_n+{\mathbf{Z}}_n{\mathbf{g}}_{n_{CNS}}+{\mathbf{Z}}_n{\mathbf{g}}_{n_{non-CNS}}+{\mathbf{e}}_n\text{for}\text{trait}\text{n}\hfill \end{array}$$

where g_CNS is a vector of random genetic effects due to the CNS genes and g_non-CNS is a vector of random genetic effects resulting from the non-CNS region.

We also tested another gene set that included candidate genes set for schizophrenia, autism, and intellectual disability (SAI).³ We matched these candidate genes with UCSC Genome Browser human genome version 18 (on which the discovery dataset was built) and retained 4,133 autosomal genes. It is noted that we excluded 479 genes flanking GWAS SNPs identified in the Swedish sample²⁸ to avoid artifact inflation in prediction accuracy. We annotated SNPs within the SAI genes (28% of the SNPs) and fitted genomic similarity matrices of the annotated SNPs and the rest of SNPs in the two-component model.

We had access to the PGC Cross-Disorder data and three independent validation datasets. The details of the PGC Cross-Disorder data with additionally available ADHD samples are described elsewhere.¹² The datasets stored in the PGC central server follow strict guidelines with local ethics committee approval. Genotype data from each study cohort were processed through the stringent PGC pipeline and imputation of autosomal SNPs was carried out with the HapMap3 reference sample.²⁹ In each imputation cohort, we retained only SNPs with MAF >0.01 and imputation R² >0.6. The number of SNPs used in this study was 745,705. We excluded certain individuals to ensure that all samples from the five disorders were completely unrelated in the conventional sense, so that no pair of individuals had a genome-wide similarity relationship greater than 0.05. The numbers of case and control subjects used in this study are shown in Table 1. All phenotypes were controlled for cohort, sex, and the first 20 principal components estimated from genome-wide SNPs. Adjustments were performed for each trait.

Table 1.

Estimates of SNP Heritability and Genetic Correlations from Multivariate Analysis of Five Psychiatric Disorders

Disorders	Cases	Controls	SNP-h2on the Liability Scale	SE
SCZ	8,826	6,106	0.235	0.011
BIP	5,867	3,328	0.218	0.017
MDD	8,770	6,506	0.286	0.023
ASD	3,086	3,163	0.130	0.024
ADHD	3,997	8,479	0.281	0.022
			Genetic Correlation	SE
BIP/SCZ	5,867/8,826	3,328/6,106	0.590	0.048
MDD/SCZ	8,770/8,826	6,506/6,106	0.365	0.047
MDD/BIP	8,770/5,867	6,506/3,328	0.371	0.060
ASD/SCZ	3,086/8,826	3,163/6,106	0.194	0.071
ASD/BIP	3,086/5,867	3,163/3,328	0.084	0.089
ASD/MDD	3,086/8,770	3,163/6,506	0.054	0.089
ADHD/SCZ	3,997/8,826	8,479/6,106	0.055	0.046
ADHD/BIP	3,997/5,867	8,479/3,328	0.160	0.059
ADHD/MDD	3,997/8,770	8,479/6,506	0.242	0.059
ADHD/ASD	3,997/3,086	8,479/3,163	−0.044	0.088

Abbreviations are as follows: SE, standard error; SCZ, schizophrenia; BIP, bipolar disorder; MDD, major depressive disorder; ASD, autism spectrum disorder; ADHD, attention deficit disorder.

In preliminary analysis, using the multivariate linear mixed model, we estimated genetic variances and genetic correlations between the five psychiatric disorders (Table 1). The estimates agreed with those reported in the previous study¹² (Figure S1) but were slightly less accurate (larger standard errors) because of the smaller sample size due to excluding genetically related samples across all five disorders rather than across only two traits in the bivariate analyses.

To evaluate the risk prediction performance of MTGBLUP, we performed within-study cross-validation of the PCG data, i.e., internal validation. We randomly split the data for each disease into a training sample containing ∼80% of individuals and a validation sample containing the remaining ∼20%³⁰ and repeated this five times. For assessing predictive performance in the internal validation, we calculated the correlation coefficient between the observed disease status and the predicted genomic risk score of the validation individuals. We also regressed observed disease status on risk scores. If the risk scores are unbiased estimates of genetic risk then the regression coefficient is expected to be 1, i.e., the covariance between true and estimated risks equals the variance of estimated risks. Deviations from 1 reflect the degree of bias of the risk scores. We averaged the correlation and regression coefficients and estimated empirical standard errors over five replicates. Using the empirical standard errors estimates, a t test was performed to assess differences in prediction accuracy between methods. In the within-study cross-validation, MTGBLUP outperformed single-trait genomic best linear unbiased prediction (STGBLUP) for all disorders: the gain in prediction accuracy was significant for schizophrenia (p < 6.0 × 10⁻⁸) and bipolar disorder (p < 6.6 × 10⁻¹¹) (Figure S2). The slope from the regression of disease status on predicted risk score ranged from 0.88 to 1.14 (Table S1), indicating that the risk scores are well calibrated.

Results obtained from a within-study validation might not reflect the true performance when SNP effects estimated from the training data are spuriously associated with the diseases. To better assess the true prediction potential of MTGBLUP, risk scores derived from the complete PCG data were validated in independent samples for schizophrenia, bipolar, and major depressive disorder. As independent validation sets, we used Swedish schizophrenia²⁸ and bipolar GWAS data³¹ and the GENRED2 major depressive disorder dataset collected by the same methods as reported for the GENRED1 dataset.³² SNPs in the validation data were processed through the same stringent quality control as the discovery data. The Swedish schizophrenia data were imputed with HapMap3 as reference. The bipolar disorder data and major depressive disorder data were imputed with the 1000 Genomes Project data as reference. Post-imputation quality control was applied to exclude poorly imputed SNPs from the validation sets. Finally, we selected SNPs that matched those in the discovery set. The number of SNPs in each validation set is shown in Table 2. Individuals were removed from the validation datasets if they had relatedness >0.05 to any one of the individuals in the discovery set. Table 2 gives the numbers of case and control subjects in the independent validation datasets before and after excluding related individuals. In the discovery set, we obtained SNP solutions by applying SNP-BLUP (Equation 3) and then projected the SNP solution to the genotypes of the validation individuals (Equation 2). For assessing predictive performance in the independent validation, the correlation and regression coefficients were used as measures of prediction accuracy and biasedness, respectively, similar to the internal validation. A likelihood ratio test (LRT) was used to test for differences in prediction accuracy between methods comparing the likelihood of a logistic regression fitting the STGBLUP to that of a logistic regression fitting the MTGBLUP and STGBLUP jointly. In the logistic regression models, case-control status was used as the dependent variable. In the validation datasets, all phenotypes were controlled for cohort, sex, and the first 20 principal components just as in the discovery dataset. This external validation confirmed the superior performance of MTGBLUP over STGBLUP (Table 3). From the LRT to test differences in prediction accuracy, the model including MTGBLUP fitted the data significantly better (p = 2.4 × 10⁻²⁴ for schizophrenia, 6.6 × 10⁻¹⁶ for bipolar disorder, and 0.010 for major depressive disorder) (Table 4). We further tested the two-components model fitting similarity matrices based on SNPs annotated in CNS genes and/or SNPs localized elsewhere (MTGBLUP-CNS and STGBLUP-CNS). Including the CNS component resulted in increased prediction accuracy for schizophrenia and bipolar disorder (Tables 3 and 4). We also tested a second annotation model replacing the CNS gene set with a SAI candidate genes set (4,133 autosomal genes)³ (MTGBLUP-SAI or STGBLUP-SAI), but found little improvement due to SAI genes for three of the disorders (Tables S2 and S3).

Table 2.

Numbers of Cases and Controls in the Independent Validation Data Sets before and after Removing Related Individuals

	SCZ (Swedish)		BIP (Swedish)		MDD (GENRED2)
	Cases	Controls	Cases	Controls	Cases	Controls
All	5,193	6,391	2,208	6,056	831	474
After cut-off QC	4,068	5,471	2,029	5,338	822	466
Number of SNPs	745,631		645,237		673,109

Abbreviations are as follows: SCZ, Swedish schizophrenia GWAS; BIP, Swedish bipolar disorder GWAS; MDD, GENRED2 GWAS.

Table 3.

Prediction Accuracy for Schizophrenia, Bipolar Disorder, and Major Depressive Disorder in Independent Validation Data Sets

	Correlation			Regression Slope
	SCZ	BIP	MDD	SCZ	BIP	MDD
STGBLUP	0.198	0.129	0.045	0.784	0.709	0.304
MTGBLUP	0.222	0.159	0.075	0.815	0.697	0.466
STGBLUP-CNS	0.203	0.132	0.045	0.789	0.719	0.306
MTGBLUP-CNS	0.224	0.162	0.076	0.807	0.690	0.476

Prediction accuracy is given as the correlation coefficient between the observed disease status and the predicted genomic risk score in the validation data. Regression deviated from one reflects the degree of bias of the risk scores.

Table 4.

p Values from the Likelihood Ratio Test Comparing Different Models

x1	x2	SCZ	BIP	MDD
		p Values from LRT
STGBLUP	MTGBLUP	2.4 × 10−24	6.6 × 10−16	1.0 × 10−2
STGBLUP	STGBLUP-CNS	9.1 × 10−6	4.6 × 10−3	5.8 × 10−1
MTGBLUP	MTGBLUP-CNS	2.4 × 10−3	5.3 × 10−3	3.3 × 10−1
STGBLUP	MTGBLUP-CNS	6.7 × 10−26	1.3 × 10−17	7.3 × 10−3

Likelihood ratio LR = −2 [logL(x₁) − logL(x₁+ x₂)] where logL(x₁) (logL(x₁+x₂)) is the log likelihood from a logistic regression with case-control status as the dependent variable and x₁ (x₁ and x₂) as independent explanatory variable.

When using independent validation samples, the slopes of the regression of the case-control status on the predictor were less than 1 (Table 3). The bias was relatively small for schizophrenia and bipolar disorder but larger for major depressive disorder. A slope less than 1 implies that the difference between the true genetic risks in a pair of individuals is less than that of the predicted genetic risk between them. The bias could be due to low predictive power (e.g., MDD) or to heterogeneity between the discovery and validation sample. In order to assess population differences, we calculated ancestry principal components from the POPRES reference sample^33,34 and projected them into the discovery and validation samples and found ancestral differences between them for each disorder (Figure S3). We estimated that the SNP correlation²¹ between the discovery and validation datasets was significantly different from 1 for schizophrenia and bipolar disorder (Table S4; the point estimate was lower for major depressive disorder but the small sample size generated a large standard error so it was not significantly different from 1). To explore whether the found heterogeneity reflects real population differences or is caused by other factors that lead to differences between the discovery and validation samples such as batch effects, we looked for evidence of heterogeneity within PGC discovery samples for schizophrenia, bipolar disorder, and major depressive disorder (Appendix B). For each disorder, we divided the discovery sample into four groups based on the 25%, 50%, and 75% quartile of the first principal component, which reflects ancestral population differences between individuals (Figure S4). Applying a reaction norm model^35,36 (Appendix B), we found significant heterogeneity attributable to the ancestral population differences for schizophrenia and bipolar disorder (Table S5 and Figure S5). This indicates that for schizophrenia and bipolar disorder, real population heterogeneity rather than batch effects contribute to the reduced SNP correlation between discovery and validation sets. Previously we reported more heterogeneity between major depressive disorder cohorts than between schizophrenia cohorts,¹² where cohorts were defined based on sample collection, genotyping platform, and imputation set. The lack of evidence of population heterogeneity for the depression sample here might reflect that population heterogeneity not detectable given other heterogeneity within these samples.

After a common epidemiological approach to assess a continuous risk factor,³⁷ individuals were stratified into deciles according to the ranked values of the genetic risk predictors. We estimated the odds ratio of case-control status by contrasting each decile to the lowest decile (Figure 1). For all disorders, the odds ratio was highest between individuals in the highest and lowest decile, ranging from 1.3 to 5.5. Generally, odd ratios from MTGBLUP were larger than those from STGBLUP. For example, for bipolar disorder MTGBLUP increased the odds ratio by up to 60% compared to STGBLUP (odds ratio of 4.4 and 2.8, respectively). The discriminant power increased more for the annotation model with the CNS genes, compared to the one-component models without annotation (Figure 1). With increasing sample sizes, the odds ratio is expected to increase further.³⁷

Figure 1.

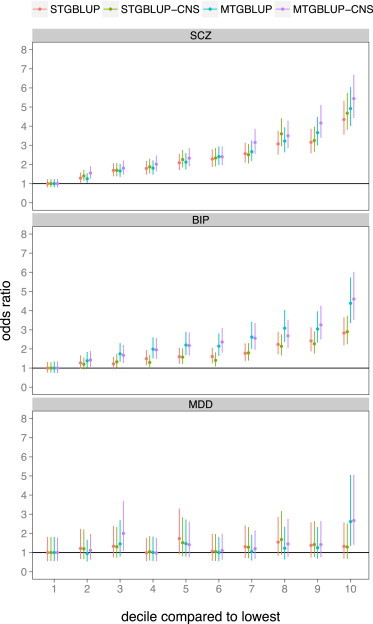
Odds Ratios of Individuals Stratified into Deciles Based on GBLUP Genetic Risk in Independent Samples, using the Decile with the Lowest Risk as the Baseline

The vertical error bars denote 95% CI. We note that the estimates for the different methods are highly correlated, and therefore the vertical error bars cannot be used to infer significance of difference between the methods (see Appendix C).

We also quantified the gain in prediction accuracy from MTGBLUP in terms of sample size. Using recent results on prediction accuracy of polygenic scores derived from quantitative genetic theory,^11,38 we inferred the sample sizes required to achieve the accuracies observed by the methods (Figure 2). We assumed prevalence of 1% for schizophrenia, 1% for bipolar disorder, and 15% for major depressive disorder. The proportion of cases in the sample was based on the real structure of the discovery data (59% for schizophrenia, 64% for bipolar disorder, and 57% for major depressive disorder). The effective number of SNPs was assumed to be 69,748 calculated with a weighted SNP method.³⁹ The observed accuracy was within the theoretical expectation for schizophrenia and bipolar disorder, but not for major depressive disorder where the actual predictive power was lower. Accuracy of risk prediction for individual traits benefited from including the correlated disorders. The gain in accuracy of MTGBLUP compared to STGBLUP was equivalent to increasing the sample size for schizophrenia, bipolar disorder, and major depressive disorder by ∼4,660 (95% confidence interval: 3,110–6,270), ∼5,560 (2,830–8,640), and ∼10,940 (730–24,440) individuals, respectively (Figure 2). Gains in accuracy were even greater with the CNS annotation model (Table S6). The 95% confidence interval was obtained according to the sampling error of the difference between the prediction accuracies (Appendix C).

Figure 2.

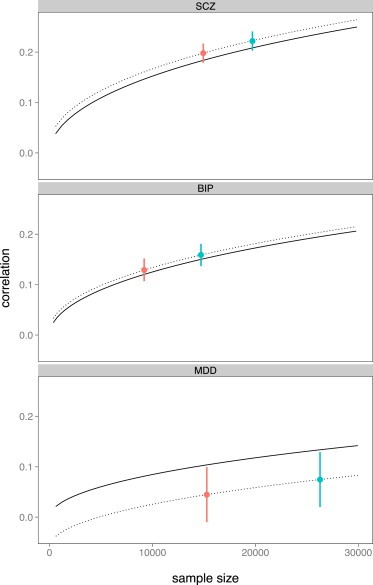
Theoretical and Observed Prediction Accuracy of STGBLUP and MTGBLUP Depending on Sample Size

Theoretical line of prediction accuracy increased with larger sample size (solid line), the observed accuracy achieved by STGBLUP with the actual sample size (red dot), and the observed accuracy achieved by MTGBLUP and inferred sample size (blue dot). The increase from MTGBLUP equates to ∼4,660 samples for schizophrenia, ∼5,550 samples for bipolar disorder, and ∼10,940 for major depressive disorder. The vertical error bars denote 95% CI. We note that the estimates for the different methods are highly correlated, and therefore the vertical error bars cannot be used to infer significance of difference between the methods (see Appendix C).

In order to test how sensitive our results on prediction are against population stratification, we re-estimated the prediction accuracy (correlation), removing potential outliers that were ±6 SD, 2 SD, 1.75 SD, 1.5 SD, 1.25 SD, or 1 SD away from the mean of the first and second principal component in the validation dataset (Figure S6). The accuracy of MTGBLUP and STGBLUP remained stable in all three diseases for which independent datasets were available. Restricting the samples to individuals whose values of the first and second principal component lay within one SD of the mean retained between 51% and 70% of the samples (Figure S6). This shows that the prediction accuracy was not substantially affected by ancestry outliers in the validation dataset.

We compared the performance of MTGBLUP with that of bivariate GBLUP (a special case of MTGBLUP). The accuracy of MTGBLUP was significantly higher than bivariate GBLUP except for a major depressive disorder risk prediction where the accuracy of MTGBLUP and that of the bivariate model involving schizophrenia and major depressive disorder was not significantly different (Table S7 and S8).

Psychiatry lags behind other fields of medicine in terms of diagnostic tests that could facilitate early diagnosis and accurate classification of disorders. The considerable heritability of psychiatric disorders implies that the genome contains a large amount of information with potential diagnostic utility. However, the highly polygenic nature of psychiatric disorders makes it very hard to exploit this information, mostly because the effect of each individual locus contributing to disease risk can be estimated only with error, and the size of the error depends on factors such allele frequency, effect size, and (crucially) sample size.

The genetic correlation between several diseases implies that a SNP contributing to risk of one disease will, on average, also be informative of the risk of the correlated diseases. Here, we have developed a multivariate method that can combine data from an arbitrary number of genetically correlated diseases, resulting in better estimates of the disease-specific SNP effects and thus generating more accurate predictors of individual risk. Our results demonstrate a significant advantage of incorporating data from multiple correlated diseases compared to single-trait analyses. Our estimates of pairwise genetic correlations obtained in independent datasets reconfirm previous results regarding the extent of genetic correlations between the five psychiatric disorders.¹² External validation demonstrated that the predictive models generalize to other populations, confirming that the correlations reflect pleiotropy between the disorders rather than artifacts.

We used a multiple random effects model that fitted two components, one due to annotated SNPs and the other due to the rest of SNPs. The prediction accuracy significantly increased when using an appropriate gene set. For example, the gain in predictive accuracy in terms of sample size equivalence increased from 4,660 to 5,080 for schizophrenia, from 5,550 to 6,220 for bipolar disorder, and from 10,940 to 11,550 for major depressive disorder when using the CNS genes annotation^12,26 (Table S6). This demonstrates that the multiple random effects model in MTGBLUP can be useful especially for psychiatric disorders where prediction accuracy is hardly improved by other advanced methods.^4,5

Zhou and Stephens⁴⁰ recently introduced a multivariate linear mixed model algorithm that is particularly suited for genome-wide association studies. Their method requires that multiple traits are measured on the same individual or that the level of missingness is sufficiently small so that missing phenotypes can be imputed. However, this algorithm is not useful when phenotypes are collected from independent datasets as in the PGC data where dependent variables are totally missing for the other four traits as is typical of disease-ascertained cohorts. Moreover, the efficiency of Zhou and Stephens’ algorithm substantially decreases when fitting multiple random effects (e.g., the annotation model).

Korte et al.⁴¹ proposed a similar model to MTGREML using ASReml⁴² that is as flexible as our method in that it can handle partial overlapping or disjoint sets of phenotypes. However, our algorithm is different from that used in ASReml and is much more efficient when using genomic data²⁰ (see Appendix A). Moreover, Korte et al. did not explore their method with respect to improvements in risk prediction.

Even though sensitivity and specificity of genetic diagnostics to predict an individual’s risk of psychiatric disorders are generally low, genetic risk scores can still be a valuable tool for research to stratify a heterogeneous population in groups with shared “genomic” characteristics. It was suggested that psychiatric diagnoses encompass several clinically similar phenotypes with distinct pathophysiology and that stratification according to individual heterogeneity is an important requirement for the development of treatments targeted at specific disease subtypes.^17–19 Our proposed multivariate approach with the annotation model is a flexible and powerful tool for such stratification. The MTGREML and MTGBLUP package and documentation are publicly available online, which we anticipate will be implemented into the GCTA package.²² Using a CPU running at 2.2 GHz, analyzing 58,128 samples with 5 disjoint sets of phenotypes (e.g., the PGC data) takes ∼7 hr per each iteration in MTGREML. Convergence is usually achieved within 10 iterations. The virtual memory required for such data is ∼45 GB. Good starting values (probably from single-trait GREML⁴¹) can reduce the number of iterations to convergence and our software has the option to provide starting values. The computational time increases cubically with sample size, e.g., analyzing sample size of 10,000 takes a few minutes per each iteration. Our software provides a parallelization option that can reduce computational burden substantially; for example, speed is increased by a factor of ten when using 20 CPUs. The number of traits hardly affects running time if phenotypes are non-overlapping.

Consortia

The members of Cross-Disorder Working Group of the Psychiatric Genomics Consortium are Devin Absher, Ingrid Agartz, Huda Akil, Farooq Amin, Ole A. Andreassen, Adebayo Anjorin, Richard Anney, Dan E. Arking, Philip Asherson, Maria H. Azevedo, Lena Backlund, Judith A. Badner, Anthony J. Bailey, Tobias Banaschewski, Jack D. Barchas, Michael R. Barnes, Thomas B. Barrett, Nicholas Bass, Agatino Battaglia, Michael Bauer, Mònica Bayés, Frank Bellivier, Sarah E. Bergen, Wade Berrettini, Catalina Betancur, Thomas Bettecken, Joseph Biederman, Elisabeth B. Binder, Donald W. Black, Douglas H.R. Blackwood, Cinnamon S. Bloss, Michael Boehnke, Dorret I. Boomsma, Gerome Breen, René Breuer, Richard Bruggeman, Nancy G. Buccola, Jan K. Buitelaar, William E. Bunney, Joseph D. Buxbaum, William F. Byerley, Sian Caesar, Wiepke Cahn, Rita M. Cantor, Miguel Casas, Aravinda Chakravarti, Kimberly Chambert, Khalid Choudhury, Sven Cichon, C. Robert Cloninger, David A. Collier, Edwin H. Cook, Hilary Coon, Bru Cormand, Paul Cormican, Aiden Corvin, William H. Coryell, Nicholas Craddock, David W. Craig, Ian W. Craig, Jennifer Crosbie, Michael L. Cuccaro, David Curtis, Darina Czamara, Mark J. Daly, Susmita Datta, Geraldine Dawson, Richard Day, Eco J. De Geus, Franziska Degenhardt, Bernie Devlin, Srdjan Djurovic, Gary J. Donohoe, Alysa E. Doyle, Jubao Duan, Frank Dudbridge, Eftichia Duketis, Richard P. Ebstein, Howard J. Edenberg, Josephine Elia, Sean Ennis, Bruno Etain, Ayman Fanous, Stephen V. Faraone, Anne E. Farmer, I. Nicol Ferrier, Matthew Flickinger, Eric Fombonne, Tatiana Foroud, Josef Frank, Barbara Franke, Christine Fraser, Robert Freedman, Nelson B. Freimer, Christine M. Freitag, Marion Friedl, Louise Frisén, Louise Gallagher, Pablo V. Gejman, Lyudmila Georgieva, Elliot S. Gershon, Daniel H. Geschwind, Ina Giegling, Michael Gill, Scott D. Gordon, Katherine Gordon-Smith, Elaine K. Green, Tiffany A. Greenwood, Dorothy E. Grice, Magdalena Gross, Detelina Grozeva, Weihua Guan, Hugh Gurling, Lieuwe De Haan, Jonathan L. Haines, Hakon Hakonarson, Joachim Hallmayer, Steven P. Hamilton, Marian L. Hamshere, Thomas F. Hansen, Annette M. Hartmann, Martin Hautzinger, Andrew C. Heath, Anjali K. Henders, Stefan Herms, Ian B. Hickie, Maria Hipolito, Susanne Hoefels, Peter A. Holmans, Florian Holsboer, Witte J. Hoogendijk, Jouke-Jan Hottenga, Christina M. Hultman, Vanessa Hus, Andrés Ingason, Marcus Ising, Stéphane Jamain, Ian Jones, Lisa Jones, Anna K. Kähler, René S. Kahn, Radhika Kandaswamy, Matthew C. Keller, John R. Kelsoe, Kenneth S. Kendler, James L. Kennedy, Elaine Kenny, Lindsey Kent, Yunjung Kim, George K. Kirov, Sabine M. Klauck, Lambertus Klei, James A. Knowles, Martin A. Kohli, Daniel L. Koller, Bettina Konte, Ania Korszun, Lydia Krabbendam, Robert Krasucki, Jonna Kuntsi, Phoenix Kwan, Mikael Landén, Niklas Långström, Mark Lathrop, Jacob Lawrence, William B. Lawson, Marion Leboyer, David H. Ledbetter, Phil H. Lee, Todd Lencz, Klaus-Peter Lesch, Douglas F. Levinson, Cathryn M. Lewis, Jun Li, Paul Lichtenstein, Jeffrey A. Lieberman, Dan-Yu Lin, Don H. Linszen, Chunyu Liu, Falk W. Lohoff, Sandra K. Loo, Catherine Lord, Jennifer K. Lowe, Susanne Lucae, Donald J. MacIntyre, Pamela A.F. Madden, Elena Maestrini, Patrik K.E. Magnusson, Pamela B. Mahon, Wolfgang Maier, Anil K. Malhotra, Shrikant M. Mane, Christa L. Martin, Nicholas G. Martin, Manuel Mattheisen, Keith Matthews, Morten Mattingsdal, Steven A. McCarroll, Kevin A. McGhee, James J. McGough, Patrick J. McGrath, Peter McGuffin, Melvin G. McInnis, Andrew McIntosh, Rebecca McKinney, Alan W. McLean, Francis J. McMahon, William M. McMahon, Andrew McQuillin, Helena Medeiros, Sarah E. Medland, Sandra Meier, Ingrid Melle, Fan Meng, Jobst Meyer, Christel M. Middeldorp, Lefkos Middleton, Vihra Milanova, Ana Miranda, Anthony P. Monaco, Grant W. Montgomery, Jennifer L. Moran, Daniel Moreno-De-Luca, Gunnar Morken, Derek W. Morris, Eric M. Morrow, Valentina Moskvina, Bryan J. Mowry, Pierandrea Muglia, Thomas W. Mühleisen, Bertram Müller-Myhsok, Michael Murtha, Richard M. Myers, Inez Myin-Germeys, Benjamin M. Neale, Stan F. Nelson, Caroline M. Nievergelt, Ivan Nikolov, Vishwajit Nimgaonkar, Willem A. Nolen, Markus M. Nöthen, John I. Nurnberger, Evaristus A. Nwulia, Dale R. Nyholt, Michael C O’Donovan, Colm O’Dushlaine, Robert D. Oades, Ann Olincy, Guiomar Oliveira, Line Olsen, Roel A. Ophoff, Urban Osby, Michael J. Owen, Aarno Palotie, Jeremy R. Parr, Andrew D. Paterson, Carlos N. Pato, Michele T. Pato, Brenda W. Penninx, Michele L. Pergadia, Margaret A. Pericak-Vance, Roy H. Perlis, Benjamin S. Pickard, Jonathan Pimm, Joseph Piven, Danielle Posthuma, James B. Potash, Fritz Poustka, Peter Propping, Shaun M. Purcell, Vinay Puri, Digby J. Quested, Emma M. Quinn, Josep Antoni Ramos-Quiroga, Henrik B. Rasmussen, Soumya Raychaudhuri, Karola Rehnström, Andreas Reif, Marta Ribasés, John P. Rice, Marcella Rietschel, Stephan Ripke, Kathryn Roeder, Herbert Roeyers, Lizzy Rossin, Aribert Rothenberger, Guy Rouleau, Douglas Ruderfer, Dan Rujescu, Alan R. Sanders, Stephan J. Sanders, Susan L. Santangelo, Russell Schachar, Martin Schalling, Alan F. Schatzberg, William A. Scheftner, Gerard D. Schellenberg, Stephen W. Scherer, Nicholas J. Schork, Thomas G. Schulze, Johannes Schumacher, Markus Schwarz, Edward Scolnick, Laura J. Scott, Joseph A. Sergeant, Jianxin Shi, Paul D. Shilling, Stanley I. Shyn, Jeremy M. Silverman, Pamela Sklar, Susan L. Slager, Susan L. Smalley, Johannes H. Smit, Erin N. Smith, Jordan W. Smoller, Edmund J.S. Sonuga-Barke, David St Clair, Matthew State, Michael Steffens, Hans-Christoph Steinhausen, John S. Strauss, Jana Strohmaier, T. Scott Stroup, Patrick F. Sullivan, James Sutcliffe, Peter Szatmari, Szabocls Szelinger, Anita Thapar, Srinivasa Thirumalai, Robert C. Thompson, Alexandre A. Todorov, Federica Tozzi, Jens Treutlein, Jung-Ying Tzeng, Manfred Uhr, Edwin J.C.G. van den Oord, Gerard Van Grootheest, Jim Van Os, Astrid M. Vicente, Veronica J. Vieland, John B. Vincent, Peter M. Visscher, Christopher A. Walsh, Thomas H. Wassink, Stanley J. Watson, Lauren A. Weiss, Myrna M. Weissman, Thomas Werge, Thomas F. Wienker, Durk Wiersma, Ellen M. Wijsman, Gonneke Willemsen, Nigel Williams, A. Jeremy Willsey, Stephanie H. Witt, Naomi R. Wray, Wei Xu, Allan H. Young, Timothy W. Yu, Stanley Zammit, Peter P. Zandi, Peng Zhang, Frans G. Zitman, and Sebastian Zöllner. Affiliations of consortium members are available in the Supplemental Data.

Published: January 29, 2015

Appendix A. Average of Hessian and Fisher Information Matrix for the Multivariate Model

The log likelihood of the multivariate model is

$$\ln L=-\frac{1}{2}\left[\ln \left|\mathbf{V}\right|+\ln |\mathbf{X}\text{'}{\mathbf{V}}^{-1}\mathbf{X}|+\mathbf{y}\text{'}\mathbf{P}\mathbf{y}\right]$$

where ln is the natural log and | | the determinant of the associated matrices. The projection matrix is defined as $\mathbf{P}={\mathbf{V}}^{-1}-{\mathbf{V}}^{-1}\mathbf{X}{(\mathbf{X}\text{'}{\mathbf{V}}^{-1}\mathbf{X})}^{-1}\mathbf{X}\text{'}{\mathbf{V}}^{-1}$ with

$$\mathbf{X}=\left[\begin{array}{ccc}{\mathbf{X}}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & {\mathbf{X}}_n\end{array}\right],\text{and}\mathbf{y}=\left[\begin{array}{c}{\mathbf{y}}_1\\ ⋮\\ {\mathbf{y}}_n\end{array}\right]\text{.}$$

The Newton-Raphson algorithm obtains the MTGREML estimates with the following equation⁴³

$${\Theta }^{(k+1)}={\Theta }^{\left(k\right)}-{\left({\mathbf{H}}^{\left(k\right)}\right)}^{-1}\frac{\partial L}{\partial \Theta }|{\Theta }^{\left(k\right)}$$ (Equation A1)

where $\Theta$ is a column vector of estimated variance components, k is the iteration round, $\partial L/\partial \Theta$ is a column vector of the first derivatives of the log likelihood function with respect to each variance component, and H is the Hessian matrix, which consists of the second derivatives of the log likelihood function with respect to the variance components. In Fisher’s scoring method, the inverse of the Hessian matrix in Equation A1 is replaced by its expected value:⁴³

$${\Theta }^{(k+1)}={\Theta }^{\left(k\right)}+{\left(F^{\left(k\right)}\right)}^{-1}\frac{\partial L}{\partial \Theta }|{\Theta }^{\left(k\right)}.$$ (Equation A2)

The derivation of the Hessian matrix and the Fisher information matrix has been described in several studies.^43,44 The Hessian matrix for the multivariate model is

$$\mathbf{H}=\frac{{\partial }^{2}L}{\partial {\sigma }_i^2\partial {\sigma }_j^2}=\frac{1}{2}\left[tr\left(\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_j^2}\mathbf{P}\right)-\mathbf{y}\text{'}\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_j^2}\mathbf{P}\mathbf{P}\mathbf{y}\right]$$ (Equation A3)

where y, P, and V are defined in the section “Multivariate Linear Mixed Model” in the main text. The Fisher information (F) matrix is

$$\mathbf{F}=E\left(\frac{{\partial }^{2}L}{\partial {\sigma }_i^2\partial {\sigma }_j^2}\right)=\frac{1}{2}\left[tr\left(\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_j^2}\mathbf{P}\right)\right].$$ (Equation A4)

Gilmour et al.⁴² and Johnson and Thompson⁴⁵ used the average of the H and F that was estimated based on Henderson’s mixed model equation (MME).⁴⁶ The MME-based average information algorithm is efficient particularly when covariance structure fitted in the model is sparse. Lee and van der Werf²⁰ introduced the direct average information algorithm where average information matrix was derived directly from the V and P matrix. When using non-zero elements of covariance structure, this direct average information algorithm is much more efficient than the MME-based average information algorithm. The equation for the iterative AI algorithm is

$${\Theta }^{(k+1)}={\Theta }^{\left(k\right)}+{\left(\mathbf{A}{\mathbf{I}}^{\left(k\right)}\right)}^{-1}\frac{\partial L}{\partial \Theta }|{\Theta }^{\left(k\right)}$$

where AI is the average information matrix and that for multivariate model can be written as

$$\mathbf{A}\mathbf{I}=\frac{1}{2}\left[\mathbf{y}\text{'}\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_j^2}\mathbf{P}\mathbf{P}\mathbf{y}\right].$$

The first derivative for each variance covariance component i can be obtained as^43,44

$$\frac{\partial L}{\partial {\sigma }_i^2}=-\frac{1}{2}tr\left(\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\right)+\frac{1}{2}\mathbf{y}\text{'}\mathbf{P}\frac{\partial \mathbf{V}}{\partial {\sigma }_i^2}\mathbf{P}\mathbf{y}.$$

Appendix B. Reaction Norm Model to Test Heterogeneity across Populations Classified by the Ancestry Principal Component

Reaction norm models have been used in ecology and evolution to study genotype × environment interaction.^35,36 Genotype × environment interaction (G × E) means that different genotypes respond different to environmental changes, i.e., norms of reaction. In the model, a random intercept and a random slope, as covariance functions, are estimated that can describe genetic and phenotypic variation across different environments. The slope of the reaction norm is often called phenotypic plasticity or environmental sensitivity. The amount of variation in slope in the population indicates the extent of G × E.^35,36 Here, we describe a reaction norm model to test heterogeneity across populations. We group each sample set into four populations by splitting them into the four quartiles of the first ancestry principal component. Whereas typically reaction norm models would compare samples with different categories of environmental factors to each other, we use the model to compare the samples in different principal component quartiles to each other. We limit our interpretation to heterogeneity across the groups and do not speculate about potential causes like G × E or G × G interaction. We apply the model to each disorder of the PGC data. Incorporating population difference among samples, the linear mixed model can be rewritten as

$$y_{ij}=b_{ij}+g_{ij}+e_{ij},$$

where y_ij is the observation for individual i in population class j (j = 1, …, P where P is the number of populations classified by the ancestry principal component, in our case four), b_ij is fixed effects, g_ij is genetic effects, and e_ij is residual effects. We applied a reaction norm model to fit functions of the ancestry principal component as covariables using Legendre polynomials.

$$y_{ij}=b_{ij}+\sum _{m=0}^{k-1}{\alpha }_{im}{f}_m\left(p_{ij}\right)+e_{ij}$$

p_ij is the average of the ancestry principal components in the j^th population class containing individual i, f_m(p_ij) is the m^th Legendre polynomials evaluated for p_ij, α_im is the m^th genetic random regression coefficients for the i^th individual, and k is the orders of fit. The genetic covariance between individual i in population class j and i′ in population class j′ is

$$cov(g_{ij},g_{i^{\prime }{j}^{\prime }})=\sum _{m=0}^{k-1}\sum _{l=0}^{k-1}{f}_m\left(p_{ij}\right)f_l\left(p_{i^{\prime }{j}^{\prime }}\right)cov({\alpha }_{im},{\alpha }_{il}).$$

This can be written in a matrix form as

$${\mathbf{V}}_g=\mathbf{F}\mathbf{K}{\mathbf{F}}^{\text{'}},$$

where F is the matrix of Legendre polynomials evaluated at given ancestry principal components and K is the covariance coefficient matrix consisting of random regression coefficients, i.e.,

$$\mathbf{K}=cov({\alpha }_{im},{\alpha }_{il})=\left[\begin{array}{ccc}var\left({\alpha }_0\right)& \cdots & cov({\alpha }_0,{\alpha }_k)\\ ⋮& \ddots & ⋮\\ cov({\alpha }_k,{\alpha }_0)& \cdots & var\left({\alpha }_k\right)\end{array}\right].$$

The optimal order of the polynomial was determined with a likelihood ratio test by comparing the likelihood of models with higher order to the null model with k = 1.

Appendix C. Estimating the Sampling Error of the Difference between Prediction Accuracies

It is assumed that there are three normalized variables with the covariance structure as below, mimicking the MTGBLUP, STGBLUP, and outcome variable.

	m	s	y
m	1	0.927	0.222
s	0.927	1	0.189
y	0.222	0.198	1

We are interested in estimating the sampling error of the difference between cor(m,y) and cor(s,y). The sampling variance of the difference (${\sigma }_d^2$) can be expressed as

$${\sigma }_d^2={\sigma }_{cor(m,y)}^2+{\sigma }_{cor(s,y)}^2-2\cdot r\cdot {\sigma }_{cor(m,y)}\cdot {\sigma }_{cor(s,y)},$$ (Equation C1)

where ${\sigma }_{cor(m,y)}^2$ is the sampling variance of cor(m,y), ${\sigma }_{cor(s,y)}^2$ is the sampling variance of cor(s,y), and r is the correlation between cor(m,y) and cor(s,y). We show here that r is approximately equal to cor(m,s).

With N records for each variable, correlations among the variables can be written as

$$cor(m,y)=E(m\cdot y)=\frac{1}{N}\sum _{i=1}^N{m}_i{y}_i$$

$$cor(s,y)=E(s\cdot y)=\frac{1}{N}\sum _{i=1}^N{s}_i{y}_i$$

$$cor(m,s)=E(m\cdot s)=\frac{1}{N}\sum _{i=1}^N{m}_i{s}_i.$$

For T replicates, the expected value of the product of cor(m,y) and cor(s,y) can be written as

$$E[E(m\cdot y)\cdot E(s\cdot y)]=\frac{1}{T}{\sum _j^T\left[\left(\frac{1}{N}\sum _{i=1}^N{m}_i{y}_i\right)\left(\frac{1}{N}\sum _{i=1}^N{s}_i{y}_i\right)\right]}_j=\frac{1}{T}{\sum _j^T\left[\left(\frac{m_1{y}_1}{N}+,\mathrm{...},+\frac{m_N{y}_N}{N}\right)\left(\frac{s_1{y}_1}{N}+,\mathrm{...},+\frac{s_N{y}_N}{N}\right)\right]}_j.$$

If m and s are uncorrelated, this reduces to

$$E[E\left(my\right)\cdot E(sy\left)\right]=E\left[E\right(m\cdot y\left)\right]\cdot E\left[E\right(s\cdot y\left)\right]$$

If m and s are correlated, there is an additional term,

$$\begin{array}{l}E\left[E\right(m\cdot y\left)E\right(s\cdot y\left)\right]\cong \hfill \\ \frac{1}{T}{\sum _j^T\left[\left(\frac{1}{N^2}\sum _{i=1}^N{m}_i{s}_i\right)\right]}_{\mathit{jj}}+E\left[E(m\cdot y)\right]\cdot E\left[E\right(s\cdot y\left)\right]=\hfill \\ \frac{1}{T}{\sum _j^T\left[\frac{1}{N}E(m\cdot s)\right]}_j+E\left[E\right(m\cdot y\left)\right]\cdot E\left[E\right(s\cdot y\left)\right]=\hfill \\ \frac{1}{N}E\left[E\right(m\cdot s\left)\right]+E\left[E\right(m\cdot y\left)\right]\cdot E\left[E(s\cdot y)\right]\hfill \end{array}$$

Therefore,

$$cov\left[E\right(m\cdot y),E(s\cdot y)]=E\left[E\right(m\cdot y\left)E\right(s\cdot y\left)\right]-E\left[E\right(m\cdot y\left)\right]\cdot E\left[E(s\cdot y)\right]\cong \frac{1}{N}E\left[E(m\cdot s)\right].$$

With $var\left[E(m\cdot y)\right]\cong var\left[E(s\cdot y)\right]\cong 1/N$, the correlation between cor(m,y) and cor(s,y) (r) can be approximated as

$$cor[E(m\cdot y),E(s\cdot y)]\cong E\left[E\left(ms\right)\right]\cong cor(m,s).$$

This expression was checked and validated by simulations (result not shown).

Here we have shown that Equation C1 can be used to estimate the sampling variance (the square of the standard error) of the difference in correlation between the STGBLUP and MTGBLUP predictors (which are themselves correlated with each other) and the outcome variable (the adjusted phenotype). This allows us to estimate the 95% confidence interval of the increase in correlation that MTGBLUP achieves over STGBLUP. Note that because the two predictors are correlated, this is a smaller confidence interval than that of the correlation between MTGBLUP and the outcome variable (which is shown in Figures 1 and 2). By using the method described above, we can transform the confidence interval from the correlation scale to the sample size scale, to get estimates of the effective increase in sample size achieved by MTGBLUP (Table S6).

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• Complex Traits Genomic Group, http://www.cnsgenomics.com/software/

• GCTA, http://www.complextraitgenomics.com/software/gcta/

• Genetic Cluster Computer, http://www.geneticcluster.org/

• International HapMap Project, http://hapmap.ncbi.nlm.nih.gov/

• Multi-trait GREML and GBLUP Analysis (MTG), https://github.com/uqrmaie1/mtgblup or http://www.cnsgenomics.com/software/

• Psychiatric Genomics Consortium, http://www.med.unc.edu/pgc/

• UCSC Genome Browser, http://genome.ucsc.edu