Short abstract
For newborns diagnosed with pulmonary atresia or severe pulmonary stenosis leading to insufficient pulmonary blood flow, cyanosis can be mitigated with placement of a modified Blalock–Taussig shunt (MBTS) between the innominate and pulmonary arteries. In some clinical scenarios, patients receive two systemic-to-pulmonary connections, either by leaving the patent ductus arteriosus (PDA) open or by adding an additional central shunt (CS) in conjunction with the MBTS. This practice has been motivated by the thinking that an additional source of pulmonary blood flow could beneficially increase pulmonary flow and provide the security of an alternate pathway in case of thrombosis. However, there have been clinical reports of premature shunt occlusion when more than one shunt is employed, leading to speculation that multiple shunts may in fact lead to unfavorable hemodynamics and increased mortality. In this study, we hypothesize that multiple shunts may lead to undesirable flow competition, resulting in increased residence time (RT) and elevated risk of thrombosis, as well as pulmonary overcirculation. Computational fluid dynamics-based multiscale simulations were performed to compare a range of shunt configurations and systematically quantify flow competition, pulmonary circulation, and other clinically relevant parameters. In total, 23 cases were evaluated by systematically changing the PDA/CS diameter, pulmonary vascular resistance (PVR), and MBTS position and compared by quantifying oxygen delivery (OD) to the systemic and coronary beds, wall shear stress (WSS), oscillatory shear index (OSI), WSS gradient (WSSG), and RT in the pulmonary artery (PA), and MBTS. Results showed that smaller PDA/CS diameters can lead to flow conditions consistent with increased thrombus formation due to flow competition in the PA, and larger PDA/CS diameters can lead to insufficient OD due to pulmonary hyperfusion. In the worst case scenario, it was found that multiple shunts can lead to a 160% increase in RT and a 10% decrease in OD. Based on the simulation results presented in this study, clinical outcomes for patients receiving multiple shunts should be critically investigated, as this practice appears to provide no benefit in terms of OD and may actually increase thrombotic risk.
Keywords: competitive flow, pulmonary atresia, multidomain, multiscale, lumped parameter network, LPN, CFD, residence time, thrombosis
1. Introduction
Neonates with pulmonary atresia or severe pulmonary stenosis in association with balanced or unbalanced ventricles represent a heterogeneous group of patients that often require initial surgical palliation by means of a systemic-to-pulmonary artery shunt [1]. The purpose of shunt insertion, connecting the systemic vessels and the PA, is to provide a source of pulmonary blood flow and ensure sufficient oxygenation. Following shunt insertion, the systemic and pulmonary circulations are arranged in parallel, such that blood travels through the aorta to both the body and lungs and returns to the right atrium (RA) through the pulmonary and systemic venous systems. In this configuration, the heart carries a higher volume load, since it must drive the systemic and pulmonary circulations in parallel, and aortic saturation is compromised due to mixing of oxygenated pulmonary and deoxygenated systemic venous blood [2].
Depending on the size of the right ventricle, some children diagnosed with pulmonary atresia or severe pulmonary stenosis also undergo subsequent palliative open-heart surgeries which are performed to unload the heart, improve oxygenation, and provide a growing and reliable source of pulmonary blood flow. In the subsequent surgeries, the systemic-to-pulmonary shunt is removed and the upper and lower body venous return is rerouted to the lungs; hence blood is pumped to the systemic and pulmonary arteries in-series rather than in parallel. In the second stage, the hemi-Fontan or bidirectional Glenn surgery, the shunt is taken down and the superior vena cava is connected to the PA, partially unloading the heart. Although systemic saturation is improved [3] compared to the first stage, the lower body and pulmonary venous return still mix and systemic saturation remains suboptimal. In the final palliative surgery, the Fontan, the inferior vena cava is also anastomosed to the PA and the right side of the heart is completely bypassed, creating an in-series circulation [4]. Although most Fontan patients achieve near-normal systematic saturation, many still suffer from morbidities including thrombosis, arrhythmias, exercise intolerance, and cardiac failure [5,6]. Despite significant improvements in surgical and management methods for the single ventricle (SV) pathway, significant morbidity and mortality remain at all three stages. In the stage one surgery, the focus of the present study, presents the highest risk, with mortality rates as high as 23% [7].
Neonates have a natural systemic-to-pulmonary connection through the PDA which normally closes after birth. Shunt placement introduces a new systemic-to-pulmonary connection in stage one surgery; however, subsequent graft failure can be caused by thrombus formation, blocking the pulmonary circulation leading to hypoxia and sudden death [8]. Because of these significant risks, some institutions have used multiple shunt insertion to supply the PA from more than one source [9,10]. In these cases, in addition to inserting a MBTS between the brachiocephalic artery (BA) and the right PA, the PDA may be kept open or a CS may be inserted between the PA and the aorta. This practice has been motivated by the perceived need for a spare connection that can prevent total blockage of the pulmonary circulation in the case of shunt blockage due to thrombosis. While this concept appears at the outset to have little downside, we hypothesize that there are several potentially negative implications of multiple shunts that may lead to undesirable hemodynamics. In the present study, we hypothesize that multiple shunts are unfavorable because (1) flow competition between the two shunts may increase the risk of thrombus formation and (2) pulmonary overcirculation may reduce OD.
We tested the above hypothesis by comparing two sets of surgical interventions in simulations: anatomies with single and multiple shunts. Anatomies with a single MBTS have been studied previously using multiscale [11–16] and in vitro [17,18] approaches. Prior multiscale studies have described the effects of shunt diameter on pulmonary and systemic saturations, pulmonary-to-systemic flow rates, OD, cardiac output, and other clinically relevant parameters but have not compared surgical approaches with single versus multiple shunts. Here, we compared surgical approaches by generating parameterized 3D models with single and multiple shunts. We systematically varied the PDA diameter to span a wide range of values, resulting in dramatic variation in total pulmonary resistance, leading in turn to global changes in the circulatory system. This situation exemplifies the need for multiscale modeling, which allows one to capture the coupled dynamics of the vascular system in a closed-loop as the 3D anatomical model is modified. Following our previous work, a lumped parameter network (LPN) is coupled to a 3D flow solver. Flow and pressure information is passed between the 3D and 0D domains, generating boundary conditions that capture the physiologic response to anatomical changes [19]. Additionally, to explore the validity of our rigid-wall assumption, a fluid–structure interaction (FSI) simulation was also performed, representing an advance over prior studies which primarily used open loop configurations and/or rigid-wall assumptions.
By automatically parameterizing shunt geometries in the 3D model, we considered a range of PDA and CS diameters, PVRs, and MBTS positions. In total, we compared 23 cases by quantifying OD, pulmonary-to-systemic flow ratio, cardiac output, heart load, and oxygen saturation in systemic and pulmonary arteries and veins. Though we did not directly model the complex biochemistry of the thrombus formation process, we compared WSS, WSSGs, OSI, and RT in segments of the PA and MBTS as surrogates for thrombotic risk. Recirculation regions are associated with high RT, which in combination with high shear stress history may increase the risk of thrombus formation [20]. In the present study, a new nondiscrete method was used for measuring RT using an advection–diffusion solver [21]. In contrast to particle-based methods, the nondiscrete method is not limited by spatial resolution issues and requires no extra simulation time for pulsatile flow [22,23]. Modeling incorporated realistic patient data and clinically realistic values, and performance of surgical scenarios with single versus multiple shunts was compared using the above metrics of thrombotic risk and physiologic response.
2. Methods
2.1. Model Construction and Simulations.
An idealized geometric model was constructed to include the systemic to pulmonary connection, the aortic arch, four upper branches, two coronary arteries, and the pulmonary arteries. Each branch was created by lofting segments of corresponding vessels along a centerline path. A complete solid model was then created by automatically joining the pulmonary-to-systemic connection to the rest of the model. This process was performed using a customized in-house version of the open source simvascular software package [24]. Models with varying shunt diameters were automatically created using a series of scripts, allowing for input of diameters and position and output of a final model. Automating the model creation process allowed us to systematically and efficiently construct and simulate a wide range of geometries. Anatomies with five PDA diameters, 0.0 mm (no PDA), 2.0 mm, 3.5 mm, 4.0 mm, and 5.0 mm, were considered. In total, ten different anatomies were constructed, including these five PDA diameters along with a 3.5 mm proximal or distal MBTS. To compare poststage one and prestage two conditions, 20 simulations were performed, coupling each of the ten models to an LPN with normal and high PVR. In addition, three cases with CS diameters of 2.0, 3.0, and 4.0 mm were studied, using high PVR and a proximal MBTS. The anatomies with CS, PDA, and proximal and distal MBTS configurations are shown in Fig. 1. In all models, the MBTS was slightly curved to make it perpendicular the PA.
Fig. 1.
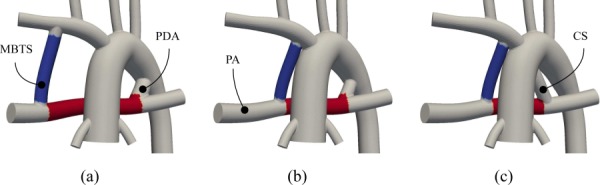
The constructed idealized models: (a) distal MBTS and a 4.0 mm PDA, (b) proximal MBTS and a 3.0 mm PDA, and (c) proximal MBTS and a 4.0 mm CS. The region between CS/PDA and MBTS inside the PA (red) and the region in the MBTS (blue) are used to compare the results of studied cases.
The computational domain was decomposed into two parts: A 3D domain where the Navier–Stokes equations were solved and a 0D domain where ordinary differential equations representing the behavior of the heart and downstream circulation were solved (Fig. 2). A rigid-wall assumption was used, since, as discussed in Sec. 2.7, the effect of wall distensibility on the solution was shown to be negligible. Since shear rate is on the order of 100 s−1, blood was assumed to behave as an incompressible Newtonian fluid [25], with density of 1060 kg/m3 and viscosity of 0.004 Pa · s. A custom in-house finite element solver was used to solve the 3D incompressible flow equations. The generalized-α method was used for time discretization [26] with a time step size of 5 × 10−4 s. In the discrete setting, a stabilized formulation was used [27,28], which allows for equal-order velocity and pressure interpolation and addresses the convective instability associated with Galerkin's method. A bipartitioned method, which includes a specialized preconditioner and an efficient parallel data structure algorithm, were used to solve the linear system of equations, achieving significant improvements in efficiency compared to standard methods [29–31]. Nonlinear iterations continued until the normalized residual was less than 5 × 10−4 or the number of iterations exceeded 8. Reducing the residual below 5 × 10−4 did not have any significant effect on the results.
Fig. 2.
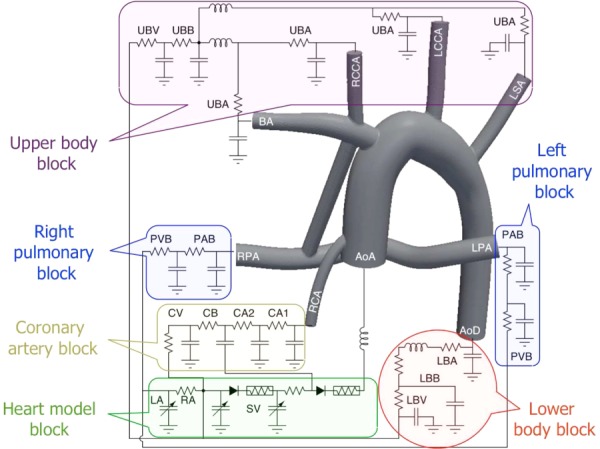
The LPN, which is coupled to the MBTS anatomy, contains blocks for the upper body arteries (UBA), upper body capillary bed (UBB), upper body veins (UBV), pulmonary artery bed (PAB), pulmonary vein bed (PVB), lower body arteries (LBA), lower body capillary bed (LBB), lower body veins (LBV), two coronary arteries (CA1 and CA2), coronary capillary bed (CB), coronary veins (CV), left atrium (LA), right atrium (RA), and single ventricle (SV). The ascending aorta (AA), descending aorta (AoD), brachiocephalic artery (BA), right common carotid artery (RCCA), left common carotid artery (LCCA), left subclavian artery (LSA), left PA (LPA), right PA (RPA), and right coronary artery (RCA) are shown in the 3D model. Note the left coronary artery, which is omitted here to make the schematic less crowded, is connected to an LPN block identical to that of the RCA.
The 3D model was meshed with tetrahedral elements using the commercial package MeshSim© (Simmetrix, Clifton Park, NY). To study mesh convergence, a single MBTS model was considered. Four interior mesh sizes of 1.0, 0.8, 0.625, and 0.5 mm were selected, producing meshes with approximately 130 k, 210 k, 400 k, and 700 k tetrahedral elements, respectively. The coronary artery wall mesh size was 40% of the interior mesh size, compared to 80% for the rest of the walls, for all mesh densities. After simulating five cardiac cycles, differences in the cardiac output between the first three meshes and the most refined mesh were 2.91%, 0.793%, and 0.524%, respectively. Hence, an interior mesh size of 0.625 mm was chosen, which produced an average of 400 k elements for all models.
The adopted LPN was very similar to the MBTS model described in the previous work [13,14,16] (Fig. 2), in which separate blocks model the upper body, lower body, pulmonary bed, coronary circulations, and the heart, each of which is partitioned into arterial, capillary, and venous bed sections. The component values were obtained from a former study that compiled clinical catheterization and angiographic data from 28 Norwood patients [11]. The MBTS flow rate can be affected by the flow to the right common carotid artery (RCCA) as well as the upper thoracic arteries. Hence, in a slight difference from the previous model, the right common carotid and right coronary arteries were included in the 3D model and the left common carotid and left subclavian arteries were independently connected to the LPN. Connecting a capacitor directly to the ascending aorta (AA) can cause nonphysiological regurgitant flow at the AA inlet. Therefore, our model directly connected the AA to a diode, and the eliminated capacitor was distributed over the rest of the domain to obtain a physiological pressure oscillation between systole and diastole (see the Appendix for the LPN values).
A multiscale approach was used to couple the 3D and 0D domains, in which ordinary differential equations governing the LPN were integrated using flow rates (Neumann boundaries) and pressure (Dirichlet boundaries) from the 3D domain as inputs [19]. The 3D and 0D domain velocity/flow rate and traction/pressure were coupled through the boundaries. The AA inlet was a coupled Dirichlet boundary, and all other outlets were coupled Neumann boundaries. The set of ordinary differential equations governing the LPN was time-advanced with a fourth order Runge–Kutta method with 1000 time steps for each nonlinear iteration of the 3D domain solver. In this formulation, after integrating the ordinary differential equations and correcting their solutions at the next time step, the pressures and flow rate are passed back to the Neumann and Dirichlet boundaries of the 3D domain, respectively. To obtain an implicit method, which is more stable numerically, the contribution of the 0D domain is incorporated in forming the 3D domain stiffness matrix, using a finite difference method following our recent work [19]. The total excessive blood volume was preserved temporally to improve cyclic convergence and accuracy, using
| (1) |
| (2) |
where P(t), C, and V(t) are pressures in the capacitors, capacitance values, and the total blood volume in the LPN, respectively. For the heart chambers, C HC was set to 1 and P HC was set to its volume. Note that the inner product of Eq. (1) with C produces the initial total blood volume, V(0).
Due to the presence of backflow in the simulation, special care was taken at coupled Neumann boundaries to avoid rapid simulation divergence by using a minimally intrusive backflow stabilization method, in which an advective stabilization term was added to the weak form following our recent work [32,33].
2.2. Residence Time Calculation.
To obtain a measure of RT, an Eulerian approach was adopted, in which the exposure time inside the region of interest is calculated by solving an advection–diffusion equation [21]. Hence, the RT and flow calculations were performed concurrently by solving an extra scalar equation. The present approach was directly derived by reformulating the particle tracking Lagrangian approach in a Eulerian framework. Denoting the time that fluid been inside the region of interest by τ(x, t)
| (3) |
is solved with H(x) defined as
| (4) |
In Eqs. (3) and (4), Ωτ, u, and are the region of interest, fluid velocity, and mesh velocity (only nonzero for the FSI simulation [34]), respectively. Physically, τ can be interpreted as the time that a parcel of fluid resides in the specified region of interest. RT is then calculated by temporally and spatially averaging τ over Ωτ × ((n − 1)T, nT] using
| (5) |
in which T and n are the cardiac cycle period and the number of simulated cycles, respectively. For more details on the RT calculation and its derivation and physical interpretation, see Ref. [21].
2.3. Wall Shear Stress Calculations.
WSS is calculated directly from velocity, using
| (6) |
| (7) |
where μ, , and are fluid viscosity, stress tensor, outward normal vector to wall, and tangential traction vector exerted on the wall at each element. The following function maps the traction to the nodes:
| (8) |
where is found such that for any test function the following holds:
| (9) |
Equation (9) is a least squares problem which produces a linear system of equations with a mass matrix on the left hand side. Calculating traction directly from velocity, as described above, requires less mesh refinement to produce mesh-independent results compared to using the traction obtained from the residual vector of the discretized Navier–Stokes equations, as described in Ref. [35].
Time averaged WSS(x) is defined from the traction obtained from Eq. (8) using
| (10) |
2.4. Wall Shear Stress Gradient Calculations.
The unit vectors tangential, s 1, and orthogonal, s 2, to the time averaged WSS vector defined at each element, are
| (11) |
The approach for finding the WSSG is similar to that of WSS. However, for bilinear shape functions, the second derivative of velocity is zero inside the elements. Therefore, the traction components obtained from Eq. (7) are decomposed into tangential and orthogonal directions, and then mapped to the nodes using
| (12) |
The time averaged WSSG(x) is then calculated as
| (13) |
2.5. Oscillatory Shear Index Calculations.
OSI(x) is directly calculated from the nodal traction [36,37] as
| (14) |
2.6. Oxygen Delivery Calculations.
Let be the total oxygen consumption, and C p, C ao, and C v be the oxygen concentration in the pulmonary vein, aorta, and systemic vein, respectively, and Q s, Q p, and Q cor be the systemic, pulmonary, and coronary flow rates, respectively. By definition the OD and coronary OD (COD) are
| (15) |
and
| (16) |
From the conservation of oxygen [13,38]
| (17) |
From Eqs. (15)–(17)
| (18) |
| (19) |
Assuming a saturation of 98% for pulmonary veins together with typical clinical data obtained from catheterization exams [11], C p and were set to and , respectively.
2.7. Fluid–Structure Interaction.
To evaluate the effect of wall distensibility on the results reported in Sec. 3, flow in a model with a 3.5 mm single proximal MBTS was simulated using both rigid-wall and FSI formulations. For the FSI simulation, the wall was modeled as a nonlinear St. Venant–Kirchhoff elastic solid, allowing for large deformation [39]. To prevent oscillation of the structure and include the effect of surrounding tissues, a damping term was added to the formulation [40]. Different material properties were used for the MBTS and the rest of the vasculature. The MBTS was modeled as a Gore-Tex conduit with density of 3.3 g/cm3, Young's modulus of 4 × 109 g/(s2 cm), and Poisson's ratio of 0.49 [41]. In all other vessels, density, Young's modulus, and Poisson's ratio were 1.06 g/cm3, 5 × 107 g/(s2 cm), and 0.49, respectively [41,42]. The closed-loop LPN described in Sec. 2.1 was used to prescribe inlet and outlet boundary conditions for the FSI simulation, with identical parameter values. Since blood can accumulate in the 3D geometry due to vessel expansion, the total excessive blood volume was corrected at the beginning of each cardiac cycle, using Eq. (2).
Variable wall thickness was calculated following the method proposed in Refs. [41] and [43]. Using this method, the wall thickness at the inlet and outlets was assumed to be 10% of the vessel diameter. To obtain the interior thickness, a Laplace equation was solved with the inlet and outlet thicknesses imposed as Dirichlet boundary conditions. The solution of the Laplace equation, a scalar field, was used to prescribe the local thickness (Fig. 3). Using the thickness at each nodal point and the normal vector to the wall, triangular surface elements were extruded to generate wedge elements. In this manner, the fluid and structure meshes match at the interface and the solid domain is three-dimensional, with stress and strain varying within the vessel wall. To prevent overlapping wall elements at the corners, thickness was reduced by an order of magnitude and stiffness and density were adjusted accordingly. Note that the model used in this section was modified to accommodate for the wall thickness and is slightly different from the 3.5 mm proximal MBTS model that is used in Secs. 3 and 4.
Fig. 3.
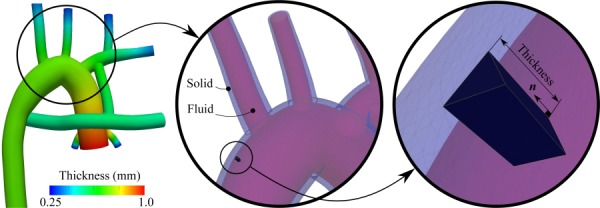
Wall thickness is calculated by solving the Laplace equation (left figure). Then, the wall of the fluid domain mesh is extruded in the normal direction to generate the solid domain mesh, i.e., vasculature wall (middle and right figures).
An arbitrary Lagrangian–Eulerian method was used to formulate the FSI problem [44], employing a quasi-direct FSI solution strategy [45], in which the fluid and structure solutions are computed in a monolithic fashion. Elastic mesh moving was employed with the aid of Jacobian-based stiffening [46,47]. The computations were performed without remeshing for ten cycles.
Figure 4 shows the geometry at peak systole. The MBTS was not deformed due to its stiffer material properties; however, other vessels were deformed to a greater or lesser degree depending on their proximity to the aortic root.
Fig. 4.
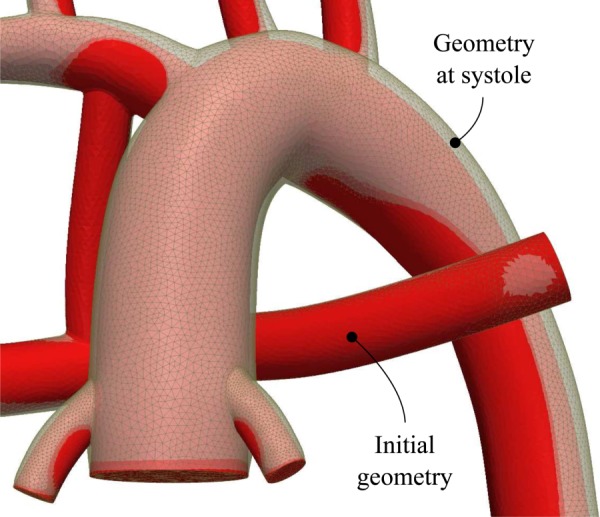
Deformation of the vessel walls at the peak systole
The rigid-wall and FSI simulation results are compared in Table 1, with a maximum difference of 3% in pulmonary-to-systemic flow ratio. All differences can be directly linked to the higher cardiac output in the FSI case, producing higher saturations, OD, and pressures. However, due to the PA expansion, RT is increased and WSS is decreased in the FSI case. Because all differences were extremely small, it was determined that rigid-wall simulations were sufficient for the present application and would not affect the final conclusions of the study.
Table 1.
Comparison between the rigid-wall and FSI simulation results, using the model with single MBTS 3
| Parameter | Unit | Rigid | FSI | Difference (%) |
|---|---|---|---|---|
| Cardiac output | L/min | 2.634 | 2.702 | 2.6 |
| pulmonary-to-systemic flow ratio | — | 0.947 | 0.974 | 2.9 |
| Aortic saturation | — | 79.8 | 80.6 | 1.0 |
| OD | 4.046 | 4.158 | 2.8 | |
| Coronary OD | 0.304 | 0.308 | 1.3 | |
| Aortic pressure | mm Hg | 98.60 | 99.07 | 0.5 |
| Pulmonary pressure | mm Hg | 12.66 | 13.00 | 2.7 |
| RT in the PA | ms | 26.5 | 26.7 | 0.8 |
| WSS in the PA | g/(s2 cm) | 81.65 | 81.44 | −0.2 |
3. Results
The single MBTS resulted in the highest systemic and COD, as shown in Table 2. Adding an extra shunt caused pulmonary hyperperfusion and systemic hypoperfusion, leading to higher saturations, but lower OD (Fig. 5). In the worst case, with a distal MBTS and normal PVR, adding a 5.0 mm PDA reduced OD by 10%. As was the case with the proximal MBTS, higher PVR increased the systemic flow rate. Increasing the systemic flow rate generally improved OD, though in an exception, COD was reduced when the MBTS position was moved from distal to proximal. The proximal position leads to blood “steal” from the aorta hindering coronary perfusion during diastole. As a result, the change in the coronary perfusion is dominated by the change in saturation, leading to lower COD [13]. Inclusion of a CS resulted in similar global hemodynamics compared to the case with an equivalent PDA diameter. Hence, the systemic to pulmonary resistance is not affected significantly by the anastomosis location of the second shunt, as long as the diameter of the second shunt is kept fixed.
Table 2.
Comparison between the anatomies. “Case” defines the distal (D) or proximal (P) MBTS (Fig. 1), high (R) or normal (N) PVR, and central shunt (C) (e.g., “DN” means a distal MBTS with normal PVR and CPR denotes the central shunt simulation with high PVR and proximal MBTS. D BT and D are the MBTS and PDA/CS diameters. HL is the heart load. , and CO are coronary, systemic, pulmonary, and AA (cardiac output) average flow rates, respectively. Sats and Satao are the oxygen saturations in the systemic veins (weighted average of superior and inferior vena cava) and aorta, respectively. OD and COD are the systemic and coronary OD, respectively.
| D BT | D | HL | Q cor | Q s | Q p | CO | Q p/Q s | Sats | Satao | OD | COD | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | mm | J/cycle | L/min | — | % | % | ||||||
| DN | 3.5 | 0.0 | 0.891 | 0.1030 | 1.362 | 1.323 | 2.684 | 0.971 | 63.21 | 80.35 | 4.098 | 0.310 |
| DR | 3.5 | 0.0 | 0.876 | 0.1043 | 1.386 | 1.254 | 2.640 | 0.905 | 62.54 | 79.38 | 4.121 | 0.310 |
| PN | 3.5 | 0.0 | 0.863 | 0.1036 | 1.399 | 1.269 | 2.667 | 0.907 | 62.91 | 79.60 | 4.170 | 0.309 |
| PR | 3.5 | 0.0 | 0.850 | 0.1049 | 1.420 | 1.205 | 2.625 | 0.849 | 62.19 | 78.63 | 4.181 | 0.309 |
| DN | 3.5 | 2.0 | 0.942 | 0.0970 | 1.283 | 1.633 | 2.916 | 1.272 | 65.51 | 83.70 | 4.022 | 0.304 |
| DR | 3.5 | 2.0 | 0.920 | 0.0992 | 1.317 | 1.524 | 2.842 | 1.157 | 64.97 | 82.69 | 4.079 | 0.307 |
| PN | 3.5 | 2.0 | 0.917 | 0.0985 | 1.324 | 1.574 | 2.898 | 1.188 | 65.54 | 83.17 | 4.124 | 0.307 |
| PR | 3.5 | 2.0 | 0.896 | 0.1001 | 1.351 | 1.476 | 2.827 | 1.092 | 64.90 | 82.18 | 4.159 | 0.308 |
| DN | 3.5 | 3.5 | 1.060 | 0.0876 | 1.148 | 2.356 | 3.504 | 2.052 | 67.76 | 88.09 | 3.788 | 0.289 |
| DR | 3.5 | 3.5 | 1.013 | 0.0907 | 1.205 | 2.129 | 3.333 | 1.767 | 67.65 | 87.03 | 3.926 | 0.296 |
| PN | 3.5 | 3.5 | 1.044 | 0.0882 | 1.179 | 2.346 | 3.526 | 1.989 | 68.26 | 88.05 | 3.889 | 0.291 |
| PR | 3.5 | 3.5 | 1.000 | 0.0921 | 1.238 | 2.113 | 3.351 | 1.706 | 68.10 | 86.95 | 4.032 | 0.300 |
| DN | 3.5 | 4.0 | 1.097 | 0.0857 | 1.123 | 2.585 | 3.708 | 2.303 | 68.17 | 88.97 | 3.740 | 0.286 |
| DR | 3.5 | 4.0 | 1.036 | 0.0890 | 1.178 | 2.302 | 3.480 | 1.955 | 68.04 | 87.86 | 3.875 | 0.293 |
| PN | 3.5 | 4.0 | 1.082 | 0.0865 | 1.151 | 2.572 | 3.723 | 2.234 | 68.65 | 88.92 | 3.833 | 0.288 |
| PR | 3.5 | 4.0 | 1.030 | 0.0906 | 1.226 | 2.274 | 3.500 | 1.854 | 68.70 | 87.73 | 4.029 | 0.298 |
| DN | 3.5 | 5.0 | 1.159 | 0.0826 | 1.087 | 2.987 | 4.074 | 2.747 | 68.72 | 90.18 | 3.673 | 0.279 |
| DR | 3.5 | 5.0 | 1.083 | 0.0871 | 1.170 | 2.592 | 3.761 | 2.216 | 69.03 | 88.99 | 3.898 | 0.290 |
| PN | 3.5 | 5.0 | 1.158 | 0.0837 | 1.134 | 2.994 | 4.128 | 2.639 | 69.62 | 90.20 | 3.831 | 0.283 |
| PR | 3.5 | 5.0 | 1.074 | 0.0877 | 1.186 | 2.597 | 3.783 | 2.190 | 69.33 | 89.01 | 3.953 | 0.292 |
| CPR | 3.5 | 2.0 | 0.897 | 0.0995 | 1.347 | 1.486 | 2.833 | 1.103 | 64.96 | 82.29 | 4.150 | 0.307 |
| CPR | 3.5 | 3.0 | 0.960 | 0.0940 | 1.277 | 1.851 | 3.128 | 1.450 | 67.11 | 85.39 | 4.083 | 0.301 |
| CPR | 3.5 | 4.0 | 1.027 | 0.0900 | 1.237 | 2.261 | 3.498 | 1.827 | 68.80 | 87.67 | 4.062 | 0.295 |
Fig. 5.
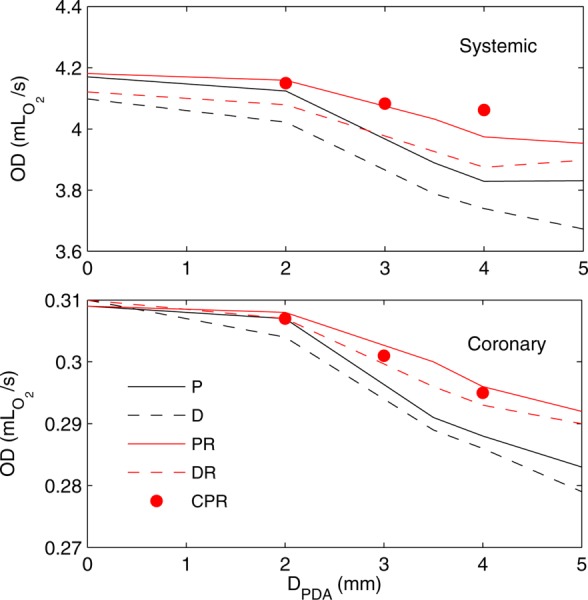
Systemic (top plot) and coronary oxygen deliveries (bottom plot) for proximal (solid) and distal (dashed) MBTS and normal PVR (black) and high PVR (red) versus PDA/CS diameter. Note the single MBTS corresponds to D PDA = 0. The results of three simulations with CS are shown with red circles, in which D PDA denotes CS diameter. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The velocity vectors inside the PA are shown for different configurations in Fig. 6 for normal (top) and high (bottom) values of PVR. The flow distribution was nearly symmetric in the models with a single MBTS. However, the right PA flow rate increased with increasing PDA diameter. Elevated flow stagnation was found in the region between the PDA and MBTS for the 2 mm PDA cases, while the flow was directed toward the right PA for the 4 mm PDA cases.
Fig. 6.
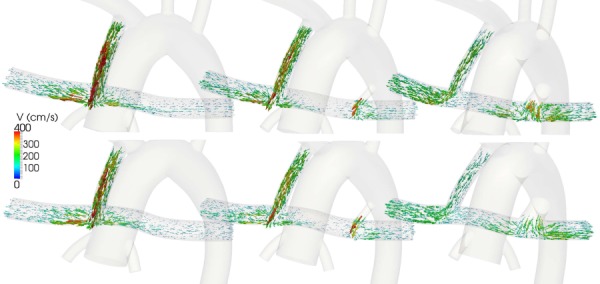
Time averaged velocity field in normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column), and a proximal MBTS and a 4 mm PDA (right column)
The cycle-averaged pressure contours and corresponding spatially averaged pressure in the PA segment and MBTS are shown in Fig. 7. Contrary to the PA, the average pressure in the aorta was not significantly affected by changes in PVR. Increasing the PDA/CS diameter increased the PA pressure, due to the higher flow rate to the pulmonary vascular bed, and reduced the AA pressure, due to the reduction in the total resistance. On the other hand, the pressure levels in the PA and AA were unaffected by the locations of the second pulmonary blood source (i.e., PDA versus CS).
Fig. 7.
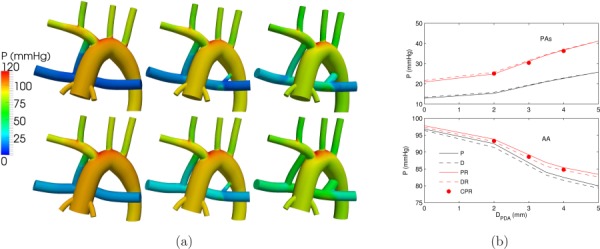
(a) Pressure contours for normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column) cases, and a proximal MBTS and a 4 mm PDA (right column). (b) Averaged pressure in the PA outlets (top plot) and in the AA (bottom plot). See Fig. 5 caption for more details.
The 3D simulations were postprocessed using Eqs. (10), (13), and (14), and the results are shown in Table 3. The tabulated pressures were averaged temporally and spatially over the PA and AA outlet and inlet surfaces. RT, WSS, OSI, and WSSG were spatially averaged either over a segment of PA wall (between the MBTS and PDA) or over the MBTS wall (see Fig. 1).
Table 3.
Comparison between the pulmonary and aortic pressures, RT, WSS, OSI, and WSSG of the studied anatomies. “PA-Seg” denoted the region between the PDA and MBTS and “BT” denotes the region in the MBTS (see red and blue regions in Fig. 1). See Table 2 caption for the other notations.
|
P (mm Hg) |
RT (ms) |
WSS (g/(s2 cm)) |
OSI (%) |
WSSG (g/(s2 cm2)) |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Case | D BT | D | PAs | AA | PA-Seg | BT | PA-Seg | BT | PA-Seg | BT | PA-Seg | BT |
| DN | 3.5 | 0.0 | 13.4 | 96.4 | 30.4 | 4.3 | 98.9 | 267 | 2.77 | 1.10 | 256 | 491 |
| DR | 3.5 | 0.0 | 21.7 | 97.3 | 32.4 | 4.5 | 91.9 | 252 | 2.17 | 0.99 | 235 | 460 |
| PN | 3.5 | 0.0 | 12.9 | 96.8 | 28.4 | 4.3 | 93.9 | 244 | 2.52 | 1.50 | 270 | 547 |
| PR | 3.5 | 0.0 | 20.9 | 97.8 | 28.3 | 4.6 | 91.5 | 232 | 2.75 | 1.56 | 268 | 525 |
| DN | 3.5 | 2.0 | 15.8 | 91.4 | 56.5 | 4.7 | 58.9 | 249 | 9.39 | 1.07 | 248 | 469 |
| DR | 3.5 | 2.0 | 25.7 | 93.1 | 57.5 | 5.0 | 58.4 | 232 | 8.09 | 1.06 | 241 | 439 |
| PN | 3.5 | 2.0 | 15.3 | 92.5 | 50.6 | 4.8 | 77.7 | 219 | 13.70 | 1.67 | 380 | 503 |
| PR | 3.5 | 2.0 | 24.9 | 93.8 | 51.5 | 5.1 | 73.8 | 206 | 11.66 | 1.70 | 339 | 477 |
| DN | 3.5 | 3.5 | 21.2 | 83.2 | 50.5 | 6.1 | 78.0 | 207 | 6.52 | 1.38 | 293 | 424 |
| DR | 3.5 | 3.5 | 34.5 | 85.8 | 58.0 | 7.0 | 67.3 | 181 | 6.92 | 1.58 | 266 | 377 |
| PN | 3.5 | 3.5 | 21.1 | 84.0 | 28.1 | 6.2 | 107.3 | 174 | 6.60 | 2.17 | 433 | 443 |
| PR | 3.5 | 3.5 | 34.2 | 86.9 | 35.8 | 7.0 | 90.7 | 154 | 10.39 | 2.31 | 385 | 397 |
| DN | 3.5 | 4.0 | 22.9 | 81.6 | 36.3 | 6.8 | 84.7 | 190 | 6.98 | 1.73 | 283 | 408 |
| DR | 3.5 | 4.0 | 37.0 | 84.6 | 44.0 | 7.8 | 74.2 | 167 | 7.64 | 1.82 | 255 | 358 |
| PN | 3.5 | 4.0 | 22.7 | 82.5 | 21.7 | 6.8 | 119.5 | 159 | 10.49 | 2.47 | 438 | 433 |
| PR | 3.5 | 4.0 | 36.7 | 85.4 | 27.0 | 7.7 | 101.4 | 140 | 9.65 | 2.54 | 378 | 381 |
| DN | 3.5 | 5.0 | 25.8 | 79.3 | 23.8 | 8.5 | 105.3 | 164 | 5.80 | 2.28 | 308 | 376 |
| DR | 3.5 | 5.0 | 41.2 | 82.6 | 28.5 | 9.9 | 90.7 | 139 | 6.59 | 2.41 | 266 | 328 |
| PN | 3.5 | 5.0 | 25.8 | 80.0 | 14.9 | 8.4 | 131.3 | 134 | 7.52 | 3.01 | 428 | 391 |
| PR | 3.5 | 5.0 | 41.2 | 83.4 | 17.5 | 9.9 | 114.0 | 113 | 8.56 | 3.09 | 366 | 329 |
| CPR | 3.5 | 2.0 | 25.1 | 93.3 | 47.9 | 5.0 | 79.0 | 211 | 5.91 | 1.76 | 256 | 493 |
| CPR | 3.5 | 3.0 | 30.4 | 88.6 | 73.7 | 5.6 | 49.4 | 190 | 15.78 | 1.90 | 242 | 460 |
| CPR | 3.5 | 4.0 | 36.3 | 84.8 | 58.6 | 6.4 | 51.5 | 167 | 11.56 | 2.16 | 224 | 422 |
The 3.0 mm CS and 3.5 mm PDA cases had the highest RT in the PA (Fig. 8). RT in the PA for the anatomy with a 3.0 mm CS was 160% higher compared to the anatomy with a single MBTS. For this particular case, WSS was 46% lower and OSI was 473% higher in the PA compared to the single MBTS, indicating disturbed and chaotic flow. This is in agreement with Fig. 6, which indicates the presence of a stagnation region between the MBTS and PDA at midrange diameters. Increasing the PDA diameter beyond 3.5 mm reduced the RT in the PA, because an imbalance between the PDA/CS and the MBTS flow led to increased flow through the PA segment. Since the PA flow rate was lower for the higher PVR cases, the RT was higher in the PA and MBTS.
Fig. 8.
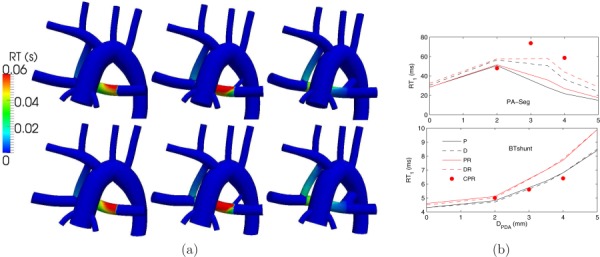
(a) RT contours for normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column), and a proximal MBTS and a 4 mm PDA (right column). (b) Spatially averaged RT in the PA segment (top plot) and in the MBTS (bottom plot). See Fig. 5 caption for more details.
Increasing the PDA/CS diameter decreased the flow rate in the MBTS and consequently WSS in the MBTS (Fig. 9). Placing the MBTS more proximally and/or increasing PVR also reduced both the MBTS flow rate and WSS. The WSS in the PA segment did not vary monotonically with the PDA/CS size. Depending on the momentum balance between the PDA/CS and MBTS, the flow was stagnant with low WSS (2 mm PDA case) or flow was unidirectional with high WSS (5 mm PDA case). In the PA segment, similar to the MBTS, lower WSS was observed at higher PVR due to the lower PA flow rate. Also, the proximal shunt generally produced higher WSS in the PA compared to the distal shunt.
Fig. 9.
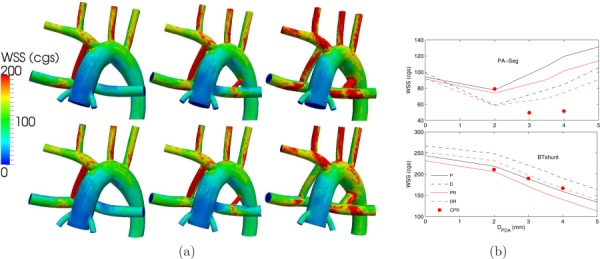
(a) WSS contours for normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column), and a proximal MBTS and a 4 mm PDA (right column). (b) Spatially averaged WSS in the PA segment (top plot) and in the MBTS (bottom plot). See Fig. 5 caption for more details.
Similar to the WSS results, higher PVR and/or larger PDA/CS led to lower WSSG due to the lower MBTS flow rate (Fig. 10). The flow in the PA decreased as a result of increasing PVR, leading to decreased WSSG. These results suggest that a distal MBTS produces a more uniform flow, hence lower WSSG in the PA segment and MBTS. Differences in WSSG in the PA segment at different PDA/CS sizes depend on the uniformity and magnitude of WSS in the PA segment.
Fig. 10.
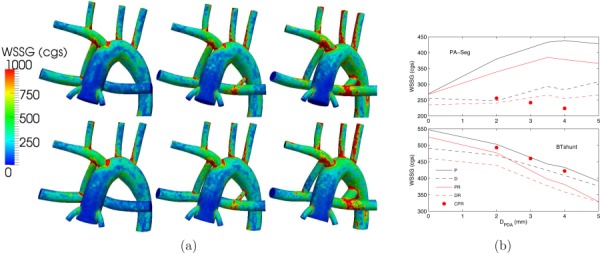
(a) WSSG contours for normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column), and a proximal MBTS and a 4 mm PDA (right column). (b) Spatially averaged WSSG in the PA segment (top plot) and in the MBTS (bottom plot). See Fig. 5 caption for more details.
Low OSI in the MBTS, with a maximum of 3.14%, compared to 15.8% in the PA segment indicates a unidirectional flow in the MBTS (Fig. 11). OSI in the PA segment correlated with the flow balance between the PDA/CS and MBTS and increased with a dominant PDA/CS or MBTS flow. Similar to WSS, more proximal shunt placement led to a higher OSI.
Fig. 11.
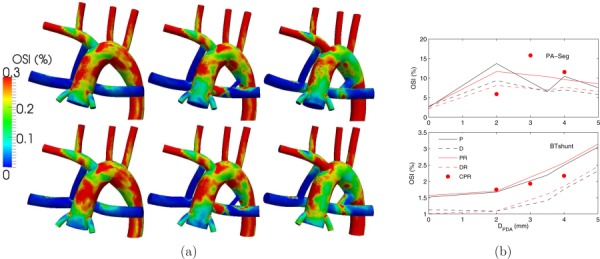
(a) OSI contours for normal PVR (top row) and high PVR (bottom row), and a single proximal MBTS (left column), a proximal MBTS and a 2 mm PDA (middle column), and a proximal MBTS and a 4 mm PDA (right column). (b) Spatially averaged OSI in the PA segment (top plot) and in the MBTS (bottom plot). See Fig. 5 caption for more details.
4. Discussion
A multiscale approach was used to simulate hemodynamics and physiology in models with single versus multiple systemic to pulmonary connections. The multiscale approach enabled predictions of global circulatory parameters, such as OD and cardiac workload, which are relevant to clinical decision-making and surgical planning. We simultaneously captured these global changes together with corresponding hemodynamic changes in the 3D domain, including WSS, WSSG, RT, and OSI. Because local hemodynamics are influenced by changes in the 0D domain, employing efficient 3D-0D coupling is essential to obtain a physiologically realistic model, allowing for more accurate predictions. To examine the effect of wall distensibility, a closed-loop FSI simulation was also performed using the same framework. Results confirmed that a rigid-wall assumption was sufficient for this study since the shunt, which primarily affects the hemodynamic outcome of the surgery, behave as a nearly rigid vessel. In summary, the results of this study suggest:
-
(1)
Pulmonary flow rate is higher with a distal MBTS compared to a proximal MBTS, which can be explained by the sharp turning of flow at the systemic anastomosis point in the proximal MBTS anatomy. This rapid change in flow direction reduces the momentum of flow perfused into the shunt, leading to reduced pulmonary flow. This reduction is consistently observed for the distal MBTS configuration with different PDA diameters in Table 2.
-
(2)
The distal MBTS configuration produces higher COD at low Q p/Q s compared to the proximal configuration, while in all other cases a proximal MBTS produces higher OD. In the presence of a PDA/CS, any increase in the pulmonary flow rate decreases OD because of pulmonary overcirculation. In general, OD to the systemic and coronary arteries is reduced by reducing PVR, increasing PDA/CS size and moving the shunt to a distal position.
-
(3)
Results are generally independent of PVR when varying PDA size or shunt positioning. Comparing the simulation results of the normal and high PVR cases, pulmonary flow rates decrease while systemic and coronary flow rates increase. At low pulmonary flow rates, changes in PVR produce insignificant changes in systemic and COD because a large portion of overall pulmonary resistance is created by the shunts, and OD is less sensitive to Q p/Q s. However, for higher PDA sizes, increasing PVR has a more pronounced effect on pulmonary flow rate, leading to higher OD.
-
(4)
The 3.5 mm PDA and 3.0 mm CS in combination with 3.5 mm MBTS are associated with the highest RT. The balance of flow momentum between the MBTS and PDA/CS generates a region between the PDA/CS and MBTS with low velocity, low WSS, high OSI, and high RT. However, as PDA/CS diameter is increased, flow in the PA becomes dominated by flow from the PDA/CS, hence flow stagnation is not observed; RT and OSI are reduced and WSS is increased. In general, the CS produces higher RT in the PA compare to a similar-sized PDA, due to increased stagnant flow in the PA caused by the anastomosis angle between the CS and PA that is opposite to that of the PDA and PA.
Effect of WSS and WSSG on local morphologic changes has been studied in Refs. [48–50]. The use of multiple shunts led to a competitive flow situation inside the PA, producing a region with high RT, especially with lower PDA diameters. WSS was lower in models with large PDAs; nevertheless, the WSS values in the shunts are sufficient for triggering platelet activation when compared with reported values of WSS for platelet activation (ranging from 120 to 300 g/(s2 cm) [51–53]). A combination of a flow stagnation region in the PA with higher WSSG and OSI, accompanied by sufficiently high WSS in the shunts is likely conductive of platelet activation and thrombus formation.
This study identified two concerning findings related to the use of multiple shunts that warrant further clinical study. First, local hemodynamic parameters, which are used here as a surrogate for assessment of thrombotic risk, suggest increased thrombotic risk in anatomies with small PDA/CS diameter. Second, insufficient systemic and COD was observed in anatomies with larger PDA/CS diameter. Together, these findings indicate that the use of multiple shunts is detrimental because it may increase thrombotic risk, while at the same time offering no benefit in terms of OD. Since OD directly relates to pulmonary flow rate, a single shunt with a larger diameter was shown to be a preferable means to provide the same pulmonary flow rate, avoiding issues of flow competition that arise with multiple shunts. The single shunt arrangement was shown in this study to have fewer adverse effects of local hemodynamic parameters, and thus likely reduced thrombotic risk, compared to the multiple shunt arrangement. In addition, the perceived benefit of introducing redundancy by using multiple shunts is compromised for two reasons. First, the individual thrombotic risks in each shunt are highly correlated, because thrombus formation relies on the production and transport of key chemical factors (e.g., thrombin) that accumulate in the blood, thereby increasing the thrombotic risk in the entire circulation and in neighboring shunts. Second, a multiple shunt configuration that is optimized for OD will become suboptimal when one of the shunts is blocked. This cannot be avoided by an initial configuration with multiple larger diameter shunts, as this leads to pulmonary hyperperfusion. For these reasons, our simulation results indicate that the use of multiple shunts has potential to worsen a patient's physiological condition, while increasing their risk of thrombosis. These findings should be corroborated by clinical studies comparing differences in patient outcomes with multiple versus single shunt configurations.
We recognize several limitations of the present study. First, this study examined a limited number of parameters, while in actual clinical scenarios there is significant interpatient variability and likely a wider range of parameters that could affect hemodynamic conditions. Second, this study examined parameter changes independently, while in actual clinical scenarios hemodynamic parameters are often tightly linked together. For example, hematocrit level, which is a function of OD, affects blood viscosity. Hence, in practice, OD, which itself depends on the cardiac output, can also effect cardiac output in a feedback loop. Third, this study used an idealized geometric model. While we do not expect changes in overall trends, it is possible that use of a patient specific model could affect local hemodynamic quantities. Despite these limitations, the simulation framework presented here enabled systematic comparison of different surgical strategies and testing of our hypothesis without confounding variables that would typically appear in a clinical study. To design more comprehensive future studies, a broader range of patients should be considered, and results should be correlated with patient outcome statistics.
Acknowledgment
Funding for this work was provided by a Leducq Foundation Network of Excellent grant, a Kaplan Fellowship, and a Burroughs Wellcome Fund Career Award at the Scientific Interface. The authors wish to thank Giancarlo Pennati, Francesco Migliavacca, and Irene Vignon-Clementel for sharing their expertise in the LPN modeling, and Ethan Kung, Sethuraman Sankaran, and Matthew Bockman for their useful comments.
Glossary
Nomenclature
- AA =
ascending aorta
- CS =
central shunt
- FSI =
fluid–structure interaction
- LPN =
lumped parameter network
- MBTS =
modified Blalock–Taussig shunt
- OD =
oxygen delivery
- OSI =
oscillatory shear index
- PA =
pulmonary artery
- PDA =
patent ductus arteriosus
- PVR =
pulmonary vascular resistance
- RT =
residence time
- WSS =
wall shear stress
- WSSG =
wall shear stress gradient
Appendix: LPN Values
The adopted LPN is very similar to the MBTS model described in Refs. [13] and [16]. The values of the LPN elements are shown in Table 4. Outside the heart model, all the resistances, capacitors, and inductances have linear behavior. To model turbulence associated with the heart valves, two resistances are included in the LPN, and the pressure drop through them is proportional to the square of their flow rates. Heart chamber pressures are considered to be composed of active and passive parts. The atrial pressure is modeled using
Table 4.
Figure 2 parameters values. and are nonlinear resistances modeling the tricuspid and aortic valves, respectively. R asd is the atrial septal defect resistance (resistance between left and right atria).
| Parameter | Value | Unit |
|---|---|---|
| R UBA | 28.0899 | mm Hg s/ml |
| C UBA | 0.04430 | ml/mm Hg |
| L UBA | 0.02138 | mm Hg s2/ml |
| R UBB | 0.64510 | mm Hg s/ml |
| C UBB | 0.15515 | ml/mm Hg |
| R UBV | 0.16529 | mm Hg s/ml |
| C UBV | 2.03945 | ml/mm Hg |
| R PAB | 0.83376 | mm Hg s/ml |
| C PAB | 0.02039 | ml/mm Hg |
| R PVB | 0.02194 | mm Hg s/ml |
| C PVB | 0.44375 | ml/mm Hg |
| R LBA | 7.02239 | mm Hg s/ml |
| C LBA | 0.07758 | ml/mm Hg |
| L LBA | 0.01069 | mm Hg s2/ml |
| R LBB | 0.64510 | mm Hg s/ml |
| C LBB | 0.07758 | ml/mm Hg |
| R LBV | 0.16529 | mm Hg s/ml |
| C LBV | 2.03945 | ml/mm Hg |
| R CA1 | 10.6739 | mm Hg s/ml |
| C CA1 | 1.9435 × 10−3 | ml/mm Hg |
| R CA2 | 10.6739 | mm Hg s/ml |
| C CA2 | 5.1827 × 10−3 | ml/mm Hg |
| R CB | 21.3477 | mm Hg s/ml |
| C CB | 7.7741 × 10−3 | ml/mm Hg |
| R CV | 10.6739 | mm Hg s/ml |
| C CV | 0.05 × 10−3 | ml/mm Hg |
| 18.5 | mm Hg/ml | |
| −0.042 | mm Hg/ml2 | |
| 4.0 | ml | |
| 0.9 | mm Hg | |
| K v | 0.062 | 1/ml |
| E a | 7.35 | mm Hg/ml |
| 1.0 | ml | |
| 0.17 | mm Hg | |
| K a | 0.484 | 1/ml |
| 4 × 10−5 | mm Hg s2/ml2 | |
| 4 × 10−4 | mm Hg s2/ml2 | |
| R sv | 0.09 | mm Hg s/ml |
| R asd | 0.001 | mm Hg s/ml |
| L ao | 0.01155 | mm Hg s2/ml |
| (A1) |
A a is modeled with a sinusoidal function which is nonzero during atrium contraction and E a, , K a, and are the constants of this model. The same model is used for the ventricle, except the active pressure, i.e., the first term in Eq. (A1), is replaced with a parabolic function
| (A2) |
All the constants of the heart model along with the rest of LPN are shown in Table 4.
Contributor Information
Mahdi Esmaily-Moghadam, Mechanical and Aerospace, Engineering Department, University of California, San Diego, CA 92093.
Bari Murtuza, Cardiac Unit, Great Ormond Street Hospital for Children and Institute of Child Health, London WC1N 3JH, UK.
Tain-Yen Hsia, Cardiac Unit, Great Ormond Street Hospital for Children and Institute of Child Health, London WC1N 3JH, UK.
Alison Marsden, Mechanical and Aerospace, Engineering Department, University of California, San Diego, CA 92093.
References
- [1]. Blalock, A. , and Taussig, H. B. , 1945, “The Surgical Treatment of Malformations of the Heart,” J. Am. Med. Assoc., 128(3), pp. 189–202. 10.1001/jama.1945.02860200029009 [DOI] [Google Scholar]
- [2]. Tamisier, D. , Vouhe, P. , Vernant, F. , Leca, F. , Massot, C. , and Neveux, J. , 1990, “Modified Blalock–Taussig Shunts: Results in Infants Less Than 3 Months of Age,” Ann. Thorac. Surg., 49(5), pp. 797–801. 10.1016/0003-4975(90)90026-3 [DOI] [PubMed] [Google Scholar]
- [3]. Glenn, W. W. , 1958, “Circulatory Bypass of the Right Side of the Heart: Shunt Between Superior Vena Cava and Distal Right Pulmonary Artery-Report of Clinical Application,” N. Engl. J. Med., 259(3), pp. 117–120. 10.1056/NEJM195807172590304 [DOI] [PubMed] [Google Scholar]
- [4]. Fontan, F. , and Baudet, E. , 1971, “Surgical Repair of Tricuspid Atresia,” Thorax, 26(3), pp. 240–248. 10.1136/thx.26.3.240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5]. Norwood, W. , Jacobs, M. , and Murphy, J. , 1992, “Fontan Procedure for Hypoplastic Left Heart Syndrome,” Ann. Thorac. Surg., 54(6), pp. 1025–1030. 10.1016/0003-4975(92)90065-C [DOI] [PubMed] [Google Scholar]
- [6]. Shachar, G. B. , Fuhrman, B. P. , Wang, Y. , Lucas, R. , and Lock, J. E. , 1982, “Rest and Exercise Hemodynamics After the Fontan Procedure,” Circulation, 65(6), pp. 1043–1048. 10.1161/01.CIR.65.6.1043 [DOI] [PubMed] [Google Scholar]
- [7]. Gaynor, J. W. , Mahle, W. T. , Cohen, M. I. , Ittenbach, R. F. , DeCampli, W. M. , Steven, J. M. , Nicolson, S. C. , and Spray, T. L. , 2002, “Risk Factors for Mortality After the Norwood Procedure,” Eur. J. Cardiothorac. Surg., 22(1), pp. 82–89. 10.1016/S1010-7940(02)00198-7 [DOI] [PubMed] [Google Scholar]
- [8]. Bartram, U. , Grünenfelder, J. , and Praagh, R. V. , 1997, “Causes of Death After the Modified Norwood Procedure: A Study of 122 Postmortem Cases,” Ann. Thorac. Surg., 64(6), pp. 1795–1802. 10.1016/S0003-4975(97)01041-2 [DOI] [PubMed] [Google Scholar]
- [9]. Corno, A. , Mazzera, E. , Marino, B. , Parisi, F. , and Marcelletti, C. , 1986, “Simultaneous Patency of Ductus Arteriosus and Surgical Shunt in Pulmonary Atresia With Intact Ventricular Septum: A Cause of Acute Myocardial Failure?,” Scand. Cardiovasc. J., 20(2), pp. 123–127. 10.3109/14017438609106488 [DOI] [PubMed] [Google Scholar]
- [10]. Zahorec, M. , Hrubsova, Z. , Skrak, P. , Poruban, R. , Nosal, M. , and Kovacikova, L. , 2011, “A Comparison of Blalock–Taussig Shunts With and Without Closure of the Ductus Arteriosus in Neonates With Pulmonary Atresia,” Ann. Thorac. Surg., 92(2), pp. 653–658. 10.1016/j.athoracsur.2011.04.008 [DOI] [PubMed] [Google Scholar]
- [11]. Migliavacca, F. , Pennati, G. , Dubini, G. , Fumero, R. , Pietrabissa, R. , Urcelay, G. , Bove, E. , Hsia, T. , and de Leval, M. , 2001, “Modeling of the Norwood Circulation: Effects of Shunt Size, Vascular Resistances, and Heart Rate,” Am. J. Physiol.: Heart Circ. Physiol., 280(5), pp. H2076–H2086. [DOI] [PubMed] [Google Scholar]
- [12]. Pennati, G. , Migliavacca, F. , Dubini, G. , and Bove, E. , 2010, “Modeling of Systemic-to-Pulmonary Shunts in Newborns With a Univentricular Circulation: State of the Art and Future Directions,” Prog. Pediatr. Cardiol., 30(1–2), pp. 23–29. 10.1016/j.ppedcard.2010.09.004 [DOI] [Google Scholar]
- [13]. Esmaily-Moghadam, M. , Migliavacca, F. , Vignon-Clementel, I. , Hsia, T. , and Marsden, A. , 2012, “Optimization of Shunt Placement for the Norwood Surgery Using Multi-Domain Modeling,” ASME J. Biomech. Eng., 134(5), p. 051002. 10.1115/1.4006814 [DOI] [PubMed] [Google Scholar]
- [14]. Esmaily-Moghadam, M. , Hsia, T.-Y. , and Marsden, A. , 2014, “The Assisted Bidirectional Glenn: A Novel Surgical Approach for First Stage Single Ventricle Heart Palliation,” J. Thorac. Cardiovasc. Surg. (in press). 10.1016/j.jtcvs.2014.10.035 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15]. Bove, E. , Migliavacca, F. , de Leval, M. , Balossino, R. , Pennati, G. , Lloyd, T. , Khambadkone, S. , Hsia, T. , and Dubini, G. , 2008, “Use of Mathematic Modeling to Compare and Predict Hemodynamic Effects of the Modified Blalock–Taussig and Right Ventricle-Pulmonary Artery Shunts for Hypoplastic Left Heart Syndrome,” J. Thorac. Cardiovasc. Surg., 136(2), pp. 312–320.e2. 10.1016/j.jtcvs.2007.04.078 [DOI] [PubMed] [Google Scholar]
- [16]. Laganà, K. , Balossino, R. , Migliavacca, F. , Pennati, G. , Bove, E. , de Leval, M. , and Dubini, G. , 2005, “Multiscale Modeling of the Cardiovascular System: Application to the Study of Pulmonary and Coronary Perfusions in the Univentricular Circulation,” J. Biomech., 38(5), pp. 1129–1141. 10.1016/j.jbiomech.2004.05.027 [DOI] [PubMed] [Google Scholar]
- [17]. Pennati, G. , Migliavacca, F. , Gervaso, F. , and Dubini, G. , 2004, “Assessment by Computational and In Vitro Studies of the Blood Flow Rate Through Modified Blalock–Taussig Shunts,” Cardiol. Young, 14(Suppl. 3), pp. 24–29. 10.1017/S1047951104006511 [DOI] [PubMed] [Google Scholar]
- [18]. Pennati, G. , Fiore, G. B. , Migliavacca, F. , Laganà, K. , Fumero, R. , and Dubini, G. , 2001, “In Vitro Steady-Flow Analysis of Systemic-to-Pulmonary Shunt Haemodynamics,” J. Biomech., 34(1), pp. 23–30. 10.1016/S0021-9290(00)00167-6 [DOI] [PubMed] [Google Scholar]
- [19]. Esmaily-Moghadam, M. , Vignon-Clementel, I. , Figliola, R. , and Marsden, A. , 2013, “A Modular Numerical Method for Implicit 0D/3D Coupling in Cardiovascular Finite Element Simulations,” J. Comput. Phys., 224, pp. 63–79. 10.1016/j.jcp.2012.07.035 [DOI] [Google Scholar]
- [20]. Bluestein, D. , Niu, L. , Schoephoerster, R. , and Dewanjee, M. , 1997, “Fluid Mechanics of Arterial Stenosis: Relationship to the Development of Mural Thrombus,” Ann. Biomed. Eng., 25(2), pp. 344–356. 10.1007/BF02648048 [DOI] [PubMed] [Google Scholar]
- [21]. Esmaily-Moghadam, M. , Hsia, T.-Y. , and Marsden, A. , 2013, “A Non-Discrete Method for Computation of Residence Time in Fluid Mechanics Simulations,” Phys. Fluids, 25(11), p. 110802. 10.1063/1.4819142 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. Kunov, M. , Steinman, D. , and Ethier, C. , 1996, “Particle Volumetric Residence Time Calculations in Arterial Geometries,” ASME J. Biomech. Eng., 118(2), pp. 158–164. 10.1115/1.2795954 [DOI] [PubMed] [Google Scholar]
- [23]. Suh, G. , Les, A. , Tenforde, A. , Shadden, S. , Spilker, R. , Yeung, J. , Cheng, C. , Herfkens, R. , Dalman, R. , and Taylor, C. , 2011, “Quantification of Particle Residence Time in Abdominal Aortic Aneurysms Using Magnetic Resonance Imaging and Computational Fluid Dynamics,” Ann. Biomed. Eng., 39(2), pp. 864–883. 10.1007/s10439-010-0202-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24]. Schmidt, J. , Delp, S. , Sherman, M. , Taylor, C. , Pande, V. , and Altman, R. , 2008, “The Simbios National Center: Systems Biology in Motion,” Proc. IEEE Inst. Electr. Electron Eng., 96(8), pp. 1266–1280. 10.1109/JPROC.2008.925454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. Valant, A. Z. , Žiberna, L. , Papaharilaou, Y. , Anayiotos, A. , and Georgiou, G. , 2011, “The Influence of Temperature on Rheological Properties of Blood Mixtures With Different Volume Expanders-Implications in Numerical Arterial Hemodynamics Simulations,” Rheol. Acta, 50(4), pp. 389–402. 10.1007/s00397-010-0518-x [DOI] [Google Scholar]
- [26]. Jansen, K. , Whiting, C. , and Hulbert, G. , 2000, “A Generalized-[Alpha] Method for Integrating the Filtered Navier–Stokes Equations With a Stabilized Finite Element Method,” Comput. Methods Appl. Mech. Eng., 190(3–4), pp. 305–319. 10.1016/S0045-7825(00)00203-6 [DOI] [Google Scholar]
- [27]. Franca, L. , and Frey, S. , 1992, “Stabilized Finite Element Methods: II. The Incompressible Navier–Stokes Equations,” Comput. Methods Appl. Mech. Eng., 99(2–3), pp. 209–233. 10.1016/0045-7825(92)90041-H [DOI] [Google Scholar]
- [28]. Brooks, A. , and Hughes, T. , 1982, “Streamline Upwind/Petrov–Galerkin Formulations for Convection Dominated Flows With Particular Emphasis on the Incompressible Navier–Stokes Equations,” Comput. Methods Appl. Mech. Eng., 32(1–3), pp. 199–259. 10.1016/0045-7825(82)90071-8 [DOI] [Google Scholar]
- [29]. Esmaily-Moghadam, M. , Bazilevs, Y. , and Marsden, A. , 2014, “A Bi-Partitioned Iterative Algorithm for Solving Linear Systems Arising From Incompressible Flow Problems,” Comput. Methods Appl. Mech. Eng. (in press). 10.1016/j.cma.2014.11.033 [DOI] [Google Scholar]
- [30]. Esmaily-Moghadam, M. , Bazilevs, Y. , and Marsden, A. L. , 2013, “A New Preconditioning Technique for Implicitly Coupled Multidomain Simulations With Applications to Hemodynamics,” Comput. Mech., 52(5), pp. 1141–1152. 10.1007/s00466-013-0868-1 [DOI] [Google Scholar]
- [31]. Esmaily-Moghadam, M. , Bazilevs, Y. , and Marsden, A. , 2014, “Impact of Data Distribution on the Parallel Performance of Iterative Linear Solvers With Emphasis on CFD of Incompressible Flows,” Comput. Mech. (published online). 10.1007/s00466-014-1084-3 [DOI] [Google Scholar]
- [32]. Esmaily-Moghadam, M. , Bazilevs, Y. , Hsia, T. , Vignon-Clementel, I. , and Marsden, A. , 2011, “A Comparison of Outlet Boundary Treatments for Prevention of Backflow Divergence With Relevance to Blood Flow Simulations,” Comput. Mech., 48(3), pp. 277–291. 10.1007/s00466-011-0599-0 [DOI] [Google Scholar]
- [33]. Bazilevs, Y. , Gohean, J. , Hughes, T. , Moser, R. , and Zhang, Y. , 2009, “Patient-Specific Isogeometric Fluid-Structure Interaction Analysis of Thoracic Aortic Blood Flow due to Implantation of the Jarvik 2000 Left Ventricular Assist Device,” Comput. Methods Appl. Mech. Eng., 198(45–46), pp. 3534–3550. 10.1016/j.cma.2009.04.015 [DOI] [Google Scholar]
- [34]. Long, C. , Esmaily-Moghadam, M. , Marsden, A. , and Bazilevs, Y. , 2014, “Computation of Residence Time in the Simulation of Pulsatile Ventricular Assist Devices,” Comput. Mech., 54(4), pp. 911–919. 10.1007/s00466-013-0931-y [DOI] [Google Scholar]
- [35]. Figueroa, C. , 2006, “A Coupled-Momentum Method to Model Blood Flow and Vessel Deformation in Human Arteries: Applications in Disease Research and Simulation-Based Medical Planning,” Ph.D. thesis, Stanford University. [Google Scholar]
- [36]. He, X. , and Ku, D. , 1996, “Pulsatile Flow in the Human Left Coronary Artery Bifurcation: Average Conditions,” ASME J. Biomech. Eng., 118(1), pp. 74–82. 10.1115/1.2795948 [DOI] [PubMed] [Google Scholar]
- [37]. Taylor, C. , Hughes, T. , and Zarins, C. , 1999, “Effect of Exercise on Hemodynamic Conditions in the Abdominal Aorta,” J. Vasc. Surg., 29(6), pp. 1077–1089. 10.1016/S0741-5214(99)70249-1 [DOI] [PubMed] [Google Scholar]
- [38]. Barnea, O. , Santamore, W. , Rossi, A. , Salloum, E. , Chien, S. , and Austin, E. , 1998, “Estimation of Oxygen Delivery in Newborns With a Univentricular Circulation,” Circulation, 98(14), pp. 1407–1413. 10.1161/01.CIR.98.14.1407 [DOI] [PubMed] [Google Scholar]
- [39]. Holzapfel, G. A. , 2000, Nonlinear Solid Mechanics: A Continuum Approach for Engineering, John Wiley & Sons, Ltd., West Sussex, UK. [Google Scholar]
- [40]. Tezduyar, T. E. , Sathe, S. , Schwaab, M. , and Conklin, B. S. , 2008, “Arterial Fluid Mechanics Modeling With the Stabilized Space–Time Fluid–Structure Interaction Technique,” Int. J. Numer. Methods Fluids, 57(5), pp. 601–629. 10.1002/fld.1633 [DOI] [Google Scholar]
- [41]. Long, C. , Hsu, M. , Bazilevs, Y. , and Feinstein, J. , 2012, “A. Marsden, Fluid-Structure Interaction Simulations of the Fontan Procedure Using Variable Wall Properties,” Int. J. Numer. Methods Biomed. Eng., 28(5), pp. 513–527. 10.1002/cnm.1485 [DOI] [PubMed] [Google Scholar]
- [42]. Coogan, J. S. , Humphrey, J. D. , and Figueroa, C. A. , 2013, “Computational Simulations of Hemodynamic Changes Within Thoracic, Coronary, and Cerebral Arteries Following Early Wall Remodeling in Response to Distal Aortic Coarctation,” Biomech. Model. Mechanobiol., 12(1), pp. 79–93. 10.1007/s10237-012-0383-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43]. Bazilevs, Y. , Hsu, M. , Benson, D. , Sankaran, S. , and Marsden, A. , 2009, “Computational Fluid-Structure Interaction: Methods and Application to a Total Cavopulmonary Connection,” Comput. Mech., 45(1), pp. 77–89. 10.1007/s00466-009-0419-y [DOI] [Google Scholar]
- [44]. Bazilevs, Y. , Calo, V. , Hughes, T. , and Zhang, Y. , 2008, “Isogeometric Fluid-Structure Interaction: Theory, Algorithms, and Computations,” Comput. Mech., 43(1), pp. 3–37. 10.1007/s00466-008-0315-x [DOI] [Google Scholar]
- [45]. Tezduyar, T. E. , Sathe, S. , Keedy, R. , and Stein, K. , 2006, “Space-Time Finite Element Techniques for Computation of Fluid-Structure Interactions,” Comput. Methods Appl. Mech. Eng., 195(17), pp. 2002–2027. 10.1016/j.cma.2004.09.014 [DOI] [Google Scholar]
- [46]. Tezduyar, T. , Aliabadi, S. , Behr, M. , Johnson, A. , and Mittal, S. , 1993, “Parallel Finite-Element Computation of 3D Flows,” Computer, 26(10), pp. 27–36. 10.1109/2.237441 [DOI] [Google Scholar]
- [47]. Stein, K. , Tezduyar, T. , and Benney, R. , 2003, “Mesh Moving Techniques for Fluid-Structure Interactions With Large Displacements,” ASME J. Appl. Mech., 70(1), pp. 58–63. 10.1115/1.1530635 [DOI] [Google Scholar]
- [48]. Rouleau, L. , Farcas, M. , Tardif, J. , Mongrain, R. , and Leask, R. , 2010, “Endothelial Cell Morphologic Response to Asymmetric Stenosis Hemodynamics: Effects of Spatial Wall Shear Stress Gradients,” ASME J. Biomech. Eng., 132(8), p. 081013. 10.1115/1.4001891 [DOI] [PubMed] [Google Scholar]
- [49]. Xu, Z. , Chen, N. , Kamocka, M. , Rosen, E. , and Alber, M. , 2008, “A Multiscale Model of Thrombus Development,” J. R. Soc., Interface, 5(24), pp. 705–722. 10.1098/rsif.2007.1202 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. Meng, H. , Wang, Z. , Hoi, Y. , Gao, L. , Metaxa, E. , Swartz, D. , and Kolega, J. , 2007, “Complex Hemodynamics at the Apex of an Arterial Bifurcation Induces Vascular Remodeling Resembling Cerebral Aneurysm Initiation,” Stroke, 38(6), pp. 1924–1931. 10.1161/STROKEAHA.106.481234 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51]. Turitto, V. , and Hall, C. , 1998, “Mechanical Factors Affecting Hemostasis and Thrombosis,” Thromb. Res., 92 (6, Supplement 2), pp. S25–S31. 10.1016/S0049-3848(98)00157-1 [DOI] [PubMed] [Google Scholar]
- [52]. Holme, P. , Orvim, U. , Hamers, M. , Solum, N. , Brosstad, F. , Barstad, R. , and Sakariassen, K. , 1997, “Shear-Induced Platelet Activation and Platelet Microparticle Formation at Blood Flow Conditions as in Arteries With a Severe Stenosis,” Arterioscler., Thromb., Vasc. Biol., 17(4), pp. 646–653. 10.1161/01.ATV.17.4.646 [DOI] [PubMed] [Google Scholar]
- [53]. Yin, W. , Shanmugavelayudam, S. , and Rubenstein, D. , 2011, “The Effect of Physiologically Relevant Dynamic Shear Stress on Platelet and Endothelial Cell Activation,” Thromb. Res., 127(3), pp. 235–241. 10.1016/j.thromres.2010.11.021 [DOI] [PubMed] [Google Scholar]


