Principles of structure building in music, language and animal song

Abstract

Human language, music and a variety of animal vocalizations constitute ways of sonic communication that exhibit remarkable structural complexity. While the complexities of language and possible parallels in animal communication have been discussed intensively, reflections on the complexity of music and animal song, and their comparisons, are underrepresented. In some ways, music and animal songs are more comparable to each other than to language as propositional semantics cannot be used as indicator of communicative success or wellformedness, and notions of grammaticality are less easily defined. This review brings together accounts of the principles of structure building in music and animal song. It relates them to corresponding models in formal language theory, the extended Chomsky hierarchy (CH), and their probabilistic counterparts. We further discuss common misunderstandings and shortcomings concerning the CH and suggest ways to move beyond. We discuss language, music and animal song in the context of their function and motivation and further integrate problems and issues that are less commonly addressed in the context of language, including continuous event spaces, features of sound and timbre, representation of temporality and interactions of multiple parallel feature streams. We discuss these aspects in the light of recent theoretical, cognitive, neuroscientific and modelling research in the domains of music, language and animal song.

1. Introduction

Human language, music and the complex vocal sequences of animal songs constitute ways of sonic communication that have evolved a remarkable degree of structural complexity. Recent discussions have focused on comparing the structure of human language to that of learned animal songs, focusing not only particularly on songbirds, but also on whales and bats [1–4]. Such comparisons addressed aspects of phonology [5,6] and syntax [7–10], aiming to distinguish features that may characterize species-specific principles of structure building and reveal whether there might also be universal principles underlying the sequential organization of complex communication sounds. One debate concerns the role of ‘recursion’ as a core mechanism of the language faculty in the narrow sense [11] that is unique both to humans and to language.

In this review, we argue that although language and recursion are important topics for comparative studies, comparisons between human music and learned songs in animals deserve more attention than they are currently receiving (see also [12–14]). Structurally and functionally, music, language and animal songs not only share certain aspects but also have important differences. A three-way comparison between language, music and animal songs therefore has the potential to benefit research in all three domains, by highlighting shared and unique mechanisms as well as hidden assumptions in current research paradigms.

We present an approach to performing such comparisons focusing on the structural organization of music, language and animal songs as well as the underlying function, motivation and context. We focus on models of structure and structure building in these domains and discuss their relations to empirical findings. Our starting point is the influential work of Shannon and Chomsky from the 1940s and 1950s. We discuss issues concerning building blocks, Shannon's n-gram models and the Chomsky hierarchy (CH) as well as their more recent extensions. Subsequently, we discuss limitations of both frameworks in relation to empirical observations from the biological and cognitive sciences and suggest ways for future research to move beyond these frameworks.

2. Building blocks and sequential structure

Before discussing models of structure building and sequence generation, we must first consider what the building blocks are from which sequences, be it in language, music and animal vocalizations, are built. One of the classic universal ‘design features' of natural languages is ‘duality of patterning’ [15], which refers to the fact that all languages show evidence of at least two combinatorial systems: one where meaningless units of sounds are combined into words and morphemes, and one where those meaningful words and morphemes are further combined into words, phrases, sentences and discourse. While many of the details are debated, the assumption that words are building blocks of sentences is uncontroversial [16]. Like language, music and animal songs combine units of sound into larger units in a hierarchical way, but the comparability of the building blocks and the nature of the hierarchies of language, music and animal songs is not at all straightforward. In particular, there is no clear analogue of a ‘word’ in music or animal songs [17,18].

From a comparative perspective, some principles of structure building may trace back to evolutionary ancient cognitive principles, whereas some structures are coined by cultural effects (such as the impact of a formal teaching tradition or notation systems on musical or linguistic structure). One recent cross-cultural review proposes a list of statistical universals of musical structure; specifically, these include the use of discrete pitches, octave equivalence, transposability, scales that commonly have seven or fewer pitches in unequal steps, the use of melody, pitch combination rules and motivic patterns as well as the use of timing, duration and beat [19] (see also [20]). The pitch continuum is discretized (based on culturally established musical scales), and so is the timing continuum by a process of beat induction (which establishes a kind of grid overlaying a musical sequence [21]). There is further some work on cross-cultural principles of melodic structure that originated from Narmour's work [22,23]. Although much more cross-cultural research is necessary [24], in the remainder of this review, we take as established that there is evidence for a number of structure building operations at work in music, which we would like to account for with formal models. These include repetition and variation [25], element-to-element implication (e.g. note–note, chord–chord) [22,26], hierarchical organization and tree structure as well as nested dependencies and insertions [27,28].

One common thread in this work is that at any point in a musical sequence listeners are computing expectations about how the sequence will continue, both regarding timing details and regarding classes of pitches or other building blocks [26,29]. Composers can play with these expectations: meet expectations, violate them or even put them on hold. Traditionally, much of the discussion of structure in music has focused on Western classical music and has built on building blocks of melody, voice-leading [30–32], outer voices [33], harmony [34–36], combinations of harmony and voice-leading [33,37,38], or complex feature combinations derived from monophonic melody [39,40] and harmony [41,42]. Although observations about Western music are clearly relevant to understanding human musical abilities, some of the complexity we find in Western music might for instance be influenced by (culture-specific) factors such as notation systems and aesthetic principles that may not necessarily generalize with respect to cognitive processes and cross-cultural principles.

In the domain of animal vocalization, there is plenty of evidence of non-trivial structure building, but the choice of building blocks for analysis is far from clear. We focus the discussion in this review primarily on learned songs of animals, which provide the most interesting comparison with language and music, as structurally particularly complex and largely learned traits (and we therefore do not say much about animal calls, which depend less or not on learning, and are perhaps more usefully compared with other, innate, human utterances such as cries, sighs and laughter). Animal songs occur primarily in a territorial or courtship setting (fighting and flirting) and are produced in the majority of bird species by both sexes [43].

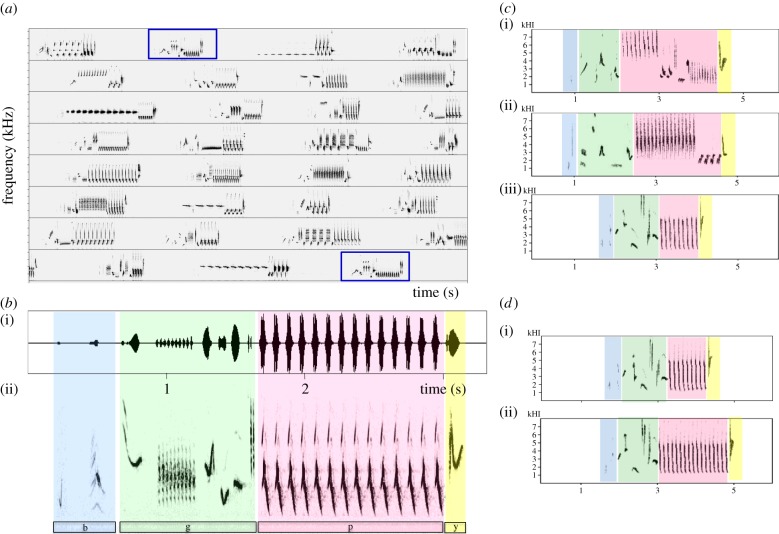
Songs usually consist of longer strings of temporally ordered, recurring, acoustically distinct elements. In contrast, calls occur in different contexts (e.g. contact, begging, alarm) and tend to be temporally and spectrally more variable [44]. Animal songs contain hierarchically structured elements (often called ‘notes') that can be combined into ‘syllables' or ‘note complexes' which in turn can constitute ‘motifs' or ‘song types'. Note that in contrast to language, repetition with little or no variation of smaller or larger units of building blocks, somewhat similar to music [25], are a typical feature of song in many bird species (figure 1).

Figure 1.

Hierarchical organization of nightingale song. Panel (a) depicts a spectrogram of ca 2 minutes of continuous nocturnal singing of a male nightingale. Shown are 30 sequentially delivered unique songs. The 31st song is the same song type as the second one (both framed). The average repertoire of a male contains about 150 unique song types, which can be delivered in variable but non-random order for hours continuously. Panel (b) illustrates the structural components of one song type. Individual sound elements are sung at different loudness (amplitude envelope in (i)) and are acoustically distinct in the frequency range, modulation, emphasis and temporal characteristics (spectrogram in (ii)). Panel (c) illustrates the structural similarities in three different song types (i,ii,iii). Song types begin usually with one or more very softly sung elements (blue, b), followed by a sequence of distinct individual elements of variable loudness (green, g). All song types contain one or more sequences of loud note repetitions (pink, p) and are usually ended by a single, acoustically distinct element (yellow, y). Panel (d) illustrates that the same song type (i,ii) can vary in the number of element repetitions in the repeated section (pink). Spectrograms courtesy of Henrike Hultsch. (Online version in colour.)

Animal songs are the product of natural and sexual selection and continue to be constrained by these forces. Finding similar structure building principles in different bird species would argue for common neurocognitive foundations for birdsong that might have parallels with those underlying human musicality [45]. In addition, research on female preference in different bird species has already revealed which elements of courtship song are particularly relevant and attractive, and those features consequently change little during the course of evolution, whereas other song features are more free to drift. Conversely, there is clear evidence from many songbird species for female preference of larger rather than smaller repertoire sizes, leading potentially to more combinatorial possibilities in sequencing and thus driving the evolution of syntactic complexity.¹

Some arguments concerning building blocks have been made based on neuroscience and motor control evidence rather than by analysis of sequences. Patel and co-workers have argued that motor constraints are similar in human and bird song and focused on the note, for example a bioacoustic gesture surrounded by silent gaps needed to inhale as the basic unit of comparison [46]. This, however, differs between bird species. Others have argued that the basic units in birdsong are smaller gestures coded by different neural ensembles and not necessarily separated by silent gaps [47]. Further larger units of sound sequences (often referred to as ‘chunks' or ‘song types' or ‘motifs') are used as building blocks for recombination. This is suggested by non-random association of particular sequences in various bird species, to which we return below.

In summary, the issues and challenges concerning the choice of building blocks are fundamental for the forms of sequential model and model representation we discuss below. However, the present state of the art offers no final word that may settle the differences between proposals for building blocks and the relations between different choices. It remains a matter of future research to explore the extent to which different types of music and animal vocalizations may require different choices of building blocks and to perform an empirical comparison of different approaches: although it seems natural to want to settle on the question of what the building blocks are before investigating how these building blocks are combined into sequences, it might be necessary to study both issues at the same time.

3. Shannon's n-grams

Shannon [48] introduced, in the slipstream of his major work on information theory, n-grams as a simple model of sequential structure in language. n-Grams define the probability of generating the next symbol in a sequence in terms of the previous (n − 1) symbols generated. When n = 2, n-grams become ‘bigrams', which simply model transitional probabilities: the probability of generating the next word only depends on what the current word is. In this respect, n-gram models are equivalent to (n − 1)th-order Markov models over the same alphabet. Shannon demonstrated with word counts from corpora that the higher n is, the better one can predict the next word (given a corpus that is sufficiently large). This insight still forms a crucial component in many engineering applications in speech recognition and machine translation [49].

n-Gram models (often simple bigrams) have also been frequently applied to bird song [50–54] and music [55,56] (see below for further details). For many bird species, bigrams in fact seem to give a very adequate description of the sequential structure. Chatfield & Lemon [51] studied the song of the cardinal, and reported that a 3-gram (trigram) model modelled song data only marginally better than a bigram model (measured by the likelihood of the data under each of these models). More recent work with birds raised with artificially constructed songs indicates that transitional probabilities between adjacent elements are the most important factor in the organization of the songs also in zebra finches and Bengalese finches [57], although there are also many examples of bird song requiring richer models as we discuss below [8,58–60].

In music research, numerous variants of n-gram models have been used predominantly in the context of modelling predictive processing [29]. The perception of tonality and key has been argued to be governed by pitch distributions that in fact correspond with unigram models [61,62]. Narmour [22] proposed a number of principles that govern melodic structure across cultures, which later work showed can be simplified considerably and put in the form of a handcrafted bigram model over melodic intervals [63–66]. In the domain of harmony, Piston's [67] table of common root progressions and Rameau's [68] theory (of the basse fondamentale) may be argued to have the structure of a first-order Markov model (a bigram model) of the root notes of chords [69,70].

All of these theoretical approaches constitute variants of Markov/n-gram models that could be encompassed by overarching generalized Markov models that learn their parameters from a corpus [29,71,72]. In fact, Markov modelling of music has been carried out early (as early as we had computers in scientific use; cf. [55,56]). In particular, general n-th order Markov models have been proposed for melody and harmony [39–42,73–75] and employed for segmentation and boundary entropy detection [76]. In practical, ecological contexts, it is a common finding that n-gram models with large values of the context length n result in suboptimal models owing to sparsity issues or overfitting. In analogy with the findings in bird song research, several music modelling studies find trigrams optimal with respect to modelling melodic structure [77] or harmonic structure [42].

The musical surface, however, is more complex than ordinary language, or potentially animal song, because of the interaction with metrical structure, which means that surface symbols, such as notes or chords, do not all have the same salience when forming a sequence. This is demonstrated by a study of harmonic structure using a corpus of seventeenth century dance music [73]: an n-gram model taking into account three-beat metrical structure (and representing each beat by one symbol) seems to favour 4-grams. This is probably because the first beat of a bar is more musically salient than the other two, in harmonic terms, and a 4-gram is able to directly capture at least some of this importance, in this representation, where a 3-gram necessarily cannot.

4. The classical Chomsky hierarchy

Shannon's n-grams are simple and useful descriptions of some aspects of local sequential structure in animal communication, music and language and have also been discussed as simple cognitive models. But what are their limitations? In theoretical linguistics, n-grams, no matter how large their n, were famously dismissed as useful models of syntactic structure in language in the foundational work of Noam Chomsky from the mid-1950s [78]. In his work, Chomsky first argued against incorporating probabilities into language models; in his view, the core issues for linguists concern the symbolic, syntactic structure of language. Chomsky proposed an idealization of language where a natural language such as English or Hebrew is conceived of as a (potentially infinite) set of sentences, and a sentence is simply a sequence of words (or morphemes).

The CH concerns different classes of formal languages that generate such sets of sequences. In the classical formulation, it distinguishes four classes: regular languages, context-free languages, context-sensitive languages and recursively enumerable languages. Each class contains an infinite number of sets, and there are subset relations between the classes: every regular language is also context-free, every context-free language is also context-sensitive and every context-sensitive language is recursively enumerable. (n-Grams, when probabilities are stripped off, correspond to a true subset of the regular languages—see below.)

For cognitive science, the relevance of the hierarchy comes from the fact that the four classes can be defined by the kinds of rules that generate structures as well as by the kind of computations needed to parse the sets of sequences in the class (the corresponding formal automaton). Informally, regular languages are the types of sets of sequences that can be characterized by a ‘flowchart’ description (finite-state automaton). Crucially, when generating or parsing the next word in a sentence of a regular language, we need only to know where we currently are on the flowchart, not how we got there.

In contrast, at all higher levels of the CH, some sort of memory is needed by the corresponding formal automaton that recognizes the language. The next level up in the classical CH are context-free languages, generated/recognized by context-free grammars (CFGs, equivalent to so-called ‘push-down automata’). CFGs consist of (context-free) rewrite rules that specify which symbols (representing a category of words or other building blocks, or categories of phrases) can be rewritten to which list of symbols. Chomsky observed that natural language syntax allows for nesting of clauses (centre-embedding), and argued that the finite-state automata are inadequate to account for such phenomena. In contrast, CFGs can express multiple forms of nesting as well as forms of counting elements in a sequence. An example of such nesting, and a CFG that can describe it, is given in table 1. Table 1 further shows a linguistic example that requires even higher complexity.

Table 1.

Example sentence, the corresponding context-free grammar and the derivation showing centre-embedding.

example sentence

context-free rules

‘either language came first or music came first’ this sentence can be derived from the start symbol S by subsequently applying rules 1a,1b,2a,3,4,5,1b,2b,3, 4,5. Note that rule 1a center-embeds a phrase of category S within a phrase of category S, which is beyond the power of finite-state automata ‘either language or music came first’ to derive this second sentence (with a so-called ellipsis), whilst maintaining the subject relation between 'language' and ‘came first’, linguists have proposed formalisms even richer than context-free grammars

(1a) S → either S or S (1b) S → NP VP (2a) NP → language (2b) NP → music (3) VP → V ADV (4) V → came (5) ADV → first

The success of the CH in linguistics and computer science and Chomsky's negative demonstration that natural language syntax is beyond the power of finite-state automata has influenced many researchers to examine the formal structures underlying animal song and music (though there is no comprehensive comparison of music-theoretical approaches in terms of the CH yet). The advantages of CFGs to express hierarchical structures, categories of events and, particularly, recursive insertion/embedding have lent themselves to a number of theoretical approaches that characterized Western tonal music [22,34–38,79–84]. Schenker's [85] seminal work constitutes the foundation of hierarchical approaches to music. However, owing to its largely informal nature, it is not clear whether its complexity is adequately expressed by a CFG or whether it requires a more complex mechanism [86] (see also the related discussion in [87]).

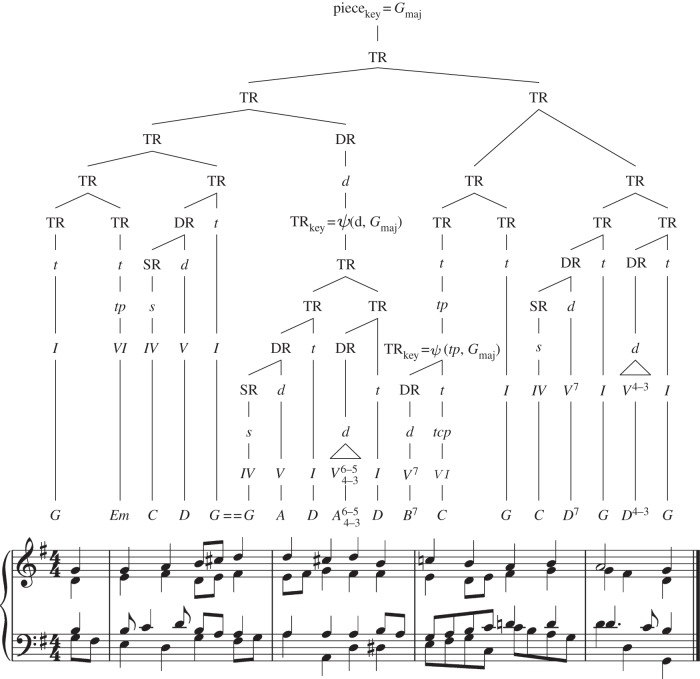
The approaches by Rohrmeier [35,36] suggest a formal argument that musical modulation (change of key and centre of tonal reference) constitutes an instance of recursive context-free embedding of a new diatonic space into an overarching one (somewhat analogous to a relative clause in language), a point considered in informal terms already by Hofstadter [88]. Figure 2 shows an example of a syntactic analysis of the harmonic structure of a Bach chorale that illustrates an instance of recursive centre-embedding in the context of modulation. Given the absence of communication through propositional semantics in music (see below), the occurrence of nested context-free structure might be explained by patterns of implication and prolongation and associated features of tension: given that an event may be prolonged (extended through another event; an idea originating from Schenker [85]), and events may be prepared/implied by other events, the possibility of multiple and recursive preparations, combined with the combinatorial play of recursion and the option to employ an event as new tonal centre, established context-free complexity as well as a straight link to a motivation through complex patterns of musical tension [89,90]. Another potential explanation for the occurrence of complex hierarchical, recursive structure in Western tonal music may be found in the notation system and the tradition of formal teaching and writing—a factor that may even be relevant for complexity differences in written and spoken languages in communities that may differ with respect to their formal education [91].

Figure 2.

Analysis of Bachs chorale ‘Ermuntre Dich, mein schwacher Geist’ according to the GSM proposed by Rohrmeier [36]. The analysis illustrates hierarchical organization of tonal harmony in terms of piece (piece), phrases (P), functional regions (TR, DR, SR), scale-degree (roman numerals) and surface representations (chord symbols). The analysis further exhibits an instance of recursive centre-embedding in the context of modulation in tonal harmony. The transitions involving 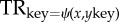denote a change of key such that a new tonic region (TR) is instantiated from an overarching tonal context of the tonal function x in the key ykey.

There are also analytical findings that suggest that principles of hierarchical organization may be found in classical North Indian music [27] that is based on a tradition of extensive oral teaching. However, more cross-cultural research on other cultures and structure in more informal and improvised music is required before more detailed conclusions may be drawn concerning structural complexity and cross-cultural comparisons.

There is currently little evidence that non-human structures or communicative abilities (either in production or in reception) exceed finite-state complexity. One structure that constitutes a core instance of context-free structures is AⁿBⁿ (in which there is the same number of As and Bs; or A_iA_jA_k … B_kB_jB_i in which the string features pairs (A_x, B_x) in a retrograde structure). Claims have been made—and been refuted—that songbirds are able to learn such instances of context-free-structures (see [92,93]; and respective responses [94–96]). Hence, further targeted research with respect to transfinite-stateness of animal song is required to shed light on this question.² By contrast, there is a number of studies arguing for implicit acquisition of context-free structure (and even (mildly) context-sensitive structure) in humans in abstract stimulus materials from language and music [97–103].

5. Limitations of the Chomsky hierarchy

Several extensions to the CH have been proposed. We introduce these by first considering one common problem in the literature, trying to decide empirically where to place language, music and animal songs on the CH. This problem is that a number of related but different issues are often conflated:

• (1) the inadequacy of (plain) n-gram models (but not necessarily of finite-state automata) for modelling music or animal songs;

• (2) the presence of long-distance dependencies (and the ability of animal or human subjects to detect them); and

• (3) the ability of subjects to process context-free languages.

Why issue (1) differs from (2) and (3) can be understood by considering the extended CH that introduces several different levels. Below the level of regular languages, ongoing research established the so-called subregular hierarchy that includes, among others, the class of strictly locally testable languages (SLTL) [104]. SLTLs constitute the non-probabilistic counterpart of n-gram models. SLTLs/n-grams do not assume underlying unobservable (hidden) structure and model the string language based on surface fragments alone. Regular languages and Markov models are therefore not equivalent, and showing the inadequacy of n-grams or SLTLs is hence not sufficient by itself to prove the need to move beyond finite-state or to the context-free level.

In reverse, the hierarchical nature of the extended CH (and methodological problems in dealing with real-world data that we outline below) creates potential issues for some arguments that the formalism producing a set of sequences is constituted by a lower class: the mere fact that a lower complexity model of structure could be built does not constitute a valid form of argument or proves that the system in question is best modelled by this type of complexity. Particularly, the fact that Markov models may be easily computed and used to describe some statistical features of corpora of music [26,105–107] does crucially not imply or even underpin an argument that a Markov model is the best model (in terms of strong generative power, compression or model comparison; see §§6,7). A Markov model may be computed from sequences generated from any deep structure and the corresponding models result in being oblivious to any other than local structure (e.g. forms of embedding or non-local dependencies).

With respect to animal songs and animal pattern recognition involving sequences of elementary units, it seems that n-gram models suffice for many species, but richer (but still finite-state) models are needed to characterize the songs of Bengalese finches [59,60], blackbirds [8,108] and other birds singing complex songs [109] (see [58] for a review). In particular, ten Cate et al. [8] argue that there are frequently observed phenomena in songs of songbird species such as blackbirds that require the power of hidden Markov models (probabilistic counterparts of regular grammars, see below); these phenomena include the optionality of elements and constraints on the number of repetitions in blackbird song.

Also in classes higher on the CH, more fine-grained distinctions have been introduced. In particular, a number of linguistic formalisms (e.g. tree-adjoining languages, combinatorial categorial grammar [110,111]) have been proposed that have been collectively referred to as mildly context-sensitive [112]. These grammars define classes of languages that are subsets of context-sensitive languages and supersets of the context-free languages. They share the expressive power to be able to express features such as cross-serial dependencies that human languages possess [113] and may be efficiently processable and learnable. We are not aware of any formally founded claims about mild context sensitivity in the domain of music or animal songs. Having introduced the extended CH, figure 3 provides a general overview of the locations of main results of structure building in language, music and animal song we discussed in the framework of the extended CH.

Figure 3.

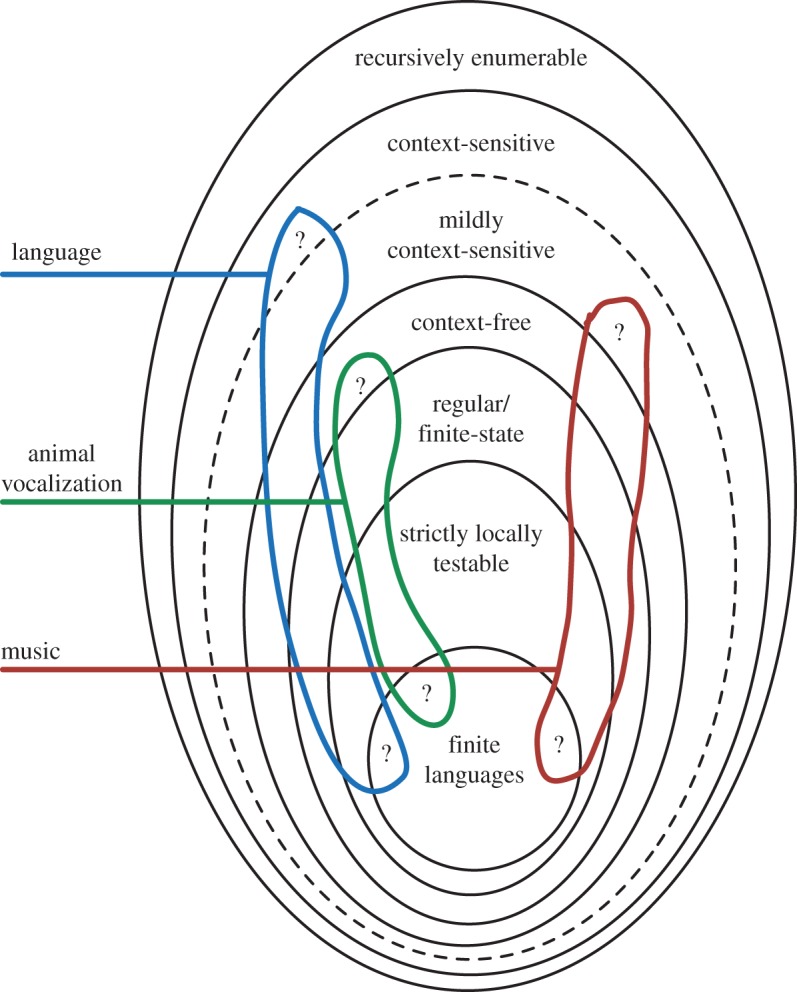
A Venn diagram of the Chomsky hierarchy of formal languages with three extensions annotated with a comparison of the hypothesized classifications of human languages, (human) music and animal vocalization. The areas marked with ‘question’ signs indicate that further research is required to settle examples for the respective class of complexity in these domains. (Online version in colour.)

However, even when considering its extensions and despite its frequent use in recent cognitive debates, the CH may not be suited for providing a good class of cognitive or structural models that capture frequent structures in language, music and animal songs. One aspect stems from the fact that the CH is by its definition fundamentally tied to rewrite rules and the structures that different types of rewrite rules constrained by different restrictions may express. One well-known issue—and an aspect that the notion of mild context-sensitivity addresses—concerns the fact that repetition, repetition under a modification (such as musical transposition) and cross-serial dependencies constitute types of structures that require quite complex rewrite rules (see also the example of context-sensitive rewrite rules expressing cross-serial dependencies in reference [114]). In contrast, such phenomena are frequent forms of form-building in music [25] and animal song. This mismatch between the simplicity of repetitive structures and the high CH class it is mapped onto might be one of many motivations to move beyond its confines.

6. Moving towards different types of models

The CH has been extensively used in recent cognitive debates on human and animal cognitive capacities, discussing the complexity of theories and processes in various domains and in characterizing different types of structures that may be learnable in artificial grammar learning and implicit learning literatures [115]. However, discussions in many of these approaches relating to the CH resulted in complex confusions concerning the distinctions between the (formal) class of a language, the formal automata producing/accepting formal languages and the complexity involved in techniques to learn such structures from examples. It is important to distinguish here that while the formal automata that accept (or generate) a class of formal language in the CH may be comparably easy, the inference procedures to learn such structures from examples (e.g. to infer CFGs) are highly complex and are likely to be underestimated in artificial grammar learning research.³

Importantly, the CH concerns a theoretical construct that organizes types of structures according to different forms of rewrite rules and has, being a theory of formal languages in conjunction with idealized formal automata, little immediate connection with cognitive motivations or constraints (such as limited memory). The fact that it defines a set of languages that happen to be organized in mutual superset relations and are well explored in terms of formal automata that produce them does not motivate its reification in terms of mental processes, cognitive constraints or neural correlates. Although the CH has been inspired research in terms of a framework that allowed for the comparison of different models and formal negative arguments against the plausibility of certain formal languages or corresponding computational mechanisms, it does not constitute an inescapable a priori point of reference for all kinds of models of structure building or processing. Such forms of formal comparison and proofs should inspire future modelling endeavours, yet better forms of structural or cognitive models may involve distinctions orthogonal to the CH and may rather be designed and evaluated in the light of modelling data and its inherent structure as well as possible.

What are some different aspects that new models of structure building and corresponding cognitive models should take into account? In order to model the complexity of ecological real-word structures, they should be able to deal with graded syntactic acceptability [116] and sequence probability, they should be grounded in considerations of descriptive parsimony, in links to semantics and form-meaning interactions, and they should not only account for production and perception, but also consider learnability and computational complexity (e.g. memory requirements, and accounting for limited memory in biological systems). Finally, formal models should be required to make predictions for empirical structures based on which they may be distinguished on an empirical basis.

One main topic in theoretical linguistics, orthogonal to the finer classifications within the CH, concerns the distinction between ‘weak generative capacity’ and ‘strong generative capacity’ that are relevant for debates in music and animal research. There are divergent definitions of these terms. Briefly, they concern the difference whether we can focus on just classes of sets of sequences (i.e. regarding models just by the surface sequences they model: ‘weak generative capacity’), or need to look at classes of structural analyses that different models can generate (i.e. regarding models in terms of the hidden underlying structure they assume to model sequences: ‘strong generative capacity’).

This is relevant, for instance, for distinguishing issue (2) long-distance dependencies, from (3) context-freeness, above. A long-distance dependency in itself is not enough to prove the inadequacy of finite-state models (as we stated above); context-freeness is necessary only when long-distance dependencies can be embedded within (unboundedly many) other long-distance dependencies. For instance, when a bird sings songs of the structure ABⁿC and DBⁿE, we observe a long-distance dependency between A and C and between D and E, but the songs can be easily modelled with finite-state automata (figure 4) by just assuming two different (hidden) states from which the Bs are generated: one for the condition starting with A and ending with C, and one for the other. This explains why some efforts to empirically demonstrate context-freeness of bird song or music may not be unconvincing from a formal language theory perspective if they are based on just demonstrating a long-distance dependency. However, a long-distance dependency does have consequences for the underlying model that can be assumed for its strong generative capacity, representational capacity and compressive power: in the example shown in figure 4, we were forced to duplicate the state responsible for generating B, in fact we require 2m states (where m is the number of non-local dependency pairs, such as A … C or D … E, that need to be encoded). Therefore, if there are multiple (finite), potentially nested non-local dependencies the number of required states grows exponentially (see also the comparable argument regarding the implicit acquisition of such structures in references [99,114]).

Figure 4.

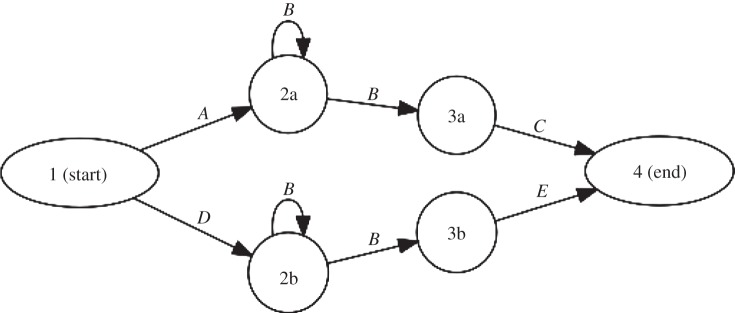
A finite-state automaton generating a repertoire consisting of two sequences: ABⁿC and DBⁿE (with n > 0). Note that the finite-state automaton is redundant in the way that it contains multiple instances of the same structure Bⁿ.

On similar grounds, one may argue that human musical capacities exceed not only Markovian, but probably also a finite-state representation (which is not a relevant or probable model here on the grounds just presented), based on empirical evidence that a recent study provided: human non-musicians were found to process non-local syntactic dependencies resulting from one level of centre-embedding in ecological music excerpts [117]. Comparable findings in animal vocalization are still missing.

This example illustrates that the CH as theoretical construct is irrelevant here in choosing the best model. If the intervening material in a long-distance dependency is very variable, even if not technically unbounded, considerations of parsimony, strong-generative capacity, elegant structure-driven compression and considerations of efficiency provide strong reasons to prefer a model other than the minimally required class in the CH or a different type of model altogether. Further, empirical testability and evaluation, for example in terms of Bayesian model comparison, come to play an important role in this context.

Another interesting situation where the distinction between weak and strong generative power matters arises when we combine a (finite-state/hidden Markov model (HMM, see below)) model of how elements are sequenced to create a song with a (finite-state/HMM) model of how songs are sequenced to create a song bout. As a simple example, consider a hypothetical bird that sings two different songs, A and B, each built up from some repertoire of elements, but showing a typical structure: song A might start with some slow introductory elements, and then continue with faster elements, whereas song B might start with fast, high-pitched elements, and continue with low-pitched ones. We can also imagine that the bird mainly uses song A in one context, and song B in another context. In such a case, the appropriate model might be a hierarchical hidden Markov model, which at the level of sequences-of-songs distinguishes different ‘states' for different contexts, and at the level of sequences-of-elements distinguishes different states for different sections (start, end) of the song. Such a model is still finite-state in terms of weak generative power—because ultimately it can be described as involving a finite number (two contexts × two sections = four states) of states, but it would be problematic to describe the model without using an account that represents the individual songs that are generated; accordingly, a model for describing song production in terms of strong generativity may potentially rather employ a formalism such as CFGs.

Other motivations to move beyond the confinements of the CH lie in the modelling of real-world structures that undermine some of the assumptions of the CH. Generally, the aspect that music involves not only multiple parallel streams of voices but also correlated streams of different features and complex timing constitutes a theme that received considerable research in the domain of music cognition, yet does not easily match with the principles that underlie the CH that is based on modelling a single sequence of words. In their cognitive model that is not only constrained to the case of music, Conklin & Witten [39] proposed successful extensions of n-gram models by combining n-gram models over different features and combined feature-spaces to optimize prediction based on the features that embody most information. They also combined predictions derived from the current piece (short-term model) with predictions derived from a corpus (long-term model). Extending this framework, the IDyOM model [40] includes a search for progressively more information-theoretically efficient representations, which are shown in turn to give rise to progressively better predictors of human expectations. The IDyOM model has been shown to be successful in the domains of music and language [56,118]. Recent modelling approaches generalized the notion of modelling parallel feature streams into dynamic Bayesian networks that combine the advantages of hidden Markov models with modelling feature streams [42,119–121].

7. Dealing with noisy data: adding probabilities

The original CH is based on a number of assumptions that turn problematic in the light of ecological data. One main problem that is particularly relevant in the domain of music or animal songs is that the notion of grammaticality or wellformedness, which is fundamental for establishing and testing symbolic rules, is much less clear than in language (where there also are problems—see [122] for an insightful discussion). Most discussions of grammatical structure in music and animal song are based on so-called positive data (i.e. examples conforming with the proposed rules) and it is significantly more difficult to establish the validity and extension of rules in the absence of negative data (i.e. where humans or animals explicitly reject a malformed sequence). It is not clear whether ungrammatical/irregular structures in music are clear-cut or distinguished in agreement by non-expert or expert subjects. This difference between the linguistic and the musical case may also in part be explained by the fact that (at least in Western music), there is large divergence between active and passive musical interaction. Furthermore, negative data are, particularly in the case of animal research, more difficult to obtain and also less clear-cut or potentially graded rather than binary.

This issue motivates a number of changes in the nature of models. Models may be grounded in foundations other than grammaticality, such as optimal prediction or compression (e.g. predictive power [56], minimum description length [123], Bayesian model comparison), strong generativity or by motivation to express form of a higher-order structure (such as semantics or musical tension; see the following section). Another important way to build better models of cognition and deal with the issues above comes from employing syntactic gradience and reintroducing the probabilities that Chomsky abandoned along with his rejection of finite-state models. Apart from a large number of recent probabilistic models (such as the ones mentioned in the previous section) that go beyond the framework of the CH, it turns out that a hierarchy of probabilistic grammars can be defined that is analogous to the classical (and extended) CH and exhibits the same expressive power, with the additional advantage that grammars from this hierarchy can straightforwardly deal with noisy data and frequency effects and lend themselves to information theoretic methodologies such as model comparison, compression or minimum description length [124,125]. n-Gram models constitute the probabilistic counterpart of SLTLs, whereas the probabilistic counterpart of finite-state automata are hidden Markov models; CFGs can be straightforwardly extended to probabilistic CFGs.

Hidden Markov models constitute one type of model that has been very successful in all domains of language, music and animal songs. Comprehensively reviewed by Rabiner [126], the HMM assumes a number of underlying (hidden) states each of which emits surface symbols from given probabilistic emission vectors, a Markov matrix defining transition probabilities between states (including remaining in the same state) and a probability vector modelling the start state. HMMs have been very successful in modelling language, music and animal songs [42,49,59,127,128].

Thanks to the probabilities, we can talk about degrees of fit, and thus select models in a Bayesian model comparison paradigm that have the highest posterior probability given the degree of fit and prior beliefs; also, the probabilistic grammar framework does not require wellformedness as a criterion, but rather can use the likelihood of observing particular sentences, songs or musical structure as a criterion [8].

8. Dealing with meaning: adding semantics

The CH of formal grammars has its limitations, but has played a major role in generating hypotheses to test, not only on natural language, but also on animal songs and music. But where does this leave semantics? Chomsky's original work stressed the independence of syntax from semantics, but that does not mean that semantics is not important for claims about human uniqueness, even for linguists working within a ‘Chomskian’ paradigm. Berwick et al. [7], for instance, use the point that birdsong crucially lacks underlying semantic representations to argue against the usefulness of bird song as a comparable model system for human language. The reason why this is so is that in natural language, the transfinite-state structure is not some idiosyncratic feature of the word streams we produce, but something that plays a key role in mediating between thought (the conceptual–intentional system in Chomsky's terms) and sound (the phonetic articulatory–perceptual system).

Crucially, the conceptual–intentional system is also a hierarchical, combinatorial system (most often modelled using some variety of symbolic logic). From that perspective, grammars from the (extended) CH describe only one half of the system; a full description of natural language would involve a transducer that maps meanings to forms and vice versa [49,129]. For instance, finite-state grammars can be turned into finite-state transducers, and CFGs into synchronous CFGs. All the classes of grammars in the CH have a corresponding class of transducers (see Knight & Graehl [130] for an overview). Depending on the type of interaction we allow between syntax and semantics, there might or might not be consequences for the set of grammatical sentences that a grammar allows if we extend the grammar with semantics. But, the extension is, in any case, relevant for assessing the adequacy of the combined model—for example we can ask whether a particular grammar supports the required semantic analysis—as well as for determining the likelihood of sentences and alternative analyses of a sentence.

Do we need transducers to model structure building in animal songs and music? There have been debates about forms of musical meaning and its neurocognitive correlates. However, a large number of researchers in the field agree that music may feature simple forms of associative meaning and connotations as well as illocutionary forms of expression, but lacks kinds of more complex forms of combinatorial semantics (see the discussion of references [131–137]). However, it is possible, as mentioned above, to conceive of complex forms of musical tension that involve nested patterns of expectancy and prolongation as an abstract secondary structure that motivates syntactic structures at least in Western tonal music and in analogy would require characterizing a transducer mapping syntactic structure and corresponding structures of musical tension in future research.

There have similarly been debates about the semantic content of animal communication. There are a few reported cases of potential compositional semantics in animal communication (cf. [138]), but these concern sequences of only two elements and thus do not come close to needing the expressiveness of finite-state or more complex transducers. For all animal vocalizations that have non-trivial structure, such as the songs of nightingales [139], blackbirds [8,108], pied butcherbirds [140] or humpback whales [141,142], it is commonly assumed that there is no combinatorial semantics underlying it. However, it is important to note that the ubiquitous claim that animal songs do not have combinatorial, semantic content is actually based on little to no experimental data. As long as the necessary experiments are not designed and performed, the absence of evidence of semantic content should not be taken as evidence of absence.

If animal songs do indeed lack semanticity, they would be more analogous to human music than to human language. The analogy to music would then not primarily be based on the surface similarity to music on the level of the communicative medium (use of pitch, timbre, rhythm or dynamics), but on functional considerations such that they do not constitute a medium to convey types of (propositional) semantics or simpler forms of meaning, but are instances of comparably free play with form and displays of creativity (see below and Wiggins et al. [143]).

Does this view on music–animal song analogies have any relevance for the study of language? There are reasons to argue it does, because music and human language may be regarded as constituting a continuum of forms of communication that is distinguished in terms of specificity of meaning [144–146])—consider, for instance, several forms of language that may be considered closer to a ‘musical use’ in terms of their use of pitch, rhythm, metre, semantics, for example motherese, prayers, mantras, poetry, nursery rhymes, forms of the utterance ‘huh’ (see [147]), etc. Drawing a strict dichotomy between music and language may further be a strongly anthropomorphic distinction that may have little match in animal communication. Animal vocalizations may be motivated by forms of meaning (that are not necessarily comparable with combinatorial semantics), for example, expressing aggression or submission, warning of predators, group cohesion, social contagion or may constitute free play of form for display of creativity, for instance (but not necessarily) in the context of reproduction. Given that structure and structure building moving from the language end to the music end is less constrained by semantic forms, more richness of structural play and creativity is expected to occur on the musical side [143].

9. Dealing with gradations: adding continuous-valued variables

A final move to a new class of successful models originates in a far research extension of the CH framework where the categorical symbols used in rewrite grammars are replaced by vectors. Thus, instead of having a rule X → YZ, where X, Y and Z are categorical objects (such as a ‘prepositional phrase’ (PP) in linguistics, or a motif in zebra finch song), we treat X, Y and Z as n-dimensional vectors of numbers (which could be binary, integer, rational or real numbers; for example [0,1,0,0,1, … ] or [0.45,0.3333,0.96, … ]). By choosing vectors at maximum distance from each other such grammars can perfectly ‘mimic’ classical, symbolic grammars (which now become the ends of a continuum—and are still important as potential attractors in learning and evolution); but, additionally, vector grammars offer a natural way to model similarity between phrase types (assuming some noisy reading of the vectors, making correct recognition of a vector less likely the further it is from its prototype; see also reference [148], for an insightful discussion of the relation between simple recurrent networks and formal grammars).

A simple example (discussed in reference [149]) is the category of the word ‘near’, which sometimes acts like an adjective (ADJ, ‘the future is near’) and sometimes like a preposition (PREP, ‘the house is near the river’). In standard symbolic as well as probabilistic grammars, this is normally modelled by having two entries in the lexicon, one with category ADJ, and the other with category PREP. Interestingly, however, ‘near’ shows behaviour inconsistent with this simple duplication approach: as a preposition, it inherits a property of adjectives, namely that it can be used as a comparative (as in ‘the house is nearer the river than the road’). In vector grammars, such cases can be dealt with by assigning ‘near’ a vector in between the cluster of prepositions and the cluster of adjectives.

In computational linguistics, vector grammars (which have a close relation to neural networks models of linguistic structure from the 1990s [150,151]) are experiencing a new wave of excitement following some successes with learning such grammars from data for practical natural language processing tasks [152–155]. These successes are due not only to the ability to represent gradedness but also (and perhaps more so) to the fact that models with continuous values allow gradual learning procedures (in these papers, the procedure is ‘backpropagation through structure’ [156]).

While vector grammars have, to the best of our knowledge, not been applied yet to music and animal vocalizations, we expect that they offer much potential in these fields. Efforts to apply symbolic grammars in these domains often encounter difficulties with dealing with phenomena that seem fundamentally continuous in nature, such as loudness and pitch variation, beat, etc. Musical examples would exhibit microdifferences in pitch corresponding with syntactic function (e.g. raised leading notes), complex note features (such as slides used in traditional North Indian rāgās) or timbre features in distorted guitar solos that may correspond with syntactic function, such as stress, intonation or timbre cues may be modified to direct attention towards elements with important syntactic functions (e.g. stability or marking departures at constituent or phrase boundaries; further empirical research is, however, required to examine such connections). Altogether vector grammars may constitute a well-suited formalism to capture the use of noisy, non-tonal and complex sounds in music across cultures that may be challenging for traditional symbolic models.

One interesting feature of vector grammars is that they are computationally more expressive than their symbolic counterparts—in fact, they result in an entirely different class of complexity that is not comparable with the models of the CH from which the models originated (this is due to the large amounts of information that the large real-valued vectors may carry). For instance, Rodriguez [157] demonstrated that a right-branching vector grammar (or, in fact, its special case, the Elman network [150]) can generate several context-free languages, even though it is well-known that right-branching symbolic grammars are finite-state. The reason is, Rodriquez argues, that small displacements in a continuous vector space can be used to implement a counter. We may expect that also other classes of symbolic grammars can be approximated by vector grammars with very simple structure (even if the non-terminals are in some sense more complex). While much theoretical work exploring their expressive power is still necessary, they provide another motivation to move on to probabilistic, non-symbolic models that move beyond the constraints of the CH.

In short, vector grammars provide a generalization over the classical symbolic grammars from the extended CH. In particular, Rodriquez's [157] results demonstrate a continuum between finite-state and (at least some) context-free languages might be used to call into question the a priori plausibility of the hypothesis that context-freeness is uniquely human (contra Fitch & Hauser [158])—a hypothesis only originating from the reification of the CH.

Following this line of reasoning, one could even argue that previous accounts have been overstated in their focus on ‘architectural’ constraints on structure building operations when discussing whether ‘animals may not be able to process context-free languages, whereas humans can’ or whether ‘music has or has no access to the recursion operation’ (see also the discussion in reference [159]). One may hypothesize, then, that the basic toolbox of structure building operations between humans, primates and birds is largely shared, but that music, language, primate and bird calls and bird and cetacean songs have recruited (perhaps in a process of cultural evolution) very different operations from that toolbox because they serve very different functions—a thought that we explore in §10.

10. Function, motivation and context

Our journey through the computational models of structure building—from Shannon's n-grams, via the CH to vector grammars and models beyond the CH—has thus uncovered many useful models for how sequences of sound might be generated and processed, which also motivate that a richer space of possibility may need to be explored before potential explanations may resort to the assumption of hard biological constraints. What could be alternative explanations for some of the differences and similarities in structure that we do observe in these domains? In this final section, we consider explanations based on function, motivation and context.

Fundamental to a cross-cultural concept of music is the form of joint group interaction: music may be a form to coordinate and synchronize a large group in terms of joint action, production and perception [145]. Music may be monological, dialogical, responsorial (individual–group) or an entire joint group-based activity [19]. This view makes it possible to understand the principles of structure building, its flexibility and constraints based on affording these forms of interactive communication. In this context, the notion of ‘absolute music’ [160] as a highly complex form of Western art is a very small subset of music of the world and a construct that constitutes an exception in an overarching cross-cultural comparison (cf. [145,161]). As mentioned above, forms of high musical complexity may stem in part from traditions of formal scholarly teaching and the use of sophisticated notational systems and probably can be correlated to uses of music in a ‘monological’ form rather than a ‘joint group-based activity’ (even when an orchestra is performing monologically for a larger audience). Further, theories of music that take such examples of absolute Western art music as basis for general claims of musical complexity and processing and specifically linking findings about complexity and recursion [37] to the debate concerning the human language faculty [28,162,163] need to be examined carefully in order to establish the extent to which the claims generalize to music across cultures (see reference [145] and the discussion in this review), because this link is not given per se. Nonetheless, observations concerning complexity in Western tonality and corresponding processing requirements may contribute important evidence towards the complexity that music cognition may reach (in terms of proofs of existence). While the considerations above do not invalidate comparisons of structural/syntactic complexity in animal vocalization, human language and music, it may further be the case that the conditions of communication and the social context of music making (such as joint group activity) may impose limits on the structural complexity that may be used. Therefore, these considerations ask for careful examination of the underlying conditions of communication.

Once the purpose of communication is not necessarily required to be grounded in propositional semantics, the question regarding the foundation of the form of communication becomes an interesting theoretical challenge (cf. [164]). From a cross-cultural perspective, music may be regarded as a tool for dealing with situations of social function and social uncertainty [165], it may be construed as a form of display, communication and regulation of emotion and tension [19,166] or an (abstract) play with structure per se [167,168]. These different forms to construct music have different implications on structure (and, of course, they are not mutually exclusive): music in social and interactive contexts is required to afford rhythmic entrainment and to build on socially established conventions of structures. The notion of music as carrier or inducer of emotions implies stronger constraints on musical structure, namely those the processing of which results in triggering the corresponding emotional mixture. In contrast, construing music as (mere) free play of form and formal complexity entails the least formal constraints.

In the above-mentioned context, many conditions of animal vocalization appear to match features of human music; as far as we can tell they are not governed by complex semantics, they are interactive and group activities but can also occur alone. Accordingly, principles of structure building in music and animal vocalization may be considerably different from the ones governing language and be constrained by different communicative motivations than the ones found in language. While simple forms of expressions such as fear or aggression encoded in prosodic structure and illocutionary speech acts may be similar in all three domains, this functional analysis suggests that syntactic structures may not necessarily converge in these domains as mere structural comparison as proposed by Jackendoff & Lerdahl [28] (see also [163]).

11. Conclusion

In this review, we have discussed different formal models of syntactic structure building, building blocks and functional motivations of structure in language, music and birdsong. With these considerations, we aim to lay a common ground for future fruitful formal analysis, shared methodologies and comparative formal and empirical research addressing common cognitive questions that were raised in these domains. Not many steps have been made to bring theoretical approaches in music and animal vocalization into common terms that can be compared with approaches established in formal and computational linguistics. These questions are fundamental to understand commonalities and differences between humans and animal cognition as well as between music and language, responding not only to Hauser, Chomsky and Fitch's provocative hypothesis concerning the ‘exceptional’ role of the human cognitive/communicative abilities [11].

Music and language may constitute a continuum in the human communicative toolkit [169,170] and forms of animal vocalizations may relate to different aspects in this spectrum (and not necessarily be related to only one of them). The level of analogy may not necessarily be based on formal considerations, but may also depend on corresponding semantics (or second tier structure), context, function and the underlying motivation of communication.

We discussed several classes of formal models that lend themselves to computational implementation and empirical evaluation. While the (extended) CH provides a useful perspective for the comparison of different theoretical approaches and predictions concerning properties of structures, it is important to bear in mind the limitations we discussed and the fact that cognitively plausible mechanisms may not be well represented in terms of the CH. The notion of grammatical gradience and other factors such as the necessary flexibility of dealing with noise and uncertainty in ecological structures motivate extensions towards probabilistic models. Finally, we have discussed recent models that add gradation and continuous-valued variable spaces. Such models link formal grammar and neural network approaches and add the power to deal with ecological structures that are inherently continuous. Finally, they predict that a single cognitively relevant framework may predict sequences of different complexity in the CH and therefore have the potential to undermine assumptions concerning categorically different cognitive capacities between human and animal forms of communication [11,171].

Funding statement

M.R. was generously supported by the MIT Department of Linguistics and Philosophy as well as the Zukunftskonzept at TU Dresden supported by the Exzellenzinitiative of the Deutsche Forschungsgemeinschaft. W.Z. is supported by the New Generation Initiative of the Faculty of Humanities at the University of Amsterdam. G.A.W. is supported by the Lrn2Cre8 and ConCreTe projects, which acknowledge the financial support of the Future and Emerging Technologies (FET) programme within the Seventh Framework Programme for Research of the European Commission, under FET grant numbers 610859 and 611733. C.S. acknowledges funding from the Excellence Clusters Languages of Emotions and Neurocure, the collaborative research grant SFB 665, and Bernstein focus area ‘neural basis of learning’, project ‘variable tunes: neural mechanisms underlying learning motor sequences (01GQ0961/TP1, BMBF).