Mutation accumulation and the formation of range limits

Abstract

The dynamics of range formation are important for understanding and predicting species distributions. Here, we focus on a process that has thus far been overlooked in the context of range formation; the accumulation of mutation load. We find that mutation accumulation severely reduces the extent of a range across an environmental gradient, especially when dispersal is limited, growth rate is low and mutations are of intermediate deleterious effect. Our results illustrate the important role deleterious mutations can play in range formation. We highlight this as a necessary focus for further work, noting particularly the potentially conflicting effects dispersal may have in reducing mutation load and simultaneously increasing migration load in marginal populations.

1. Introduction

The formation and limitation of species ranges is a longstanding subject of interest in ecology and evolution ([1], reviewed in [2,3]). Understanding geographical ranges is a particularly current topic due to the recognition that anthropogenic climate and habitat change could result in substantial genetic and demographic effects that ultimately shape species' distributions. A considerable body of theory demonstrates the importance and interplay between ecological and evolutionary drivers of metapopulation range formation [4–11], of which environmental gradients play a potentially key role [4,5]. A particularly important paper on the evolutionary influences on range formation by Kirkpatrick & Barton [6] investigated the roles of local adaptation and gene flow for a species along an environmental gradient, showing that stable range limits arise when immigration of maladapted individuals to the periphery prevents local adaptation. This finding corroborated the most commonly invoked explanation for range limit formation, i.e. that gene flow from core populations disrupts selection at the periphery (gene swamping) [7,8]. Similarly, Alleaume-Benharira et al. [9] found that increasing immigration into marginal populations resulted in gene swamping; however, immigration also alleviated the effects of genetic drift by re-introducing genetic variation, purging poorly adapted alleles. Migration can therefore have opposing effects for patterns of local adaptation [9].

While previous studies [7–9] have examined the effect of migration load on patterns of local adaptation and range formation, few studies have examined the effect of mutation load. Here, we term mutation load as the build up of (environmentally independent) deleterious mutations, as a consequence of inbreeding and genetic drift. Existing theory on mutation load has demonstrated that large-effect mutations are typically rapidly purged [10,11] and are therefore of less influence on population dynamics. However, intermediate to mildly deleterious mutations can be a potent force, accumulating and becoming locally fixed as strong stochastic effects overcome selection [12]. In stochastic simulations, the stability and viability of metapopulations in homogeneous landscapes were hugely affected by mutations of intermediate deleterious effect, but the influence of deleterious mutations scaled with connectivity [13]. Populations were much less extinction-prone when they were better connected to neighbouring patches and consisted of few larger populations rather than several small populations [14]. While the above studies highlight the importance of mutation load for metapopulations in homogeneous landscapes, small populations at the limits of an environmental gradient are also vulnerable to inbreeding. Thus, it is possible that the accumulation of mutation load can result in the extinction of marginal populations, limiting a species' range. Here, we use a relatively simple individual-based model to establish whether the accumulation of mutation load can, in principle, limit a species' range along an environmental gradient. We also conduct an initial exploration of how the extent of this effect may vary according to genetic and demographic factors.

2. Material and methods

We simulate the dynamics of a metapopulation inhabiting a one-dimensional array of patches structured along a linear environmental gradient in patch capacity (K), with slope b = 0.5. Capacity of a site at position x (K_x) is set by the equation

where K_C = 50 is the maximum capacity at one end of the species range. The gradient stretches across 100 patches and ranges from a maximum K = K_C to K = 0. Patches are connected by dispersal; individuals disperse from their natal patch in either direction along the array; however the boundaries at both ends of the landscape are absorbing, that is, individuals dispersing beyond the length of the landscape die. All individuals have the potential to disperse and the distance dispersed in continuous space (d) is drawn from a normal distribution: d ∼ |Norm(0, σ)|. Individuals disperse from the centre of the natal patch, in either direction along the one-dimensional landscape, and settle in the discrete patch they land within. However, depending on the standard deviation (σ) of the dispersal kernel, a proportion of individuals remain in the natal patch; e.g. for σ = 0.5, the emergent probability of emigration, m = 0.32. After dispersal, if the population density in a patch is greater than K, a randomly selected number of individuals survive until the local population size equals K. Individuals are monoecious and diploid, and mating is random within patches and can occur between any two individuals per offspring. The probability of self-fertilization is the same as that of mating with any other individual in the patch. The number of offspring an individual produces is drawn from a Poisson distribution with mean λ.

At initialization, all individuals have a genome consisting of 1000 independent, unlinked non-deleterious diploid loci. In subsequent generations, mutations occur with a probability (m_g) per individual and are unidirectional (non-deleterious to deleterious, we assume no backward mutations). Mutation sites are randomly selected from non-deleterious loci; thus, the total genomic mutation rate remains constant but the genewise mutation rate increases over time as mutations accumulate. Offspring inherit each allele randomly from each parent and survival at birth is a function of genetic load. The effect of deleterious alleles (s) is constant across loci, and their dominance coefficient is calculated as h = 1/(2 + 20s) (as in [13]). The viability of an individual (w) follows the multiplicative model:

where h_z is the number of heterozygote deleterious loci and h_o is the number of homozygote deleterious loci. Generations are discrete; once all adults have mated they die.

At initialization, all patches are filled to capacity; the simulation runs for 3000 generations. We record the mean genetic viability of each sub-population in each cell along the landscape, through time. We investigate the influence of mutation effect size, dispersal and growth rate on metapopulation range formation over 30 replicates for each parameter combination.

3. Results and discussion

Table 1 shows that mutation load can substantially increase the minimum carrying capacity (K) required for population persistence. However, the dispersal of individuals from patches of higher carrying capacity into more marginal conditions can sustain populations in patches of lower K than would be possible if the landscape were homogeneous. Thus, the marginal patches effectively persist as evolutionary sinks maintained by immigration from the higher density core areas. This has potentially important consequences for range formation that have thus far been overlooked. While the influx of individuals to the range margins can prevent local adaptation [6], it can also alleviate the effects of mutation load, providing a genetic rescue effect. Indeed, we find that increasing dispersal or growth rate, subsequently increasing the number of individuals moving within the metapopulation, increases the range extent (figures 1 and 2). Previous theory has demonstrated that increased dispersal and patch capacity can alleviate the effects of drift and maladaptation in small peripheral populations [9,15,16]. Undoubtedly, here the mechanism is similar; increasing immigration increases genetic variation within peripheral patches, diluting the frequency of deleterious mutations and relieving the effects of inbreeding. Thus, our results are in accordance with existing work; increasing gene flow leads to larger effective population sizes in the margins which counteracts drift [9]. However, our results serve to highlight that this effect is important not only for local adaptation but also for inbreeding and mutation load, in the context of range formation. Furthermore, at the range limit, given the small local K, a large proportion of matings involve selfing. In a set of additional simulations, we prevented selfing, such that individuals alone in a patch were unable to reproduce. In these simulations, we find that the range extent is reduced even further. This highlights an important consideration for sexual species: Allee effects; in this case a lack of mating opportunities at the range margin may present additional restrictions during range formation.

Table 1.

For homogeneous landscapes, simulations were run for each value of K (ranging from 1 to 50) and the minimum K allowing for persistence is shown. This is compared with the K of the smallest inhabited patch on the environmental gradient for the equivalent parameter settings. Data shown are the mean of 30 replicates.

mutation effect size	standard deviation of dispersal kernel (emergent migration rate)	minimum K before more than 50% of replicates go extinct in homogeneous landscape	K of smallest inhabited patch on gradient
0.0	0.25 (0.05)	2	2
0.025	0.25 (0.05)	33	33
0.05	0.25 (0.05)	23	22
0.0	0.5 (0.32)	2	1
0.025	0.5 (0.32)	13	9
0.05	0.5 (0.32)	10	6
0.0	0.75 (0.5)	1	1
0.025	0.75 (0.5)	10	3
0.05	0.75 (0.5)	9	6
0.0	1.0 (0.62)	1	1
0.025	1.0 (0.62)	8	4
0.05	1.0 (0.62)	6	3

Figure 1.

(a) Metapopulation range extent through time. The lighter shading in the background shows the persistence and range extent of the metapopulation without mutation accumulation. Darker shading in the foreground shows the persistence and range extent of the metapopulation with mutation accumulation. Standard deviation of the dispersal kernel σ = 0.25 (m = 0.05), growth rate λ = 2 and mutation effect size s = 0.025. (b) For the same settings as (a), transect of mean viability (w) in patches across the range at generation 2900. Error bars represent the standard error of 30 replicates. (c) Snapshots of range extent for increasing dispersal neighbourhoods. Growth rate λ = 2 and mutation effect size s = 0.025.

Figure 2.

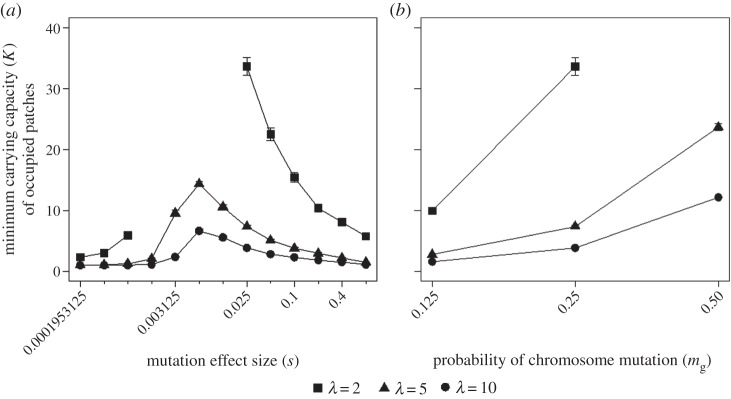
Minimum K of occupied patches on the environmental gradient for (a) different mutation effect sizes (m_g) and growth rates (λ), and (b) different probability of mutations (m_g) and growth rates (λ), σ = 0.25 (m = 0.05). Points represent the mean and standard error over 30 replicates. Missing points are simulations with an unstable range extent resulting in extinction before generation 3000.

In our simulations, mutation load has the strongest effect on species' range formation when dispersal is limited (figure 1c), growth rate is low, the probability of mutation is high (figure 2b) and mutations are of intermediate deleterious effect (figure 2a); in some cases, the accumulation of mutation load more than halves the range extent. Furthermore, we find a U-shaped relationship between effect size and range formation which we explain as follows. For mutations of large effect, the metapopulation is rapidly purged of load, and thus the range extent is affected little (figure 2). As effect size decreases, stochastic effects become more important than selection and mutations increasingly accumulate due to drift [13]. For small marginal populations, the strength of drift is much greater; this increases the rate of mutation accumulation and patch extinction, in turn reducing range size. For small growth rates, this effect is so severe that the entire metapopulation goes extinct (figure 2a, missing points for λ = 2). However, as effect size becomes extremely small, mutations still accumulate but are almost neutral and hence do not induce patch extinctions or limit range formation. Therefore, while Higgins & Lynch's [13] comparison of mutation effect sizes demonstrated that mutations of intermediate deleterious effect accelerate extinction timescale in metapopulations, here we show that they can also limit range formation, without necessarily causing complete extinction, for species structured across environmental gradients.

The simulations in our study are on a linear landscape; this arrangement is rare in nature and restricts gene flow as individuals can only disperse in one dimension. To identify the effects of mutation load, we have excluded demographic stochasticity from population regulation; however, it would also be interesting to consider how the two interact for range formation in two-dimensional landscapes. Our results indicate that for small, slow-growing populations with limited dispersal, mutation load may play an influential role in range formation and species persistence, especially in marginal regions. We therefore emphasize the need for future studies on range formation to include and consider mutation load, and its evolution, alongside other more commonly considered evolutionary forces such as local adaptation and dispersal.

Data accessibility

Data available from the Dryad Digital Repository (doi:10.5061/dryad.4tr2v).

Funding statement

The work of K.B. was supported by the EU (FP7-IEF) Marie Curie Fellowship, project RANGESHIFT. R.C.H. and J.M.J.T. acknowledge support of Natural Environment Research Council, UK.

Conflict of interests

We declare no conflicts of interest.