Locally adaptive, spatially explicit projection of US population for 2030 and 2050

Significance

Oak Ridge National Laboratory (ORNL) is a leader in population distribution and dynamics research, particularly in developing gridded population datasets. For this study, ORNL researchers leverage their expertise in intelligent dasymetric modeling to construct large-scale, national level, spatially distributed population projections for the contiguous United States. The model presented here departs from other spatially explicit projection models by accounting for socioeconomic and cultural characteristics that influence spatial population growth at smaller scales, while still projecting population at a large scale. The resulting projected population distribution can be exploited for long-term urban and infrastructure planning, and scientific modeling for climate change.

Abstract

Localized adverse events, including natural hazards, epidemiological events, and human conflict, underscore the criticality of quantifying and mapping current population. Building on the spatial interpolation technique previously developed for high-resolution population distribution data (LandScan Global and LandScan USA), we have constructed an empirically informed spatial distribution of projected population of the contiguous United States for 2030 and 2050, depicting one of many possible population futures. Whereas most current large-scale, spatially explicit population projections typically rely on a population gravity model to determine areas of future growth, our projection model departs from these by accounting for multiple components that affect population distribution. Modeled variables, which included land cover, slope, distances to larger cities, and a moving average of current population, were locally adaptive and geographically varying. The resulting weighted surface was used to determine which areas had the greatest likelihood for future population change. Population projections of county level numbers were developed using a modified version of the US Census’s projection methodology, with the US Census’s official projection as the benchmark. Applications of our model include incorporating multiple various scenario-driven events to produce a range of spatially explicit population futures for suitability modeling, service area planning for governmental agencies, consequence assessment, mitigation planning and implementation, and assessment of spatially vulnerable populations.

Impacts, adaptations, and vulnerability of population have come into sharp focus in recent years, particularly in light of concerns around global climate change (1). Whether through increased susceptibility to vector-borne disease (2), food scarcity, or extreme weather events, the general consensus is that large populations will be affected by the impacts of climate change (3). Nearly every climate change model predicts some magnitude of sea level rise (4), and whereas a considerable segment of the world’s population lives in close proximity to coastal areas (5–8), rising sea levels increase the risk of storm surge, coastal flooding, and other storm-related hazards (4, 9). The aforementioned scenarios require the examination of tools and data that are necessary to quantify populations at risk to these predicted adverse events, so that appropriate countermeasures can be taken when attempting to allocate potential resources. Spatially explicit gridded population estimates have repeatedly proven their usefulness for planning needs, including those of public health, the environment, disaster mitigation, preparedness and assistance, and service area planning for local, regional, and national governments.

Originally pioneered by Semenov-Tian-Shansky (10) and popularized by Wright (11), dasymetric modeling is a key technique for spatial disaggregation of population data. Unlike choropleth maps, which assume a uniform distribution of population within an arbitrary spatial unit, the dasymetric approach uses ancillary data at a finer spatial resolution to distribute population from source zones (i.e., census regions) to more precise target zones (e.g., grid cells). Land use\land cover is the best indicator and most prolific in this respect (12, 13), where land use or land cover categories for each cell are weighted based on the likelihood of population. Over time, refinement of the dasymetric mapping technique has led to the development of intelligent dasymetric models using multiple ancillary spatial data to refine the allocated population distribution (14, 15). Developed at Oak Ridge National Laboratory, LandScan USA (3 arc-seconds ∼ 90 m) (13) and LandScan Global (30 arc-seconds ∼ 1 km) (12) use intelligent dasymetric modeling to produce high-resolution raster population distribution data. However, current distributions of population are of limited use in long-term socioeconomic planning. Therefore, projecting future distributions is of the utmost importance for urban development, critical infrastructure siting, or assessing the impacts of climate change. In the context of climate change modeling, as reported by the Intergovernmental Panel on Climate Change, long-term demographic projections have been an essential component of scientific analysis for future greenhouse gas scenario generation (16).

Recent spatially explicit population projections have ranged in scale from metropolitan (17), state (18), national (19), to global levels (20). However, due to computational intensity, most large-scale spatially explicit projection models do not account for local subtleties, rather they apply generalized trends across multiple regions. Some existing spatial projection methodologies project population counts as part of the spatially modeled scenario. For instance, the California Urban Futures (CUF) model (21) uses linear regression to estimate residential population numbers that are then allocated to geographic units based on various weights. Similarly, the Spatially Explicit Regional Growth Model (SERGoM) projects changes in housing density resulting from variables such as urban proximity and county level population growth rates (19), thus population change is accounted for within these two models. However, all models intrinsically have the capacity to incorporate exogenously derived population estimates (i.e., third party entity) and urbanization rates to allocate or downscale projected population on top of an existing, current population distribution developed by another organization (20). Other spatial projection procedures are similar in that multiple sources are used to independently validate the projected population counts (12, 13).

For the development of the spatial allocation procedure, methodologies typically follow either a straightforward procedure that reflects current trends and patterns or a more complex procedure that integrates a multivariate statistical model (22, 23). The former includes population trend extrapolations, prorates of the current spatial population structure, and cellular automaton. Trend extrapolation procedures look at the individual cell and project population change by either the total population change per cell or by the change in the share of growth per cell (23, 24). Another procedure assumes new population will conform to the current spatial structure of the population. In this particular case, the same spatial structure of population at a specific point in time is prorated to match anticipated population counts (20, 25, 26). Cellular automata provide a general representation of urban development by simulating the development of adjacent cells through multiple iterations (27–29). Whereas ref. 27 uses cellular automata to project both urban expansion and spatial population growth, refs. 28, 29 merely attempt to model spatial expansion of urban areas, using population as an explanatory response to the observed changes rather than modeling population growth.

More complex procedures model change in the spatial structure of population by incorporating multiple variables which seek to understand the relationship between census counts and the associated variables (22, 23). The most straightforward of these methods uses a population gravity model, which is based on the assumption that existing population attracts additional population. The methodology used by the International Institute for Applied Systems Analysis primarily uses this technique to project generalized global trends (30), and Jones and O’Neil (1) modify this procedure by accounting for many geographical limitations, such as distance-decay rates, border effects, influence of window size, and adding in a suitability mask to prevent certain areas from being developed. The methodologies used by the California Futures Model (17, 21) and in the Florida 2060 report (18) incorporate existing population as attractors for new growth as well as variables such as land cover, infrastructure, zoning, and the financial housing market to produce potential urban development surfaces, which are in turn used to distribute new population. Similarly, the SERGoM procedure (19) incorporates a myriad of physical and socioeconomic variables to model growth, although this method projects changes in housing density rather than population, because its primary purpose is for modeling and monitoring land use.

To date, most spatial projection methods have been founded on projecting residential population (1, 17–19, 21), urban population (31), or purely urban growth (28, 29) at coarse resolutions for national and global scales by applying generic, regional growth patterns or varying climate change scenarios, ignoring the underlying subtleties which influence spatial population growth (20, 23, 25, 30). Whereas metropolitan and state level spatially explicit projection models do account for the local subtleties and variation in population growth and historical land use change trends, due to varying formats, varying spatial resolutions, research gaps, and the impracticality of coordinating with every state and local organization, agglomerating all of the fine scale, localized, residential projections into one national level projection distribution becomes a difficult task to orchestrate. Even if this task were feasible, the resulting output would be a residential projection, and although these models may be appropriate for modeling the impacts of climate change at coarse resolutions, the mobility of population means people are not confined to their place of residence. Whereas existing models that project residential population are beneficial to numerous applications, planning for infrastructure needs, energy consumption, and emergency response relies heavily upon ambient population distributions, or a 24-h average of population, rather than a static, residential population count (12, 13). For example, given the safety and security concerns associated with nuclear energy, planning the optimal site for future construction entails identifying areas of low public interest, requiring the potential site to have the smallest footprint in terms of encountering population. Because an ambient population is essentially the likelihood of population being at any place during a 24-h day and it accounts for diurnal population movements, such as commuting to and from work or school, an ambient population dataset is more suitable for this type of modeling. The concept of ambient population has been discussed in greater detail elsewhere; further information can be found in refs. 12, 13.

Therefore, to account for local factors which affect population change at the national level, we have deviated from the LandScan USA (13) and LandScan Global (12) projects by incorporating both population gravity and multivariate methods to construct spatially explicit population projections for the 3,109 counties in the contiguous United States for 2030 and 2050. This locally adaptive, spatially explicit model projects an ambient population distribution dataset for each target year based on a business as usual scenario, and assumes no significant, disruptive changes to our socioeconomic, political, legal, and physical environment. The aim of this research is not only to produce a valid, functional dataset, but also to demonstrate a method for estimating a national level, ambient population distribution for an extended timeframe that, in future use, can be applied to specific scenario-driven events. The novelty of our model is ingrained in the fact that although the geographic scope pertains to the national level, population projections, variables, and weights were adapted to address local characteristics of the individual counties to create a fine-resolution population distribution.

Materials and Methods

Population Projections.

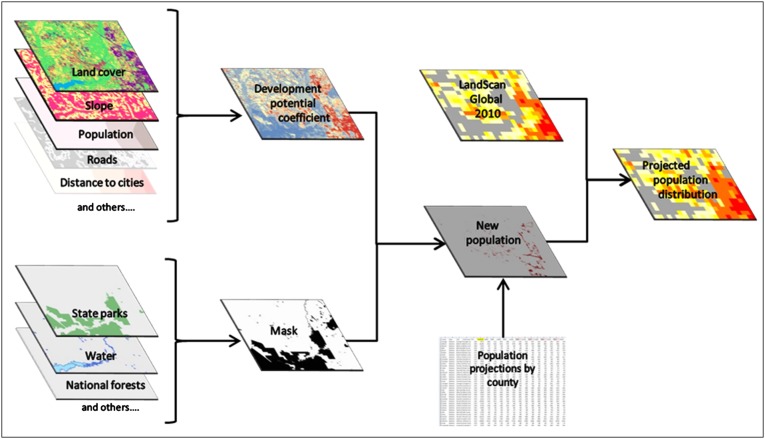
A simplified flow diagram of our methods is shown in Fig. 1, where we first project population at the county level. Local variables and weights which influence the spatial facet of population growth were then combined to create a potential development coefficient, which is the identification of lands most suitable for population growth. The projected population was then allocated to its spatial location using the coefficients calculated in the previous step. This projected population, in turn, is added to the current population distribution to generate the projected population distribution. Further details on the methods used for each step can be found in the ensuing paragraphs.

Fig. 1.

Logic diagram of the locally adaptive, spatially explicit population projection model.

As conducted by the US Census Bureau, projections of US population are available at the state level through 2030 (32) and the national level through 2050 (33). However, our model requires these data at the county level to control for spatial demographic variation when modeling US population distributions for 2030 and 2050. The cohort-component method (34) was used to calculate projected population counts for each county (See SI Materials and Methods for further detail on cohort-component method):

$$P_{x+n}=P_x+\left(B_{x,x+n}-D_{x,x+n}\right)+(I{M}_{x,x+n}-O{M}_{x,x+n}),$$

where the projected population $P_{x+n}$ is equivalent to current population $P_x$ plus the net difference between births $B$ and deaths $D$, and net migration between in-migration $IM$ and out-migration $OM$, projected to occur in a given time interval $x,x+n$. The 2010 US Census population counts were used as the base population count. These data were stratified by county, sex, and 5-y age cohorts (0–4, 5–9,…,90+). Data on 2009 birth and death rates were available for each 5-y age–sex cohort from the National Center for Health Statistics. Migration data come from the Internal Revenue Service (IRS) and are for 2009–2010, the most recent year available. However, age- or sex-specific migration rates were not available, so the same migration rate was assumed for all age and sex groups. Using these data, we were able to calculate age-specific fertility rates, survivability rates, migration rates, and sex ratios, which were then used to project county populations every 5 y up to 2050. When our county projections were summed to a national total and compared with the official US Census projections for 2030 and 2050, our modified method itself had a national overprojection of 9.8% for 2030 and 14.7% for 2050. Therefore, county level figures were adjusted proportionately so the sum of all counties matched the total US Census national projection (33). Although county-specific migration patterns by age and sex were not available, we ultimately incorporated these specific rates by adjusting the county projections to match the US Census Bureau’s projected state and national totals, which do account for age and sex domestic and international migration patterns.

Variables and Weight Selection.

For distributing the projected population to its spatial location, based on recent literature, we used several variables to create a potential development coefficient (i.e., identification of areas likely to become populated) for the population distribution algorithm. Variables, weights, and methodologies selected for implementation build on the techniques used by LandScan and incorporate several aspects of population gravity models used in other spatially explicit population projection models. Fig. S1 provides a visual representation of the locally adaptive weighting process for two counties; relative ranking of variables from greatest to least significance can be found in Table S1. For the purpose of this research, all analysis was conducted at a 1-arc-second (∼ 30 m) resolution and aggregated to 3 arc-seconds for population allocation.

From a purely quantitative standpoint, certain geographic areas may exhibit all of the characteristics deemed highly suitable for development, such as gentle to no slope or within close proximity to current infrastructure. However, federal, state, and/or local policies have created inequalities in the spatial distribution of developable lands due to the frequent subjection of planning controls (27). To prevent future population from being allocated to areas where policies, planning, and/or common sense would likely prohibit development (28), the 2012 Homeland Security Infrastructure Program (HSIP) dataset (35) and National Land Cover Data (NLCD) 2006 (36) were used to mask or exclude areas such as national parks, cemeteries, and wetlands. A complete list of exclusion areas, along with the corresponding data source, can be found in Table S2.

Slope and land cover, both quintessential dasymetric mapping variables, were used as the foundation for the model. Slope was used in our model to prevent development from occurring in impractical locations, and due to its deterministic behavior when quantifying the development potential of an individual site (12, 13, 21, 28). Digital Terrain Elevation Data Level 2 was used to extract slope values that were found within the 2010 US Census Urban Areas (37) and weighted with respect to the proportion it represented. Along with slope, a land cover weighting scheme was devised using the National Urban Change Indicator (NUCI) data* and NLCD 1992 (38). To determine which land cover classes had the highest probability of becoming developed within the local environment, a county level land cover change analysis was conducted using NLCD 1992 as the baseline (“from class”) and NUCI data as the resulting land cover class (“to class”). Because the most recent year of the NUCI data was 2008, using the NLCD 1992 as the baseline allowed us to collect a larger sample and explore historical county level land cover change trends, rather than the small temporal window offered if we had used the NCLD 2006 as our baseline. The prior land cover class of all change pixels was recorded using NLCD 1992. The number of urban change cells was then normalized to account for the total number of cells represented by each land cover class per county. The land cover classes within a particular county were then weighted based on their probability of urban change. To calculate this probability for each county, we used the following formula:

$$P_{L{C}_i}=\frac{{\displaystyle {\sum }_{k=1}^{n}NUC{I}_{L{C}_i,k}}}{A_{L{C}_{it}}},$$

$$NUC{I}_{L{C}_i}=\{\begin{array}{l}1\hspace{0.17em}if\hspace{0.17em}L{C}_i\hspace{0.17em}\mathrm{\Delta }\hspace{0.17em}Urban\hfill \\ 0\hspace{0.17em}\mathrm{otherwise}\hfill \end{array},$$

where $P_{L{C}_i}$ is the probability that land cover class $i$ will change to urban $k$, and $A_{L{C}_{it}}$ is land cover class $i$ for each geographic area $A$ at the baseline time $t$.

For the suitability aspect, diverse techniques that strive to account for the socio-cultural potential of an area to become developed were incorporated. These techniques centered on gravity-based variables such as population and infrastructure amenities. Current population not only represents present distributions, but also acts as a proxy for existing amenities and represents an underlying attractant which may not be quantifiable, known, or fully understood (1). To integrate certain intangible socio-cultural–economic drivers of development within a local environment, a moving average of the current population was included. Specifically, for each cell, the per-cell average of the population in all cells within a 4-mile radius was calculated. The 4-mile radius serves as the median distance of trips as recorded by the National Household and Travel Survey 2009 (NHTS) (39). These cells were then ranked and weighted based on their values. Furthermore, using the NHTS as a measure of distance allowed us to factor in the mobility of people and their willingness to travel to resources.

Similarly, cities from NAVTEQ. 2011 (35) with population ≥30,000, ≥50,000, and ≥100,000 were used as a positive predictive factor for future population. For all cells, the distance to the nearest city in each of the three city classifications was calculated. These distances were then classified into 12 categories at set percentages (10, 20, 30…90, 95, and 99%) of distances for all nonzero trips in the NHTS (39). For example, the 30% threshold corresponds to a trip distance of 2 miles, meaning that at least 30% of nonzero trips are 2 miles in length or shorter. Using this method, cities with a larger population were also encompassed in the cities with a smaller population threshold. To account for this overlap, weights given to larger cities were increasingly smaller. In similar fashion, the distance from each cell to the nearest NavtEq. 2011 interstate exit (35) was calculated and then classified in the same method as the distance to cities. The rationale for including highway exits is that new population and development tends to cluster and conform to the existing highway structure as observed in a case study of the Austin, TX metropolitan statistical area (40).

Roads were also used as an attractiveness variable for potential growth because they offer an avenue for development and access to resources. Using NAVTEQ. 2011 (35), roads were buffered by five concentric rings, each with a radius of 30 m. Weights, which were inversely related to the distance to the roadway, were then applied to the roadway buffers. This weighting scheme was applied to mimic sprawl, which is primarily characterized by commercial strip development and low-density development along roadways outside cities and suburbs, and has been the dominant trend in US population growth in recent history (19, 40).

Lastly, city limits from NAVTEQ. 2011 were selected from the HSIP dataset (35) and used as a binary variable; that is, cells were either within city limits or not. Given that everything else is equal, areas within city limits are theoretically more likely to become developed than if they were outside city limits. The potential development coefficient was finalized by summing all of the weighted variable grids and multiplying by the mask–exclusion areas. The development coefficient grid was then aggregated to 3 arc-seconds for allocating population.

Population Allocation.

It is unlikely that projected new population will develop and occupy only the periphery of urban areas in a uniform manner. Therefore, our projection model had to account for both the proportion of additional people that went into the current urban areas (infill) as well as that which was at the edge of or beyond current urban areas (sprawl). To calculate these different rates of spatial allocation, we classified projected new population as either infill or sprawl based on current county level patterns of urban population to urban land area. Here, we used “infill” as an all-inconclusive term combining infill development and urban redevelopment, similar to the CUF model (21).

As seen in Fig. S2, the percentage of population residing within a county’s US Census Urban Area is strongly correlated (Pearson’s r = 0.572, P < 0.0001) with the percentage of that county’s urban area (37). To determine what percentage of new population would be distributed as infill, we calculated a logarithmic function, set at a threshold to capture 95% of the counties (n = 2,954). In this way, we have the scenario of maximum new urban land to be developed without straying from the reality of the current demographic situation. The logarithmic formula used to calculate county-specific spatial allocation rates is as follows, where x represents the percentage of urban area per county and y the infill rate:

$$y=\frac{\text{ln}\left(\frac{x}{0.0055}\right)}{5.16}.$$

For example, holding constant the current ratio of urban population to urban area, a predominately urban county, such as Mecklenburg County, NC, will have an infill rate of 97%, whereas a predominately rural county, such as Floyd County, IA, will only have 7% of projected population growth classified as infill. Respectively, the counties will have 3% and 93% of population growth classified as sprawl.

Gross urban density (GUD) was used to constrain sprawl growth (18), making the assumption that spatially, population growth for each county would occur at the current density of people per unit of urban area. GUD was calculated by taking the 2010 urban population per county and dividing it by the 2010 US Census Urban Areas (37), resulting in a ratio of people per urban cell, per county. The number of cells needed to accommodate the projected growth was calculated by taking the projected population growth for each county and dividing it by the county’s GUD. For counties that contained no urban area as defined by the US Census, LandScan USA 2010 Night and Day were averaged and used to calculate the number of cells occupied by population. The population for each nonurban county was then divided by the number of occupied cells, producing a ratio of the average number of people per cell. Population growth for these counties was then divided by this ratio, resulting in the number of cells needed to accommodate growth in counties with no urban area. Coupling GUD with infill and sprawl allocation rates essentially embeds a pycnophylactic smoothing process within the model to prevent drastic fluctuations in the distribution of population (i.e., population cliffs).

This potential development grid was then separated into urban and nonurban areas. Infill population was distributed to existing urban areas, whereas sprawl population was distributed to nonurban areas, constrained to the number of cells determined by the current GUD. The infill and sprawl coefficient surfaces were weighted with their respective population of the total projected county growth to create a county level likelihood coefficient as follows:

$$P{C}_{County\hspace{0.17em}}=\hspace{0.17em}\frac{Total\hspace{0.17em}populatio{n}_{County}}{{{\displaystyle \sum }}_1^n{W}_{i,j}},$$

where $PC$ is the population coefficient, $n$ is the number of cells describing the area, and $W$ is the weight of the individual cell $i,j$. Subsequently, population for a given area, whether infill or sprawl, allocated to each weighted cell by the calculated likelihood (population coefficient) of being populated as shown below (13):

$$Population{\hspace{0.17em}}_{Celli,j}=PC{\hspace{0.17em}}_{County}\times W_{i,j}.$$

For counties that were projected to lose population, the entire population total for each county was distributed using LandScan USA 2010 Night and Day average population distribution as the coefficient grid. Once the population was distributed for each scenario, infill, sprawl, and population loss grids were mosaicked to create a continuous surface of population growth and decline. This grid was then aggregated to a spatial resolution of 30 arc-seconds and added to LandScan Global 2010 for the area covering the contiguous United States, resulting in the projected population distribution for 2030. This process was repeated to achieve the projected population distribution for 2050.

Results

The final output of this model was a gridded, 30 arc-second, ambient population distribution of the contiguous United States for both the years 2030 and 2050, depicting one of many possible projected population futures. Using LandScan Global 2010 as the baseline population distribution, for the years 2030 and 2050, only the population change that was projected to occur throughout our study period was distributed. For 2010, the population of the contiguous United States was 306,675,006, with projected populations of 371,029,047 for 2030 and 436,126,074 for 2050 (Fig. S3 displays the entire projected distribution for 2050; Fig. S4 provides more detail with a 3D visualization of the San Francisco Bay area).

To address the validity of our results, we used two separate validation procedures for the population projections and the model’s spatial distribution algorithm. Due to shifts and annexations affecting county boundaries during the time period 2000–2010, 5 counties were withheld from analysis, leaving 3,104 counties for validation. To validate the accuracy of the cohort-component population projection, we projected county level population to 2010 using the 2000 US Census as our baseline. We scaled our projections to the 2010 US Census national projection. We then compared our projections with the 2010 US Census. To remove any bias between the actual census and the projections, we scaled the 2010 US Census county population counts to the projected national total. This left us with an observed population and predicted population, both scaled to a common number. We calculated the error as a percentage of the US Census projection (Fig. S5). On average, our county level projections were overestimated by 3.72% with an SE of 0.27% and an SD of 14.93%.

Error associated with our population projections can be classified into two categories. The first category deals with erratic population trends. These cases can be attributed to anomalies such as natural disasters and economic downturns, as well as other socioeconomic processes that tend to be sporadic and unpredictable. St. Bernard Parish, LA, Orleans Parish, LA, and Monroe County, FL all have large overestimations of population (Fig. S5). The two Louisiana parishes experienced drastic decreases in population because of a mass exodus due to the catastrophic effects of Hurricane Katrina. These parishes have yet to rebound to prehurricane population counts. Similarly, Monroe County, FL experienced a large magnitude of population loss due to increased cost of living, dwindling job market, and a seasonal economy.

The second category of error is associated with a large relative change in population as opposed to a small absolute change. The large error exhibited for counties that are projected to have a large relative change in population can be traced back to limitations associated with the cohort-component method. Historical variation is not strongly accounted for in the cohort-component method, and therefore the future population of slower-growing areas will be overestimated and faster-growing areas will be underestimated. Historical variation in population growth trends can be similarly compared with fractals. Depending on the temporal resolution of interest, a county will display a general pattern of growth or decline over a span of several years. However, if the temporal focus is narrowed, it becomes apparent that these general patterns are the aggregation of more subtle trends which fluctuate from high to low or vice versa, even within the smallest timeframe. Depending on the current position of oscillation in the cycle of population growth–decline, extrapolating from this sample can cause an increase in error when projecting population counts. Cases such as this become more pronounced in counties that have smaller initial population counts. For example, if county A has a population of 1,000 and was projected to have a population of 1,800, the absolute change is small (800); however, relative to the total population of the county, there is population change of 80%. Instances such as this can be seen with Terrell County, TX, Greely County, KS, and San Juan County, CO (Fig. S5).

For spatial validation of our model, we compared the relationship between the quantity of NUCI change observed per county and the quantity of change in urban area per county as defined by the US Census between the years 2000 and 2010. The Spearman’s rho correlation coefficient for the two variables revealed a statistically significant positive correlation (r = 0.363, P = 0.000). There were additional attempts to validate the projected spatial distribution of population, such as back-casting population using LandScan 2000 as our baseline, projecting that baseline to 2010, and then comparing our modeled output with LandScan 2010. However, this proved to be a flawed and biased validation method due to technological advancements and continual improvements in the quality, accuracy, and validity of model inputs for the LandScan algorithm. As such, using LandScan 2000 as our baseline would be erroneous from the beginning because the data were limited to the technology available at that time. For example, light detection and ranging (LiDAR) building footprints were not widely available at this time and were not used as input to LandScan 2000. However, introducing LiDAR data into the model in subsequent versions of LandScan allowed a finer geographic detail to be captured with regard to the spatial distribution of population. Data such as LiDAR, as well as technological advancements, have greatly increased the spatial accuracy of LandScan. Thus, comparing between versions of LandScan introduces significant bias, especially in terms of an ambient population. Nonetheless, urban area and built-up infrastructure, both directly accounted for within our model, are indicative of ambient population and diurnal population movements. Given the relationship between NUCI change and urban change per county, as well as the emphasis we placed upon these inputs in the spatial projection model, we feel it is a suitable basis for validation of the model.

Discussion

The ambient nature of the resulting distribution takes into account the breadth of human activity space, not just residential areas. Most national censuses are concerned with residential population, which is based primarily on where people reside rather than where they work or travel. Although our population projections are derived from residential population counts, our distribution is ambient because of the variables and weights selected for allocation. The moving average of population was ambient in the fact that the weights were derived from averaging LandScan USA Day with LandScan USA Night. Furthermore, whereas other variables, such as slope, are indicative of where any future development may or may not occur, others serve a more ambiguous purpose. These variables not only represent the spatial potential for residential growth but also commercial expansion. The distinction between ambient and residential population is important because an ambient distribution is a preferable format for emergency response purposes. In the event of a crisis, the entire population will not be within their place of residence. Unless specifically a residential area, the census would indicate zero population. Therefore, an ambient distribution gives a more likely representation of population throughout a 24-h timeframe (12).

Projecting an ambient population distribution from census counts is challenging. Because our population projections were based on residential population counts aggregated to the county level, we do not directly incorporate metropolitan county-to-county same-day migration. However, the ratio of population to urban area and built-up infrastructure, both directly accounted for within our model, are indicative of ambient population and diurnal population movements. Furthermore, LandScan USA does account for cross-county commuting. Using this dataset as our baseline, along with the moving average of population for LandScan USA Day, places even greater emphasis on an ambient distribution. Additionally, aggregating residential projections to the county level allows for more flexibility than projecting population at finer geographies. However, temporal population dynamics are extremely complex processes that require the development of high-resolution temporal models that can capture and predict the social and cultural intricacies of a population and their movement patterns (12, 13). Thus, further research is required to directly account for future temporal dynamics.

Uncertainty is intrinsic in all population projections, particularly at smaller geographic units. A general rule is the smaller the geographic unit, the greater the difficulty in developing accurate population forecasts. In turn, this uncertainty is exacerbated the further the projection from the base year, explaining our relatively large SD among county level projections. Conventional techniques for addressing uncertainty revolve around constructing a range of projection scenarios (e.g., high, medium, and low) by applying different assumptions using the specific projection method (34). However, this technique does not fully quantify the uncertainty and, because we were projecting population based on business as usual, we only provided one particular scenario, most closely resembling a medium projection. Due to the limitations of the data and the assumptions that were made, several factors may have contributed to overestimations or underestimations in our population projections. For example, our migration rates were derived from IRS data, implicating only the people who filed tax returns in 2009–2010 were included in our calculation of migration rates. However, we scaled our projections to match the official projections released by the US Census Bureau, which do account for domestic and international migration, because using tax returns may not fully capture age- and sex-specific migration trends as they exclude certain socioeconomic sectors of the population. Similarly, we modeled spatial population growth assuming no significant disruptions to our socioeconomic, political, legal, and physical environment. Based on this premise, we assume population growth trends as well as gross urban density will remain constant. However, the ease and functionality of this model permits it to be adaptable, allowing for calibration and the incorporation of new data with relative ease. Looking forward, we anticipate adapting this model to various scenario-driven events where hypothetical policy alterations may either constrain or increase gross urban density and population growth, similar to ref. 17.

In our model, we define sprawl solely as population growth outside US Census-defined urban areas; it should be noted that the literature on sprawl is much more extensive and comprehensive as illustrated by the varying degrees of designation in refs. 19, 41–43). Because our objective, for this modeled scenario, was to model spatial population change given the current demographic landscape, we could reasonably assume that new urban population for each county would parallel present patterns. Although we factored in separate allocation rates and potential change surfaces for infill and sprawl, even within the same metropolitan area, there are subtle, finer detailed subprocesses of growth and decline that create a more dynamic illustration of spatial population change than the previous dichotomy of declining city centers or suburban growth (44). Because we cannot predict which areas within a metropolis are going to decay or be revitalized (44), or accurately simulate the timing, location, and nature of major infrastructure investments, such as a major corporate relocation or the construction of new roadways (45), we can only base coefficients on the current investment of infrastructure amenities. However, our model can accommodate a variety of potential development scenarios by tailoring the inputs to simulate unique climatic-driven events across multiple scales. By manipulating GUD to mimic either a more conservative or liberal sprawl pattern, modifying spatial allocation rates (sprawl and infill) to represent changing values and sentiment on the socioeconomic, cultural, and political landscape, or tailoring the land cover weights to signify the implementation of policies that would incentivize land protection or redevelopment, such as urban renewal, allow for a broader range of future population scenarios to be modeled as opposed to current routine.

Lastly, one of the most challenging issues we addressed was population loss. Although some models suggested using the inverse of the coefficients from the potential growth surface for declining areas (1), we instead reallocated the total population for the counties with projected population loss so that all cells absorbed some magnitude of the population loss. Although trends in recent decades have shown the occurrence of population loss oscillating between rural areas and the urban core, a new US Census report has shown population to be increasing in many downtowns (46). However, at the national scale, these trends vary significantly throughout both space and time (44, 47). Thus, population loss will continue to be problematic to model without data of greater geographic detail on the spatial location of decline.

Conclusion

Changes in climate-induced disaster patterns, epidemiological events, and human conflict, as well as infrastructure planning, underscore the criticality of quantifying and mapping current population. Moreover, spatial distribution of future population allows for improved adaptation and mitigation strategies. In contrast with current large-scale, spatially explicit population projections that typically rely on a population gravity model to determine areas of future growth, our projection model accounts for multiple components that affect population distribution. This model was used to simulate population growth using a range of both theoretical and empirical growth constraints with the purpose of producing one of many conceivable spatially explicit population projection scenarios for the years 2030 and 2050. Through broadening the applications of the intelligent dasymetric modeling approach, we developed a locally adaptive and geographically varying population allocation model that accounts for multiple socioeconomic factors, with the ability to accommodate multiple scenario-driven population futures. Acknowledging future population distribution is a complex interaction of climate change, land cover change, and migration; future research should systematically approach incorporating all three dimensions into the modeling framework.