Direct laser manipulation reveals the mechanics of cell contacts in vivo

Significance

The shaping of tissues and organs relies on the ability of cells to adhere together and deform in a coordinated manner. It is, therefore, key to understand how cell-generated forces produce cell shape changes and how such forces transmit through a group of adhesive cells in vivo. In this context, we have developed an approach using laser manipulation to impose local forces on cell contacts in the early Drosophila embryo. Quantification of local and global shape changes using our approach can both provide direct measurements of the forces acting at cell contacts and delineate the time-dependent viscoelastic properties of the tissue. The latter provides an explicit relationship, the so-called constitutive law, between forces and deformations.

Abstract

Cell-generated forces produce a variety of tissue movements and tissue shape changes. The cytoskeletal elements that underlie these dynamics act at cell–cell and cell–ECM contacts to apply local forces on adhesive structures. In epithelia, force imbalance at cell contacts induces cell shape changes, such as apical constriction or polarized junction remodeling, driving tissue morphogenesis. The dynamics of these processes are well-characterized; however, the mechanical basis of cell shape changes is largely unknown because of a lack of mechanical measurements in vivo. We have developed an approach combining optical tweezers with light-sheet microscopy to probe the mechanical properties of epithelial cell junctions in the early Drosophila embryo. We show that optical trapping can efficiently deform cell–cell interfaces and measure tension at cell junctions, which is on the order of 100 pN. We show that tension at cell junctions equilibrates over a few seconds, a short timescale compared with the contractile events that drive morphogenetic movements. We also show that tension increases along cell interfaces during early tissue morphogenesis and becomes anisotropic as cells intercalate during germ-band extension. By performing pull-and-release experiments, we identify time-dependent properties of junctional mechanics consistent with a simple viscoelastic model. Integrating this constitutive law into a tissue-scale model, we predict quantitatively how local deformations propagate throughout the tissue.

During the development of an organism, cells change their shape and remodel their contacts to give rise to a variety of tissue shapes. Analysis of tissue kinematics has revealed that epithelial tissue morphogenesis is partly controlled by actomyosin contractility. The spatiotemporal deployment and coordination of actomyosin contractility produce shrinkage and extension of cell surfaces and interfaces, which can drive tissue invagination, tissue folding, or tissue extension (1). Understanding the mechanical nature of these processes requires force measurements in vivo; however, measurements in developing epithelia are limited, and most methods have been indirect. They rely on either force inference from image analysis (2–4) or laser dissection experiments at cell (5, 6) or tissue scales (7, 8), which provide the relative magnitude and direction of stresses from cell or tissue shape changes. In contrast, mechanical approaches have been developed in recent years to impose or measure stresses of cells in contact, including cell monolayer micromanipulation (9), pipette microaspiration on cell doublets (10), and traction force microscopy on migrating epithelia (11) and single-cell doublets (12). Recently, an elegant method using deformable cell-sized oil microdroplets has provided absolute values of stresses at the cell level in cell cultures and embryonic mesenchymes (13) but not yet in live epithelia. In this context, we sought a direct in vivo method for tension measurements and mechanical characterization at cell contacts and developed an experimental approach combining optical tweezers with light-sheet microscopy.

To probe epithelial mechanics in a live organism, we chose the early epithelium of the Drosophila embryo as a model system. It consists of a simple sheet of cells that spread over the yolk and are in contact with each other through E-cadherin–based adhesion. During early embryogenesis at the blastula stage just after the end of cellularization, epithelial cells have very similar hexagonal shapes, suggesting that cell junctions have similar mechanical properties and that the internal pressure of these cells is homogeneous. At the later gastrula stage, cells undergo shape changes at distinct regions in the embryo. On the ventral side of the embryo, apical cell constriction of a few rows of cells drives tissue invagination (14), whereas on the ventrolateral side of the embryo, cell intercalation, a process whereby cells exchange neighbors by polarized remodeling of their junctions, drives tissue extension. The latter morphogenetic movement is driven by an anisotropic distribution of Myosin-II (Myo-II), which is more concentrated along junctions aligned with the dorsal/ventral (D/V) axis (15). Laser dissection of cortical actomyosin networks at cell junctions in the ventrolateral tissue has shown that such an anisotropic distribution of Myo-II causes an anisotropic cortical tension (6). However, the absolute values of tensile forces have not yet been measured, and more generally, the mechanics of cell–cell interfaces in vivo are largely unknown. Here, we addressed this issue by analyzing local mechanical measurements at cell junctions during tissue morphogenesis and determining the contribution of Myo-II to tension in this context. We determined the time-dependent response of cell–cell interfaces to forced deflection and delineated a viscoelastic model of junctions. Finally, we explored the propagation of local forces within the epithelial tissue.

Results and Discussion

To probe the mechanics of cell–cell interfaces, we devised a setup combining optical tweezers and light-sheet microscopy (Fig. 1A and Fig. S1). This combination allows imaging of a whole tissue at a high acquisition rate while manipulating objects in vivo. Light-sheet microscopy is also more advantageous than confocal microscopy, because it reduces photobleaching (15). Our light-sheet setup was designed from an upright microscope: a light sheet sections the sample horizontally, and the fluorescent light is collected by a high numerical aperture objective lens pointing downward (16) (Fig. 1A and Fig. S1). The laser trap is produced by a near-IR laser light focused by the collection objective lens into the sample and moved by galvanometric mirrors in the plane of the epithelium (Fig. 1A and Fig. S1). Optical tweezers experiments usually require the use of a glass or polystyrene bead to apply a force onto an attached molecule or cellular structure. We found that the cell–cell interfaces can be manipulated directly without the need of an external probe (Fig. 1B, three snapshots of deflected membrane interfaces and trap positions and C and Movie S1). It is likely that direct manipulation is possible because of a positive refraction index difference between the interface and the interior of the cells as revealed by quantitative phase imaging of the epithelial cells (Fig. S2). However, the value of this mismatch is difficult to determine because of the geometry of the tissue.

Fig. 1.

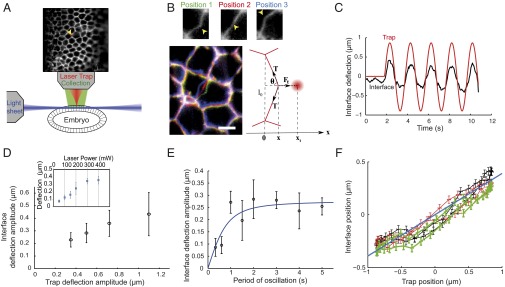
Characterizing the deflection of cell–cell interfaces imposed by optical tweezers. (A) Schematic of the setup. The embryo is optically sectioned by a light sheet and imaged while a laser trap (red) allows manipulation. Upper shows the epithelium labeled by a membrane marker (GAP43::mcherry) and the laser trap position (yellow arrowhead). (B) Separate images of the interface in three different positions of deflection (yellow arrowheads in Upper). Lower Left is a merge of Upper images (position 1 in green, position 2 in red, and position 3 in blue). Also, a schematic of deflection with distribution of forces labeled is in Lower Right. (Scale bar: 5 µm.) (C) Representative plot of deflection vs. time showing both trap (red line) and interface (black line) positions. (D) Amplitude of interface deflection as a function of trap movement amplitude and (Inset) laser trap power; 7–13 independent measurements per data point. Error bars represent 1 SD. (E) Interface deflection amplitude over the trap oscillation period. (F) Interface position as a function of trap position during a few cycles of laser oscillation (amplitude = 0.5 µm, period = 2 s). Successive cycles are in different colors (black, first cycle; red, second cycle; green, third cycle). The blue line represents a linear fit.

Using the direct application of the laser, we imposed a sinusoidal movement to the trap perpendicular to a cell interface and centered on it, and we imaged the resulting deflection in the adherens junction plane (Fig. 1C). The interface deflection followed the trap movement but with lower amplitude, suggesting that the interface resists the mechanical load imposed by the laser trap (Fig. 1C).

To explore the regime of deformation that the laser trap imposes to the interfaces, we varied the amplitude of the trap sinusoidal movement while keeping the period of oscillation constant. The amplitude of the interface deflection increases with the trap amplitude, but it deviates from a linear relationship for trap amplitude larger than 1 µm (Fig. 1D). Then, we varied the laser power while keeping the trap amplitude and the period of oscillation constant. We found that the interface deflection amplitude also increases linearly with the laser power up to 300 mW (Fig. 1D, Inset). Together, these results confirm that, in the case of small deformations (for comparison, the average length of an interface is 4.5 µm), the trap acts as a linear spring, with stiffness $k_t$ that is linearly proportional to the laser power. Therefore, all of the experiments are carried out within this range of deformation (<1-µm trap amplitude) and with power 200 mW unless otherwise stated.

To estimate the trap stiffness on the cell interfaces and thus, the forces directly applied by the laser, we implemented a two-step procedure using beads. First, we determined the trap stiffness on beads: single 0.46-µm-diameter beads injected in the cytosol were trapped and moved in a stepwise fashion between two trap positions separated by 0.5 µm (Fig. S3A). The resulting relaxation of the bead toward the new trap position was exponential. The characteristic time is set by the ratio of the drag coefficient, $6\pi \eta R$, over the trap stiffness on the bead, with $\eta$ as the viscosity and R as the bead radius. An effective value of the viscosity was estimated independently by analyzing bead motion in the cytosol in the absence of trap to measure its mean square displacement (Fig. S4) (17). Relating the diffusion constant $D$ to viscosity by the Stokes–Einstein equation ($k_B\mathrm{\Theta }=6\pi \eta DR$), where $k_B$ is the Boltzmann constant and $\mathrm{\Theta }$ is the temperature, we found that the effective viscosity of the cytosol is 3.6 ± 0.1 Pa⋅s (mean ± SE; 1,350 beads). Using this value, we could, thus, estimate the trap stiffness on beads to be 120 ± 50 pN⋅µm⁻¹ at 200-mW laser excitation (mean ± SD; 20 measurements). Second, we compared the deformation produced by direct application of the focused laser on the interface with that induced by beads pushed against the cell–cell interfaces (Fig. S3 B–D and Movie S2). The former was only two- to threefold larger than the latter (2.5 ± 0.4; mean ± SD; five measurements), indicating that the trap stiffness on the interfaces was two- to threefold smaller than that on beads. Thus, the trap stiffness on interfaces was estimated to be $k_t$ = 50 ± 30 pN⋅µm⁻¹ at 200-mW laser excitation and in the regime of small deformations.

The resistance to deformation can arise from not only the mechanical properties of the interface and its apposed cortical elements, including the actomyosin cytoskeleton, but also, the viscous cytosol. To determine whether the resistance to deformation is time-dependent, we varied the period of oscillation while keeping the trap amplitude constant (0.5 µm) (Fig. 1E). For periods larger than or equal to 1 s, which correspond to mean speeds smaller than 2 µm⋅s⁻¹, the amplitude was constant. The constancy of the deflection amplitude at speeds below 2 µm⋅s⁻¹ indicates that the force applied by the trap and that produced by the interface are in quasistatic equilibrium. At low speeds of deformation (speed < 2 µm⋅s⁻¹), we can, thus, assume that the shape of the interface mainly results from the balance of forces between the trapping force $F_t$ and the tension of the interface $T$: $F_t=2T\cos \theta$, where $\theta$ is the angle that the interface makes with respect to the trapping force (Fig. 1B). Because the vertices of the cell–cell contact did not move significantly during the deformation (Fig. S5), we could neglect the contribution of other cells and use this simple local equilibrium formula.

For small deformations (that is, for maximal deflections much smaller than the initial junction length l₀), $\text{cos}\theta \approx 2x/l_0$ and $F_t\approx k_t(x_t-x)$, where $x$ is the position of the interface, and $x_t$ is the position of the trap. The tension of the interface, thus, approximates as $T\approx k_t{l}_0\left(x_t/x-1\right)/4$. We found that, within experimental error, the ratio $x_t/x$ remains constant during periodic oscillations (Fig. 1F), indicating that the preexisting tension $T$ of the interface is not significantly modified during small deformations. Importantly, this result also implies that tension measurements, while relying on geometrical and physical approximations, do not require a mechanical model of cell contacts. Thus, tension values can be obtained as a simple linear function of the ratio between the interface deflection and the trap position. Using our estimate of $k_t$ = 50 pN⋅µm⁻¹ and the ratio $x_t/x$ = 1.88 ± 0.4 (mean ± SD; 16 measurements), we found that tension $T$ at cell–cell interfaces is on the order of 44 ± 22 pN at the end of cellularization. The tensions reported here are in the same range as cortical tensions measured on single cells (18) but two to three orders of magnitude below cell–cell forces in cell aggregates on adhesive substrates in vitro (12).

We observed that, for periods smaller than 1 s (speed > 2 µm⋅s⁻¹), the deflection was reduced (Fig. 1E). This loss of amplitude is the characteristic signature of viscous damping, presumably related to the viscous drag in the cytosol. To test whether damping was, indeed, caused by the viscosity of the cytosol, we performed relaxation experiments after instantaneous release of the trap (Fig. S6A). At the onset of relaxation, tension is balanced only by viscous damping: $2T\cos \theta =C_{\eta }{v}_0$, where $v_0$ is the initial relaxation velocity, and $C_{\eta }$ is the damping coefficient. Measuring $v_0$ (Fig. S6A) and using the mean tension value of 44 pN, this equation provided an indirect measurement of $C_{\eta }$, which is on the order of 2 ± 1 × 10⁻⁵ m⋅Pa⋅s. To determine viscosity, $C_{\eta }$ should be rescaled by both a typical length scale L of deformation and a geometric coefficient g: $\eta =C_{\eta }/Lg$. In the plane of junctions, the deformation extends to the whole contact line (4–5 µm). We found a similar value for the deformation along the apicobasal direction (Fig. S6B). The deformation is, thus, likely to be akin to a 2D Gaussian, with a typical width of 4–5 µm. Therefore, we took $L=4.5$ µm and $g=16$, which corresponds to disk approximation. The viscosity associated with the observed damping is, thus, on the order of 1 Pa⋅s, which is consistent with our previous measurements of cytosol viscosity using beads. This value is also consistent with microrheological measurements made in the cytosol of Caenorhabditis elegans embryo (19).

During tissue morphogenesis, cells undergo cell shape changes driven by Myo-II contractile events, which induce interface deformation at various speeds up to about 0.1 µm⋅s (20, 21). The condition of low speeds (speed < 2 µm⋅s⁻¹) is, thus, always fulfilled during cell shape changes driven by Myo-II contractility during tissue morphogenesis of Drosophila, indicating that short-time viscous damping should play no role in the process.

Using direct optical manipulation, we then probed how cell–cell tensions change during tissue morphogenesis of the early germ band of the Drosophila. Before gastrulation movements, at the end of stage 5, cells form a regular lattice with isotropic shapes (Fig. 2A, Top) (6, 22, 23). Later, at the end of stage 6 and the onset of stage 7, the total concentration of Myo-II increases at adherens junctions, and its distribution becomes anisotropic, with higher levels along interfaces parallel to the D/V axis (Fig. 2A, Middle and Bottom) (6, 22, 23). This anisotropic distribution of Myo-II has been shown to drive polarized junction shrinkage and cell intercalation (6, 22, 23). We found that the deflection amplitude of cell–cell interfaces caused by the optical trap is reduced by twofold from the end of stage 5 to the onset of stage 7, indicating a tension increase (Fig. 2B). Moreover, at stage 7, cell–cell interfaces with a direction close to the D/V axis are about 2.5 times more tense than those along the horizontal axis (Fig. 2C and Fig. S7, tension normalized to junction size). The anisotropy of tension is consistent with a previous report, which estimated the relative values of tension from laser nanodissection (6).

Fig. 2.

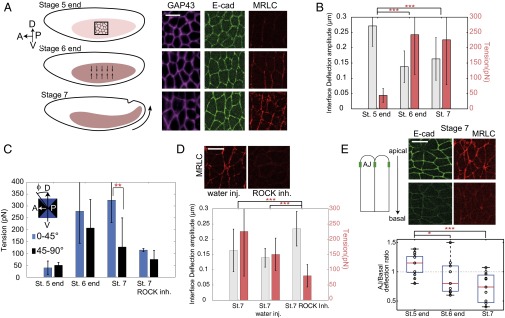
Tension at cell contacts before and during germ-band elongation in wild type (WT) and perturbed embryos. (A, Left) Schematic of tissue elongation and images at three different stages: before elongation (stage 5 end), at the onset of Myo-II accumulation at cell junctions (stage 6 end), and during tissue extension (stage 7). A, anterior; D, dorsal; P, posterior; V, ventral. (A, Right) Images showing the cell interface (purple, GAP43::mcherry), E-cadherin (E-cad; green), and Myo-II [red, regulatory light chain of Myo-II (MRLC)] at the different stages. (B) Interface deflection amplitude (gray bars) and tension (red bars) at the adherens junction plane for different stages (16, 24, and 14 different interfaces measured at stage 5 end, stage 6 end, and stage 7, respectively). (C) Interface deflection amplitude at different stages for different junction orientation along and perpendicular to the D/V axis. (D) Interface deflection amplitude (gray bars) and tension (red bars) in the adherens plane in Rho-associated protein kinase (ROCK) inhibitor-injected embryos and control embryos (WT, 14 interfaces; water-injected, 11 interfaces; ROCK inhibitor, 15 interfaces). Error bars represent 1 SD. (E) Ratio between the interface deflection at the adherens junction (AJ) plane and in a more basal plane (3 µm below the adherens junctions) at different stages. The red line is the median, the box edges are the lower and upper quartiles, and the whiskers display the total range of measurements. t Test. inh., inhibitor; inj., injected; St., stage. *Not significant; **P value < 0.01; ***P value < 0.001. (Scale bar: 10 µm.)

Inhibition of Myo-II activity by injection of Rho-associated protein kinase (ROCK) inhibitor resulted in a significant reduction of the tension at cell junctions at stage 7 (Fig. 2D) and a loss of tension anisotropy (Fig. 2C), which confirms that the significant increase in tension measured between stages 5 and 7 can be attributed to Myo-II activity. Given that a single molecular motor of Myo-II produces a few piconewtons of force (24), the range of forces measured here suggests that the increase in tensions from stage 5 to stage 7 could be powered by only a few dozens of motors.

The E-cadherin junctions, where we performed the experiments presented above, are restricted to a thin 1-µm section and localized about 1–2 µm below the apical surface (25, 26) (Fig. 2D, Upper Left). Because Myo-II accumulates at the adherens junction plane at the end of stage 6 and the onset of stage 7, we wondered if this might translate into different mechanical properties at the adherens junction plane compared with more basal positions. Measurements of interface deflection by laser trap at different positions along the apicobasal axis showed that, during tissue morphogenesis, there is a gradual polarization of the tension along this axis (Fig. 2E, Lower). Whereas at stage 5, tension at adherens junctions is the same as in a more basal plane, it becomes larger at stage 7. The fact that we measure the same deformation at the adherens junction plane and 3 µm more basally at stage 5 end when Myo-II is very apical and not junctional also suggests that the apical cortex does not have a significant contribution to the restoring force. Altogether, these results show that optical tweezers can be robustly used to measure tension at cell contacts in vivo and that this method can reveal planar-polarized as well as apicobasal anisotropies of tension in a developing organism.

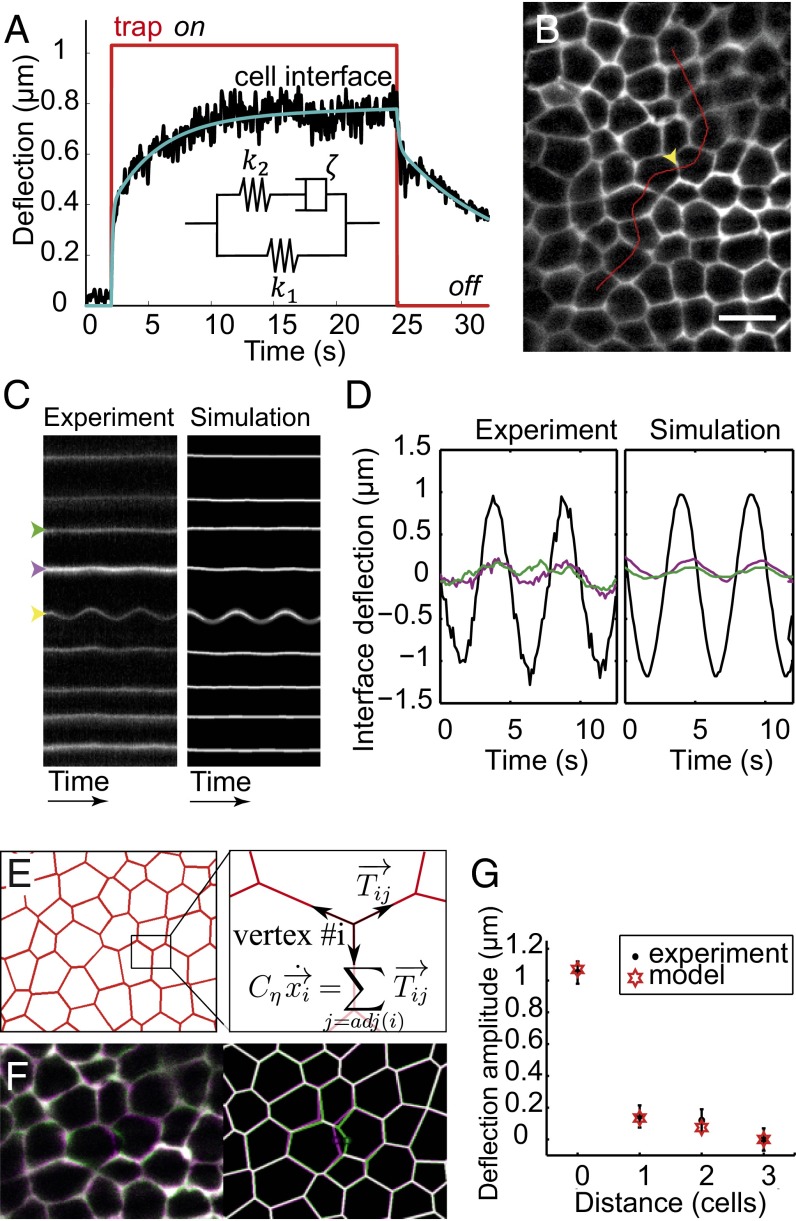
We then explored in more detail the mechanical response of cell–cell contacts to forced deflection at different temporal and spatial scales. First, we performed pull-and-release experiments, which have been used in vitro on single cells with optical and magnetic tweezers (27) but have never been applied in vivo. Pull-and-release experiments consist of switching the laser trap on and off at a few hundred nanometers distance from the junction and then monitoring the deflection of the cell–cell interface both toward (trap on) and away from (trap off) the trap (Fig. 3A). At these short timescales, the mechanical response of an epithelial tissue should result from both the constitutive mechanics of its actomyosin cortex and viscous friction exerted by the cytosol. In other words, modeling deflection dynamics requires both a cortical constitutive equation and a force balance equation between the cortical restoring force, the trapping force, and the viscous friction. The pull-and-release curves obtained show that the dynamics are not purely exponential and exhibit at least two characteristic times in the range of 1–10 s (Fig. 3A and Fig. S8A). We considered different types of viscoelastic constitutive models coupled to the force balance equation to fit the experimental data and found that a so-called standard linear solid (SLS) model, composed of a Maxwell arm (a spring and a dashpot) in parallel with a spring, is the best and simplest model to correctly account for the observed behavior (Fig. 3A, solid blue curve and Inset, SLS model). Indeed, we can rule out Kelvin–Voigt and Maxwell models, which predict simple exponential relaxation (Fig. S8B). Notably, the SLS model also fits well to the periodic experiments described above (Fig. 1E, solid blue curve). In particular, the 1-s timescale is consistent with the drop of deflection amplitude observed for periods of oscillation below 1 s, which can, therefore, be attributed to the viscous drag in the cytosol. The existence of another timescale (10 s) denotes the fact that the cortex itself is not purely elastic but viscoelastic (hence, the SLS model). These two timescales can be derived analytically; indeed, one is determined by the friction in the cytosol, whereas the other is given by the viscous component of the cortex constitutive equation. Importantly, both these viscoelastic timescales are under 1 min; neither the experiments nor the model deals with the long-term dynamics (minutes to hours), which presumably imply creep and therefore, fluid-like behavior (9, 28).

Fig. 3.

Mechanical model of the interface and tissue response. (A) Deflection of the interface in a pull-and-release (trap on–trap off) experiment. The model (blue line) accurately fits the experimental data (black). (Inset) The simplest analogous viscoelastic model is a Maxwell arm in parallel with a spring. For a trap stiffness, $k_t$ = 50 pN⋅μm⁻¹, and fit parameters values are $k_1$ = 15 pN⋅μm⁻¹, $k_2$ = 55 pN⋅μm⁻¹, $\zeta$ = 1.5 × 10⁻⁴ m⋅Pa⋅s, and $C_{\eta }$ = 1.5 × 10⁻⁵ m⋅Pa⋅s. Note that this value of $C_{\eta }$ is consistent with our previous estimate (2 ± 1 × 10⁻⁵ m⋅Pa⋅s). The same parameter values are used in the simulations. (B) Deflection perpendicular to the interfaces is tracked over time along lines perpendicular to cell interfaces (red), which allows measurement of deformation away from the targeted interface (yellow arrowhead). (Scale bar: 10 µm.) (C) Kymograph of interface deflections in the (Left) experimental and (Right) simulated tissues. Only the interfaces adjacent to the target interface display significant deflection. (D) Deflection of the target (black) and neighbor (at one- and two-cells distance; magenta and green, respectively) interfaces in the (Left) experimental and (Right) simulated tissues. (E) In the model, the movement of a vertex results from a balance between tension from adjacent bonds and viscous friction. (F) Overlay of the undeformed (purple) and deformed (green) tissue in the (Left) experimental and (Right) simulated tissue. (G) Spatial decay of interface deflections over the neighboring cells. Comparison between experiments and simulations.

During tissue morphogenesis, the integration of local forces shapes the tissue (1). Challenging questions are whether local forces produce long-range deformation and at what speed the mechanical information propagates. Thus, having established a model for the mechanics of single-cell interfaces, we then asked how single-cell deformation propagates throughout the tissue. We imposed the local deflection of a cell interface using sinusoidal oscillations, and we tracked the deflection of neighboring interfaces away from this point. For that purpose, we plotted kymographs along lines perpendicular to cell interfaces (Fig. 3B). The target interface was oscillated using a deflection amplitude of 1 ± 0.1 μm (Fig. 3C, Left), which is larger than in the experiments presented so far, to facilitate the detection of propagation. We observed that the neighboring interfaces within a distance of one to two cells also deflected periodically but with much lower amplitudes and a small phase shift (Fig. 3 C, Left and D, Left and Fig. S9 A–D), indicating that the deformation typically decays over a distance of one to two cells.

To evaluate the ability of our simple mechanical model to reproduce these data, we first transposed the single-junction model to a network of contacts as observed in vivo. Each contact is considered as an SLS element (again, with viscoelastic parameters $k_1$, $k_2$, and $\zeta$) pulling on its vertices (Fig. 3A). The displacement of each vertex then results from the force balance between tensile forces exerted by adjacent contacts and external damping, $C_{\eta }\dot{x}$, caused by cytosol viscosity (Fig. 3E). We were then able to simulate the mechanical response of the tissue to periodic manipulations in the extracted experimental geometry, imposing only the sinusoidal displacement at the midpoint of the target interface (Fig. 3F).

To quantitatively assess the accuracy of the model, we plotted kymographs in the simulated tissues along the same lines as in the experiments (Fig. 3C, Right and Fig. S9). The parameter values that we estimated from the single-interface experiments faithfully reproduce the tissue-scale observation: one or two neighboring cells deform away from the source point of deflection (Fig. 3 C, D, and G and Movie S3). The propagation is a bit more efficient transverse (Fig. S9C) than perpendicular to deformation (Fig. 3G). Taking higher or lower viscosity for the cytosol into account leads to shorter or longer propagation distance, respectively, which does not correctly reproduce the observed behavior (Fig. S9E). Note that our model underestimates the speed of propagation (Fig. 3D), which suggests that constant volume constraints and/or transmission through the apical cortex may contribute to propagation. The speed of propagation can be experimentally estimated by the phase delay between the trapped interface’s deflection and that of its neighbors (Fig. 3D, time shift between black and magenta curves). At a one-cell distance (∼7 μm), we measured a time delay of 150 ± 85 ms (95% confidence interval), which corresponds to a propagation speed with a typical phase velocity of 45 μm⋅s⁻¹. This speed is much larger than the speed of actomyosin flows, which are observed in different systems, including Drosophila and C. elegans (0.1 µm⋅s⁻¹) (21, 29).

Conclusion

Here, we studied the mechanical properties of cell–cell contacts during tissue morphogenesis and how local deformation propagates within a tissue. We provide absolute values of tensions at cell interfaces, whereas previous work estimated relative values based on assumptions of the viscous properties at cell junctions. Surprisingly, the small forces produced by optical tweezers are sufficient to produce significant deflection of cell interfaces, and we could estimate that tension at cell interfaces is in the 100-pN range during early stages of tissue morphogenesis. These findings suggest that the forces that remodel cell–cell contacts during tissue morphogenesis and drive the shrinkage or extension of cell contacts can be powered by a small number of molecular motors. Fluctuations in cell shape, which are observed during these events, might, thus, result from stochastic fluctuations in motor numbers.

The possibility of absolute tension measurements at cell contacts might be beneficial to force inference methods (2–4), which provide relative tensions based on the geometry of the contact network. It might, indeed, allow experimental validation of the inference and can also be used to calibrate the inferred tensions.

Our study has provided a predictive mechanical model of cell contacts. Modeling the constitutive mechanics of epithelia by quantifying how forces dynamically cause deformations is crucial for understanding epithelial morphogenesis events, which was suggested as early as 1981 in the pioneering work by Odell et al. (30). Since then, a variety of mechanical descriptions have been proposed; however, testing of the underlying hypotheses has been limited because of the lack of in vivo experimental tools. Notably, so-called vertex models (31), usually based on energy minimization, do not incorporate energy dissipation and thus, cannot predict the tissue dynamics. Here, we propose a vertex-based model, which bridges usual vertex models and continuum mechanics with finite elements approaches that integrate viscoelastic constitutive behavior (32, 33). In addition, it captures the nontrivial two-timescale relaxation dynamics evidenced by pull-and-release experiments. Finally, here, we intentionally restricted our analysis to timescales and speeds faster than the changes in contractility to deal with steady shape patterns. We believe that the approach that we have established here is now ready to explore additional timescales and probe long-term irreversible deformation of cell contacts.

Materials and Methods

Experiments and Data Analysis.

Optical manipulation was done using a custom-built two-colors (488 and 516 nm) light-sheet microscope (16) coupled with a single-beam gradient trap (1,070-nm wavelength, ytterbium fiber laser; IPG). A 100× water-immersion lens (1.1 N.A.; Nikon) was used for imaging as well as introducing the optical trap in the imaging plane. Galvanometric mirrors controlled laser trap position deflection to produce sinusoidal oscillations or step movements. Before every in vivo experiment, the relationship between galvanometer voltages and laser trap position was calibrated using fluorescent beads (localization precision of 25 nm). During experiments, both images and position of the galvanometers were simultaneously recorded. Kymographs of interface deflection were extracted from movies along lines perpendicular to the interfaces and fitted at each time step by a Gaussian to determine the interface position with subpixel resolution (localization precision of 35 nm).

Quantification of E-cadherin::GFP and Squash::GFP was done in a spinning-disk microscope (Perkin-Elmer) using a 100× oil immersion lens (Nikon).

Details on sample preparation are in SI Materials and Methods.

Model.

In the single-junction model (Figs. 1E, fit and 3A), the horizontal restoring force $f$ is related to the deflection $x$ of the interface through the SLS constitutive mechanics of the cortex:

$$\dot{f}+\frac{k_2}{\zeta }f=\left(k_1+k_2\right)\hspace{0.17em}\dot{x}+\frac{k_1{k}_2}{\zeta }x.$$

Variables k₁ and k₂ are elastic parameters (newtons per meter), $\zeta$ is a viscous parameter (meter⋅pascal⋅second), and the dot denotes a temporal derivative. The force balance at the interface simply reads

$$f=k_t\left(x_t-x\right)-C_{\eta }\dot{x},$$

where $k_t$ and $x_t$ are the stiffness and position of the optical trap, respectively, and $C_{\eta }$ is the damping coefficient in the cytosol. Combining these two equations yields two characteristic timescales: one related to $\zeta$ (the viscous component of the cortex) and one related to $C_{\eta }$ (the damping coefficient of the cytosol).

In the tissue-scale model, each bond has a viscoelastic dynamics given by the same model:

$$\dot{T}+\frac{k_2}{\zeta }T=\left(k_1+k_2\right)\hspace{0.17em}\dot{X}+\frac{k_1{k}_2}{\zeta }X,$$

where $T$ is the tension, and $X$ is the elongation. At vertex i, tensions of adjacent interfaces [j = adj(i)] are balanced only by viscous damping. The force balance, thus, is

$$C_{\eta }\dot{\overrightarrow{x_i}}={\displaystyle \sum }_{j=adj\left(i\right)}\overrightarrow{T_{ij\hspace{0.17em}}},$$

which provides direct access to vertices displacements. The midpoint of the target interface is treated as a two-way vertex in the simulations. Its movement is imposed to mimic the considered experiment.