Low spatial coherence electrically pumped semiconductor laser for speckle-free full-field imaging

Significance

There has been an intense search for the ideal light sources for high-speed, full-field imaging applications ranging from next-generation microscopes and laser projectors to digital holography and photolithography. Traditional lasers, although providing the required brightness (i.e., power per mode), exhibit high spatial coherence, which introduces coherent artifacts such as speckle, corrupting image formation. At the other extreme, low spatial coherence sources such as thermal sources and light emitting diodes (LEDs) avoid speckle but lack sufficient power per mode for high-speed imaging. In this work, we demonstrate a new type of semiconductor laser based on a chaotic cavity, which combines low spatial coherence with high power per mode. Such a laser could enable a wide range of full-field imaging applications.

Abstract

The spatial coherence of laser sources has limited their application to parallel imaging and projection due to coherent artifacts, such as speckle. In contrast, traditional incoherent light sources, such as thermal sources or light emitting diodes (LEDs), provide relatively low power per independent spatial mode. Here, we present a chip-scale, electrically pumped semiconductor laser based on a novel design, demonstrating high power per mode with much lower spatial coherence than conventional laser sources. The laser resonator was fabricated with a chaotic, D-shaped cavity optimized to achieve highly multimode lasing. Lasing occurs simultaneously and independently in ∼1,000 modes, and hence the total emission exhibits very low spatial coherence. Speckle-free full-field imaging is demonstrated using the chaotic cavity laser as the illumination source. The power per mode of the sample illumination is several orders of magnitude higher than that of a LED or thermal light source. Such a compact, low-cost source, which combines the low spatial coherence of a LED with the high spectral radiance of a laser, could enable a wide range of high-speed, full-field imaging and projection applications.

Spatial coherence is a defining characteristic of laser emission. High spatial coherence allows focusing electromagnetic energy to a small spot or collimation of an optical beam over a long distance. However, spatial coherence can also introduce coherent artifacts such as speckle, because any uncontrolled scattering in the imaging system can cause multipath interference. These artifacts have limited the use of lasers in full-field imaging applications ranging from traditional wide-field microscopes to laser projectors, holography, and photolithography systems. Instead, traditional low spatial coherence sources such as thermal light sources and light-emitting diodes (LEDs) are still used for illumination in most full-field imaging applications, despite having lower power per mode, poor collection efficiency, and less spectral control than lasers. These limitations are particularly pronounced in applications requiring high-speed imaging or imaging in absorbing or scattering media, prompting the use of raster-scanning–based laser imaging systems. For parallel imaging and projection applications, the ideal illumination source would combine the high power per mode of a laser with the low spatial coherence of an LED. The common approach to achieve this combination is by reducing the effective spatial coherence of a traditional laser using, e.g., a spinning diffuser (1), a colloidal solution (2), or a microelectromechanical mirror (3). However, these techniques require averaging over many speckle patterns in time, mitigating the advantage of using bright sources such as lasers or superluminescent diodes for high-speed imaging applications. Another approach to suppress speckle is by taking advantage of the low temporal coherence of broadband sources like superluminescent diodes (SLDs) and supercontinuum sources (4). However, these sources maintain high spatial coherence and still produce speckle with notable contrast in most imaging contexts (5). Moreover, this approach cannot be adopted for applications that rely on narrowband illumination such as deep UV photolithography with excimer lasers.

An alternative and more effective approach is to design a laser that generates light in an intermediate number of spatial modes, producing sufficiently low spatial coherence to suppress speckle, while maintaining higher power per mode than an LED or a thermal light source. To this end, we recently demonstrated that a random laser (5, 6) and a degenerate laser (7) can be engineered to efficiently control the spatial coherence of emission. However, the required optical pumping, together with the large size and cost of these systems, may limit their use outside of a research setting. Similar functionality has also been realized by combining many independent lasers to synthesize a low spatial coherence laser source. For example, a recently developed vertical cavity surface-emitting laser (VCSEL) array combines ∼1,000 mutually incoherent lasers on a single chip (8). However, this approach requires a relatively large chip because the lasers must be sufficiently separated to remain uncoupled. In addition, the individual VCSELs typically lase in a single longitudinal mode due to the short cavity length, limiting the ability to generate broadband emission required for imaging modalities such as optical coherence tomography (OCT) and laser ranging.

In this work, we demonstrate a chip-scale electrically pumped semiconductor laser that produces intense emission with low spatial coherence. Specifically, we designed a chaotic microcavity to support highly multimode lasing and experimentally realized lasing in ∼1,000 mutually incoherent modes in a single cavity. The lasing emission was used as an illumination source for speckle-free full-field imaging. The chaotic cavity laser was compared with a standard Fabry–Perot (FP) cavity laser that produced emission with high spatial coherence. The chaotic microcavity laser was fabricated by photolithography and wet etching and hence was relatively simple and compatible with mass production. The lasing performance was robust against cavity shape deformation and boundary roughness. Such a compact, low-cost laser with low spatial coherence and high radiance could enable a wide range of high-speed, full-field imaging and projection applications.

Results

Chaotic Cavity Design.

To achieve multimode lasing, the cavity must support a large number of resonances with a similar quality (Q) factor. The Q factor is proportional to the lifetime of a cavity resonant mode and inversely proportional to its lasing threshold. In the absence of gain saturation, the modes with similar Q would lase at a similar pump threshold. Thus, the second goal in the cavity design is to minimize mode competition for gain, so that the first few lasing modes do not deplete the gain and prevent other modes from lasing. A promising approach to satisfying these requirements was to use a 2D “chaotic cavity” design. The term refers to planar dielectric cavities in which the ray dynamics are chaotic over all or much of the phase space (9, 10). Such cavities do not lead to chaotic laser dynamics [as has been realized in other types of laser systems (11)]. Instead the presence of ray chaos leads to many pseudorandom spatial modes that, on average, fill the entire cavity uniformly (with independent Gaussian fluctuations on the wavelength scale). In such a cavity there will be no subset of strongly preferred high Q modes, and a large enough cavity of this type will support many modes with similar thresholds.

In this work, we used a fully chaotic cavity consisting of a disk of radius, R, with a section removed along a chord with length parameterized by r₀ as shown in Fig. 1A, referred to as a “D-shaped cavity.” This D-shaped geometry is known to support chaotic ray dynamics (12, 13) and has been used previously to improve the pumping efficiency of fiber amplifiers (14). Compared with an on-chip random laser that consists of numerous subwavelength scatterers (e.g., air holes) (15), the chaotic microcavity laser not only is simpler and less expensive to fabricate, but also has lower loss from out-of-plane scattering and nonradiative recombination of carriers at the semiconductor/air interface.

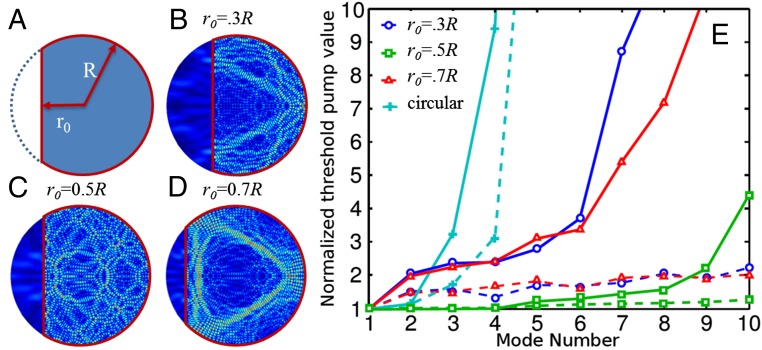
Fig. 1.

Design and simulation of D-cavity lasers to optimize multimode lasing. (A) A schematic of the D-shaped cavity that consists of a circle with a flat edge at a distance r₀ from the center. (B–D) Numerically calculated (false color) amplitude of the electric field distribution for the highest Q mode in cavities of radius R = 5 μm and r₀ = 0.3R, 0.5R, and 0.7R, respectively. The modes have transverse-magnetic (TM) polarization with the electric field perpendicular to the cavity plane. The mode in the cavity of r₀ = 0.5R displays the most uniform spatial intensity distribution. (E) Calculated pump thresholds of the first 10 lasing modes in four cavities of r₀ = R (circle), 0.7R, 0.5R, and 0.3R, normalized to the threshold of the first lasing mode. Dashed lines show noninteracting thresholds reflecting the Q-value distribution of the passive cavity. The r₀ = 0.5R cavity has the narrowest distribution of Q values, which is favorable for multimode lasing at relatively low pump values. Solid lines show interacting thresholds, calculated from SALT up to the fifth lasing threshold and extrapolated using the single-pole approximation (SPA)-SALT approximation (17) up to the 10th lasing threshold. Mode competition causes the actual thresholds to increase compared with the noninteracting estimates, but has the weakest effect for the r₀ = 0.5R cavity shape (due to reduced localization of the lasing modes as discussed in the text). Hence the r₀ = 0.5R cavity is optimal for maximizing the number of lasing modes.

In a circular cavity, light can be confined by total internal reflection at the cavity boundary, forming a whispering gallery mode (WGM) with a small leakage rate and a high Q factor. By introducing the flat cut, the high-Q WGMs of a circular cavity are eliminated (SI Text). If one neglects outcoupling loss and treats the system as an ideal “billiard,” then, for 0 < r₀ < R, it has been shown (9, 10) that the ray motion is fully chaotic, meaning that no stable periodic ray orbits exist. Quantizing the wave equation on such a domain will lead to many chaotic modes, spread over the full cavity, with similar Q values and hence a similar lasing threshold. Although the system is fully chaotic for all values of r₀, as the value of r₀ approaches zero or R, the cavity approaches the nonchaotic limit (of a full or semicircle) and exhibits weaker instability in the ray motion leading to wave solutions that are much less random and uniform in space. Thus, one would expect the optimal value for generating states with similar Q values is r₀ = 0.5R.

However, narrowing the distribution of lasing thresholds by designing a cavity to have similar Q values is only one aspect of maximizing the number of lasing modes. One must also reduce the mode competition that prevents modes with somewhat lower Q values from turning on once the first few modes are lasing. One cannot evaluate this effect using only Q values and a linear analysis; it is determined by nonlinear cross-gain saturation and spatial hole burning in the active cavity. Because chaotic modes overlap in space, it is not immediately clear that mode competition is minimized by choosing the geometry with the most chaotic wave solutions.

To address this question theoretically we use steady-state ab initio laser theory (SALT), a relatively new approach, which treats the cavity geometry and modal interactions exactly, assuming that a stable multimode steady state exists (16–18). Specifically, we investigate the effect of mode competition on the lasing thresholds as a function of cavity shape and compare the results to the expected thresholds in the absence of mode competition (Fig. 1E). First, we investigate the effect of the Q-value distribution alone, without including mode competition. The dashed lines connecting the data points in Fig. 1E are the noninteracting pump thresholds for the first 10 lasing modes calculated for a circular microdisk and three D-shaped cavities with varying values of r₀. For each cavity shape, the pump was normalized to be unity at the first threshold. As expected, the lowest (normalized) thresholds for each mode (n = 2, 3, … 10) occur for r₀ = 0.5R; this reflects the narrow distribution of Q values in the most chaotic cavity shape. In contrast, e.g., for the circular cavity, there are two high-Q whispering gallery modes that turn on at nearly the same pump value and then the next modes within the gain spectrum have much lower Q and require much higher relative pumps to reach threshold.

Next, we present the full nonlinear calculation at a pump value corresponding to five modes lasing, shown by the data points joined by the solid lines in Fig. 1E. This demonstrates the additional effect of mode competition. Once the laser is significantly above threshold, so that the effects of gain saturation are strong, all cavity shapes have their corresponding thresholds pushed to higher pump values, reducing the number of modes lasing at a given pump. The difference between the dashed and solid lines represents the effect of mode competition. The simulations clearly show that the most chaotic cavity, with r₀ = 0.5R, has the weakest mode competition and the largest number of modes lasing for the same normalized pump. Fig. 1 A–C illustrates the qualitative reason for this behavior. For the less chaotic shapes (r₀ = 0.3R, 0.7R, shown in Fig. 1 B and D), the lasing modes are still somewhat localized in space, apparently near some unstable periodic orbits closer to the boundary. The spatial localization of these modes makes their mode competition stronger, clamps the gain, and makes it difficult for many modes to lase simultaneously. The extreme case, of course, is the circular cavity, for which the high-Q WGMs are all highly peaked close to the cavity boundary, and the fourth lasing mode turns on at 9.5 times the first threshold pump, whereas the D-shaped cavity laser with r₀ = 0.5R has a fourth mode threshold only 2% higher than the first threshold. Note that the cavities we simulated are much smaller than those we fabricated, due to numerical constraints on 2D calculations of this type. In the larger cavities used in our experiments many more modes are expected to lase simultaneously for the same pump and shape. Nevertheless, the simulations were a valuable guide for determining the optimal cavity design, as confirmed by the experiments.

Experimental Realization of the D Cavity Laser.

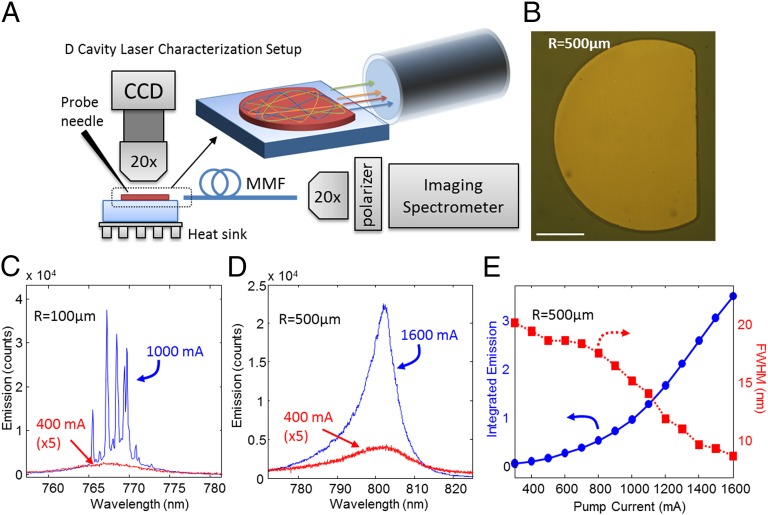
We then fabricated the D-shaped cavity with the optimized geometry of r₀ = 0.5R. To realize lasing with electrical pumping, we used a commercial laser diode wafer consisting of a P-I-N junction with gain provided by a GaAs quantum well. D-shaped cavities with radius R ranging from 100 μm to 500 μm were fabricated using standard photolithography and wet etching techniques and characterized using the experimental setup shown schematically in Fig. 2A. The optical image of a D cavity of R = 500 μm is shown in Fig. 2B.

Fig. 2.

Experimental realization of the D-cavity laser. (A) Schematic of the experimental setup to characterize the D-cavity laser. A microscope is used to image the chip from above to align the probe needle to a single cavity. Electrical current is injected through the needle to the cavity, and the emission is collected from the edge of the cavity with a multimode fiber as shown in Inset. The end facet of the multimode fiber is then imaged by a 20× objective onto the entrance slit of an imaging spectrometer through a linear polarizer. (B) Optical microscope image of the R = 500-μm D cavity taken from above. (Scale bar, 250 μm.) (C) The emission spectra collected from a D cavity with R = 100 μm and r₀ = 0.5R at a pump current of 400 mA (red line) and 1,000 mA (blue line). The emission spectrum collected at 400 mA was magnified 5× for clarity. At 1,000 mA, discrete narrow peaks appear in the emission spectrum. (D) The emission spectra collected from a D cavity with R = 500 μm and r₀ = 0.5R at a pump current of 400 mA (red line) and 1600 mA (blue line). A dramatic narrowing of the emission spectrum was observed at high pump current. (E) Spectrally integrated emission intensity and emission bandwidth as a function of the pump current for the D cavity with R = 500 μm and r₀ = 0.5R. As the emission intensity grows nonlinearly with the pump current, the emission bandwidth drops quickly.

To reduce thermal effects, the pump current was turned on for 1 μs and repeated at a rate of 1 kHz. At low pump current, the electroluminescence spectrum of the quantum well was broad and smooth (red line in Fig. 2 C and D). As the pump current increased, the emission spectrum narrowed due to amplification of spontaneous emission (ASE). When the current exceeded a threshold value, discrete narrow peaks appeared in the emission spectra of smaller D cavities (e.g., R = 100 μm or 250 μm), as seen in Fig. 2C. The full width at half maximum (FWHM) of these peaks is less than 0.1 nm. The intensity of these peaks grew rapidly with pump current. These results indicate the onset of lasing action. The number of lasing peaks increased with the cavity size as expected and merged to a continuous band in the cavities of R = 500 μm (blue line in Fig. 2D). The spectrally integrated emission intensity grew superlinearly with the current (blue circles in Fig. 2E), whereas the emission bandwidth (defined by the FWHM) was reduced (red squares in Fig. 2E). These data provide further evidence for lasing. Note that the light–current (L-I) curve did not exhibit an abrupt transition, because the measured emission was from a large number of modes with slightly different lasing thresholds. We also note that the emission spectrum in the R = 100-μm cavity was blue shifted by ∼35 nm compared with the R = 500-μm cavity. This blue shift is attributed to the increased pump current density required to achieve lasing in the smaller cavity that supported lower Q modes. We also tested lasing in a FP cavity and a circular microdisk cavity fabricated on the same wafer as the D-shaped cavity. The FP cavity consisted of a 2-mm-long and 100-μm-wide ridge waveguide with the semiconductor–air interfaces at both cleaved ends acting as mirrors. The FP-cavity laser displayed a sharp threshold in the L-I curve and a narrow emission spectrum with FWHM ∼ 0.3 nm above threshold (SI Text). The circular microdisk cavity with a radius of 100 μm displayed a similar lasing behavior and a relatively narrow emission spectrum consisting of a few peaks above threshold (SI Text).

Spatial Coherence Characterization.

Next we characterized the spatial coherence of the D-cavity laser and the FP-cavity laser by collecting emission with a 1-m-long, step-index multimode fiber (core diameter = 105 μm, numerical aperture = 0.22) and measuring the speckle contrast at the end of the fiber. Speckle is formed in a multimode fiber by interference of the guided modes with different propagation constants. The speckle contrast is defined as C = σ_I/<I>, where σ_I is the SD of the intensity and <I> is the average intensity. Because the chaotic lasing modes in the D cavities have different emission patterns, they will excite the fiber modes with different relative phase and amplitude, thus generating distinct speckle patterns. If these modes lase independently, then their emission is mutually incoherent and they do not interfere, causing their speckle patterns to add in intensity. Thus, the speckle contrast, C, decreases as C = M^−1/2, where M is the number of uncorrelated speckle patterns (19). Hence, from the speckle contrast at the end of the multimode fiber, we can estimate the number of independent lasing modes in the cavity. Because polarization mixing in the fiber could also reduce the speckle contrast, a linear polarizer was placed in front of the camera to eliminate this effect. In addition, a multimode fiber may reduce the effective spatial coherence of broadband emission (4), which was ignored in our estimation of the number of independent lasing modes, as justified in Methods.

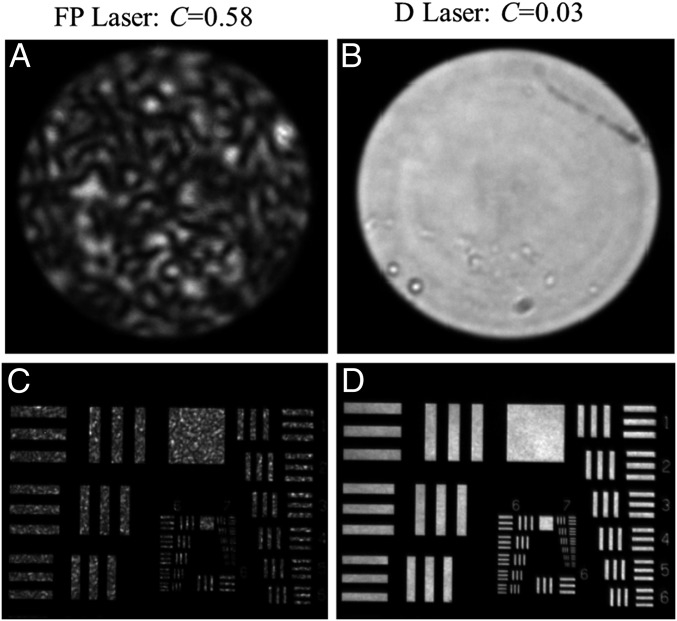
An optical image of the speckle pattern at the output facet of the multimode fiber by emission from the FP-cavity laser is shown in Fig. 3A. This speckle pattern was recorded during a 1-μs interval of current injection; however, the speckle pattern remained unchanged over multiple intervals, indicating that the same lasing modes were excited each time. The size of the speckle grains at the end of the multimode fiber is dictated by the numerical aperture of the multimode fiber, whereas the speckle contrast is determined by the number of mutually incoherent lasing modes coupled into the fiber. The FP-cavity laser emission produced high-contrast speckle, revealing high spatial coherence. The measured speckle contrast was C = 0.58, implying that the FP-cavity laser supported only ∼3 independent transverse modes. Although the FP cavity was made of a 100-μm-wide ridge waveguide that supports ∼450 transverse modes, strong mode competition in this cavity limited lasing to just a few transverse modes. In contrast, the D-cavity laser emission produced speckle with very low contrast, as seen in Fig. 3B. The measured contrast of C = 0.03 suggested that ∼1,000 modes lased simultaneously and independently in the D cavity, as a result of suppression of mode competition. The low speckle contrast in Fig. 3B confirms that the D-cavity laser produced emission with low spatial coherence suitable for full-field imaging applications We also characterized the spatial coherence of the 100-μm radius D-shaped cavity and the 100-μm radius circular microdisk (SI Text). We found that the 100-μm radius D-shaped cavity produced speckle with contrast of ∼0.1, indicating lasing in ∼100 modes, whereas the circular microdisk produced speckle with contrast of ∼0.25, indicating lasing in ∼15 modes, confirming that the chaotic cavity shape plays an essential role in reducing the spatial coherence of the laser emission.

Fig. 3.

Spatial coherence of the D-cavity laser and application to full-field imaging. (A and B) Optical images of the speckle pattern at the end of a 1-m-long multimode fiber by emission from the FP-cavity laser (A) and the D-cavity laser (B). The FP-cavity laser emission produced high-contrast speckle (C = 0.58), indicating that lasing was limited to ∼3 transverse modes, whereas the D-cavity laser produced low-contrast speckle (C = 0.03), implying independent lasing in ∼1,000 modes. (C and D) The emission from the end of the multimode fiber was used to illuminate an Air Force resolution test chart in transmission mode through an immobile ground glass diffuser. The high spatial coherence of the FP-cavity laser produced a speckled image (C) whereas the low spatial coherence of the D-laser emission gave a high-quality image with low speckle contrast (D).

Speckle-Free Imaging.

Finally, we demonstrated that the D-cavity lasers could be used as an illumination source for full-field speckle-free imaging. The laser output from the sidewall of the D cavity provides a line emission that is coherent in the direction perpendicular to the cavity plane and incoherent in the direction parallel to the cavity plane. Such a line source may be directly applied to line scanning in parallel OCT or confocal imaging. Alternatively, we can make a 2D incoherent light source by coupling the laser emission to a multimode fiber. The fiber mixes the degrees of spatial coherence in different directions, making the degree of spatial coherence (or incoherence) isotropic. We used the output from the multimode fiber to illuminate an Air Force resolution test chart in transmission mode through an immobile ground glass diffuser (Thorlabs DG10-600-MD). Fig. 3 C and D shows the images of the Air Force test chart illuminated by the FP-cavity laser and the D-cavity laser. The speckle, clearly seen with the FP-cavity laser illumination, was not visible with the D-cavity laser illumination.

In addition to providing speckle-free illumination, the D-cavity laser produces much higher power per mode than traditional low spatial coherence sources such as thermal light sources and LEDs. This is because the D-cavity laser concentrates emission in ∼1,000 spatial modes, whereas thermal sources and LEDs, with the spatial coherence length on the order of a wavelength, distribute light in many more spatial modes. From an imaging perspective, thermal light sources and LEDs are very inefficient, because only ∼1,000 modes are required to suppress speckle below the level observable by humans (20). As a quantitative comparison, we estimated the photon degeneracy of the D laser, a measure of the number of photons per coherence volume. The photon degeneracy parameter δ = (P δz)/(hν c M), where P is the emission power, δz is the temporal coherence length, hν is the photon energy, c is the speed of light, and M is the number of spatial modes (21). The temporal coherence length of the R = 500-μm D-cavity laser was estimated to be δz = 35 μm based on the 8-nm emission bandwidth. The output from the D-cavity laser is nearly isotropic in the plane of the disk, and the multimode fiber collected ∼15% of the total emission, which was ∼4 mW during the 1-μs pump pulse. The estimated value of δ is ∼10², which is four to five orders of magnitude higher than that of a thermal source (at 4,000 K δ ∼ 10⁻³) (21) and of a high-efficiency LED (δ ∼ 10⁻²) (22). The greatly improved photon degeneracy could be used to achieve much higher imaging speeds in light-limited full-field imaging applications. Moreover, we expect that with proper packaging and thermal management, the D-cavity laser will operate in a continuous wave (CW) at even higher power. Also, it may be possible to improve the emission collection efficiency by optimizing the chaotic cavity shape for directional emission or adding a reflecting boundary along the circular edge of the D cavity. In addition, the pulsed operation of D-cavity lasers may be used for speckle-free stroboscopic imaging (23).

Discussion

Finally, we compare the D-cavity laser to SLDs based on ASE, which share some similar characteristics. For example, both the D-cavity laser and SLDs exhibit a superlinear increase of emission intensity with pump and produce relatively broadband emission. However, SLDs maintain relatively high spatial coherence and cannot be used in full-field imaging applications without producing speckle. This is because the SLDs are typically realized in a ridge waveguide geometry where gain competition suppresses the amplification of high-order transverse spatial modes. The key distinction between a SLD and a traditional laser is that SLDs exhibit low temporal coherence (and hence broadband emission). This has made SLDs a popular light source for applications such as OCT that require broadband emission with high power per mode. By contrast, the D-cavity laser achieves both low temporal coherence and low spatial coherence. Moreover, from a full-field imaging perspective, the distinction between ASE and laser emission is less important than achieving low spatial coherence while maintaining high photon degeneracy. The D-cavity laser matches these requirements and illustrates the potential for tailoring the spatial and temporal coherence of lasers for target application.

In summary, we have demonstrated a chip-scale, electrically pumped semiconductor laser that combines low spatial coherence and high power per mode. The chaotic cavity shape was selected and optimized to enable highly multimode lasing. We fabricated the D-cavity laser with standard photolithography and wet chemical etching. It supported ∼1,000 independent lasing modes, combining to produce low spatial coherence emission. We confirmed that the laser emission could be used as an illumination source for speckle-free full-field imaging. By designing the laser to support enough spatial modes to suppress speckle, without the overabundance of modes present in traditional low spatial coherence sources, much higher power per mode was reached. Such a compact, low-cost, and bright source with low spatial coherence could enable a wide range of high-speed, full-field imaging and ranging applications.

Methods

Modeling.

The modeling presented in Fig. 1 was performed using SALT. We considered uniform pumping of the cavity and used open boundary conditions. The 2D cavity has an effective index of refraction 3.5 and is surrounded by air. The gain spectrum is centered at 1,000 nm with a full width at half maximum of 30 nm.

Wafer Structure.

The D-cavity laser was fabricated using a commercial laser diode wafer consisting of a P-I-N junction (Q-Photonics QEWLD-808). The epitaxial structure was grown on an n-type GaAs wafer and consisted of a 1,500-nm n-type Al_0.55Ga_0.45As layer, an undoped 200-nm Al_0.3Ga_0.7As layer with a 10-nm GaAs quantum well in the center, a 1,500-nm p-type Al_0.55Ga_0.45As layer, and a 300-nm p-type GaAs contact layer. With current injection, the AlGaAs quantum well provides optical gain near λ = 800 nm. The layered structure results in vertical confinement of light in the undoped Al_0.3Ga_0.7As layer via index guiding. The fundamental guided mode has the peak intensity at the location of the GaAs quantum well and experiences the highest gain.

Laser Fabrication.

The D cavities were fabricated by photolithography and wet etching. Once the cavity shape was defined by photolithography, electrical contacts consisting of 20 nm of Ti and 300 nm of Au were deposited by electron-beam evaporation. After liftoff, the metal contacts were used as etch masks and the wafer was wet etched to a depth of ∼2 μm in a solution of phosphoric acid and hydrogen peroxide in water. This etching depth exceeds the waveguiding layer of Al_0.3Ga_0.7As, ensuring that light in the guided mode experienced a high refractive index contrast at the boundary of the D cavity due to the semiconductor–air interface. This high index contrast ensured strong optical confinement and formation of high-Q resonances that experienced total internal reflection for a wide range of incident angles. Finally, a backside electrical contact consisting of 25 nm of Ni and 350 nm of AuGe was deposited via electron beam evaporation. For comparison, standard FP cavities in ridge waveguide geometry were fabricated on the same wafer.

Optical Characterization.

The experimental setup for lasing characterization is drawn schematically in Fig. 2A. Electrical current was injected through the top contact with a Tungsten probe needle. The emission was then collected with a multimode fiber and directed to the entrance slit of a spectrometer (Acton Research Corporation Spectra Pro-300i). The emission spectrum was recorded as a function of pump current. The sample was mounted on a heat sink and operated at room temperature. To reduce thermal effects, the pump current was turned on for 1 μs and repeated at a rate of 1 kHz. Because 1 μs was much longer than the response times of the material and the cavity, the system reached quasi-steady state.

Spatial Coherence Characterization.

The contrast of the speckle pattern formed at the end facet of a multimode fiber was used to estimate the number of mutually incoherent lasing modes coupled into the fiber. However, a multimode fiber may reduce the effective spatial coherence of broadband emission (4), if the linewidth of individual lasing modes exceeds the spectral correlation width of the fiber (24). The spectral correlation width determines the change in wavelength required to produce an uncorrelated (distinct) speckle pattern. Our estimation of the number of independent lasing modes assumed that the spectral width of each lasing mode was smaller than the spectral correlation width of the fiber (∼0.1 nm), consistent with the observation of narrow lasing peaks of width <0.1 nm from smaller D cavities. In the FP-cavity laser, there could be numerous longitudinal modes that correspond to a single transverse mode, but all these longitudinal modes would have the same emission pattern and create identical speckle in the fiber. Hence, only different transverse modes generated distinct speckle patterns and reduced the speckle contrast.