Highlight text
Combining experimental and theoretical approaches to characterize the carbon acquisition of a cyanobacterium, this paper improves interpretations of C isotope fractionation by accounting for the important role of intracellular C cycling.
Key words: Carbon acquisition, carbon-concentrating mechanism (CCM), CO2, cyanobacteria, leakage, NDH, ocean acidification.
Abstract
To predict effects of climate change on phytoplankton, it is crucial to understand how their mechanisms for carbon acquisition respond to environmental conditions. Aiming to shed light on the responses of extra- and intracellular inorganic C (Ci) fluxes, the cyanobacterium Trichodesmium erythraeum IMS101 was grown with different nitrogen sources (N2 vs NO3 –) and pCO2 levels (380 vs 1400 µatm). Cellular Ci fluxes were assessed by combining membrane inlet mass spectrometry (MIMS), 13C fractionation measurements, and modelling. Aside from a significant decrease in Ci affinity at elevated pCO2 and changes in CO2 efflux with different N sources, extracellular Ci fluxes estimated by MIMS were largely unaffected by the treatments. 13C fractionation during biomass production, however, increased with pCO2, irrespective of the N source. Strong discrepancies were observed in CO2 leakage estimates obtained by MIMS and a 13C-based approach, which further increased under elevated pCO2. These offsets could be explained by applying a model that comprises extracellular CO2 and HCO3 – fluxes as well as internal Ci cycling around the carboxysome via the CO2 uptake facilitator NDH-14. Assuming unidirectional, kinetic fractionation between CO2 and HCO3 – in the cytosol or enzymatic fractionation by NDH-14, both significantly improved the comparability of leakage estimates. Our results highlight the importance of internal Ci cycling for 13C composition as well as cellular energy budgets of Trichodesmium, which ought to be considered in process studies on climate change effects.
Introduction
Cyanobacteria are ancient organisms responsible for oxygenation of the atmosphere during times when CO2 concentrations were about two orders of magnitude higher than today (cf. Buick, 1992; Kasting and Siefert, 2002). Possibly due to their origin at that time, the CO2-fixing enzyme RubisCO of cyanobacteria has one of the lowest affinities among all autotrophic organisms (Badger et al., 1998; Tortell, 2000). Consequently, cyanobacteria are dependent on high activities of carbon-concentrating mechanisms (CCM) for increasing the CO2 concentration in the vicinity of RubisCO. Currently, due to ongoing anthropogenic CO2 combustion, the availability and speciation of inorganic C (Ci) in seawater is changing at a rapid pace (IPCC, 2007). In view of this ocean acidification (Caldeira and Wickett, 2003), a number of studies in recent years have focused on the mechanisms of C acquisition and CO2 responses of different groups of phytoplankton (e.g. Rost et al., 2008). Among these studies, the abundant N2-fixing cyanobacterium Trichodesmium stands out by showing an exceptionally high stimulation of biomass production and N2 fixation in response to elevated pCO2 (e.g. Hutchins et al., 2007; Levitan et al., 2007; Kranz et al., 2009). Further studies on the underlying reasons for these CO2 effects show a decrease in Ci affinity at high pCO2 (Kranz et al., 2009; Kranz et al., 2010). Given the high energy demand of the CCM in cyanobacteria, a reallocation of energy between Ci acquisition and N2 fixation was suggested to stimulate production at high pCO2 (Kranz et al., 2010).
Cellular Ci affinities of Trichodesmium are determined by the interplay of several transporters and structural adaptations composing the CCM. In order to understand pCO2 responses of the CCM as well as potential changes in energy demand, it is necessary to distinguish between these different components. While CO2 can diffuse through the cell membrane without energy investments, the low equilibrium concentrations, slow interconversion with HCO3 – (Zeebe and Wolf-Gladrow, 2007), and its tendency to leak out of the cell compromise the use of CO2 as the predominant Ci source. Therefore, cyanobacteria have evolved energy-dependent transporters for taking up HCO3 –, which can be accumulated in the cell more efficiently (Badger et al., 2006). Trichodesmium has been found to cover ~90% of its C demand using HCO3 – (Kranz et al., 2009; Kranz et al., 2010). Uptake of HCO3 – in this species is catalysed by the Na+-dependent transporter BicA, which is fuelled by Na+/HCO3 – symport or via an H+/Na+ antiport mechanism (Price et al., 2008).
Cyanobacterial RubisCO is localized in distinct compartments within the cell, the so-called carboxysomes. The protein shells of these microbodies are permeable to HCO3 – but pose a diffusion barrier for CO2 (Dou et al., 2008; Espie and Kimber, 2011), allowing significant accumulation of CO2 in the vicinity of RubisCO. Inside the carboxysomes, transformation of HCO3 – to CO2 is accelerated by carbonic anhydrase (CA; reviewed by Espie and Kimber, 2011). In addition to direct HCO3 – uptake and CO2 diffusion, CO2 uptake in Trichodesmium is facilitated by the NDH-14 complex, which converts CO2 to HCO3 – in the cytoplasm, presumably in a CA-like reaction (Price et al., 2002). The protein complex is thought to be located on the thylakoid membrane and form part of the photosynthetic/respiratory electron transport chain, being fuelled by electrons donated from NADPH or ferredoxin, which are subsequently transferred to the plastoquinone pool (Price et al., 2002). After the hydration of CO2, a proton is thought to be released into the thylakoid lumen, contributing to the pH gradient necessary for ATP synthesis and making the reaction irreversible in the light (Price et al., 2002).
Conversion of CO2 to HCO3 – by the NDH complex has been proposed to drive internal Ci recycling to minimize loss via CO2 efflux (Maeda et al., 2002; Price et al., 2002). Due to the strong CO2 accumulation required in cyanobacteria, CO2 efflux is a major challenge in these organisms. Despite the interplay of the carboxysome and proposed recapture of CO2 by the NDH-14 complex, efflux of CO2 has been shown to equal ~50–90% of gross Ci uptake in Trichodesmium (Kranz et al., 2009; Kranz et al., 2010). Next to the C source (CO2 vs HCO3 –), leakage (i.e. CO2 efflux : gross Ci uptake) can strongly affect isotopic composition of organic C produced during photosynthesis (Burkhardt et al. 1999, Sharkey and Berry, 1985), and thus measurements of 13C fractionation can provide complementary information on this aspect of CCM regulation (e.g. Laws et al., 1997; Keller and Morel, 1999; Rost et al., 2006; Tchernov and Lipschultz, 2008). In fact, differences in leakage estimates based on membrane inlet mass spectrometry (MIMS; Badger et al., 1994) and C isotope fractionation (Sharkey and Berry, 1985) have been attributed to internal Ci cycling driven by NDH (Kranz et al., 2010).
In a previous study (Eichner et al., 2014), the energy allocation to different physiological processes in Trichodesmium under varying energetic states was addressed by altering the cellular energy budget through addition of different nitrogen sources: while N2 fixation is a highly energy-demanding process with a high demand for ATP, NO3 – requires very little ATP (only for uptake) but instead has a high electron demand. The study highlighted the dependence of energy reallocation on the stoichiometry in energy demands (ATP vs NADPH) of the different pathways involved. The energy demand of the CCM in Trichodesmium remains uncertain, however, especially because the regulation of internal Ci fluxes is as yet poorly characterized. To shed light on the extra- and intracellular Ci fluxes under the different energetic conditions, Trichodesmium was grown with different pCO2 levels and N sources (N2 vs NO3 –), and a combination of different methods, including MIMS and 13C fractionation measurements, as well as modelling, was employed. While MIMS provides a useful tool to investigate Ci fluxes across the cell membrane, internal fluxes cannot be directly measured and were therefore modelled. Model calculations of internal Ci fluxes made use of the measured extracellular Ci fluxes and the isotopic composition of particulate organic C (δ13CPOC), which reflects the integrated effects of extra- and intracellular Ci fluxes. Hereby, a common model of 13C fractionation (Sharkey and Berry, 1985) was extended by including internal fluxes around the carboxysome.
Materials and methods
Culture conditions
Trichodesmium erythraeum IMS101 was grown in semi-continuous batch cultures at 25°C and 150 μmol photons m–2 s–1 with a 12 h : 12h light : dark cycle. Cultures were grown in 0.2-μm-filtered artificial seawater (YBCII medium; Chen et al., 1996) and kept in exponential growth phase by regular dilution with culture medium. Culture bottles were continuously bubbled with 0.2-μm-filtered air with pCO2 levels of 380 and 1400 μatm. Prior to experiments, cells were allowed to acclimate to the respective pCO2 for at least 2 weeks. Cultures in which pH had drifted by >0.09 units compared to cell-free reference media were excluded from further analysis. In treatments with NO3 – as the N source, 0.2-μm-filtered NaNO3 was added to achieve mean concentrations of 97±2 µmol l–1 in the experiments, and these never fell below 65 µmol l–1. Cultures were acclimated to NO3 – for at least 1 week before measurements. Samples for the analysis of dissolved inorganic C (DIC) were filtered through 0.2 μm filters and measured colourimetrically (QuAAtro autoanalyzer, Seal, Norderstedt, Germany). Average precision was ±5 μmol kg–1. The pH values of the acclimation media were measured potentiometrically (pH meter pH3110, WTW, Weilheim, Germany). For further details on culture conditions as well as carbonate chemistry parameters, see Eichner et al. (2014).
MIMS measurements
Cellular Ci fluxes (Fig. 1) were obtained using a custom-made MIMS system (Rost et al., 2007), applying a disequilibrium approach described by Badger et al. (1994). Assays were performed in YBCII medium buffered with HEPES (50mM, pH 8.0) at acclimation temperature and light intensity, unless otherwise specified. To account for the diurnal cycle of Ci fluxes in Trichodesmium, measurements were performed three times over the day, during time intervals from 0 to 1.5, 5.5 to 7, and 9 to 10.5h after beginning of the photoperiod. CO2 and O2 fluxes were measured as a function of DIC, starting with concentrations close to zero (media bubbled with CO2-free air), which were subsequently increased by step-wise addition of NaHCO3 up to concentrations of ~5000 μM. As the assay medium is buffered, unlike the conditions during acclimation of the cells, the HCO3 –:CO2 ratio stayed constant over the investigated DIC range. DIC-saturated rates of photosynthesis (Vmax) and half-saturation concentrations [K1/2 (DIC)] were obtained by fitting a Michaelis-Menten function to the data. Net O2 evolution was converted to C fixation (F fix) assuming a photosynthetic quotient (PQ) of 1.34 (Williams and Robertson, 1991). Net CO2 uptake (F cyt, netCO2) was calculated from the steady-state rate of CO2 depletion at the end of the light period and corrected for the CO2/HCO3 – interconversion in the medium (F ext, db). Using C fixation and net CO2 uptake, HCO3 – uptake rates (F cyt, HCO3–) could be derived by a mass balance equation:
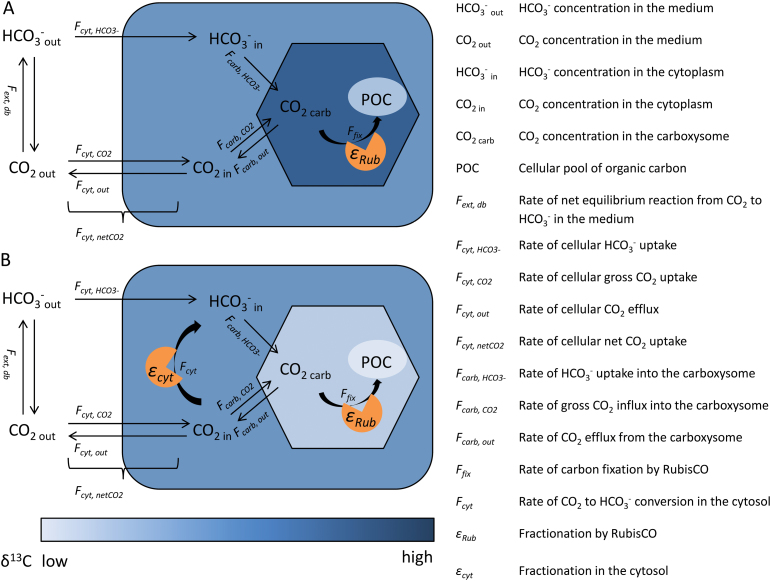
Fig. 1.
Schematic diagram showing the cellular Ci pools and fluxes characterized by measurements and modelling. Fluxes and concentrations in the external medium and fluxes over the cell membrane as well as C fixation (F fix) were measured by MIMS, while fluxes in and out of the carboxysome were modelled. Shading intensity denotes δ13C values of different cellular C pools (including POC and Ci in the cytosol and carboxysome). (A) Fractionation during C fixation by RubisCO leads to depletion of POC in 13C and enrichment of 13C in the carboxysomal Ci pool. (B) Fractionation during internal Ci cycling, e.g. via NDH, leads to 13C depletion of the carboxysomal Ci pool. Consequently, the POC formed is isotopically lighter than in scenario A. This figure is available in colour at JXB online.
| (1) |
For normalization of the CO2 and O2 traces, duplicate samples for chlorophyll a (chl a) analysis were taken after each measurement. Chl a was extracted in acetone for >12h and determined fluorometrically (TD-700 fluorometer, Turner Designs, Sunnyvale, CA, USA; Holm-Hansen and Rieman, 1978).
Leakage estimation
Cellular leakage was estimated by two different methods. Firstly, leakage was determined by MIMS measurements using the disequilibrium approach (Badger et al., 1994). Cellular leakage (L MIMS) is defined as the ratio of CO2 efflux (F cyt, out) to gross Ci uptake [i.e. the sum of HCO3 – (F cyt, HCO3–) and gross CO2 uptake (F cyt, CO2)]:
| (2) |
F cyt, out was estimated from the initial increase in CO2 concentration after switching off the light (Badger et al., 1994). These estimates are based on the assumption that the rate of diffusive CO2 efflux during the light phase is well represented by the rate of CO2 efflux during the first ~20 s of the subsequent dark phase. As leakage calculated by this approach is based on O2 measurements that are converted to C fluxes, the sensitivity to different PQ values was tested by varying PQ between 1.0 and 1.7, yielding deviations of not more than 15% of leakage estimates (i.e. 0.06 units).
In the second approach, leakage was estimated from the isotopic fractionation during POC formation (ε p), which was calculated from the difference in isotopic composition between POC (δ13CPOC) and CO2 (δ13CCO2) in the medium according to Freeman and Hayes (1992). Duplicate samples for analysis of δ13CPOC were filtered onto pre-combusted GF/F filters and acidified with 200 μl HCL (0.2M) to remove all Ci prior to analysis. δ13CPOC was measured with an EA mass spectrometer (ANCA SL 2020, SerCon Ltd, Crewe, UK). For analysis of the isotopic composition of DIC (δ13CDIC), filtered samples were fixed with HgCl2 (final concentration 110mg l–1). Subsequent to acidification of the samples, isotopic composition of CO2 in the headspace was analysed with an isotope ratio mass spectrometer (GasBench-II coupled to Delta-V advantage, Thermo, Bremen, Germany). The isotopic composition of CO2 was calculated from δ13CDIC, following a mass balance equation (Zeebe and Wolf-Gladrow, 2007). Leakage (L 13C) was subsequently derived using an extended equation from Sharkey and Berry (1985):
| (3) |
where ε Rub is the intrinsic discrimination of 13C by RubisCO (assumed to be +25‰; Roeske and O’Leary, 1984; Guy et al., 1993) and ε db represents the equilibrium fractionation between CO2 and HCO3 – (–9‰; Mook et al., 1974). The fractional contribution of HCO3 – to gross Ci uptake (a cyt), being introduced by Burkhardt et al. (1999), has been determined by MIMS measurements for the respective treatments. These calculations assume an equilibrium situation and further consider the cell as a single compartment.
Results and discussion
General CCM characteristics
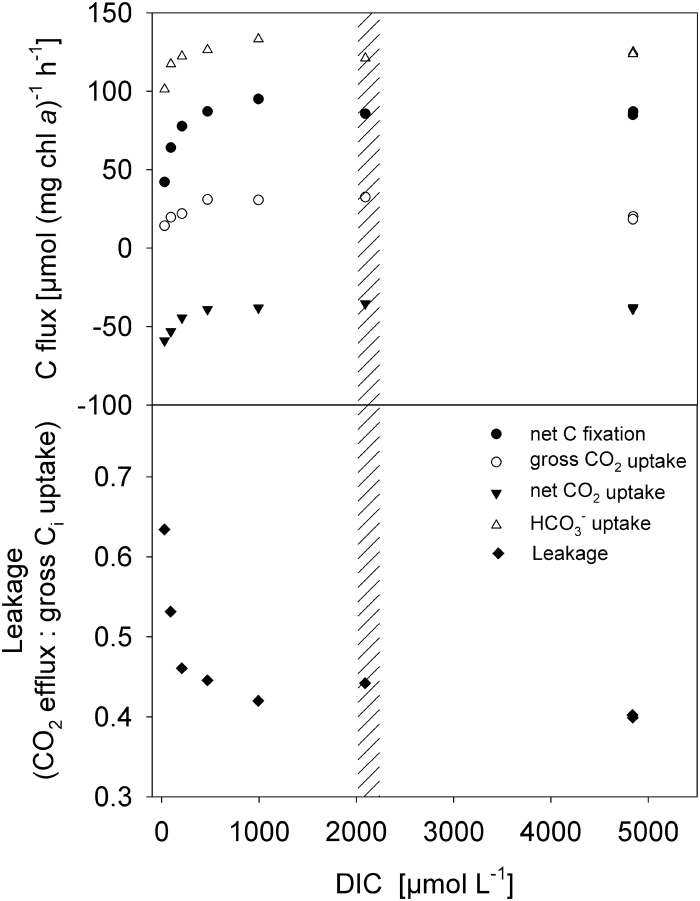
MIMS measurements showed a highly efficient CCM with a high capacity for regulation of Ci affinity over the diurnal cycle as well as with different pCO2 levels, in agreement with previous studies on Trichodesmium (e.g. Kranz et al., 2009; Kranz et al., 2010). Half-saturation DIC concentrations for C fixation (K1/2) ranged between ~20 and 500 µmol DIC l–1 (Supplementary Figure S1), which is equivalent to ~0.2 and 4 µmol CO2 l–1 and is thus substantially lower than the KM of cyanobacterial RubisCO (105–185 µmol CO2 l–1; Badger et al., 1998). Taking the ratio of KM to K1/2 as a measure of CO2 accumulation in the vicinity of RubisCO (assuming a KM of 150 µmol CO2 l–1), our data suggest accumulation factors between ~35 and 900 and indicate that the degree of RubisCO saturation is always larger than 80%. Accordingly, under the applied external CO2 concentrations, concentrations in the carboxysome typically exceed 600 µmol CO2 l–1. The CCM was primarily based on active HCO3 – uptake, accounting for 82±4% of gross Ci uptake (Table 1). As gross Ci uptake was approximately twice as high as net C fixation at acclimation DIC (~2100 µmol CO2 l–1), leakage measured by MIMS ranged between 0.3 and 0.7 (i.e. CO2 efflux equalled 30–70% of gross Ci uptake; Table 1). As a consequence of the high HCO3 – contribution and the high CO2 efflux, the net fluxes of CO2 were generally directed out of the cell (cf. negative values for net CO2 uptake: Table 1, Fig. 2).
Table 1.
Diurnal cycle of Ci fluxes measured by MIMS under acclimation DIC levels (~2100 µmol l–1) in Trichodesmium acclimated to two different pCO2 levels (380 vs 1400 µatm) and N sources (N2 vs NO3 –)a
| 380 µatm –NO3 – | 380 µatm +NO3 – | 1400 µatm –NO3 – | 1400 µatm +NO3 – | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Morning | Midday | Evening | Morning | Midday | Evening | Morning | Midday | Evening | Morning | Midday | Evening | |
| Net C fixation | 91±15 | 57±14 | 87±3 | 95±20 | 56±22 | 70±18 | 80±13 | 39±14 | 61±4 | 91 | 61±19 | 63±16 |
| Gross Ci uptake | 157±18 | 144±24 | 167±17 | 135±23 | 128±16 | 143±25 | 144±7 | 124±9 | 142±6 | 144 | 127±22 | 131±17 |
| HCO3 – uptake | 134±18 | 117±22 | 133±12 | 118±21 | 108±14 | 113±14 | 126±11 | 95±9 | 112±2 | 120 | 97±17 | 102±12 |
| Gross CO2 uptake | 23±4 | 27±4 | 34±6 | 17±3 | 20±2 | 30±13 | 18±4 | 28±5 | 30±6 | 24 | 30±9 | 29±6 |
| Net CO2 uptake | –45±10 | –60±12 | –46±9 | –23±2 | –52±8 | –42±11 | –46±5 | –56±8 | –51±4 | –28 | –36±8 | –39±9 |
| HCO3 –:Ci uptake | 0.85±0.03 | 0.81±0.03 | 0.80±0.02 | 0.87±0.01 | 0.84±0.01 | 0.80±0.06 | 0.88±0.03 | 0.77±0.04 | 0.79±0.03 | 0.83 | 0.76±0.05 | 0.78±0.01 |
| CO2 efflux | 69±12 | 87±13 | 79±13 | 40±3 | 72±6 | 72±8 | 64±7 | 85±14 | 81±3 | 53 | 66±4 | 67±10 |
| Leakage | 0.44±0.05 | 0.61±0.05 | 0.47±0.03 | 0.30±0.03 | 0.57±0.11 | 0.51±0.04 | 0.45±0.07 | 0.69±0.10 | 0.57±0.01 | 0.37 | 0.53±0.07 | 0.52±0.07 |
a All Ci fluxes are given in µmol C (mg chl a)–1 h–1. Errors are standard deviations for biological replicates (1 SD; n = 3 except 1400 +NO3 – morning with n = 1).
Fig. 2.
Example showing the dependence of Ci fluxes measured by MIMS in Trichodesmium on the DIC concentration in the assay. Data shown were measured in the evening in a culture grown at 380 µatm pCO2 without NO3 –. The shaded area denotes the range of acclimation DIC levels.
Diurnal changes in Ci fluxes
The diurnal cycle was characterized by low K1/2 values in the morning and a downregulation of C fixation rates at midday (ANOVA, P < 0.001; Supplementary Figure S1A and B). Leakage estimated by MIMS at acclimation DIC was lowest in the morning, increased towards midday, and decreased again towards the evening (ANOVA, P < 0.05; Table 1). Leakage estimates for DIC levels approaching zero (obtained by curve fits of leakage plotted over DIC concentration; Fig. 2) varied even more over the course of the day, yielding values around 0.3 in the mornings, while at midday and in the evening ratios approached 1.0 (data not shown). These diurnal changes in leakage could be explained by the concurrent changes in the ratio of HCO3 – to CO2 uptake (Table 1, Supplementary Figure 1C), which were characterized by low CO2 fluxes in the mornings (ANOVA, P < 0.05; Table 1), while HCO3 – uptake was higher in the morning than at midday, and increased again towards the evening (ANOVA, P < 0.05; Table 1). Over the day, a higher share of HCO3 – uptake, which is less prone to diffuse out of the cell, was thus correlated with lower leakage.
Effects of different pCO2 levels and N sources
The affinity for Ci was downregulated at elevated pCO2, as indicated by high K1/2 values under these conditions (Supplementary Figure 1B). Under acclimation DIC, however, Ci fluxes (C fixation, Ci uptake, and CO2 uptake and efflux) were not significantly affected by pCO2 (ANOVA, P > 0.05; Table 1), reflecting the cells’ capacity to achieve similar C fixation over a range of pCO2 levels by regulating their CCM. Regarding the N source, C fixation rates and CO2 uptake under acclimation DIC were equally unaffected (ANOVA, P > 0.05; Table 1). Although cells mainly used HCO3 – as a Ci source in all treatments, HCO3 – uptake at acclimation DIC decreased slightly with increasing pCO2 (~10%; ANOVA, P < 0.05; Table 1, Supplementary Figure 1C), but was not affected by N source (ANOVA, P > 0.05; Table 1). Interestingly, CO2 efflux was affected by the N source (ANOVA, P < 0.01; Table 1), with ~20% lower efflux in NO3 – users compared to N2 fixers, possibly due to differences in internal pH caused by the uptake/accumulation of NO3 – vs NH4 + in the cell. One could also speculate that growing cells on NO3 – reduces the general membrane permeability, since NH4 + transfer between cells is only necessary under N2-fixing conditions, which could also affect the permeability for CO2. Leakage at acclimation DIC estimated by MIMS was, however, not significantly affected by pCO2 or N source at any time of the day (ANOVA, P > 0.05; Table 1).
Offsets in leakage estimates
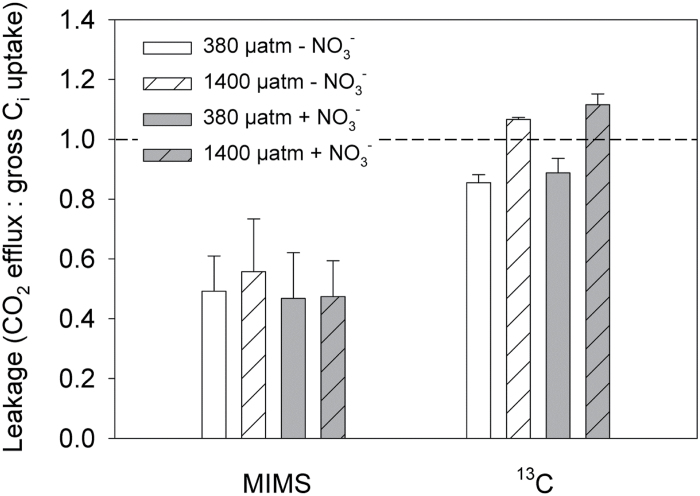
High leakage values obtained in MIMS measurements reflect the strong Ci accumulation necessary for C fixation in cyanobacteria due to the poor CO2 affinity of their RubisCO. However, leakage estimates obtained from δ13C values (L 13C, eqn 3) even exceeded MIMS-based estimates. Overall fractionation during formation of POC (ε p) was not significantly affected by N treatment (ANOVA, P > 0.05) but increased with pCO2 (ANOVA, P < 0.0001), ranging from 14.4±1.0‰ at 380 µatm to 19.9±0.9‰ at 1400 µatm pCO2. Consequently, leakage estimates based on ε p (eqn 3) also increased with pCO2, while estimates from MIMS measurements at acclimation DIC were constant over the range of pCO2 levels. L 13C was calculated to range between 0.82 and 1.14, exceeding MIMS-based measurements by ~30–60% (Fig. 3) and even reaching theoretically impossible values (>1). A similar discrepancy between these two approaches, which was equally dependent on pCO2 acclimation, has been observed previously (Kranz et al., 2010). In the following paragraph, possible reasons for the deviations between estimates are outlined.
Fig. 3.
Leakage estimates by MIMS (mean values of measurements conducted at three time points over the day; Badger et al., 1994) and 13C fractionation (Sharkey and Berry, 1985) determined in Trichodesmium grown under two pCO2 levels and N sources (n ≥ 3).
Following the approach by Badger et al. (1994), leakage is directly calculated from the measured CO2 efflux and gross Ci uptake. As CO2 efflux cannot readily be determined during the light due to the concurrent Ci uptake, the rise in the CO2 signal directly after switching off the light is taken as an estimate of CO2 efflux during the light phase, assuming that the accumulated Ci pool and therewith gross CO2 efflux are initially at the pre-darkness level (Badger et al., 1994). If active Ci uptake as well as C fixation by RubisCO do not cease immediately upon darkening, leakage estimates could be biased and likely to be underestimated. Despite these potential uncertainties, this is a more direct approach than the alternative method, which infers leakage from the isotopic composition of cells. The 13C-based approach makes use of the effect of leakage on ε p (eqn 3; Sharkey and Berry, 1985). Briefly, while the intrinsic fractionation by RubisCO (ε Rub) generally causes organic material to be depleted in 13C (Fig. 1A), variation in ε p can be induced by changes in the Ci source and/or leakage. Consequently, any errors in estimates of ε Rub or a cyt, but also any unaccounted process affecting ε p, would cause 13C-based leakage estimates to be biased.
Kranz et al. (2010) suggested that internal Ci cycling within the cell may affect ε p in general. The CO2 dependence of the offset between MIMS- and 13C-based leakage estimates was furthermore suggested to reflect a CO2 effect on the NDH complex driving this internal Ci cycling (Kranz et al., 2010), in line with early observations of the Ci dependence of CO2 uptake by the NDH complex (Price and Badger, 1989a,c). In Fig. 1, the effects of internal Ci cycling on isotopic composition are illustrated. While Fig. 1A assumes an equilibrium situation and does not include any internal Ci cycling, Fig. 1B illustrates non-equilibrium situations caused by internal Ci cycling. The degree of 13C enrichment in the cytosol and within the carboxysome, according to this concept, would be dependent on the type of kinetic fractionation in the cytosol. This could include complete or incomplete unidirectional fractionation as well as enzymatic fractionation by the NDH complex. Accounting for these processes requires the introduction of a second compartment. The approach taken here can be considered as an extension of the model of Sharkey and Berry (1985), which considers the cell as one compartment. In order to avoid errors being introduced by large uncertainties, e.g. in permeability of the plasma membrane and carboxysome in Trichodesmium, a flux-based model that is independent of these assumptions is employed, rather than a full kinetic model. Our approach is similar to the model of Schulz et al. (2007), but disequilibrium situations are also considered.
Internal Ci fluxes and fractionation—model setup
To test our concept (Fig. 1) and quantitatively describe the possible effect of internal cycling on δ13C, intracellular Ci fluxes and their effects on isotopic ratios in different cellular Ci pools were modelled. For parameterizations, HCO3 – and gross CO2 fluxes measured by MIMS as well as measured fractionation values ε p were used. The model is based on flux balance equations for the individual isotope species. The flux balance of total C (12C + 13C) in the cytosol and in the carboxysome, respectively, is given by the following equations:
| (4) |
| (5) |
As about 99% of C is 12C, i.e. , the flux balance equations for 13C can be derived by multiplying the fluxes (F) with the isotopic ratio R = 13C/12C. The isotopic fractionation factor α db is defined by the isotopic ratio of CO2 divided by the isotopic ratio of HCO3 –, i.e. . Using the equilibrium fractionation (ε db), the fractionation factor between CO2 and HCO3 - can be calculated for the external medium as well as for the cytosol according to:
| (6) |
| (7) |
While the equilibrium value ε db is –9‰ (i.e. CO2 is isotopically lighter than HCO3 –; Mook et al., 1974), ε cyt can significantly deviate from this value due to kinetic effects. The uncatalysed conversion of HCO3 – to CO2 shows a kinetic fractionation of –22‰, whereas the formation of HCO3 – from CO2 is associated with a kinetic fractionation of +13‰ (Marlier and O’Leary, 1984). Hence, the actual value of ε cyt is determined by the disequilibrium between CO2 and HCO3 – in the cytosol, which depends on all fluxes in and out of the cytosol, and on the internal CO2 and HCO3 – concentrations, which cannot be calculated in the framework of a flux-based model. Assuming a unidirectional conversion of CO2 to HCO3 – in the cytosol, a value of +13‰ for ε cyt will be adopted. By setting ε cyt to +30‰, a potential fractionation by the NDH-14 complex will be taken into account. The situation where the conversion of CO2 to HCO3 – in the cytosol is not completely unidirectional will be considered by setting ε cyt to +8‰.
The R associated with F fix can be written in terms of the isotopic fractionation against 13C by RubisCO described by the factor α Rub = R carb / R POC, where R carb is the isotopic ratio of CO2 in the carboxysome and R POC is the isotopic ratio of POC. The value of α Rub is calculated from the intrinsic RubisCO fractionation ε Rub (assuming an intermediate value of +25‰; Roeske and O’Leary, 1984; Guy et al., 1993):
| (8) |
Given the isotopic ratios (R) of CO2 and the isotopic fractionation factors between HCO3 – and CO2 expressed as α bd = 1/α db, the flux balance equations for 13C can be derived from eqns 4 and 5 for the cytosol and the carboxysome, respectively:
| (9) |
| (10) |
R cyt is the isotopic ratio of CO2 in the cytosol. The overall isotopic fractionation by the cell is defined with respect to the isotopic composition of CO2 in the external medium (R ext):
| (11) |
The ratio R ext/R carb reflects the impact of the inner compartment on the isotopic fractionation and can be calculated from flux balance eqns 9 and 10. Eqn 10 can be solved for R cyt, which in turn is substituted into eqn 9, yielding the ratio:
| (12) |
This solution is valid for arbitrary combinations of fluxes as long as the constraints imposed by flux balance equations 4 and 5 are obeyed:
| (13) |
Given the fractional contribution of HCO3 – to total Ci uptake into the cytosol (a cyt) and the carboxysome (a carb), as well as the leakage out of the cytosol (L cyt) and the carboxysome (L carb), eqns 6 to 8 and 11 to 13 can be used to derive the overall isotopic fractionation:
| (14) |
Solving the approximated solution for L cyt yields the following:
| (15) |
The approximate solution can be considered as a generalization of the original function given by Sharkey and Berry (1985), accounting for two compartments. The authors assumed that the cell takes up HCO3 – into a single compartment and subsequently converts it to CO2; hence there is no HCO3 – inside the cell. The compatibility of our model with the original function can be confirmed by comparing ε p for L carb = 1 (i.e. no second compartment) and a carb = 0 (i.e. only CO2 uptake into the carboxysome).
As pointed out by Schulz et al. (2007), diffusive CO2 fluxes generally need to be added to cellular fluxes measured by MIMS (Badger et al., 1994) when relating them to 13C fractionation. For membrane permeability exceeding 10–4 cm s–1, as proposed for a diatom (~10–2 cm s–1; Hopkinson et al., 2011), diffusive CO2 fluxes are high and internal CO2 concentrations approach those of the cell’s exterior (Supplementary Figure S2). In this case, gross CO2 efflux estimated by MIMS would be underestimated, which could explain part of the discrepancy between MIMS-based leakage and estimates based on eqn 4 (Sharkey and Berry, 1985). While there is, to our knowledge, no recent data on the membrane permeability of cyanobacteria available, older studies on cyanobacteria state significantly lower values, approaching 10–5 cm s–1 (Badger et al., 1985; Marcus et al., 1986), which are in line with diffusive CO2 fluxes being low enough to allow for considerable CO2 accumulation in the cell (Supplementary Figure S2). Using this permeability, the effect of diffusive CO2 influx on leakage obtained by our model was estimated, yielding maximum changes in the order of a few percent, which were thus neglected. In view of the uncertainties in this parameter, measurements of membrane permeability of cyanobacteria are needed to improve future estimates of internal C fluxes.
Internal Ci fluxes and fractionation—model application
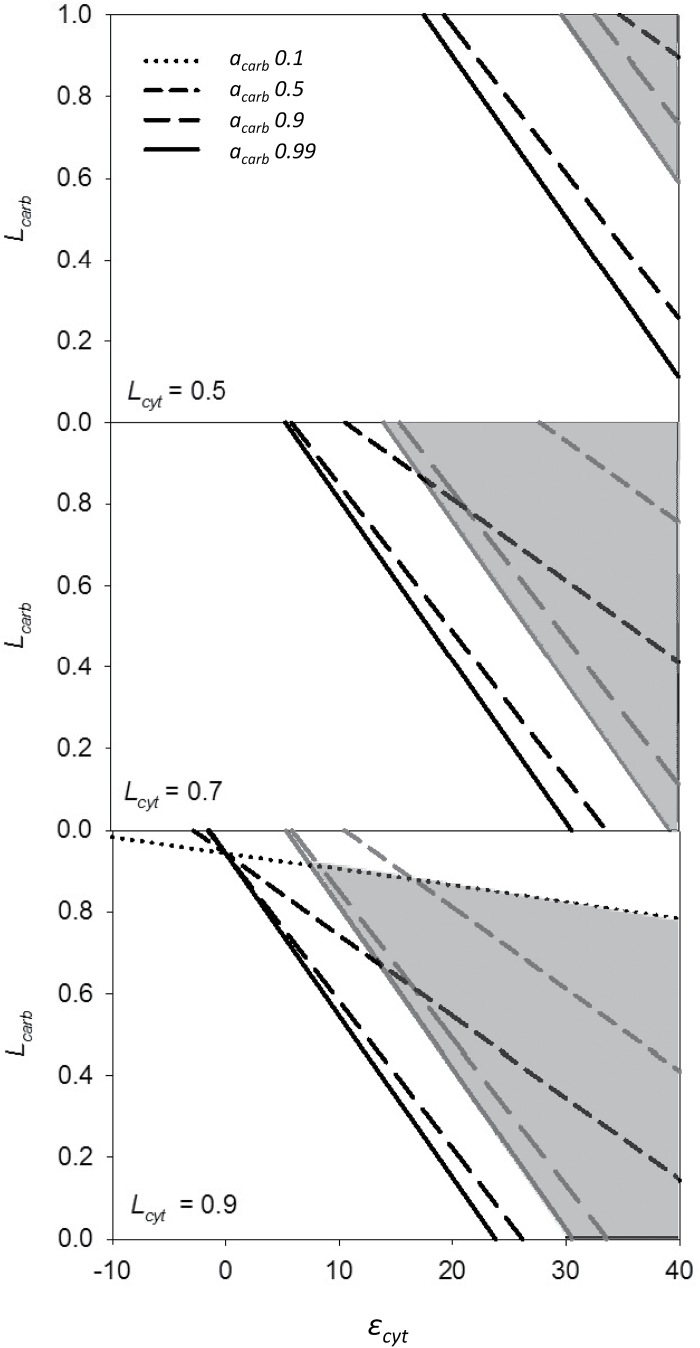
To test the sensitivity of our model, the potential effect of changes in a cyt on ε p was quantified, using the maximum variability observed in our study (0.84 vs 0.76) while leaving all other parameters constant. This variability can explain a change in ε p by not more than 0.7‰. Thus, a cyt can be excluded as a main driver behind the variability in ε p (or leakage estimates), even if variability in a cyt is severely underestimated. Applying the model to our measured fluxes and ε p values, a range of different possible scenarios for intracellular fluxes and fractionation in the cytosol is obtained (Fig. 4).
Fig. 4.
Interrelationship between L carb, ε cyt, and a carb in the model, depicted for different values of L cyt and ε p. The shaded areas mark the range of possible values for L carb and ε cyt that could reconcile our measurements of isotopic composition with measured external Ci fluxes. Black and grey lines are based on ε p measured in cells acclimated to 380 and 1400 µatm pCO2, respectively.
According to these interrelations, while at L cyt according to our MIMS measurements (0.5), only a very high fractionation in the cytosol (ε cyt) can explain our results, at L cyt ≥ 0.7, there is a large range of possible combinations of parameters (see shaded areas in Fig. 4). As we aim to find parameters that can explain ε p in both of our pCO2 treatments, the high ε p measured in cells grown at 1400 µatm constrains the range of possible values, while εp of cells grown at 380 µatm could be explained by a larger range of values for a carb and L carb (Fig. 4). High values for a carb and L carb (both approaching 1) allow for a larger range of possible values of ε cyt to explain our measured ε p (Fig. 4). Due to the high contribution of HCO3 – to Ci uptake and the additional conversion of CO2 to HCO3 – by the NDH complex, a carb is likely to be close to 1, most probably exceeding a cyt measured in our experiment (0.82). Moreover, high diffusive CO2 influx into the carboxysome seems unlikely in view of the supposed function of the carboxysome as a diffusion barrier to CO2 (e.g. Reinhold et al., 1989). While comparison experiments with CA knockout mutants with intact and broken carboxysomes confirmed that the carboxysome shell impedes diffusion of CO2 (Dou et al., 2008), the pores in the hexamer protein subunits of the shell are supposed to be permeable to small, negatively charged molecules such as HCO3 – (Tsai et al., 2007; Klein et al., 2009; Espie and Kimber, 2011). Despite the low CO2 permeability, high rates of CO2 efflux, and thus high L carb, are likely due to the very high accumulation factor (two to three orders of magnitude; this study and Kaplan et al., 1980). A value for L carb of 0.9 is therefore used in the model scenarios described in the following (Table 2). Using eqn 13, the following expression for the ratio of internal to external Ci fluxes can be derived:
Table 2.
Different scenarios of external and internal Ci fluxes that can reconcile measurements of Ci fluxes by MIMS and ε p values obtained in this study (scenarios 1, 2 and 4 to 6) and by Kranz et al. (2010, scenario 3)a
| Scenario | pCO2 | ε p | a cyt | L MIMS | L 13C | L cyt | L carb | a carb | ε cyt |
|---|---|---|---|---|---|---|---|---|---|
| Measured | Modelled | ||||||||
| 1 | 1400 | 20 | 0.8 | 0.5 | 1.1 | 0.8 | 0.9 | 1 | 13 |
| 2 | 380 | 14 | 0.8 | 0.5 | 0.8 | 0.6 | 0.9 | 1 | 13 |
| 3 | 180 | 7 | 0.8 | 0.4 | 0.6 | 0.4 | 0.9 | 1 | 13 |
| 4 | 1400 | 20 | 0.8 | 0.5 | 1.1 | 0.9 | 0.9 | 1 | 8 |
| 5 | 1400 | 20 | 0.8 | 0.5 | 1.1 | 0.5 | 0.9 | 1 | 30 |
| 6 | 380 | 14 | 0.8 | 0.5 | 1.1 | 0.6 | 0.9 | 0.7 | 20 |
a ε p, a cyt, and L MIMS were measured; L 13C was calculated from ε p according to Sharkey and Berry (1985); remaining values are model input parameters and model results (L cyt , L carb, a carb, and ε cyt).
| (16) |
For the chosen value for L carb of 0.9 and the measured L cyt of 0.5, eqn 16 yields a ratio of internal vs external Ci cycling of 5.
Compared to estimates based on Sharkey and Berry (1985), our model significantly improved the compatibility of leakage estimates with those obtained by MIMS measurements (Table 2). The maximum fractionation that could be achieved in an uncatalysed reaction from CO2 to HCO3 – is +13‰ (O’Leary et al., 1992). With this kinetic fractionation, ε p values measured for the two pCO2 levels can be explained by leakage values from the cytosol (L cyt) of 0.8 and 0.6, respectively (scenarios 1 and 2, Table 2), which are significantly lower than the estimates based on the function by Sharkey and Berry (L 13C = 1.1 and 0.8, respectively). The remaining difference to leakage estimates obtained by MIMS (L MIMS = 0.5) could be explained by an underestimation of leakage by the MIMS approach, as discussed above. Assuming that the conversion between CO2 and HCO3 – in the cytosol was not completely unidirectional, ε cyt could range between +13‰ and –9‰ (equilibrium fractionation; O’Leary et al., 1992). To simulate this intermediate scenario, an ε cyt of +8‰ is assumed (senario 4, Table 2), yielding an L cyt of 0.9 for the high CO2 treatment.
Kinetic fractionation could be achieved by the NDH complex or by creation of a strong disequilibrium in the cytosol, minimizing the back-reaction from HCO3 – to CO2. Mutants of Synechococcus expressing human CA in the cytosol were unable to accumulate Ci (Price and Badger, 1989b), suggesting that HCO3 – is accumulated in the cytosol, and that a chemical disequilibrium in the cytosol favours the reaction from HCO3 – to CO2 rather than the opposite direction. This strongly argues for a fractionating enzyme instead of a purely chemical disequilibrium driving unidirectional CO2 to HCO3 – conversion in the cytosol. Assuming that NDH not only drives the unidirectional conversion of CO2 to HCO3 – but also discriminates against 13C during the reaction, leakage estimates by our model can be further reconciled with MIMS-based estimates. In a scenario assuming an upper estimate for ε cyt of +30‰ (scenario 5, Table 2), which is within the range of fractionation measured in other enzymes such as RubisCO, our MIMS-measured data can be reproduced even for the high pCO2 treatment (L MIMS = L cyt = 0.5; Table 2). Note that in combination with one of the other factors discussed above, such as an underestimation of L carb or of MIMS-based leakage estimates, enzymatic fractionation less than +30‰ could also explain our measurements (cf. e.g. scenarios with ε cyt of 13‰; Table 2). Although CA and NDH have been proposed to have similar reaction mechanisms (Price et al., 2002), our model results suggest that the fractionation by the NDH complex is different from that of CA (1‰ for conversion of CO2 to HCO3 –; Paneth and O’Leary, 1985). This might be due to the fact that the subunit carrying out the hydration reaction in the NDH-14 complex (chpX) is embedded in a larger functional unit including the transmembrane proton channel and is associated with the electron transport chain. To confirm the differences in fractionation between these enzyme complexes, however, further work using experimental approaches would be necessary, e.g. by comparing cyanobacterial mutant strains.
Since our MIMS measurements showed that leakage was unaffected by pCO2 and the slight changes in a cyt could not explain the observed variation in ε p, a carb and/or ε cyt would need to vary with pCO2 to explain the observed CO2-dependence of ε p. An increase in the activity of the NDH complex could yield an increase in a carb as well as ε cyt and therewith ε p. With an increase in a carb from 0.7 to 1 and an increase in ε cyt from 20 to 30‰, the measured increase in ε p between 380 and 1400 µatm can be explained, almost reproducing MIMS-measured leakage in both scenarios (scenarios 5 and 6, Table 2). A higher activity of NDH at high pCO2 may seem unexpected in view of its supposed role as part of the CCM. However, in contrast to other components of the CCM such as HCO3 – transporters, the reaction catalysed by the NDH complex contributes to ATP regeneration rather than consuming energy, and thus a downregulation of NDH at high pCO2 would not provide any energetic benefit to the cell. A positive correlation with pCO2 might be coupled to the small CO2 effect on a cyt (Table 1; Supplementary Figure 1C), increasing the activity of the NDH complex at high pCO2 levels in the acclimations in response to a higher availability of its substrate CO2. Note that the change in a cyt may have been underestimated in our study due to the constant pH in MIMS measurements. Due to its function as a proton pump in the thylakoid membrane, activity of the NDH complex can increase the ratio of ATP to NADPH available in the cell. The production of ATP by high NDH activity at high pCO2 could, in turn, contribute to the increased ATP requirement to fuel N2 fixation in Trichodesmium under ocean acidification (e.g. Kranz et al., 2010; Eichner et al., 2014).
Kranz et al. (2010) compared leakage estimates based on MIMS and 13C for Trichodesmium grown under different pCO2 levels as well as light intensities. Applying our model to this data set, MIMS-based leakage estimates could be reproduced with unidirectional fractionation for a low pCO2 treatment with light intensities similar to our experiment (200 µmol photons m–2 s–1; scenario 3, Table 2). In high pCO2 and low light treatments, the difference between L MIMS and L cyt was larger and could consequently only be reconciled with ε cyt values larger than +30‰. Short-term exposure to high light intensities (300 µmol photons m–2 s–1) in our experiment affected CO2 efflux in cells acclimated to high pCO2 (ANOVA, P < 0.05; data not shown). Such light sensitivity generally suggests CO2 efflux to be closely associated to photosynthetic electron transport. As this light effect was only observed under high pCO2, i.e. conditions associated with higher NDH activity according to our model results, the interrelation of CO2 efflux and the NDH complex is further corroborated. The observed light effects on CO2 efflux (this study) and ε p (Kranz et al., 2010) impose interesting questions with regard to a potential regulation of the NDH complex by the electron transport chain (redox state and/or proton gradient), which should be investigated in future studies. A better understanding of the regulation of the NDH complex is essential to improve confidence in explaining the effects of pCO2 as well as light on internal Ci fluxes and potential feedbacks on cellular energy budgets of this key N2 fixer.
Conclusion and outlook
This study demonstrates that internal Ci fluxes via the NDH-14 complex need to be considered not only in terms of cellular Ci acquisition, but also with regard to 13C fractionation and cellular energy status. The comparison of direct measurements of Ci fluxes with estimates based on isotopic composition revealed that 13C fractionation in Trichodesmium cannot be adequately described by only considering external Ci fluxes.
Compatibility with direct leakage measurements was improved by applying a model accounting for internal Ci fluxes around the carboxysome, e.g. via the NDH complex, providing a generalization of the model of Sharkey and Berry (1985) applicable for two compartments. In these model calculations, a large fraction of HCO3 – uptake into the carboxysome (0.7–1, Table 2) and high leakage from the carboxysome (>0.9, Table 2) are assumed, in accordance with the current understanding of carboxysome functioning. A large range of fractionation values for the cytoplasm, representing uncatalysed, unidirectional fractionation as well as enzymatic fractionation by the NDH complex, could significantly improve compatibility of leakage estimates (Table 2), even though the exact interplay of these processes still has to be resolved. While the lack of recent literature data on membrane permeability of cyanobacteria clearly demands future measurements, our model calculations are insensitive to this parameter within a certain range of permeability estimates (<10–4 m–2 s–1). Similarly, the model is independent of other potentially uncertain assumptions such as permeability of the carboxysome and pH values for the different compartments. Once future studies improve confidence in these parameters, a kinetic model can be used to predict internal concentrations and individual Ci fluxes. The agreement of model results with measured values could further be improved by accounting for possible 13C enrichment of CO2 leaking out of the cell as well as a disequilibrium situation in the surroundings of the cell (altering the isotopic signature of HCO3 – taken up).
The model applied here could also be used to improve estimates of leakage based on 13C signatures for other species in which several compartments and/or internal Ci fluxes play an important role. For phytoplankton groups that are relevant in terms of paleo-proxies, this could have important implications for the interpretation of C isotope signals.
Supplementary material
Supplementary Figure S1. DIC-saturated rates of C fixa tion (Vmax), half saturation DIC concentrations (K1/2) and HCO3 – : Ci uptake ratios measured at three time points during the day in Trichodesmium grown under two pCO2 levels and N sources (N2 and NO3 –).
Supplementary Figure S2. The dependence of intracellular CO2 concentrations on membrane permeability.
Funding
This work was supported by the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013), ERC grant agreement (205150), and the US National Science Foundation (EF 1040965).
Supplementary Material
Acknowledgements
We thank Ulrike Richter, Klaus-Uwe Richter, and Jana Hölscher for technical assistance at AWI, Gert-Jan Reichart and Mirja Hoins for δ13C-DIC measurements at Utrecht University, and Dieter Wolf-Gladrow as well as François M. M. Morel for constructive comments on the manuscript.
Glossary
Abbreviations:
- acarb
fractional contribution of HCO3 – to total Ci uptake into the carboxysome
- acyt
fractional contribution of HCO3 – to total Ci uptake into the cytosol
- CA
carbonic anhydrase
- CCM
carbon-concentrating mechanism
- chl a
chlorophyll a
- Ci
inorganic carbon
- DIC
dissolved inorganic carbon
- K1/2
half-saturation concentration
- L13C
leakage calculated from 13C fractionation
- Lcarb
modelled leakage from the carboxysome
- Lcyt
modelled leakage over the plasma membrane
- LMIMS
leakage estimated by MIMS
- MIMS
membrane inlet mass spectrometry
- POC
particulate organic carbon
- PQ
photosynthetic quotient
- Vmax
maximal rate
- εcyt
13C fractionation in the cytosol
- εdb
13C equilibrium fractionation in the external medium
- εp
total 13C fractionation during POC formation
- εRub
13C fractionation by RubisCO.
References
- Badger MR, Andrews TJ, Whitney SM, Ludwig M, Yellowlees DC. 1998. The diversity and co-evolution of Rubisco, plastids, pyrenoids and chloroplast-based CO2-concentrating mechanisms in algae. Canadian Journal of Botany 76, 1052–1071. [Google Scholar]
- Badger MR, Bassett M, Comins HN. 1985. A model for HCO3 − accumulation and photosynthesis in the cyanobacterium Synechococcus sp. Theoretical predictions and experimental observations. Plant Physiology 77, 465–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badger MR, Palmqvist K, Yu JW. 1994. Measurement of CO2 and HCO3 - fluxes in cyanobacteria and microalgae during steady-state photosynthesis. Physiologia Plantarum 90, 529–536. [Google Scholar]
- Badger MR, Price GD, Long BM, Woodger FJ. 2006. The environmental plasticity and ecological genomics of the cyanobacterial CO2 concentrating mechanism. Journal of Experimental Botany 57, 249–265. [DOI] [PubMed] [Google Scholar]
- Buick R. 1992. The antiquity of oxygenic photosynthesis: evidence from stromatolites in sulphate-deficient Archaean lakes. Science 255, 74–77. [DOI] [PubMed] [Google Scholar]
- Burkhardt S, Riebesell U, Zondervan I. 1999. Effects of growth rate, CO2 concentration, and cell size on the stable carbon isotope fractionation in marine phytoplankton. Geochimica et Cosmochimica Acta 63, 3729–3741. [Google Scholar]
- Caldeira K, Wickett ME. 2003. Anthropogenic carbon and ocean pH. Nature 425, 365–365. [DOI] [PubMed] [Google Scholar]
- Chen Y-B, Zehr JP, Mellon M. 1996. Growth and nitrogen fixation of the diazotrophic filamentous nonheterocystous cyanobacterium Trichodesmium sp. IMS 101 in defined media: evidence for a circadian rhythm. Journal of Phycology 32, 916–923. [Google Scholar]
- Dou Z, Heinhorst S, Williams EB, Murin CD, Shively JM, Cannon GC. 2008. CO2 fixation kinetics of Halothiobacillus neapolitanus mutant carboxysomes lacking carbonic anhydrase suggest the shell acts as a diffusional barrier for CO2 . The Journal of Biological Chemistry 283, 10377–10384. [DOI] [PubMed] [Google Scholar]
- Eichner M, Kranz SA, Rost B. 2014. Combined effects of different CO2 levels and N sources on the diazotrophic cyanobacterium Trichodesmium . Physiologia Plantarum 152, 316–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Espie GS, Kimber MS. 2011. Carboxysomes: cyanobacterial RubisCO comes in small packages. Photosynthesis Research 109, 7–20. [DOI] [PubMed] [Google Scholar]
- Freeman KH, Hayes JM. 1992. Fractionation of carbon isotopes by phytoplankton and estimates of ancient CO2 levels. Global Biogeochemical Cycles 6, 185–198. [DOI] [PubMed] [Google Scholar]
- Guy RD, Fogel ML, Berry JA. 1993. Photosynthetic fractionation of stable isotopes of oxygen and carbon. Plant Physiology 101, 37–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holm-Hansen O, Riemann B. 1978. Chlorophyll a determination: improvements in methodology. Oikos 30, 438–447. [Google Scholar]
- Hopkinson BM, Dupont CL, Allen AE, Morel FMM. 2011. Efficiency of the CO2-concentrating mechanism of diatoms. Proceedings of the National Academy of Sciences, USA 108, 3830–3837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchins DA, Fu F-X, Zhang Y, Warner ME, Feng Y, Portune K, Bernhardt PW, Mulholland MR. 2007. CO2 control of Trichodesmium N2 fixation, photosynthesis, growth rates and elemental ratios: Implications for past, present and future ocean biogeochemistry. Limnology and Oceanography 552, 1293–1304. [Google Scholar]
- IPCC. 2007. Summary for policymakers. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL, eds. Climate change 2007: the physical science basis. Contribution of working group I to the fourth assessment report of the Intergovernmental Panel on Climate Change. Cambridge and New York: Cambridge University Press. [Google Scholar]
- Kaplan A, Badger MR, Berry JA. 1980. Photosynthesis and the intracellular inorganic carbon pool in the bluegreen alga Anabaena variabilis - response to external CO2 concentration. Planta 149, 219–226. [DOI] [PubMed] [Google Scholar]
- Kasting JF, Siefert JL. 2002. Life and the evolution of earth’s atmosphere. Science 296, 1066–1068. [DOI] [PubMed] [Google Scholar]
- Keller K, Morel FMM. 1999. A model of carbon isotopic fractionation and active carbon uptake in phytoplankton. Marine Ecology Progress Series 182, 295–298. [Google Scholar]
- Klein MG, Zwart P, Bagby SC, Cai F, Chisholm SW, Heinhorst S, Cannon GC, Kerfeld CA. 2009. Identification and structural analysis of a novel carboxysome shell protein with implications for metabolite transport. Journal of Molecular Biology 392, 319–333. [DOI] [PubMed] [Google Scholar]
- Kranz SA, Levitan O, Richter K-U, Prasil O, Berman-Frank I, Rost B. 2010. Combined effects of CO2 and light on the N2 fixing cyanobacterium Trichodesmium IMS101: Physiological responses. Plant Physiology 154, 334–345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kranz SA, Sültemeyer D, Richter K-U, Rost B. 2009. Carbon acquisition in Trichodesmium: the effect of pCO2 and diurnal changes. Limnology and Oceanography 54, 548–559. [Google Scholar]
- Laws EA, Bidigare RR, Popp BN. 1997. Effect of growth rate and CO2 concentration on carbon isotopic fractionation by the marine diatom Phaeodactylum tricornutum . Limnology and Oceanography 42, 1552–1560. [Google Scholar]
- Levitan O, Rosenberg G, Setlik I, Setlikova E, Grigel J, Klepetar J, Prasil O., Berman-Frank I. (2007). Elevated CO2 enhances nitrogen fixation and growth in the marine cyanobacterium Trichodesmium . Global Change Biology 13, 531–538. [Google Scholar]
- Maeda S, Badger MR, Price GD. 2002. Novel gene products associated with NdhD3/D4-containing NDH-1 complexes are involved in photosynthetic CO2 hydration in the cyanobacterium Synechococcus sp. PCC7942. Molecular Microbiology 43, 425–435. [DOI] [PubMed] [Google Scholar]
- Marcus Y, Schwarz R, Friedberg D, Kaplan A. 1986. High CO2 requiring mutant of Anacystis nidulans R2. Plant Physiology 82, 610–612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marlier JF, O’Leary MH. 1984. Carbon kinetic isotope effects on the hydration of carbon dioxide and the dehydration of bicarbonate ion. Journal of the American Chemical Society 106, 5054–5057. [Google Scholar]
- Mook W, Bommerson J, Staverman W. 1974. Carbon isotope fractionation between dissolved bicarbonate and gaseous carbon dioxide. Earth and Planetary Science Letters 22, 169–176. [Google Scholar]
- O’Leary M, Madhavan S, Paneth P. 1992. Physical and chemical basis of carbon isotope fractionation in plants. Plant, Cell and Environment 15, 1099–1104. [Google Scholar]
- Paneth P, O’Leary MH. 1985. Carbon isotope effect on dehydration of bicarbonate ion catalyzed by carbonic anhydrase. Biochemistry 24, 5143–5147. [DOI] [PubMed] [Google Scholar]
- Price GD, Badger MR. 1989a. Ethoxyzolamide inhibition of CO2 uptake in the cyanobacterium Synechococcus PCC7942 without apparent inhibition of internal carbonic anhydrase activity. Plant Physiology 89, 37–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GD, Badger MR. 1989b. Ethoxyzolamide inhibition of CO2-dependent photosynthesis in the cyanobacterium Synechococcus PCC7942. Plant Physiology 89, 44–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GD, Badger MR. 1989c. Expression of human carbonic anhydrase in the cyanobacterium Synechococcus PCC7942 creates a high CO2-requiring phenotype. Evidence for a central role for carboxysomes in the CO2 concentrating mechanism. Plant Physiology 91, 505–513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price GD, Badger MR, Woodger FJ, Long BM. 2008. Advances in understanding the cyanobacterial CO2-concentrating-mechanism (CCM): functional components, Ci transporters, diversity, genetic regulation and prospects for engineering into plants. Journal of Experimental Botany 59, 1441–1461. [DOI] [PubMed] [Google Scholar]
- Price GD, Maeda S, Omata T, Badger MR. 2002. Modes of inorganic carbon uptake in the cyanobacterium Synechococcus sp. PCC7942. Functional Plant Biology 29, 131–149. [DOI] [PubMed] [Google Scholar]
- Reinhold L, Zviman M, Kaplan A. 1989. A quantitative model for inorganic carbon fluxes and photosynthesis in cyanobacteria. Plant Physiology and Biochemistry 27, 945–954. [Google Scholar]
- Roeske C, O’Leary M. 1984. Carbon isotope effects on the enzyme-catalyzed carboxilation of ribulose bisphosphate. Biochemistry 23, 6275–6285. [DOI] [PubMed] [Google Scholar]
- Rost B, Kranz SA, Richter KU, Tortell PD. 2007. Isotope disequilibrium and mass spectrometric studies of inorganic carbon acquisition by phytoplankton. Limnology and Oceanography: Methods 5, 328–337. [Google Scholar]
- Rost B, Richter K-U, Riebesell U, Hansen PJ. 2006. Inorganic carbon acquisition in red tide dinoflagellates. Plant, Cell and Environment 29, 810–822. [DOI] [PubMed] [Google Scholar]
- Rost B, Zondervan I, Wolf-Gladrow D. 2008. Sensitivity of phytoplankton to future changes in ocean carbonate chemistry: current knowledge, contradictions and research directions. Marine Ecology Progress Series 373, 227–237. [Google Scholar]
- Schulz KG, Rost B, Burkhardt S, Riebesell U, Thoms S, Wolf-Gladrow DA. 2007. The effect of iron availability on the regulation of inorganic carbon acquisition in the coccolithophore Emiliania huxleyi and the significance of cellular compartmentation for stable carbon isotope fractionation. Geochimica et Cosmochimica Acta 71, 5301–5312. [Google Scholar]
- Sharkey TD, Berry JA. 1985. Carbon isotope fractionation of algae influenced by an inducible CO2-concentrating mechanism. In: Lucas WJ, Berry JA, eds. Inorganic carbon uptake by aquatic photosynthetic organisms. Rockville: American Society of Plant Physiologists, 389–401. [Google Scholar]
- Tortell PD. 2000. Evolutionary and ecological perspectives on carbon acquisition in phytoplankton. Limnology and Oceanography 45, 744–750. [Google Scholar]
- Tchernov D, Lipschultz F. 2008. Carbon isotopic composition of Trichodesmium spp. colonies off Bermuda: effects of colony mass and season. Journal of Plankton Research 30, 21–31. [Google Scholar]
- Tsai Y, Sawaya MR, Cannon GC, Cai F, Williams EB, Heinhorst S, Kerfeld CA, Yeates TO. 2007. Structural analysis of CsoS1A and the protein shell of the Halothiobacillus neapolitanus carboxysome. PLoS Biology 5 10.1371/journal.pbio.0050144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams PJL, Robertson JE. 1991. Overall planktonic oxygen and carbon dioxide metabolisms: the problem of reconciling observations and calculations of photosynthetic quotients. Journal of Plankton Research 13 , 153–169. [Google Scholar]
- Zeebe RE, Wolf-Gladrow DA. 2007. CO2 in seawater: equilibrium, kinetics, isotopes. Amsterdam: Elsevier Science B.V. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.