Abstract
In image-guided radiotherapy (IGRT) of disease sites subject to respiratory motion, soft tissue deformations can affect localization accuracy. We describe the application of a method of 2D/3D deformable registration to soft tissue localization in abdomen. The method, called registration efficiency and accuracy through learning a metric on shape (REALMS), is designed to support real-time IGRT. In a previously developed version of REALMS, the method interpolated 3D deformation parameters for any credible deformation in a deformation space using a single globally-trained Riemannian metric for each parameter. We propose a refinement of the method in which the metric is trained over a particular region of the deformation space, such that interpolation accuracy within that region is improved. We report on the application of the proposed algorithm to IGRT in abdominal disease sites, which is more challenging than in lung because of low intensity contrast and nonrespiratory deformation. We introduce a rigid translation vector to compensate for nonrespiratory deformation, and design a special region-of-interest around fiducial markers implanted near the tumor to produce a more reliable registration. Both synthetic data and actual data tests on abdominal datasets show that the localized approach achieves more accurate 2D/3D deformable registration than the global approach.
Index Terms: Abdomen, image-guided radiotherapy (IGRT), radiation oncology, 2D/3D registration
I. Introduction
The goal of the image-guided radiation therapy (IGRT) process is to localize tumors and target organs in three-dimensional (3D) at treatment time. The advent of so-called on-board imaging systems mounted on medical linear accelerators makes possible the acquisition of two-dimensional (2D) planar images during radiation treatment for monitoring internal patient motion. This has motivated the use of 2D/3D registration for target localization and patient positioning just prior to treatment, and for tracking target motion during treatment delivery [1]. A challenge in lung and abdominal disease sites subject to respiratory motion is that organ deformation may occur, thus requiring incorporation of deformation in the registration process. In this context, the patient’s treatment-time 3D deformations can be computed by performing image registration between the treatment-time on-board planar images (X-ray) and the treatment-planning 3D image (CT). Chou et al. [2] recently introduced a real-time 2D/3D deformable registration method, called registration efficiency and accuracy through learning metric on shape (REALMS). At treatment-planning time REALMS learns a Riemannian metric that measures the distance between two projection images. At treatment time it interpolates the patient’s 3D deformation parameters using a kernel regression with the learned distance metric. REALMS can locate the target in less than 10 ms at treatment time, which shows potential to support real-time registration. However, the previously reported method approximates the Riemannian metric by using a linear regression over the global deformation space between the projection image intensity differences and the deformation parameter differences. Therefore, the accuracy highly depends on how well this relationship can fit into a global linear model.
We describe an improvement scheme for REALMS using local metric learning. The global deformation space is divided into several local subspaces, and a local Riemannian metric is learned in each of these subspaces. At treatment time it first determines into which subspace the deformation parameters fall, and it then interpolates the deformation parameters within the subspace using the local metric and local training deformation parameters. Local metric learning makes REALMS more accurate by fitting a better linear relationship between the projection differences and the parameter differences in each subspace to yield a good local metric.
In this paper, we investigate this localized REALMS with several abdominal IGRT cases. Registration with abdominal images is more challenging than in lung for two reasons. First, in addition to respiratory deformations during the patient’s breathing cycle, there are other deformations in the abdomen, such as digestive deformations, between planning time and treatment time, which makes the learned metric inappropriate for treatment-time registration. Second, the formation of the deformation space depends on accurate deformable 3D/3D registration among planning-time RCCTs (respiratory-correlated CTs), but a challenge is the low intensity contrast in the abdomen. We propose several methods in this paper that show promise in dealing with these problems. To our knowledge, this study represents the first attempt at 2D/3D deformable registration with abdominal image sets.
The rest of the paper is organized as follows. In Section II, we discuss some of the background research work (alternative methods) for 2D/3D registration. In Section III, we describe the interpolative scheme and metric learning in the REALMS framework. In Section IV, we introduce the localized approach to make REALMS more accurate. In Section V, we describe some specific situations for localized REALMS in the abdomen, including an updated deformation model for the composition of respiratory deformation and digestive deformation. Finally in Section VI, we discuss the results of synthetic tests and real tests on abdominal cases.
II. Related Work
A number of 2D/3D registration methods [3]–[6] were designed to optimize over a 2D/3D rigid transformation that minimizes a similarity measurement between a simulated DRR (digitally-reconstructed radiographs) and the treatment planar image. With GPU parallelization recent optimization-based 2D/3D registration methods [7][8] are able to localize the tumor within 1 s assuming rigid target volume motion. For nonrigid motion in lung and abdomen, in order to lower the number of deformation parameters and produce reasonable deformations, a common approach is to adopt a deformation model based on principal component analysis (PCA) [9] from the patient’s respiration-correlated CT (RCCT), consisting of a set of (typically 10) 3D CT images over one breathing cycle. The PCA model can efficiently represent the deformation with only a few deformation parameters and corresponding eigenvectors. Li et al. [10], [11] used a gradient-descent optimization scheme on GPUs to find the optimal PCA scores that minimized the difference between DRRs and on-board projections. However, the image mismatch term often introduces a nonconvex objective function which can be trapped in local minima. In order to avoid local minima and to reduce the registration time, a bootstrap-like approach [10], [11] was adopted, and the optimizations were initialized by registration results from previous time points.
Li et al. [12] used an efficient MAP (maximum a posterior) estimator to solve for PCA coefficients of the entire lung motion from the 3D position of a single marker, but according to their experiments, solving for more than two PCA coefficients from three coordinates could lead to an overfitting problem. Other methods have used neural networks to model rigid [13]–[15], or nonrigid transformations [16] and to achieve efficient computation at registration time. However, they cannot support both rigid and nonrigid 2D/3D registration.
Chou et al. [17], [18] recently proposed a regression-based approach, CLARET, to estimate deformation parameters. CLARET first learns a linear regression between projection intensities and deformation parameters at planning time. Then at treatment time the learned regression is iteratively applied to refine the deformation parameters. However, CLARET still involves computationally demanding production of DRRs in each registration iteration. Reference [19] introduced a localized version of CLARET that could avoid generating DRRs at treatment time. It uses graph cuts to separate the whole deformation space and learns a linear regression independently in each division. At treatment time it uses a decision forest to classify a target projection into a partition, and the learned regression for that training partition is noniteratively applied to the target projection image. Even though localized CLARET achieves a large improvement in registration speed at treatment time, it is still slower than REALMS due to the voting procedure of the decision forest in each registration.
III. REALMS Framework
A. Deformation Modeling at Planning Time
As described in [2], REALMS first models the deformation with a shape space, in which each deformation is formed by a linear combination of basis deformations calculated through PCA analysis. For deformations due to respiration, we use a set of RCCT images {Jτ |τ = 1, 2, …, 10} of the patient at planning time that records a cyclically varying target area. Chou et al. [2] computed a Fréchet mean image J̅ as well as the diffeomorphic deformations ϕ from J̅ to each image Jτ and performed a statistical analysis based on the 10 deformations. Here, we use an alternative approach, in which we pick a reference image Iref from the 10 RCCTs. Iref is chosen as the closest phase to the average phase of the breathing cycle represented by the RCCTs according to the position of a fiducial marker implanted in the patient. We compute a 3D/3D registration between each of the other nine images and Iref to yield a set of nine deformations {ϕτ |τ = 1, 2, …, 9}.
We use an LDDMM (large deformation diffeomorphicmetric mapping) framework described in Foskey et al. [20]. The diffeomorphic deformation ϕτ from the reference Iref to each of the nine RCCTs Iτ is computed using a fluid-flow registration
| (1) |
where L is some suitable differential operator, Iτ (x) is the intensity of the pixel at position x, υτ (x, t) is the fluid-flow velocity at position x and flow time t, α is the weighting variable on image dissimilarity, and ϕτ (x) describes the overall deformation up to time t at position x: .
We follow a greedy approach to optimize the energy function. At each time step, we choose the velocity field that improves the image match most rapidly, given the current deformation. This optimization does not update velocity fields once they are first estimated or take future velocity fields into account. In such a case, the gradient is proportional to
| (2) |
which means the image force exerted on each point at each time step is along the direction of greatest change in image intensity, and the magnitude and sign of the force are determined by the difference in intensity between the two images. The difference in intensity is adjustable by means of the display window, which in this study is adjusted so as to enhance soft tissue contrast in the abdominal organs.
Using the calculated diffeomorphic deformation set {ϕτ |τ = 1, 2, …, 9}, our method finds a set of linear deformation basis vectors by PCA analysis. The scores on each represent ϕτ in terms of these basis vectors
| (3) |
We have found that the first three eigenmodes are sufficient to capture more than 95% of the total variation, meaning a deformation can be approximately represented by its first three PCA scores. Then we let c = (c1, c2, c3) form the 3D parametrization of the deformation. This three-tuple forms a 3D parameter space (also referred to as the deformation space or the shape space).
B. Treatment-Time Registration
At treatment time, REALMS uses kernel regression [(4)] to interpolate the patient’s three 3D deformation parameters c = (c1, c2, c3) separately from the on-board projection image Ψ (θ). Each parameter ci is interpolated as a weighted sum of N parameters from a set of N training deformation parameters {cγ |γ = 1, 2, …, N}. These training deformation parameters are evenly sampled in the shape space at planning time, and the corresponding training DRRs {P(Iref ◦ T(cγ); θ) |γ = 1, 2, …, N)} are generated as well. P simulates the DRRs with deformation parameters cγ according to the treatment-time imaging geometry, e.g., the projection angle θ.
In the treatment-time registration, each deformation parameter ci in c can be estimated with the following kernel regression:
| (4) |
where the exponential part gives the weight for , and K normalizes the overall weight. denotes the squared distance between the on-board projection image and the γth DRR: P(Iref ◦ T(cγ); θ). Moreover, we use a Riemannian metric tensor Mi to determine using
| (5) |
| (6) |
where ΔI denotes the intensity difference between the two images.
C. Metric Learning at Planning Time
At planning time, REALMS learns a metric tensor Mi with a corresponding kernel width βi for the patient’s ith deformation parameter ci. To limit the number of degrees of freedom in the metric tensor, we structure Mi as a rank-1 matrix formed by a basis vector ai: Mi = aiaiT. We assume that this basis vector presents a linear relationship between the intensity difference between two projection images and their parameters’ difference
| (7) |
Therefore, REALMS learns ai by applying a linear regression [(7)] between a set of N intensity difference data R = (ΔI1, ΔI2, …, ΔIN)T and the corresponding parameter difference data , where
| (8) |
| (9) |
Finally, we solve for ai by
| (10) |
In such a case, the squared distance function denotes a weighted intensity distance between the on-board projection and the γth DRR [(11)]. This distance is also consistent with their parameter difference, which provides a meaningful weight in the kernel regression
| (11) |
Chou et al. have pointed out that the basis vector ai can be refined by using a leave-one-out (LOO) training strategy after the linear regression. In our work, the learned regression is directly used as the basis vector. We select the optimal kernel width βi from a number of candidates that minimizes synthetic tests’ error [described in Section VI-A].
IV. Localized REALMS
A. Localized Interpolation Strategy
The accuracy of kernel regression highly depends on the quality of the learned metric Mi. Traditional (global) REALMS uses linear regression to learn the underlying basis vector ai. Therefore, ai uses a linear model to approximate the relationship between intensity difference and parameter difference in the overall shape space. Usually this approximation is not sufficiently accurate because the linear property does not hold for the entire shape space. However, if the basis vector is tailored for a particular region of the shape space, the approximation will be more accurate in that region. Moreover, the patient’s 3D deformation parameter c is more related to nearby parameter values in the shape space. Therefore, we introduce a localized interpolation method based on REALMS. Localized REALMS will place the N training deformation parameters closer to the target parameters’ position, so that both a robust linear regression and an accurate interpolation will be achieved in that local region.
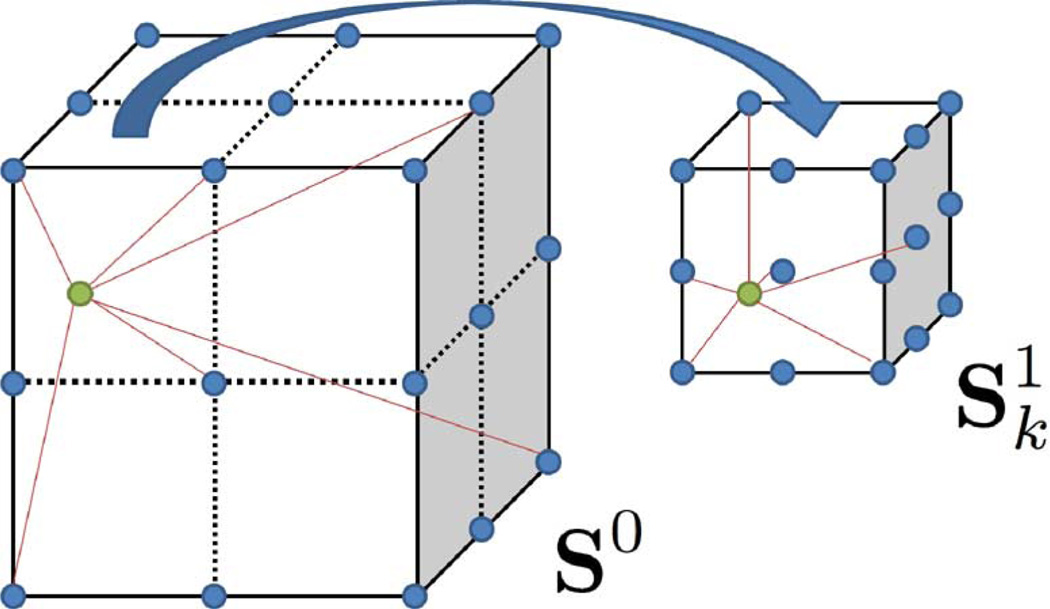
In the localized REALMS approach, we first divide the global shape space S0 into several first level subspaces (k = 1, 2, …, S), where k denotes the kth subspace, and S is the number of subspaces. At treatment-planning time, each subspace has its own N deformation parameters sampled and corresponding DRRs generated. Then a local metric is learned for the kth subspace. is still decomposed by a basis vector , which is learned by a local linear regression from its own deformation parameters and their corresponding DRRs. The treatment-time registration first decides to which subspace the deformation parameters c belong. If c locates in , an interpolation is applied using its local metric and local training DRRs to yield a finer result (Fig. 1).
Fig. 1.
Global REALMS first determines the subspace to which the parameters belong. Next, localized REALMS does a finer interpolation using local training parameters and the local metric. Green dots denote target parameters. Blue dots denote training parameters.
B. Subspace Division and Selection
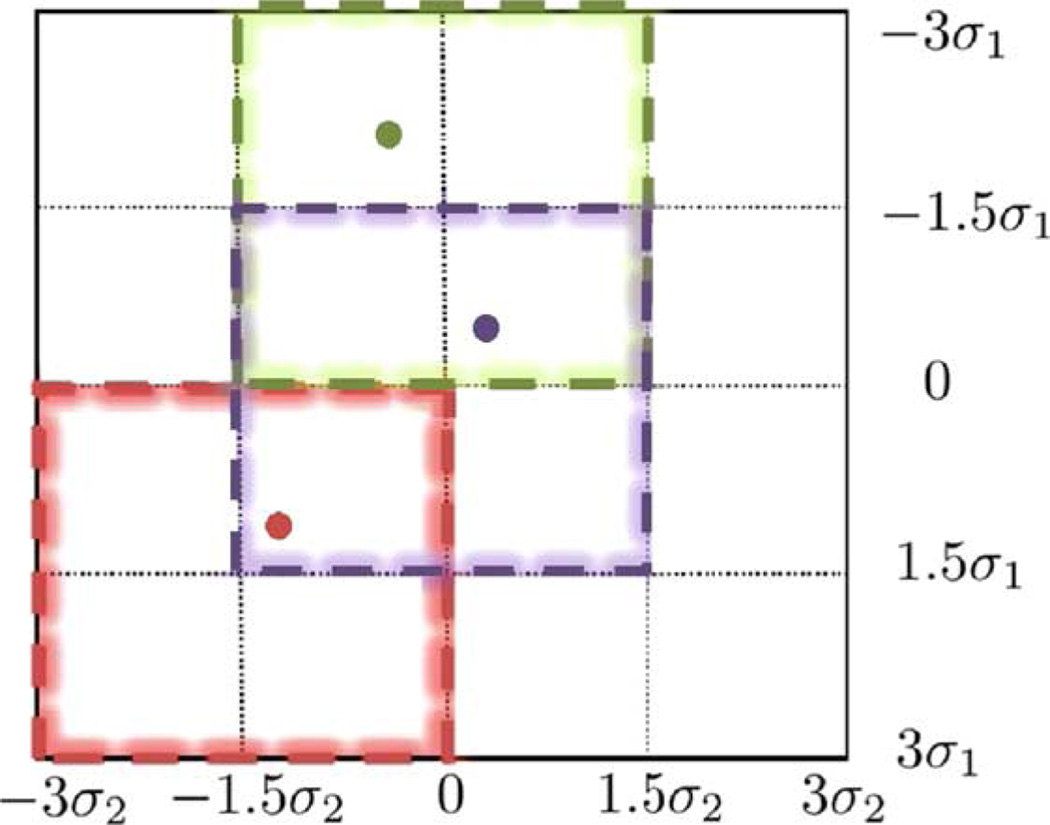
There are many ways to divide global space into subspaces. Chou et al. [19] used normalized graph cuts to separate the shape space and trained a decision forest for deciding into which subspace a target projection image should be classified. In our work, we uniformly divide the global shape space by considering that the global shape space can be viewed as a 3D box. The length in each dimension is 6σi (from to −3σi to 3σi), where σi is the standard deviation of the scores on the principal component . We take three subintervals in each dimension: −3σi to 0σi, −1.5σi to 1.5σi, 0σi to 3σi. The combinations of subintervals of three dimensions yield 27 overall subspaces. Each of these subspaces is also a 3D box, where the length in each dimension is half of the global shape space. Fig. 2 shows an example of a 2D version of the shape space constructed by the first two principal components of deformation. In this 2D case, we divide the global 2D space into 16 grids, and a subspace can be viewed as a sliding window defined on these grids, so there are nine subspaces in total. Three example subspaces are presented in different colors.
Fig. 2.
Subspaces division in 2D. Global shape (shown as black) space consisting of the first two principal components is a 2D square. Edges of all subspaces are along black lines. Global REALMS determines the initial position of deformation parameters. Localized REALMS chooses the corresponding subspace. Three examples are shown in different colors.
To choose the subspace to which the target parameters belong, we use global REALMS to compute a first round interpolation over the whole space. The estimated parameter values indicate a position in the global 3D shape space. Then, localized REALMS chooses the subspace with its centre closest to the initial estimated position. In Fig. 2, each colored dot indicates the estimated 2D position of the parameter values. The corresponding chosen subspace is denoted by the 2D square of the same color.
Localized REALMS can be extended to a multi-scale approach, in which the level of localization can be added if an ith level subspace is divided into several (i + 1)th level subspaces (k′ = 1, 2, …, N′). In this case, a metric tensor should be learned respectively for every subspace on every level. The interpolation determined in will identify which subspace to choose on the next level for applying a further local interpolation.
C. Kernel Regression Versus Locally Weighted Regression
There are two popular locally weighted training techniques: kernel regression and locally weighted regression (LWR) [21], [22]. Localized REALMS is based on kernel regression, but it is intrinsically related to LWR.
Kernel regression is a zero-order method trying to find a weighted average of nearby training outputs given a query point. On the other hand, LWR fits a local linear model using a distance weighted regression. Given a query point q, LWR solves a weighted least squares problem, ending up with a linear model fits locally to the data near the query point
| (12) |
The weighting function K is a standard Gaussian kernel, and the square distance function
| (13) |
measures the Euclidean distance between the query point q and the training data xi. Therefore, LWR explicitly fits a local linear model to the data with the distance defined in a standard Euclidean space. On the other hand, localized REALMS finds a locally weighted average with the distance defined by a metric, which is learned from a local linear regression. In other words, localized REALMS is a kernel regression with first-order information implicitly built in.
V. Localized Realms in the Abdomen
The findings by Chou et al. [2] indicate that REALMS performs reasonably well in lung. However, there are additional challenges posed by registration in abdomen. We describe these special problems and propose several methods to address them.
A. Nonrespiratory Deformation
In lung IGRT, the deformation between treatment time and planning time images is almost entirely respiratory deformation. However in the abdomen, there also exists nonrespiratory deformation caused by the digestive system. Changes in filling of the stomach, duodenum and bowel will cause deformation of these organs. There can also be changes of gas filling in these same organs. These factors will induce nonrespiratory deformations of nearby target organs, such as the pancreas. Therefore in the abdomen, the digestive process may deform the target organ to different positions for each treatment, and respiration will impose further cyclic deformations. However, since the learning stage and the interpolation stage in REALMS are both based on the intensity difference caused only by respiratory deformation, REALMS is not credible for finding these nonrespiratory deformations. In other words, REALMS alone only learns and produces deformations modeled by the parameter space formed from the patient’s respiratory variation.
To deal with this problem, we first assume that only respiratory deformation occurs during treatment and that nonrespiratory deformation only happens between planning time and treatment time. In the long term, we can address this problem by taking a new reference CT at the beginning of treatment and apply the old deformation space based on the new reference. However, for the time being, we act as if the nonrespiratory deformation is a 3D rigid translation vector with respect to the abdominal region around the target organ. The rationale is to first estimate a translation vector at the beginning of treatment time registration, and we translate the planning reference image Iref as well as the deformation principal components (, ϕ̅) by the vector to compensate for nonrespiratory deformation. Following rigid translation correction, the remaining deformations at treatment time with respect to the new Iref are all respiratory deformations and can be determined by REALMS. Therefore, at treatment registration, the intensity difference ΔI is still generated using (5), where Iref now is the translated reference image, and T(cγ) generates deformations from the translated deformation principal components.
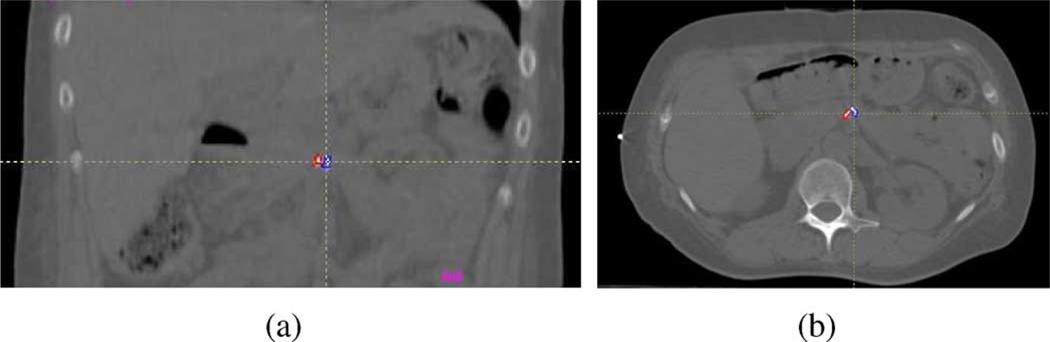
We make use of fiducial markers to compute the rigid translation vector. These are small radiopaque markers (Visicoil, RadioMed Corp., Bartlett, TN, USA), 20 mm long × 1 mm diameter, which are implanted in or near the target abdominal organ at planning time (Fig. 3). In addition, the Visicoil markers have a hollow core designed to reduce artifacts in CT and CBCT, thereby minimizing deleterious effects on the deformable 3D/3D registration. The markers curl up and take on irregular shapes upon implantation. Their high contrast with respect to surrounding tissues allows them to be easily located in CT, projection images and even in coarse CT reconstructions from projection images. Therefore, we can compute the translation vector from the positional difference of a fiducial marker between planning time and treatment time.
Fig. 3.
Two fiducial markers delineated by red and blue outlines. (a) Coronal slice of the reference CT. (b) An axial slice of the reference CT.
In our application, the treatment time images are obtained with a kilovoltage cone-beam CT (CBCT) system [23] mounted on a medical linear accelerator (TrueBeam, Varian Medical Systems, Palo Alto, CA, USA). Immediately prior to the start of radiation treatment, a CBCT scan is acquired, consisting of 660 projection images over a 360 arc around the patient while simultaneously recording respiration with a position monitor placed on the patient’s abdomen (Real-time Position Management System, Varian Medical Systems). The projection images are sorted into 10 respiratory bins and each bin is reconstructed using an implementation of the FDK algorithm [24] (Varian iTools version 1.0.32.0), yielding a sequence of 10 preRT-CBCT images over the patient’s respiratory cycle. We extract fiducial positions from each of these reconstructions and compute a mean fiducial marker position for treatment time. In addition, we locate the fiducial positions in the 10 RCCT images and compute a mean fiducial position at planning time. Finally, the translation vector is the difference between the two mean fiducial positions.
B. Contrast Issues
Because soft tissue contrast in CT images of the abdomen has lower contrast than in lung, it is more challenging to achieve accurate deformable registration between RCCT images, which in turn affects the accuracy of the deformation space. To address this problem, the LDDMM 3D/3D registration uses a narrower intensity window (−100 to +100 HU), which encompasses the soft tissue intensity range of abdominal structures.
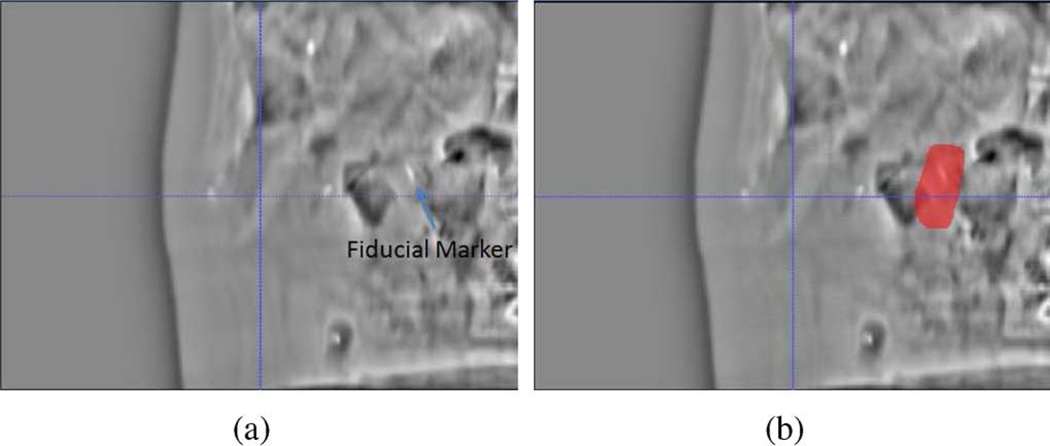
The robustness of REALMS highly depends on the intensity difference information between DRR and projection image caused by deformation. However there are two factors which adversely affect projection images in abdomen. First, because of the similar intensities of soft tissue organs, it is not possible to reliably localize them in the projection images or determine their deformations. Second, movement of gas pockets in the abdomen induces variable high contrast intensity patterns in the projection images, which yields inconsistent intensity differences between planning time and treatment time. Our solution is to focus our region of interest (ROI) on one or more fiducial markers visible in the images (Fig. 4). Because the fiducial is usually very distinct in the images, and soft tissue deformation is implied by its displacement, we use the intensity change in a small region around the fiducial to indicate the overall deformation in the surrounding soft tissue organs. In our experiments, we used a 4 cm × 6 cm square ROI including the fiducial marker, and perform REALMS learning and interpolation only using the pixels in that area.
Fig. 4.
(a) DRR generated from the mean CT [deformed from the reference CT by c = (0, 0, 0)]. (b) Red area indicates the region-of-interest for computing intensity differences between DRR and projection image.
C. DRRs Versus On-Board Radiographs
REALMS requires comparable intensities between DRRs and real projection images. To account for variations caused by X-ray scatter that produces inconsistent projection intensities, we normalize both training DRRs and the on-board projection image Ψ(θ). In particular, we use the localized Gaussian normalization introduced in [25], which has shown promise in removing the undesired scattering artifacts. In addition, the histogram matching scheme described in [17] is used to produce intensity-consistent radiographs.
Due to the different image resolutions, a fiducial marker usually has very distinct appearances in DDRs and on-board projections. DRRs are simulated from CTs, in which the optical resolution (the minimum distance at which two fiducial markers can be distinguished in the image) is approximately 3 mm, while an on-board radiograph has an approximate optical resolution of 1 mm in the projection plane (measured manually over three patient datasets). On the other hand, CT has an anisotropic pixel size of 1 mm × 1 mm × 2 mm (2 mm in axial direction), while a radiograph has an approximate pixel size of 0.3 mm × 0.3 mm. Consequently the fiducial markers appear more blurred in DRRs than in on-board projection images. We use a simple blurring technique on the latter to yield an image with comparable resolution to the DRR (Fig. 5). We convolve the on-board projection image with an anisotropic mean kernel with ηy rows and ηx columns
where ηx and ηy is the blurring width in each dimension. For each dimension, the blurring width is the product of the ratio between optical resolutions and the ratio between pixel sizes in that dimension.
Fig. 5.
(a) Fiducial appearance in a DRR. (b) Fiducial appearance in a cone-beam projection before convolution. (c) Fiducial appearance in a cone-beam projection after convolution with a blurring kernel.
In our case
| (14) |
| (15) |
For computational convenience with a discretized image, we set ηx = 9, and ηy = 15.
VI. Results
A. Evaluation Measurement
We tested localized REALMS on three patients datasets in abdomen. In each dataset, segmentations of the pancreas, duodenum and fiducial markers were drawn on the reference RCCT image by a medical physicist experienced in radiation treatment planning. In addition, each patient dataset included a reconstructed CBCT at end expiration (EE) with corresponding segmentations drawn by the same observer. The CBCT at end expiration was acquired by respiration gating of the on-board imaging system, such that rotation of the gantry and acquisition of projection images occurred within a gate centered at expiration and encompassing approximately 25% of the respiratory cycle [23]. The 2D/3D registration is evaluated by first determining the deformation parameters of the reference CT and then deforming the reference segmentation by these parameters. The quality of the registration is measured between the estimated segmentation and the target (manual or synthetically deformed) segmentation. The evaluation tests made use of two types of measurement. When the ground truth deformation is known for every voxel of the target segmentation, such as in the synthetic data tests (Section VI-B), we use mTRE (mean target registration error) to evaluate the average deformation error over all the voxels between the estimated and target segmentation. When the ground truth deformation of the target is not known, such as in tests of the actual data (Section VI-C), we alternatively measure the registration error by the magnitude of the 3D target centroid difference (TCD), which is the centroid distance between two segmentations. Note that TCD may overestimate the error because of inconsistencies in manual segmentations between reference CT and target CBCT.
B. Synthetic Data Tests
The tests of synthetic data made use of the RCCT datasets. As stated in Section IV-B, the global shape space was divided into 27 subspaces. We evenly sampled 343 training deformation parameters {cγ |γ = 1, …, 343} in the global shape space and each subspace. The corresponding training DRRs {P(Iref ◦ T(cγ); θ) |γ = 1, 2, … N} were generated as well (dimension: 512 × 384). For each patient, an ROI was independently selected based on the fiducial position and the projection angle, which can best reveal the fiducial marker in the projection images. The target CTs in the tests were synthetically deformed from the reference CT Iref by normally distributed random samples of the 3D deformation parameters c = (c1, c2, c3). DRRs were generated from these synthetically deformed target CTs to represent test on-board cone-beam projection images. The quality of the registration was measured by using the average mTRE of the target organ (duodenum) over all the test cases.
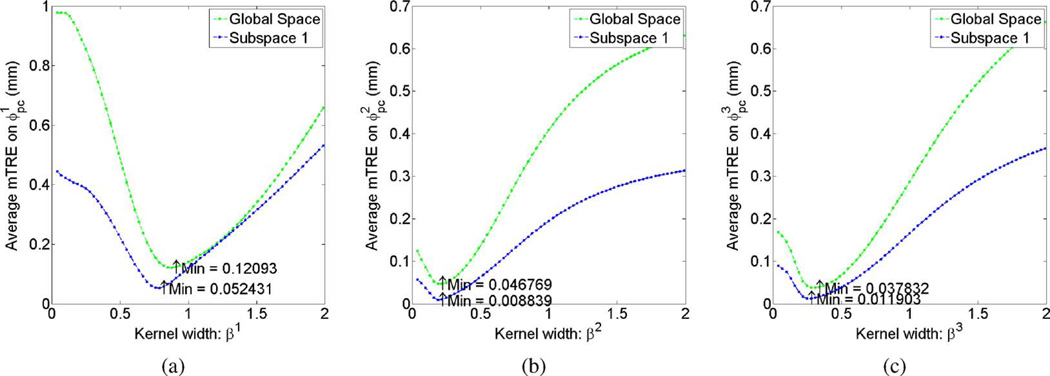
We first investigated whether interpolation in a local region yielded more accurate registration. Thirty DRRs were tested for each subspace as well as the global space. As shown in Fig. 6, interpolation in a subspace yielded a lower mTRE than did global interpolation for each candidate kernel width.
Fig. 6.
Average mTREs over 30 test cases induced by the interpolation error of the (a) first, (b) second, (c) third deformation parameter versus different kernel widths. Green: 30 test cases sampled in the global parameter space and interpolated from global training images. Blue: 30 test cases sampled in the first subspace and interpolated from local training images.
Next, the kernel width resulting in the least mTRE was selected separately for each subspace and global space, and used to test global REALMS and localized REALMS on an independent set of 128 test images sampled from the global shape space. As shown in Table I, localized REALMS reduced the global REALMS registration error by an average of 74.2%. Further, global REALMS showed a 97% success rate in choosing the correct subspace for the local interpolation.
TABLE I.
Average mTREs Over 128 Test Cases Projected Onto the Each Deformation Principal Component
| Dataset# | REALMS Method | (mm) | (mm) | (mm) | Overall (mm) |
|---|---|---|---|---|---|
| 1 | Global | 0.110 ± 0.081 | 0.027 ± 0.024 | 0.036 ± 0.032 | 0.101 ± 0.078 |
| 1 | Localized | 0.037 ± 0.030 | 0.009 ± 0.007 | 0.011 ± 0.009 | 0.032 ± 0.027 |
| 2 | Global | 0.275 ± 0.246 | 0.215 ± 0.164 | 0.174 ± 0.178 | 0.350 ± 0.278 |
| 2 | Localized | 0.069 ± 0.063 | 0.030 ± 0.026 | 0.036 ± 0.075 | 0.080 ± 0.088 |
| 3 | Global | 0.210 ± 0.193 | 0.062 ± 0.061 | 0.070 ± 0.073 | 0.101 ± 0.093 |
| 3 | Localized | 0.048 ± 0.042 | 0.012 ± 0.012 | 0.011 ± 0.012 | 0.023 ± 0.022 |
C. Actual Data Tests
Tests of actual data consisted of registration of the reference CT with actual on-board cone-beam projection images at the EE (End-Expiration) phase in the three patient datasets. The rigid translation and resolution normalization described in Section V were carried out prior to deformable registration. The same training methodology was used as in the synthetic data tests. The learned metrics and the selected kernel widths were used to estimate deformation parameters. The quality of the registration was measured by the magnitude of 3D target centroid differences (TCDs) of the target organ (duodenum) between the REALMS-estimated segmentation and the manual segmentations in the reconstructed CBCT at end expiration.
As shown in Table II, localized REALMS outperformed global REALMS in all cases. Localized REALMS reduced the registration error of global REALMS by an average of 30% in average. The TCDs in the first two patient cases were approximately 2 mm, consistent with the accuracy needed for clinical application.
TABLE II.
Magnitude of Target Centroid Differences of the Duodenum Before and After Registration for Three Patient Datasets
| Dataset# | Initial (mm) | Global (mm) | Localized (mm) | Time (ms) |
|---|---|---|---|---|
| 1 | 6.901 | 6.826 | 2.475 | 25.83 |
| 2 | 7.321 | 2.58 | 1.961 | 25.93 |
| 3 | 6.797 | 6.216 | 6.098 | 34.01 |
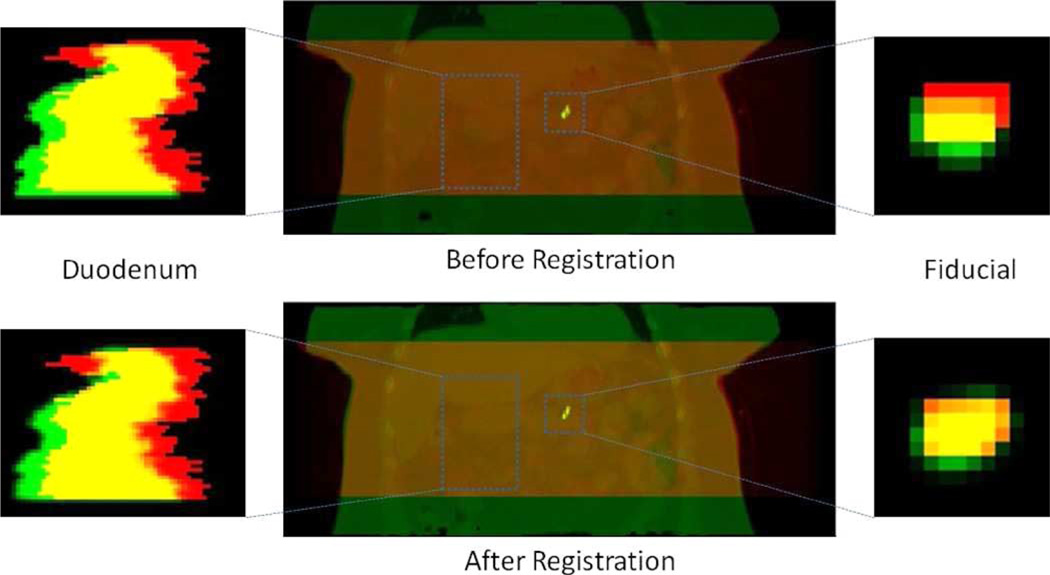
Fig. 7 shows an example (dataset 2) image overlays of the reference CT and target (CBCT) segmentations. The duodenum and the fiducial marker are more closely aligned following registration. We note that in dataset 3, localized REALMS achieves only a small improvement in TCD of the duodenum (Table II). Inspection of the fiducial marker following registration (Fig. 8) shows that it is correctly aligned (TCD: 1.19 mm) whereas the duodenum alignment is improved only in the superior–inferior direction (i.e., vertically in the images). This indicates that the deformation shape space derived from the RCCT has captured only part of the remaining deformation in the CBCT after rigid correction. There remains a significant displacement of the duodenum in the patient’s left–right direction (5.8 mm) which may have been induced by the digestive deformation, e.g., caused as changes in stomach or bowel filling. In this particular dataset, the rigid translation based on mean fiducial position difference may not be sufficiently accurate for modeling duodenal deformation. The duodenum is the portion of the small bowel that connects to the stomach, whereas the fiducial marker is implanted in the pancreas, an organ adjacent to the duodenum. Inspection of the reference CT and CBCT images showed a larger amount of stomach and bowel gas in the CBCT than in the CT (data not shown). Since the fiducial marker is approximately 5 cm distant from the duodenum and adjacent to a different part of the stomach, it is likely subject to different gas-induced deformations than is the duodenum. We did not attempt to incorporate such deformations into the REALMS shape space in this study.
Fig. 7.
Top left: Image overlay of a coronal slice of the duodenum segmentation before registration. Segmentation from the reference CT is in green and from reconstructed CBCT in red. Yellow is the overlapping region. Bottom left: Green denotes the duodenum segmentation deformed by the estimated deformation parameters. Top center: Image overlays of the reference CT (green) and the reconstructed CBCT (red). Bottom center: Images overlays of the estimated CT (green) and the reconstructed CBCT (red). Top and bottom right: Coronal image overlays of the fiducial marker segmentation.
Fig. 8.
Top left: Image overlay of a coronal slice of the duodenum segmentation before registration. Segmentation from the reference CT is in green and from reconstructed CBCT in red. Yellow is the overlapping region. Bottom left: Green denotes the duodenum segmentation deformed by the estimated deformation parameters. Top center: Image overlays of the reference CT (green) and the reconstructed CBCT (red). Bottom center: Images overlays of the estimated CT (green) and the reconstructed CBCT (red). Top and bottom right: Coronal image overlays of the fiducial marker segmentation.
VII. Discussion
A. Registration Based on a Fiducial Marker
An alternative application of REALMS is to obtain organ deformation directly. This approach is applicable to sites such as lung in which the tumor is visible in the 2D images. Such an approach in lung has been investigated by Li et al. [11] and by Chou et al. [18]. Since the current study focuses on abdomen where, unlike in lung, soft tissue contrast is low, there are no soft tissue organs visible in the radiographs. In pancreas, even the diaphragm is outside the radiograph field-of-view (Fig. 4). Hence, our 2D/3D registration approach has been to focus on the fiducial markers as the most reliable match structures in this site.
In fact, some alternative methods [9], [12] derived the overall regional deformation simply based on fiducial markers or surrogate signals by noticing that it is easier to solve for the PCA scores from a sparse subset of the whole region, such as the position of a single voxel. However, in our abdominal 2D/3D registration context, it is still inadequate to use the fiducial marker alone to determine the composite deformation. As mentioned before, there are two kinds of deformation in the abdomen, and we only use the information derived from a single fiducial marker to correct for the digestive deformation. Experiments (Fig. 8) suggested that this might not be able to sufficiently capture the digestive deformation. We have also tried using a fiducial marker alone to determine the respiratory deformation, and experiments showed that it failed to accurately determine the deformation far away from the target organ. In our application, what we can measure at treatment is just a 2D position of a single fiducial marker in the projection image, so it is difficult to use two values to accurately estimate three PCA scores. This argument was also suggested by Li’s [12] result. According to their experiments, solving for more than two PCA coefficients from three coordinates could even lead to an overfitting problem and give large errors.
B. Breathing Magnitude
In clinical use cases in which 2D/3D registration is carried out on radiographs acquired over the entire respiratory cycle, there can be circumstances in which patient breathing is shallower in the RCCT at simulation but deeper at treatment. The organ deformations at treatment would extend outside the shape space derived from the RCCT, thereby requiring extrapolation of the model. In the REALMS framework, each eigenvector of the PCA analysis represents a principal deformation mode caused by respiration. We constrain the coefficients (c values) of the first three deformation modes to be from −3σi to 3σi (i = 1, 2, 3), assuming the magnitude of respiratory deformation can be captured by this range. If the breathing is way deeper at treatment, we can relax the range constraint for each deformation mode and have training c parameters with even larger magnitudes, so that the target c parameters can be achieved by interpolation. Here, we assume that a deformation with a large magnitude can be recovered by increasing the magnitudes of principal deformation coefficients.
Our study examined gated CBCT in which all projection images were acquired at the same point in the respiratory cycle, near end expiration. Hence, these data were less likely to be affected by larger breathing amplitudes. What was observed, however, was that the positions of the fiducial markers in the gated CBCT were outside the range of positions observed in the RCCT, hence the need for a rigid registration to compensate for nonrespiratory deformations.
VIII. Conclusion
In this work, we have presented a new algorithm for improving the accuracy of a previously developed 2D/3D deformable registration method, called REALMS. Rather than carrying out a kernel regression with a globally trained metric as in the prior method, the improved algorithm divides the deformation space into several subspaces and learns a local metric in each subspace. After determining the subspace to which the deformation parameters belong, each parameter is interpolated using the local metric from local training samples. We evaluated the performance of our proposed method in patient abdominal image sets, which posed additional challenges relative to previously test image sets such as lung, caused by low soft tissue contrast in the abdominal images and the presence of nonrespiratory deformations caused by changes in the contents of digestive organs. Several methods were introduced for processing abdominal images. First, to account for digestive changes, a 3D rigid translation was applied between the planning time and treatment time images by aligning to the respiration-averaged position of an implanted fiducial marker as a surrogate for soft tissue positions. Second, to facilitate 2D/3D deformable registration in low-contrast projection images, differences between the DRR and target projection images was computed within an ROI around the fiducial. Third, a convolution of projection images with a blurring kernel was applied to yield fiducial appearances consistent with those in the lower-resolution DRRs. Evaluation of synthetic data and actual data show that the proposed localized method improves registration accuracy when accounting for respiratory deformation alone. Two of the three actual data cases demonstrate the method’s potential utility for clinical use in abdominal IGRT. However, the method’s accuracy can be limited when the proposed fiducial-based 3D rigid translation is insufficient to approximate the digestive deformation. Future work will include modeling of the digestive deformation between planning time and treatment time, updating the deformation space and the reference image at treatment setup time and evaluating the method on more abdominal patient datasets.
Acknowledgments
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health. This work was supported by the National Cancer Institute under Award R01-CA126993 and Award R01-CA126993-02S1.
Footnotes
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Qingyu Zhao, Department of Computer Science, University of North Carolina, Chapel Hill, NC 27599 USA..
Chen-Rui Chou, Department of Computer Science, University of North Carolina, Chapel Hill, NC 27599 USA..
Gig Mageras, Memorial Sloan-Kettering Cancer Center, New York, NY 10021 USA..
Stephen Pizer, Department of Computer Science, University of North Carolina, Chapel Hill, NC 27599 USA..
References
- 1.Markelj P, Tomazevic D, Likar B, Pernus F. A review of 3D/2D registration methods for image-guided interventions. Med. Image Anal. 2012;16(3):642–661. doi: 10.1016/j.media.2010.03.005. [DOI] [PubMed] [Google Scholar]
- 2.Chou C, Pizer S. Real-time 2D/3D deformable registration using metric learning. MCV: Recognit. Techniq. Appl. Med. Imag. 2012;7766:1–10. [Google Scholar]
- 3.Russakoff D, Rohlfing T, Maurer C. Fast intensity-based 2D–3D image registration of clinical data using light fields. Proc. IEEE Int. Conf. Comput. Vis. 2003;1:416–422. [Google Scholar]
- 4.Russakoff D, Rohlfing T, Mori K, Rueckert D, Ho A, Adler JR, Maurer CR. Fast generation of digitally reconstructed radiographs using attenuation fields with application to 2D–3D image registration. IEEE Trans. Med. Imag. 2005 Nov.24(11):1141–1454. doi: 10.1109/TMI.2005.856749. [DOI] [PubMed] [Google Scholar]
- 5.Khamene A, Bloch P, Wein W, Svatos M, Sauer F. Automatic registration of portal images and volumetric CT for patient positioning in radiation therapy. Med. Image Anal. 2006;10(1):96–112. doi: 10.1016/j.media.2005.06.002. [DOI] [PubMed] [Google Scholar]
- 6.Munbodh R, Jaffray DA, Moseley DJ, Chen Z, abd JPSK, Cathier P, Duncan JS. Automated 2D–3D registration of a radiograph and a cone beam CT using line-segment enhancement. Med. Phys. 2006;33(5):1398–1411. doi: 10.1118/1.2192621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gendrin C, Furtado H, Weber C, Bloch C, Figl M, Pawiro SA, Bergmann H, Stock M, Fichtinger G, Georg D, Birkfellner W. Monitoring tumor motion by real time 2D/3D registration during radiotherapy. Radiother. Oncol. 2012;102(2):274–280. doi: 10.1016/j.radonc.2011.07.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Furtado H, Steiner E, Stock M, Georg D, Birkfellner W. Realtime 2d/3d registration using kV-MV image pairs for tumor motion tracking in image guided radiotherapy. Acta Oncol. 2013 Oct.52(7):1464–1471. doi: 10.3109/0284186X.2013.814152. [DOI] [PubMed] [Google Scholar]
- 9.Zhang Q, Pevsner A, Hertanto A, Hu Y, Rosenzweig K, Ling C, Mageras G. A patient-specific respiratory model of anatomical motion for radiation treatment planning. Med. Phys. 2007;34(12):4772–4781. doi: 10.1118/1.2804576. [DOI] [PubMed] [Google Scholar]
- 10.Li R, Lewis J, Jia X, Gu X, Folkerts M, Men C, Song W, Jiang S. 3D tumor localization through real-time volumetric X-ray imaging for lung cancer radiotherapy. Med. Phys. 2011;38(5):2783–2794. doi: 10.1118/1.3582693. [DOI] [PubMed] [Google Scholar]
- 11.Li R, Jia X, Lewis JH, Gu X, Folkerts M, Men C, Jiang S. Realtime volumetric image reconstruction and 3D tumor localization based on a single X-ray projection image for lung cancer radiotherapy. Med. Phys. 2010;37(6):2822–2826. doi: 10.1118/1.3426002. [DOI] [PubMed] [Google Scholar]
- 12.Li R, Lewis J, Jia X, Zhao T, Liu W, Lamb J, Yang D, Low D, Jiang S. On a PCA-based lung motion model. Phys. Med. Biol. 2011;56(18):6009–6030. doi: 10.1088/0031-9155/56/18/015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Banks S, Hodge W. Accurate measurement of three-dimensional knee replacement kinematics using single-plane fluoroscopy. IEEE Trans. Biomed. Eng. 1996 Jun.43(6):638–649. doi: 10.1109/10.495283. [DOI] [PubMed] [Google Scholar]
- 14.Freire L, Gouveia A, Godinho F. FMRI 3D registration based on Fourier space subsets using neural networks; Proc. IEEE Eng. Med. Biol. Soc. Conf; 2010. pp. 5624–5627. [DOI] [PubMed] [Google Scholar]
- 15.Zhang J, Ge Y, Ong S, Chui C, Teoh S, Yan C. Rapid surface registration of 3D volumes using a neural network approach. Image Vis. Comput. 2008;26(2):201–210. [Google Scholar]
- 16.Wachowiak M, Smolikova R, Zurada J, Elmaghraby A. A supervised learning approach to landmark-based elastic biomedical image registration and interpolation. Proc. 2002 Int. Joint Conf. Neural Netw. 2002;2:1625–1630. [Google Scholar]
- 17.Chou C, Frederick B, Liu X, Mageras G, Chang S, Pizer S. CLARET: A fast deformable registration method applied to lung radiation therapy. Proc. 4th Int. MICCAI Workshop Pulmonary Image Anal. 2011:113–124. [Google Scholar]
- 18.Chou C, Frederick B, Mageras G, Chang S, Pizer S. 2D/3D image registration using regression learning. Comput. Vis. Image Understand. 2013;117(9):1095–1106. doi: 10.1016/j.cviu.2013.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chou C, Pizer S. Local regression learning via forest classification for 2d/3d deformable registration. Proc. MICCAI Workshop Med. Comput. Vis. 2013;8331:24–33. [Google Scholar]
- 20.Foskey M, Davis B, Goyal L, Chang S, Chaney E, Strehl N, Tomei S, Rosenman J, Joshi S. Large deformation three-dimensional image registration in image-guided radiation therapy. Phys. Med. Biol. 2005;50:5869–5892. doi: 10.1088/0031-9155/50/24/008. [DOI] [PubMed] [Google Scholar]
- 21.Li R, Lewis J, Berbeco R, Xing L. Real-time tumor motion estimation using respiratory surrogate via memory-based learning. Phys. Med. Biol. 2012;57(15):4771–4786. doi: 10.1088/0031-9155/57/15/4771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Atkeson C, Moore A, Schaal S. Locally weighted learning. Artif. Intell. Rev. 1997;11:11–73. [Google Scholar]
- 23.Kincaid RE, Yorke ED, Goodman KA, Rimner A, Wu AJ, Mageras GS. Investigation of gated cone-beam CT to reduce respiratory motion blurring. Med. Phys. 2013;40(7):041717. doi: 10.1118/1.4795336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Feldkamp LA, Davis LC, Kress JW. Practical cone-beam algorithm. J. Opt. Soc. Am. A. 1984;1(6):612–619. [Google Scholar]
- 25.Cachier P, Pennec X. 3D non-rigid registration by gradient descent on a gaussianwindowed similarity measure using convolutions. Proc. Math. Methods Biomed. Image Anal. 2000:182–189. [Google Scholar]