A Simple Method for Rectified Noise Floor Suppression: Phase-Corrected Real Data Reconstruction With Application to Diffusion-Weighted Imaging

Abstract

Diffusion-weighted MRI is an intrinsically low signal-to-noise ratio application due to the application of diffusion-weighting gradients and the consequent longer echo times. The signal-to-noise ratio worsens with increasing image resolution and diffusion imaging methods that use multiple and higher b-values. At low signal-to-noise ratios, standard magnitude reconstructed diffusion-weighted images are confounded by the existence of a rectified noise floor, producing poor estimates of diffusion metrics. Herein, we present a simple method of rectified noise floor suppression that involves phase correction of the real data. This approach was evaluated for diffusion-weighted imaging data, obtained from ethanol and water phantoms and the brain of a healthy volunteer. The parameter fits from monoexponential, biexponential, and stretched-exponential diffusion models were computed using phase-corrected real data and magnitude data. The results demonstrate that this newly developed simple approach of using phase-corrected real images acts to reduce or even suppress the confounding effects of a rectified noise floor, thereby producing more accurate estimates of diffusion parameters.

In the last several decades, diffusion-weighted imaging (DWI) has played a pivotal role in the diagnosis and treatment of numerous diseases, especially stroke and cancer, due to their sensitivity to the microscopic motion of tissue water (1–3). DWI has been predominantly used to evaluate intracranial diseases, but in recent years an ever-increasing number of extracranial diseases have also benefited from this imaging application (4,5). As clinical DWI advances, more effort has been made to understand and exploit the complex diffusion properties of tissue. Often this takes the form of higher resolution and the inclusion of images with a greater range and magnitude of b-values. Unfortunately, the signal-to-noise ratios (SNR) at both higher spatial resolutions and diffusion weightings are significantly reduced. Until technical advances are made that diminish or circumvent the confounding noise, techniques must be established to accommodate lower SNR images.

The noise properties of MR images have been exhaustively studied (6–9). The raw signal, generated by radio-frequency quadrature detection hardware, is recorded by two channels and subsequently transformed into complex data. Intrinsic to the MR hardware, each raw signal channel is confounded by white noise having a zero mean gaussian probability distributions (8). After the complex data are placed into k-space, it is subsequently transformed, by means of the Fourier transform, a linear operator, into complex image space. Therefore, noise in the real and the imaginary images each maintain their zero mean gaussian probability distribution. The ubiquitously analyzed magnitude images are calculated by the root sum of squares of the real and imaginary images, a nonlinear operation that combines the noise distributions. This operation transforms the noise into the Rician probability distribution, an asymmetric distribution with a positive expectation value, giving rise to a rectified noise floor (6). Most MR applications produce magnitude images in the high SNR regimen such that it is reasonable to ignore the influence of the rectified noise floor. In situations where the SNR is inherently poor, the MR signal of interest approaches the magnitude image’s rectified noise floor. When the low SNR cannot be avoided, the rectified noise floor cannot be ignored, especially when biophysical models are used to fit data that span the noise regimens.

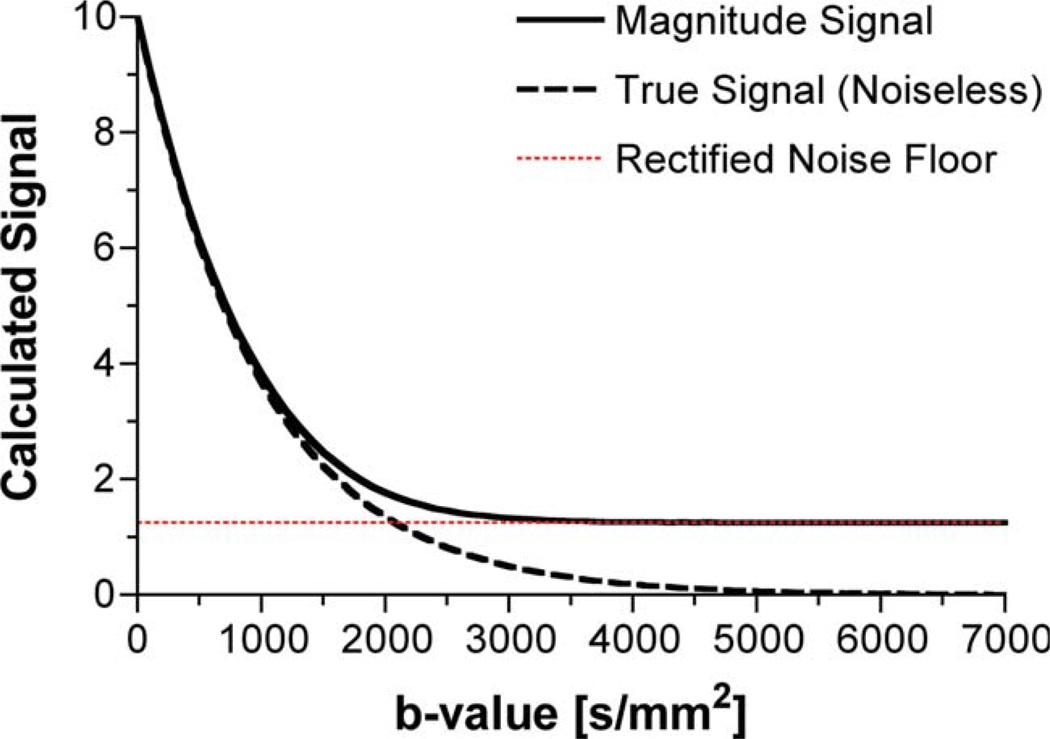
DWI, due to its intrinsic signal attenuation, is a low SNR candidate, particularly at high b-values in voxels of fast diffusion rates. Current clinical sequences typically assume a simplified diffusion model not confounded by a rectified noise floor. Specifically, the standard two-point DWI (b = 0 and 1000 sec/mm²) method was chosen to maintain both an optimal diffusion-to-noise ratio and optimal SNR. In recent years, the diffusion-weighted (DW) signal attenuation in many tissue types, including brain, has been shown to be nonmonoexponential for a larger range of b-values (b = 0 to 6000 sec/mm²) (10–13). Consequently, more complex models, e.g., biexponential and stretched-exponential diffusion models (11,14), have been implemented to describe the nature of the diffusion-weighted signal attenuation observed for this larger range of diffusion weightings. However, these models are used to fit to data that may span, on a voxelwise scale, a large range of SNRs for parameter estimation. Fitting any multicompartment model to data that span both high and low SNR regimens may introduce additional artificial compartments solely due to the presence of the rectified noise floor. As the b-value increases, the rectified noise floor increasingly dominates the signal, as depicted by the simulated diffusion data shown in Fig. 1. At high b-values, the SNR of an image as a whole may be large enough to ignore the noise floor; however, this will not be true on a voxelwise basis.

FIG 1.

The effect of the rectified noise floor on the diffusion weighted signal as a function of the signal-to-noise ratio. The data were generated in Matlab by adding normally distributed noise to both the real and imaginary signal having an original phase angle of zero. The “true signal” estimate of the diffusion attenuation curve was generated using an ADC of 1000 µm²/sec. The rectified noise floor is calculated by taking the root mean sum of squares of the noise added to the real and imaginary channels. Both the magnitude signal and the rectified noise floor represent the mean value of 10⁵ iterations. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

In this regard, several authors have attempted to correct for the noise bias in diffusion-weighted images (6,7,15). Even if these methods are applied, the noise probability distributions are SNR dependent and thus b-value dependent. For non-diffusion-weighted sequences, the simple solution is to increase SNR so that the noise can be considered gaussian by increasing the number of complex signal averages. However, in diffusion imaging complex signal averaging can only be performed after a correction for motion-induced phase errors (16). Due to the motion sensitivity of diffusion-weighted sequences, the resultant phase variations of the diffusion-encoded data only allow for magnitude signal averaging, which results in a non-gaussian noise distribution. However, even if complex signal averaging could be performed to increase the SNR, since SNR only increases as the square root of the number of averages, this solution is not practical in most clinical situations. Therefore, for DWI, the more realistic solution is one that does not require additional acquisition time but eliminates the signal bias and maintains the same probability distribution for the noise at all SNR. We propose that phase-corrected real data reconstruction may provide the solution to this challenge.

Phase-corrected (PC) real data reconstruction is a technique that attempts to maintain the original signal and the original white noise of zero mean gaussian probability distribution generated during acquisition (17–19). Unlike magnitude image reconstructions that discard phase information, this technique phase corrects the real and imaginary images. Ideally, the phase correction rotates all of the signal of interest into the real image, leaving only noise in the imaginary image. Therefore, instead of discarding signal information contained in the phase images, real images are generated containing the signal of interest plus noise, while the imaginary images, which only contain noise, are discarded. By working with the real images directly, the original zero-mean white-noise gaussian distribution is preserved. Furthermore, the resulting real images, unlike the magnitude images, possess both positive and negative values, allowing for a true zero-mean background noise, completely eliminating the rectified noise floor.

Previous phase-corrected real data reconstruction techniques utilize several different techniques, including a least-squares fit of the phase to a low-order polynomial (17,20) or a low-resolution phase image (19) to phase correct the complex data. Here, we propose a new and simpler phase-correction technique that relies upon low-pass-filtered complex images to phase correct the complex data. This technique ensures that the phase-corrected real and imaginary images have normally distributed noise while moving almost the entire signal into the real image. Initial evaluation of this approach is undertaken here by processing diffusion data obtained in phantoms and healthy human brain tissue. The new phase-correction technique is compared to standard magnitude reconstruction methods in the context of the most common model fits of diffusion data.

THEORY

The Phase-Corrected Real-Data Reconstruction Technique

The phase-corrected real-data reconstruction can be easily incorporated into any MR data reconstruction algorithm. First, both the real and imaginary images are spatially filtered, using a square (i.e., 3 × 3, 5 × 5, 7 × 7, …) uniformly weighted convolution kernel to generate low-frequency phase images. Using the low-frequency phase images, the original complex images, defined as

$$S(x,y)=\text{Re}(x,y)+i\text{Im}(x,y),$$ [1]

are rotated, by complex rotation,

$$S_{\mathit{\text{PC}}}(x,y)=S(x,y)e^{i\widehat{\mathrm{\varphi }}(x,y)}$$ [2]

where x and y are voxel coordinates and φ̂(x, y) is the voxelwise estimate of the low-frequency phase used to calculate the phase-corrected complex images, S_PC(x, y). Regardless of the degree of rotation, the magnitude of S_PC(x, y) remains constant. After the complex rotation, a normality test may be performed on each imaginary image to ensure that the phase-corrected imaginary image contains only noise, not signal. After the phase-corrected imaginary image meets the normality conditions, it is assumed to contain only noise and therefore can be discarded. The remaining image, the phase-corrected real image, contains the signal of interest plus white noise, with the original gaussian probability distribution.

Biophysical Diffusion Models

Many models have been used to parameterize the diffusion-weighted signal decay of brain tissue, each having various assumptions and interpretations. It is not the purpose of this paper to address these issues or even the sources of the signal decay. Instead, the purpose of this paper is to present a simple method for noise floor suppression. To that end, a comparison of diffusion-weighted parameterization of standard magnitude images and phase-corrected real images is made. Here, we briefly describe the most common diffusion analysis models, which will be used to parameterize the diffusion data in this study.

Monoexponential Model

For b-values less than approximately 1500 sec/mm², the diffusion-weighted signal of brain tissue exhibits mono-exponential signal decay. Biophysically, the monoexponential model,

$$S(b)=S_0{e}^{-\mathit{\text{bADC}}},$$ [3]

represents a parameterization of the tissue’s apparent diffusion coefficient (ADC). If any of the diffusion-weighted images have signals that enter the low SNR regimen, a constant noise term, N_floor, can be added to model the rectified noise floor in magnitude images,

$$S(b)=S_0{e}^{-\mathit{\text{bADC}}}+N_{\mathit{\text{floor}}}.$$ [4]

For the purpose of comparison, both monoexponential models were implemented to determine the influence of modeling the rectified noise floor as a constant in magnitude images.

Biexponential Model

For b-values exceeding approximately 1500 sec/mm², the diffusion-weighted signal of brain tissue exhibits biexponential signal decay (11,21). For the biexponential model,

$$S(b)=A_1{e}^{-{\mathit{\text{bADC}}}_1}+A_2{e}^{-{\mathit{\text{bADC}}}_2},$$ [5]

where A₁ and A₂ are the proton pool signal amplitudes and ADC₁ and ADC₂ are the respective ADCs. Diffusion-weighted measurements made at the higher b-values are more likely to approach the rectified noise floor, but the biexponential model commonly excludes a term to model the rectified noise floor. Therefore, we hypothesize that phase-corrected real images will enhance the overall fit of the biexponential model by eliminating the confounding effects of the rectified noise floor from the data.

Stretched-Exponential Model

A significant body of literature has shown that within the in vivo brain, diffusion-weighted signal attenuation is nonmonoexponential over an extended range of b-values (0–6000 sec/mm²) (10–13). Due to the uncertainty of the biophysical mechanism of the diffusion-weighted signal decay, the stretched-exponential model was introduced (10),

$$S(b)=S_0{e}^{-{(\mathit{\text{bDDC}})}^{\alpha }},$$ [6]

where DDC is the distributed diffusion coefficient and a is the stretching parameter, also known as the heterogeneity index, a unitless quantity that ranges from 0 to 1, with 1 being the least heterogeneous or completely homogeneous. Unlike the previous model, this model makes no assumptions about the number of proton pools contributing to the diffusion-weighted signal decay. Like the biexponential model, the rectified noise floor is a potential confounding factor that is often ignored when fitting the model to the diffusion-weighted signal. Therefore, it is our hypothesis that the phase-corrected real images are also likely to benefit the stretched-exponential model fit of the diffusion-weighted data.

MATERIALS AND METHODS

Phantom Study

In order to assess the effects of noise on these diffusion models, DWI experiments of deionized water and ethanol were performed at room temperature. These solutions are known to have monoexponential diffusion and meet the assumptions for the monoexponential diffusion model. Data were collected on a 9.4-T system (Bruker, Berlin, Germany) equipped with 400 mT/m gradients using the standard spin warp, diffusion-weighted, spin-echo sequence with pulse repetition time = 2000 msec, echo time = 108 msec, δ = 25 msec, Δ = 30 msec, and 15 b-values linearly spaced between 0 and 7000 sec/mm². Four 2 mm-thick slices with a field of view 40 × 40 mm and matrix size 128 × 128 were collected at each b-value. In order to verify the natural noise distribution from the scanner hardware, an additional image was collected with identical imaging parameters but with 0° excitation and refocusing pulses and without diffusion weighting. The real and imaginary data were used for the phase-corrected real reconstruction.

Human Study

Diffusion-weighted images of a healthy subject were acquired on a 3.0-T GE scanner (GE Healthcare, Milwaukee, WI) equipped with 40 mT/m gradients and running software version 11.0. A commercial quadrature coil was used for radiofrequency transmission and reception. High b-value diffusion-weighted images were acquired using a custom, lipid-suppressed, single-shot, spin-echo, spiral-out sequence with a field of view 22 cm², matrix sizes of 96 × 96 or 128 × 128, pulse repetition time = 10,000 msec, slice thickness = 5mm, skip = 1.5mm, and 22 slices. To minimize eddy currents, the time width of the ramps of the diffusion gradients was lengthened to 400 µsec and the maximum gradient amplitude of the diffusion gradients was limited to 22 mT/m. Timing parameters for the sequence were chosen based on the maximum b-value of 7000 sec/mm². This resulted in values of δ = 44 msec, Δ = 50 msec, and echo time = 100 msec. The amplitudes of the diffusion gradients were incremented over 15 steps from 0 to 22 mT/m, corresponding to b-values ranging linearly from 0–7000 sec/ mm². Spiral images were reconstructed offline using custom software developed at our institution. The subject gave informed written consent under guidelines approved by the institutional review board at our institution.

Statistical Analysis

Since the ethanol and water phantoms are known single compartments, the estimates of the ADC and DDC from all the models were compared to one another using a one-way analysis of variance to compare the parameter estimates of ADC obtained from both the magnitude and the PC real reconstruction techniques. Post hoc, the Bonferroni’s multiple comparison test was used to compare each combination of model and reconstruction method on the estimated ADC. For the human study, only a qualitative analysis was performed.

Theoretical and Practical Implications

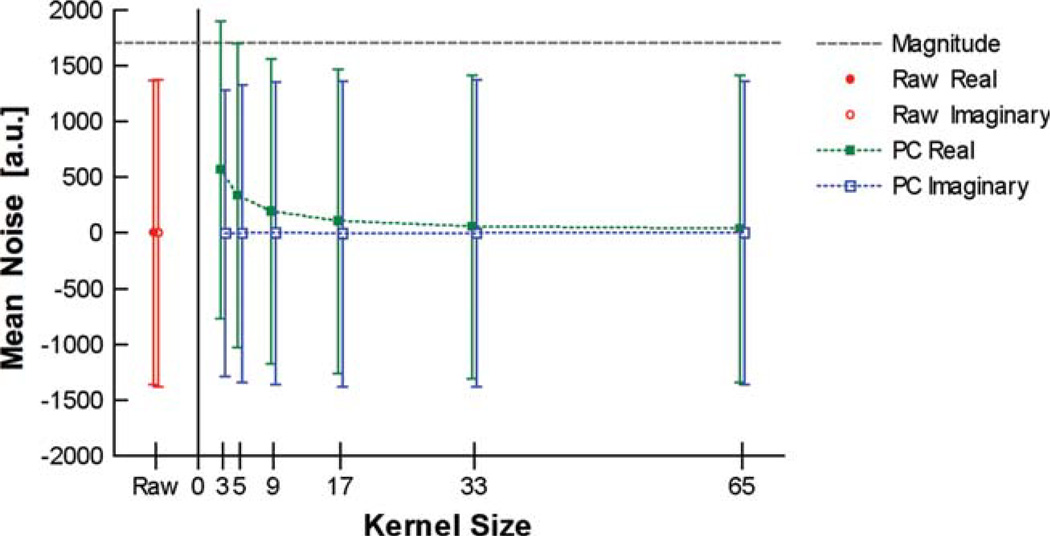
Due to the high spatial frequencies found within most images, the estimated phase will never match the actual phase. If the phase estimate equals the actual phase, then the phase-corrected real images should in theory have no noise bias. Practically, since the PC real method relies on a low-resolution estimate of the phase, a small noise floor may exist. Furthermore, the filtering kernel directly affects the phase estimate and consequently the degree of the noise floor present in the final PC real data. The size of the image kernel that is implemented directly affects the mean value of the noise in the final PC real data. Figure 2 was generated from noise-only images, using various kernel sizes in order to determine the effect the kernel size has on the signal bias. This figure clearly demonstrates that the larger the kernel size, the smaller the signal bias. However, the larger the kernel size, the more high-frequency spatial information is left behind in the imaginary image. A kernel size of one voxel estimates the exact phase and consequently generates the magnitude image. Note that, even using a small kernel of 3 × 3, the signal bias is much smaller than the signal bias of the magnitude images. For the purpose of this study, a 3 × 3 kernel was chosen, which has signal bias but leaves little if any high-frequency spatial information in the imaginary image. Though this kernel was best suited for the noise conditions of the images presented, further investigation is warranted to optimize this choice under other conditions. The type of filtering kernel can also affect the noise floor. However, for smaller kernel sizes a uniformly weighted convolution kernel was found to reduce the noise over a gaussian weight convolution kernel. (Data not included.)

FIG 2.

The effects of the phase correction’s kernel size on the mean noise of the phase-corrected real and imaginary images. The size of the filtering kernel determines the degree of noise offset seen in the PC real imaged. As the size of the filtering kernel increases, the mean of the PC real noise approached the original mean of zero. The standard deviation of the PC imaginary is reduced at smaller kernel sizes but maintains a zero mean for all kernel sizes. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Boundary Effects Simulation

A simulation was performed to consider the effects of nonuniform phase variation, as can be seen between gray and white matter. Fourier space data were generated on a point-by-point basis in the simulation. For each k-space point, acquired at time t, an image-space representation of the phantom was generated as:

$$S(x,y)=\rho e^{-t/{T_2}^{\ast }(x,y)}{e}^{-t\Delta {\omega }_0(x,y)}{e}^{-\mathit{\text{bADC}}},$$ [7]

where ρ is the phantom proton spin density, T₂* is the phantom T₂* map, Δω₀ is the chemical shift of the tissue being imaged, b is the simulated b-value, and ADC is the simulated ADC. The Fourier transform of the image-space representation for the time point was made and the desired k-space point extracted for the simulated k-space data.

The phantom included gray and white matter components with proton spin densities of 1.2 and 1.0 and T₂*s of 40 msec and 30 msec, respectively. The proton spin density of cerebrospinal fluid was set to zero. The gray and white matter masks were extracted from a Brainweb template (22). A chemical shift of 0.01 ppm between gray and white matter was assumed (23). The simulation thus yielded a discrete phase difference between gray and white matter, with no other phase being simulated. A global ADC of 0.76 µm²/msec was simulated within the brain, with b-values ranging in steps of 1000 sec/ mm² from 0 to 8000 sec/mm². A 96 × 96 data acquisition was simulated, with each k-space line acquired instantaneously and with line acquisitions spaced by 1 msec. Normally distributed noise was added to the real and imaginary components of the simulated images such that the strongest signal in the b = 0 sec/mm² image held a magnitude SNR of 100.

The phase-corrected real reconstruction method was then applied to the simulated data, and the ADC was calculated for each voxel.

RESULTS

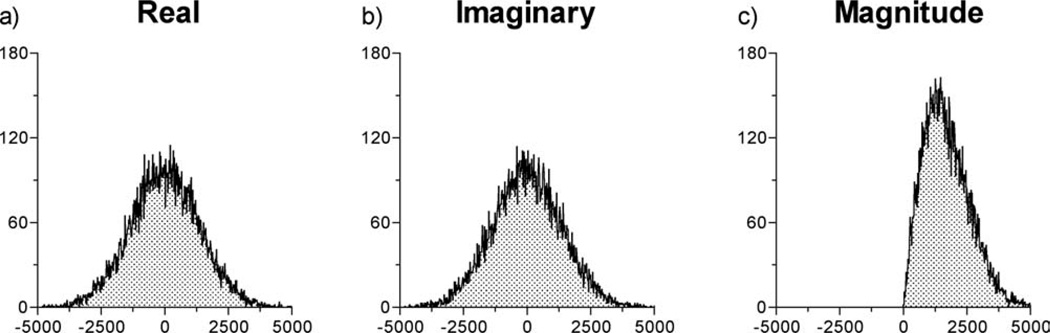
Histograms were generated of noise-only images to verify the original noise distributions of the complex and magnitude images. Figure 3 displays the histograms generated from 16,328 voxels of the magnitude, real, and imaginary images of a single 2 mm slice through a water phantom acquired with the zero degree excitation and refocusing pulses. The noise obtained in both the real and imaginary channels passed the Kolmogorov-Smirnov test for normality (P < 0.05), verifying the assumption that the scanner noise is gaussian. The histogram of the corresponding magnitude image exhibits the special case of the Rician distribution (i.e., the Rayleigh distribution) and clearly demonstrates the source of the rectified noise floor.

FIG 3.

Histograms taken from a single slice of the noise-only magnitude, real, and imaginary images. The complex data were obtained using a standard line scan sequence using a 0° flip angle of a cylindrical phantom. Each histogram represents 16,384 voxels. Both the real and the imaginary image data passed the Kolmogorov-Smirnov test for normality (P < 0.05). Note that the magnitude image data, unlike the original real and imaginary image data, have a different noise distribution, the Raleigh distribution.

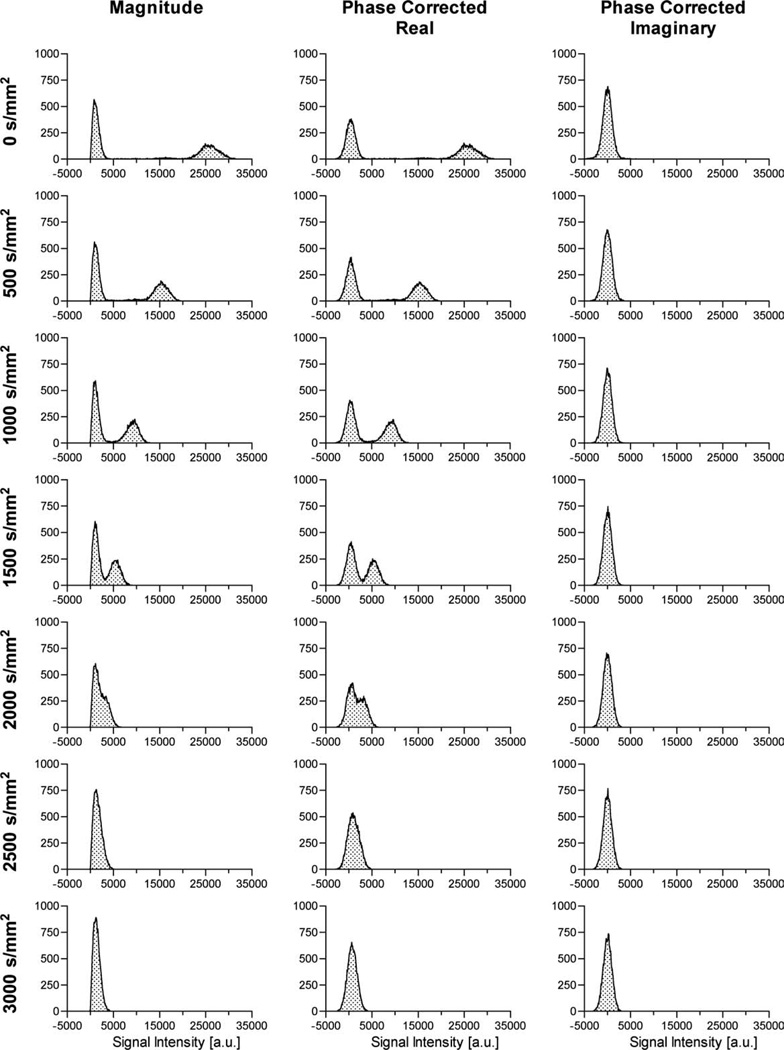
Figure 4 demonstrates the effect that diffusion weighting has on magnitude, phase-corrected real, and phase-corrected imaginary images as a function of b-value. Each histogram was generated from all voxels contained within the same single 2mm slice of the ethanol phantom. As the diffusion weighting increases, the ability to separate noise from signal diminishes. At the resolution used in this study (312.5-µm × 312.5-µm × 2-mm) and assumed diffusion coefficient of 1100 µm²/msec, which is slightly larger than the typical range of ADC values (500–1000 µm²/msec) of human gray/white matter in vivo, the distributions of the signal and the noise begin to overlap at b = 1500 sec/mm². Due to the shape of the noise distribution from the magnitude image, it appears to overlap the signal distribution at a lower b-value than for the PC data. Differences in the degree of overlap of signal and noise are most apparent at b-values of 1500 and 2000 sec/mm². As expected, the phase correction successfully removed the signal from the imaginary images for the entire range of b-values, or, alternatively, for all ranges of signal-to-noise ratios. In addition, the noise distribution of the phase-corrected imaginary image remained practically unchanged. Similarly, the noise distribution for the phase-corrected real image at 0 sec/mm² appears to be relatively centered about zero, with a mean and standard deviation of 398 ± 1007. However, the combined signal and noise distribution at 3000 sec/mm², for the phase-corrected real data, maintains a positive bias, with a mean and standard deviation of 715 ± 1041, indicating the presence of signal. At that same diffusion weighting, the magnitude data exhibits a Rician distribution.

FIG 4.

Histograms of the magnitude, phase-corrected real, and phase-corrected imaginary images as a function of b-value (0–3000 sec/mm² from top to bottom), taken from a single 2 mm slice of an ethanol phantom.

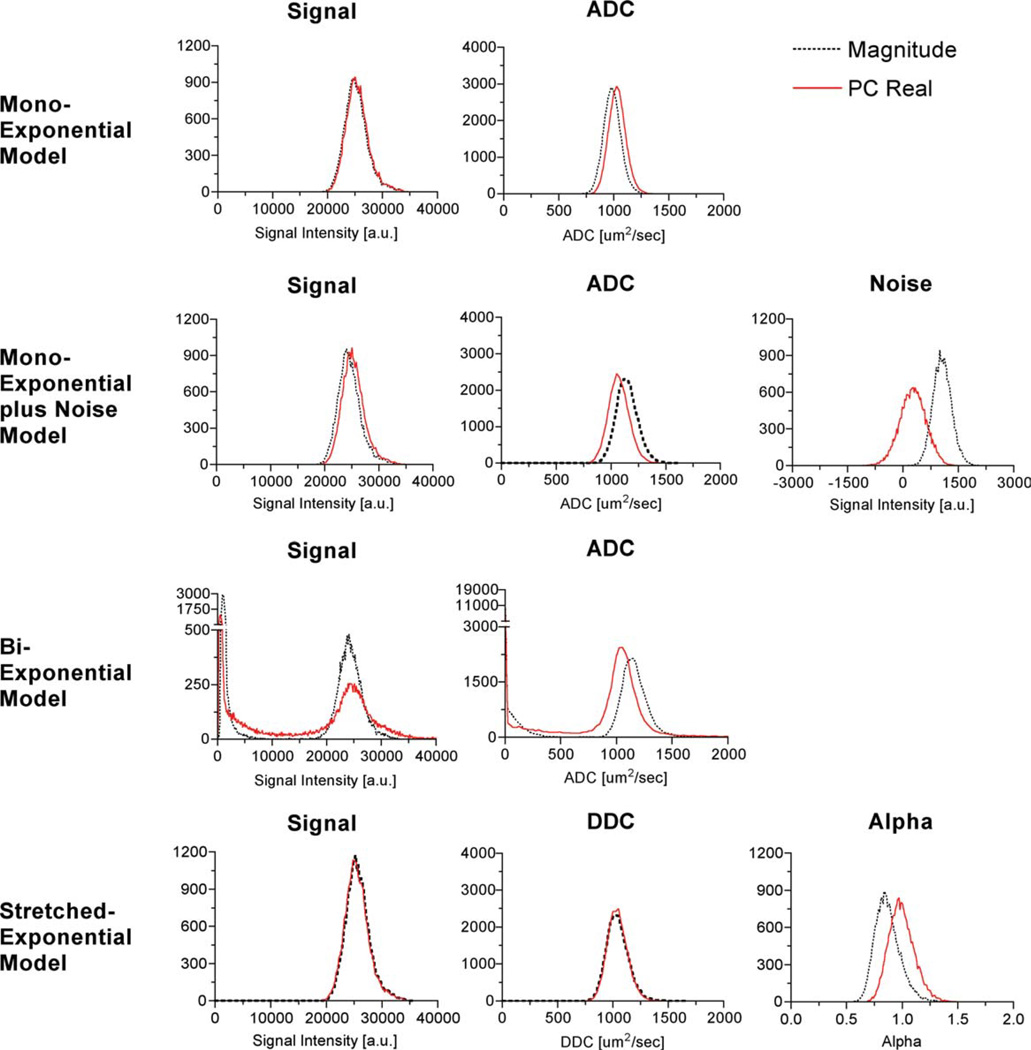
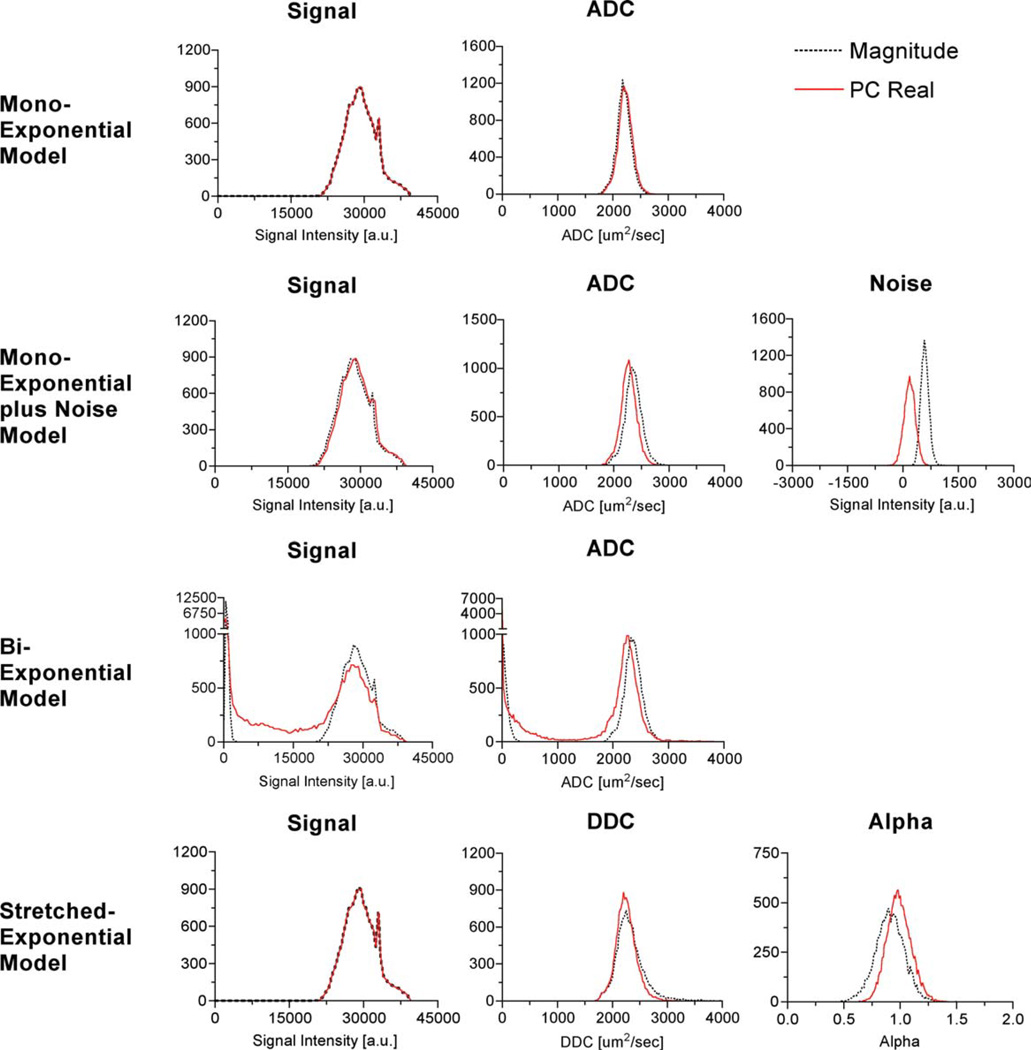
An analysis of parameter distributions for each of the diffusion models described above was performed to compare the standard magnitude and PC real reconstruction techniques. Figures 5 and 6 each show histograms of the voxelwise parameter fits of the diffusion-weighted images obtained from the ethanol (n = 22,120) and water phantom (n = 14,139), respectively, calculated over the extended range of b-values (0 to 7000 sec/mm²) from both the magnitude and the PC real images. For each phantom, single regions of interest located within the phantom on the b = 0 mm²/sec image from all four slices were manually constructed. Table 1 summarizes mean and the standard error of the mean for estimated diffusion coefficients for each model and reconstruction technique for both ethanol and deionized water. The biexponential model fits of signals A₁ and A₂, as well as the ADCs, ADC₁ and ADC₂, were plotted together to produce a histogram of each respective parameter. All models and both reconstruction techniques produced statistically significant differences in the estimates of diffusion coefficients, i.e., ADC, ADC₁, ADC₂, and DDC, for both ethanol and water.

FIG 5.

Histograms of the signal and diffusion parameter fits of the ethanol phantom at room temperature for the monoexponential, monoexponential plus noise, biexponential, and the stretched-exponential models. Each model was voxelwise fit to the data. The published diffusion coefficient of room temperature ethanol is 1100 ± 200 µm²/msec (31). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

FIG 6.

Histograms of the signal and diffusion parameter fits of the water phantom at room temperature for the monoexponential, monoexponential plus noise, biexponential, and the stretched-exponential models. Each model was voxelwise fit to the data. The published diffusion coefficient of room temperature water is 2200 ± 200 µm²/msec (31). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Table 1.

Mean ADC/DDC Between Models and Reconstruction Techniques^*

	Monoexponential model, ADC		Monoexponential + noise, ADC		Stretched-exponential model, DDC
	Magnitude	PC real	Magnitude	PC real	Magnitude	PC real
Ethanol	986.5 ± 0.52	1031 ± 0.52	1145 ± 0.65	1070 ± 0.63	1041 ± 0.67	1040 ± 0.62
Deionized water	2197 ± 1.1	2221 ± 1.1	2352 ± 1.4	2267 ± 1.2	2326 ± 2.3	2250 ± 1.6

^*The mean and the standard error of the mean for the various models and methods were calculated. Parameters were calculated from the same data set obtained from the homogeneous water and ethanol phantoms. For reference, the published diffusion coefficient of room temperature ethanol is 1100 ± 200 µm²/msec and water is 2200 ± 200 µm²/msec (31).

A comparison of the distributions of the parameter fits for the two reconstruction techniques for the fast-diffusing fluid, water, and the slow-diffusing fluid, ethanol, yielded slightly different results. Differences between the two reconstruction techniques were larger for the faster-diffusing fluid for all models except for the monoexponential model without the noise term. When applying the monoexponential model, the ADC estimates from the PC real images are higher than from the standard magnitude images. The monoexponential model fit to the PC real data from ethanol without the term for the noise floor resulted in an increased ADC compared to the fit to the magnitude data. This would be expected since the noise acts to slow the observed attenuation. By suppressing the noise floor, the signal decays more rapidly, which corresponds to an increase in the ADC. Using the same model for the water phantom resulted in a small change, which is expected, given the higher ADC of water. Alternatively, applying the monoexponential + noise and the biexponential models to the PC real images resulted in a reduction of the estimated diffusion coefficient. The biexponential model applied to the PC real data reduced the number of voxels that showed a theoretically nonexistent slow diffusing compartment/component. Furthermore, the diffusion estimate using the magnitude data estimated a relatively higher diffusion coefficient than would be expected from ethanol. Interestingly, the DDC from the stretched-exponential model had the smallest difference between the two reconstruction techniques. This suggests that the DDC provides the most robust diffusion coefficient estimate of a single-compartment fluid, regardless of reconstruction technique. The parameter fit of a greatly benefited from the PC real reconstruction. For a single-fluid compartment, the parameter a should be distributed around 1.0, i.e., have a monoexponential behavior, as shown with PC real reconstruction. Alternatively, the a fits of the standard magnitude data are distributed around a value less than 1.0, which can be directly attributed to the rectified noise floor. In summary, the PC real reconstruction technique benefits the multicompartment models more than the single-compartment model of single-compartment fluids.

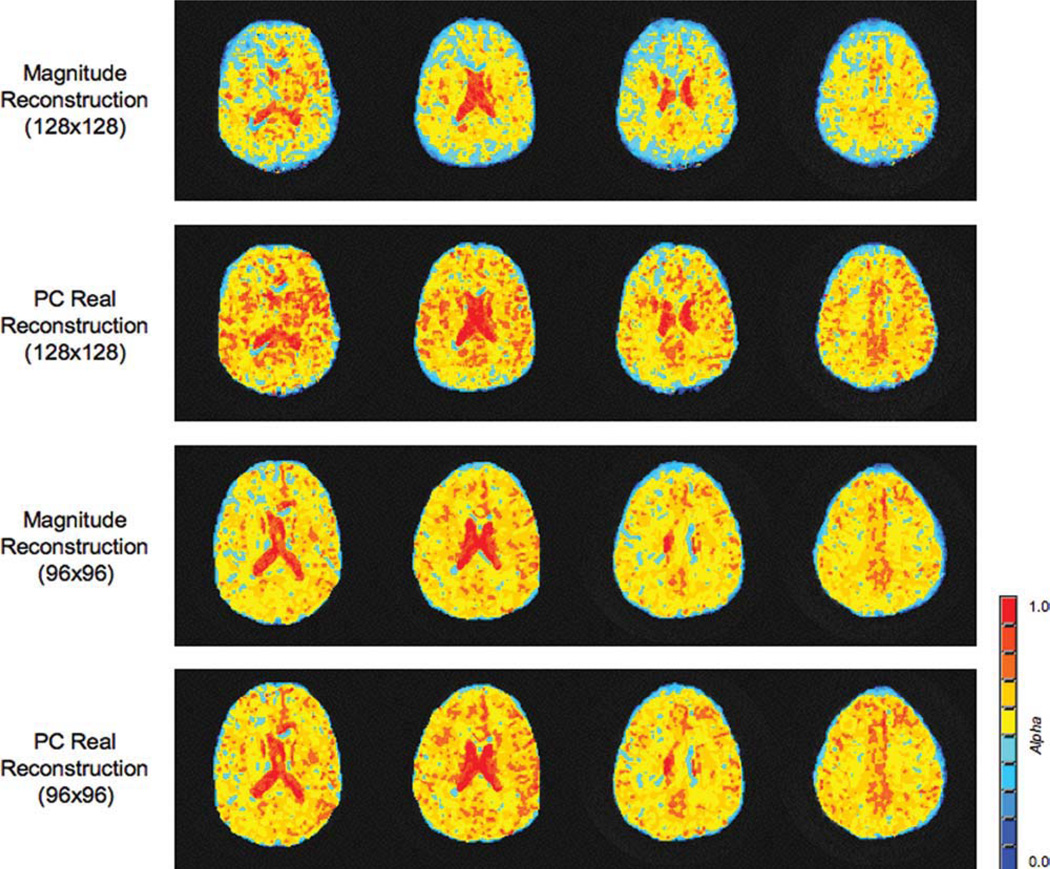
Figure 7 displays α maps obtained from the stretched-exponential model of a human subject collected with different in-plane resolutions. The larger matrix size produced larger differences between the two data types, though differences are seen with the smaller 96 × 96 matrix size. Comparing the a maps of the two matrix sizes, the standard magnitude data produces qualitatively larger differences in the maps. The smaller matrix estimated larger values of α than the larger matrix counterpart.

FIG 7.

α Parameter maps obtained from the stretched-exponential model of a human subject. All four sets of images were obtained using the same field of view and slice thickness. Two different matrix sizes were collected to demonstrate the effect that the SNR can have on the parameter fits of the stretched-exponential model. Note the lower overall values of α obtained with the standard reconstruction compared to the PC real reconstruction technique. As the matrix size decreases for the same field of view, i.e., the voxel volume increases, an increase in the corresponding SNR is observed. Consequentially, the standard magnitude reconstruction underestimates a if the SNR is reduced. However, for a sufficiently high SNR, both reconstruction techniques yield similar results. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

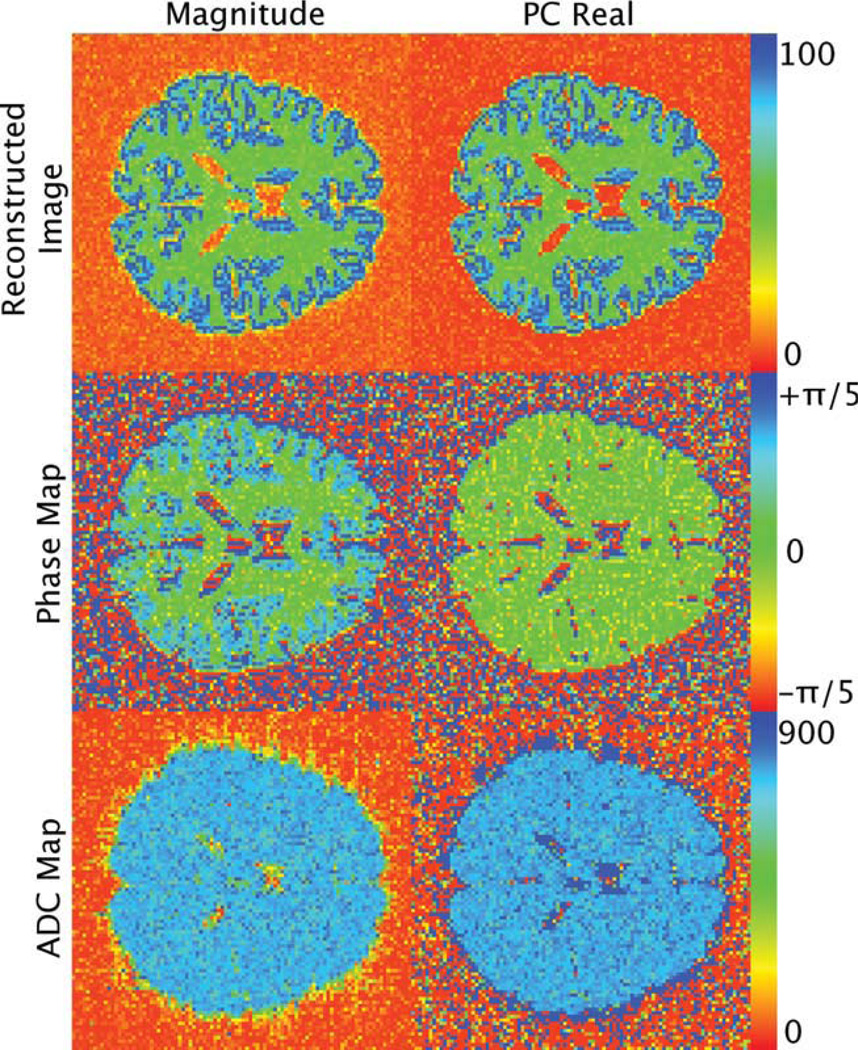
Figure 8 displays the phase maps for the PC real data and the magnitude data obtained from the boundary effects simulation b = 2000 sec/mm², giving the data an SNR range of 12 to 22. The corresponding calculated ADC maps are also presented. Notice that the reconstructed PC real images have a lower background signal intensity over the reconstructed magnitude images. At this low SNR range, the boundary effects are negligible in the phase image of the PC real data. Likewise, boundary effects were not observed in the calculated ADC maps.

FIG 8.

Reconstructed images, phase maps, and ADC maps for the magnitude and PC real reconstruction techniques obtained from the border effect simulation. The reconstructed images are of the b = 2000 msec/mm² image and consequentially have an SNR range of 12 to 22. The corresponding calculated ADC maps are also presented. The boundary effects are negligible in the phase maps and ADC map of the PC real data. The reconstructed images were normalized to the maximum value. The phase maps are displayed in units of radians. The ADC maps are displayed in units of micrometers squared per millisecond.

DISCUSSION

A simple method for rectified noise floor suppression using phase-corrected real reconstructed images was presented. In demonstrating this technique, DW model parameterization of the PC real data was found to be statistically different compared to that of the standard magnitude data for all diffusion models of the single-compartment fluids, ethanol and water. The largest differences were seen in the multiexponential models; however, the single-compartment models also benefited. Finally, the benefit of PC real data was successfully demonstrated in a healthy volunteer, for whom a low-SNR high-resolution a parameter map was generated using a stretched exponential model.

Diffusion-weighted MR is an intrinsically low-SNR imaging application, given the signal attenuation that results with the application of diffusion-weighted gradients. Furthermore, since the DW signal attenuation is a function of both b-value and the underlying diffusion properties within the tissue, regional difference in SNR will exist. This may be especially true in pathologic conditions, such as stroke and brain tumor, which either have a low initial SNR or larger bulk diffusion coefficients. In these instances, the signal intensities are more prone to approach the rectified noise floor at higher diffusion weighting.

The noise floor may introduce varying degrees of systematic errors into the estimates of the underlying biophysical diffusion process. The magnitude data can be partially corrected; however, the phase-corrected real reconstruction technique diminishes the need for such correction.

Growing evidence suggests a more complex behavior of the diffusion-weighted signal than a simple monoexponential decay over a larger range of higher b-values, further decreasing the minimum image SNR. Consequently, more complex models are likely to systematically model the RNF as an additional diffusion compartment. With magnitude images, these systematic errors will not be uniform throughout; instead, they will be a function of the initial signal and the intrinsic properties of the parenchyma. Use of phase-corrected real images will significantly diminish the rectified noise floor and therefore eliminate the potential of modeling the noise as biophysical diffusion. Overall, phase-corrected real reconstruction appears to be the most beneficial to the multicompartment models, which are prone to model noise as another false compartment. The single-compartment models, one of which models noise, showed little benefit from the PC real data reconstruction since the bulk diffusion coefficient dominates the signal attenuation and noise can be separately accounted for.

The phantom study demonstrates that the rectified noise floor that exists in standard magnitude data increases the systematic error. This effect is amplified as the intrinsic diffusion coefficient of a fluid increases. Faster diffusing spins will attenuate the signal at a lower b-value than slower diffusing protons. Fitting a biophysical diffusion model to data from a pool of faster-moving spins increases the confounding effects of the rectified noise floor. The PC real reconstruction had the effect of minimizing or even eliminating the rectified noise floor and its confounding effects on the estimated diffusion coefficients.

Several theories that exist to explain the source of the nonmonoexponential DW signal decay include the multiple physical compartments and subcompartments themselves. Regardless of those theories, since DWI reflects structures that are orders of magnitude smaller than the resolvable voxel, partial-voluming effects may contribute to some of the nonmonoexponential behavior. As resolution increases, these effects will be diminished, but at the cost of SNR, for which the phase-corrected real images will be even more beneficial.

The single-shot spiral sequence employed in this study utilized lipid suppression to reduce the chemical shift contribution to off-resonant signal. The effect of off-resonance is an accrual of phase over the duration of the readout. For an echo-planar imaging trajectory, which is more commonly used for DWI, the dominant off-resonance effect is one-dimensional shift in the phase-encode direction. For a spiral trajectory, the dominant off-resonance effect is a two-dimensional blurring. For longer readouts and very long echo times, the phase accumulation may be large, resulting in higher spatial frequency in the phase image that would not be completely corrected with the low-resolution phase estimate. For the PC real reconstruction method, an incorrect phase estimate results in a reduced attenuation of the noise floor. For the spiral acquisition, off-resonance results in blurring allowing the corresponding low-resolution phase image to retain a suitable estimate of the phase. Of course, the effective resolution of the image is reduced as a result of the off-resonance blurring effects. Eddy currents have the potential to contribute high-frequency phase that would result in poor estimate of the phase. To avoid eddy currents, the maximum slew rate must be reduced to avoid these effects. Furthermore, cardiac gating can minimize phase distortions caused by flowing blood and cerebrospinal fluid flow.

In echo-planar imaging acquisitions, magnetic field inhomogeneities cause both phase variation and image warping. The phase-correction method addresses such phase variations through the removal of the locally smoothed phase. Geometric warping, associated with the temporally accruing phase over the image acquisition, is thus not addressed through the phase-correction method. Therefore, any calculations with this method will contain B-field-related warping. Such distortion may be removed with the acquisition of a magnetic field map and subsequent time- or frequency-segmented magnetic field correction (24). The application of such a magnetic field correction can further smooth the phase of the reconstructed image by removing magnetic-field-associated phase variation. Thus, the assumption of a smoothly varying magnetic field can be improved with such a correction. Nevertheless, calculations in this manuscript yield acceptable results in the uncorrected, warped space.

With regard to other phase-correction techniques mentioned in the introduction, the diffusion estimates derived using these other methods are expected to yield similar results, for if the other methods estimate the same phase as the approach described here, then equivalent PC real data would result and consequently produce similar diffusion estimates. As such, this work does not represent a comparative study of phase-corrected real methodology, although such a study would certainly be beneficial to the field. Rather, this study represents a simple approach, where parameters are selected empirically to minimize the signal in the phase-corrected imaginary channel and thus reduce or eliminate the rectified noise floor. In addition, this study provides some initial results to demonstrate the significance of this issue in the evaluation of diffusion imaging data, especially under conditions of low SNR.

In this work, the spatial averaging is performed in the complex domain instead of in the phase domain. The purpose of this is to avoid the confounds of phase jumps in the circular phase data. Other methods can be considered that include phase unwrapping prior to computation of the average of the phase data.

Boundary effects were found to be negligible for the low-SNR images. This was observed both in the phase images and the calculated ADC maps. However, as SNR increases or as kernel size increases, the boundary effects become more prevalent. Therefore, it is not recommended that the proposed technique be used under these circumstances. The PC real method includes the spatial averaging of the observed phase before rotating the observed data into the real channel. This spatial averaging assumes a smoothly varying phase and can be violated in cases of true, discrete phase steps. Such phase steps can occur at tissue boundaries, as seen in the simulation at the gray/white matter boundaries with large SNR and when large smoothing kernels are utilized.

As the phase-correction method relies upon a smoothly varying phase in the local neighborhood of a voxel, techniques that utilize information from more distant voxels can confound the phase-correction results. Thus, results from this study most certainly do not generalize to lower acquired spatial resolutions or larger smoothing kernel dimensions. We would recommend that the technique only be utilized in resolutions equal to or greater than those utilized in this manuscript, and with kernel sizes comparable to those studied here.

In general, any MR application that relies on low-SNR images will greatly benefit by using the real data analysis technique presented here. Diffusion tensor imaging has great potential to benefit from the PC real reconstruction. For fibers parallel to the diffusion-encoding direction, the SNR is often poor and may severely compromise metrics such as diffusion anisotropy. Minimizing noise bias using the PC real reconstruction for the directions parallel to fibers would permit spatial resolution improvements in the calculation of diffusion anisotropy. Relaxometry has the potential to benefit from the technique. Estimating transverse relaxation rates, T₂ or T₂*, relies on signal attenuation as a function of echo time much like diffusion-weighted imaging relies on b-value. In addition, multiexponential analysis has been applied to the evaluation of transverse relaxation of muscle water protons (25–28) and other nuclei such as sodium-23 (17,29,30), all of which may benefit from the approach describe here.

The purpose of the paper was to draw attention to the deleterious effects of the rectified noise floor and present a simple improvement over the standard magnitude reconstruction. It should be noted that a detailed comparison with other potential methods would be greatly beneficial to this area of study.

CONCLUSION

With DWI, which has an intrinsically low SNR, the rectified noise floor can confound diffusion model parameterization. The data presented here demonstrate that the approach of using phase-corrected real images acts to reduce or even suppress these confounding effects. Consequently, more accurate estimates of single, multiexponential, and stretched-exponential diffusion values result when using phase-corrected real data, rather than magnitude data. Other MRI applications, which may suffer from low SNR, such as diffusion tensor imaging and multiexponential analysis of transverse relaxation or sodium-23 data, are expected to likewise benefit from the phase-corrected real reconstruction technique.