Abstract
We examine the increasing variance of earnings of white men over the 1970s and 1980s by focusing on changes in the covariance structure of earnings. Using data from the Michigan PSID from 1969–1987, we find that about half of the increase has arisen from an increase in the variance of the permanent component of earnings and half from an increase in the variance of the transitory component, where the transitory component is composed of serially correlated shocks that die out within three years. We thus find that increases in the variability of earnings are of equal importance to increases in the dispersion of permanent earnings in explaining recent increases in earnings inequality.
Considerable recent attention has been focused on the increase in earnings inequality in the U.S. over the 1970s and 1980s; see Levy and Murnane (1992) for a comprehensive list of the many studies. A growing body of research has shown that inequality in earnings grew over this period not only from an increase in returns to education and experience but also from an increase in inequality within groups of workers of similar age and education. Furthermore, the increase in inequality appears to have occurred throughout the earnings distribution, for the proportion of high-earnings workers as well as of low-earnings workers increased during the 1970s and 1980s. An increase in the dispersion of wage rates has also accompanied that of earnings.
While this literature has firmly established that an increase in the cross-sectional dispersion of earnings and wages has occurred--that is, that the variance of the marginal distribution of earnings and wages has gone up-- it has not been established whether the autocovariance structure of earnings and wages--that is, the structure of earnings dynamics--has also shifted. Our study examines this question.
The simplest and most widely known autocovariance structure assumes earnings to be composed of a permanent component and a white-noise transitory component. For this simple model the question we examine is whether the increase in the cross-sectional variance of earnings has arisen from a increased variance of the permanent component or of the transitory component-- the latter would imply that there has been an increase in the variability of earnings. However, the literature on earnings dynamics has established that the earnings process is more complex than the simple model implies, containing both random walks and serially-correlated transitory components (Lillard and Willis (1978), Lillard and Weiss (1979), Hause (1977, 1980), MaCurdy(1982), Abowd and Card (1989); see Atkinson et al., 1992, for a survey). We therefore examine whether the parameters of such a more complex process have shifted over time in more general ways.
We also examine trends in earnings mobility. We show that the degree of earnings mobility in an economy is closely related to the autocovariance structure of earnings and, more specially, to the relative magnitudes of its permanent and transitory components. Earnings mobility is positively (negatively) related to the variance of the transitory (permanent) component. Trends in the variances of these two components can therefore be expected to have effects on mobility as well.
We find that the variance of the transitory component of earnings has increased over the 1970s and 1980s in approximately equal magnitude to an increase in the variance of the permanent component. This finding--of a substantial increase in the variability of earnings--has significant implications for research on the causes of increased dispersion, for most hypotheses to date have implicitly presumed the dispersion to have arisen from an increased permanent variance. Changes in the price of human capital (skill) arising from labor demand shifts (e.g., from skill-based technical change as argued by Bound and Johnson, 1992); changes in the dispersion of the quantity of human capital generated by the educational system; increases in the magnitude and dispersion of rents; and other factors all presumably have considerable persistence (see Levy and Murnane for references). Possible explanations for an increased transitory variance are quite different--for example, from an increase in competition both domestic and foreign; the decline of regulation, unions and administered prices; the increase in temporary employment; and change in other factors that increase overall turbulence.
The paper is composed of four sections. The first section briefly discusses the panel data to be used and how it is formulated for estimation of dynamic earnings processes. The second section provides the main results of the paper. The third section extends the results to a discussion of a mobility, while the fourth section takes up several additional issues of importance.
I. Data and Variable Construction
We use the Panel Study on Income Dynamics (PSID), a longitudinal survey which has followed a sample of households from the civilian non-institutional population of the U.S. since 1968. Approximately 5,000 households were interviewed in the initial year of the survey, including a supplementary low-income sample (the SEO) which we also include in our analysis (sample weights are used throughout). Members of the original 1968 households and their offspring have been followed through 1988, the most recent year of data available at the time this analysis was conducted. The primary advantage of the PSID is its long period of coverage and its conformity with cross-sectional measures of inequality.1 A disadvantage of the PSID is that relatively little information is available on the education and earnings of individuals who are not heads of households.
Following the practice of most previous studies of inequality, we analyze only white males. There are larger sample sizes for whites than for blacks, and the problem of zero earnings is less of a problem for males than for females. We restrict our sample to heads of household 20–59 who had positive hours of work and earnings in the year prior to interview and who were not in school. Our sample--white male heads of household--is likely to have a smaller transitory earnings variance than other groups in the population, and should therefore provide us with a lower bound estimate of earnings variability in the labor force as a whole.
We include every annual observation for each individual for which these restrictions are met; thus the sample is not “continuous” (i.e., there are missing years for some individuals). This permits us to maximize the sample size used for the construction of each element of the covariance matrix.2 The earnings and wage measures we examine are the log of real annual earnings (wage and salary only) in the year prior to interview, and the log of real weekly earnings in that year. We exclude the first two years of the survey, 1968 and 1969, because wage and salary earnings data asked in those years were bracketed. Thus our analysis includes the years 1970–1988 and our earnings and wage measures cover the period 1969–1987. The real figures are obtained by deflating the nominal values by the GNP personal consumption expenditure deflator (base 1982).3 Our final sample includes 2,781 individuals with a total of 25,194 person-year observations.
We conduct most of our work with residuals that are obtained from regressions of these earnings and wage measures on a set of education, age, and year variables; however, we also conduct extra tests using unadjusted earnings and wages. Regressions are estimated separately for each year and by 10-year age interval (20–29, 30–39, 40–49, 50–59), each regression containing education dummies for 0–8, 9–11, 12, 13–15, and 16+ years. We choose this level of disaggregation to maintain a minimum of 250 observations per regression; there are 78 regressions altogether (4 age categories, 19 years).4 Using the residuals from these regressions, we calculate earnings and wage variances in each year within each age interval. We also follow individuals forward through time (up to age 59) and compute covariances between their residuals at different ages. We follow different cohorts separately, and thereby obtain variances and covariances at the same age but at different calendar points in time. This will provide the basis for our examination of whether the covariance structure of earnings has shifted.
The covariance matrix pooled over all ages and years has 553 elements, consisting of 76 variances and 477 covariances. The construction of the matrix is elaborate in more detail in Appendix A.
II. Main Results
Simple Permanent-Transitory Models
The simplest and most well-known model of the earnings structure is the canonical permanent-transitory model with white-noise transitory component. Let yia be the level of earnings (or, in our case, its residual) for individual i at age a. Then
| (1) |
where μi is a time-invariant individual component with variance and νia is a serially uncorrelated transitory component with variance . The variances and covariances in the data can be used in a simple fashion to estimate and because and . Hence the permanent variance can be estimated by the autocovariances and the transitory variance can be estimated from the difference between the variances and covariances. The variance of the permanent component is thus synonomous with persistence of earnings. Whether that variance has been increasing over time can be determined by examining whether covariances have been rising; and trends in the transitory variance can be detected by shifts in the difference between variances and covariances.
Another simple method of estimating changes in the permanent variance is to estimate the variance of average earnings (or its residual) over two separate calendar periods. Changes in the transitory variance can be estimated by the change in the variance of the deviations around the two averages. We have conducted an analysis of this type in a prior study (Gottschalk and Moffitt, 1994). However, in addition to requiring the choice of arbitrary calendar time intervals, that method is problematic if the permanent variance does not shift abruptly at interval endpoints but instead trends smoothly upward. In that case, deviations from average earnings during the early and later parts of the interval will be incorrectly attributed to transitory earnings. To instead analyze trends year-by-year requires the approach we are taking.5
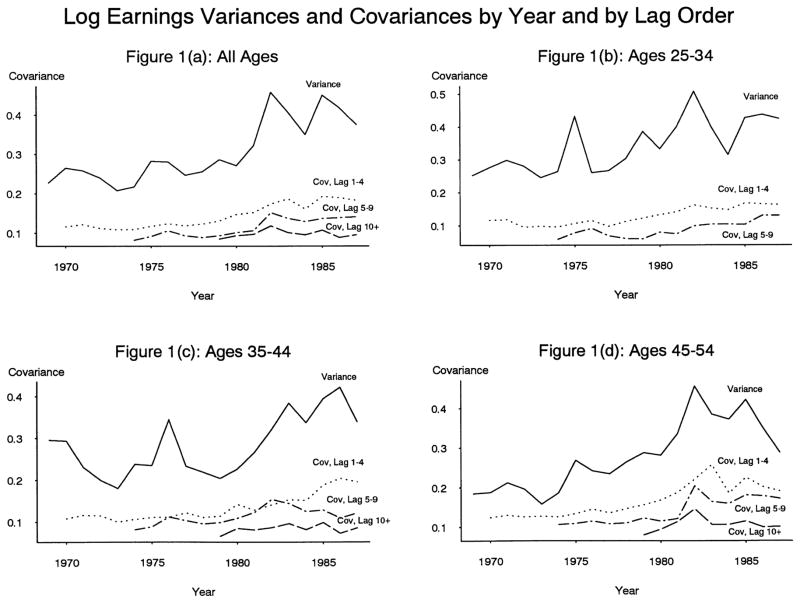
Figures 1(a)–(d) show trends in variances and in covariances at different lag orders for different age groups.6 For all age groups variances have been increasing, consistent with cross-sectional evidence from the CPS. However, the figures also show unmistakable evidence of an increase in covariances as well. The covariance increases are larger for the older age groups and for the low-order covariances, but are positive in almost all cases (though there is some hint of a decline in the final year or two at the older ages). It is also clear from the figures that, although the variance shows considerable fluctuation--much related to the business cycle--the gap between the variance and the covariances has been growing over time, especially between the variances and the high-order covariances. Because this gap proxies the transitory variance, there is graphical evidence that that variance has increased.7
Figure 1.
Log Earnings Variances and Covariances by Year and by Lag Order
Table 1 provides a regression method of summarizing these patterns, using all 553 individual variances and covariances in our data (see Appendix A). The model in column 1 has only an intercept and a “diagonal” dummy variable (D) equal to 1 if the element is a variance (i.e., it falls on the diagonal of the covariance matrix) and 0 if not, and thus has no time trends (for illustration). The use of the diagonal dummy is convenient for summarizing the difference between variances, which lie on the diagonal, and covariances, which do not. In terms of the canonical permanent-transitory model, therefore, the intercept in column (1) is an estimate of and the coefficient on D is an estimate of . The regression shows an average covariance of approximately .13 and an average transitory variance of .18, implying a total variance of approximately .31 and a correlation coefficient of .41, an estimate close to other estimates of random effects earnings models.
Table 1.
Descriptive Covariance Regressions for Log Annual Earnings
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| Intercept | .1253* (.0006) | .0846* (.0045) | .0823* (.0049) | .0878* (.0082) |
| D | .1811* (.0050) | .1296* (.0080) | .1319* (.0087) | .1656* (.0132) |
| t | - | .0058* (.0003) | .0061* (.0003) | .0059* (.0003) |
| Dt | - | .0059* (.0005) | .0056* (.0005) | .0014 (.0012) |
| A2 | - | .0023* (.0003) | .0023* (.0003) | .0012 (.0004) |
| DA2 | - | −.0029* (.0003) | −.0029* (.0003) | −.0038* (.0005) |
| (A2−A1) | - | −.0165* (.0014) | −.0168* (.0014) | −.0135* (.0015) |
| (A2−A1)2/100 | - | .0476* (.0068) | .0537* (.0068) | .0712* (.0085) |
| U2 | - | - | .0065* (.0010) | .0059* (.0009) |
| DU2 | - | - | .0097* (.0027) | .0101* (.0027) |
| U1 | - | - | .0020 (.0011) | .0021* (.0011) |
| tA2/10 | - | - | - | .0010* (.0003) |
| tDA2/10 | - | - | - | .0012* (.0005) |
| t(A2−A1)/10 | - | - | - | −.0042* (.0011) |
| Chi-squareda (df) | 2272 (551) | 1029 (545) | 1138 (542) | 1101 (539) |
Notes: Standard errors in parentheses
significant at the 10 percent level n=553
Unemployment rate is for all U.S. male civilians 20 and over.
D=diagonal dummy; A2 = the older age minus 20; A1 = the younger age minus 20; t = year at age A2 minus 1969; U2 = unemployment rate at age A2; U1 = unemployment rate at age A1
Statistic=ne’S−1e, where e is the vector of estimated residuals and S is their empirical covariance matrix.
The other columns show estimates of how the intercept and slope coefficient have trended over time by including year (“t”) in level form and interacted with D, controlling for age effects in the covariances and variances, for distance off the diagonal, and for the unemployment rate. The simplest specification in the second column shows that covariances trended at .0058 per year and that the transitory variance trended at .0059 per year, estimates which are not significantly different from one another. Thus the permanent and transitory variances appear to have trended upward at approximately the same rate. Including the unemployment rate (column 3) shows procyclical variances and covariances but does not affect the variance trends.8 The fourth column, which permits the covariances to trend at different rates at different distances off the diagonal, shows strongly what was apparent in the figures, namely, that the low-order covariances have increased more rapidly than the high-order covariances.
Table 2 allows the coefficients on t and Dt to differ for the periods 1969–1980 and 1981–1987. The most striking finding in the table is the much greater relative growth of the permanent variance in the 1970s and the relatively greater rate of growth of the transitory variance in the 1980s. Indeed, in the 1970s the transitory variance appears to have fallen, or at least not to have changed significantly. This pattern holds both for all the elements of the covariance matrix as well as for the low-order elements shown in the lower portion of the table, where it is also seen that the relatively greater rate of growth of the low-order covariances relative to high-order covariances was concentrated in the 1980s as well. Put differently, the low-order covariances almost doubled from the earlier period to the later one, whereas all covariances (and by implication the high-order ones) grew much less over the same period of time. As we shall show in the next section, this pattern is a result of the same forces that cause the coefficient on Dt (i.e., the “transitory” variance) to rise faster in the 1980s than in the 1970s.
Table 2.
Log Annual Earnings Covariance Regressions by Lag Order and Time Period: Selected Coefficients
| All Years | 1969–1980 | 1981–1987 | |
|---|---|---|---|
| All Lag Orders | |||
| t | .0061* (.0004) | .0056* (.0008) | .0066* (.0008) |
| Dt | .0056* (.0008) | −.0008 (.0014) | .0183* (.0022) |
| Lag Orders 1–3 | |||
| t | .0066* (.0007) | .0049* (.0013) | .0093* (.0017) |
| Dt | .0051* (.0011) | −.0001 (.0019) | .0156* (.0031) |
Notes: Standard errors in parentheses
significant at the 10 percent level
Acronyms: see Table 1
Also included in regressions: D, A2, DA2, A2−A1, (A2−A1)2, U2, DU2, U1
More Realistic Earnings Dynamics Models
Both the Figures and the regressions in Table 1 show that the canonical permanent-transitory model is an incorrect description of the autocovariance structure of earnings. The existing literature on earnings dynamics (see Atkinson et al., 1992 for a survey) finds this to be the case as well. Most importantly, the past literature has found the transitory component to be strongly serially correlated, but arising from an ARMA process of low order (e.g., of order no greater than 2).
Table 3, which displays the covariances and correlations of log annual earnings in our data over all years combined, shows covariance and correlation patterns that are similar to those found in prior work. Covariances and correlations fall rapidly over the first two or three orders and then decline at a much slower rate at higher orders. The covariances and correlations do not fall to zero, but appear to asymptote, consistent with the presence of an individual effect (i.e., between periods sufficiently far apart, only μ is in common). These patterns would appear to be reasonably well fit by a model with a time-invariant individual effect (to explain the asymptote) plus a low-order ARMA error, the AR component to explain the long declining tail and the other, MA, component to explain the more rapid decline in the first one or two orders.
Table 3.
Log Annual Earnings Covariances and Correlations by Age (pooled over years)
| Leads | Covariance
|
Correlation
|
||||||
|---|---|---|---|---|---|---|---|---|
| 20–29 | 30–39 | 40–49 | 50–59 | 20–29 | 30–39 | 40–49 | 50–59 | |
| 0 | .35 (.009) | .30 (.008) | .27 (.008) | .32 (.011) | 1.0 | 1.0 | 1.0 | 1.0 |
| 1 | .17 (.005) | .18 (.005) | .18 (.005) | - | .63 | .74 | .80 | - |
| 2 | .13 (.005) | .15 (.004) | .17 (.005) | - | .51 | .64 | .73 | - |
| 3 | .12 (.005) | .14 (.004) | .15 (.005) | - | .43 | .59 | .69 | - |
| 4 | .11 (.005) | .13 (.005) | .15 (.005) | - | .40 | .55 | .66 | - |
| 5 | .11 (.006) | .12 (.005) | .15 (.006) | - | .37 | .50 | .65 | - |
| 6 | .09 (.005) | .11 (.005) | .15 (.007) | - | .34 | .49 | .64 | - |
| 7 | .09 (.005) | .12 (.006) | .14 (.007) | - | .32 | .51 | .61 | - |
| 8 | .10 (.006) | .12 (.006) | .13 (.006) | - | .35 | .49 | .58 | - |
| 9 | .09 (.006) | .11 (.006) | .12 (.006) | - | .32 | .46 | .53 | - |
| 10 | .09 (.007) | .11 (.007) | .12 (.006) | - | .34 | .47 | .49 | - |
| 11 | .07 (.007) | .12 (.009) | - | - | .29 | .46 | - | - |
| 12 | .09 (.010) | .11 (.008) | - | - | .29 | .47 | - | - |
| 13 | .09 (.012) | .10 (.008) | - | - | .29 | .48 | - | - |
| 14 | .08 (.011) | .10 (.007) | - | - | .28 | .43 | - | - |
| 15 | .10 (.013) | .10 (.009) | - | - | .32 | .45 | - | - |
| 16 | .09 (.015) | .10 (.010) | - | - | .29 | .42 | - | - |
| 17 | .09 (.018) | .11 (.013) | - | - | .30 | .45 | - | - |
| 18 | .10 (.025) | .11 (.019) | - | - | .37 | .37 | - | - |
Notes: Cell sample sizes range from 183 to 7358.
Standard errors in parentheses
Another important feature of the autocovariance structure is the notable positive correlation of covariances and correlations with age, holding the order constant. An ARMA model stationary in age is not capable of explaining such a pattern; instead some non-stationary age-related process is required. To capture this pattern we will test for a random walk in age, since random walks generate increasing covariances over time.
Table 4 shows the results of fitting several error components models to the 553 variances and covariances, although, for the moment, not allowing any parameters to vary with calendar time. The models estimated are shown in the notes to the table. The standard errors are computed from the empirical covariance matrix of the residuals (see Appendix B).
Table 4.
Error Components Models for Log Real Annual Earnings (no calendar time effects)
| RE + AR (1) | RE + ARMA (1, 1) | Random-Walk RE + ARMA (1, 1) | Random-Growth RE + ARMA (1, 1) | ||
|---|---|---|---|---|---|
| (I) | (II) | (III) | (IV) | ||
|
|
.114 (.008) | .070 (.012) | .090 (.015) | .092 (.005) | |
| ρ | .354 (.017) | .906 (.026) | .622 (.025) | .657 (.069) | |
|
|
.167 (.013) | - | - | - | |
| θ | - | −.670 (.017) | −.344 (.045) | −.362 (.092) | |
|
|
- | .188 (.013) | .169 (.016) | .166 (.007) | |
|
|
- | - | .159a (.025) | - | |
|
|
- | - | - | .462a (.069) | |
| Chi-squared (df) | 2388 (550) | 2262 (549) | 2094 (548) | 2080 (548) |
Notes: Standard errors in parentheses
All coefficients significant at 10 percent level
RE=random effect
Parameter multiplied by 100
| Model I: | (1) εia = μi + νia |
| (2) νia = ρνi, a−1 + ηia | |
| Model II: | (1), (2), plus |
| (3) ηia = ξia + θξi, a−1 | |
| Model III: | (2), (3), plus |
| (1′) εia = μia + νia | |
| (4) μia = μi, a−1 + ωia | |
| with | |
| Model IV: | (2), (3), plus |
| (1″) εia = μi + aϕi + νia |
All primary error components assumed independent.
The first column fits a model with an individual permanent component and an AR(1) transitory component, while the second column expands the transitory component to an ARMA(1,1). All parameters are significant. The high value of the estimated ρ is consistent with the slow decline in autocorrelations and the large negative estimate for θ implies that the autocorrelations drop off from order 1 to order 2, both as were seen in Table 3. The variance of the individual effect is significant, reflecting the non-zero asymptote. The third and fourth columns of the table attempt to capture the increasing covariances of earnings with age, in one case with a random walk in the individual effect and in the other case by a random growth rate (Hause, 1977, 1980; Lillard and Weiss, 1979). Both models show significant age effects, and the fit is essentially the same for both. The choice is therefore arbitrary in our case, so we pick the random walk specification based on findings from other studies which have used fourth-moments to distinguish the two.9 In other results, we tested ARMA(1,2) and ARMA(2,1) specifications for the transitory effect while maintaining the random-walk specification for the individual effect. In neither case was the fit significantly improved and in neither case was the additional parameter significant. An ARMA(1,1) with a random-walk individual effect hence fits our data adequately.10
These results are fairly consistent with past work on earnings dynamics. Our model is a bit more refined than early models such as Lillard and Willis (1978), who assumed only an individual effect and an AR(1) transitory effect. But recent, more flexible specifications, such as those tested by MaCurdy (1982) and Abowd and Card (1982), find strong MA components as well as random walk components. Both MaCurdy and Abowd-Card find that an MA(2) specification adequately fits the covariance matrix of earnings differences, for example. Our random-walk-plus-ARMA(1,1) model in levels implies an ARMA(1,2) model in differences, slightly different than MaCurdy and Abowd-Card. But the magnitude of our estimated AR(1) implies a rapid fade-out in differences, so the difference with the differenced MA(2) is not large.11
Our main interest is in allowing the parameters of the process to change with calendar time. To introduce time-varying parameters into the model, we estimate the following specification:
| (2) |
| (3) |
| (4) |
Equation (2) shows the log earnings (or earnings residual) of person i at age a in year t to be composed of an individual effect (μiat) with a time-varying factor loading (αt), and a transitory effect (νiat). The individual effect could represent latent unobservable human capital whose price (αt) shifts with calendar time. The individual effect follows a random walk as shown in (3) and the transitory effect follows the ARMA(1,1) process shown in (4). As conventional in these models, we assume the forcing variables ωiat, ξiat, and the initial value of the individual effect (μi1t) to be independently distributed over age and time and w.r.t. each other.
Aside from the variance of the initial individual effect, there are five parameters in the model--αt, ρt, θt, and the variances of ωiat and ξiat-- which, together, determine the pattern of variances and covariances. We permit all five to vary linearly with calendar time (and, subsequently, with year dummies):
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
The factor loading αt is normalized to 1 at t=0 (1969 in our data), and we let to establish the baseline variance of the individual effect.
A “permanent” effect in this model is not permanent in the literal sense since the individual effect is permitted to shift over the life cycle and with calendar time. The distinction between the two components in (2) is, instead, based upon a decomposition of shocks into those that are mean-reverting and those that are not. Our decomposition defines permanent shocks to be those that are non-mean-reverting and transitory shocks to be those that are mean-reverting.
We estimate the model by minimum distance using the form suggested by Chamberlain (1984) for the estimation of covariance structures. The mapping of the model (2)–(9) into the variances and covariances necessary for the estimation is given in Appendix B. Robust standard errors are computed from the empirical covariance matrix of the residuals in the moment equations.
Table 5 shows estimates of the model. Initial testing revealed that the time trend coefficients were significant only for αt and the variance of ξiat, so column (1) shows a specification with only these two time effects allowed. The year coefficient for αt is .029, implying that its factor loading (or the “price of permanent unobserved human capital”) increased by approximately 52 percent over the 18-year period 1969–1987 (1.52 = 1 + .029*18). Thus the model strongly confirms the existence of an increase in the variance of the permanent component. At the same time, the variance of ξiat--which is a two-period transitory component--almost doubled over the period, increasing from .117 in 1969 to .207 in 1987 (.207 = .117 + .005*18). Thus the model also confirms that there was a strong increase in the transitory component. However, because of the presence of the autoregressive process, the increase in the transitory variance persists over time in its effect on the variance of the total transitory component, νiat (see equation (4)). But this effect dies out at the rate ρ2, implying, at our estimates of that parameter, that the impact is negligible after three years.
Table 5.
Error Components Models for Log Annual Earnings with Calendar Time Effects
| (1) | (2) | ||
|---|---|---|---|
| αt: | |||
| Year | .029* (.003) | .023* (.006) | |
| Var(ξiat): | |||
| Year | .005* (.001) | .005* (.001) | |
| Constant | .117* (.009) | .118* (.010) | |
| ρt: | |||
| Year | - | .008 (.015) | |
| Constant | .641* (.063) | .578* (.191) | |
| θt: | |||
| Year | - | −.003 (.018) | |
| Constant | −.367* (.078) | −.352* (.227) | |
| Var(ωiat):a | |||
| Year | - | .001 (.010) | |
| Constant | .100* (.013) | .110* (.017) | |
|
|
.056* (.003) | .061* (.006) | |
| Chi-Squared (df) | 1082 (546) | 1076 (543) | |
Notes: Standard errors in parentheses
significant at 10 percent level
Year=0 in 1969, = 1 in 1970, etc.
Parameters multiplied by 100.
The second column in Table 5 shows that the time trends in the other three parameters of the covariance matrix are insignificant. The magnitude of the trend coefficient for ρ is not trivial, implying an increase from .578 to .722 over the period and hence a strengthening of the low-order covariances and a longer persistence of transitory shocks. However, the large standard error on the coefficient makes this result highly uncertain.12
These estimates provide an interpretation of figure 1 and an explanation for the differing rates of growth of low-order and high-order covariances. The estimates imply that covariances of earnings within three years of one another reflect not only the permanent component but also the serially-correlated transitory component. Thus they imply that it is incorrect to associate off-diagonal elements with the permanent variance per se, as the simple canonical model assumes. The more rapid increase in the low-order covariances in Figure 1 (and Table 1) than of the high-order covariances simply reflects the fact that the former captures the increasing transitory variance as well as the increasing permanent variance, whereas the latter reflects only the increasing permanent variance. This also implies that, within the simple permanent-transitory model discussed earlier in this section, it is the gap between the variance and the high-order covariances-- not the low-order covariances--that measures the total transitory variance, and this has clearly risen in Figure 1.
One way of assessing the relative importance of the increase in the variance of the permanent component (αtμiat) and the transitory component (νiat) is to calculate what the increase in the total variance would have been from 1969 to 1987 had each parameter increased separately. Table 6 shows the results of such an exercise, obtained by calculating the variance of yiat assuming no change in the parameters from 1969–1987, and by then calculating what the 1987 variance would have been had each of the parameters increased by the magnitudes implied by the coefficients in the second column of Table 5.13 The results show that the increase in the permanent variance accounted for approximately 40 percent of the increase in total variance and the increase in the transitory variance accounted for approximately 50 percent, with the remainder accounted for by changes in other parameters.14 Thus, although the change in the transitory variance accounts for slightly more of the change than that of the permanent variance, the two are roughly equal in importance for practical purposes.15
Table 6.
Effects of Parameter Changes on Log Annual Earnings Variances, 1969–1987
| Variances by Age
|
||||
|---|---|---|---|---|
| 20 | 30 | 40 | 50 | |
| 1969 Values of all Parameters | .179 | .199 | .210 | .221 |
| 1987 Value of αt only | .240 | .273 | .296 | .318 |
| 1987 Values of αt and Variance of ξiat | .338 | .379 | .401 | .423 |
| 1987 Values of αt, Variance of ξiat, and θt | .338 | .372 | .394 | .416 |
| 1987 Values of all Parameters | .338 | .401 | .423 | .445 |
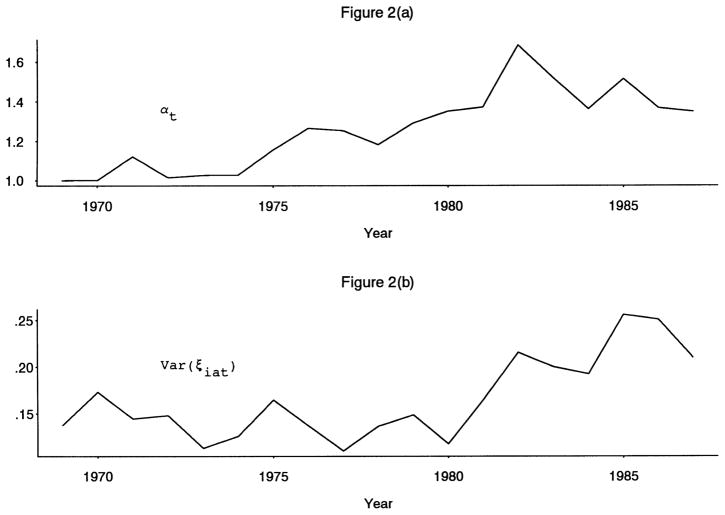
The estimates thus far have restricted year effects to a linear trend; yet, at minimum, Table 2 indicated that there may be different trends in the 1970s and 1980s. We therefore reestimate the model in column (1) of Table 5, allowing αt and Var(ξiat) to take on different values in each year 1969–1987. As shown in Figure 2, the increase in the two parameters occurred in quite different periods. While the permanent variance grew, on average, through about 1982 or 1983, it leveled off or fell subsequently. The transitory variance, on the other hand, showed essentially no trend until 1980 or 1981, when it began to rise. Although it showed a slight decline after 1984, it was still unambiguously higher in the late 1980s than in the early 1980s, opposite to the pattern for the permanent variance. Thus we find additional evidence indicating relatively higher growth rates of the permanent variance in the 1970s and of the transitory variance in the 1980s.16
Figure 2.
Estimated Trends in Permanent and Transitory Components
III. Mobility
Mobility, defined as a change in individual ranks within a distribution, is closely related to the covariance structure. For example, an increase in an earnings covariance between any two points in time will necessarily lower mobility because earnings in the two periods are more closely related. However, a stronger statement than this can be made. In Appendix C we show that if earnings follow a joint normal distribution, the probability of a change in individual ranks between any two points in time is a function only of the correlation coefficient between earnings at those two points, and not a function of the absolute levels of either of the variances at the two points in time or the covariance.
The intuition for this result is particularly strong in the canonical permanent-transitory model, where the correlation coefficient between earnings at any two points is equal to the fraction of the variance accounted for by the permanent component, or . The degree of mobility in this model thus hinges only on the relative sizes of the permanent and transitory variances. A rise in the permanent variance, which increases the average distance between the earnings of different individuals, lowers the chance of a change in rank; a rise in the transitory variance, on the other hand, makes the chance of a change in rank more likely. But a proportional increase in the permanent and transitory variances has no effect on mobility; the two effects exactly cancel. Therefore, to the extent that the permanent and transitory variances have risen at about the same rate, as suggested by our previous results, this model would show little change in mobility.
We should note that the value of the correlation coefficient in a more realistic model, such as one with serially-correlated transitory components, varies depending upon the distance between the two points under consideration. With serially-correlated but mean-reverting transitory components, correlation coefficients fall with that distance and hence mobility is likely to be greater over longer periods. In addition, if mobility is defined instead on the basis of average earnings over multiple years rather than earnings in a single year, and if it is a change in the rank of mean earnings that is considered, mobility is likely to be lower since the transitory component is a smaller portion of the total variance when earnings are averaged over multiple years.17
Since our estimated error components model reported in the last section provides a full accounting for the changes in correlation coefficients (i.e., over different distances and intervals) that have occurred during the 1970s and 1980s, a mobility analysis may at first blush appear redundant; that is, our estimated error components model should by itself determine trends in mobility. However, an examination of transition rates between quantiles of the earnings distribution can provide more detail on whether any changes in mobility have occurred at different parts of the distribution (e.g., at top and bottom). We therefore provide a simple quantile analysis of mobility in this section.
Our mobility analysis uses the same data set and covariance structure as used in the previous analyses except that variance elements are eliminated since they are not relevant to mobility. This leaves us with 477 observations, each of which corresponds to a pair of ages in two particular years. Instead of computing covariances for each such cell, we compute quantile mobility rates using five quantiles (i.e., quintiles).18
Table 7 shows the year-to-year rates of mobility in the sample between quintiles, pooled over all years and ages. Mobility at the upper and lower quintiles is less than in the middle quintiles.19 At the upper and lower ends there is an approximate one-third chance of changing rank from one year to the next, as opposed to an approximately fifty-fifty chance for the middle quintiles. The mobility table is also remarkable for its symmetry.
Table 7.
One-Year Quintile Mobility Rates for Log Annual Earnings: All Years and Ages
| Quintile at t−1 | Sum | Quintile Distribution at t
|
||||
|---|---|---|---|---|---|---|
| Bottom Fifth | Next to Bottom Fifth | Middle Fifth | Next to Top Fifth | Top Fifth | ||
| Bottom Fifth | 100 | 67 | 21 | 8 | 3 | 1 |
| Next to Bottom Fifth | 100 | 20 | 49 | 22 | 7 | 2 |
| Middle Fifth | 100 | 7 | 21 | 44 | 22 | 6 |
| Next to Top Fifth | 100 | 4 | 7 | 20 | 47 | 22 |
| Top Fifth | 100 | 2 | 3 | 7 | 20 | 69 |
Notes: 477 observations per row
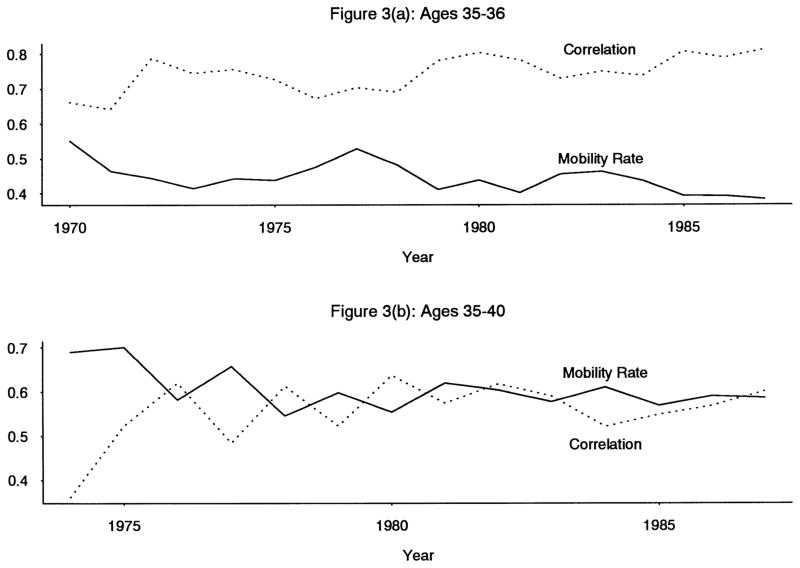
Our interest is, once again, in how these mobility rates have changed over time conditional on age. As we discussed previously, the overall shape of mobility trends should follow those of the covariance analysis closely, but should depend primarily upon trends in the correlation coefficients rather than in the covariances. Figures 3(a)–(b) show the trends in both the correlation coefficient and the mobility rate between the illustrative ages 35 and 36 (“short”) and between 35 and 40 (“long”).20 The measure of mobility we use is the sum of the off-diagonal elements in each row of Table 7 (i.e., one minus the probability of staying in the same quintile). This measure is the inverse of what is known as the “immobility ratio” (Atkinson et al., 1992). As expected, the correlation coefficients and mobility rates in both diagrams show an extremely close inverse relationship. The one-year-apart correlation coefficient between ages 35 and 36 shows a slight upward trend in the 1970s but a steeper trend in the 1980s, reflecting the pattern of the transitory variance. Correspondingly, there was very little trend in one-year-apart mobility until the late 1970s, when short-term mobility dropped sharply. The five-year-apart correlation coefficient rose steadily over the late 1970s, albeit with considerable fluctuation, but leveled off in the 1980s; correspondingly, five-year mobility dropped steadily in the 1970s but leveled off in the 1980s. These patterns closely reflect the relative patterns of the transitory and permanent variances discussed previously.
Figure 3.
Mobility Rates and Correlation and Coefficients by Year and Age
Table 8 shows the results of a regression analysis of the mobility rates for all quintiles, all ages, and lag orders. The first row shows that while there was only a small net decline in overall mobility (over all lag orders), a significant decline in mobility occurred in the top and the bottom two quintiles. The subsequent rows of the table show overall mobility rates consistent with Figure 3, falling significantly only for short-term mobility in the 1980s and only for long-term mobility in the 1970s. However, as in the first row, the trends seem to be concentrated in the upper and lower tails of the distribution. Indeed, for the lowest fifth of earners even short-term mobility declined in the 1970s, which is an indirect indication that the variance of serially-correlated transitory shocks has been increasing for that group over the entire period, not just over the 1980s.
Table 8.
Year Coefficients in Quintile Mobility Regressions
| All | Initial Quintile Location
|
|||||
|---|---|---|---|---|---|---|
| Bottom Fifth | Next to Bottom Fifth | Middle Fifth | Next to Top Fifth | Top Fifth | ||
| All Lag Orders | ||||||
| Year | −.0020* (.0004) | −.0040* (.0008) | −.0028* (.0008) | −.0010 (.0007) | −.0007 (.0007) | −.0020* (.0007) |
| Lag Orders 1–4 | ||||||
| 1969–1980 | −.0013 (.0011) | −.0051* (.0018) | −.0008 (.0019) | .0001 (.0019) | .0006 (.0017) | −.0017 (.0017) |
| 1981–1987 | −.0025* (.0014) | −.0022 (.0023) | −.0038 (.0024) | −.0026 (.0024) | −.0017 (.0021) | −.0026 (.0022) |
| Lag Orders 5+ | ||||||
| 1969–1980 | −.0067* (.0017) | −.0083* (.0035) | −.0035 (.0034) | −.0014 (.0030) | −.0087* (.0034) | −.0108* (.0034) |
| 1981–1987 | −.0005 (.0009) | −.0027 (.0018) | −.0044* (.0018) | −.0004 (.0015) | .0021 (.0018) | .0020 (.0018) |
Notes: Standard errors in parentheses
significant at the 10 percent level
Sample sizes are 477 for all-lag-order sample, and 198 and 279 for the 1–4 lag-order and 5+ lag-order samples, respectively.
Dependent variable: fraction of population in the relevant age-year-quintile cell that changed quintiles over the lag orders shown.
Independent variables in addition to time trends: A2, A2−A1, and (A2−A1) squared (see notes to Table 2 for definitions).
IV. Additional Issues
Weekly Wages and Weeks of Work
An important secondary question is the extent to which the increase in instability in earnings profiles signified by the increase in transitory variances has been a result of increasing instability in wage rates or in employment. The literature on the overall increase in cross-sectional dispersion of earnings indicates that a majority of that increase has arisen from increases in the cross-sectional dispersion of wage rates rather than of weeks of work, hours of work, and employment in general (Levy and Murnane, 1992; Burtless, 1990, Table 7). However, there is no necessary reason for the lesser importance of dispersion in cross-sectional employment measures to follow through for the relative importance of permanent and transitory variances. In fact, the literature on life cycle labor supply analysis and on business cycle fluctuations indicates that employment fluctuates with a greater variance than wages, suggesting that transitory components in employment might be considerably stronger than permanent components.
Figures comparable to figure 1 but with trends in the variances and covariances of log real weekly wages and the log of annual weeks worked (available upon request) indicate that both variances and covariances of log weekly wages rose and that they did so in the same pattern as for log real earnings (i.e., with the same relative patterns for high-order and low-order covariances). Clear evidence of increases in the variances and covariances of weeks of work also appear, although the increases in covariances are much weaker than for earnings or wages. This pattern is consistent with a greater relative importance of transitory factors for weeks worked.
Table 9 shows estimates of several models for log real weekly wages and log annual weeks worked. The descriptive regressions show that the increasing variance of log real weekly wages is equally shared between diagonal and off-diagonal elements, as was the case for annual earnings. However, the coefficients are only approximately two-thirds the magnitude of the Table 2 results, thus confirming a role for increasing dispersion in weeks of work. This is further confirmed by the results for log and absolute weeks worked in the table, which indicate increasing diagonal and off-diagonal elements but greater relative trends for the diagonal elements. This pattern is also consistent with a greater relative importance of increases in transitory variances for weeks worked. The estimates of the error components models shown in the lower half of the table confirm this and show that increases in transitory variances were particularly marked for weeks of work. However, it should be stressed that transitory variances have increased for real weekly wages as well.
Table 9.
Covariance Analysis of Real Weekly Wages and Annual Weeks of Work
These analyses exclude any consideration of changes in the proportion of the population with no weeks worked at all during the year. Those percentages are relatively small for our sample of prime-age white males but have increased over the period. For those 20–29, for example, the percent without work at all during the year increased from 0.4 percent in 1969 to 2.7 percent in 1987. The corresponding percents for those 30–39, 40–49, and 50–59 are, respectively, 0 to 1.7, 1.8 to 2.2, and 8.0 to 11.3.21 Our results thus far already indicate increases in the variance of weeks worked in the worker subsample, and our data indicate even larger increases in that variance when nonworkers are included.
Estimates of the descriptive and error components models for absolute weeks of work inclusive of zeros, comparable to those shown in the last column of Table 9, show stronger trends in the permanent variance and weaker trends in the transitory variance.22 We speculate that an entire year without work may be an indication of a serious wage or employment problem that reflects a permanent condition.
Between-Group Trends
The analysis thus far has been conducted entirely on the residuals from earnings and wage regressions, regressions containing education dummies and estimated separately by year and age interval. An important question is whether our results on the relative importance of trends in the variances of the permanent and transitory components of these within-cell earnings components apply as well to log earnings itself. The answer depends upon the relative importance of trends in the permanent and transitory variances of the between-cell components, which in our case are the components accounted for by education and age differences in earnings.
There is a much larger literature on trends in education and age differences in earnings than on trends in the within component, the literature showing markedly different trends in both over the 1970s and 1980s for both within and between components (see Levy and Murnane for a review). Our education and age coefficients follow the same general pattern over time as those in the past literature, which have been mainly estimated on the CPS, and therefore we do not present them.23 Instead, we take a simpler approach to this question by reestimating the models we reported in Section IV on log earnings itself rather than on the regression residuals; the difference in results will be an indirect indication of the importance of trends in the between-group variances. Thus, we work with 553 cells of a covariance matrix of log annual earnings over all years, age groups, and lag orders, constructed as described previously for the regression residuals.
The estimates of the descriptive regressions (not shown) indicate that the permanent variance is considerably more important when the “between” is included. Estimates of average permanent and transitory components for the specification in column (1) of Table 1 are .172 and .185, respectively, implying a correlation coefficient of approximately .48 as opposed to our prior estimate of .41. This is to be expected since education levels in our sample are essentially constant for each individual and, therefore, will mainly contribute to the permanent component of earnings. Estimates of trend coefficients comparable to those in columns (2) and (3) of Table 1 show, moreover, approximately the same coefficients on Dt (.0057 and .0056 in the two columns) but somewhat higher coefficients on D (the average covariance) of .0066 and .0068. This higher value reflects a net increase in educational differentials over the period. Estimates of column (4) for the new covariance matrix reveals, however, the same pattern of greater increases of high-order covariances than low-order covariances as found previously.
In order to contrast the within-group and total results we estimate the error components model on both and simulate the implied permanent and transitory variances. The steady-state values in 1969 and 1987 are shown in Table 10.24 As suggested by the descriptive analysis, the results show a higher level of the permanent variance for total log earnings. In addition, there was a slightly greater rate of increase in the permanent variance when the between is included. However, the magnitudes of the changes induced by including trends in the between are not large, and hence none of our substantive findings (e.g., that upward trends in transitory variance are important) are affected.25
Table 10.
Steady-State Variance Components Implied by the Estimated Error Components Models
| Within | Total | |||||
|---|---|---|---|---|---|---|
| Permanent | Transitory | Rho | Permanent | Transitory | Rho | |
| Age 20 | ||||||
| 1969 | .061 | .118 | .34 | .088 | .118 | .43 |
| 1987 | .122 | .216 | .36 | .154 | .212 | .42 |
| Age 30 | ||||||
| 1969 | .072 | .127 | .36 | .109 | .127 | .46 |
| 1987 | .144 | .258 | .36 | .192 | .256 | .43 |
Notes: The permanent variance is the estimated value of Var(μiat) at 1969 and 1987 values. The transitory variance is the estimated value of Var(νiat) at 1969 and 1987 values of the parameters. The model estimates in column (1) of Table 5 and the analogous estimates for total log earnings are used.
V. Summary and Conclusions
In this paper we have examined the source of the increasing cross-sectional variance of male earnings in the U.S. over the 1970s and 1980s by determining its origins in the covariance structure of earnings. Using data from the Michigan Panel Study of Income Dynamics from 1969–1987 for white males, we find that about half of the increase in variance within education and age groups has arisen from an increase in the variance of the permanent component of earnings and half from an increase in the variance of the transitory component, where the transitory component reflects shocks that die out within three years. We thus find that increases in transitory shocks are of equal importance to increases in the dispersion of permanent earnings in explaining recent increases in earnings inequality. Indeed, the increase in transitory shocks was especially great in the 1980s. Other results show that the increase in transitory shocks appears in weekly wages as well as annual earnings, although even greater in annual weeks of work. We also find that transitory shocks are still very important when trends in the variance across education and age groups are considered.
Our investigation of earnings mobility indicates that mobility changed very little over the period, but with a slight fall in long-term mobility in the 1970s and a slight fall in short-term mobility in the 1980s, the latter reflecting the increase in short-term covariances arising from a higher variance of serially-correlated transitory shocks. These mobility declines are concentrated in the top and bottom quintiles of the earnings distribution.
Our study has been largely a statistical accounting exercise aimed at determining the relative contributions of different error component variances to the upward trend in overall cross-sectional variances, rather than a search for causes. We have conducted a rudimentary exploration of the latter type in Gottschalk and Moffitt (1994), where we found that while some of the increasing transitory variance is a result of a decline in unionization (union jobs have lower transitory variances) and industry shifts, these do not provide a sufficient explanation by themselves--transitory variances have increased within unionized and non-unionized jobs, within all industrial sectors, and even for workers who have stayed with the same firm for up to 10 years. Further work in exploring the sources of increased variability would therefore appear warranted.
Acknowledgments
This project was supported by grants from the U.S. Department of Health and Human Services through the Institute for Research on Poverty and from the U.S. Department of Labor through the National Bureau of Economic Research. The authors would like to thank Richard Blundell, Charles Brown, James Heckman, Costas Meghir, Gary Solon, and the members of seminars and workshops at several universities for comments on this version of the paper, as well as Thomas MaCurdy for comments on an earlier version. For assistance on the project, the authors would like to thank Amit Dar, Philip Merrigan, Reema Nayar, Renya Reed, Robert Reville, and Thomas Vanderveen at Brown University and Alpay Filizteken at Boston College.
Appendix A. Structure of the Autocovariance Matrix
The cells used to construct the autocovariance matrix from the data are broken out separately by age and year, in order to examine trends in the matrix elements over time but holding age constant. The only difficulty in constructing the matrix is the necessity to group the data into age intervals. As noted in the text, we group the data from age 20 through 59 into 4 ten-year age groups (20–29,30–39,40–49,50–59). In each year t of the data, we follow the individuals in each of these four groups through to year t+1, year t+2, etc. until either the end of our data is reached (1988) or until the age interval in question reaches beyond age 59 (e.g., the 40–49 cohort in 1969 can be followed through to 1979, when the individuals are 50–59, but no further26). Covariances are then calculated between the initial year, t, and each subsequent year.27 A fresh set of cohorts is begun in each year, starting in 1969, and continuing through 1987; the four cohorts (i.e., age groups) started in each year are again followed over time.
Table A-1 shows the cells of the data. The ages shown are in the midpoints of the intervals (“25” for 20–29, “26” for 21–30, etc.). The beginning of the table showed the variances of earnings in the 20–29 group for each of the years 1969 through 1987. The next set of rows shows the autocovariances of earnings between the individuals 20–29 in the initial year and 21–30 (“26”) in the following year, computed separately for each year pair 1969–1970 through 1986–1987. The next set of rows shows the autocovariances of earnings of individuals 20–29 in the initial year and 22–31 two years later, which are observed for year pairs 1969–1971 through 1985–1987. Thereafter the covariances between all future years for the cohorts begun in each year. There are 553 cells in total.
This method of grouping ensures that every individual variance and covariance in the panel is included uniquely in one cell. There are many alternative methods of grouping the data and computing the autocovariance matrix, but there is no reason for any one to be preferred to another except for convenience. Our method is designed to make trends over time, holding age constant, particularly easy to discern.
Table A-1.
Elements of the Autocovariance Matrix for Log Annual Earnings
| Lower Age | Upper Age | Lower Year | Upper Year | Covariance | Correlation |
|---|---|---|---|---|---|
| 25 | 25 | 69 | 69 | 0.25238188 | 1.00000000 |
| 25 | 25 | 70 | 70 | 0.27661610 | 1.00000000 |
| 25 | 25 | 71 | 71 | 0.29885597 | 1.00000000 |
| 25 | 25 | 72 | 72 | 0.28129703 | 1.00000000 |
| 25 | 25 | 73 | 73 | 0.24614233 | 1.00000000 |
| 25 | 25 | 74 | 74 | 0.26469568 | 1.00000000 |
| 25 | 25 | 75 | 75 | 0.43190508 | 1.00000000 |
| 25 | 25 | 76 | 76 | 0.26104279 | 1.00000000 |
| 25 | 25 | 77 | 77 | 0.26704491 | 1.00000000 |
| 25 | 25 | 78 | 78 | 0.30346186 | 1.00000000 |
| 25 | 25 | 79 | 79 | 0.38524288 | 1.00000000 |
| 25 | 25 | 80 | 80 | 0.33242864 | 1.00000000 |
| 25 | 25 | 81 | 81 | 0.39948014 | 1.00000000 |
| 25 | 25 | 82 | 82 | 0.50573263 | 1.00000000 |
| 25 | 25 | 83 | 83 | 0.39997789 | 1.00000000 |
| 25 | 25 | 84 | 84 | 0.31458814 | 1.00000000 |
| 25 | 25 | 85 | 85 | 0.42641570 | 1.00000000 |
| 25 | 25 | 86 | 86 | 0.43640994 | 1.00000000 |
| 25 | 25 | 87 | 87 | 0.42371208 | 1.00000000 |
| 25 | 26 | 69 | 70 | 0.11633512 | 0.63167875 |
| 25 | 26 | 70 | 71 | 0.13821284 | 0.59565863 |
| 25 | 26 | 71 | 72 | 0.11342464 | 0.52259787 |
| 25 | 26 | 72 | 73 | 0.14004715 | 0.63837205 |
| 25 | 26 | 73 | 74 | 0.11546026 | 0.59151964 |
| 25 | 26 | 74 | 75 | 0.12219645 | 0.58660671 |
| 25 | 26 | 75 | 76 | 0.15682258 | 0.60795617 |
| 25 | 26 | 76 | 77 | 0.13151195 | 0.66666760 |
| 25 | 26 | 77 | 78 | 0.14674520 | 0.65900616 |
| 25 | 26 | 78 | 79 | 0.16755935 | 0.65699472 |
| 25 | 26 | 79 | 80 | 0.20299283 | 0.72175769 |
| 25 | 26 | 80 | 81 | 0.19808092 | 0.68160385 |
| 25 | 26 | 81 | 82 | 0.18401466 | 0.50621530 |
| 25 | 26 | 82 | 83 | 0.20191927 | 0.54819073 |
| 25 | 26 | 83 | 84 | 0.16691218 | 0.63894878 |
| 25 | 26 | 84 | 85 | 0.19559662 | 0.67716967 |
| 25 | 26 | 85 | 86 | 0.21750304 | 0.64041851 |
| 25 | 26 | 86 | 87 | 0.21225842 | 0.61792656 |
| 25 | 27 | 69 | 71 | 0.09866807 | 0.48208527 |
| 25 | 27 | 70 | 72 | 0.09279338 | 0.40253686 |
| 25 | 27 | 71 | 73 | 0.09156946 | 0.47025502 |
| 25 | 27 | 72 | 74 | 0.10232635 | 0.49919795 |
| 25 | 27 | 73 | 75 | 0.09184921 | 0.44692778 |
| 25 | 27 | 74 | 76 | 0.10757963 | 0.47142084 |
| 25 | 27 | 75 | 77 | 0.10857410 | 0.49677680 |
| 25 | 27 | 76 | 78 | 0.12459753 | 0.54874119 |
| 25 | 27 | 77 | 79 | 0.13440083 | 0.57530542 |
| 25 | 27 | 78 | 80 | 0.11694031 | 0.48949713 |
| 25 | 27 | 79 | 81 | 0.17531619 | 0.61783509 |
| 25 | 27 | 80 | 82 | 0.16787270 | 0.49590720 |
| 25 | 27 | 81 | 83 | 0.16025237 | 0.51150350 |
| 25 | 27 | 82 | 84 | 0.16942197 | 0.50655937 |
| 25 | 27 | 83 | 85 | 0.16584386 | 0.52905995 |
| 25 | 27 | 84 | 86 | 0.15056479 | 0.53802160 |
| 25 | 27 | 85 | 87 | 0.17926115 | 0.56929064 |
| 25 | 28 | 69 | 72 | 0.07961085 | 0.42257982 |
| 25 | 28 | 70 | 73 | 0.08624263 | 0.38756770 |
| 25 | 28 | 71 | 74 | 0.10617399 | 0.47172091 |
| 25 | 28 | 72 | 75 | 0.09528073 | 0.40358414 |
| 25 | 28 | 73 | 76 | 0.09396649 | 0.43700238 |
| 25 | 28 | 74 | 77 | 0.07332420 | 0.34859434 |
| 25 | 28 | 75 | 78 | 0.11595002 | 0.41771346 |
| 25 | 28 | 76 | 79 | 0.08888380 | 0.45289509 |
| 25 | 28 | 77 | 80 | 0.11372574 | 0.50108722 |
| 25 | 28 | 78 | 81 | 0.10697949 | 0.39753841 |
| 25 | 28 | 79 | 82 | 0.15448279 | 0.39266133 |
| 25 | 28 | 80 | 83 | 0.13684763 | 0.48681720 |
| 25 | 28 | 81 | 84 | 0.13347704 | 0.48255631 |
| 25 | 28 | 82 | 85 | 0.15756926 | 0.42125528 |
| 25 | 28 | 83 | 86 | 0.14326366 | 0.43837657 |
| 25 | 28 | 84 | 87 | 0.14502792 | 0.52028730 |
| 25 | 29 | 69 | 73 | 0.07543691 | 0.37479200 |
| 25 | 29 | 70 | 74 | 0.05999891 | 0.29206800 |
| 25 | 29 | 71 | 75 | 0.11876027 | 0.46597082 |
| 25 | 29 | 72 | 76 | 0.10376712 | 0.42085803 |
| 25 | 29 | 73 | 77 | 0.07791934 | 0.39243477 |
| 25 | 29 | 74 | 78 | 0.06333104 | 0.30477997 |
| 25 | 29 | 75 | 79 | 0.10030708 | 0.36463545 |
| 25 | 29 | 76 | 80 | 0.09770953 | 0.45692784 |
| 25 | 29 | 77 | 81 | 0.08504214 | 0.37234993 |
| 25 | 29 | 78 | 82 | 0.14263073 | 0.40694904 |
| 25 | 29 | 79 | 83 | 0.11128236 | 0.34348803 |
| 25 | 29 | 80 | 84 | 0.12104363 | 0.48395931 |
| 25 | 29 | 81 | 85 | 0.15265122 | 0.42626753 |
| 25 | 29 | 82 | 86 | 0.14965524 | 0.33430411 |
| 25 | 29 | 83 | 87 | 0.11615068 | 0.41339401 |
| 25 | 30 | 69 | 74 | 0.05852007 | 0.28428150 |
| 25 | 30 | 70 | 75 | 0.07869137 | 0.38110584 |
| 25 | 30 | 71 | 76 | 0.11547119 | 0.42340466 |
| 25 | 30 | 72 | 77 | 0.07950265 | 0.35977812 |
| 25 | 30 | 73 | 78 | 0.04002073 | 0.21406528 |
| 25 | 30 | 74 | 79 | 0.05501892 | 0.23861011 |
| 25 | 30 | 75 | 80 | 0.10003192 | 0.35299469 |
| 25 | 30 | 76 | 81 | 0.08818811 | 0.36814051 |
| 25 | 30 | 77 | 82 | 0.13497743 | 0.50148070 |
| 25 | 30 | 78 | 83 | 0.14750095 | 0.42098171 |
| 25 | 30 | 79 | 84 | 0.12826679 | 0.43084562 |
| 25 | 30 | 80 | 85 | 0.10694778 | 0.37990074 |
| 25 | 30 | 81 | 86 | 0.15954503 | 0.46707946 |
| 25 | 30 | 82 | 87 | 0.19699868 | 0.42347796 |
| 25 | 31 | 69 | 75 | 0.07785410 | 0.36591022 |
| 25 | 31 | 70 | 76 | 0.06443509 | 0.32312146 |
| 25 | 31 | 71 | 77 | 0.06429405 | 0.29175863 |
| 25 | 31 | 72 | 78 | 0.07307886 | 0.38113335 |
| 25 | 31 | 73 | 79 | 0.05034927 | 0.25201528 |
| 25 | 31 | 74 | 80 | 0.06154955 | 0.29281806 |
| 25 | 31 | 75 | 81 | 0.07181829 | 0.22511274 |
| 25 | 31 | 76 | 82 | 0.08387374 | 0.37335981 |
| 25 | 31 | 77 | 83 | 0.10869648 | 0.34439521 |
| 25 | 31 | 78 | 84 | 0.12169507 | 0.42629244 |
| 25 | 31 | 79 | 85 | 0.09761055 | 0.31206388 |
| 25 | 31 | 80 | 86 | 0.13714024 | 0.47061075 |
| 25 | 31 | 81 | 87 | 0.10243348 | 0.36542198 |
| 25 | 32 | 69 | 76 | 0.09471803 | 0.41971012 |
| 25 | 32 | 70 | 77 | 0.05070792 | 0.22384846 |
| 25 | 32 | 71 | 78 | 0.04703889 | 0.23764678 |
| 25 | 32 | 72 | 79 | 0.06941981 | 0.32537881 |
| 25 | 32 | 73 | 80 | 0.05873525 | 0.29395281 |
| 25 | 32 | 74 | 81 | 0.05499573 | 0.23045075 |
| 25 | 32 | 75 | 82 | 0.10716559 | 0.43277929 |
| 25 | 32 | 76 | 83 | 0.08582790 | 0.27044687 |
| 25 | 32 | 77 | 84 | 0.09595455 | 0.36425277 |
| 25 | 32 | 78 | 85 | 0.12242578 | 0.40690334 |
| 25 | 32 | 79 | 86 | 0.10859377 | 0.33586166 |
| 25 | 32 | 80 | 87 | 0.11165113 | 0.40749023 |
| 25 | 33 | 69 | 77 | 0.08103649 | 0.36672029 |
| 25 | 33 | 70 | 78 | 0.06063010 | 0.31175362 |
| 25 | 33 | 71 | 79 | 0.06243404 | 0.29113196 |
| 25 | 33 | 72 | 80 | 0.10182218 | 0.46635152 |
| 25 | 33 | 73 | 81 | 0.06337081 | 0.26750401 |
| 25 | 33 | 74 | 82 | 0.08950424 | 0.42171494 |
| 25 | 33 | 75 | 83 | 0.10376041 | 0.28737979 |
| 25 | 33 | 76 | 84 | 0.08254653 | 0.31776590 |
| 25 | 33 | 77 | 85 | 0.11165876 | 0.38523698 |
| 25 | 33 | 78 | 86 | 0.15237092 | 0.46245530 |
| 25 | 33 | 79 | 87 | 0.11451762 | 0.40080550 |
| 25 | 34 | 69 | 78 | 0.08296506 | 0.41443325 |
| 25 | 34 | 70 | 79 | 0.06167349 | 0.32375240 |
| 25 | 34 | 71 | 80 | 0.07751481 | 0.34202613 |
| 25 | 34 | 72 | 81 | 0.09557326 | 0.39507951 |
| 25 | 34 | 73 | 82 | 0.07879655 | 0.31880094 |
| 25 | 34 | 74 | 83 | 0.07418957 | 0.23843042 |
| 25 | 34 | 75 | 84 | 0.09042044 | 0.26223610 |
| 25 | 34 | 76 | 85 | 0.07505823 | 0.25648842 |
| 25 | 34 | 77 | 86 | 0.09404648 | 0.33094745 |
| 25 | 34 | 78 | 87 | 0.12590517 | 0.45942639 |
| 25 | 35 | 69 | 79 | 0.06543087 | 0.33224462 |
| 25 | 35 | 70 | 80 | 0.08361872 | 0.35077237 |
| 25 | 35 | 71 | 81 | 0.10130704 | 0.40228552 |
| 25 | 35 | 72 | 82 | 0.11177885 | 0.49345778 |
| 25 | 35 | 73 | 83 | 0.09474978 | 0.33424135 |
| 25 | 35 | 74 | 84 | 0.06696919 | 0.25255336 |
| 25 | 35 | 75 | 85 | 0.09963772 | 0.28460584 |
| 25 | 35 | 76 | 86 | 0.07984423 | 0.29585403 |
| 25 | 35 | 77 | 87 | 0.09608901 | 0.38417229 |
| 25 | 36 | 69 | 80 | 0.08543528 | 0.37546050 |
| 25 | 36 | 70 | 81 | 0.07692504 | 0.28490531 |
| 25 | 36 | 71 | 82 | 0.09017109 | 0.43294206 |
| 25 | 36 | 72 | 83 | 0.11494263 | 0.31571937 |
| 25 | 36 | 73 | 84 | 0.05657153 | 0.23756236 |
| 25 | 36 | 74 | 85 | 0.04857361 | 0.17567050 |
| 25 | 36 | 75 | 86 | 0.07106139 | 0.19493965 |
| 25 | 36 | 76 | 87 | 0.06911677 | 0.27977718 |
| 25 | 37 | 69 | 81 | 0.06430834 | 0.28440934 |
| 25 | 37 | 70 | 82 | 0.07953987 | 0.35822704 |
| 25 | 37 | 71 | 83 | 0.11632399 | 0.33113468 |
| 25 | 37 | 72 | 84 | 0.09623319 | 0.30468022 |
| 25 | 37 | 73 | 85 | 0.10688008 | 0.31351192 |
| 25 | 37 | 74 | 86 | 0.04394220 | 0.14786917 |
| 25 | 37 | 75 | 87 | 0.09772782 | 0.32263907 |
| 25 | 38 | 69 | 82 | 0.06382157 | 0.28097040 |
| 25 | 38 | 70 | 83 | 0.07748352 | 0.27928911 |
| 25 | 38 | 71 | 84 | 0.10867363 | 0.31895856 |
| 25 | 38 | 72 | 85 | 0.14270788 | 0.37922260 |
| 25 | 38 | 73 | 86 | 0.05545543 | 0.18790020 |
| 25 | 38 | 74 | 87 | 0.06369242 | 0.26578764 |
| 25 | 39 | 69 | 83 | 0.07637790 | 0.30371474 |
| 25 | 39 | 70 | 84 | 0.06046641 | 0.21564954 |
| 25 | 39 | 71 | 85 | 0.11885353 | 0.33141715 |
| 25 | 39 | 72 | 86 | 0.07812950 | 0.23960532 |
| 25 | 39 | 73 | 87 | 0.05905213 | 0.24421106 |
| 25 | 40 | 69 | 84 | 0.10017744 | 0.36831807 |
| 25 | 40 | 70 | 85 | 0.09822473 | 0.26115192 |
| 25 | 40 | 71 | 86 | 0.10582135 | 0.33492992 |
| 25 | 40 | 72 | 87 | 0.07944614 | 0.30528294 |
| 25 | 41 | 69 | 85 | 0.07648787 | 0.22863580 |
| 25 | 41 | 70 | 86 | 0.05921662 | 0.23618920 |
| 25 | 41 | 71 | 87 | 0.11893127 | 0.42156702 |
| 25 | 42 | 69 | 86 | 0.08850931 | 0.28819706 |
| 25 | 42 | 70 | 87 | 0.08503483 | 0.34087897 |
| 25 | 43 | 69 | 87 | 0.10043580 | 0.36543209 |
| 35 | 35 | 69 | 69 | 0.29575627 | 1.00000000 |
| 35 | 35 | 70 | 70 | 0.29373972 | 1.00000000 |
| 35 | 35 | 71 | 71 | 0.23090994 | 1.00000000 |
| 35 | 35 | 72 | 72 | 0.19957159 | 1.00000000 |
| 35 | 35 | 73 | 73 | 0.18023090 | 1.00000000 |
| 35 | 35 | 74 | 74 | 0.23808636 | 1.00000000 |
| 35 | 35 | 75 | 75 | 0.23458647 | 1.00000000 |
| 35 | 35 | 76 | 76 | 0.34440097 | 1.00000000 |
| 35 | 35 | 77 | 77 | 0.23282476 | 1.00000000 |
| 35 | 35 | 78 | 78 | 0.21873077 | 1.00000000 |
| 35 | 35 | 79 | 79 | 0.20391977 | 1.00000000 |
| 35 | 35 | 80 | 80 | 0.22575833 | 1.00000000 |
| 35 | 35 | 81 | 81 | 0.26517069 | 1.00000000 |
| 35 | 35 | 82 | 82 | 0.32012594 | 1.00000000 |
| 35 | 35 | 83 | 83 | 0.38348632 | 1.00000000 |
| 35 | 35 | 84 | 84 | 0.33689053 | 1.00000000 |
| 35 | 35 | 85 | 85 | 0.39398481 | 1.00000000 |
| 35 | 35 | 86 | 86 | 0.42165217 | 1.00000000 |
| 35 | 35 | 87 | 87 | 0.33897801 | 1.00000000 |
| 35 | 36 | 69 | 70 | 0.10799405 | 0.62738270 |
| 35 | 36 | 70 | 71 | 0.11873585 | 0.64975896 |
| 35 | 36 | 71 | 72 | 0.13604364 | 0.77529695 |
| 35 | 36 | 72 | 73 | 0.12144991 | 0.74850054 |
| 35 | 36 | 73 | 74 | 0.12894967 | 0.75818783 |
| 35 | 36 | 74 | 75 | 0.14176807 | 0.69900552 |
| 35 | 36 | 75 | 76 | 0.13050343 | 0.67368649 |
| 35 | 36 | 76 | 77 | 0.16464134 | 0.71879334 |
| 35 | 36 | 77 | 78 | 0.11531758 | 0.71537523 |
| 35 | 36 | 78 | 79 | 0.12927109 | 0.75750547 |
| 35 | 36 | 79 | 80 | 0.14554272 | 0.83374069 |
| 35 | 36 | 80 | 81 | 0.13293863 | 0.70135582 |
| 35 | 36 | 81 | 82 | 0.19851673 | 0.74479164 |
| 35 | 36 | 82 | 83 | 0.19998343 | 0.67991527 |
| 35 | 36 | 83 | 84 | 0.17502639 | 0.72943404 |
| 35 | 36 | 84 | 85 | 0.22216544 | 0.76894690 |
| 35 | 36 | 85 | 86 | 0.25730562 | 0.77270412 |
| 35 | 36 | 86 | 87 | 0.22992805 | 0.79621907 |
| 35 | 37 | 69 | 71 | 0.11326541 | 0.58458088 |
| 35 | 37 | 70 | 72 | 0.10775334 | 0.60624414 |
| 35 | 37 | 71 | 73 | 0.11308605 | 0.72981096 |
| 35 | 37 | 72 | 74 | 0.09850006 | 0.60809306 |
| 35 | 37 | 73 | 75 | 0.11624987 | 0.66477877 |
| 35 | 37 | 74 | 76 | 0.13438354 | 0.59479556 |
| 35 | 37 | 75 | 77 | 0.12446262 | 0.60690191 |
| 35 | 37 | 76 | 78 | 0.12175314 | 0.63027885 |
| 35 | 37 | 77 | 79 | 0.10919921 | 0.63408922 |
| 35 | 37 | 78 | 80 | 0.11489002 | 0.70376926 |
| 35 | 37 | 79 | 81 | 0.13080792 | 0.67157580 |
| 35 | 37 | 80 | 82 | 0.14594004 | 0.60538630 |
| 35 | 37 | 81 | 83 | 0.14802777 | 0.59296476 |
| 35 | 37 | 82 | 84 | 0.18385733 | 0.54007643 |
| 35 | 37 | 83 | 85 | 0.19080162 | 0.66990303 |
| 35 | 37 | 84 | 86 | 0.20717688 | 0.69794514 |
| 35 | 37 | 85 | 87 | 0.19602736 | 0.70958374 |
| 35 | 38 | 69 | 72 | 0.10002642 | 0.51154300 |
| 35 | 38 | 70 | 73 | 0.08640619 | 0.56832930 |
| 35 | 38 | 71 | 74 | 0.10096207 | 0.56665153 |
| 35 | 38 | 72 | 75 | 0.08329954 | 0.54106813 |
| 35 | 38 | 73 | 76 | 0.09783600 | 0.52078480 |
| 35 | 38 | 74 | 77 | 0.10811593 | 0.61893031 |
| 35 | 38 | 75 | 78 | 0.09036375 | 0.55967314 |
| 35 | 38 | 76 | 79 | 0.11673417 | 0.55901296 |
| 35 | 38 | 77 | 80 | 0.13581815 | 0.69706610 |
| 35 | 38 | 78 | 81 | 0.12584093 | 0.60538425 |
| 35 | 38 | 79 | 82 | 0.11600084 | 0.52903474 |
| 35 | 38 | 80 | 83 | 0.12331923 | 0.59596576 |
| 35 | 38 | 81 | 84 | 0.13009112 | 0.56713480 |
| 35 | 38 | 82 | 85 | 0.18628058 | 0.54793500 |
| 35 | 38 | 83 | 86 | 0.19491268 | 0.65958365 |
| 35 | 38 | 84 | 87 | 0.18369060 | 0.68003395 |
| 35 | 39 | 69 | 73 | 0.07755548 | 0.50012662 |
| 35 | 39 | 70 | 74 | 0.09690851 | 0.47449027 |
| 35 | 39 | 71 | 75 | 0.10168147 | 0.55483884 |
| 35 | 39 | 72 | 76 | 0.08385627 | 0.42354181 |
| 35 | 39 | 73 | 77 | 0.08919678 | 0.56513403 |
| 35 | 39 | 74 | 78 | 0.11603696 | 0.58675609 |
| 35 | 39 | 75 | 79 | 0.10149781 | 0.53643158 |
| 35 | 39 | 76 | 80 | 0.17218863 | 0.69409284 |
| 35 | 39 | 77 | 81 | 0.12327679 | 0.58143160 |
| 35 | 39 | 78 | 82 | 0.10227251 | 0.52635389 |
| 35 | 39 | 79 | 83 | 0.14048602 | 0.60455185 |
| 35 | 39 | 80 | 84 | 0.11636288 | 0.53672026 |
| 35 | 39 | 81 | 85 | 0.15313519 | 0.53239444 |
| 35 | 39 | 82 | 86 | 0.15704782 | 0.53300832 |
| 35 | 39 | 83 | 87 | 0.17248239 | 0.62100705 |
| 35 | 40 | 69 | 74 | 0.08112916 | 0.37933330 |
| 35 | 40 | 70 | 75 | 0.11984755 | 0.53736040 |
| 35 | 40 | 71 | 76 | 0.11150620 | 0.43347122 |
| 35 | 40 | 72 | 77 | 0.08898410 | 0.51808885 |
| 35 | 40 | 73 | 78 | 0.08754521 | 0.54220403 |
| 35 | 40 | 74 | 79 | 0.09002747 | 0.49557796 |
| 35 | 40 | 75 | 80 | 0.12404980 | 0.60337486 |
| 35 | 40 | 76 | 81 | 0.14039209 | 0.60424036 |
| 35 | 40 | 77 | 82 | 0.11882276 | 0.61461105 |
| 35 | 40 | 78 | 83 | 0.12693847 | 0.54609357 |
| 35 | 40 | 79 | 84 | 0.09475936 | 0.44967260 |
| 35 | 40 | 80 | 85 | 0.12176836 | 0.47993331 |
| 35 | 40 | 81 | 86 | 0.13116267 | 0.57826009 |
| 35 | 40 | 82 | 87 | 0.16255441 | 0.52122396 |
| 35 | 41 | 69 | 75 | 0.05651727 | 0.25158133 |
| 35 | 41 | 70 | 76 | 0.10825400 | 0.38012324 |
| 35 | 41 | 71 | 77 | 0.10597530 | 0.54365253 |
| 35 | 41 | 72 | 78 | 0.10430018 | 0.53364146 |
| 35 | 41 | 73 | 79 | 0.10608943 | 0.56844010 |
| 35 | 41 | 74 | 80 | 0.11702395 | 0.61962651 |
| 35 | 41 | 75 | 81 | 0.14037138 | 0.59988745 |
| 35 | 41 | 76 | 82 | 0.19139425 | 0.58485586 |
| 35 | 41 | 77 | 83 | 0.12554693 | 0.55712686 |
| 35 | 41 | 78 | 84 | 0.10569432 | 0.45149954 |
| 35 | 41 | 79 | 85 | 0.13433820 | 0.50996248 |
| 35 | 41 | 80 | 86 | 0.09627442 | 0.43771926 |
| 35 | 41 | 81 | 87 | 0.12103767 | 0.52310531 |
| 35 | 42 | 69 | 76 | 0.11610103 | 0.51252548 |
| 35 | 42 | 70 | 77 | 0.10175541 | 0.49230691 |
| 35 | 42 | 71 | 78 | 0.11040124 | 0.57061544 |
| 35 | 42 | 72 | 79 | 0.09094121 | 0.48584131 |
| 35 | 42 | 73 | 80 | 0.10432545 | 0.61240867 |
| 35 | 42 | 74 | 81 | 0.11982831 | 0.55731284 |
| 35 | 42 | 75 | 82 | 0.16925654 | 0.57168687 |
| 35 | 42 | 76 | 83 | 0.18662131 | 0.63410442 |
| 35 | 42 | 77 | 84 | 0.13155154 | 0.50626558 |
| 35 | 42 | 78 | 85 | 0.11069693 | 0.44023007 |
| 35 | 42 | 79 | 86 | 0.11391833 | 0.49777507 |
| 35 | 42 | 80 | 87 | 0.10697071 | 0.51559679 |
| 35 | 43 | 69 | 77 | 0.11597465 | 0.48248416 |
| 35 | 43 | 70 | 78 | 0.09771238 | 0.43497969 |
| 35 | 43 | 71 | 79 | 0.11573113 | 0.52846091 |
| 35 | 43 | 72 | 80 | 0.08904726 | 0.46565233 |
| 35 | 43 | 73 | 81 | 0.10974553 | 0.49809136 |
| 35 | 43 | 74 | 82 | 0.12218862 | 0.50318561 |
| 35 | 43 | 75 | 83 | 0.15370061 | 0.57952494 |
| 35 | 43 | 76 | 84 | 0.15568707 | 0.54548330 |
| 35 | 43 | 77 | 85 | 0.12849729 | 0.45370867 |
| 35 | 43 | 78 | 86 | 0.09855969 | 0.47362676 |
| 35 | 43 | 79 | 87 | 0.11581614 | 0.54499438 |
| 35 | 44 | 69 | 78 | 0.07731330 | 0.34285575 |
| 35 | 44 | 70 | 79 | 0.09092584 | 0.43150032 |
| 35 | 44 | 71 | 80 | 0.10954453 | 0.51532161 |
| 35 | 44 | 72 | 81 | 0.10342399 | 0.43460711 |
| 35 | 44 | 73 | 82 | 0.16680586 | 0.57790590 |
| 35 | 44 | 74 | 83 | 0.12880958 | 0.49143840 |
| 35 | 44 | 75 | 84 | 0.13706969 | 0.54201022 |
| 35 | 44 | 76 | 85 | 0.14758292 | 0.46770053 |
| 35 | 44 | 77 | 86 | 0.10594947 | 0.41480395 |
| 35 | 44 | 78 | 87 | 0.09936566 | 0.49410779 |
| 35 | 45 | 69 | 79 | 0.07930485 | 0.35734477 |
| 35 | 45 | 70 | 80 | 0.10178299 | 0.48580665 |
| 35 | 45 | 71 | 81 | 0.12228159 | 0.51510462 |
| 35 | 45 | 72 | 82 | 0.09430867 | 0.33026370 |
| 35 | 45 | 73 | 83 | 0.11164080 | 0.51196058 |
| 35 | 45 | 74 | 84 | 0.14807400 | 0.59480858 |
| 35 | 45 | 75 | 85 | 0.14520793 | 0.56503630 |
| 35 | 45 | 76 | 86 | 0.12132591 | 0.42830640 |
| 35 | 45 | 77 | 87 | 0.08282760 | 0.40402788 |
| 35 | 46 | 69 | 80 | 0.08614411 | 0.38205010 |
| 35 | 46 | 70 | 81 | 0.11827860 | 0.53585980 |
| 35 | 46 | 71 | 82 | 0.20187612 | 0.59900647 |
| 35 | 46 | 72 | 83 | 0.08080180 | 0.35022378 |
| 35 | 46 | 73 | 84 | 0.13069770 | 0.60935116 |
| 35 | 46 | 74 | 85 | 0.13187763 | 0.49723125 |
| 35 | 46 | 75 | 86 | 0.10593031 | 0.44907824 |
| 35 | 46 | 76 | 87 | 0.10969483 | 0.43622209 |
| 35 | 47 | 69 | 81 | 0.09974853 | 0.43268432 |
| 35 | 47 | 70 | 82 | 0.15902232 | 0.56729410 |
| 35 | 47 | 71 | 83 | 0.11843594 | 0.48975207 |
| 35 | 47 | 72 | 84 | 0.07165584 | 0.39273026 |
| 35 | 47 | 73 | 85 | 0.12392844 | 0.52648532 |
| 35 | 47 | 74 | 86 | 0.10948550 | 0.50505418 |
| 35 | 47 | 75 | 87 | 0.09193293 | 0.42156245 |
| 35 | 48 | 69 | 82 | 0.12698106 | 0.41563058 |
| 35 | 48 | 70 | 83 | 0.11753844 | 0.47656642 |
| 35 | 48 | 71 | 84 | 0.09405469 | 0.47117984 |
| 35 | 48 | 72 | 85 | 0.08240910 | 0.41220891 |
| 35 | 48 | 73 | 86 | 0.10413944 | 0.44080374 |
| 35 | 48 | 74 | 87 | 0.09303585 | 0.49249451 |
| 35 | 49 | 69 | 83 | 0.10091445 | 0.39934180 |
| 35 | 49 | 70 | 84 | 0.09015872 | 0.45513756 |
| 35 | 49 | 71 | 85 | 0.11079876 | 0.47588498 |
| 35 | 49 | 72 | 86 | 0.07164230 | 0.34317330 |
| 35 | 49 | 73 | 87 | 0.10072712 | 0.50871371 |
| 35 | 50 | 69 | 84 | 0.10108034 | 0.47189658 |
| 35 | 50 | 70 | 85 | 0.10439749 | 0.47644525 |
| 35 | 50 | 71 | 86 | 0.09567998 | 0.45294817 |
| 35 | 50 | 72 | 87 | 0.08599539 | 0.40434647 |
| 35 | 51 | 69 | 85 | 0.10383210 | 0.43212285 |
| 35 | 51 | 70 | 86 | 0.08846481 | 0.45288614 |
| 35 | 51 | 71 | 87 | 0.11258039 | 0.51408156 |
| 35 | 52 | 69 | 86 | 0.09716044 | 0.44397917 |
| 35 | 52 | 70 | 87 | 0.11740437 | 0.48110302 |
| 35 | 53 | 69 | 87 | 0.11416182 | 0.41074034 |
| 45 | 45 | 69 | 69 | 0.18450732 | 1.00000000 |
| 45 | 45 | 70 | 70 | 0.18762559 | 1.00000000 |
| 45 | 45 | 71 | 71 | 0.21260064 | 1.00000000 |
| 45 | 45 | 72 | 72 | 0.19622150 | 1.00000000 |
| 45 | 45 | 73 | 73 | 0.15778624 | 1.00000000 |
| 45 | 45 | 74 | 74 | 0.18656541 | 1.00000000 |
| 45 | 45 | 75 | 75 | 0.26861350 | 1.00000000 |
| 45 | 45 | 76 | 76 | 0.24174888 | 1.00000000 |
| 45 | 45 | 77 | 77 | 0.23420209 | 1.00000000 |
| 45 | 45 | 78 | 78 | 0.26441058 | 1.00000000 |
| 45 | 45 | 79 | 79 | 0.28745096 | 1.00000000 |
| 45 | 45 | 80 | 80 | 0.28096509 | 1.00000000 |
| 45 | 45 | 81 | 81 | 0.33564005 | 1.00000000 |
| 45 | 45 | 82 | 82 | 0.45541647 | 1.00000000 |
| 45 | 45 | 83 | 83 | 0.38459008 | 1.00000000 |
| 45 | 45 | 84 | 84 | 0.37185514 | 1.00000000 |
| 45 | 45 | 85 | 85 | 0.42152591 | 1.00000000 |
| 45 | 45 | 86 | 86 | 0.34952142 | 1.00000000 |
| 45 | 45 | 87 | 87 | 0.28788574 | 1.00000000 |
| 45 | 46 | 69 | 70 | 0.12415186 | 0.79348734 |
| 45 | 46 | 70 | 71 | 0.13166740 | 0.81163386 |
| 45 | 46 | 71 | 72 | 0.12863474 | 0.82304806 |
| 45 | 46 | 72 | 73 | 0.13862347 | 0.87038045 |
| 45 | 46 | 73 | 74 | 0.13570983 | 0.86070611 |
| 45 | 46 | 74 | 75 | 0.14612226 | 0.78290837 |
| 45 | 46 | 75 | 76 | 0.17768590 | 0.83083201 |
| 45 | 46 | 76 | 77 | 0.14029805 | 0.75754916 |
| 45 | 46 | 77 | 78 | 0.16328858 | 0.73217632 |
| 45 | 46 | 78 | 79 | 0.18280427 | 0.76025639 |
| 45 | 46 | 79 | 80 | 0.22136823 | 0.81324685 |
| 45 | 46 | 80 | 81 | 0.22921152 | 0.88526701 |
| 45 | 46 | 81 | 82 | 0.28535136 | 0.81286425 |
| 45 | 46 | 82 | 83 | 0.31366553 | 0.77304395 |
| 45 | 46 | 83 | 84 | 0.20215241 | 0.77754417 |
| 45 | 46 | 84 | 85 | 0.24213282 | 0.82924466 |
| 45 | 46 | 85 | 86 | 0.23775723 | 0.77618131 |
| 45 | 46 | 86 | 87 | 0.21223617 | 0.86042142 |
| 45 | 47 | 69 | 71 | 0.12848324 | 0.78067712 |
| 45 | 47 | 70 | 72 | 0.12317067 | 0.77336302 |
| 45 | 47 | 71 | 73 | 0.12089597 | 0.72752448 |
| 45 | 47 | 72 | 74 | 0.12862652 | 0.78044227 |
| 45 | 47 | 73 | 75 | 0.12587253 | 0.71461933 |
| 45 | 47 | 74 | 76 | 0.14562659 | 0.72551218 |
| 45 | 47 | 75 | 77 | 0.14434890 | 0.78803348 |
| 45 | 47 | 76 | 78 | 0.15121667 | 0.75420824 |
| 45 | 47 | 77 | 79 | 0.15835363 | 0.74282666 |
| 45 | 47 | 78 | 80 | 0.16979023 | 0.74665160 |
| 45 | 47 | 79 | 81 | 0.18792305 | 0.75879846 |
| 45 | 47 | 80 | 82 | 0.21245219 | 0.64661513 |
| 45 | 47 | 81 | 83 | 0.23838206 | 0.69135480 |
| 45 | 47 | 82 | 84 | 0.18394933 | 0.69626621 |
| 45 | 47 | 83 | 85 | 0.21366987 | 0.69386177 |
| 45 | 47 | 84 | 86 | 0.23437112 | 0.77185127 |
| 45 | 47 | 85 | 87 | 0.21680244 | 0.71730719 |
| 45 | 48 | 69 | 72 | 0.12492398 | 0.74455867 |
| 45 | 48 | 70 | 73 | 0.12866905 | 0.75795486 |
| 45 | 48 | 71 | 74 | 0.12590696 | 0.71727696 |
| 45 | 48 | 72 | 75 | 0.13379141 | 0.70806834 |
| 45 | 48 | 73 | 76 | 0.12666606 | 0.69194649 |
| 45 | 48 | 74 | 77 | 0.13553801 | 0.73665650 |
| 45 | 48 | 75 | 78 | 0.13910216 | 0.77403928 |
| 45 | 48 | 76 | 79 | 0.13870509 | 0.73082841 |
| 45 | 48 | 77 | 80 | 0.14330316 | 0.67370814 |
| 45 | 48 | 78 | 81 | 0.15775888 | 0.68453991 |
| 45 | 48 | 79 | 82 | 0.19335256 | 0.59734172 |
| 45 | 48 | 80 | 83 | 0.23128612 | 0.70558171 |
| 45 | 48 | 81 | 84 | 0.17316764 | 0.69753670 |
| 45 | 48 | 82 | 85 | 0.25492586 | 0.66752297 |
| 45 | 48 | 83 | 86 | 0.18188307 | 0.54399355 |
| 45 | 48 | 84 | 87 | 0.18189091 | 0.73814206 |
| 45 | 49 | 69 | 73 | 0.12112981 | 0.73876290 |
| 45 | 49 | 70 | 74 | 0.11065046 | 0.68589170 |
| 45 | 49 | 71 | 75 | 0.12782530 | 0.59630672 |
| 45 | 49 | 72 | 76 | 0.12983524 | 0.69034977 |
| 45 | 49 | 73 | 77 | 0.12236924 | 0.72040496 |
| 45 | 49 | 74 | 78 | 0.13129965 | 0.66002213 |
| 45 | 49 | 75 | 79 | 0.14352933 | 0.73242269 |
| 45 | 49 | 76 | 80 | 0.13613068 | 0.65258827 |
| 45 | 49 | 77 | 81 | 0.17348321 | 0.73389920 |
| 45 | 49 | 78 | 82 | 0.18967184 | 0.57297328 |
| 45 | 49 | 79 | 83 | 0.24327555 | 0.75832928 |
| 45 | 49 | 80 | 84 | 0.18120065 | 0.72333408 |
| 45 | 49 | 81 | 85 | 0.18940768 | 0.65303267 |
| 45 | 49 | 82 | 86 | 0.15052001 | 0.48627933 |
| 45 | 49 | 83 | 87 | 0.15163712 | 0.52937859 |
| 45 | 50 | 69 | 74 | 0.10595853 | 0.69689056 |
| 45 | 50 | 70 | 75 | 0.10740767 | 0.59456272 |
| 45 | 50 | 71 | 76 | 0.12509121 | 0.62695063 |
| 45 | 50 | 72 | 77 | 0.12764210 | 0.69993807 |
| 45 | 50 | 73 | 78 | 0.11146100 | 0.62089458 |
| 45 | 50 | 74 | 79 | 0.13645481 | 0.72100349 |
| 45 | 50 | 75 | 80 | 0.14015426 | 0.71166312 |
| 45 | 50 | 76 | 81 | 0.14228485 | 0.68174878 |
| 45 | 50 | 77 | 82 | 0.27442679 | 0.72990877 |
| 45 | 50 | 78 | 83 | 0.16644934 | 0.61055788 |
| 45 | 50 | 79 | 84 | 0.19195626 | 0.71259508 |
| 45 | 50 | 80 | 85 | 0.21580317 | 0.73455694 |
| 45 | 50 | 81 | 86 | 0.18837655 | 0.67068228 |
| 45 | 50 | 82 | 87 | 0.18004192 | 0.56108297 |
| 45 | 51 | 69 | 75 | 0.11017644 | 0.58582978 |
| 45 | 51 | 70 | 76 | 0.10598551 | 0.62950711 |
| 45 | 51 | 71 | 77 | 0.10387774 | 0.56799145 |
| 45 | 51 | 72 | 78 | 0.12982331 | 0.67451179 |
| 45 | 51 | 73 | 79 | 0.12190785 | 0.71636895 |
| 45 | 51 | 74 | 80 | 0.11943817 | 0.64809972 |
| 45 | 51 | 75 | 81 | 0.13743028 | 0.67526210 |
| 45 | 51 | 76 | 82 | 0.24390376 | 0.65324241 |
| 45 | 51 | 77 | 83 | 0.21548279 | 0.71901995 |
| 45 | 51 | 78 | 84 | 0.13898516 | 0.63751855 |
| 45 | 51 | 79 | 85 | 0.21833860 | 0.72082696 |
| 45 | 51 | 80 | 86 | 0.21576172 | 0.69664288 |
| 45 | 51 | 81 | 87 | 0.16075924 | 0.55834693 |
| 45 | 52 | 69 | 76 | 0.11258549 | 0.51728146 |
| 45 | 52 | 70 | 77 | 0.09897096 | 0.57823989 |
| 45 | 52 | 71 | 78 | 0.11500808 | 0.60762162 |
| 45 | 52 | 72 | 79 | 0.12980932 | 0.68059063 |
| 45 | 52 | 73 | 80 | 0.10820331 | 0.62321354 |
| 45 | 52 | 74 | 81 | 0.11690633 | 0.63276818 |
| 45 | 52 | 75 | 82 | 0.17534886 | 0.60304985 |
| 45 | 52 | 76 | 83 | 0.17508725 | 0.67606120 |
| 45 | 52 | 77 | 84 | 0.18123254 | 0.63847351 |
| 45 | 52 | 78 | 85 | 0.15021171 | 0.60967338 |
| 45 | 52 | 79 | 86 | 0.18861341 | 0.66028879 |
| 45 | 52 | 80 | 87 | 0.20414454 | 0.62637655 |
| 45 | 53 | 69 | 77 | 0.10026401 | 0.52977759 |
| 45 | 53 | 70 | 78 | 0.09789989 | 0.56913478 |
| 45 | 53 | 71 | 79 | 0.11192195 | 0.61013270 |
| 45 | 53 | 72 | 80 | 0.10823988 | 0.54873668 |
| 45 | 53 | 73 | 81 | 0.10266486 | 0.58421503 |
| 45 | 53 | 74 | 82 | 0.14038564 | 0.42919335 |
| 45 | 53 | 75 | 83 | 0.15006270 | 0.61103059 |
| 45 | 53 | 76 | 84 | 0.15129720 | 0.61150573 |
| 45 | 53 | 77 | 85 | 0.17369149 | 0.59869221 |
| 45 | 53 | 78 | 86 | 0.13227547 | 0.60695741 |
| 45 | 53 | 79 | 87 | 0.18631318 | 0.59992570 |
| 45 | 54 | 69 | 78 | 0.09505115 | 0.52934985 |
| 45 | 54 | 70 | 79 | 0.11191512 | 0.64250813 |
| 45 | 54 | 71 | 80 | 0.09770058 | 0.54895333 |
| 45 | 54 | 72 | 81 | 0.10575867 | 0.51437867 |
| 45 | 54 | 73 | 82 | 0.18349166 | 0.60220801 |
| 45 | 54 | 74 | 83 | 0.11290932 | 0.50741697 |
| 45 | 54 | 75 | 84 | 0.13213210 | 0.56788281 |
| 45 | 54 | 76 | 85 | 0.14440478 | 0.44198949 |
| 45 | 54 | 77 | 86 | 0.16777826 | 0.57943321 |
| 45 | 54 | 78 | 87 | 0.12792258 | 0.53694397 |
| 45 | 55 | 69 | 79 | 0.11060217 | 0.61021201 |
| 45 | 55 | 70 | 80 | 0.10992745 | 0.61344591 |
| 45 | 55 | 71 | 81 | 0.09653611 | 0.49851443 |
| 45 | 55 | 72 | 82 | 0.13830385 | 0.36875467 |
| 45 | 55 | 73 | 83 | 0.10459329 | 0.45267594 |
| 45 | 55 | 74 | 84 | 0.12097583 | 0.47870097 |
| 45 | 55 | 75 | 85 | 0.11828959 | 0.38711642 |
| 45 | 55 | 76 | 86 | 0.13427016 | 0.47481047 |
| 45 | 55 | 77 | 87 | 0.14171002 | 0.51670066 |
| 55 | 55 | 69 | 69 | 0.17728938 | 1.00000000 |
| 55 | 55 | 70 | 70 | 0.30183911 | 1.00000000 |
| 55 | 55 | 71 | 71 | 0.29061541 | 1.00000000 |
| 55 | 55 | 72 | 72 | 0.28286051 | 1.00000000 |
| 55 | 55 | 73 | 73 | 0.24741125 | 1.00000000 |
| 55 | 55 | 74 | 74 | 0.18012075 | 1.00000000 |
| 55 | 55 | 75 | 75 | 0.19401375 | 1.00000000 |
| 55 | 55 | 76 | 76 | 0.27513949 | 1.00000000 |
| 55 | 55 | 77 | 77 | 0.25312508 | 1.00000000 |
| 55 | 55 | 78 | 78 | 0.23749102 | 1.00000000 |
| 55 | 55 | 79 | 79 | 0.26942362 | 1.00000000 |
| 55 | 55 | 80 | 80 | 0.24637073 | 1.00000000 |
| 55 | 55 | 81 | 81 | 0.28905820 | 1.00000000 |
| 55 | 55 | 82 | 82 | 0.54746327 | 1.00000000 |
| 55 | 55 | 83 | 83 | 0.45761974 | 1.00000000 |
| 55 | 55 | 84 | 84 | 0.37930624 | 1.00000000 |
| 55 | 55 | 85 | 85 | 0.55924920 | 1.00000000 |
| 55 | 55 | 86 | 86 | 0.46763581 | 1.00000000 |
| 55 | 55 | 87 | 87 | 0.45397922 | 1.00000000 |
Appendix B. The Minimum Distance Method and the Mapping of the Covariance Model
Minimum Distance Method
Let sim =yijyik, where yij and yik are the log earnings (or residuals) for individual i for age-year “locations” j and k, and where m=1, …, M is the moment generated by the product of residuals at locations j and j′. In our case, M=553. Posit the model
| (B1) |
where θ is a Lx1 vector of parameters. Then the set of M equations in (B1) constitutes an SUR system whose efficient estimation requires an initial consistent estimate of the covariance matrix of the εim. However, following the findings and recommendations of Altonji and Segal (1991) on bias in estimating covariance structures of this type, we employ the identity matrix for the estimation.28 Hence we choose θ to minimize the sum of squared residuals:
| (B2) |
or, equivalently, since f is not a function of i,
| (B3) |
where s̄m is the mean (over i) of sim (i.e., a covariance).
To obtain standard errors, we apply the extension of Eicker-White methods in the manner suggested by Chamberlain, using the residuals from (B1), each of which we denote eim. Let Ω be the MxM covariance matrix of the eim, each element of which is estimated by:29
| (B4) |
Let the NMxNM covariance matrix of individual residuals be
Then
| (B5) |
where G is the NMxL matrix of gradients ∂f(θ, j, k)/∂θ.
We experienced considerable difficulty in obtaining positive definite covariance matrices from (B5) in some of our larger models because of the amount of noise in the Ω matrix, which has over 150,000 unique elements. Consequently, we set many elements of that matrix to zero and we smoothed many others with polynomial functions of age and year to obtain our standard error estimates.
Mappings
For Table 1 and related tables in the paper, f is just a linear regression function of age, year, and other variables corresponding to the location of the element in the covariance matrix. For the models presented in Tables 4 and 5, a mapping from the assumed error-components process to f is required. For the models in Table 4, which are independent of calendar time, the covariances (f) implies are easily obtained, but this is not the case for the models in Table 5 where the covariances are functions of calendar time. For those, we derive f at each age and year by recursively deriving successive variances and covariances over the life cycle for each cohort beginning at the beginning of the life cycle (age 20) and proceeding forward simultaneously in age and year. No initial conditions problems per se are presented in our model because the life cycle has a finite start date and end date by assumption; no stationarity assumptions are made or required in either age or calendar time.
For brevity we will present the mapping only for the most complex model, that in equations (2)–(4). Letting δt =Var(ξiat) and ψt=Var(ωiat), we have:
| (B6) |
| (B7) |
| (B8) |
| (B9) |
| (B10) |
| (B11) |
| (B12) |
| (B13) |
| (B14) |
| (B15) |
Equations (B6) and (B7) provide recursion relationships for the variances and covariances, respectively, of equation (2) in the text. Equations (B8)–(B11) are recursion relationships for the variances and covariances of the permanent component, while (B12)–(B15) are recursion relationships for the variances and covariances of the transitory component. Conditional on values of the initial 2 permanent variance ( ) and the five parameters αt, ρt, θt, ψt, and δt, all variances and covariances can be calculated by starting at a=1 for each cohort (each cohort begins at a=1 at a different calendar time, t) and by moving recursively forward over the life cycle using the formulae.
Appendix C. Relation of Mobility to Covariance Structure
Assume we have a random sample of n individuals with earnings observed at two points in time. We denote the earnings of individual i at time t as yit (i=1, …, n; t=1, 2). Although earnings are independent across individuals we assume that they are correlated over time for the same individual. We also assume that the two earnings observations for each individual follow a bivariate normal distribution, with means zero and with and . Let P denote the probability that there are no changes in rank in the distribution from t=1 to t=2. We shall demonstrate that ∂P/∂ρ > 0 and that P is independent of .
Ordering the individuals from i=1 to i=n by rank, we have:
| (C1) |
since there are n! possible orderings of the n individuals, each ordering with the same probability.
It is sufficient to compare only the change in relative rank for any given pair of individuals i and j, since the result will generalize to all pairs. Let
| (C2) |
Defining
| (C3) |
| (C4) |
we have that w1 and w2 are distributed bivariate normal with means zero and with and . Hence
| (C5) |
| (C6) |
where b is the unit bivariate normal density and where . Thus P′ is only a function of ρ and not a function of .
The partial derivative of a bivariate normal cumulative distribution function w.r.t. ρ is equal to the bivariate density evaluated at the upper limits. Hence ∂P′/∂ρ = b(0, 0; ρ) > 0.
Footnotes
In prior work, we have treated each wave of the PSID as an independent cross section and we have compared trends in earnings differentials to those in the CPS (Gottschalk and Moffitt, 1992). We found overall conformity of the direction of the trends in the two data sets in both within-group and between-group earnings differentials.
Attrition in the PSID has reached approximately 50 percent by 1988, and therefore a continuous-sample restriction would severely reduce the sample size and hinder the analysis. Fortunately, despite this heavy attrition, there is little evidence of significant attrition bias in the PSID in the studies that have examined it to date (Becketti et al., 1988; Fitzgerald, Gottschalk, and Moffitt, forthcoming).
We delete the top and bottom one-percent of the earnings and wage observations within each age-year covariance cell. These outliers introduce noise into the trends in variances and covariances. This trimming also eliminates the top-coded earnings observations in the PSID. Results on untrimmed data show the same patterns as those we present below but with larger standard errors.
The regression coefficients are available upon request.
In addition, if the transitory component is serially correlated, the variance of average earnings will be affected by the variance of the transitory component as well. The method we use in this paper confirms the crude estimate in Gottschalk and Moffitt (1994).
The variances and covariances are averaged over the age groups in question and over the single-order lags (e.g., over the first, second, third, and fourth-order lags for the plot “lag 1–4”).
The difference in the growth rates of high-order and low-order covariances, and their different implications for the growth of the transitory variance, will be discussed further below.
However, variances are more procyclical than covariances (as can also be seen in Figures 1(a)–(d)), an indirect indication that transitory variances are more procyclical than “permanent” variances. We should note that the unemployment rates are detrended.
That the two models fit approximately the same is not surprising since the random growth model implies variances rising over the life cycle with the square of age whereas the random walk model implies linearly increasing variances. There is relatively little curvature in the life cycle profile of variances in our data, which is no doubt the reason for the similarity of fit. Abowd and Card (1989) examined fourth moments of the data and found the random walk model to provide a superior fit than the random growth model because earnings differences were weakly correlated over time.
We make no attempt to explicitly identify measurement error components although such error will unquestionably enter in various places. Although classical measurement error could be captured by the innovations in the MA process, more recent work on error in earnings reports suggests that measurement error is serially correlated (Bound et al., 1990; Bound and Krueger, 1991). Hence the parameters θt and ρt could pick up some measurement error as well. Unfortunately, the Bound-Krueger and Bound et al. studies only had two periods of validated earnings data, and hence AR and MA components of measurement error could not be identified.
At the third lag, for example, the covariance of differences is reduced by ρ raised to the sixth power, which in our case (ρ=.662) is .084. It falls further at higher lags. Although it is clear from Table 1 that our data require a first-order autoregressive parameter to explain the decline in autocovariances after the second lag, the magnitude may be too small for statistical significance when estimation is conducted in differences. Another possible explanation for this minor difference is that we have a panel of 19 periods, whereas MaCurdy and Abowd-Card only had panels of 10 and 11, respectively; our longer panel may give us more power in detecting small autoregressive influences at longer lags.
The chi-squared statistics for both specifications are far above the one-percent critical values of 600–624, implying considerable unexplained variation in the model. However, replacing the time trends with year dummies, whose results will be discussed momentarily, reduce the chi-squareds to 739.
The order of parameter change in Table 6 does not materially affect these conclusions because the permanent and transitory components are additive in the total variance and hence do not interact. For example, introducing the change in the variance of ξ first increases the four variances from their 1969 values to .277, .305, .317, and .328 for the four respective ages shown in the Table.
The change induced by the trend coefficient for the variance of the random walk is negligible in magnitude and hence is not broken out separately; the changes in the last row are entirely due to the change in ρ.
An alternative computation is to compute the “steady-state” variances implied by the values of the parameters in 1987, and to compare these to the 1969 steady-state variances shown in the first row of Table 6. The 1987 variances in Table 6 reflect the historical experience of the shocks from 1969 to 1987 and, because of the autoregressive structure of the model, do not represent the steady-state values. However, because the autoregressive lag in the variances is so short--of negligible importance after three years--the 1987 steady-state variances differ from those in the last row of Table 6 only at the second decimal place.
The increase in transitory variance could in principle be the result of increasing measurement error in the PSID, but there is no evidence that it did so or any reason to think it would have increased more in the 1980s. Nor is there any evidence that there has been a change in the accuracy of earnings data in the PSID. The fraction of earnings observations that are imputed, combining what the PSID calls “major” and “minor” imputations, is only 1.6 percent in our sample averaged over all years. This low percent probably reflects better reporting among prime-age white males than other population groups. More important, the fraction has not changed over the period, varying only between .6 percent and 2.1 percent, with a slight downward trend over time. As a consequence, estimates of the model shown in Table 6 change only at the third or fourth decimal place when imputed earnings observations are deleted. In addition, there has been no change in the coding procedures used to detect “erroneous” earnings. Those procedures are documented for coders, and the same documents have been used for the entire PSID.
Over the entire lifetime, for example, an increase in the permanent variance must both increase the variance of lifetime earnings and lower mobility between average earnings in the first part of the life cycle and in the second part, at least as long as transitory components die out within those parts.
The limited number of observations in the sample prevent us from disaggregating the quantiles further. Some prior analyses in the literature have been able to use a finer set of quantiles by pooling the data across years and across ages. However, not only have we found pooling across years to be incorrect, both our descriptive and error components analysis showed the necessity of conditioning on age.
This is to be expected since persons in the upper (lower) quintiles can only move down (up), whereas persons in the middle quintiles can move in either direction.
Given our age grouping, “35” stands for 30–39, “36” stands for 31–40, and “40” stands for 35–44.
These trends by themselves have no necessary implication for our prior results. Mean weeks of work have fallen in our sample whether these zero-weeks observations are included or not (although they have fallen more when the zeros are included than when they are not). More important, a change in mean weeks worked, negative or positive, has no necessary implication for changes in variances.
For the descriptive regressions, the off-diagonal and diagonal coefficients are 1.296 and 1.109, respectively, both significant at the 10 percent level. The magnitudes are considerably larger than those for conditional weeks worked because variances and covariances showed larger absolute increases over the period. Estimates of the error components model reduce the magnitude and significance level of the trend in the transitory component, and increase them for the permanent component.
A detailed comparison of the PSID and CPS in this dimension can be found in our prior benchmarking exercise (Gottschalk and Moffitt, 1992).
The sum of the permanent and transitory components of the within values are almost identical to the values given in Table 6. As noted previously, the steady-state predicted values from the model are essentially identical to the values predicted historically because the latter only include the influence of “history”--that is, the fact that variances have been growing over time and hence have not been at their steady-state value for the whole period--but history is unimportant after approximately three years.
To some extent the small magnitude of the change induced by including the between simply reflects the relatively small R-squareds in all log earnings regressions when only education and age are the explanators; hence trends in the covariance structure of total log earnings are dominated by trends in the covariance structure of the residuals. Note as well that the correlation coefficients in Table 11 imply even less reduction in mobility than was found for the within analysis. The trends in the correlation coefficients arise from the size of the proportionate increase in the permanent variance, not its absolute size, and the proportionate increase in that variance is smaller for the between than for the within.
The individuals in age group 50–59 cannot be followed at all. However, their earnings are used to construct diagonal elements of the covariance matrix (i.e., variances rather than covariances).
To compute the covariances between those who are, say, 20–29 in 1970 and (hence) 30–39 in 1980, we use only those who are present in both years.
Abowd and Card (1989) also used the identity matrix because of problems similar to those discussed by Altonji and Segal.
Each individual in our data set contributes to only a subset of the moments in Ω (see Appendix A); we do not adjust the notation in (B4) for this, but instead leave it implicit.
Contributor Information
Robert A. Moffitt, Johns Hopkins University
Peter Gottschalk, Boston College.
References
- Abowd J, Card D. On the Covariance Structure of Earnings and Hours Changes. Econometrica. 1989 Mar;57:411–445. [Google Scholar]
- Altonji J, Segal L. Mimeographed. Northwestern University; 1991. Small Sample Bias in GMM Estimation of Covariance Structures. [Google Scholar]
- Atkinson AB, Bourguignon F, Morrison C. Empirical Studies of Earnings Mobility. Harwood Publishers; 1992. [Google Scholar]
- Baker M. Working Paper 9209. Institute for Policy Analysis, University of Toronto; 1992. Growth Rate Heterogeneity and the Covariance Structure of Life Cycle Earnings. [Google Scholar]
- Becketti S, Gould W, Lillard L, Welch F. The Panel Study After Fourteen Years: An Evaluation. Journal of Labor Economics. 1988 Oct;6:472–492. [Google Scholar]
- Bound J, Brown C, Duncan G, Rodgers W. Measurement Error in Cross-Sectional and Longitudinal Labor Market Surveys: Validation Study Evidence. In: Hartog J, Ridder G, Theeuwes J, editors. In Panel Data and Labor Market Studies. New York and Amsterdam: North-Holland; 1990. [Google Scholar]
- Bound J, Krueger A. The Extent of Measurement Error in Longitudinal Earnings Data: Do Two Wrongs Make a Right? Journal of Labor Economics. 1991 Jan;9:1–24. [Google Scholar]
- Bound J, Johnson G. Changes in the Structure of Wages in the 1980s: An Evaluation of Alternative Explanations. American Economic Review. 1992 Jun;82:371–392. [PubMed] [Google Scholar]
- Burtless G. Earnings Inequality over the Business and Demographic Cycles. In: Burtless G, editor. A Future of Lousy Jobs. Washington: Brookings; 1990. [Google Scholar]
- Chamberlain G. Panel Data. In: Griliches Z, Intriligator M, editors. Handbook of Econometrics. Amsterdam: North-Holland; 1984. [Google Scholar]
- Fitzgerald J, Gottschalk P, Moffitt R. Mimeographed. Brown University; 1995. A Study of Sample Attrition in the Michigan Panel Study of Income Dynamics. [Google Scholar]
- Gottschalk P, Moffitt R. Part I of Final Report to the U.S. Department of Labor. Providence: Brown University; 1992. Earnings and Wage Distributions in the NLS, CPS, and PSID. [Google Scholar]
- Gottschalk P, Moffitt R. The Growth of Earnings Instability in the U.S. Labor Market. Brookings Papers on Economic Activity. 1994;2:217–272. [Google Scholar]
- Hause J. The Covariance Structure of Earnings and the On-the-Job Training Hypothesis. Annals of Economic and Social Measurement. 1977;6:335–365. [Google Scholar]
- Hause J. The Fine Structure of Earnings and the On-the-Job Training Hypothesis. Econometrica. 1980;48:1013–1029. [Google Scholar]
- Levy F, Murnane R. Earnings Levels and Earnings Inequalities: A Review of Recent Trends and Proposed Explanations. Journal of Economic Literature. 1992 Sep;30:1333–81. [Google Scholar]
- Lillard L, Weiss Y. Components of Variation in Panel Earnings Data: American Scientists, 1960–1970. Econometrica. 1979 Mar;47:437–454. [Google Scholar]
- Lillard L, Willis R. Dynamic Aspects of Earnings Mobility. Econometrica. 1978 Sep;46:985–1012. [Google Scholar]
- MaCurdy T. The Use of Time Series Processes to Model the Error Structure of Earnings in a Longitudinal Data Analysis. Journal of Econometrics. 1982 Jan;18:83–114. [Google Scholar]