VIDA: A Voxel-Based Dosimetry Method for Targeted Radionuclide Therapy Using Geant4

Abstract

We have developed the Voxel-Based Internal Dosimetry Application (VIDA) to provide patient-specific dosimetry in targeted radionuclide therapy performing Monte Carlo simulations of radiation transport with the Geant4 toolkit. The code generates voxel-level dose rate maps using anatomical and physiological data taken from individual patients. Voxel level dose rate curves are then fit and integrated to yield a spatial map of radiation absorbed dose. In this article, we present validation studies using established dosimetry results, including self-dose factors (DFs) from the OLINDA/EXM program for uniform activity in unit density spheres and organ self- and cross-organ DFs in the Radiation Dose Assessment Resource (RADAR) reference adult phantom. The comparison with reference data demonstrated agreement within 5% for self-DFs to spheres and reference phantom source organs for four common radionuclides used in targeted therapy (¹³¹I, ⁹⁰Y, ¹¹¹In, ¹⁷⁷Lu). Agreement within 9% was achieved for cross-organ DFs. We also present dose estimates to normal tissues and tumors from studies of two non-Hodgkin Lymphoma patients treated by ¹³¹I radioimmunotherapy, with comparison to results generated independently with another dosimetry code. A relative difference of 12% or less was found between methods for mean absorbed tumor doses accounting for tumor regression.

Introduction

Radiation therapy using radiopharmaceuticals should be performed with patient-individualized calculation of doses to tumors and normal tissues that might express toxicity or tumor control probability. Dosimetry using standardized reference models based on the Radiation Dose Assessment Resource (RADAR) schema has been established for many years and is implemented in the OLINDA/EXM software.¹ OLINDA/EXM provides some customization with the ability to adjust reported doses for patients' specific organ masses. However, the use of standardized phantoms has two major shortcomings when applied to patient dosimetry for targeted radionuclide therapy (TRT). The dosimetric quantity reported, mean absorbed dose to a target organ, assumes uniform activity in the source region(s). Evidence indicates that deterministic biological effects including tumor response and normal tissue toxicity are not well predicted by the mean absorbed dose and may be significantly influenced by nonuniform doses and temporally changing dose rates.² Also, although OLINDA/EXM allows calculation of self-dose to unit density spheres, which might be used to estimate tumor dose estimates, contributions to tumor dose from other organs and tissues cannot be included. Dose contributions to and from distant regions due to high energy photons may be non-negligible for radionuclides with significant γ emissions.³

Many of the limitations with using fixed-geometry methods for dose calculations in TRT can be overcome using image-based techniques. It is generally accepted that voxel-based dosimetry incorporating the spatial and temporal distribution of activity from sequential SPECT provides greater accuracy and permits assessment of tumor dose–response and normal tissue toxicity. Image-based approaches to patient-individualized dosimetry have been demonstrated by several groups, including 3D-ID,⁴ updated to include radiobiological dose assessment as 3D-RD,^5,6 SIMDOS,⁷ RMDP,⁸ and an adaptation of dose planning method (DPM).⁹ These codes employ various methods for photon and electron transport, including point kernel convolution and Monte Carlo (MC) simulation. They generally rely on manual segmentation of the patient anatomy and quantitative spatial distributions of activity to produce three-dimensional (3D) maps of radiation dose and dose-volume histograms (DVHs). This approach not only provides improved results compared with fixed geometry dosimetry with standardized phantoms, but also takes considerable time and effort to perform.

Here, we describe the development of voxel-based internal dosimetry application (VIDA), a 3D image-based dosimetry technique using the Geant4 MC tool kit for voxel-by-voxel absorbed dose calculation. Geant4's radioactive decay module provides a general method for assessing dose from any type of radionuclide through direct sampling of the decay scheme. VIDA was validated using two independent techniques. The first method applies a simple geometry of a spherical source in a semi-infinite scattering medium. The self-dose to spheres of various masses was determined assuming a uniformly distributed activity. The second approach compares dose factors (DFs) for selected target organs in a standard male reference phantom assuming uniform activity in the source organ. In addition, VIDA was used to estimate doses from SPECT studies of two patients with non-Hodgkin lymphoma (NHL), with comparison of our results to those calculated previously with another 3D dosimetry code.

Materials and Methods

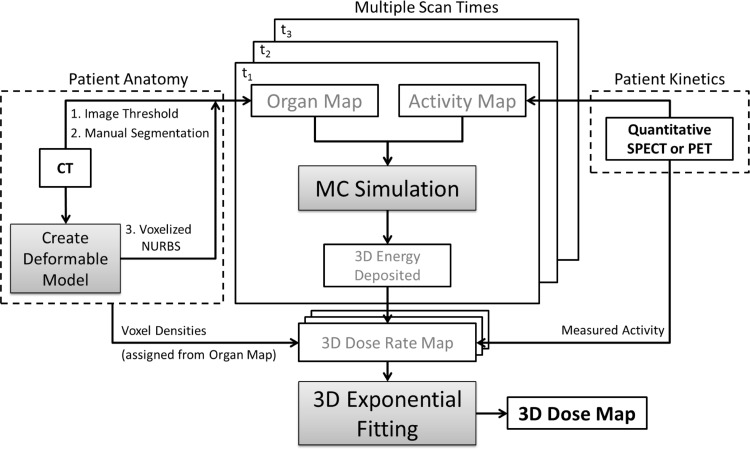
VIDA allows for patient-specific dosimetry methods by coupling 3D anatomical data (CT) with functional images (SPECT or PET). The application consists of two main components (Fig. 1), the Geant4 simulation code to generate 3D maps of voxel-level absorbed energy and a custom exponential fitting tool for radiopharmaceutical kinetics modeling developed in MATLAB. Detailed descriptions of these two elements of VIDA and the methods used to validate the application follow.

FIG. 1.

VIDA procedure flow with key components and inputs. 3D, three-dimensional; MC, Monte Carlo; VIDA, voxel-based internal dosimetry application.

MC simulation

Geant4^10,11 is an open source, integrated radiation transport package that simulates many particle types and their interactions based on a user-specified geometry. Particle interactions are tracked through materials in the simulation environment and energy deposition is scored in selected target regions. VIDA was created from an existing application that traced mono-energetic photons and electrons uniformly distributed in a standard anthropomorphic phantom.¹²

The material definitions implemented in VIDA include air, soft tissue, lung, and whole skeleton (Table 1) derived from data tabulated in ICRU Publication 46 Appendix A.¹³ The simulation geometry and voxel materials are defined by an organ identification map constructed from one of two methods. Organs of interest and tumor volumes can be outlined on the patient CT using conventional segmentation methods. For multiple time points, manual segmentation of each CT can be time-prohibited and tissue maps of relevant materials can be quickly created for simulation using density thresholds. Organ identification can also be defined by a patient-specific anatomical model produced from Non-Uniform Rational B-Spline (NURBS) standard phantoms.^14,15 The NURBS phantom is rendered over the CT images and custom transformation algorithms are applied to morph the body contour and organ surfaces to match patient anatomy. The deformed NURBS model is then converted to voxel format matching the resolution of the quantitative activity images. The method of quick adaption of an existing body model to an individual patient and its usefulness in patient-specific dosimetry will be reported a separate publication.

Table 1.

Material Definitions in Voxel-Based Internal Dosimetry Application Monte Carlo Simulation

		Chemical composition (% by mass)
Material	Density (g/cm3)	H	C	N	O	Elements Z>8
Air	0.00121	—	0.01	75.53	23.18	Ar (1.28)
Soft tissuea	1.03	10.5	25.6	2.7	60.2	Na (0.1), P (0.2), S (0.3), Cl (0.2), K (0.2)
Lungb	0.26	10.3	10.5	3.1	74.9	Na (0.2), P (0.2), S (0.3), Cl (0.3), K (0.2)
Whole skeletonc	1.35	6.5	28.6	3.6	41.7	Na (0.1), Mg (0.1), P (5.9), S (0.2), Cl (0.1), K (0.1), Ca (13.2), Fe (0.1)

^aAverage adult male.

^bAdult healthy, inflated.

^cComposite material defined using average density and elemental compositions of adult whole bones (excluding cranium and mandible).

Decay events are generated voxel-by-voxel based on an activity map from quantitative SPECT or PET imaging. Events created inside each voxel are assumed uniformly distributed and assigned a random position and direction vector. VIDA employs the radioactive decay module in Geant4 to produce primary particles using data including branching ratios, decay energies and transition probabilities, and energies for nuclear de-excitation. A detailed overview of the radioactive decay package is found in Sauf et al.¹⁶ The physics models implemented in VIDA are a modified version of the standard electromagnetic package with options to improve electron particle transport. The energy interval in VIDA was set from 10 eV to 50 MeV and divided into 220 bins to increase the sampling of interaction cross sections for particle energies in targeted therapy. Atomic de-excitation processes, including Auger emissions, were activated to handle atomic shell vacancies.

The energy deposited due to primary decay, secondary particles, and subsequent γ emission from isomeric transitions is tallied for each voxel. The voxel-level deposited energy is used to create 3D dose rate maps that are integrated over time to produce DVHs and average whole organ doses. VIDA is compiled using Geant4 9.4 and is run on the Vanderbilt University multi-node Advanced Computing Center for Research and Education (ACCRE) with the capability of being split into multiple parallel jobs for decreased run-time. For a geometry matrix of 256×256×80, simulation of one million decay events requires ∼3 hours of CPU time and 300 MB of memory on a 2.3-GHz Nehalem processor (Intel).

Exponential fitting

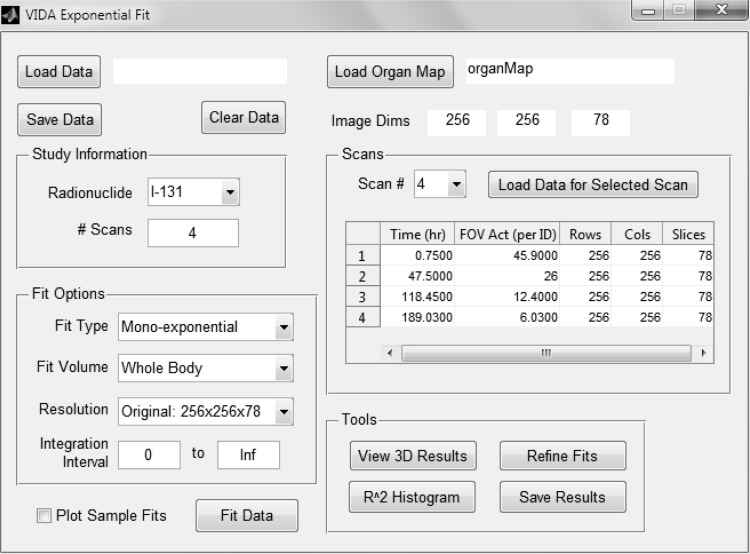
Patient kinetics modeling is performed by the exponential fitting module in VIDA. This module (Fig. 2) consists of a MATLAB-based graphical user interface for curve fitting by iterative least squares estimation using the nonlinear regression model in the Statistics Toolbox (Release 2012a). The user has a choice of fit functions depending on uptake kinetics and number of sequential scans. Instantaneous activity uptake, resulting in exponentially decaying dose rates, can be fit to a mono-exponential or bi-exponential function of the general form:

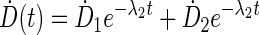FIG. 2.

Screen capture of MATLAB-based exponential fitting tool in VIDA.

Initial guesses for the rate components (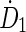 and 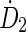) are derived from the time-sequence data and elimination constants (λ₁ and λ₂) from the physical half-life of the radionuclide of interest. The fitting algorithm automatically detects voxels with noninstantaneous uptake (i.e., tumor) and fits these data to a bi-exponential including the (0, 0) point of the form:

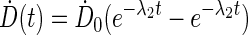The voxel dose is computed by integration of the fitted function based on a time interval supplied by the user, with a default range of zero to infinity.

The exponential fitting tool in VIDA provides the user with several other options. The user may choose to fit the entire body in the image field of view or select specific organs and tumors based on the organ map. Also, the user may specify the resolution of the resulting dose map. A scaled map with voxel dimensions twice as large in the transverse plane is created by fitting a voxel dose curve to the data in the corresponding 2×2×1 cell in the original array. This option decreases the overall processing time and may facilitate regression convergence when data are only available for a limited number time points.

Evaluation tools are provided by the exponential fitting module to assess the results. The user can plot a histogram of the coefficients of determination (R²) for all fitted voxels. Fits with R² values below a user-defined threshold may be refined by rerunning the regression using an array of different initial coefficient values to optimize R². The user can also evaluate the dose results in a three plane viewer and plot the data and fitted curve for a selected voxel.

Dose to uniform activity spheres

VIDA was used to determine DFs in unit-density spheres ranging in size from 10 to 1000 g. For consistency with patient modeling, each sphere was “voxelized” into an array large enough to include the surrounding scattering medium. Spatial resolution was chosen to limit the error in sphere mass from digitally approximating the surface to less than 0.5%. The spheres were defined as tissue-equivalent material surrounded by a scattering medium of water. Tissue composition was taken from MIRD Pamphlets 3 and 8^17,18 to facilitate comparison to previously published results.

Uniform activity was simulated for common radionuclides used in targeted internal therapy including ⁹⁰Y, ¹³¹I, ¹¹¹In, and ¹⁷⁷Lu. For each simulation, 1 million events were tracked resulting in absorbed energies within the sphere with relative errors of less than 0.5%. Relative error is defined as the 1σ standard deviation of the tally (energy deposited) divided by the average tally.¹⁹ Self-DFs were calculated and compared to the unit density sphere model in OLINDA/EXM.¹

Organ S values in adult male phantom

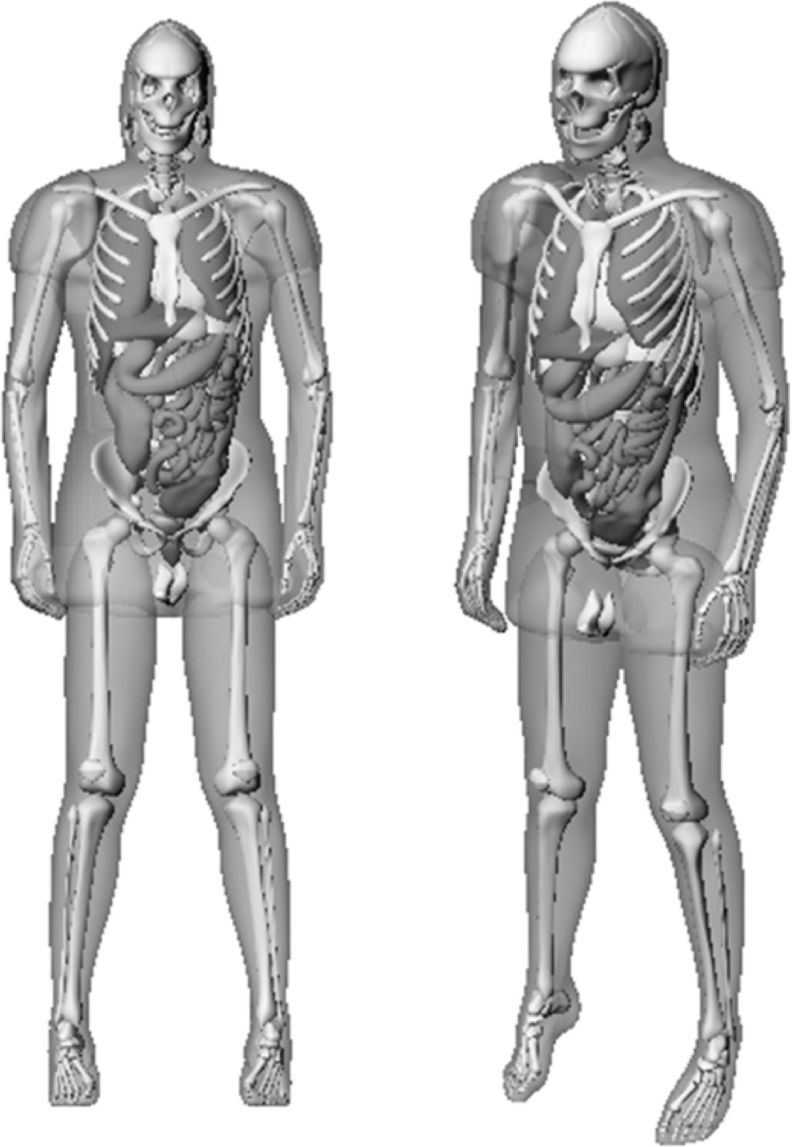
DFs for selected organs were determined using the RADAR reference adult male phantom¹² (Fig. 3). The phantom anatomy is a modified version of the NURBS-based cardiac-torso (NCAT) phantom^14,15 with ICRP publication 89²⁰ adult male reference organ masses. An organ map was created by rendering the phantom in voxel format with resolution of 1.5×1.5×5.0 mm. Any voxels outside of the boundary of the phantom were defined as air. Instead of using the default materials defined in Table 1, simulation materials were changed to the densities and compositions of soft tissue, lungs, and bone²¹ used to generate new specific absorbed fractions (SAFs)¹² to aid comparison between our results and the reference data.

FIG. 3.

Anterior views of the RADAR adult male NURBS phantom. NURBS, Non-Uniform Rational B-Spline; RADAR, Radiation Dose Assessment Resource.

Simulations were performed for the same radionuclides as the uniform spheres (⁹⁰Y, ¹³¹I, ¹¹¹In, and ¹⁷⁷Lu) with three different organs designated as the source of radioactivity (liver, spleen, and pancreas). These organs were chosen as representative sources centrally located in the body with varying shape. Each run generated 5 million decay events uniformly throughout the source organ, resulting in relative errors of less than 2% in the total energy deposited in each target volume. DFs were determined using the average dose deposited in each target organ and compared to reference data. Target volumes included the three source organs and also the lungs and kidneys to evaluate self-dose and cross-organ doses to distant structures that may be of interest in TRT dosimetry.

Radioimmunotherapy patient dosimetry

Individualized dosimetry was performed for two follicular NHL patients treated with ¹³¹I-labeled tositumomab (Bexxar^®) using multiple SPECT/CT scans. These patients provided written informed consent for the additional SPECT/CT scans not included in the normal treatment protocol. The clinical treatment protocol has been previously described in the literature²² and is briefly outlined here. Each patient was imaged at three time points after administration of a diagnostic tracer of 185 MBq. Therapeutic doses of 3.74 GBq (patient 1) and 3.43 GBq (patient 2) were administered to deliver a nominal whole-body absorbed dose of 75 cGy based on post-tracer imaging. Patients were imaged at three time points post-therapy, with a delay for the first scan of ∼48 hours due to dead time and exposure considerations (patient 1, 47.5 hours; patient 2, 48.58 hours). Additional details of image acquisition, reconstruction, and activity quantification are included elsewhere.^22–24

Voxel-based dosimetry

VIDA was used to obtain a dose rate map at each time point. A map defining different materials for simulation (Table 1) was automatically generated from the CT images in a preprocessing step using MATLAB. Density maps were created using calibration of HUs to material density as a bi-linear fit based on data from Schneider et al.²⁵ Air was defined for voxel densities less than 0.15 g/cm³, lung by a range of 0.15 to 0.61 g/cm³, soft tissue between 0.61 and 1.17 g/cm³, and whole bone greater than 1.17 g/cm³. Activity maps were sampled using 20 million events, resulting in relative errors in the deposited energy of less than 1% in whole organs and a maximum of 10% for individual voxels in the tumor and organs of interest. No partial volume correction (PVC) was performed, as tumor volumes exceeded 100 mL. The voxel-tallied energy deposited was converted to absorbed dose using voxel masses derived from the simulation tissue densities. Instantaneous dose rate maps per administered activity were generated by scaling the dose deposited in each voxel by the ratio of actual field-of-view activity to simulated activity.

Target definition and image registration

Tumors and normal tissue organs were segmented on the high resolution first post-tracer CT image (512×512×196 matrix, 0.977×0.977×2.0 mm voxel size) using a combination of manual and semi-automatic segmentation techniques included in the ITK/SNAP toolkit.²⁶ Normal organ volumes were verified and tumors were identified by a subspecialty radiologist with experience in both body CT and nuclear medicine.

CT-based registration of serial dose rate images was performed with an affine rigid registration algorithm based on maximizing mutual information²⁷ developed by the Vanderbilt University Institute of Imaging Science. The CT images were down-sampled to a resolution of 256×256×78 (1.954×1.954×5.0 mm) to match the slice thickness of the SPECT data and to expedite registration. The CT image set of the first post-tracer scan was assigned to be the reference image in the registration algorithm. All other time points were registered to the reference image by first performing CT–CT registration and applying the transformation matrices to the corresponding dose rate maps.

Conversion to 3D absorbed dose

Each 3D deposited energy map from the MC simulation was converted to an instantaneous dose rate map using voxel masses calculated from the materials in Table 1. Voxel-level dose rate curves were fit to a mono-exponential decay function for both the pretherapy tracer data and the post-therapy scans using the exponential fitting tool in VIDA. An absorbed dose map with voxel dimensions of 3.908×3.908×5.0 mm³ (128×128×78 array) was generated using the option to fit voxel curves to the corresponding 2×2×1 cell array of the higher resolution dose rate maps. This resolution was chosen to improve processing time without affecting accuracy due to the already limited resolution of the SPECT camera (full width at half maximum ≤3.9 mm).

Tumor dosimetry

Malignant lymphomas can be highly sensitive to radiation, leading to measurable changes in volume within the first few days of treatment.²⁸ The effect of tumor regression on absorbed tumor dose was investigated by defining tumor volumes of interest (VOIs) on the CT at each time point. The average absorbed tumor dose was calculated by fitting the volume-adjusted dose rate curve. A comparison was made to mean absorbed tumor doses from the DPM MC software^9,22,29 using the same tumor VOIs to minimize error due to differences in segmentation between institutions.

Results

Dose to uniform activity spheres

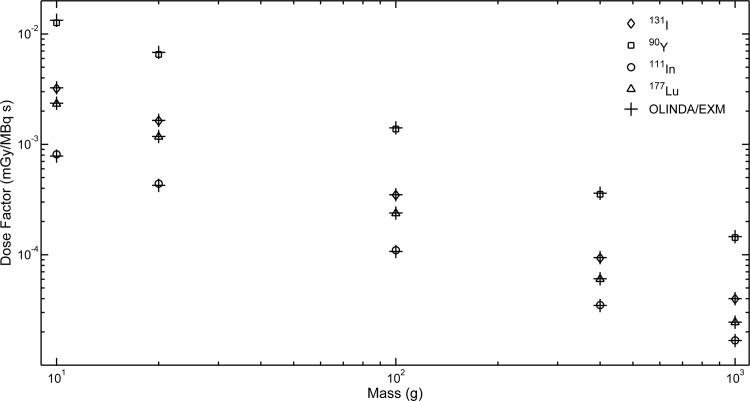
DFs for self-dose to uniform activity spheres are shown in Figure 4. The differences between VIDA and OLINDA/EXM (Table 2) ranged from 0.4% to 5%, with the largest deviations occurring in the smallest sphere. DFs for ⁹⁰Y show the largest difference between the two models with a range of 2%–5%.

FIG. 4.

Dose factors comparison between VIDA and OLINDA/EXM for unit density soft tissue spheres of different masses.

Table 2.

Relative Percent Differences in Voxel-Based Internal Dosimetry Application and OLINDA/EXM Sphere Dose Factors

Mass (g)	Diameter (cm)	131I	90Y	111In	177Lu
10	2.7	−1.4	−5.0	3.8	−1.3
20	3.4	−0.9	−4.1	3.8	−0.9
100	5.8	−0.9	−2.5	2.8	−0.7
400	9.1	−0.9	−2.3	0.9	−0.7
1000	12.4	−0.5	−2.1	0.4	−0.4

Relative % difference defined as 100×(DF_VIDA−DF_OLINDA)/DF_OLINDA. DF, dose factor.

Organ DFs in the adult male phantom

Results for the reference phantom study are presented in Table 3. Cross-organ DFs are omitted for ⁹⁰Y because β-emission energy is mostly absorbed locally. Any dose deposited in target regions far from the source organ is mainly due to bremsstrahlung radiation and results in low scoring statistics. Deviations in the DFs for organ self-dose ranged between 0.6% and 5%. The difference in cross-organ DFs spanned from 0% to 9% with lower VIDA results compared with OLINDA/EXM for almost all source-target organ pairs.

Table 3.

Dose Factors for Source and Target Organs in the Radiation Dose Assessment Resource Adult Male Phantom

Organ		DF (mGy/MBq-s)
		VIDA	OLINDA	% Diffa	VIDA	OLINDA	% Diffa
Source	Target		131I			90Y
Liver	Lungs	8.05E–07	8.09E–07	−0.5	—	—	—
	Liver	2.27E–05	2.28E–05	−0.4	7.89E–05	8.05E–05	−2.0
	Kidneys	1.11E–06	1.14E–06	−2.7	—	—	—
	Spleen	3.05E–07	3.29E–07	−7.6	—	—	—
	Pancreas	1.09E–06	1.11E–06	−1.8	—	—	—
Spleen	Lungs	4.67E–07	4.70E–07	−0.6	—	—	—
	Liver	3.07E–07	3.16E–07	−2.9	—	—	—
	Kidneys	2.40E–06	2.36E–06	1.7	—	—	—
	Spleen	2.35E–04	2.32E–04	1.3	9.16E–04	9.26E–04	−1.1
	Pancreas	1.35E–06	1.36E–06	−0.7	—	—	—
Pancreas	Lungs	5.36E–07	5.62E–07	−4.7	—	—	—
	Liver	1.08E–06	1.13E–06	−4.5	—	—	—
	Kidneys	8.31E–07	8.84E–07	−6.2	—	—	—
	Spleen	1.35E–06	1.43E–06	−5.8	—	—	—
	Pancreas	2.44E–04	2.49E–04	−2.0	9.49E–04	9.94E–04	−4.6

			111In			177Lu
Liver	Lungs	8.80E–07	8.92E–07	−1.4	9.57E–08	8.93E–08	6.9
	Liver	1.01E–05	9.91E–06	1.9	1.35E–05	1.36E–05	−0.7
	Kidneys	1.23E–06	1.27E–06	−3.2	1.16E–07	1.18E–07	−1.7
	Spleen	3.16E–07	3.47E–07	−9.4	2.84E–08	3.12E–08	−9.4
	Pancreas	1.20E–06	1.24E–06	−3.3	1.12E–07	1.14E–07	−1.8
Spleen	Lungs	5.04E–07	5.05E–07	−0.2	4.68E–08	4.64E–08	0.9
	Liver	3.17E–07	3.34E–07	−5.1	2.82E–08	3.03E–08	−7.2
	Kidneys	2.65E–06	2.65E–06	0.0	2.69E–07	2.58E–07	4.2
	Spleen	7.58E–05	7.19E–05	5.3	1.60E–04	1.59E–04	0.6
	Pancreas	1.48E–06	1.50E–06	−1.3	1.41E–07	1.41E–07	0.0
Pancreas	Lungs	5.80E–07	6.11E–07	−5.2	5.41E–08	5.67E–08	−4.7
	Liver	1.20E–06	1.27E–06	−5.7	1.10E–07	1.16E–07	−5.3
	Kidneys	9.13E–07	9.81E–07	−7.2	8.55E–08	9.16E–08	−6.9
	Spleen	1.48E–06	1.58E–06	−6.5	1.41E–07	1.49E–07	−5.5
	Pancreas	7.95E–05	7.81E–05	1.8	1.66E–04	1.70E–04	−2.4

^aRelative difference defined as 100×(DF_VIDA−DF_OLINDA)/DF_OLINDA.

Radioimmunotherapy patient dosimetry

SPECT/CT images with tumor outlines and resulting dose maps for each patient are shown in Figure 5. Tumor DVHs (Fig. 6) were generated using volumes from the first post-tracer scan. The first post-tracer time point, scaled by the ratio of activity administered for the therapy and tracer studies, was included in the therapy data set due to the lack of an early imaging time point. Mean absorbed doses to tumor and organs were calculated and compared to results from DFs derived from the RADAR adult male reference phantom¹² and the unity density sphere model (Table 4). Organ doses are reported only if the entire volume was included in the field of view. Reference doses were adjusted for differences in organ masses between the patient and phantom.

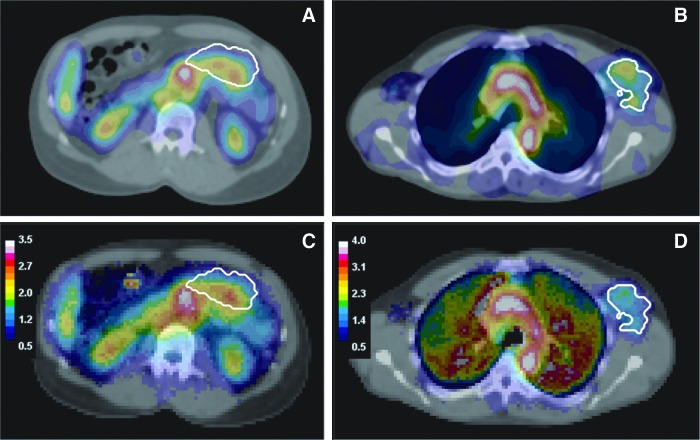
FIG. 5.

Fused SPECT/CT images for patient 1 (A) and patient 2 (B) with matching 3D dose maps overlaid on CT for patient 1 (C) and patient 2 (D). The dose maps are displayed in units of Gy. Color images available online at www.liebertpub.com/cbr

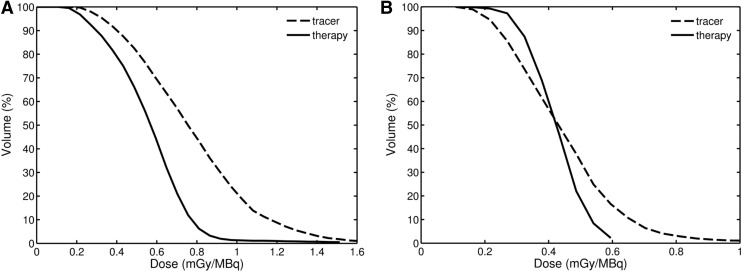
FIG. 6.

Tumor dose-volume histograms from tracer and therapy scans for patient 1 (A) and patient 2 (B). The tumor volumes were taken from the first post-tracer scan.

Table 4.

Voxel-Based Internal Dosimetry Application and Radiation Dose Assessment Resource Reference Mean Absorbed Doses to Organs and Tumors and Percent Differences (in Parentheses) from Post-Therapy Dosimetry

	Patient 1		Patient 2
Organ	VIDA dose (cGy)	RADAR dose (cGy)	VIDA dose (cGy)	RADAR dose (cGy)
Lungs	—	—	221	254 (−13%)
Heart	411	438 (−6%)	311	380 (−18%)
Spleen	186	191 (−3%)	183	160 (14%)
Liver	223	210 (6%)	—	—
Kidneys	190	160 (19%)	—	—
Tumor	196	187 (5%)	150	135 (11%)

Relative difference defined as 100×(D_VIDA−D_RADAR)/D_RADAR.

RADAR, Radiation Dose Assessment Resource.

Between the initial tracer study and the last imaging point post-therapy, significant decreases in both tumor volumes occurred (Table 5). When accounting for shrinkage, the tumor dose differed as much as 16% compared with the mean absorbed dose to a static volume. The comparison of mean tumor doses accounting for changing volume between VIDA and DPM agree within 12% or less.

Table 5.

Comparison of Mean Absorbed Tumor Doses Between Voxel-Based Internal Dosimetry Application and Dose Planning Method

	Patient 1: abdominal tumor	Patient 2: Lt. axillary tumor
Initial tumor volume (mL)	269	226
Total tumor shrinkage	53%	23%

	VIDA	DPM	VIDA	DPM
Predicted dose, static vol. (cGy)	291	—	153	—
Predicted dose, changing vol. (cGy)	292	261 (12%)	154	164 (−6.1%)
Delivered dose, static vol. (cGy)	196	—	150	—
Delivered dose, changing vol. (cGy)	252	266 (−5.3%)	151	162 (−6.8%)

Relative difference defined as 100×(D_VIDA−D_DPM)/D_DPM.

DPM, dose planning method.

Discussion

There has been significant focus on developing methods of image-based 3D dose calculations with the goal of providing patient-specific dosimetry for internal therapy. We have created VIDA, an application designed for individualized dosimetry using the Geant4 toolkit. In the simulation, patient geometry is represented by a 3D map of integer organ identification numbers instead of assigning voxel density and composition directly from CT images as done in the Geant4 DICOM application. The reasoning for this approach is to permit modeling patient anatomy using a NURBS-based deformable phantom that can be digitized to a 3D organ map. For multiple time points, tissue maps using density thresholds can be quickly created for simulation purposes in a preprocessing step such as those used in the RIT patient studies. We believe our approach of implementing uniform density organs based on a map of identification numbers offers adequate flexibility for tissue definition and introduces negligible uncertainty in particle transport compared to other sources of errors in the dose estimates.

VIDA was designed to generate dose rate maps at each time point for voxel-based integration of the total absorbed dose. Although this technique requires additional simulations, the rational for this approach is twofold. The determination of instantaneous dose rates permits inclusion of tumor regression over scan times in the absorbed dose estimates. Also, incorporation of radiobiological models requires 3D absorbed dose rate images at each time point rather than the simulation of absorbed dose from a single map of cumulated activity. A similar approach of generating multiple dose rate maps has been implemented in other dosimetry studies.^{22,24,29–31} However, if desired, the user can use the exponential fitting tool in VIDA to create a map of cumulated activity for input in the MC simulation to determine the integrated dose in each voxel with only one run.

Due to the inherent flexibility of MC simulation tools such as Geant4, verification of the results is of the utmost importance. Efforts relating to the validation of Geant4 have been extensively published and include topics relevant to our application such as radioactive decay simulation³² and electromagnetic processes of low energy electrons.³³ Here, VIDA was validated under several conditions including dose to uniform activity spheres and organ DFs from various sources in an anthropomorphic phantom and was achieved excellent concordance between our results and reference data.^1,34

The agreement in DFs for the spheres was within 5% and improved with increasing mass, due to the decreased likelihood of an electron escaping the source volume before complete energy absorption. For all sphere sizes, the largest differences occurred for ⁹⁰Y, a pure β emitter. The discrepancy is most likely due to different methods used to sample the β energy spectrum. OLINDA/EXM applies a single SAF for the average energy of the β emission spectrum, whereas β particles created in a decay event in Geant4 are assigned energies by sampling the β-Fermi-function.¹⁶ β emissions with energy higher than the spectrum mean have a longer range in tissue and higher interaction likelihood; however, there is also an increased possibility of these electrons exiting the sphere without being scored, which results in less total energy absorbed reflected by the lower DFs from VIDA.

For radionuclides that undergo β decay (¹³¹I, ⁹⁰Y, and ¹⁷⁷Lu), DFs calculated from VIDA for spheres and the majority of source/target pairs in the reference phantom are slightly lower compared with OLINDA/EXM. However, all self-DFs from VIDA are higher for ¹¹¹In. ¹¹¹In decays by electron capture and dose is locally deposited by low energy Auger electrons and small yield internal conversion electrons. The difference in ¹¹¹In self-DFs may be due to error in the interpolation of SAFs for the very low energy Auger electrons by OLINDA/EXM and improved low energy electron transport models in Geant4 compared to MNCP4B; nonetheless, the differences are small.

Several other groups have performed simulations for internal radiotherapy using Geant4. Amato et al. reported absorbed fractions for monoenergetic photons and electrons in ellipsoids.^35,36 Using these data, they specified the average energy deposited per disintegration of ¹³¹I as a function of the generalized radius. The energy deposited per disintegration of ¹³¹I by VIDA for the two smallest spheres (10 and 20 g) was 201 and 205 keV respectively. These energies are in excellent agreement with Amato et al. for ellipsoidal sources with generalized radii of 1.34 cm (201 keV) and 1.68 cm (206 keV).³⁶ A 3D dosimetry application RAYDOSE³⁷ uses the General Particle Source to create spatial distributions of decay events slice by slice based on patient PET images. RAYDOSE was validated using DFs for water spheres based on imaging a phantom containing activity-filled spheres of various sizes. For ¹³¹I and ¹⁷⁷Lu, RAYDOSE DFs were within 1%–3% of OLINDA/EXM and agree with the evaluation of VIDA and OLINDA/EXM for spheres of comparable sizes. Although RAYDOSE and VIDA are similar applications, we were unable to compare organ DFs and patient-specific doses because RAYDOSE has only been validated based on activity distributions in physical phantoms and has not yet been applied to clinical patient studies. Another Geant4 dosimetry application GRNT³⁸ uses the command line interface to define phantom geometry, simulation materials, and the particle emission spectrum. GRNT was validated by comparing organ DFs from the MIRD-5 phantom to RADAR reference data. The relative differences found using GRNT for liver as the source organ were ∼5% for self-DFs and 1%–10% for cross-organ DFs to the kidneys, lungs, pancreas, spleen for ¹³¹I and ⁹⁰Y, which are similar to those from VIDA.

To assess VIDA's treatment of nonuniform activity distributions and clinical utility, SPECT-based tumor and organ dosimetry was performed for patients receiving ¹³¹I radioimmunotherapy. Patient mean absorbed organ doses were compared to doses from a reference phantom with relative differences less than 20% (Table 4). The differences could be caused by several different factors. The reference dose calculations were performed based on activity in user-specified source organs. Activity in the rest of the field of view was assigned to the body remainder. The dose to target organs from the body remainder activity is calculated based on a uniform distribution of this activity spread across the entire volume in the phantom (including arms and legs). Thus, we would expect the reference organ doses to be lower compared to VIDA where dose is deposited from activity in the field of view closer to the target organs. Also, there are slight differences in the material densities and compositions in VIDA compared to those used to generate the SAFs for the RADAR reference phantom. The lung density is lower in VIDA by more than 10%, which may account for the underestimation of lung dose for patient 2. Tumor doses were also compared to self-irradiation doses using the uniform sphere model in OLINDA/EXM. As expected, the tumor doses from VIDA are larger by 5%–11% due to the contribution from the remaining body.

Tumor DVHs were generated based on the predicted and delivered dose maps (Fig. 6). Tumor volumes were defined based on segmentation of CT from the first post tracer scan. It is difficult to assess the impact of tumor regression on 3D dose heterogeneities, and mass changes across the imaging time period were not incorporated in the DVHs. Both patients exhibit more conformal dose distributions for the delivered tumor dose compared with the tracer-predicted distribution. The maximum delivered dose is also lower compared with the predicted DVH. One possible explanation for these differences is an increased antibody clearance in tumor cells after treatment due to radiobiological damage caused by the tracer dose, as previously suggested by Eary et al.³⁹

When we account for changes in tumor volumes, the tracer-predicted tumor doses concur with the delivered therapeutic dose within 16%. For both patients, the tracer scans over-predict the delivered dose, although the difference for patient 2 is very small. This trend is consistent with a previously reported study.²² The therapy-delivered mean absorbed doses were compared to results from DPM MC using the same tumor volumes. With the exception of the tracer study for patient 1, the tumor doses from VIDA are lower by 5%–7% compared to DPM. Our dose rates for the changing tumor volumes were derived from mean values from the 3D energy deposited maps for the tumor VOI defined at each time point. These volume-averaged dose rates were fit to a bi-exponential curve and directly integrated to determine the mean tumor dose. In comparison, the calculation of the mean tumor-absorbed dose using DPM involves a piecewise integration of the absorbed dose rates over three time periods using a mixed model fit.⁴⁰ These varying approaches may account for the discrepancies in tumor dose, even though the differences in tumor absorbed-dose rates between the two simulations were less than 2%.

Many contributing factors make estimating the uncertainty in organ and tumor doses for patient studies difficult. When performing voxel-based patient dosimetry using MC, there are many sources of error including the quantification of the activity distribution, the fidelity of the registration process between the serial SPECT/CT scans, and the ability to properly define organ and tumor volumes. Also, fitting voxel dose rates with a limited number of time points may introduce additional uncertainty. Acquisition of more than three sequential SPECT scans post-tracer or post-therapy administration would aid the fitting process but may be prohibitive in the clinical environment.

The 3D OSEM reconstruction methods used for the patient studies in this work have produced quantitative results within 10% for volumes 16 mL and larger without PVC.²³ Furthermore, the organ and tumor volumes in the patient studies presented here are sufficiently large, preventing partial volume effects from being a significant source of error in estimates of the average absorbed dose. MIRD Pamphlet 23 recommends PVC for objects less than dimensions of 3×FWHM of the spatial resolution of reconstructed images, but currently a well-validated method for voxel-based corrections for SPECT has yet to be developed.⁴¹ Therefore, voxel-level PVC was not applied before using the activity distributions in VIDA. To mitigate the uncertainty in reported doses due to partial volume effects, we limited the voxel resolution of the 3D dose map to 3.908×3.908×5 mm³, a factor of four larger than the original reconstructed image resolution and on the order of the intrinsic FWHM of the SPECT system used to acquire the data.

Image registration accuracy for 3D internal dosimetry has been discussed previously.^42–44 Availability of high resolution co-registered SPECT/CT images in our patient studies permitted CT-based registration. Thus, possible errors in SPECT-SPECT registration from poor spatial resolution and temporal variability in the activity distributions were avoided. A mutual information rigid registration algorithm was used in this study. Nonrigid techniques have been shown to provide the most robust results; however, only small differences in doses for volumes of interest were found between rigid and nonrigid registration.⁴⁴ Nonetheless, rigid registration may affect the accuracy of the 3D dose to the axillary tumor in patient 2, as nonrigid movements are more likely to occur in the neck and shoulder region of the body. An effort to quantify the effects of mis-registration on 3D patient dose was beyond the scope of this study.

Organ segmentation may also contribute to the uncertainty in reported doses. Errors in structure are typically small compared with those from image registration; however, erosion or dilation of the volume by only one voxel can contribute as much of 7% difference in activity.⁴² Because volume of interest definition is typically a subjective task reliant on human observation, it is difficult to predict the true magnitude of the error. The tumor volumes were identical in VIDA and DPM to avoid segmentation uncertainties in our relative dose comparisons, but no assessment was done to determine the error in the defined volumes outlined by the radiologist compared to the true physical volumes.

Recent emphasis has been placed on not only calculating 3D absorbed doses (Gy) in TRT, but also the biological response of different tissues considering the dose rates being delivered, and tissue-specific radiosensitivity parameters.^5,24,30 This research describes our initial work to develop and validate a functioning dosimetry program for our use; in future development of the code we hope to include consideration of radiobiological parameters.

Conclusion

We have developed VIDA, an application for patient-specific dosimetry in targeted therapy using the Geant4 MC toolkit to model radiation absorption in tissue from internal emitters. The simulation generates voxel-level dose rate maps based on anatomical and quantitative functional imaging. It has been benchmarked with results using the RADAR formalism including self-DFs for uniform activity spheres and organ self-dose and cross-organ doses in a standard phantom. VIDA has been applied to patient studies for ¹³¹I radioimmunotherapy for NHL, with tumor doses that are in excellent agreement with results from the DPM MC algorithm. The future aim of this work is to employ VIDA in conjunction with patient-specific organ maps created from a deformable NURBS anatomical model.

Acknowledgments

The authors thank Jennifer Whisenant for assistance with image registration. This work was supported in part by grant R01 EB001994 awarded by the National Institutes of Health, United States Department of Health and Human Services. This work was also supported in part by grants P50 CA098131 and P30 CA068485 awarded by the National Institutes of Health, United States Department of Health and Human Services, and the AUR_CE Radiology Research Academic Fellowship.

Disclosure Statement

No conflicting financial interests exist.