Abstract
Objective
Physicians classify patients into those with or without a specific disease. Furthermore, there is often interest in classifying patients according to disease etiology or subtype. Classification trees are frequently used to classify patients according to the presence or absence of a disease. However, classification trees can suffer from limited accuracy. In the data-mining and machine learning literature, alternate classification schemes have been developed. These include bootstrap aggregation (bagging), boosting, random forests, and support vector machines.
Study design and Setting
We compared the performance of these classification methods with those of conventional classification trees to classify patients with heart failure according to the following sub-types: heart failure with preserved ejection fraction (HFPEF) vs. heart failure with reduced ejection fraction (HFREF). We also compared the ability of these methods to predict the probability of the presence of HFPEF with that of conventional logistic regression.
Results
We found that modern, flexible tree-based methods from the data mining literature offer substantial improvement in prediction and classification of heart failure sub-type compared to conventional classification and regression trees. However, conventional logistic regression had superior performance for predicting the probability of the presence of HFPEF compared to the methods proposed in the data mining literature.
Conclusion
The use of tree-based methods offers superior performance over conventional classification and regression trees for predicting and classifying heart failure subtypes in a population-based sample of patients from Ontario. However, these methods do not offer substantial improvements over logistic regression for predicting the presence of HFPEF.
Keywords: Boosting, classification trees, Bagging, random forests, classification, regression trees, support vector machines, regression methods, statistical methods, prediction, heart failure
1. Introduction
There is an increasing interest in using classification methods in clinical research. Classification methods allow one to assign subjects to one of a mutually exclusive set of states. Accurate classification of disease states (disease present/absent) or of disease etiology or subtype allows subsequent investigations, treatments, and interventions to be delivered in an efficient and targeted manner. Similarly, accurate classification of disease states permits more accurate assessment of patient prognosis.
Classification trees employ binary recursive partitioning methods to partition the sample into distinct subsets [1-4]. While their use is popular in clinical research, concerns have been raised about the accuracy of tree-based methods of classification and regression [2,4]. In the data mining and machine learning literature, alternatives to and extensions of classical classification trees have been developed in recent years. Many of these methods involve aggregating classifications over an ensemble of classification trees. For this reason, many of these methods are referred to as ensemble methods. Ensemble-based methods include bagged classification trees, random forests, and boosted trees. Alternate classification methods include support vector machines.
In patients with acute heart failure (HF) there are two distinct subtypes: HF with preserved ejection fraction (HFPEF) vs. HF with reduced ejection fraction (HFREF). The distinction between HFPEF and HFREF is particularly relevant in the clinical setting. While the treatment of HFREF is based on a multitude of large randomized clinical trials, the evidence-base for the treatment of HFPEF is much smaller, and more focused on related comorbid conditions [5]. While the overall prognosis appears to be similar within the two subtypes of HF, there are important differences in cause-specific mortality, which would be relevant in risk stratification and disease management [6]. The diagnosis of HFREF vs. HFPEF is ideally made using results from echocardiography. While echocardiography should ideally be done in all HF patients at some point in their clinical care, this test is not always performed even in high resource regions, and treatment decisions may need to be made before echocardiographic data are available. In one US Medicare cohort, more than one-third of HF patients did not undergo echocardiography in hospital [7].
The current study had two objectives. First, to compare the accuracy of different methods for classifying HF patients according two disease sub-types: HFPEF vs. HFREF, and for predicting the probability of patients having HFPEF in a population-based sample of HF patients in Ontario, Canada. Second, to compare the accuracy of the prediction of the presence of HFPEF using methods from the data-mining literature with that of conventional logistic regression.
2. Methods for classification and prediction
In this section, we describe the different methods that will be used for classification and prediction. For classification, we restrict our attention to binary classification in which subjects are classified as belonging to one of two possible categories. Our case study will consist of patients with acute HF, which is further classified as HF with preserved ejection fraction (HFPEF) and HF with reduced (HFREF). By prediction we mean prediction of the probability of an event or of being in a particular state. In our case study, this will be the predicted probability of having HFPEF. We consider the following classification methods: classification trees, bagged classification trees, random forests, boosted classification trees, and support vector machines. For prediction, we consider the following methods: logistic regression, regression trees, bagged regression trees, random forests, and boosted regression trees.
2.1 Classification and regression trees
Classification and regression trees employ binary recursive partitioning methods to partition the sample into distinct subsets [3]. At the first step, all possible dichotomizations of all continuous variables (above vs. below a given threshold) and of all categorical variables are considered. Using each possible dichotomization, all possible ways of partitioning the sample into two distinct subsets is considered. That binary partition that results in the greatest reduction in impurity is selected. This process is then repeated iteratively until a predefined stopping rule is satisfied. For classification, a subject's class can be determined using the status that was observed for the majority of subjects within that subset to which the given subject belongs (i.e. classification by majority vote). For prediction, the predicted probability of the event for a given subject can be estimated using the proportion of subjects who have the condition of interest amongst all the subjects in the subset to which the given subject belongs.
Advocates for classification and regression trees have suggested that these methods allow for the construction of easily interpretable decision rules that can be easily applied in clinical practice. Furthermore, it has been suggested that classification and regression tree methods are adept at identifying important interactions in the data [8-10] and in identifying clinical subgroups of subjects at very high or very low risk of adverse outcomes [11]. Advantages of tree-based methods are that they do not require the specification of the parametric nature of the relationship between the predictor variables and the outcome. Additionally, assumptions of linearity that are frequently made in conventional regression models are not required for tree-based methods.
We grew classification and regression trees using the tree function from the tree package for the R statistical programming language [12,13]. In our study we used the default criteria in the tree package for growing regression trees: at a given node, the partition was chosen that maximized the reduction in deviance; the smallest permitted node size was 10; and a node was not subsequently partitioned if the within-node deviance was less than 0.01 of that of the root node. Once the initial regression tree had been grown, the tree was pruned. The optimal number of leaves was determined by identifying the tree size that minimized the tree deviance when 10-fold cross-validation was used in the derivation sample.
2.2 Bagging classification or regression trees
Bootstrap aggregation or bagging is a generic approach that can be used with different classification and prediction methods [4]. Our focus is on bagging classification or regression trees. Repeated bootstrap samples are drawn from the study sample. A classification or regression tree is grown in each of these bootstrap samples. Using each of the grown regression trees, classifications or predictions are obtained for each study subject. Finally, for each study subject, a prediction is obtained by averaging the predictions obtained from the regression trees grown over the different bootstrap samples. For each study subject, a final classification is obtained by a majority vote across the classification trees grown in the different bootstrap samples. We used the bagging function from the ipred package for the R statistical programming language to fit bagged regression trees [14]. All parameter values were set to the default values in the bagging function. In our application of bagging, we used 100 bootstrap samples.
2.3 Random forests
The Random Forests approach was developed by Brieman [15]. The Random Forests approach is similar to bagging classification or regression trees, with one important modification. When one is growing a classification or regression tree in a particular bootstrap sample, at a given node, rather than considering all possible binary splits on all candidate variables, one only considers binary splits on a random sample of the candidate predictor variables. The size of the set of randomly selected predictor variables is defined prior to the process. When fitting random forests of regression trees, we let the size of the set of randomly selected predictor variables be ⌊p / 3 ⌋, where p denotes the total number of predictor variables and ⌊ ⌋ denotes the floor function. When fitting random forests of classification trees, we let the size of the set of randomly selected predictor variables be √p (these are the defaults in the R implementation of random forests). We grew random forests consisting of 500 regression or classification trees. Predictions or classifications are obtained by averaging predictions across the regression trees or by majority vote across the classification trees, respectively. We used the randomForest function from the RandomForest package for R to estimate random forests [16]. All parameter values were set to their defaults.
2.4 Boosting
One of the most promising extensions of classical classification methods is boosting. Boosting is a method for combining “the outputs from several ‘weak’ classifiers to produce a powerful ‘committee’” [4]. A ‘weak’ classifier has been described as one whose error rate is only slightly better than random guessing [4]. Breiman has suggested that boosting applied with classification trees as the weak classifiers is the “best off-the-shelf” classifier in the world [4].
When focusing on classification, we used the AdaBoost.M1 algorithm proposed by Freund and Schapire [17]. Boosting sequentially applies a weak classifier to series of reweighted versions of the data, thereby producing a sequence of weak classifiers. At each step of the sequence, subjects that were incorrectly classified by the previous classifier are weighted more heavily than subjects that were correctly classified. The classifications from this sequence of weak classifiers are then combined through a weighted majority vote to produce the final prediction. The reader is referred elsewhere for a more detailed discussion of the theoretical foundation of boosting and its relationship with established methods in statistics [18,19]. The AdaBoost.M1 algorithm for boosting can be applied with any classifier. However, it is most frequently used with classification trees as the base classifier [4]. Even using a ‘stump’ (‘stump’ is a classification tree with exactly one binary split and exactly two terminal nodes or leaves) as the weak classifier has been shown to produce substantial improvement in prediction error compared to a large classification tree [4]. Given the lack of consensus on optimal tree depth, we considered four versions of boosted classification trees: using classification trees of depth one, two, three, and four as the base classifiers. For each method we used sequences of 100 classification trees. We used the ada function from the ada package for R for boosting classification trees, which implements the AdaBoost.M1 algorithm [20].
Generalized boosting methods adapt the above algorithm for use with regression, rather than with classification [4,21]. We considered four different base regression models: regression trees of depth one, regression trees of depth two, regression trees of depth three, and regression trees of depth four. These have also been referred to as regression trees with interaction depths one through four. For each method, we considered sequences of 10,000 regression trees. We used the gbm function from the gbm package for boosting regression trees [22].
2.5 Support vector machines
Support vector machines (SVMs) are based on the fact that with an appropriate function to a sufficiently high dimension, data from two categories can always be separated by a hyperplane [23]. A SVM is the separating hyperplane that maximizes the distance from the nearest subjects with and without the outcome. Subjects are then classified according to which side of the hyperplane they lie on. Readers are referred elsewhere for a more extensive treatment of SVMs [4,23]. We used the svm function from the e1071 package for R [24].
2.6 Logistic regression
Finally, conventional logistic regression can be used to obtain predicted probabilities of being in a particular state or of the occurrence of a specific outcome. Unlike the methods described above, logistic regression results in only a predicted probability of an event, and not a binary classification. We used the lrm function from the Design package for the R statistical programming language to estimate the logistic regression models [25].
3. Methods
3.1 Data Sources
The Enhanced Feedback for Effective Cardiac Treatment (EFFECT) Study was an initiative to improve the quality of care for patients with cardiovascular disease in Ontario [26,27]. The EFFECT study consisted of two phases. During the first phase, detailed clinical data on patients hospitalized with HF between April 1, 1999 and March 31, 2001 at 103 acute care hospitals in Ontario, Canada were obtained by retrospective chart review. During the second phase, data were abstracted on patients hospitalized with HF between April 1, 2004 and March 31, 2005 at 96 Ontario hospitals. Data on patient demographics, vital signs and physical examination at presentation, medical history, and results of laboratory tests were collected for this sample.
In the EFFECT study, detailed clinical data were available on 9,943 and 8,339 patients hospitalized with a diagnosis of HF during the first and second phases of the study, respectively. After excluding subjects with missing data on key variables and for whom ejection fraction could not be determined, 3,697 and 4,515 subjects were available from the first and second phases, respectively, for inclusion in the current study. The first and second phases of the EFFECT study will be referred to as the EFFECT-1 and EFFECT-2 samples, respectively (these were referred to as the EFFECT Baseline sample and the EFFECT Follow-up sample, respectively, in the original EFFECT publication [27]).
For the purposes of our analyses, only participants with available left ventricular ejection fraction (LVEF) assessment by cardiac imaging were included. Participants were classified as having HFPEF (LVEF > 45%) or HFREF (LVEF ≤ 45%). This distinction is clinically relevant, as the treatment for HFPEF and HFREF are distinct: whereas the treatment of HFREF with beta-blockers, ACE inhibitors, and aldosterone blockers is well-substantiated, the treatment of HFPEF is much less defined, and focuses more on underlying co-morbid conditions [5].
As candidate variables for classifying HF subtype or for predicting the presence of HFPEF, we considered 34 variables denoting demographic characteristics, vital signs, presenting signs and symptoms, results of laboratory investigations, and previous medical history. These variables are listed in Table 1.
Table 1.
Comparison of patients with HFPEF and HFREF in EFFECT-1 and EFFECT-2 samples.
| EFFECT-1 sample | EFFECT-2 sample | |||||
|---|---|---|---|---|---|---|
| Variable | HFREF | HFPEF | P-value | HFREF | HFPEF | P-value |
| N=2,529 | N=1,168 | N=2,776 | N=1,739 | |||
| Age (years) | 75.0 (66.0-81.0) | 77.0 (70.0-83.0) | <.001 | 76.0 (67.0-82.0) | 79.0 (71.0-85.0) | <.001 |
| Male | 1,547 (61.2%) | 423 (36.2%) | <.001 | 1,686 (60.7%) | 643 (37.0%) | <.001 |
| Heart rate on admission (bpm) | 96.0 (78.0-113.0) | 90.0 (74.0-110.0) | <.001 | 94.0 (76.0-112.0) | 86.0 (70.0-105.0) | <.001 |
| Systolic blood pressure on admission (mm Hg) | 142.0 (122.0-164.0) | 156.0 (134.0-180.0) | <.001 | 140.0 (120.0-161.0) | 150.0 (131.0-173.0) | <.001 |
| Respiratory rate on admission | 24.0 (20.0-30.0) | 24.0 (20.0-28.0) | 0.853 | 24.0 (20.0-28.0) | 22.0 (20.0-28.0) | 0.156 |
| History of hypertension | 1,245 (49.2%) | 675 (57.8%) | <.001 | 1,784 (64.3%) | 1,264 (72.7%) | <.001 |
| Diabetes mellitus | 919 (36.3%) | 374 (32.0%) | 0.01 | 1,055 (38.0%) | 661 (38.0%) | 0.997 |
| Current smoker | 415 (16.4%) | 130 (11.1%) | <.001 | 382 (13.8%) | 157 (9.0%) | <.001 |
| History of coronary artery disease | 1,339 (52.9%) | 345 (29.5%) | <.001 | 1,519 (54.7%) | 579 (33.3%) | <.001 |
| Atrial fibrillation | 594 (23.5%) | 396 (33.9%) | <.001 | 752 (27.1%) | 619 (35.6%) | <.001 |
| Left bundle branch block | 530 (21.0%) | 55 (4.7%) | <.001 | 540 (19.5%) | 109 (6.3%) | <.001 |
| Any ST elevation | 371 (14.7%) | 70 (6.0%) | <.001 | 169 (6.1%) | 35 (2.0%) | <.001 |
| Any T wave inversion | 905 (35.8%) | 319 (27.3%) | <.001 | 864 (31.1%) | 414 (23.8%) | <.001 |
| Neck vein distension | 1,575 (62.3%) | 671 (57.4%) | 0.005 | 1,826 (65.8%) | 1,115 (64.1%) | 0.254 |
| s3 | 351 (13.9%) | 92 (7.9%) | <.001 | 245 (8.8%) | 72 (4.1%) | <.001 |
| s4 | 122 (4.8%) | 44 (3.8%) | 0.149 | 97 (3.5%) | 39 (2.2%) | 0.017 |
| Rales > 50% of lung field | 299 (11.8%) | 101 (8.6%) | 0.004 | 361 (13.0%) | 206 (11.8%) | 0.253 |
| Pulmonary edema | 1,298 (51.3%) | 588 (50.3%) | 0.579 | 1,750 (63.0%) | 1,042 (59.9%) | 0.036 |
| Cardiomegaly | 1,012 (40.0%) | 393 (33.6%) | <.001 | 1,377 (49.6%) | 691 (39.7%) | <.001 |
| Cerobrovascular disease / transient ischemic attack | 379 (15.0%) | 189 (16.2%) | 0.349 | 432 (15.6%) | 326 (18.7%) | 0.005 |
| Previous AMI | 1,145 (45.3%) | 239 (20.5%) | <.001 | 1,281 (46.1%) | 401 (23.1%) | <.001 |
| Peripheral arterial disease | 376 (14.9%) | 132 (11.3%) | 0.003 | 404 (14.6%) | 206 (11.8%) | 0.01 |
| Chronic obstructive pulmonary disease | 362 (14.3%) | 206 (17.6%) | 0.009 | 577 (20.8%) | 378 (21.7%) | 0.446 |
| Dementia | 124 (4.9%) | 68 (5.8%) | 0.242 | 168 (6.1%) | 133 (7.6%) | 0.036 |
| Cirrhos | 23 (0.9%) | 12 (1.0%) | 0.731 | 19 (0.7%) | 13 (0.7%) | 0.806 |
| Cancer | 282 (11.2%) | 132 (11.3%) | 0.893 | 292 (10.5%) | 186 (10.7%) | 0.851 |
| Hemoglobin | 12.7 (11.3-14.1) | 12.3 (10.7-13.5) | <.001 | 12.7 (11.2-14.0) | 12.1 (10.7-13.4) | <.001 |
| White blood cell count | 8.9 (7.1-11.4) | 9.1 (7.1-11.5) | 0.527 | 8.7 (7.0-11.4) | 8.8 (7.0-11.4) | 0.901 |
| Sodium | 139.0 (136.0-141.0) | 139.0 (136.0-141.0) | 0.574 | 139.0 (136.0-141.0) | 139.0 (136.0-142.0) | 0.681 |
| Glucose | 7.7 (6.1-11.2) | 7.2 (6.0-10.1) | <.001 | 7.4 (6.0-10.5) | 7.1 (5.9-9.6) | 0.004 |
| Urea | 8.3 (6.1-12.2) | 7.6 (5.6-11.4) | <.001 | 8.3 (6.2-12.1) | 8.1 (5.9-11.5) | 0.006 |
| Creatinine | 108.0 (86.0-142.0) | 98.0 (76.0-136.0) | <.001 | 110.0 (87.0-146.0) | 100.0 (79.0-134.0) | <.001 |
| eGFR (ml/min/1.73 m2) | 55.1 (39.3-71.9) | 57.3 (39.2-75.8) | 0.06 | 54.9 (38.9-70.9) | 54.6 (39.7-74.2) | 0.301 |
| Potassium | 4.2 (3.9-4.6) | 4.2 (3.8-4.6) | 0.008 | 4.2 (3.9-4.6) | 4.2 (3.8-4.6) | <.001 |
Note: Dichotomous variables are reported as N (%), while continuous variables are reported as median (25th percentile – 75th percentile). The Kruskal-Wallis test and the Chi-squared test were used to compare continuous and categorical baseline characteristics, respectively, between patients with HFPEF and those with HFREF
In each of the two samples, the Kruskal-Wallis test and the Chi-squared test were used to compare continuous and categorical baseline characteristics, respectively, between patients with HFPEF and those with HFREF. Furthermore, characteristics were compared between patients in the EFFECT-1 sample and those in the EFFECT-2 sample.
3.2 Comparison of predictive ability of different regression methods
We examined the predictive accuracy of each method using the EFFECT-1 sample as the model derivation sample and the EFFECT-2 sample as the model validation sample. Using each prediction method, a model was developed for predicting the probability of HFPEF using the subjects in the EFFECT-1 sample. We then applied the developed model to each subject in the EFFECT-2 sample to estimate that subject's predicted probability of having HFPEF. Note that the derivation and validation samples consist of patients from the same jurisdiction (Ontario). Furthermore, most acute hospitals that cared for HF patients were included in both of these two datasets. However, the derivation and validation samples are separated temporally (1999/2000 and 2000/2001 vs. 2004/2005). The study design ensured that there was very little overlap in patients between the two study periods.
The tree-based methods considered as candidate variables all 34 variables described in Table 1. Two separate logistic regression models were fit to predict the probability of the presence of HFPEF. First, we fit a logistic regression model that contained all 34 variables as main effects. No variable reduction was performed. Restricted cubic splines (cubic splines that are linear in the tails) with four knots were used to model the relationship between each continuous covariate and the log-odds of having HFPEF [28]. Second, we fit a logistic regression model that contained 14 predictor variables that previously had been identified as important predictors of HF disease sub-types using data from the Framingham Heart Study (age, sex, heart rate, systolic blood pressure, CHD history, history of hypertension, diabetes mellitus, current smoker, hemoglobin, eGFR, atrial fibrillation, left bundle branch block, any ST elevation, and any T wave inversion) [29].
Predictive accuracy was assessed using two different metrics. First, we calculated the area under the receiver operating characteristic (ROC) curve (abbreviated as the AUC), which is equivalent to the c-statistic [28,30]. Second, we calculated the Brier Score [28] (mean squared prediction error), which is defined as , where N denotes the sample size, P̂i is the predicted probability of the outcome and Yi is the observed outcome (1/0). We used the val. prob function from the Design package to estimate these two measures of predictive accuracy.
We also examined the calibration of the predictions obtained using each method. For each method, subjects in the validation sample were divided into ten groups defined by the deciles of the predicted probability of the presence of HFPEF. Within each of the ten groups, the mean predicted probability of HFPEF was compared with the observed probability of having HFPEF.
3.3 Comparison of accuracy of classification for different classification methods
Classification models were developed that considered all 34 variables described in Table 1 as potential predictor variables. As above, accuracy of classification was assessed using the EFFECT-1 sample as the model derivation sample and the EFFECT-2 sample as the model validation sample. For each subject in the validation sample, a true HF sub-type was observed (HFPEF vs. HFREF) and a classification was obtained (HFPEF vs. HFREF) for each classification method developed in the EFFECT-1 sample. Accuracy of classification was assessed using sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV) [31].
4. Results
4.1 Description of study sample
Comparisons of baseline characteristics between patients with and without preserved ejection fraction in the EFFECT-1 and EFFECT-2 samples are reported in Table 1. In each of the EFFECT-1 and EFFECT-2 samples there were statistically significant differences in 24 of the 34 baseline covariates between subjects with HFPEF and subjects with HFREF. Comparisons of baseline characteristics of patients in the EFFECT-1 sample with those of patients in the EFFECT-2 sample are reported in Table 2. There were significant differences in 20 of the 34 baseline covariates between the two samples. Importantly, the proportion of patients with HFPEF was modestly higher in the EFFECT-2 sample than it was in the EFFECT-1 sample (31.6% vs. 38.5%). The higher proportion of patients with HFPEF in the EFFECT-2 sample could reflect a higher average age and greater prevalence of risk factors such as hypertension and atrial fibrillation over time, which are more commonly associated with HFPEF.
Table 2. Comparison of EFFECT-1 and EFFECT-2 samples.
| Variable | EFFECT-1 Sample (N=3,697) |
EFFECT-2 Sample (N=4,515) |
P-value |
|---|---|---|---|
| HFPEF | 1,168 (31.6%) | 1,739 (38.5%) | <.001 |
| Age (years) | 75.0 (68.0-82.0) | 77.0 (68.0-83.0) | <.001 |
| Male | 1,970 (53.3%) | 2,329 (51.6%) | 0.124 |
| Heart rate on admission (bpm) | 94.0 (77.0-112.0) | 91.0 (74.0-110.0) | <.001 |
| Systolic blood pressure on admission (mm Hg) | 147.0 (126.0-170.0) | 144.0 (124.0-166.0) | <.001 |
| Respiratory rate on admission | 24.0 (20.0-30.0) | 23.0 (20.0-28.0) | <.001 |
| History of hypertension | 1,920 (51.9%) | 3,048 (67.5%) | <.001 |
| Diabetes mellitus | 1,293 (35.0%) | 1,716 (38.0%) | 0.005 |
| Current smoker | 545 (14.7%) | 539 (11.9%) | <.001 |
| History of coronary artery disease | 1,684 (45.6%) | 2,098 (46.5%) | 0.407 |
| Atrial fibrillation | 990 (26.8%) | 1,371 (30.4%) | <.001 |
| Left bundle branch block | 585 (15.8%) | 649 (14.4%) | 0.067 |
| Any ST elevation | 441 (11.9%) | 204 (4.5%) | <.001 |
| Any T wave inversion | 1,224 (33.1%) | 1,278 (28.3%) | <.001 |
| Neck vein distension | 2,246 (60.8%) | 2,941 (65.1%) | <.001 |
| s3 | 443 (12.0%) | 317 (7.0%) | <.001 |
| s4 | 166 (4.5%) | 136 (3.0%) | <.001 |
| Rales > 50% of lung field | 400 (10.8%) | 567 (12.6%) | 0.015 |
| Pulmonary edema | 1,886 (51.0%) | 2,792 (61.8%) | <.001 |
| Cardiomegaly | 1,405 (38.0%) | 2,068 (45.8%) | <.001 |
| Cerobrovascular disease / transient ischemic attack | 568 (15.4%) | 758 (16.8%) | 0.081 |
| Previous AMI | 1,384 (37.4%) | 1,682 (37.3%) | 0.865 |
| Peripheral arterial disease | 508 (13.7%) | 610 (13.5%) | 0.762 |
| Chronic obstructive pulmonary disease | 568 (15.4%) | 955 (21.2%) | <.001 |
| Dementia | 192 (5.2%) | 301 (6.7%) | 0.005 |
| Cirrhos | 35 (0.9%) | 32 (0.7%) | 0.233 |
| Cancer | 414 (11.2%) | 478 (10.6%) | 0.376 |
| Hemoglobin | 12.5 (11.2-13.9) | 12.4 (11.0-13.8) | 0.035 |
| White blood cell count | 9.0 (7.1-11.4) | 8.8 (7.0-11.4) | 0.105 |
| Sodium | 139.0 (136.0-141.0) | 139.0 (136.0-141.0) | 0.399 |
| Glucose | 7.5 (6.0-10.9) | 7.3 (6.0-10.1) | <.001 |
| Urea | 8.1 (5.9-12.0) | 8.2 (6.1-11.9) | 0.371 |
| Creatinine | 105.0 (84.0-140.0) | 106.0 (84.0-142.0) | 0.679 |
| eGFR (ml/min/1.73 m2) | 56.0 (39.3-73.2) | 54.8 (39.3-72.0) | 0.219 |
| Potassium | 4.2 (3.9-4.6) | 4.2 (3.9-4.6) | 0.236 |
Note: Dichotomous variables are reported as N (%), while continuous variables are reported as median (25th percentile – 75th percentile). The Kruskal-Wallis test and the Chi-squared test were used to compare continuous and categorical baseline characteristics, respectively, between patients in the two phases of the EFFECT sample.
4.2 Comparison of predictive ability of different regression methods
The predictive accuracy of the different methods for predicting the probability of the presence of HFPEF is reported in Table 3. The AUC in the EFFECT-2 sample of the different models developed in the EFFECT-1 sample ranged from a low of 0.683 for the regression tree to a high of 0.780 for the non-parsimonious logistic regression model. Boosted regression trees of depths three and four had AUCs that were very similar to that of the non-parsimonious logistic regression model (0.772 and 0.774, respectively). The Brier Score in the EFFECT-2 sample of the different models developed in the EFFECT-1 sample ranged from a high of 0.2152 for the regression tree to a low of 0.1861 for the non-parsimonious logistic regression model.
Table 3.
Accuracy of prediction in EFFECT-2 sample.
| Prediction method | AUC or c-statistic | Brier Score |
|---|---|---|
| Regression tree | 0.683 | 0.2152 |
| Bagged regression tree | 0.733 | 0.2079 |
| Random forest | 0.751 | 0.1959 |
| Boosted regression tree (depth 1) | 0.752 | 0.2049 |
| Boosted regression tree (depth 2) | 0.768 | 0.1962 |
| Boosted regression tree (depth 3) | 0.772 | 0.1933 |
| Boosted regression tree (depth 4) | 0.774 | 0.1918 |
| Logistic regression (full model) | 0.780 | 0.1861 |
| Logistic regression (simple model) | 0.766 | 0.1914 |
For both measures of predictive accuracy, the use of conventional regression trees resulted in predicted probabilities of the presence of HFPEF with the lowest accuracy. A non-parsimonious logistic regression resulted in the greatest out-of-sample predictive accuracy when using the EFFECT-2 sample as the validation sample. Boosted regression trees of depth three and four had predictive accuracy that approached that of the non-parsimonious logistic regression model.
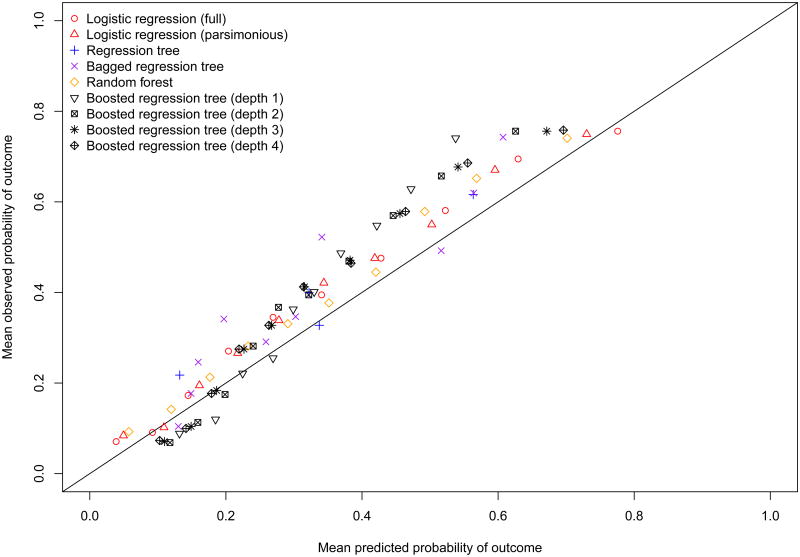
The calibration of each of the prediction methods is described graphically in Figure 1. While all methods tended to under-estimate the probability of the presence of HFPEF, the two logistic regression models and the random forests resulted in estimates that displayed the best calibration. The under-estimation of the predicted probability of HFPEF or miscalibration was most likely due to the differences in the prevalence of HFPEF between the two samples. As noted above, the prevalence of HFPEF was modestly higher in the EFFECT-2 sample than it was in the EFFECT-1 sample.
Figure 1. Calibration of prediction methods in EFFECT Follow-up sample.
4.3 Comparison of accuracy of classification for different classification methods
The sensitivity, specificity, PPV, and NPV of the different classification methods are reported in Table 4. The sensitivity in the EFFECT-2 sample of the different models developed in the EFFECT-1 sample ranged from a low of 0.378 for the random forest to a high of 0.500 for the boosted classification tree of depth four. Specificity ranged from a low of 0.820 for the conventional classification tree and the boosted classification trees of depth four to a high of 0.897 for the random forest. PPV ranged from a low of 0.616 for the classification tree to a high of 0.696 for the random forest. The NPV ranged from a low of 0.697 for the random forest to a high of 0.726 for the boosted classification tree of depth two.
Table 4.
Sensitivity and specificity of classification in EFFECT-2 sample.
| Classification method | Sensitivity | Specificity | Positive predictive value | Negative Predictive value |
|---|---|---|---|---|
| Classification tree | 0.462 | 0.820 | 0.616 | 0.709 |
| Bagged classification tree | 0.451 | 0.849 | 0.653 | 0.712 |
| Random forest | 0.378 | 0.897 | 0.696 | 0.697 |
| Boosted classification tree (depth 1) | 0.453 | 0.876 | 0.695 | 0.719 |
| Boosted classification tree (depth 2) | 0.491 | 0.847 | 0.667 | 0.726 |
| Boosted classification tree (depth 3) | 0.492 | 0.828 | 0.642 | 0.722 |
| Boosted classification tree (depth 4) | 0.500 | 0.820 | 0.635 | 0.724 |
| Support vector machines | 0.401 | 0.887 | 0.690 | 0.703 |
5. Discussion
Classification plays an important role in modern clinical research. The objective of binary classification schemes or algorithms is to classify subjects into one of two mutually exclusive categories based upon their observed characteristics. In clinical research, a common binary classification is diseased/non-diseased, different disease subtypes, or disease etiology. Classification trees are a commonly-used binary classification method. In the data mining and machine learning fields, improvements to classical classification trees have been developed. Many of these methods involve aggregating classifications across a set of classification trees. There is limited research comparing the performance of different classification/prediction methods for predicting the presence of disease, disease etiology, or disease subtype.
We compared the performance of modern classification and regression methods with classification and regression trees to classify patients with HF into one of two mutually exclusive categories HFPEF (HF with preserved ejection fraction) vs. HFREF (HF with reduced ejection fraction), or to predict the probability of the presence of HFPEF. We found that modern classification methods offered improved performance over conventional classification trees for classifying HF patients according to disease subtype. Several observations warrant comment. First, when focusing on predicting the probability of the presence of HFPEF, conventional regression trees had lower predictive accuracy compared to all other methods that we examined. Second, logistic regression had the best predictive accuracy for predicting the presence of HFPEF. Third, when focusing on classification, boosted classification trees of depth four had the highest sensitivity. Fourth, random forests had the highest specificity for classifying patients according to disease subtype.
The current study had a very limited focus: comparing the ability of different methods to predict or classify disease subtype in patients hospitalized with HF in Ontario. Our conclusions about the relative performance of different classification and prediction methods should be restricted to this patient population and to this specific classification scheme (i.e. HFPEF vs. HFREF). Readers should not conclude that logistic regression will have superior predictive ability compared to ensemble-based methods in all settings and for all conditions or outcomes. However, recent studies in patients with cardiovascular disease merit discussion. A recent study which examined the predictive ability of ensemble-based methods for predicting the probability of short-term mortality in patients hospitalized with either acute myocardial infarction or with HF found that ensemble methods resulted in improved predictive accuracy compared to conventional regression trees [32]. However, ensemble-based methods did not result in improved predictive performance compared to conventional logistic regression. In a different study focusing on classifying patients with HF according to mortality outcomes, boosted classification trees were found to result in minor to modest improvement in accuracy of classification compared to conventional classification trees [33].
Comparisons similar to the above have been conducted by other authors. Wu et al., comparing the performance of logistic regression, boosting, and support vector machines to predict the subsequent development of HF, found that the former two methods had comparable performance, while the latter method had the poorest performance [34]. Maroco et al., compared ten different classifiers for predicting the evolution of mild cognitive impairment to dementia [35]. They concluded that random forests and linear discriminant analysis had the best performance for predicting progression to dementia. While these two studies focused on disease incidence, a third study compared three methods for predicting survival in patients with breast cancer [36]. They found that a decision tree resulted in the greatest accuracy, followed by artificial neural networks, with logistic regression resulting in the lowest accuracy. In an extensive set of analyses, Caruana and Niculescu-Mizil compared the performance of ten prediction/classification algorithms on 11 binary classification problems using eight performance metrics [37]. They found that bagged trees, random forests, and neural networks resulted in the best average performance across the different metrics and datasets. In general, they found that conventional classification trees and logistic regression had inferior performance to the best-performing methods. In a related study, Caruana et al. examined the effect of dimensionality (i.e. the number of available predictor variables) on the relative performance of different classification algorithms [38]. They found that as dimensionality increases, the relative performance of the different algorithms changes. They also observed that random forests tended to perform well across all dimensions.
There are several limitations to the current study. First, as noted above, our conclusions are limited to the relative performance of methods for classification/prediction of disease subtype in patients hospitalized with HF. Our conclusions are not intended to be generalized to other patient populations or to other outcomes and conditions. Second, for some of the prediction and classification methods, we used the default settings in the given statistical software package for estimating the given model (e.g. regression trees). Similarly for random forests, we used the default setting for the size of the random sample of predictor variables that was considered at each split of a given tree. However, for other methods, no such default specification existed. In particular, for boosted classification and regression trees, there is limited research on the optimal depth of the fitted trees. Furthermore, it is possible that the optimal tree depth may vary across settings and outcomes. Due to limited research on optimal tree depth, we grew four different sets of boosted trees, with tree depths of 1, 2, 3, and 4. For this reason, concluding that boosted trees had the best performance amongst the different modern prediction methods risks resulting in an incorrect conclusion since comparable tuning parameters were not varied for the other prediction methods. Our finding that boosted trees of depth four tended to have superior performance compared to boosted trees of other depths merits replication in other datasets, in other settings, and for other outcomes. However it should be noted that boosted trees of this depth performed well for predicting cardiovascular mortality in an earlier study [32].
In summary, we found that modern, flexible tree-based methods from the data mining and machine learning literature offer substantial improvement in prediction and classification of HF sub-type compared to conventional classification and regression trees. However, conventional logistic regression was able to more accurately predict the probability of the presence of HFPEF amongst patients with HF compared to the methods proposed in the data mining and machine learning literature.
What is new?
Key finding
Modern data mining and machine learning methods offer advantages for predicting and classifying heart failure (HF) patients according to disease subtype: HF with preserved ejection fraction (HFPEF) vs. HF with reduced ejection fraction (HFREF), compared to conventional regression and classification trees.
Conventional logistic regression performed at least as well as modern methods from the data mining and machine learning literature for predicting the probability of the presence of HFPEF in patients with HF.
What this adds to what was known?
Boosted trees, bagged trees, and random forests do not offer an advantage over conventional logistic regression for predicting the probability of disease subtype in patients with HF.
What is the implication, what should change now?
Conventional logistic regression should remain a standard tool in the analyst's toolbox when predicting disease subtype in patients with HF.
Analysts interested in classifying HF patients according to disease subtype should use ensemble-based methods rather than conventional classification trees.
Acknowledgments
This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. This research was supported by an operating grant from the Canadian Institutes of Health Research (CIHR) (MOP 86508). Dr. Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation. Dr. Tu is supported by a Canada Research Chair in health services research and a Career Investigator Award from the Heart and Stroke Foundation. Dr. Lee is a clinician-scientist of the CIHR. The data used in this study were obtained from the EFFECT study. The EFFECT study was funded by a Canadian Institutes of Health Research (CIHR) Team Grant in Cardiovascular Outcomes Research.
Footnotes
Declaration of conflicting interests: The authors declare that there is no conflict of interest.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Breiman L, Friedman JH, Olshen RA, Stone CJ. Classification and Regression Trees. Chapman & Hall/CRC; Boca Raton: 1998. [Google Scholar]
- 2.Austin PC. A comparison of regression trees, logistic regression, generalized additive models, and multivariate adaptive regression splines for predicting AMI mortality. Statistics in Medicine. 2007;26(15):2937–2957. doi: 10.1002/sim.2770. [DOI] [PubMed] [Google Scholar]
- 3.Clark LA, Pregibon D. Tree-Based Methods. In: Chambers JM, Hastie TJ, editors. Statistical Models in S. Chapman & Hall; New York, NY: 1993. pp. 377–419. [Google Scholar]
- 4.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning Data Mining, Inference, and Prediction. Springer-Verlag; New York, NY: 2001. [Google Scholar]
- 5.Hunt SA, Abraham WT, Chin MH, Feldman AM, Francis GS, Ganiats TG, Jessup M, Konstam MA, Mancini DM, Michl K, Oates JA, Rahko PS, Silver MA, Stevenson LW, Yancy CW. 2009 focused update incorporated into the ACC/AHA 2005 Guidelines for the Diagnosis and Management of Heart Failure in Adults: a report of the American College of Cardiology Foundation/American Heart Association Task Force on Practice Guidelines: developed in collaboration with the International Society for Heart and Lung Transplantation. Circulation. 2009;14(119):e391–e479. doi: 10.1161/CIRCULATIONAHA.109.192065. [DOI] [PubMed] [Google Scholar]
- 6.Lee DS, Gona P, Vasan RS, Larson MG, Benjamin EJ, Wang TJ, Tu JV, Levy D. Relation of disease pathogenesis and risk factors to heart failure with preserved or reduced ejection fraction: insights from the framingham heart study of the national heart, lung, and blood institute. Circulation. 2009;24(119):3070–3077. doi: 10.1161/CIRCULATIONAHA.108.815944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Masoudi FA, Havranek EP, Smith G, Fish RH, Steiner JF, Ordin DL, Krumholz HM. Gender, age, and heart failure with preserved left ventricular systolic function. Journal of the American College of Cardiology. 2003;42(2):217–223. doi: 10.1016/s0735-1097(02)02696-7. [DOI] [PubMed] [Google Scholar]
- 8.Sauerbrei W, Madjar H, Prompeler HJ. Differentiation of benign and malignant breast tumors by logistic regression and a classification tree using Doppler flow signals. Methods of Information in Medicine. 1998;37(3):226–234. [PubMed] [Google Scholar]
- 9.Gansky SA. Dental data mining: potential pitfalls and practical issues. Advances in Dental Research. 2003;17:109–114. doi: 10.1177/154407370301700125. [DOI] [PubMed] [Google Scholar]
- 10.Nelson LM, Bloch DA, Longstreth WT, Jr, Shi H. Recursive partitioning for the identification of disease risk subgroups: a case-control study of subarachnoid hemorrhage. Journal of Clinical Epidemiology. 1998;51(3):199–209. doi: 10.1016/s0895-4356(97)00268-0. [DOI] [PubMed] [Google Scholar]
- 11.Lemon SC, Roy J, Clark MA, Friedmann PD, Rakowski W. Classification and regression tree analysis in public health: methodological review and comparison with logistic regression. Ann Behav Med. 2003;26(3):172–181. doi: 10.1207/S15324796ABM2603_02. [DOI] [PubMed] [Google Scholar]
- 12.R Core Development Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2005. Ref Type: Computer Program. [Google Scholar]
- 13.Ripley B. tree: Classification and regression trees [1.0-28] 2010 Ref Type: Computer Program. [Google Scholar]
- 14.Peters A, Hothorn T. ipred: Improved Predictors [0.8-8] 2009 Ref Type: Computer Program. [Google Scholar]
- 15.Breiman L. Random Forests. Machine Learning. 2001;45(1):5–32. [Google Scholar]
- 16.Liaw A, Wiener M. Classification and Regression by random Forest. R News. 2002;2(3):18–22. [Google Scholar]
- 17.Freund Y, Schapire R. Machine Learning: Proceedings of the Thirteenth International Conference. Morgan Kauffman; San Francisco, California: 1996. Experiments with a new boosting algorithm; pp. 148–156. [Google Scholar]
- 18.Buhlmann P, Hathorn T. Boosting algorithms: Regularization, prediction and model fitting. Statistical Science. 2007;22:477–505. [Google Scholar]
- 19.Friedman J, Hastie T, Tibshirani R. Additive logistic regression: A statistical view of boosting (with discussion) The Annals of Statistics. 2000;28:337–407. [Google Scholar]
- 20.Culp M, Johnson K, Michailidis G. ada: ada: an R package for stochastic boosting [2.0-2] 2010 Ref Type: Computer Program. [Google Scholar]
- 21.McCaffrey DF, Ridgeway G, Morral AR. Propensity score estimation with boosted regression for evaluating causal effects in observational studies. Psychological Methods. 2004;9(4):403–425. doi: 10.1037/1082-989X.9.4.403. [DOI] [PubMed] [Google Scholar]
- 22.Ridgeway G. gbm: Generalized Boosted Regression Models [1.6-3.1] 2010 Ref Type: Computer Program. [Google Scholar]
- 23.Duda RO, Hart PE, Stork DG. Pattern classification. Wiley-Interscience; New York: 2001. [Google Scholar]
- 24.Dimitriadou E, Hornik K, Leisch F, Meyer D, Weingessel A. e1071: Misc Functions of the Department of Statistics (e1071), TU Wien [1.5-24] 2010 Ref Type: Computer Program. [Google Scholar]
- 25.Harrell FE. Design: Design Package [2.3-0] 2009 Ref Type: Computer Program. [Google Scholar]
- 26.Tu J, Donovan LR, Lee DS, Austin PC, Ko DT, Wang JT, Newman AM. Quality of Cardiac Care in Ontario - Phase 1. 1. Toronto, ON: Institute for Clinical Evaluative Sciences; 2004. Ref Type: Report. [Google Scholar]
- 27.Tu JV, Donovan LR, Lee DS, Wang JT, Austin PC, Alter DA, Ko DT. Effectiveness of public report cards for improving the quality of cardiac care: the EFFECT study: a randomized trial. Journal of the American Medical Association. 2009;302(21):2330–2337. doi: 10.1001/jama.2009.1731. [DOI] [PubMed] [Google Scholar]
- 28.Harrell FE., Jr . Regression modeling strategies. Springer-Verlag; New York, NY: 2001. [Google Scholar]
- 29.Ho JE, Gona P, Pencina MJ, Tu JV, Austin PC, Vasan RS, Kannel WB, D'Agostino RB, Lee DS, Levy D. Discriminating clinical features of heart failure with preserved vs. reduced ejection fraction in the community. European Heart Journal. 2012;33(14):1734–1741. doi: 10.1093/eurheartj/ehs070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Steyerberg EW. Clinical prediction models: a practical approach to development, validation, and updating. Springer; New York, NY: 2009. [Google Scholar]
- 31.Zhou X, Obuchowski N, McClish D. Statistical Methods in diagnostic medicine. Wiley-Interscience; New York: 2002. [Google Scholar]
- 32.Austin PC, Lee DS, Steyerberg EW, Tu JV. Regression trees for predicting mortality in patients with cardiovascular disease: what improvement is achieved by using ensemble-based methods? Biometrical Journal. 2012;54(5):657–673. doi: 10.1002/bimj.201100251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Austin PC, Lee DS. Boosted classification trees result in minor to modest improvement in the accuracy in classifying cardiovascular outcomes compared to conventional classification trees. American Journal of cardiovascular Disease. 2011;1(1):1–15. [PMC free article] [PubMed] [Google Scholar]
- 34.Wu J, Roy J, Stewart WF. Prediction Modeling Using EHR Data: Challenges, Strategies, and a Comparison of Machine Learning Approaches. Medical Care. 2010;48(6, Suppl 1):S106–S113. doi: 10.1097/MLR.0b013e3181de9e17. [DOI] [PubMed] [Google Scholar]
- 35.Maroco J, Silva D, Rodrigues A, Guerreiro M, Santana I, de Mendonca A. Data mining methods in the prediction of Dementia: A real-data comparison of the accuracy, sensitivity and specificity of linear discriminant analysis, logistic regression, neural networks, support vector machines, classification trees and random forests. BioMed Central Research Notes. 2011;4(299):1–14. doi: 10.1186/1756-0500-4-299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Delen D, Walker G, Kadam A. Predicting breast cancer survivability: a comparison of three data mining methods. Artificial Intelligence in Medicine. 2004;34:113–127. doi: 10.1016/j.artmed.2004.07.002. [DOI] [PubMed] [Google Scholar]
- 37.Caruana R, Niculescu-Mizil A. International Conference on Machine Learning ICML '06 Proceedings of the 23rd international conference on Machine learning. New York, NY: ACM; 2006. An empirical comparison of supervised learning algorithms; pp. 161–168. Ref Type: Conference Proceeding. [Google Scholar]
- 38.Caruana R, Karampatziakis N, Yessenalina A. International Conference on Machine Learning ICML '08 Proceedings of the 25th international conference on Machine learning. New York, NY: ACM; 2008. An empirical evaluation of supervised learning in high dimensions; pp. 96–103. Ref Type: Conference Proceeding. [Google Scholar]