Abstract
Perhaps the greatest paradox in the hydrocephalus field is the failure of researchers to consistently measure transmantle pressure gradients (ventricle to subarachnoid space) in either human or animal models of the communicating form of the disorder. Without such a gradient, conceptualization of how ventricular distention occurs is difficult. Based on evidence from both a mathematical model [35] and experiments in skin [51], we observed that the intraventricular injection of anti-β1 integrin antibodies in rat brains results in a reduction of periventricular pressures to values below those monitored in the ventricles. In addition, many of these animals developed hydrocephalus [30]. We conclude that the dissociation of β1 integrins from the surrounding matrix fibers generates pressure gradients favouring ventricular expansion suggesting a novel mechanism for hydrocephalus development. Several issues, however, need further clarification. If hydrostatic pressure declines in the periventricular tissues then fluid absorption must occur. Aquaporin-4 (AQP4) is a likely candidate for this absorption as it is the predominant water channel in the brain. Indeed, when capillary function is negated, periventricular interstitial fluid pressures increase after anti-β1 integrin antibody administration. This suggests that capillary absorption of parenchymal water may play a pivotal role in the generation of pressure gradients in our hydrocephalus model. Focusing on these issues, we present two poroelastic models to investigate the role of intramantle pressure gradients in ventriculomegaly and to determine if integrin-matrix disassociation represents a complete causative mechanism for hydrocephalus development.
Keywords: Hydrocephalus, β1 Integrins, Aquaporin-4, Brain Biomechanics, Poroelasticity
1. Introduction
The term hydrocephalus represents a family of disorders characterized by expansion of the ventricles within the brain. In obstructive hydrocephalus, an observable blockage within the cerebrospinal fluid (CSF) system impairs CSF flow leading to ventriculomegaly. In communicating hydrocephalus however, there is no obvious impediment to CSF movement and the reason for ventricular expansion is unknown. Hydrocephalus can be caused by a wide variety of developmental abnormalities or injuries. Genetic factors are believed to contribute to the development of congenital hydrocephalus and as of 2006, more than 40 mutants and 9 genes have been identified in animal models and humans [54]. Most of the gene products are the cytokines and growth factors involved in brain development. In humans, however, only one hydrocephalus gene has been identified (X-linked) encoding for the cell adhesion molecule L1 [14]. Additionally, there are many cases of hydrocephalus that occur as part of complex syndromes that are difficult to interpret. In contrast to the congenital form, acquired hydrocephalus occurs after development of the brain and can be due to many causes such as trauma, hemorrhage, infection, and tumors.
Hydrocephalus afflicts people of all ages. The incidence of infantile hydrocephalus is approximately one in every 500 live births, making it one of the most common birth defects [16, 45]. In children, this condition is especially damaging as up to 78% of children with treated hydrocephalus still su er debilitating neurological deficits [6, 18]. Additionally, the increasing numbers of aging patients with Normal Pressure Hydrocephalus (NPH), further substantiate the need for better management of this disorder [38]. Gait disturbance, urinary incontinence and dementia in conjunction with expanded ventricles define idiopathic NPH usually in the sixth or seventh decade of life [25]. Secondary NPH is thought to occur from subarachnoid hemorrhage, meningitis, head trauma or stroke and can affect individuals at all ages.
Treatment of hydrocephalus involves the insertion of a catheter called a shunt into a brain ventricle with diversion of CSF to another site of absorption in the body (usually the abdominal cavity). Alternatively, the endoscopic third ventriculostomy technique is used in which a channel in the floor of the third ventricle is opened surgically. This allows CSF flow to the basal cisterns of the brain. Unfortunately, half a century of research has produced little improvement in shunt survival [11]. Approximately 40% of shunts fail and require further surgery within a year, and 60% fail by two years [45]. The overall cost for shunt treatments has been estimated at 1 billion per year in the United States and shunt malfunctions represent at least half of this expense [9, 5, 33]. It is clear that fresh approaches are needed to understand the causes and therapeutic potential of this disorder [4, 49].
2. Physiological and Molecular Mechanisms in the Brain Interstitium
In this section we discuss some existing theories for hydrocephalus development as well as a promising new theory based on a molecular mechanism in the brain interstitium.
2.1. Does a CSF absorption deficit cause hydrocephalus?
It would seem intuitively obvious that pressures within the ventricular system would have to be greater than those in the subarachnoid space for ventricular enlargement to occur and yet, some investigators have failed to measure suitable gradients in various models or have measured gradients that were very small [36, 42, 44]. Others have postulated that some factor (possibly a change in compliance) causes the ventricular pulse pressure amplitude to exceed the amplitude of the pulsation in the subarachnoid space (SAS), thus initiating a transmantle pulse pressure gradient and ventricular dilation [12]. The mathematical principles on which this idea is based have been disputed [47] and the idea seems to be falling out of favour. Historically, hydrocephalus has been viewed as a ‘plumbing problem’ representing (in the communicating type) an imbalance between CSF production and absorption. Since overproduction of CSF is relatively rare [26], many have assumed that an impediment to CSF absorption through the arachnoid projections or extracranial lymphatic vessels increases ventricular pressure and causes ventricular enlargement. This concept, however, is problematic.
In the communicating hydrocephalus model we use, the ventricular and subarachnoid compartments are in communication with one another and thus, pressure would likely increase in both compartments equally if CSF outflow is obstructed. It is, of course, possible that very small transmantle pressure gradients (1 mm Hg or less) induced by some impediment to CSF flow are capable of expanding the ventricles as postulated by Levine [22] and mathematically analyzed in the case of infant hydrocephalus by Wilkie et al. [52]. Levine argued that diminutive gradients exist since pressures are diminished towards the periphery of the brain due to the absorption of interstitial fluid into the brain capillaries. The capillary absorption of water becomes a critical element in his mathematical formulation, a concept that we will return to shortly. If Levine's suppositions are correct, then a decline in CSF absorption with a concomitant increase in global CSF outflow resistance could play an important role in hydrocephalus development. The postulated small pressure gradients, however, have never been directly verified. In addition, while hydro-cephalus is associated with elevations in CSF outflow resistance, the opposite is not necessarily true, as elevations in CSF outflow resistance do not always correlate with hydrocephalus. In pseudotumor cerebri for example, CSF outflow resistance is often high without hydrocephalus being present [50]. Furthermore, in previous studies from our group, it was clear that a lymphatic CSF absorption deficit occurred in ageing rats and yet no hydrocephalus was present in these animals [29]. In conclusion, it is not apparent whether an impediment to CSF drainage represents a pivotal event in hydrocephalus development or whether it is a ‘co-conspirator’ in the pathogenesis of ventricular enlargement with some other factor denoting the definitive cause.
2.2. An alternative explanation for ventricular expansion
There may be many pathophysiological mechanisms that lead to ventricular expansion, but Dr. Pickards Cambridge group [35] has developed a particularly interesting sidebar to this issue that could be relevant to at least some forms of hydrocephalus. Based on a finite element analysis of a poroelastic model, these authors postulated that ventricular expansion may result from a relative reduction in interstitial fluid pressure in the periventricular area leading to the formation of a ventricle-parenchymal rather than a ventricle-SAS pressure gradient. No mechanism was identified or proposed but studies carried out in non-CNS tissues may provide a clue as to how this might occur.
Rubin and colleagues [40] have proposed that fibroblasts in the skin regulate interstitial fluid pressure by exerting a tensile force on matrix elements, which restrains the interstitial gel from swelling. A lowering of interstitial fluid pressure can be induced by various types of inflammatory reactions, certain prostaglandins, and Cytochalasin D. The data with the F actin-disrupting agent Cytochalasin D supported a role for extracellular and intracellular cytoskeletal linkages in pressure regulation [3]. These factors appear to regulate the balance between grip and release by altering cell-matrix-integrin interactions leading to compaction or tissue swelling which in turn affects interstitial pressure [41]. This phenomenon appears to occur in the trachea as well [53]. Furthermore, injections of anti β1 integrin antibodies into skin simulated the inflammatory effects by inducing a significant reduction of interstitial fluid pressure [51]. Indeed, the anti-inflammatory effects of alpha-trinositol appear to relate to its ability to modulate β1 integrin function with a concomitant reversal of the interstitial pressure lowering effect [40]. Therefore, integrin-matrix interactions appear to be prime candidates for regulating this phenomenon. We may then ask if the brain parenchyma can modulate tissue pressure similarly.
Integrins are cell surface glycoproteins that mediate cell-matrix interactions by providing a physical transmembrane link between the extracellular matrix and the cell cytoskeleton [17]. Believed to have many important roles in CNS function [27], β1 integrins are expressed on choroidal and ependymal cells and throughout the neuropil on glial cells and vascular structures [15, 34, 55]. With this in mind, we tested if the intraventricular injection of function blocking anti β1 integrin antibodies in rats could lower periventricular interstitial fluid pressure relative to that measured in the ventricular system and determined if similar injections could induce ventricular enlargement. We measured ventricular and periventricular interstitial fluid pressures with a micropipette servo-null system. Following the intraventricular injection of anti β1 or anti α2β1 integrin antibodies, we measured a decline in periventricular pressures to values significantly below those monitored in the ventricular system. This pressure drop occurred rapidly (within 20 minutes after antibody injection) and remained below baseline for the duration of the experiments. Additionally, after 2 weeks, more than two thirds of these animals developed hydrocephalus [30]. These effects were not observed with injections of the immunoglobulin isotype controls.
2.3. Issues that need to be resolved
Rather than simply being a passive participant, it would appear that the brain interstitium assumes an active role in regulating interstitial fluid pressure. This concept provides a guide to the development of linkages between the physiological and molecular domains that regulate the pressure gradients associated with hydrocephalus. A number of key issues, however, need to be examined as it is unlikely that the drop in parenchymal pressure is orchestrated solely by the dissociation of integrin-matrix interactions. As outlined in more detail below, a particularly important question relates to the possible movement of ventricular CSF into the surrounding tissues and its subsequent fate in the interstitium. In the textbook view, all CSF is removed from the subarachnoid space by bulk flow through the arachnoid granulations and villi that project into the cranial venous sinuses. Recent evidence also suggests that a significant proportion of CSF moves through the cribriform plate into lymphatic vessels located in the olfactory turbinates [20]. One of the intriguing features of Levine's article relates to the absorption of parenchymal water by the capillaries. This process may be important in understanding how pressure gradients favourable to ventricular expansion are created. If the periventricular tissue pressure declines, one would expect that CSF would be drawn into the parenchyma from the ventricles due to the pressure gradient, thus negating the pressure drop.
Recent consultations with members of the Centre for Mathematical Medicine at the Fields Institute [2] have indicated that, in order for pressure to be lower in the parenchyma than in the ventricles, some removal of fluid must occur from the tissues. This concept is echoed in the papers of Levine [21, 22] as noted earlier and, interestingly, is a necessary condition for ventricular enlargement in the Pickard Cambridge model as well [35]. Our recent data supports this view. In the skin studies, the vascular administration of a saturated KCL solution was an effective tool to negate the passage of water from the capillaries into the tissues; a phenomenon that would dampen the drop in interstitial fluid pressure [3, 37]. By stopping the heart, the capillaries would largely collapse and the capillary hydrostatic pressures would fall to zero. Similarly, under these conditions it seems unlikely that significant amounts of water would be able to move in the opposite direction i.e. from the tissues into the capillary network, as presumably, the osmotic pressure of the capillary contents would be much reduced due to the paucity of solutes in the collapsed vessels.
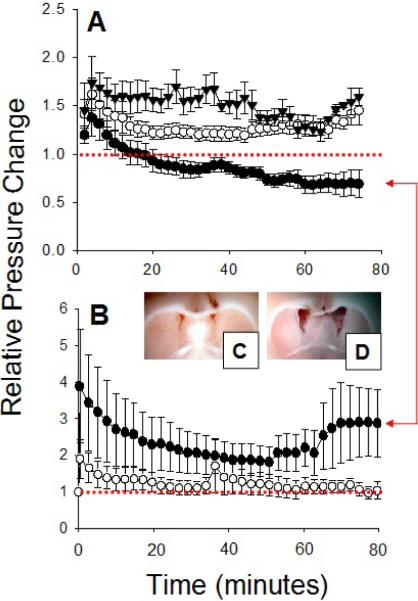
With this assumption, we performed experiments in which micropipettes were placed in the periventricular interstitium and Hamilton syringe needles were placed in a ventricle for antibody injection. Pressures were measured for around 30 minutes at which point, KCL was administered into a femoral vein to stop the heart. Once a new stable baseline was attained, antibodies to the β1 integrins or the iso-type control immunoglobulin were injected into a lateral ventricle and interstitial pressures were monitored. Under these conditions, periventricular interstitial fluid pressures increased after anti β1 integrin antibody administration. The injection of isotype IgG controls resulted in pressures that returned to pre-injection levels (see Figure 1). These results suggest that water moves into the tissues from the ventricles secondary to the matrix expansion (β1 integrin-matrix disruption) and that interstitial fluid couldn't be removed from parenchymal tissues in the KCL-treated animals (due to capillary collapse). These data support the hypothesis that the capillary absorption of parenchymal water may play a pivotal role in the generation of pressure gradients in our hydrocephalus model.
Figure 1.
Impact of intraventricular anti β1 integrin antibodies on pressures within the brain of rats. (A) Intact animals. (●) Antibodies to the β1 integrins cause a drop in periventricular interstitial fluid pressures below averaged pre-injection levels (red dotted line). (▼) Isotype immunoglobulin controls cause an elevation of periventricular interstitial fluid pressures, which remain higher than pre-injection levels for the duration of the experiment. (○) Antibodies to the β1 integrins cause an elevation of ventricular (CSF) pressures, which remain consistently higher than the interstitial pressures in the brain parenchyma. The difference between the data designated by ○ and ● represents a pressure dient that favours hydrocephalus gra-development. (B) Animals with heart stopped with KCL. (●) Antibodies to the β1 integrins increase periventricular interstitial fluid pressures above averaged pre-injection levels (red dotted line). (○) Isotype immunoglobulin controls resulted in interstitial fluid pressures that returned to baseline (pre-injection levels). These results suggested that water moves into the tissues from the ventricles secondary to the matrix expansion and that interstitial fluid couldn't be removed from parenchymal tissues due to capillary collapse. Red arrows denote comparison between effects of the anti β1 integrin antibodies in intact (A) and heart-stopped animals (B). Image of the brain following intraventricular injection of isotype immunoglobins control showing normal ventricle size (C) and following intraventricular injection of antibodies to the β1 integrins showing enlarged ventricles (D). (A), (C), and (D) are taken from [30].
At this point, the mechanisms contributing to the movement of water into the capillaries is unclear. We suspect that the blood brain barrier (BBB) is not involved. Astrocytic processes surrounding select microvessels in the adult primate express β1 integrins as do the endothelial cells themselves [55]. Endothelial cells and astrocytes maintain the basal lamina and support the barrier properties associated with the BBB. It is possible therefore, that the anti-integrin antibodies affect water transport at two levels, the matrix and the blood vessels. At this point, we do not know if injection of the anti β1 integrin antibodies affects barrier function, but we suspect that they do not since studies have shown that the conditional deletion of astrocytic β1 integrins has no affect on BBB permeability [39]. In addition, any disruption of the BBB would likely increase the movement of water and solutes from the capillaries into the tissues and negate the pressure drop.
Also, it seems unlikely that hydrostatic pressure gradients are responsible for fluid absorption. First, capillary pressure is much higher than the (reduced) pressures we measured in the experiments discussed earlier, so no such gradient favouring capillary absorption would exist. Second, even if the tissue pressure was greater than the capillary pressure, interstitial solutes would be held up at the capillary membrane because of the blood brain barrier. This would increase the concentration of solutes at the membrane, increasing the pericapillary osmotic pressure and limiting any further water absorption; a process termed osmotic buffering [13]. Osmotic forces on the other hand, may be the key to this water absorption, although how this might occur remains quite speculative.
Under normal circumstances, the movement of certain solutes from the blood to the brain tissues occurs via carrier-mediated processes across the capillary wall [10]. We might imagine that this results in a concentration gradient of solutes with the highest concentration existing in the pericapillary area and lower concentrations being present beyond the capillary as the fluid diffuses to and mixes with, the surrounding tissue water. When matrix-integrin interactions are disrupted, water moves presumably from the ventricle into the periventricular tissues due to the now-formed ventricular-parenchymal pressure gradient. This movement, which occurs in the opposite direction to the normal flow from the tissues to the CSF compartment [13], might be expected to dilute the relatively higher solute concentration in the immediate vicinity of the capillary. If this is the case, then the pericapillary tissue osmotic pressure may decline relative to that in the vasculature and alter the Starling's forces such that water is absorbed into capillary blood. Another possibility is that astrocytes have the ability to modify osmolytes in the surrounding tissues [32]. In any event, a small imbalance of osmotic forces in the brain may be important. For example, a concentration difference of 1.0 mOsm for an impermeable solute generates an equivalent hydrostatic driving pressure of 19.3 mm Hg [13]. This brings us to the aquaporins.
Aquaporin-4 (AQP4) is the predominant water channel in the brain [1] and is expressed on endothelial cells and astrocytic foot processes that surround capillary endothelial cells [8, 19]. These proteins appear to function as bi-directional channels that facilitate water movement driven by hydrostatic or osmotic forces [8, 28]. Analysis of AQP4 null mice revealed that the loss of this gene is well tolerated with no overt defects during development [24]. The importance of AQP4 in water regulation is most apparent when null animals are challenged with various stresses. AQP4 null mice display reduced cellular swelling in models of cytotoxic cerebral edema and increased brain swelling in models of vasogenic edema, strongly indicating that AQP4 plays a role in water homeostasis in the brain [8, 31, 48]. We do not envisage aquaporin activity as the initiating event in the hydrocephalus development associated with matrix-integrin disruption. Nevertheless, it seems that aquaporins may play a significant role in our model of hydrocephalus. The conditional deletion of β1 integrins in astrocytes disrupted AQP4 expression in the end feet regions of the cells [39] suggesting that β1 integrin-AQP4 relationships may be worth exploring in future studies.
3. Mathematical Modeling
The above description of this new molecular mechanism for hydrocephalus development leads one to ask certain mathematical and mechanical questions, the two, perhaps, most pressing of which, we now attempt to answer. The first question, regarding the physical presence of these intramantle pressure gradients, asks “does the pressure gradient essentially exist only near the periventricular area with a relatively small spatial localization (an inverted spike in pressure), or is the pressure reduced almost entirely throughout the parenchyma, only rising back to normal levels near the boundaries (a trough)”? In answer, we present a poroelastic model and predict the ventricular enlargement that occurs due to pressure gradients with both spike and trough spatial distributions. The second question considers the action of the anti β1 integrin antibodies and asks “do the observed and assumed macroscopic mechanical effects of these antibodies represent a complete mechanism sufficient to induce hydrocephalus”? To answer this question, we present a poroelastic model that incorporates antibody diffusion throughout the parenchyma and ties the mechanical properties of the tissue to the action of these antibodies. These questions were first addressed in the 2009 OCCAM-Fields-MITACS Biomedical Problem Solving Workshop [2], and we summarize the results below.
3.1. Intramantle Pressure Gradient Distributions
Biot's [7] theory of consolidation describes the behaviour of a porous linearly elastic material saturated in a viscous fluid. Many mathematical models of hydrocephalus use consolidation theory to describe the behaviour of brain tissue [21, 43, 46]. A simplified geometry (usually spherical or cylindrical in shape) is generally assumed to reduce the partial differential equations to one spatial dimension. Here we modify the poroelastic model developed by Levine [21] to investigate the effects that the spatial distribution of an intramantle pressure gradient has on tissue displacement and ventricle enlargement. A spherical geometry is assumed with the hollow inner region representing the ventricles, the outer region representing the SAS, and the thick wall representing the brain parenchyma, see Figure 2.
Figure 2.
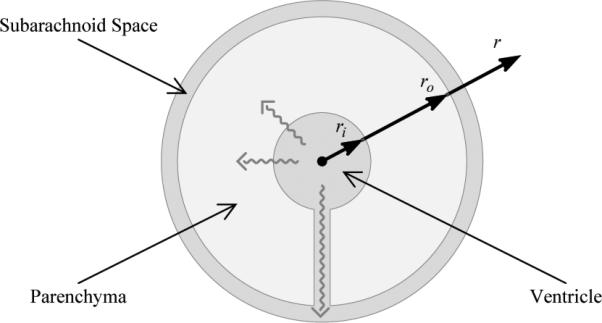
A simplified spherical brain geometry. The internal spherical void represents the ventricles from which CSF may either flow out through the parenchyma or out through a channel representing the foramena and aqueduct. We consider this channel to be small enough that it has a negligible effect on tissue displacement. The thick wall of the sphere represents the parenchyma, and the outer region represents the SAS and skull.
3.1.1. Tissue Displacement
Levine's [21] equation for radial displacement is obtained from the quasi-static version of Biot's theory [7] assuming both the displacement and pressure are radially symmetric. Thus, the relation between radial displacement u(r) and pore pressure P(r) is
| (1) |
where G is the shear modulus and v is the Poisson's ratio of the saturated poroelastic solid. The parameter α, according to Biot [7], represents the ratio of the volume of fluid squeezed out to the volume change of the parenchyma if the parenchyma is compressed while allowing fluid to escape.
For (1), boundary conditions are prescribed at the inner, ri, and outer, ro, boundaries of the brain. At the inner boundary, the normal component of the forces acting on the fluid and solid phases must be equal, this gives
| (2) |
At the outer boundary, we have two possible conditions. The first imposes the same condition on the forces at the outer boundary as was imposed at the inner boundary. That is,
| (3) |
which describes the case of infant hydrocephalus where the unfused skull plates may deform to accommodate the ventricular and parenchymal distension. The second possibility, describing adult hydrocephalus, imposes
| (4) |
which enforces zero tissue displacement at the outer boundary due to the rigid skull.
Both of these boundary conditions are approximations to the physical system. In reality, the infant skull provides some resistive force to prevent enlargment and the adult skull is not fused with the brain parenchyma (which excludes the possibility of tissue contraction near the skull). Furthermore, in the following we assume the brain tissue solid matrix to be incompressible. Thus, if the parenchyma is compressed, the volume loss must be due to fluid loss or pore shrinkage. Hence α = 1 and conditions (2) and (3) enforce zero radial solid stress at these boundaries.
3.1.2. Pressure Distribution
Throughout the brain parenchyma, pore pressure can be related to CSF flow through the pores via Darcy's law. Levine [21] writes these equations as
| (5) |
| (6) |
| (7) |
Here, Vr(r) is the pore CSF velocity, which corresponds to ϕv(r), where ϕ is the volume fraction of CSF at a given point and v(r) is the radial velocity at that same point. Equation (5) is Darcy's law where k’ is the hydraulic permeability of the parenchyma. Equation (6) is Starling's law which relates the volume of CSF absorbed per unit volume of the parenchyma per unit time (Vab) to the pressure difference across the capillary wall. Here k̂ is the absorbtion coefficient. Note that this equation assumes the blood pressure and net colloid osmotic pressures sum to zero, leaving the pore pressure, P , as the driving force behind the transfer of fluid from the interstitium to the capillaries. Finally, equation (7) describes the increment of fluid content in the parenchyma (ζ(r, t) = ϕ−ϕ0, if ϕ0 is the initial volume fraction of fluid in the parenchyma). The two factors affecting the volume fraction of fluid are the absorbtion of fluid by capillaries and the divergence of the fluid flow. The notation ζt denotes the time derivative of ζ. In the quasi-static case, where ζt = 0, this simplifies to
| (8) |
The boundary conditions, as suggested by Levine [21], are
where Pv is the pressure difference between the ventricles and the SAS. In communicating hydrocephalus, however, the ventricular space and the subarachnoid space are connected via the cerebral aqueduct, and no significant pressure gradients have been observed [23], so the boundary conditions should be closer to
| (9) |
where Pss is the steady-state fluid pressure in both the ventricles and the SAS.
3.1.3. Radial Displacement and Ventricular Expansion
In the brain, the absorbtion and permeability coefficients may vary spatially and thus, by choosing k̂ and k’ appropriately, we can obtain a pressure profile of any desired shape. For now, we assume that these coefficients are constant and define their ratio as . Pressure profiles for various values of the ratio k are obtained by solving (8) subject to (9) in MAPLE.
Figure 3 illustrates the dependence of the pressure distribution on the ratio k as well as the dependence of the parenchymal displacement (determined by (1) with adult hydrocephalus boundary conditions (2) and (4)) on the pressure profile. When absorption is equal to permeability (k = 1), pressure drops only slightly mid-parenchyma which causes negligible deformation. When absorption dominates permeability (k << 1), significant drops in pressure occur mid-parenchyma and the tissue is displaced inwards at both boundaries of the brain. The inward displacement of the cortical surface may be avoided by overlaying a small transmantle pressure gradient; at 1 mm Hg or less, this would not have been detected in the measurements of Linninger et al. [23] due to transducer sensitivity.
Figure 3.
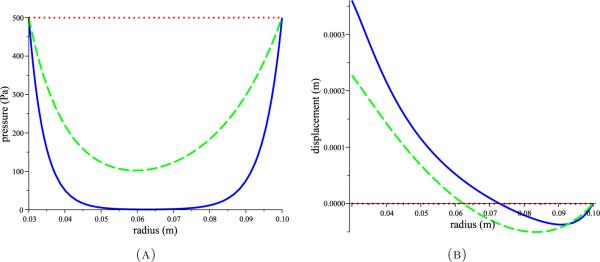
Pressure profiles (A) obtained by solving (8) with (9) for various values of k, and the corresponding tissue displacements (B) obtained by solving (1) with (2) and (4). Red dotted curves for k = 1 and blue solid and green dashed curves for k << 1 all with G = 8 kPa and v = 0.35 as estimated by Tenti et al.[46].
To investigate the dependence of displacement on the shape of the pressure distribution through the parenchyma, inverted spike profiles were constructed to compare with the trough profiles of Figure 3. The constructed pressure profiles and their corresponding displacements according to (1) with (2) and (4) are shown in Figure 4. The pressure spikes cause the majority of the parenchyma to move inward while the ventricle walls move outward creating compression in the middle of the parenchyma. The trough profiles, on the other hand, cause the majority of the parenchyma to move outward while a region near the outer boundary moves inward, again creating compression of the parenchyma.
Figure 4.
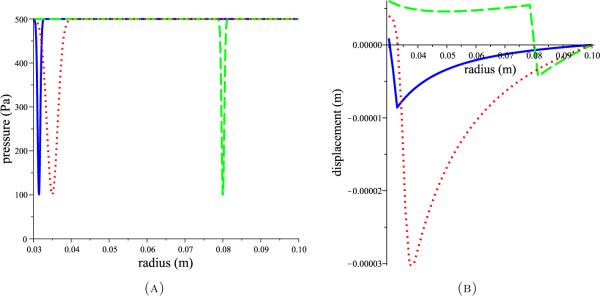
Three hypothetical inverted spike (A) pressure profiles (red dotted, blue solid, and green dashed lines) and the corresponding tissue displacements (B) (shown with same line colour and style) obtained by solving (1) with (2) and (4). Parameter values of G = 8 kPa and v = 0.35 [46] were used.
3.1.4. Discussion
The spatial distribution of an intramantle pressure gradient seems to affect the spatial location of the tissue compression resulting from the overall ventricular enlargement. The enlargements predicted by this model are small compared to those observed in Johnston's animal experiments [30]. A few possible explanations for this discrepancy are that the material parameters of the animal brain tissue were unknown, so rough estimates were used, that Biot's model assumes linearity, so large displacements are inaccuratly predicted, and that the expansion seen in the animal experiments occurred over weeks whereas these model predictions are equilibrium solutions. The time scale on which these equilibrium states are obtained is unknown and may in fact be quite small depending on the material properties of the parenchyma. Thus, it is possible that large displacements may occur if these pressure distributions reoccur transiently and in response to each transient the parenchyma actively restructures its extracellular environment.
3.2. A Complete Physical Mechanism
Peña et al. [35] showed through a finite element simulation that a drop in parenchymal pressure coupled with a reduced elastic modulus is sufficient to enlarge ventricles in a poroelastic model. In order to maintain a low pressure region inside the parenchyma, they assumed that CSF was absorbed by the parenchyma but no physical explanations for the absorption process or for the reduced elasticity were given. To investigate the potential role of anti β1 integrin antibodies in reducing the interstitial fluid pressure observed in the parenchyma, we hypothesize that the dissociation of β1 integrins from the extracellular matrix creates a drop in local parenchymal pressure by changing the mechanical properties of the tissue, such as the elasticity, permeability, and absorption coefficients.
More specifically, the antibodies bind to the β1 integrins protruding from cell membranes which prevents integrin attachment to the extracellular matrix. Normal tissues are held in a state of tension by these cell-matrix connections, and when the integrins are blocked, we hypothesize that the tension may be relaxed, increasing cell motility, decreasing tissue rigidity, and decreasing the local fluid pressure.
3.2.1. Model Derivation
To test this hypothesis, we developed a model at the macroscopic scale that considers the concentration of antibodies in the parenchyma and their overall effect on tissue mechanics [2]. The flow of CSF and antibodies through the tissue necessitates the use of a poroelastic model. Material parameters, such as elasticity and permeability, are assumed to be affected by the β1 integrin antibodies and thus have a spatial and temporal dependence determined by the antibody concentration history. The concentration of antibodies is governed by a convection-diffusion equation.
Neglecting inertia in the conservation of momentum at steady-state gives
| (10) |
Here, τ is the total stress tensor defined by
| (11) |
where λ = λ(x, t) and G = G(x, t) are the Lamé parameters of elasticity which depend on space and time due to the antibody concentration history, p is the hydrostatic pressure, and the strain is assumed to be linear,
| (12) |
The displacement of the tissue is denoted by u and (·)T denotes the transpose operator.
Combining (10)–(12) gives the equation of motion
| (13) |
The first three terms on the right hand side give the standard equation of motion in linear poroelasticity and the rest arises due to the spatial variability of λ and G. Darcy's law, in this framework, is
| (14) |
where, ϕ is the porosity (or the fluid volume fraction which is equivalent in a saturated media), W is the filtration of the fluid (defined to be the velocity of the fluid relative to the solid phase), and k’ = k’(x, t) is the hydraulic permeability.
Applying conservation of mass to the fluid and solid phases gives
where Q(x, t) represents absorption of CSF (possibly due to osmotic pressure gradients and aquaporins) and depends on the antibody concentration. Adding these two equations gives
Taking the divergence of Darcy's Law (14) and substituting into the above equation gives a second equation relating pressure to displacement:
| (15) |
Finally, the concentration of antibodies in the parenchyma is governed by the convection-diffusion equation,
| (16) |
where D is the diffusion coefficient and α is an absorption constant. The initial condition c(x, 0) = 0 is prescribed so that initially the antibody concentration is zero.
The remaining model parameters are assumed to satisfy the following evolution equations and initial conditions:
| (17) |
| (18) |
| (19) |
| (20) |
| (21) |
where v, γ, μ, and p are positive constants, k is the initial permeability of the parenchyma, η is the viscosity of the CSF, H(·) is the Heaviside function, the subscript crit denotes the critical value (maximum or minimum), and the subscript 0 denotes the initial value.
We assume the same spherical geometry as above to obtain radially symmetric solutions. Boundary conditions are thus prescribed at the ventricle, r = ri, and SAS, r = ro, boundaries. The pressure at the ventricle wall must equal the pressure in the ventricle, p(ri) = pi, and the pressure at the cortical surface must equal the pressure in the subarachnoid space, p(ro) = po. Note that for communicating hydrocephalus, pi should approximately equal po, or at least pi – po ≤ 1 mmHg.
The boundary condition for displacement arises due to the continuity of stress at each boundary. That is, the effective stress at each boundary is zero:
Note that these conditions represent infant hydrocephalus where the cranial sutures are unfused and so the skull may enlarge. For adult hydrocephalus, where the skull is rigid, the outer boundary condition should be changed to u(ro) = 0.
Finally, the boundary conditions for the concentration of antibodies are
The inner condition represents an exponentially decaying source of antibodies in the ventricle which approximates the bolus injection draining through the aqueduct. The outer condition represents absorption of the antibodies through the normal CSF absorption mechanisms (arachnoid villi or lymphatic drainage).
3.2.2. Sensitivity to permeability and absorption
Equations (13) and (15) are coupled equations for displacement and pressure, but the assumption of a quasi-static state, ut = 0, decouples these equations leaving a single equation for pressure:
| (22) |
This assumption requires that the tissue deforms only in response to changes in the pressure distribution, whereas in reality, tissue deformation may occur for other reasons and it affects the pressure.
As a first approximation, we solve (22) with prescribed functions for hydraulic permeability and absorption (either constants or linear functions of r are assumed). The linear functions used are k’ = 0.05(1 – r) and Q = 800(1 – r) and the constants used are k’ = 0.05(1 – 0.2) and Q = 800(1 – 0.2) for 0.2 ≤ r ≤ 0.8. These functions and values are not physical and were chosen for simplicity; Figure 5 shows the results.
Figure 5.
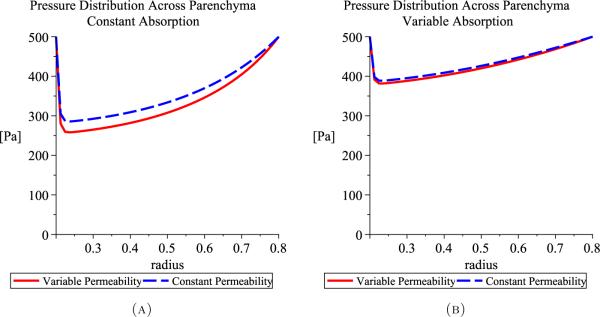
Pressure distributions through the parenchyma assuming constant permeability or variable permeability for either constant absorption (A) or variable absorption (B).
As shown in the simulated pressures in Figure 5, variable permeability slightly lowers the minimum of the pressure curve and absorption strongly affects the shape of the pressure profile. This results from (22), since the only solution with Q(r, t) = 0 is p = pi = po. Thus, absorption in the parenchyma, and hence osmotic pressure, significantly affects the hydrostatic pressure distribution throughout the brain tissue but permeability does not, so hydraulic permeability, k’(x, t), may be assumed constant to further simplify the model.
3.2.3. Discussion
We presented a new model capable of simulating the effects of anti β1 integrin antibodies on brain tissue. Future work will include numerically solving the above model and comparing the results to those obtained with Levine's model above. We will also consider incorporating a more direct role for osmotic pressure and aquaporins in the parenchymal absorption of CSF. The large number of model parameters that must be estimated from experimental data are a limitation of the proposed model.
The preliminary investigations presented here indicate that our assumed mechanical alterations resulting from the injection of anti β1 integrin antibodies provides the necessary environmental changes in the parenchyma for the development of hydrocephalus. A drop in interparenchymal pressure combined with the required increase in CSF absorption by the parenchyma (possibly due to osmotic pressures and aquaporins) creates the necessary conditions for ventricular enlargement. Add to this, the possibility that antibodies may decrease the elasticity of brain tissue and even more favourable conditions for hydrocephalus progression are created.
4. Summary
We investigated intramantle pressure gradients as a possible force to enlarge the ventricles and we presented a poroelastic model incorporating the effects of the antibodies on the tissue parameters. This analysis seems to indicate that the anti β1 integrin antibodies may provide a complete mechanism for hydrocephalus development when combined with a new pathway for fluid absorption, possibly due to osmotic pressures and the aquaporins. This promising new theory for the pathogenesis of hydrocephalus may lead to the possibility of pharmacological treatments for the condition and warrants further investigations both experimentally and mathematically.
Acknowledgements
This research was supported in part by the Canadian Institutes of Health Research (GN and MJ), by the Natural Sciences and Engineering Research Council of Canada (KPW), and by the National Cancer Institute, Award Number U54CA149233 (KPW). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
Contributor Information
KATHLEEN P. WILKIE, Center of Cancer Systems Biology, St. Elizabeth's Medical Center, Tufts University School of Medicine, Boston, MA, USA
GURJIT NAGRA, Faculty of Medicine, University of Toronto, Department of Laboratory Medicine and Pathobiology, Brain Sciences Program, Sunnybrook Health Sciences Centre, Toronto, ON, CAN.
MILES JOHNSTON, Faculty of Medicine, University of Toronto, Department of Laboratory Medicine and Pathobiology, Brain Sciences Program, Sunnybrook Health Sciences Centre, Toronto, ON, CAN.
References
- 1.Badaut J, Lasbennes F, Magistretti PJ, Regli L. Aquaporins in brain: distribution, physiology, and pathophysiology. J Cereb Blood Flow Metab. 2002;22:367–378. doi: 10.1097/00004647-200204000-00001. [DOI] [PubMed] [Google Scholar]
- 2.Begg R, Wilkie K. Proceedings of the OCCAM-Fields-MITACS Biomedical Problem Solving Workshop. Fields Institute; Toronto, Canada: 2009. A mechanism for ventricular expansion in communicating hydrocephalus. http://www.fields.utoronto.ca/programs/scientific/08-09/biomedical/ [Google Scholar]
- 3.Berg A, Rubin K, Reed RK. Cytochalasin D induces edema formation and lowering of interstitial fluid pressure in rat dermis. Am J Physiol Heart Circ Physiol. 2001;281:H7–13. doi: 10.1152/ajpheart.2001.281.1.H7. [DOI] [PubMed] [Google Scholar]
- 4.Bergsneider M, Egnor MR, Johnston M, Kranz D, Madsen JR, McAllister II JP, Stewart C, Walker ML, Williams MA. What we don't (but should) know about hydro-cephalus. J Neurosurg (3 Suppl Pediatrics) 2006;104:157–159. doi: 10.3171/ped.2006.104.3.157. [DOI] [PubMed] [Google Scholar]
- 5.Del Bigio MR. Cellular damage and prevention in childhood hydrocephalus. Brain Pathology. 2004;14:317–324. doi: 10.1111/j.1750-3639.2004.tb00071.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Del Bigio MR, McAllister II JP. In: Pathophysiology of hydrocephalus, Pediatric Neurosurgery. Choux M, Di Rocco R, Hockley AD AD, Walker ML, editors. Churchill Livingstone; 1999. [Google Scholar]
- 7.Biot MA. General theory of three-dimensional consolidation. J App Phys. 1941;12(2):155–164. [Google Scholar]
- 8.Bloch O, Manley GT. The role of aquaporin-4 in cerebral water transport and edema. Neurosurg Focus. 2007;22(5):E3. doi: 10.3171/foc.2007.22.5.4. [DOI] [PubMed] [Google Scholar]
- 9.Bondurant CP, Jimenez DF. Epidemiology of cerebrospinal fluid shunting. Pediatr Neurosurg. 1995;23:254–258. doi: 10.1159/000120968. [DOI] [PubMed] [Google Scholar]
- 10.Bradbury MW. The blood-brain barrier. Transport across the cerebral endothelium. Circ Res. 1985;57:213–222. doi: 10.1161/01.res.57.2.213. [DOI] [PubMed] [Google Scholar]
- 11.Drake JM, Kestle JR, Milner R, Cinalli G, Boop F, Piatt J, Jr, Haines S, Schiff SJ, Cochrane DD, Steinbok P, MacNeil N. Randomized trial of cerebrospinal fluid shunt valve design in pediatric hydrocephalus. Neurosurg. 1998;43:294–303. doi: 10.1097/00006123-199808000-00068. [DOI] [PubMed] [Google Scholar]
- 12.Egnor M, Zheng L, Rosiello A, Gutman F, Davis R. A model of pulsations in communicating hydrocephalus. Pediatr Neurosurg. 2002;36:281–303. doi: 10.1159/000063533. [DOI] [PubMed] [Google Scholar]
- 13.Fenstermacher JD. Volume regulation of the central nervous system. In: Staub NC, Taylor AE, editors. Edema (New York) Raven Press; 1984. pp. 383–404. [Google Scholar]
- 14.Fransen E, Lemmon V, Van CG, Vits L, Coucke P, Willems PJ. Crash syndrome: clinical spectrum of corpus callosum hypoplasia, retardation, adducted thumbs, spastic paraparesis and hydrocephalus due to mutations in one single gene L1. Eur J Hum Genet. 1995;3(5):273–284. doi: 10.1159/000472311. [DOI] [PubMed] [Google Scholar]
- 15.Grooms SY, Terracio L, Jones LS. Anatomical localization of β-1 integrin-like immunoreactivity in rat brain. Exp Neurol. 1993;122:253–259. doi: 10.1006/exnr.1993.1125. [DOI] [PubMed] [Google Scholar]
- 16.Gupta N, Park J, Solomon C, Kranz DA, Wrensch M, Wu YW. Long-term outcomes in patients with treated childhood hydrocephalus. J Neurosurg. 2007;106:334–339. doi: 10.3171/ped.2007.106.5.334. [DOI] [PubMed] [Google Scholar]
- 17.Hynes RO. Integrins: bidirectional, allosteric signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 18.Kang JK, Lee IW. Long-term follow-up of shunting therapy. Child's Nerv Syst. 1999;15(11–12):711–717. doi: 10.1007/s003810050460. [DOI] [PubMed] [Google Scholar]
- 19.Kobayashi H, Minami S, Itoh S, Shiraishi S, Yokoo H, Yanagita T, Uezono Y, Mohri M, Wada A. Aquaporin subtypes in rat cerebral microvessels. Neurosci Lett. 2001;297:163–166. doi: 10.1016/s0304-3940(00)01705-5. [DOI] [PubMed] [Google Scholar]
- 20.Koh L, Zakharov A, Johnston M. Integration of the subarachnoid space and lymphatics: Is it time to embrace a new concept of cerebrospinal fluid absorption? Cerebrospinal Fluid Res. 2005;2(6) doi: 10.1186/1743-8454-2-6. doi: 10.1186/1743–8454–2–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Levine DN. The pathogenesis of normal pressure hydrocephalus: a theoretical analysis. Bull Math Biol. 1999;61:875–916. doi: 10.1006/bulm.1999.0116. [DOI] [PubMed] [Google Scholar]
- 22.Levine DN. Intracranial pressure and ventricular expansion in hydrocephalus: have we been asking the wrong question? J Neurol Sci. 2008;269:1–11. doi: 10.1016/j.jns.2007.12.022. [DOI] [PubMed] [Google Scholar]
- 23.Linninger AA, Tsakiris C, Zhu DC, Xenos M, Roycewicz P, Danziger Z, Penn R. Pulsatile cerebrospinal fluid dynamics in the human brain. IEEE Trans Biomed Eng. 2005;52(4):557–565. doi: 10.1109/TBME.2005.844021. [DOI] [PubMed] [Google Scholar]
- 24.Manley GT, Fujimura M, Ma T, Noshita N, Filiz F, Bollen AW, Chan P, Verkman AS. Aquaporin-4 deletion in mice reduces brain edema after acute water intoxication and ischemic stroke. Nat Med. 2000;6:159–163. doi: 10.1038/72256. [DOI] [PubMed] [Google Scholar]
- 25.Marmarou A, Young HF, Aygok GA. Estimated incidence of normal pressure hydro-cephalus and shunt outcome in patients residing in assisted-living and extended-care facilities. Neurosurg Focus. 2007;22:E1. doi: 10.3171/foc.2007.22.4.2. [DOI] [PubMed] [Google Scholar]
- 26.Milhorat TH. Neurosurgery. In: Wilkins RH, Rengachary SS, editors. Neurosurgery (New York) McGraw-Hill; 1985. pp. 2135–2139. [Google Scholar]
- 27.Milner R, Campbell IL. The integrin family of cell adhesion molecules has multiple functions within the CNS. J Neurosci Res. 2002;69:286–291. doi: 10.1002/jnr.10321. [DOI] [PubMed] [Google Scholar]
- 28.Nagelhus EA, Mathiisen TM, Ottersen OP. Aquaporin-4 in the central nervous system: cellular and subcellular distribution and coexpression with KIR4.1. Neuroscience. 2004;129(4):905–913. doi: 10.1016/j.neuroscience.2004.08.053. [DOI] [PubMed] [Google Scholar]
- 29.Nagra G, Johnston MG. Impact of ageing on lymphatic cerebrospinal fluid absorption in the rat. Neuropathol Appl Neurobiol. 2007;33:684–691. doi: 10.1111/j.1365-2990.2007.00857.x. [DOI] [PubMed] [Google Scholar]
- 30.Nagra G, Koh L, Aubert I, Kim M, Johnston M. Intraventricular injection of antibodies to β1-integrins generates pressure gradients in the brain favoring hydrocephalus development in rats. Am J Physiol Regul Integr Comp Physiol. 2009;297(5):R1312–21. doi: 10.1152/ajpregu.00307.2009. [DOI] [PubMed] [Google Scholar]
- 31.Papadopoulos MC, Manley GT, Krishna S, Verkman AS. Aquaporin-4 facilitates reabsorption of excess fluid in vasogenic brain edema. FASEB J. 2004;18(11):1291–3. doi: 10.1096/fj.04-1723fje. [DOI] [PubMed] [Google Scholar]
- 32.Pasantes-Morales H, Cruz-Rangel S. Brain volume regulation: Osmolytes and aquaporin perspectives. Neuroscience. 2010;168(4):871–84. doi: 10.1016/j.neuroscience.2009.11.074. [DOI] [PubMed] [Google Scholar]
- 33.Patwardhan RV, Nanda A. Implanted ventricular shunts in the United States: the billion-dollar-a-year cost of hydrocephalus treatment. Neurosurg. 2005;56:139–145. doi: 10.1227/01.neu.0000146206.40375.41. [DOI] [PubMed] [Google Scholar]
- 34.Paulus W, Baur I, Schuppan D, Roggendorf W. Characterization of integrin receptors in normal and neoplastic human brain. Am J Pathol. 1993;143:154–163. [PMC free article] [PubMed] [Google Scholar]
- 35.Peña A, Harris NG, Bolton MD, Czosnyka M, Pickard JD. Communicating hydro-cephalus: the biomechanics of progressive ventricular enlargement revisited. Acta Neurochir Suppl. 2002;81:59–63. doi: 10.1007/978-3-7091-6738-0_15. [DOI] [PubMed] [Google Scholar]
- 36.Penn RD, Lee MC, Linninger AA, Miesel K, Lu SN, Stylos L. Pressure gradients in the brain in an experimental model of hydrocephalus. J Neurosurg. 2005;102:1069–1075. doi: 10.3171/jns.2005.102.6.1069. [DOI] [PubMed] [Google Scholar]
- 37.Reed RK, Rubin K, Wiig H, Rodt SA. Blockade of β1-integrins in skin causes edema through lowering of interstitial fluid pressure. Circ Res. 1992;71:978–983. doi: 10.1161/01.res.71.4.978. [DOI] [PubMed] [Google Scholar]
- 38.Rekate HL. Adults with hydrocephalus treated in infancy and childhood. Seminars in Neurosurg. 2002;13(1):19–28. [Google Scholar]
- 39.Robel S, Mori T, Zoubaa S, Schlegel J, Sirko S, Faissner A, Goebbels S, Dimou L, Gotz M. Conditional deletion of β1-integrin in astroglia causes partial reactive gliosis. Glia. 2009;57:1630–1647. doi: 10.1002/glia.20876. [DOI] [PubMed] [Google Scholar]
- 40.Rodt SA, Reed RK, Ljungstrom M, Gustafsson TO, Rubin K. The anti-inflammatory agent alpha-trinositol exerts its edema-preventing effects through modulation of β1 integrin function. Circ Res. 1994;75:942–948. doi: 10.1161/01.res.75.5.942. [DOI] [PubMed] [Google Scholar]
- 41.Rubin K, Sundberg C, Ahlen K, Reed RK. Integrins: transmembrane links between the extracellular matrix and the cell interior. In: Reed RK, McHale NG, Bert JL, Winlove CP, Laine GA, editors. Interstitium, Connective Tissue and Lymphatics (London) Portland Press Ltd.; 1995. pp. 29–40. [Google Scholar]
- 42.Shapiro K, Kohn IJ, Takei F, Zee C. Progressive ventricular enlargement in cats in the absence of transmantle pressure gradients. J Neurosurg. 1987;67:88–92. doi: 10.3171/jns.1987.67.1.0088. [DOI] [PubMed] [Google Scholar]
- 43.Smillie A, Sobey I, Molnar Z. A hydrostatic model of hydrocephalus. J Fluid Mech. 2005;539:417–443. [Google Scholar]
- 44.Stephensen H, Tisell M, Wikkelso C. There is no transmantle pressure gradient in communicating or noncommunicating hydrocephalus. Neurosurgery. 2002;50:763–771. doi: 10.1097/00006123-200204000-00016. [DOI] [PubMed] [Google Scholar]
- 45.Stewart C. What is hydrocephalus. 2007 http://www.brainchildfoundation.org/hydro.html.
- 46.Tenti G, Sivaloganathan S, Drake JM. Brain biomechanics: Steady-state consolidation theory of hydrocephalus. Can Appl Math Q. 1999;7(1):93–110. [Google Scholar]
- 47.Tenti G, Sivaloganathan S, Drake JM. The synchrony of arterial and CSF pulsations is not due to resonance. Pediatr Neurosurg. 2002;37(4):221–222. doi: 10.1159/000065400. [DOI] [PubMed] [Google Scholar]
- 48.Verkman AS, Binder DK, Bloch O, Auguste K, Papadopoulos MC. Three distinct roles of aquaporin-4 in brain function revealed by knockout mice. Biochim Biophys Acta. 2006;1758:1085–1093. doi: 10.1016/j.bbamem.2006.02.018. [DOI] [PubMed] [Google Scholar]
- 49.Walker ML. Looking at hydrocephalus: where are we now, where are we going? Child’s Nerv Syst. 2005;21:524–527. doi: 10.1007/s00381-005-1219-0. [DOI] [PubMed] [Google Scholar]
- 50.Wall M. Idiopathic intracranial hypertension (pseudotumor cerebri) Curr Neurol Neurosci Rep. 2008;8:87–93. [PubMed] [Google Scholar]
- 51.Wiig H, Rubin K, Reed RK. New and active role of the interstitium in control of interstitial fluid pressure: potential therapeutic consequences. Acta Anaesthesiol Scand. 2003;47(2):111–121. doi: 10.1034/j.1399-6576.2003.00050.x. [DOI] [PubMed] [Google Scholar]
- 52.Wilkie KP, Drapaca CS, Sivaloganathan S. A nonlinear viscoelastic fractional derivative model of infant hydrocephalus. Appl Math Comput. 2011;217:8693–704. [Google Scholar]
- 53.Woie K, Koller ME, Heyeraas KJ, Reed RK. Neurogenic inflammation in rat trachea is accompanied by increased negativity of interstitial fluid pressure. Circ Res. 1993;73:839–45. doi: 10.1161/01.res.73.5.839. [DOI] [PubMed] [Google Scholar]
- 54.Zhang J, Williams MA, Rigamonti D. Genetics of human hydrocephalus. J Neurol. 2006;253:1255–66. doi: 10.1007/s00415-006-0245-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Del Zoppo GJ, Milner R. Integrin-matrix interactions in the cerebral microvasculature. Arterioscler Thromb Vasc Biol. 2006;26:1966–1975. doi: 10.1161/01.ATV.0000232525.65682.a2. [DOI] [PubMed] [Google Scholar]