Abstract
Sexual traits vary tremendously in static allometry. This variation may be explained in part by body size-related differences in the strength of selection. We tested this hypothesis with in two populations of vervet monkeys, using estimates of the level of condition dependence for different morphological traits as a proxy for body size-related variation in the strength of selection. In support of the hypothesis, we found that the steepness of allometric slopes increased with the level of condition dependence. One trait of particular interest, the penis, had shallow allometric slopes and low levels of condition dependence, in agreement with one of the most consistent patterns yet detected in the study of allometry, that of genitalia exhibitting shallow allometries.
ADDITIONAL KEYWORDS: Chlorocebus, primate, scaling relationships, sexual selection
INTRODUCTION
Think about different athletes that interest you, and you will probably visualize differences in bodily proportions. How does this variation in proportions arise? This question may be asked with the quantitative framework of allometry, the study of how structure sizes scale on body size (Huxley 1932). The main descriptor of scaling is the allometric slope (b), which is obtained from log-log regressions of trait size on body size. When traits have b = 1, they vary in proportion to body size (they exhibit isometry). Traits with b > 1 are disproportionately large in large individuals and exhibit positive allometry (also known as hyperallometry). And traits with b < 1 are disproportionately small in large individuals and exhibit negative allometry (also known as hypoallometry). We refer to variation between b > 1 and b < 1 in terms of steep vs. shallow allometries, respectively.
Allometry can be studied at various levels: between species or higher taxa (in what is known as evolutionary allometry); within species among developmental stages (ontogenetic allometry); and within species among individuals of the same developmental stage (static allometry). At any level, variation in allometric patterns challenges biologists to provide explanations in terms of sources of selection and developmental constraints (Huxley 1932; Gould 2002; Eberhard et al., 2009). Here we focus on variation in static allometry.
Perhaps the greatest amount of variation in static allometry occurs in sexual traits. Some ornaments and weapons have very steep allometries (Kodric-Brown et al., 2006; Bonduriansky, 2007). But sexual ornaments may also show isometry, or even quite shallow allometries (Cuervo & Møller, 2001; Bonduriansky, 2007; Schulte–Hostedde et al., 2011). And it does not seem simple to predict which ornament will have what kind of allometry. The spectacular tail coverts of male resplendent quetzals, for example, scale shallowly with body size (with b = 0.38), whereas the apparently more modest central tail feathers of male common tailor birds scale very steeply with body size (b = 9.01; Cuervo & Møller, 2001). And then there is a large class of sexual traits, genitalia, that predominantly exhibit shallow allometries (Eberhard et al., 1998; Eberhard, 2009).
Why would sexual traits vary so much in their static allometry? Here we focus on a hypothesis that posits an interplay between the form of selection (stabilizing vs. directional) and body size-related differences in the net benefit of trait size increase (Bonduriansky, 2007; Eberhard et al., 2009; and see also Green, 1992; Eberhard et al., 1998; Bonduriansky & Day, 2003). According to this hypothesis, stabilizing selection on trait size favors shallow allometries (Eberhard et al., 1998, 2009). By contrast, the effect of directional selection varies according to whether the net benefits of increase in trait size vary with body size — i.e., according to whether the strength of net directional selection varies with body size (Bonduriansky, 2007; Eberhard et al., 2009). This is because selection favoring larger ornaments should result in isometry if males of all sizes benefit equally from larger ornaments; but it should result in steeper allometries if larger males benefit to a greater extent from larger ornaments; and it should result in shallower allometries if smaller males are the ones that most benefit from bearing larger ornaments (Eberhard et al., 2009; cf. Bonduriansky & Day, 2003; Bonduriansky, 2007).
This hypothesis will be challenging to test in full, because this would require measuring the form and strength of selection, asking whether the latter varies with body size, and assembling a collection of such measures for a number of species. Nevertheless, partial tests of the hypothesis are possible. There is evidence that traits under stabilizing selection have shallower allometries than traits under directional selection (Rodríguez & Al-Wathiqui, 2012a; Rodríguez et al., 2014a). Another test approximated body size-related variation in the net benefits of trait increase with variation in the level of condition dependence of different traits, finding that more highly condition dependent traits under directional selection have steeper allometries (Rodríguez et al., 2014a). This test used behavioral traits, however, and it remains to be seen whether morphological traits follow the same patterns.
Here we focus on body size-related variation in the net benefits of trait increase, and we test its role with morphological traits. We approximate this body size-related variation in the net benefits of trait increase with variation in the level of condition dependence of different traits. The rationale for this proxy is that traits whose expression is related to individual condition are likely to have greater costs of expression for smaller individuals (Bonduriansky, 2007; see also Rowe & Houle, 1996; Shingleton et al., 2007). In other words, we reason that the expression of costly traits (those related to condition) should be relatively cheaper for larger individuals, and thereby bring them higher benefits.
This rationale leads to the prediction that there should be a positive relationship between the level to which different structures are related to individual condition and the steepness of their allometry. This is a simplistic prediction, as it assumes that all traits are under directional selection. Nevertheless, support for the prediction would help explain variation in allometry, although lack of support would be inconclusive.
We tested this prediction with a suite of morphological traits in two populations of vervet monkeys, Chlorocebus aethiops (Primates: Cercopithecidae) (Fig 1). We tested the prediction in three ways. First, we assessed the relationship between b and condition dependence across all traits. Second, we categorized traits according to expected differences in b and condition dependence, and we tested for a relationship between b and condition dependence across categories (Table 1). We placed each sexual trait in its own category to explore variation in condition dependence and b among them, as follows: (i) The penis. We focus on vervet penes because genitalia predominantly exhibit shallow static allometries (Eberhard et al., 1998; Eberhard, 2009; Voje et al., 2014). An apparent exception in vertebrates may be due to mixing of adult age groups (Eberhard, 2009; Rodríguez et al., in review), and our b estimates account for this. Also, genitalia tend to show low condition dependence (Arnqvist & Thornhill, 1998; House & Simmons, 2007; Rodríguez & Al-Wathiqui, 2011). (ii) The testes. Both the penis and the testes are part of a colorful sexual display (Cramer et al., 2013) (Fig. 1). (iii) The canines. The other categories correspond to: (iv) non-sexual body traits (e.g., thigh length); and (v) non-sexual body traits involving girth measurements (e.g., thigh girth), which are closely related to condition (Rutenberg et al., 1987). Third, a difference in overall condition between populations (Table 1) allowed us to test for an effect on the expression of trait allometries. We reasoned that the relationship between condition dependence and b should be stronger in the population in better condition, where variation in trait developmental architecture should be emphasized, whereas such variation would be curbed in the population in worse condition.
Figure 1.

An adult male vervet monkey, Chlorocebus aethiops pygerythrus, from South Africa. Photo by Jennifer Danzy Cramer.
Table 1.
Measures that we used to describe trait allometries in two vervet monkey populations. All traits were measured in cm unless otherwise indicated. We report least square mean ± SE values and tests for population differences in trait means (see text). Significant differences in boldface
| type of trait | trait | C. a. sabaeus, St Kitts and Nevis (mean ± SE, n) | C. a. pygerythrus, South Africa (mean ± SE, n) | F, P |
|---|---|---|---|---|
| body mass | mass (kg) | 5.95 ± 0.26, 104 | 5.47 ± 0.24, 99 | 10.47, 0.0014 |
| estimate of body size | lower leg length | 19.9 ± 0.3, 89 | 19.8 ± 0.2, 99 | 0.69, 0.41 |
| body traits (lengths) | body | 38.9 ± 1.7, 89 | 39.4 ± 1.7, 99 | 0.61, 0.44 |
| head (excl. the face) | 10.5 ± 0.3, 89 | 10.5 ± 0.3, 89 | 0.003, 0.96 | |
| upper arm | 16.4 ± 0.4, 89 | 15.6 ± 0.4, 98 | 17.26, < 0.0001 | |
| lower arm | 16.2 ± 0.3, 89 | 16.0 ± 0.3, 97 | 1.64, 0.21 | |
| upper leg (thigh) | 18.6 ± 0.6, 89 | 18.2 ± 0.5, 99 | 3.50, 0.06 | |
| sternal notch-pubic symphasis | 36.5 ± 9757, 80 | 37.0 ± 9600, 97 | 0.00, 1.00 | |
| girth traits | chest | 35.7 ± 1.6, 89 | 32.8 ± 1.6, 98 | 43.19, < 0.0001 |
| upper arm | 15.4 ± 0.8, 84 | 14.1 ± 0.8, 98 | 19.23, < 0.0001 | |
| upper leg (thigh) | 22.4 ± 0.9, 84 | 21.7 ± 0.8, 99 | 2.83, 0.09 | |
| body mass indeces | human BMI * | 7.9 ± 0.5, 70 | 7.2 ± 0.5, 89 | 12.62, 0.0005 |
| primate BMI ** | 39.9 ± 4.3, 70 | 36.0 ± 4.2, 99 | 10.35, 0.0016 | |
| condition | mass~body length residuals | 0.67 ± 0.38, 89 | 0.13 ± 0.37, 94 | 16.74, < 0.0001 |
| sexual traits | canine length | 1.9 ± 0.2, 22 | 1.7 ± 0.03, 87 | 1.43, 0.34 |
| testes volume (cc) | 15.4 ± 1.1, 91 | 15.9 ± 0.6, 95 | 0.21, 0.66 | |
| penis length | 6.6 ± 0.4, 32 | 6.9 ± 0.3, 88 | 0.94, 0.33 |
human BMI = mass / (head + body + upper leg + lower leg / 100)2
primate BMI = mass / (body / 100)2
These tests rely on variation among trait types to address the problem of variation in sexual allometries. We consider this to be a strength — if correct, the hypothesis identifies a general rule about the evolution and expression of allometry.
MATERIALS AND METHODS
We worked with two populations of vervet monkeys, representing two subspecies. We chose these two populations from a broader project (The International Vervet Research Consortium) because they offered the largest sample sizes for the traits in which we were interested. We sampled sexually mature males of C. a. sabaeus at a colony at St. Kitts and Nevis, and of C. a. pygerythrus at South Africa. Measurements were taken by researchers who were members of the International Vervet Research Consortium. In our analyses, we took measurer ID into account to reduce the potential for among-measurer differences to influence our results. Vervets were wild-caught according to the procedure described by Grobler & Turner (2010). Briefly, vervets were anesthesized while in traps, and measurements were taken from the anesthetized individuals. Vervets remained anesthetized for approx. 30 min, and were then freed and allowed to return to the wild after data collection. Individual micro-chipping ensured that each male was measured only once. Researchers used measuring tape to take linear measures of seven body traits, three sexual traits (including penis length), and measures of the girth of three body parts (Table 1) (details in Turner et al., 1997). Sample sizes vary among traits (Table 1) because it was not always possible to take all measurements for all individuals — vervets were measured only while sedation lasted, and they were never given additional sedation to complete measures. Our sample included three age categories of sexually mature vervet males (with fully developed testes). Individuals were assigned to one of the three age categories (subadult, mature adult, older adult) according their stage in the dental eruption sequence (details in Cramer et al., 2013).
Estimating allometric slopes (b)
We conducted all analyses in JMP (v. 7.0.1) (SAS Institute, Cary, NC, USA). We used OLS regression of log10-log10 data to estimate b. There has been debate about the use of OLS regression in studies of allometry, due to the concern that it may bias estimates of b downwards by not taking into account measurement error in the x-axis (e.g., Green, 1999). However, recent work shows that OLS regression does not underestimate b unless measurement error is very large (Al-Wathiqui & Rodríguez, 2011; Kilmer & Rodríguez, in prep.). Further, a popular alternative (RMA regression) confounds scaling with dispersion (it estimates b with the ratio of the standard deviations in x and y; Eberhard et al., 1999), and it may force apparent isometry (b = 1) due to the variance-homogenizing effect of the log-log transformation. OLS regression is therefore indicated for allometric studies (Eberhard et al., 1999; Voje & Hansen 2013; Cassidy et al., 2014; Voje et al., 2014; Kilmer & Rodríguez, in prep.).
We approximated body size (x-axis in allometric plots) with the body measurement that we considered to have the best-defined landmarks, lower leg length (Table 1). We were concerned that body length (Table 1) might not have such strictly defined landmarks. Lower leg length was significantly correlated with body length and mass (Pearson product-moment correlation pooling across all individuals: r = 0.28 and 0.50, respectively; P < 0.0001 in both cases), and thus offers a good proxy for body size. Since there is no concern that measurement error in y may bias OLS regression, we retained body length as a y-axis trait. To include testes volume in allometric analyses we used the log10 of the cubic root of the volume measures.
Our estimates of b had to account for two potential confounding factors, for which we added terms to the basic standard least squares statistical model used to estimate b, as follows: To account for potential measurer differences, we included terms for measurer ID and its interaction with the x-axis (random terms, REML method). We also needed to account for variation in the age of the adult vervets sampled. In animals that continue to grow at least some structures during adulthood, as in vertebrates, mixing individuals of different adult ages confounds static allometry with ontogenetic allometry and may overestimate b (Eberhard, 2009; Rodríguez et al., in review). For example, if genitalia reach full size at an intermediate adult age, they might appear to have a steeper allometry across adult ages than among adults of comparable age. We therefore included terms for age and its interaction with the x-axis. An alternative is to use only individuals of one adult age category (results of which we also report), but our approach better prevents overestimation of b (Rodríguez et al., in review).
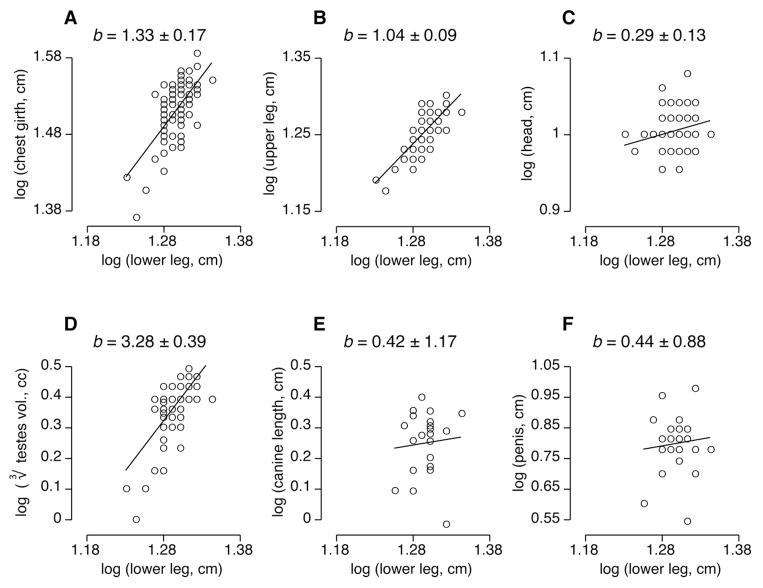
We show examples of the raw data and b estimates in Fig. 2. These b values then became the data for our tests. We use b estimates regardless of whether they are significantly different from zero, because we view them as descriptors of relative allometric steepness (cf. Eberhard et al., 1998). This approach emphasizes effect sizes rather than statistical significance (Nakagawa & Cuthill, 2007).
Figure 2.
Examples of allometric (log10-log10) plots, showing how different structures scale relative to the length of lower leg (our estimate of body size) in vervet monkeys. All x-axes span two log units; y-axes span two (A–C) or five log units (D–E). (A) Chest girth shows weak positive allometry (b > 1). (B) The length of the upper leg shows near perfect isometry (b = 1). (C) The head shows negative allometry (b < 1). Allometric slopes (b) given ± 1 SE. Data from the St. Kitts and Nevis site for males of all adult ages for illustrative purposes.
We also tested for population differences in trait allometries and sizes. To test for differences in b, we added to the above models a population × lower leg length interaction. We do not report these full models to save space; instead, we focus on the interaction. To test for population differences in trait means, we used models with each trait as the dependent variable and the following independent variables: population, measurer ID (random term, REML method), and adult age category. This is analogous to testing for differences in trait intercepts in allometry plots, but focusing on means. We report population term from these models.
Testing for a relationshp between b and condition dependence
Estimating individual condition and trait levels of condition dependence
To estimate the level of condition dependence for each trait, we first calculated individual condition for each male, and we then related variation in condition to variation in trait sizes. We consider individuals that are relatively heavy for their size to be in better condition than individuals that are light for their size. This view of condition is based on resources acquired and carried on the body (e.g., muscle and fat; Hunt et al., 2004), rather than on the health of cellular processes (Hill, 2011). Both views are important, but our measure allowed field sampling with minimal disturbance for the vervets. Alternatives such as experimental manipulation of condition with diet treatments (Kotiaho, 1999; Tomkins et al., 2004) were not an option for this study.
We tested several alternatives for describing mass relative to body size. These included the residuals of an OLS regression of mass on body length; human and primate body mass indices (BMIs); and the girth of the chest, upper arm and thigh (Table 1). All of these measures were highly correlated with each other. For example, the mean for Pearson’s correlation between the mass~body length residuals and the other condition measures was r = 0.77 ± 0.02 (averaging within and then across populations). We selected the mass~body length residuals as our measure of individual condition. We are aware of debate around this measure (Jakob et al., 1996; Green, 2001; Tomkins et al., 2004; Peig & Green, 2009, 2010). But we consider that it is well suited for our purposes. It has been validated as a metric of general applicability (Schulte–Hostedde et al., 2005). Also, of particular relevance for our study, the girth of the upper arm correlates well with lean muscle mass in primates (Rutenberg et al., 1987), and indeed this was one of the measures that correlated highly with our metric (see above). We used the mass~body length residuals rather than upper arm girth itself because the former is more widely used.
Once we estimated individual condition, we calculated the level of condition dependence of each trait. We used models with condition as the independent variable, and z-scores for each trait as the dependent variable. With z-scores, the slope of the trait~condition relationship is equivalent to Pearson’s correlation (r). This r was the measure of condition dependence for each trait. Note that our measure of condition is independent of body size — a male can be in good or poor condition irrespective of his size — and therefore independent of our description of allometry; e.g., a male can bear a relatively large or small trait irrespective of whether he his relatively heavy or light for his size. Thus, the b~condition dependence relationship asks whether relatively heavy or light males produce larger or smaller traits across body sizes.
Testing the condition dependence prediction
We tested this prediction in three ways. First, we asked if b varied with the level of condition dependence of each trait. The statistical model included b as the dependent variable, and the following independent variables: condition dependence, population, and their interaction (Table 2). In this test, the data (b and condition dependence) come from traits that are correlated with each other, which introduces the risk of spurious significance. But the usual correctives are not appropriate for our study. Generating suites of uncorrelated traits with Principal Components Analysis would detract from our focus on traits of interest (e.g., the penis). And corrections against spurious significance compromise statistical power (Nakagawa, 2004). But note that this problem is likely to be minor in our tests: our data involve allometric scalings and relationships between scalings and condition dependence, which are more likely to be independent of each other than the traits themselves. Also, correlations between traits were often weak: range: r = 0.03–0.86; mean: r = 0.40; median: r = 0.41; and 75% were below 0.53. Nevertheless, we took advantage of a pattern in these correlations to assess the risk of spurious significance. Correlations between traits on the same limb were higher (mean r = 0.64) than correlations between traits on different body parts (mean r = 0.38) (F1,153 = 5.16, P = 0.024). We therefore repeated the above test with only one trait per limb. Results robust to this exclusion would suggest that our analysis is not unduly affected by data obtained from correlated traits.
Table 2.
Test of the condition dependence hypothesis to explain variation in trait allometries, with two vervet monkey populations. Significant terms in boldface
| factor | df num, denom | F, P |
|---|---|---|
| condition dependence | 1, 20 | 8.54, 0.0084 |
| population | 1, 20 | 0.37, 0.55 |
| condition dependence × population | 1, 20 | 1.38, 0.25 |
Second, we assessed the relationship between condition dependence and b across categories for different trait types: penis; testes; canines; body traits; and girth body traits. We tested for differences in b and condition dependence among these trait types with standard least squares models including the following independent variables: trait type, population, and their interaction (Table 3). We obtained least square mean ± SE values for condition dependence and b for these trait types from these models, and we calculated Pearson’s correlation (r) between the mean values for b and condition dependence.
Table 3.
Comparison of allometric slopes (b) and condition dependence among trait types (penis, testes, canines, body traits, girth body traits; see text) in vervet monkeys. Significant terms in boldface
| test for differences in b | test for differences in condition dependence | |||
|---|---|---|---|---|
| factor | df num, denom | F, P | df num, denom | F, P |
| trait type | 4, 14 | 11.19, 0.0003 | 4, 14 | 3.40, 0.038 |
| population | 1, 14 | 0.22, 0.65 | 1, 14 | 0.00, 0.99 |
| trait type × population | 4, 14 | 5.99, 0.005 | 4, 14 | 0.58, 0.68 |
Third, we tested for population differences in the relationship between b and condition dependence. This difference is tested by the condition dependence × population interaction in the above model (Tables 2).
RESULTS
We tested for a positive relationship between a trait’s level of condition dependence and the steepness of its allometric slope (b). We found this relationship in both populations (Table 2; Fig. 3A). Excluding the non-significant interaction did not alter the result (term for condition dependence: F1,21 = 8.39, P = 0.0086). The pattern also remained when we repeated the test including only one trait per limb, although the term for condition dependence became marginally-significant (F1,13 = 4.39, P = 0.056) due to lowered power. Thus, the pattern that we detect is not forced by correlated traits. The result was also the same with males of only one age category (mature adults): term for condition dependence: F1,20 = 5.11, P = 0.035.
Figure 3.
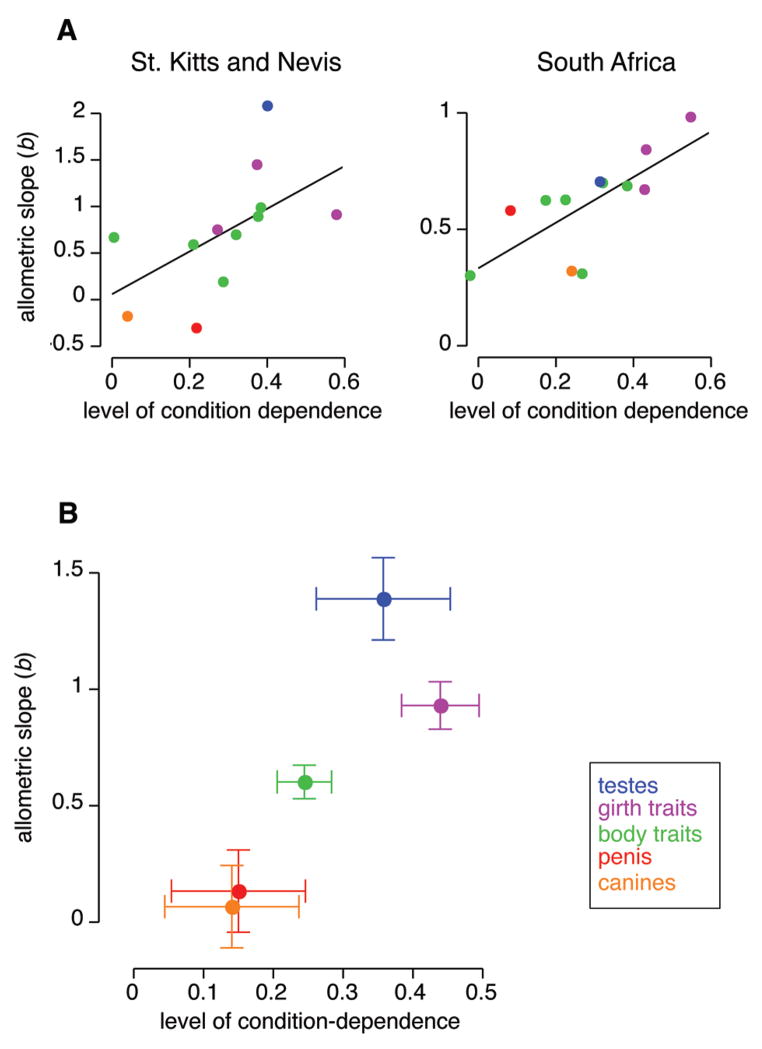
Relationship between the level of condition dependence of different traits and their allometric slope (b), in two vervet monkey populations. (A) Across all traits. (B) Across trait types, showing least square means ± 1 SE.
We then assessed the b~condition dependence relationship across trait types. Both b (y-axis in Fig. 3B) and condition dependence (x-axis in Fig. 3B) varied significantly among trait types (Table 3). Populations varied in how b (but not condition dependence) differed among trait types (compare interaction terms in Table 3; Fig. 3A). Across trait types, the b~condition dependence relationship was strong and positive (Fig. 3B). The correlation between the least square mean values for b and condition dependence among trait types was r = 0.87, P = 0.058; marginal significance is due to low power with n = 5 data points, but the relationship is of large effect size (Nakagawa & Cuthill, 2007).
The b~condition dependence relationship differed between populations, with b having a broader range in the population in better condition (St. Kitts and Nevis) (Fig. 3A). However, this difference was not significant (interaction term in Table 2).
We found population differences in several traits (Table 1), but little evidence of differences in allometry. The sexual traits varied the most in allometry (Fig. 3), but the lower leg × population interaction was significant only for the penis (Table 4), and this variation remained within the realm of negative allometry (red symbols in Fig. 3A). The trait that varied the least in allometry was the head (b = 0.18 for St. Kitts and Nevis; b = 0.31 for South Africa).
Table 4.
Test for population differences in vervet monkey allometry. We report only the term that tests for population differences (lower leg × population interaction) extracted from the full models detailed in the text. Significant term in boldface
| trait | test for the interaction | |
|---|---|---|
| df num, denom | F, P | |
| body | 1, 1 | 3.23, 0.32 |
| head | 1, 2.889 | 0.006, 0.94 |
| upper arm | 1, 46.66 | 0.11, 0.74 |
| lower arm | 1, 66.75 | 0.00, 0.99 |
| upper leg (thigh) | 1, 127 | 0.16, 0.69 |
| sternum-pubis | 1, 1 | 0.09, 0.82 |
| chest girth | 1, 162.7 | 0.62, 0.43 |
| upper arm girth | 1, 136 | 0.84, 0.36 |
| lower leg (thigh) girth | 1, 76.33 | 0.46, 0.50 |
| canine | 1, 62.38 | 0.62, 0.44 |
| testes | 1, 171.4 | 0.20, 0.65 |
| penis | 1, 109.4 | 8.26, 0.005 |
DISCUSSION
Study of the allometry of sexual traits reveals an astounding amount of variation. This variation may be explained in part by an interplay between the form of selection and body size-related differences in the strength of selection (Bonduriansky, 2007; Eberhard et al., 2009). We tested a component of this hypothesis with morphological traits in vervet monkeys, using trait differences in condition dependence as a proxy for body size-related variation in the net benefits of trait increase. We found support for the prediction that there should be a positive relationship between condition dependence and the steepness of allometry, and this pattern was robust across diverse trait types. But we found only weak support for the prediction that variation in the expression of trait allometries as a function of condition dependence would be greater for a population in better overall condition. We therefore interpret our findings as tentative support for the hypothesis.
We also offer some caveats to this interpretation. First, further work with other study species is required to assess how vulnerable our findings are to problems arising from use of data generated from traits correlated with each other. Second, our test involved over-simplification of the full hypothesis: we lack information about the form of selection, and we approximated body size-related variation in the net benefits of trait increase with the level of condition dependence of different traits. Thus, our test was asymmetric: the support we find is encouraging, but negative results would have been inconclusive. Nevertheless, to date there is agreement among studies using morphological and behavioral traits that both the form of selection and condition dependence have predictable influences allometry (Rodríguez & Al-Wathiqui 2012a; Rodríguez et al., 2014a; this study). Third, we categorized several body traits as non-sexual (Table 1), but vervets exhibit sexual size dimorphism (Turner et al., 1997). Thus, overall male size in vervets reflects the effect of sexual selection (Lindenfors et al., 2007). Although this represents sex differences in intercept rather than slope, it may also influence the evolution of trait allometries. Addressing this interesting question will require further work comparing male and female allometries. Finally, we note that the evolution of allometry is likely to be influenced by many factors. For instance, sexual structures with forceful or coercive functions (e.g., weapons) may evolve steeper allometries than sexual structures that function in other ways (e.g., displays) (Eberhard, 2009; cf. Rodríguez et al., 2014a). Also along those lines, whether structures function by contacting the body of the mating partner or from a distance may also influence allometry (Eberhard et al., 1998; Eberhard, 2002, 2009; Kilmer & Rodríguez, unpub.). The combinations of functions that traits perform (e.g., genitalia have sexually-selected functions such as contact courtship and naturally-selected functions like insemination) may also influence the evolution of allometries (House & Simmons, 2003; Eberhard, 2009; Rodríguez & Al-Wathiqui, 2012a).
Against the background of high diversity in sexual allometries, the predominantly shallow allometry of animal genitalia stands out as a remarkably consistent pattern, with the apparent exception of vertebrate genitalia (Eberhard, 2009). We were thus especially interested in the allometry of vervet penes. After accounting for variation in adult age, which may bias b estimates upward (Rodríguez et al., in review), vervet penes showed negative allometries and low condition dependence, in agreement with the overall pattern across animal groups (Eberhard et al., 1998; Eberhard, 2009). This offers insight into potential sources of selection on vervet penes. In spite of their showiness (Fig. 1), they are unlikely to have evolved as indicators of size or condition, or as coercive structures (cf. Eberhard et al., 1998, 2009). The head also had consistently shallow allometries — in agreement with a widespread trend for brain size to exhibit shallow static, developmental, and evolutionary allometries (Huxley, 1932; Striedter, 2005) — although it did not have especially low levels of condition dependence, being below the 20th percentile for b, but only below the 48th percentile for condition dependence.
Implicit in our discussion of the evolution of allometry is the notion that it can be molded by selection. There is, however, debate on whether selection can modify allometry (Eberhard & Gutiérrez, 1991; Emlen & Nijhout, 2000; Frankino et al., 2005; Eberhard et al., 2009), or whether such patterns mainly represent constraints (Gould, 2002; and see Egset et al., 2011, 2012). We take the large amount of variation in sexual allometries (Cuervo & Møller, 2001; Bonduriansky, 2007; Schulte–Hostedde et al., 2011) as suggestive of their potential to be shaped by selection. Also suggestive are the relationship between b and condition dependence (this study; Rodríguez et al., 2014a), and variation in allometry according to the form of selection on different traits (Rodríguez & Al-Wathiqui 2012a; Rodríguez et al., 2014a). Further, evidence of genetic variation in how allometry responds to environmental inputs during development — i.e, of genotype × environment interaction in allometry (Rodríguez & Al-Wathiqui, 2012b) — suggests that allometry may respond differently to selection in different environments. Finally, we point to evidence of (slow) evolutionary divergence in allometry (Voje & Hansen, 2013; Voje et al., 2014). In our comparison of two vervet monkey populations, we found that trait sizes varied more commonly than trait allometries. But our sample of only two populations may underestimate the extent of divergence in trait allometries.
We conclude by emphasizing that a complete explanation for the evolution of allometry will likely involve many variables. It is encouraging, however, that approximations such as ours can explain some of the variation observed in trait allometries.
Acknowledgments
We thank Gerlinde Höbel, Joey Kilmer, and three anonymous reviewers for constructive comments to the manuscript. We are indebted to the individuals who participated in field work for the International Vervet Research Consortium. We especially acknowledge the veterinarians who worked in the field — Lizanne Meiring, Peter How, Murray Stokoe, Ben Kigbu. Permissions to conduct this work were graciously granted from the Department of Environmental Affairs of the Republic of South Africa, and the Provincial Departments of Environmental Affairs of the South African Provinces of the Free State, Eastern Cape, KwaZulu Natal and Limpopo. We also acknowledge permissions from the St. Kitts Biomedical Research Fundation. We are indebted to the University of the Free State, South Africa, for logistic support. IACUC and ARC permissions for this project were obtained from the University of Wisconsin-Milwaukee and the University of California, Los Angeles. This research was supported by NIH grant R01RR0163009.
References
- Al-Wathiqui N, Rodríguez RL. Allometric slopes not underestimated by Ordinary Least Squares regression. Annals of the Entomological Society of America. 2011;104:562–566. [Google Scholar]
- Arnqvist G, Thornhill R. Evolution of animal genitalia: patterns of phenotypic and genotypic variation and condition dependence of genital and non-genital morphology in water strider (Heteroptera: Gerridae: Insecta) Genetical Research. 1998;71:193–212. [Google Scholar]
- Bonduriansky R. Sexual selection and allometry: a critical reappraisal of the evidence and ideas. Evolution. 2007;61:838–849. doi: 10.1111/j.1558-5646.2007.00081.x. [DOI] [PubMed] [Google Scholar]
- Bonduriansky R, Day T. The evolution of static allometry in sexually selected traits. Evolution. 2003;57:2450–2458. doi: 10.1111/j.0014-3820.2003.tb01490.x. [DOI] [PubMed] [Google Scholar]
- Cassidy EJ, Bath E, Chenoweth SF, Bonduriansky R. Sex–specific patterns of morphological diversification: evolution of reaction norms and static allometries in neriid flies. Evolution. 2014;68:368–383. doi: 10.1111/evo.12276. [DOI] [PubMed] [Google Scholar]
- Cramer JD, Gaetano TJ, Gray JP, Grobler JP, Lorenz J, Freimer N, Schmitt CA, Turner TR. Variation in scrotal color among widely distributed vervet monkey populations (C. a. pygerythrus and C. a. sabaeus) American Journal of Primatology. 2013;75:752–762. doi: 10.1002/ajp.22156. [DOI] [PubMed] [Google Scholar]
- Cuervo JJ, Møller AP. Components of phenotypic variation in avian ornamental and non–ornamental feathers. Evolutionary Ecology. 2001;25:53–72. [Google Scholar]
- Eberhard WG. The relation between aggressive and sexual behavior and allometry in Palaeosepsis dentatiformis flies (Diptera: Sepsidae) Journal of the Kansas Entomological Society. 2002;75:317–332. [Google Scholar]
- Eberhard WG. Static allometry and animal genitalia. Evolution. 2009;63:48–66. doi: 10.1111/j.1558-5646.2008.00528.x. [DOI] [PubMed] [Google Scholar]
- Eberhard WG, Gutiérrez EE. Male dimorphisms in beetles and earwigs and the question of developmental constraints. Evolution. 1991;45:18–28. doi: 10.1111/j.1558-5646.1991.tb05262.x. [DOI] [PubMed] [Google Scholar]
- Eberhard WG, Huber BA, Rodríguez RL, Briceño RD, Salas I, Rodríguez V. One size fits all? Relationships between the size and degree of variation in genitalia and other body parts in twenty species of insects and spiders. Evolution. 1998;52:415–431. doi: 10.1111/j.1558-5646.1998.tb01642.x. [DOI] [PubMed] [Google Scholar]
- Eberhard WG, Huber BA, Rodríguez RL. Don’t forget the biology: a reply to Green. Evolution. 1999;53:1624–1627. doi: 10.1111/j.1558-5646.1999.tb05428.x. [DOI] [PubMed] [Google Scholar]
- Eberhard WG, Rodríguez RL, Polihronakis M. Pitfalls in understanding the functional significance of genital allometry. Journal of Evolutionary Biology. 2009;22:435–445. doi: 10.1111/j.1420-9101.2008.01654.x. [DOI] [PubMed] [Google Scholar]
- Egset CK, Bolstad GH, Rosenqvist G, Endler JA, Pélabon C. Geographical variation in allometry in the guppy (Poecilia reticulata) Journal of Evolutionary Biology. 2011;24:2631–2638. doi: 10.1111/j.1420-9101.2011.02387.x. [DOI] [PubMed] [Google Scholar]
- Egset CK, Hansen TF, Le Rouzic A, Bolstad GH, Rosenqvist G, Pélabon C. Artificial selection on allometry: change in elevation but not slope. Journal of Evolutionary Biology. 2012;25:938–948. doi: 10.1111/j.1420-9101.2012.02487.x. [DOI] [PubMed] [Google Scholar]
- Emlen DJ, Nijhout HF. The development and evolution of exaggerated morphologies in insects. Annual Review of Entomology. 2000;45:661–708. doi: 10.1146/annurev.ento.45.1.661. [DOI] [PubMed] [Google Scholar]
- Frankino WA, Zwaan BJ, Stern DL, Brakefield PM. Natural selection and developmental constraints in the evolution of allometries. Science. 2005;307:718–720. doi: 10.1126/science.1105409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gould SJ. The structure of evolutionary thought. Cambridge, MA: Belknap Press; 2002. [Google Scholar]
- Green AJ. Positive allometry is likely with mate choice, competitive display and other functions. Animal Behaviour. 1992;43:170–172. [Google Scholar]
- Green AJ. Allometry of genitalia in insects and spiders: one size does not fit all. Evolution. 1999;53:1621–1624. doi: 10.1111/j.1558-5646.1999.tb05427.x. [DOI] [PubMed] [Google Scholar]
- Green AJ. Mass/length residuals: measures of body condition or generators of spurious results? Ecology. 2001;82:1473–1483. [Google Scholar]
- Grobler JP, Turner TR. A novel trap design for the collection and sedation of vervet monkeys (Chlorocebus aethiops) South African Journal of Wildlife Research. 2010;40:163–168. [Google Scholar]
- Hill GE. Condition-dependent traits as signals of the functionality of vital cellular processes. Ecology Letters. 2011;14:625–634. doi: 10.1111/j.1461-0248.2011.01622.x. [DOI] [PubMed] [Google Scholar]
- House CM, Simmons LW. Genital morphology and fertilization success in the dung beetle Onthophagus taurus: an example of sexually selected male genitalia. Proceedings of the Royal Society of London B. 2003;270:447–455. doi: 10.1098/rspb.2002.2266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- House CM, Simmons LW. No evidence for condition-dependent expression of male genitalia in the dung beetle Onthophagus taurus. Journal of Evolutionary Biology. 2007;20:1322–1332. doi: 10.1111/j.1420-9101.2007.01346.x. [DOI] [PubMed] [Google Scholar]
- Hunt J, Bussière L, Jennions MD, Brooks R. What is genetic quality? Trends in Ecology & Evolution. 2004;19:329–333. doi: 10.1016/j.tree.2004.03.035. [DOI] [PubMed] [Google Scholar]
- Huxley JS. Problems of relative growth. London, UK: Methuen & Co; 1932. (Republished by Ulan Press.) [Google Scholar]
- Jakob EM, Marshall SD, Uetz GW. Estimating fitness: a comparison of body condition indices. Oikos. 1996;77:61–67. [Google Scholar]
- Kilmer JT, Rodríguez RL. OLS regression is indicated for allometric studies. doi: 10.1111/jeb.12986. In prep. [DOI] [PubMed] [Google Scholar]
- Kodric-Brown A, Sibly RM, Brown JH. The allometry of ornaments and weapons. Proceedings of the National Academy of Sciencies USA. 2006;103:8733–8738. doi: 10.1073/pnas.0602994103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kotiaho JS. Estimating fitness: comparison of body condition indices revisited. Oikos. 1999;87:399–400. [Google Scholar]
- Lindenfors P, Gittleman JL, Jones KE. Sexual size dimorphism in mammals. In: Fairbairn DJ, Blackenhorn WU, Székely T, editors. Sex, size, and gender roles. Evolutionary studies of sexual size dimorphism. New York: Oxford University Press; 2007. pp. 16–26. [Google Scholar]
- Mcardle BH. The structural relationship-regression in biology. Canadian Journal of Zoology. 1988;66:2329–2339. [Google Scholar]
- Nakagawa S. A farewell to Bonferroni: the problems of low statistical power and publication bias. Behavioral Ecology. 2004;15:1044–1045. [Google Scholar]
- Nakagawa S, Cuthill IC. Effect size, confidence interval and statistical significance: a practical guide for biologists. Biological Reviews. 2007;82:591–605. doi: 10.1111/j.1469-185X.2007.00027.x. [DOI] [PubMed] [Google Scholar]
- Peig J, Green AJ. New perspectives for estimating body condition from mass/length data: the scaled mass index as an alternative method. Oikos. 2009;118:1883–1891. [Google Scholar]
- Peig J, Green AJ. The paradigm of body condition: a critical reappraisal of current methods based on mass and length. Functional Ecology. 2010;24:1323–1332. [Google Scholar]
- Rodríguez RL, Al–Wathiqui N. Genotype × environment interaction is weaker in genitalia than in mating signals and body traits in Enchenopa treehoppers (Hemiptera: Membracidae) Genetica. 2011;139:871–884. doi: 10.1007/s10709-011-9591-z. [DOI] [PubMed] [Google Scholar]
- Rodríguez RL, Al–Wathiqui N. Causes of variation in sexual allometry: a case study with the mating signals and genitalia of Enchenopa treehoppers (Hemiptera: Membracidae) Ethology Ecology & Evolution. 2012a;24:187–197. [Google Scholar]
- Rodríguez RL, Al–Wathiqui N. Genotype × environment interaction in the allometry of body, genitalia, and signal traits in Enchenopa treehoppers (Hemiptera: Membracidae) Biological Journal of the Linnean Society. 2012b;105:187–196. [Google Scholar]
- Rodríguez RL, Araya-Salas M, Gray DA, Reichert MS, Symes LB, Wilkins MR, Safran RJ, Höbel G. How acoustic signals scale with individual body size: common trends across diverse taxa. Behavioral Ecology. 2014a in press. [Google Scholar]
- Rodríguez RL, Cramer JD, Schmitt CA, Gaetano TJ, Grobler JP, Freimer NB, Turner TR. Age confounds estimates of static allometric slopes in a vertebrate. Ethology Ecology & Evolution. doi: 10.1080/03949370.2014.986767. In review. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rowe L, Houle D. The lek paradox and the capture of genetic variance by condition dependent traits. Proceedings of the Royal Society of London B. 1996;263:1415–1421. [Google Scholar]
- Rutenberg GW, Coelho AM, Jr, Lewis DS, Carey KD, McGill HC., Jr Body composition in baboons: evaluating a morphometric method. American Journal of Primatology. 1987;12:275–285. doi: 10.1002/ajp.1350120305. [DOI] [PubMed] [Google Scholar]
- Schulte–Hostedde AI, Zinner B, Millar JS, Hickling GJ. Restitution of mass–size residuals: validating body condition indices. Ecology. 2005;86:155–163. [Google Scholar]
- Schulte-Hostedde AI, Kuula S, Martin C, Schank CCM, Lesbarrères D. Allometry and sexuall dimorphic traits in male anurans. Journal of Evolutionary Biology. 2011;24:1154–1159. doi: 10.1111/j.1420-9101.2011.02256.x. [DOI] [PubMed] [Google Scholar]
- Shingleton AW, Frankino WA, Flatt T, Nijhout HF, Emlen DJ. Size and shape: the developmental regulation of static allometry in insects. BioEssays. 2007;29:536–548. doi: 10.1002/bies.20584. [DOI] [PubMed] [Google Scholar]
- Sokal RR, Rohlf FJ. Biometry. 5. New York, NY: Freeman and Company; 1995. [Google Scholar]
- Striedter GF. Principles of brain evolution. Sunderland, MA: Sinauer; 2005. [Google Scholar]
- Tomkins JL, Radwan J, Kotiaho JS, Tregenza T. Genic capture and resolving the lek paradox. Trends in Ecology & Evolution. 2004;19:323–328. doi: 10.1016/j.tree.2004.03.029. [DOI] [PubMed] [Google Scholar]
- Turner TR, Anapol F, Jolly CJ. Growth, development, and sexual dimorphism in vervet monkeys (Cercopithecus aethiops) at four sites in Kenya. American Journal of Physical Anthropology. 1997;103:19–35. doi: 10.1002/(SICI)1096-8644(199705)103:1<19::AID-AJPA3>3.0.CO;2-8. [DOI] [PubMed] [Google Scholar]
- Voje KL, Hansen TF. Evolution of static allometries: adaptive change in allometric slopes of eye span in stalk-eyed flies. Evolution. 2013;67:453–467. doi: 10.1111/j.1558-5646.2012.01777.x. [DOI] [PubMed] [Google Scholar]
- Voje KL, Hansen TF, Egset CK, Bolstad GH, Pélabon C. Allometric constraints and the evolution of allometry. Evolution. 2014;68:866–885. doi: 10.1111/evo.12312. [DOI] [PubMed] [Google Scholar]