Mixture modeling methods for the assessment of normal and abnormal personality I: Cross-sectional models

Abstract

Over the past 75 years, the study of personality and personality disorders has been informed considerably by an impressive array of psychometric instruments. Many of these tests draw on the perspective that personality features can be conceptualized in terms of latent traits that vary dimensionally across the population. A purely trait-oriented approach to personality, however, may overlook heterogeneity that is related to similarities among subgroups of people. This paper describes how factor mixture modeling (FMM), which incorporates both categories and dimensions, can be used to represent person-oriented and trait-oriented variability in the latent structure of personality. We provide an overview of different forms of FMM that vary in the degree to which they emphasize trait- versus person-oriented variability. We also provide practical guidelines for applying FMMs to personality data, and we illustrate model fitting and interpretation using an empirical analysis of general personality dysfunction.

The study of personality traits has been an organizing force in psychology over the past century that has provided important insights into health behaviors (Bogg & Roberts, 2004), diatheses for psychopathology (Krueger & Markon, 2006), motivation (Humphreys & Revelle, 1984), and dysfunctional personality configurations that are associated with psychosocial impairment (Leary, 1957), to name just a few domains. In brief, a personality trait is a latent, unobservable predisposition to feel, think, or behave in a certain fashion (Allport, 1927; W. Mischel & Shoda, 1995). Individual differences in personality are typically thought to vary continuously across people such that the relative levels of one or more traits may reflect an individual’s personality style (i.e., a trait profile). Although the expression of traits often varies across situations (Fleeson, 2001; Walter Mischel, 2004), there is increasing evidence that personality structure typically stabilizes in adolescence (Caspi, Roberts, & Shiner, 2005) and that traits are linked with important outcomes, such as interpersonal aggression (Blair, 2001) and mental health treatment utilization (Lahey, 2009).

The broader field of normal and abnormal personality assessment has flourished in the past 75 years. There has been a proliferation of broad multidimensional measures of personality, such as the Multidimensional Personality Questionnaire (Tellegen & Waller, 2008) and the NEO-PI-R (Costa & McCrae, 1992), that reflect overlapping theories of personality and that provide convergent information about major traits (Markon, Krueger, & Watson, 2005). In addition, broad inventories of personality dysfunction have been developed to describe abnormal traits (e.g., the Schedule for Nonadaptive and Adaptive Personality: L. A. Clark, Simms, Wu, & Cassilas, in press; the Temperament and Character Inventory: Cloninger, Przybeck, & Svrakic, 1994; or the Dimensional Assessment of Personality Pathology: Livesley & Jackson, 2009), and these, too, are largely convergent in their content (L. A. Clark & Livesley, 2002). Furthermore, normal and abnormal personality traits may fall along related continua, with abnormal traits potentially representing extreme or maladaptive variants of normative traits (Samuel, Simms, Clark, Livesley, & Widiger, 2010; Stepp et al., 2012; Walton, Roberts, Krueger, Blonigen, & Hicks, 2008; Widiger & Simonsen, 2005). In addition to personality measures that are more comprehensive than specific, some researchers have developed focused inventories that seek to describe a certain aspect of personality, such as impulsivity (Whiteside & Lynam, 2001).

Altogether, a rich ecosystem of personality tests has developed that provides extensive resources for clinicians and researchers alike to probe a wide array of traits in applied, research, and clinical settings. This conceptual article seeks to build upon these important accomplishments by describing and illustrating how factor mixture modeling (FMM), an extension of factor analysis that allows for latent subgroups, can potentially enhance and inform the development of psychometric personality tests, and how FMM may provide scientifically rich information about the latent structure of personality.

The breadth and depth of the content assessed by modern personality tests is remarkable, yet it is interesting that the machinery underlying test development is often quite similar across measures. The majority of personality tests — and more broadly, psychological tests — have been developed following an established approach to construct validation that was well articulated decades ago (L. A. Clark & Watson, 1995; Loevinger, 1957; Nunnally & Bernstein, 1994). Although psychometric theory has contributed to major advances in personality assessment, we wish to draw attention to three premises of conventional test development efforts that may not hold in some datasets: 1) a trait falls along a continuum that is approximately normally distributed, 2) the true level of a trait can best be approximated by multiple items that provide overlapping information, and 3) the latent structure of a test characterizes the entire sample and is not markedly different for one or more subgroups, latent or observed.

We illustrate below how FMM may be particularly useful in cases where one or more of these premises is invalid, such as a personality trait that is not normally distributed or data where response patterns reflect both underlying traits and unique latent subgroup characteristics. Such scenarios are not accommodated by traditional methods. We also describe how a range of latent structure models can be conceptualized within the FMM framework, from those that allow for no latent subgroups (e.g., CFA) to those that impose no factorial structure, instead emphasizing distinctive response profiles (e.g., latent class analysis or latent profile analysis). Whereas the two extremes — latent trait models and latent profile models — have been widely used to study personality, the middle ground (i.e., hybrid models), where variation can exist both in terms of profiles and traits, has only recently been described (Lubke & Muthén, 2005; Teh, Seeger, & Jordan, 2005). For example, using FMMs in a large epidemiological sample of adolescents, Lubke and colleagues (2007) tested whether inattention and hyperactivity-impulsivity are best conceptualized as subtypes of attention deficit hyperactivity disorder (ADHD), or whether these features are continuous traits in the population. They found that a dimensional representation of inattention and hyperactivity-impulsivity fit the data better than categorical models, refuting the existence of subtypes. In addition, FMMs identified two latent classes of ADHD severity: persons with mild or absent symptoms (approximately 93% of the sample) and those with moderate to severe symptoms consistent with the syndrome.

Factor analytic techniques, specifically exploratory factor analysis (EFA) and confirmatory factor analysis (CFA), have long predominated structural analyses of personality tests (Cattell, 1946; Eysenck & Eysenck, 1976; Eysenck, 1947). Both EFA and CFA seek to summarize the covariation among observed responses to a number of psychometric items using a few latent dimensions. An associated assumption is that the traits are normally distributed in the population. Moreover, within an item response theory framework (Embretson & Reise, 2000), tests are often developed by selecting psychometric items that provide maximal information about a latent trait across the range of possible trait levels.

Within the personality assessment tradition, there has been a division between nomothetic approaches, which seek to summarize the predominant personality dimensions within a group, and idiographic approaches, which focus on the unique characteristics and emergent properties that characterize an individual (Beck, 1953; Bem, 1983). Factor analytic models fall squarely within the nomothetic tradition because they focus on the relationship between observed responses and latent dimensions (i.e., they are trait-oriented), and the same response–trait mapping is assumed to hold for all individuals in the population. As a result, they represent individual characteristics exclusively in terms of relative standing on a number of continuous traits. It is unlikely that any analytic method based solely on psychometric data can capture the uniqueness of an individual, yet by allowing for variation in terms of both latent dimensions and latent response profiles, FMMs may provide greater leverage on person-oriented research questions about whether distinctive subgroups are mixed within the dataset. Indeed, the term “mixture model” refers to the idea that the observed data reflect a mixture of subpopulations with distinct distributions or response patterns.

Thus, both idiographic assessment and the person-oriented analyses enabled by FMMs are conceptually related by an emphasis on identifying configurations of traits that may provide information about emergent personality signatures that characterize individuals or related groups. For example, negative emotionality and positive emotionality may be unidimensional traits in a sample of outpatients with mood disorders, yet they may be strongly negatively correlated in one latent subgroup (e.g., anhedonic individuals), whereas another group exhibits no correlation between traits (e.g., hypomanic individuals). Knowledge about latent subgroups can help to inform clinical decisions because personality profiles represent a pattern of traits that is greater than the sum its parts — profiles help to define personality dynamics that emerge from certain combinations of traits (e.g., narcissistic vulnerability emerges from a unique combination of exquisite sensitivity to shame, entitled expectations, and difficulties with emotion regulation).

An introduction to factor mixture modeling

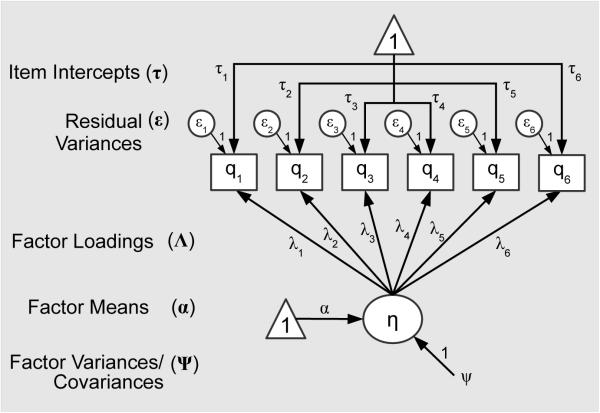
Factor mixture models build directly upon a traditional CFA framework, which we review briefly to provide a context for FMMs. In CFA, one or more latent factors/traits, η, are linked to the responses via a set of factor loadings, Λ, that represent the degree to which shared variability among items is captured by an underlying latent trait (see Figure 1). Response variability not explained by the latent trait structure is captured by a set of residual item variances, ε. Because latent traits in CFA are defined by the regression of items on latent traits, a set of item intercepts¹, τ, is also typically modeled, each representing the mean level of an item at a factor score (i.e., trait level) of zero.² Latent traits are assumed to be normally distributed, and in the case of a single latent trait, to have mean α and variance σ. In a multi-trait CFA, variances and covariances among latent traits are modeled as a matrix, Ψ.³

Figure 1.

A graphical depiction of the common factor model.

Note. This figure largely follows the reticular action model notation (McArdle & McDonald, 1984), whereby latent variables are denoted by circles and observed variables are denoted by rectangles. Triangles containing the number one denote the inclusion of mean/intercept structure in the model for the variables pointed to by the path arrows.

In the personality assessment literature, several studies have characterized how the latent structure of personality differs across cultures, between sexes, or as a function of genetics (Eaves et al., 1989; McCrae, Costa Jr, Del Pilar, Rolland, & Parker, 1998; J. Yang et al., 1999). A majority of these studies have used multiple-groups CFA techniques to examine whether the number, form, or interpretation of latent traits differed across known or established subgroups. This analytic technique allows one to test whether measurement parameters can be constrained to be equal between subgroups (e.g., men vs. women) without significantly degrading model fit (Byrne, Shavelson, & Muthén, 1989). If the measurement model differs between groups, it suggests that the personality test does not perform equivalently and that the underlying constructs may differ.

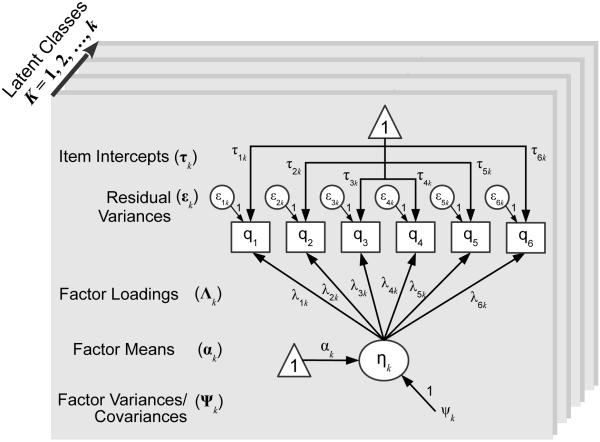
The general factor mixture model can most easily be understood as a multiple-groups CFA where the groups are unknown a priori. Instead, latent subgroups are estimated in FMMs and emerge because of qualitative differences in one or more aspects of the latent trait model. For example, if there were two relatively distinct levels of antagonistic personality, such that some individuals were quite antagonistic, whereas others had little or no antagonism, an FMM could help to identify such bimodality at the latent trait level and to disaggregate individuals into high vs. low subgroups, something not possible using traditional factor analytic techniques. The principal innovation of FMM is that item responses are jointly represented by a latent measurement model (composed of one or more continuous traits) and by an unordered categorical latent variable that distinguishes among K latent classes⁴. The probabilities of class membership are estimated by multinomial regression, such that an individual is assigned a set of posterior probabilities that sum to 1.0 and describe the probability of being in each class.

Any of the parameters in the traditional CFA — factor means, factor variances/covariances, factor loadings, residual variances, or item intercepts — can be allowed to vary across latent subgroups in a FMM framework (see Figure 2), yet the form and interpretation of the subgroups differs considerably depending on which aspects of the measurement model are free to vary across classes. Thus, the general FMM extends CFA by providing the possibility for unique estimates of measurement parameters in each latent class, k. The range of factor mixture models can be organized along a gradient that varies from forms that emphasize dimensions (e. g., CFA is a special case of a FMM where a measurement model is estimated in a single class — the entire sample) to those that emphasize categories (e.g., latent class/profile analysis, where classes differ in their response profiles in the absence of any latent trait structure) (Masyn, Henderson, & Greenbaum, 2010). We describe a subset of FMMs along the dimensional-categorical spectrum that we hope will be of greatest relevance to personality researchers (more comprehensive treatments of FMM can be found in Lubke & Muthén, 2005; Masyn et al., 2010; and Muthén, 2008)

Figure 2.

A graphical depiction of the general factor mixture model.

Measurement invariance in FMM

Prior to describing different forms of FMMs, we review measurement invariance in latent trait models. This is important because the extent to which measurement parameters are allowed to vary across latent classes in FMMs directly influences the form of the classes and their substantive interpretation. Exactly as in multiple-groups CFA, increasing restrictions can be placed on the measurement model across latent classes in order to enforce similarity of the trait model (Meredith, 1993). When only factor loadings are constrained to be equal across latent classes in FMM, the level of measurement invariance (MI) is weak (for a more detailed discussion, see Widaman & Reise, 1997). Enforcing equality of both item intercepts and factor loadings across classes is called strong MI. Finally, adding the restriction of equal residual item variances across classes is conventionally called strict MI.

For latent traits to have an identical meaning across latent classes in FMMs — that is, for factor scores to be on the same scale and thus comparable across classes — strict MI must hold (Lubke & Muthén, 2005; Masyn et al., 2010)⁵. When intercepts, residual variances, and/or factor loadings vary across latent classes, the underlying scale of the latent trait is not comparable across classes. Thus, when strict MI is enforced in FMM, differences in factor means, factor variances/covariances, and factor scores across latent classes can be interpreted on the same scale. But when strict MI is not enforced, the measurement model and latent trait scales only apply within each latent class, and only latent trait differences among individuals within a class are interpretable, whereas between-class comparisons on factor scores or latent means are not valid (Masyn et al., 2010). Below, we distinguish between FMMs that enforce strict MI versus those that do not.

Forms of FMM

In order to illustrate the potential relevance of FMMs for studies of normal and abnormal personality, we will focus on a simple example: the measurement of a general liability for personality disorder (PD). This is topical in light of the Section III (Emerging Models and Measures) model for diagnosing PDs in DSM-5, which emphasizes that personality dysfunction can be understood and diagnosed generally by assessing for disruptions in representations of self and others (Skodol et al., 2011). Related studies have explored whether a general liability for PDs can be identified using self-reported personality traits (Morey et al., 2011) or existing DSM diagnostic criteria (Langbehn et al., 1999). Although there is an increasing consensus that the identification of PDs generally should have primacy over the particular type of dysfunction (Pilkonis, Hallquist, Morse, & Stepp, 2011), the optimal approach for the diagnosis of a PD remains elusive. We focus here on whether a single dimension of general PD (GPD) liability can be identified using existing diagnostic criteria.

Factor Analysis: An FMM with no latent classes

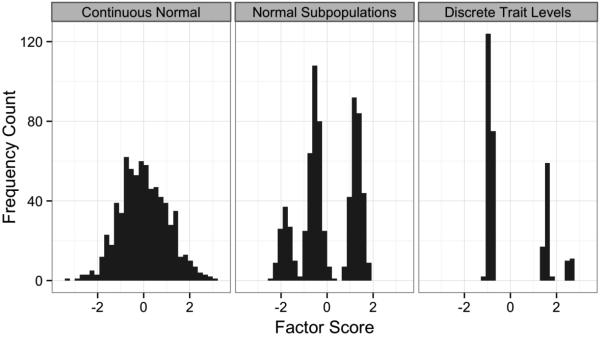
Factor analysis is the most trait-oriented model considered here, and it can be conceptualized as an FMM where the number of latent classes is one — i.e., measurement parameters do not vary as a function of class. Such a latent trait model represents responses strictly in terms of one or more continuous dimensions, and individuals’ standing relative to each other can be quantified in terms of interval-scaled factor scores that represent the degree of “trait-ness” (see Figure 3, left panel). In the case of GPD, a unidimensional latent trait model would represent personality dysfunction as a normally distributed, continuous dimension along which people vary by degree.

Figure 3.

Latent trait distributions for continuous normal, semi-parametric, and non-parametric factor models.

Note. Data were simulated from unidimensional factor mixture models with 1) a single normal trait distribution representing the population (left panel); 2) three normal subpopulations representing latent subgroups with unique factor means and variances; and 3) three discrete subpopulations representing latent subgroups differing only in latent means. All data were then analyzed using a unidimensional confirmatory factor analysis model, and the resulting factor scores were plotted to illustrate relevant variations in latent structure.

Latent means and variances FMM: a semi-parametric factor model

Some latent traits may not be normally distributed, but may nevertheless have a continuous, if “lumpy” or highly skewed, distribution that can be well represented by an FMM. In particular, a CFA model can be extended to allow for non-normal latent trait distributions by testing an FMM where latent classes vary in their factor means and variances, while maintaining strict MI for the factor model. This form of FMM produces a semi-parametric factor analysis (SP-FA; Ng & McLachlan, 2003; Teh et al., 2005) whereby a non-normal trait distribution is treated as a mixture of normally distributed subgroups, each having a distinct factor mean and variance that help to capture the features of the latent distribution (see Figure 3, middle panel). Because strict MI is enforced, the underlying factor scores can be compared directly between and within classes (i.e., the factor represents the same latent trait across classes). In order to interpret the results of an SP-FA model, it is useful to plot the latent trait distribution, as well as the means and variances of each latent class, to assess how the latent trait deviates from normality and how the latent classes help to represent such non-normality. In some cases, a latent distribution may be strikingly non-normal (e.g., bimodal) whereas other traits may exhibit more subtle non-normality, such as a skewed distribution (De Boeck, Wilson, & Acton, 2005). In the case of GPD, the semi-parametric FA model would still represent the trait along a single dimension with factor scores across classes that could be compared quantitatively, but the model would allow for a non-normal factor distribution, such as would occur if some individuals had low or absent levels of dysfunction, whereas others had clinically significant PDs.

Latent means FMM: A non-parametric factor model

The traditional factor analytic model assumes that latent traits follow a multivariate normal distribution, whereas the SP-FA form of FMM relaxes this assumption using a set of latent subgroups, each having a unique factor mean and variance, to approximate a continuous, non-normal distribution. The assumption that latent traits follow any parametric distribution (e.g., normal or mixture of normals) can also be relaxed using an FMM where a strict MI factor model is enforced across a set of latent subgroups that differ only in terms of the factor means. In this form of FMM, factor variances within each class are fixed at zero, resulting in a non-parametric factor analysis (NP-FA; also called a located latent class analysis) that represents the distribution of the latent trait using a set of discrete points along a continuum, and individuals in each subgroup are assumed to be homogeneous in their latent level of the trait (see Figure 3, right panel). Like FA and SP-FA models, NP-FA represents traits along shared dimensions, but models the possibility that the latent trait is best captured by a discrete number of levels. For example, an NP-FA model could be used to test a truly dichotomous conception of personality dysfunction as a rare trait, where many individuals do not manifest personality problems, whereas others have specific level of clinically significant dysfunction.

Factor mixture models that allow for measurement parameters to vary over classes

When measurement model parameters vary across latent classes in an FMM (i.e., violations of strict MI), the underlying factors and factor scores are typically not comparable among subgroups (Lubke & Muthén, 2005). Yet an FMM that permits item intercepts, factor loadings, and/or residual variances to vary across classes opens a new set of modeling possibilities that may capture meaningful heterogeneity in the latent structure of personality. For example, allowing factor loadings to vary across latent classes could reveal that personality dysfunction is best represented by certain features (e.g., antagonism) in some groups, and by different features in others (e.g., dependency), while still representing personality dysfunction as a unidimensional trait. As in multiple-groups CFA, measurement invariance can be relaxed selectively for certain types of parameters (e.g., allowing residual variances to vary while constraining factor loadings to be invariant), but because the latent subgroups in FMM reflect heterogeneity not accommodated by the measurement model, the form of the latent classes depends precisely on which parameters are free to vary across classes.

More specifically, freeing measurement parameters across latent subgroups is likely to absorb response heterogeneity in the measurement model and result in relatively fewer subgroups, whereas constraining some or most measurement parameters to be invariant across classes may result in the extraction of additional subgroups to capture the same source of heterogeneity (Lubke & Neale, 2008). Only in the special (and artificial) case of Monte Carlo simulation studies does one know what model generated the observed responses, and in practice, the goal of most latent structure analyses is to develop a reasonably good, parsimonious model of the responses that is psychologically interpretable. Consequently, because there are an inordinate number of possible FMM configurations that could be tested by relaxing measurement invariance for one or more parameters, we encourage those interested in testing noninvariant FMMs to choose plausible models a priori. For example, if one is interested in comparing the factor variance/covariance relationships across classes, but the factor means and scores need not be comparable, then item intercepts could be freed across latent subgroups while enforcing invariance for factor loadings and residual variances (Lubke & Muthén, 2005). On the other hand, if one is interested in whether observed responses reflect different traits across latent subgroups, then factor loadings, intercepts, and residual variances could be allowed to vary across latent subgroups, potentially at the risk of a more complex model that is acutely sensitive to the features of the observed data. Much like traditional multiple-groups CFA (Byrne et al., 1989), partial measurement invariance is possible in FMM, which can be accomplished by identifying a well-fitting FMM that imposes strict MI followed by a series of FMMs that relax measurement parameters for selected items (for example, see Hallquist & Pilkonis, 2012).

LCA/LPA: A fully categorical mixture model

Latent class analysis (LCA; or in the case of continuous items, latent profile analysis, LPA) is a special case of FMM that provides the most categorical, person-oriented view of personality traits. In LCA/LPA, a categorical latent variable captures the possibility that response profiles arise because there are latent subgroups of individuals with distinctive combinations of features, not because of shared variance among features that represents latent traits. In fact, the LCA/LPA model assumes that there is no association among the items within a latent subgroup (i.e., the items are independent conditional on latent class membership). This assumption can conceptualized within the FMM framework as a model that forces all factor loadings across latent classes to be zero, precluding the possibility that some underlying dimensions explain covariation among items. That is, the conventional LCA/LPA model attempts to parse heterogeneity strictly in terms of latent subgroups and does not permit residual associations among items (Hagenaars & McCutcheon, 2002). Similarly, in CFA, the basic model assumes that associations among items are entirely captured by one or more factors (i.e., the residual item covariances are constrained to be zero, another example of conditional independence).

In practice, however, the conditional independence assumption is often violated in both factor analytic and latent class models, particularly in personality and clinical data that have complex latent structures. To achieve good model fit in CFA models, residual covariation among items is often accommodated by including one or more error covariance terms (Brown, 2006). The development of FMM was motivated in part by an interest in relaxing the restrictive and often implausible conditional independence assumption in LCA/LPA models by allowing for residual associations among items within each latent class (McLachlan, Do, & Ambroise, 2004; Muthén & Asparouhov, 2006). Similarly, residual item covariation in factor models may arise because of unique characteristics of latent subgroups mixed within the data, a possibility accommodated by FMMs.

Items that reflect overlapping approximations of related traits are unlikely to be represented appropriately by LCA/LPA models because the covariation among items may lead to the spurious extraction of putative latent subgroups that would be better conceptualized as one or more dimensions (Muthén & Asparouhov, 2006). For example, anhedonia and dysphoria are unlikely to be completely independent within a latent class because they reflect mood state, and their inclusion in an LCA/LPA model may identify spurious cut points along a continuous dimension (e.g., low, medium, and high depressed mood). In such cases, LCA/LPA profiles will differ quantitatively, not qualitatively, an effect the late Dr. Richard Todd referred to as the “salsa pattern” for the mild, medium, and hot levels of spice it evokes, although capsaicin level is actually dimensional (R. R. Althoff, personal communication, October 26, 2012)

Thus, LCA/LPA may be most useful as a technique to classify individuals into subgroups on the basis of multiple personality traits that are relatively uncorrelated and that are conceptually distinct. In the case of general personality dysfunction, an LCA/LPA model would capture the possibility that personality dysfunction does not vary dimensionally, but instead that symptoms are expressed differently across latent subgroups (e.g., a predominantly odd/eccentric type versus an emotionally dysregulated type).

Model building, estimation, and comparison in FMM

As with all statistical models, one can improve the fit of an FMM to the data by increasing the complexity of the model, either by freeing additional measurement parameters within latent classes, or by adding additional classes. Yet improved fit comes at the cost of parsimony and replicability, and the interpretability of FMMs that permit considerable measurement model variation across classes often suffers considerably. At the extreme, one could test an FMM where a unique EFA solution is estimated in each latent class, potentially giving rise to completely different factor structures across latent subgroups. Models of this type may be conceptually appealing in certain instances, but in practice they quickly become complicated, difficult to interpret, and computationally unstable. Although there has not been a focused exploration of model building strategies in FMM (S. L. Clark et al., under review; Masyn et al., 2010), we offer some suggestions that may facilitate the development of tractable and interpretable FMMs.

First, it is often useful to begin the model building process by fitting an exploratory factor analysis (EFA) to the item-level data. The EFA provides an initial summary of the extent to which items can be summarized by one or more latent traits and also may help to establish the number, form, and interrelationships of latent traits. If one has an a priori idea about the latent trait structure for a personality test, then a CFA model can also be tested initially to validate the proposed structure (cf. Hopwood & Donnellan, 2010). If one is interested in exploring how a trait may be differentially expressed across latent subgroups (e.g., allowing factor loadings to vary), it may be advantageous to use factor analytic methods to identify a set of items that are reasonably unidimensional prior to testing FMMs that relax measurement invariance across classes. Although FMMs that model multiple traits can certainly be tested, the emergence of latent classes in a multi-trait FMM where one or more measurement parameters are free to vary for each trait will result in latent classes that reflect subgroup-specific patterns on all traits. Consequently, latent classes in multi-trait FMMs may be more difficult to interpret when measurement parameters are allowed to vary for multiple traits. Another advantage of testing unidimensional factor models as a precursor to FMMs is that one can plot the resulting factor scores to ascertain whether the latent trait is approximately normal, or whether semi-parametric or non-parametric FA models may better represent the data (cf. Figure 3).

After exploring a purely dimensional model, we recommend testing an LCA/LPA model next to get a sense of person-related variability that may reflect subgroups with distinctive response patterns. In cases where the underlying structure of the data is purely dimensional, because LCA/LPA does not include a trait model, an LCA/LPA is likely to find subgroups that differ primarily in their mean level across items, such as a situation where three latent classes are used to capture low, medium, and high levels of an underlying trait. Thus, if an LCA/LPA fails to identify subgroups with qualitatively distinct response profiles, this may provide initial evidence that the latent structure is better approximated by a model that includes a trait structure, such as CFA or FMM (Markon & Krueger, 2006). In contrast, evidence of distinct response profiles in LCA/LPA may be indicative of subgroups that differ phenotypically and/or of multiple traits underlying the observed responses.

After fitting the purely dimensional and purely categorical models, one can begin to test FMMs that allow for responses to vary both in terms of distinct subgroups and relationships among items that reflect latent traits. For example, if an interpretable factor model were identified using EFA/CFA to represent antagonism, disinhibition, and negative emotionality, one could extend this model using FMM to explore whether a single covariance matrix adequately summarizes the associations among these traits, or whether there are latent subgroups that show different patterns of associations. This would be accomplished by using the CFA solution as the measurement model in an FMM, holding the measurement parameters to be equal across latent classes, while freeing the variances and covariances. The use of FMM should be guided, to the extent possible, by a priori theory about latent traits and subgroups, particularly because there are an overwhelming number of model variants that could be tested, and it is unlikely that a comparison among a spate of models will yield an optimal psychological theory. One should also be clear whether the major goal of using FMM is to model non-normality in an otherwise fairly conventional latent trait structure (i.e., FMMs that enforce strict invariance) or whether one is more interested in modeling latent subgroups that differ in qualitatively interesting ways, such as factor loadings (Masyn et al., 2010). Some of the most informative applications of FMMs to date have compared models that reflect plausible competing conceptions about the latent structure of psychopathology and that draw directly on prior theory (e.g., Lubke et al., 2007; Shevlin & Elklit, 2012).

Estimating the optimal number of classes in FMM

In any model that includes a categorical latent variable (e.g., LCA/LPA or any of the forms of FMM), an important part of model estimation is to determine the number of latent classes that provides an optimal fit to the data, ideally approximating the “true” number of classes that gave rise to the responses (McLachlan & Peel, 2000). Because each form of FMM differs in the parameters that are free to vary across latent classes, one would not typically expect that the optimal number of classes for one type of FMM (e.g., NP-FA) would be the same as another (e.g., LCA/LPA). Thus, for each form of FMM, one typically estimates models with an increasing number of classes until some stopping criterion is reached. The goal of iteratively increasing the number of latent classes is to find the optimal point between model parsimony and accuracy (Burnham & Anderson, 2002), where additional classes may help to capture meaningful interindividual heterogeneity not accounted for by one or more latent traits. Although the best approach to identify the optimal number of latent classes remains a topic of study (Nylund, Asparouhov, & Muthén, 2007), the bootstrapped likelihood ratio test (BLRT) has received considerable support in simulation studies and is useful as a primary stopping criterion. Alternatively, as one increases the number of latent classes for a given form of FMM, models can be compared using information criteria, such as the Akaike Information Criterion (AIC; Akaike, 1974) or the Bayesian Information Criterion (BIC; Schwarz, 1978). The BLRT tests the improvement in model fit of a k-class model relative to a model with k-1 classes using parametric bootstrap resampling to generate an empirical distribution of the log-likelihood difference test statistic (Feng & McCulloch, 1996; McLachlan, 1987). A significant BLRT p-value (conventionally p < .05) indicates that the k-class model fits the data significantly better than the model with k-1 classes, accounting for the additional parameters added by increasing the number of latent classes. Thus, one typically fits an increasing number of classes in FMM models until a non-significant BLRT p-value is obtained, indicating that the addition of more latent classes does not improve model fit.

Model selection criteria including the AIC and BIC attempt to balance model fit (often represented by the model log-likelihood, which represents the probability of the observed data given the model parameter estimates) and model parsimony by penalizing models that include many more parameters while not fitting the data much better. Some criteria also include a correction for sample size. There is a host of model selection criteria that draw on information theory and Bayesian inference (Claeskens & Hjort, 2008) and that differ in their philosophical and statistical underpinnings (Burnham & Anderson, 2002; Vrieze, 2012). In general, however, when comparing two models, the model that has a lower value for the model selection criterion (e.g., AIC or BIC) is preferred as having a better complexity-fit tradeoff.

Choosing the best representation of latent structure

When selecting the FMM that best represents the data, whether comparing those of the same form that differ only in the number of latent classes or those with completely different parameterizations, one must weigh both fit criteria and model interpretability. For example, model selection criteria or the BLRT may prefer a five-class FMM with no clear conceptual separation among the classes, whereas a four-class model yields psychologically interesting classes that align with an a priori theory. This scenario is analogous to traditional personality test development strategies where one might choose a solution with fewer factors than suggested by some criterion (e.g., Kaiser-Guttman or parallel analysis) because the factor structure is more interpretable. Indeed, FMMs sometimes yield solutions where an additional class is quite small in relative size (e.g., 3% of the sample) and represents an uncommon response profile that may not constitute a meaningful latent class (McLachlan & Peel, 2000).

That said, researchers are often interested in latent subgroups that are rare (e.g., a subset of individuals with narcissistic personality may also have sadistic features that are a topic of study), and FMMs may provide leverage on such questions. If one wishes to use FMMs to identify uncommon latent subgroups (e.g., 5% or less of the population of interest), having a large sample (preferably n = 1,000 or more) is critical. This recommendation reflects that for a given sample size, the statistical power of model selection criteria is much weaker for resolving rare subgroups in FMMs (Ning & Finch, 2004), which may lead to false negatives in smaller samples. In addition, accurate estimation of latent subgroup parameters (e.g., means) is poor for rare subgroups in small samples (e.g., fewer than 200 total observations; Nylund et al., 2007). Thus, the identification of a rare latent subgroup in a small sample may be more reflective of sampling variability that would not be expected to replicate in an independent sample. For these reasons, although it is a somewhat arbitrary rule of thumb, we suggest that researchers observe particular caution when interpreting FMM subgroups smaller than n = 15 as substantively interesting (see also Wright et al., 2013).

For each form of FMM that is of interest, one first identifies the optimal number of latent classes based on stopping criteria and model interpretability, as described above. Next, the best models for each form of FMM can be compared to each other to decide which candidate provides the best representation of the latent structure of the data. Because different forms of FMMs are not usually restricted variants of each other (i.e., the models are not nested), the BLRT cannot be used to compare candidate models (e.g., NP-FA versus LCA). Thus, other model selection criteria must be used to inform a decision about the best model. Although a full review of model selection criteria is beyond the scope of this article (for more details, see Burnham & Anderson, 2002; Claeskens & Hjort, 2008; Vrieze, 2012), the corrected AIC (Sugiura, 1978) is often a useful criterion for choosing among different forms of FMM:

$$AI{C}_c=-2\log \left(L(\widehat{\theta }\mid y)\right)+2k+\frac{2k(k+1)}{n-k-1}$$ (1)

where $\log \left(L(\widehat{\theta }\mid y)\right)$ is the log-likelihood of the model, k is the number of parameters, and n is the sample size. Relative to the AIC, the AIC_C includes a penalty for the ratio of number of parameters relative to the sample size, which is crucial to avoid overfitting the data (i.e., selecting an overly complex model) in finite samples, particularly when there are fewer than 40 cases per parameter (Burnham & Anderson, 2002; C. M. Hurvich & Tsai, 1991; Clifford M. Hurvich & Tsai, 1989).

In practice, it is common for model selection criteria to favor different models, which can make it difficult to decide among candidate FMMs. Although the AIC and BIC are sometimes described as complementary criteria, their statistical properties are fundamentally different (Y. Yang, 2005). The BIC is a consistent criterion, meaning that as sample size increases, it will tend to select the model that generated the data if the true model is among those tested. In contrast, the AIC is an efficient criterion, meaning that as sample size increases, it will select the model that minimizes prediction error (i.e., the difference between model-predicted values and the empirical data for a novel set of observations; Y. Yang, 2005). In most psychological studies, the processes that give rise to the observed data are probably quite complex and it is unlikely that the “true model” is among those tested. Rather, many latent structure studies in personality research are concerned with identifying a model that provides a good approximation of the data, knowing that the model is probably simpler than the truth. Consequently, model selection criteria that are efficient (e.g., AIC and AIC_C) may be preferable over consistent criteria (e.g., BIC) in most psychological research (see also Hallquist & Pilkonis, 2010; Vrieze, 2012).

From a pragmatic perspective, however, due to differences in the penalty terms for the number of parameters and sample size, the BIC favors models with fewer parameters than the AIC or AIC_C (Burnham & Anderson, 2002). Consequently, relative to the AIC_C, the BIC will often prefer models with fewer latent classes within a given form of FMM. Similarly, when choosing among different forms of FMM, BIC typically prefers CFAs and FMMs that enforce strict MI over FMMs that permit measurement parameters to vary across classes. One option when comparing candidate models is to consider those that fit best according to either AIC_C or BIC and to rely on theory, interpretability, and additional model checks (e.g., residual diagnostics; Wang, Brown, & Bandeen-Roche, 2005) to decide on the optimal model.

Although most model selection criteria cannot be used in a null hypothesis testing framework to decide whether one model fits significantly better than another, the evidence in favor of one model relative to other candidates can be quantified by subtracting the AIC_C of one model from the AIC_C of the best-fitting model (i.e., the model with the smallest AIC_C value; this approach also applies to inferences based on BIC). Burnham and Anderson (2002) describe the following rule-of-thumb for interpreting AIC differences: models within 0–2 points of the best model have substantial support, of 4–7 points indicate substantially less support, and differences greater than 10 suggest almost no support of the poorer model relative to the best-fitting model. More specific comparisons of model evidence can be conducted by computing a set of standardized weights based on AIC differences for all candidate models, where the weights sum to 1.0 across models and indicate the evidence in favor of that model (for details, see Burnham & Anderson, 2002). We encourage researchers interested in the latent structure of personality to conduct careful comparisons of model evidence among different forms of FMM, rather than making a binary decision about one model fitting better than another. In cases where two distinct FMMs are relatively similar in their level of support (e.g., AIC differences in the 0–2 range), it suggests that the underlying structure can be interpreted in more than one way, a scenario that should prompt a careful review of relevant theory and one’s a priori hypotheses about the latent structure.

Model validation: External variables and replication

In addition to parsimony and interpretability, candidate FMMs should be evaluated on the basis of theoretically meaningful differences between classes on additional variables not included in the model (for examples, see Hallquist & Pilkonis, 2012; Lenzenweger, Clarkin, Yeomans, Kernberg, & Levy, 2008; Wright et al., 2013). This step is particularly crucial if the intent of the analysis is to identify latent subgroups that differ qualitatively in personality or clinical presentation. For example, if an LCA/LPA model were to suggest that a subgroup of individuals with PDs was much more socially withdrawn, one would hope that this subgroup would also report higher anxiety on a social stress task, such as public speaking. The ability to discern meaningful differences among latent classes depends in part on the uncertainty associated with assigning individuals to one of the latent classes. To the extent that individuals have a high probability of being in a single class, the model is said to have high entropy, a statistic that varies from 0, reflecting complete uncertainty about assignment, to 1, reflecting complete certainty (Celeux & Soromenho, 1996). Identifying differences among classes on additional variables may be difficult when entropy is low because of uncertainty about class assignment, which degrades the statistical power of between-class comparisons (S. L. Clark et al., under review). In addition, low entropy suggests that differences among classes may be more subtle than striking, potentially raising questions about whether classes differ more in degree than kind.

An additional consideration with FMMs is whether the best-fitting model can be replicated in an independent sample. Mixture models are sensitive to the characteristics of the sample, and subtypes may reflect unique features of one sample that are not present in another (Eaton, Krueger, South, Simms, & Clark, 2011). It is potentially unlikely that two samples that differ considerably in composition (e.g., psychiatric inpatients versus college undergraduates) will be optimally represented by the same FMM. This issue is analogous to similar concerns in latent trait models, where items may function differently across samples (Embretson & Reise, 2000) and the form or number of traits may be difficult to cross-validate. Despite these limitations, one should hope that the latent structure of personality and psychopathology, whether measured by traits, subgroups, or both, is relatively robust across samples, and examples of replicable PD subtypes have been published (cf. Hallquist & Pilkonis, 2012; Lenzenweger et al., 2008).

An illustration of fitting FMMs: General liability for PDs

To illustrate the fitting and interpretation of FMMs, we describe below a basic analysis of the general liability for PDs. In a mixed sample of 303 psychiatric outpatients and community participants (for more details, see Morse & Pilkonis, 2007), we tested whether DSM-III-R PD symptoms that were most correlated with the total PD symptom count might represent a unidimensional trait reflecting general personality dysfunction (GPD). First, we computed polychoric correlations of all 83 DSM-III-R PD criteria (American Psychiatric Association, 1987), which were rated 0 (absent), 1 (present), and 2 (strongly present), with the total symptom score. Symptom ratings were derived from semistructured clinical interviews followed by diagnostic discussions among clinicians (Morse & Pilkonis, 2007; Pilkonis, Kim, Proietti, & Barkham, 1996). We rank-ordered the item-total correlations and retained the top eight criteria (i.e., the top 10%) as potential indicators of GPD (see Table 1). Although these criteria might simply represent a unitary GPD dimension, there may also be evidence for latent subtypes, which we explore below.

Table 1.

Eight DSM-III-R PD criteria with the highest correlations with the total number of PD symptoms.

PD Criterion	Description	Item-Total r
Narcissistic #1	Reacts to criticism with feelings of rage, shame, or humiliation (even if not expressed)	.74
Histrionic #1	Constantly seeks or demands reassurance, approval, praise	.73
Histrionic #7	Is self-centered, actions being directed toward obtaining immediate satisfaction; has no tolerance for the frustration of delayed gratification	.72
Narcissistic #4	Believes that his or her problems are unique and can be understood only by other special people	.71
Borderline #4	Inappropriate, intense anger or lack of control of anger, recurrent physical fights	.65
Paranoid #4	Bears grudges or is unforgiving of insults or slights	.64
Dependent #9 & Avoidant #1	Is easily hurt by criticism or disapproval	.63
Borderline #6	Marked and persistent identity disturbance manifested by uncertainty about at least two of the following: self-image, sexual orientation, long-term goals or career choice, type of friends desired, preferred values	.61

The eight putative GPD criteria were internally consistent, Cronbach’s alpha = 0.79, with an average inter-item correlation of r = 0.32. To explore whether these items were reasonably unidimensional according to conventional test development approaches, we computed McDonald’s hierarchical omega, ω_h, which provides an estimate of the item variance attributable to single common factor (Zinbarg, Yovel, Revelle, & McDonald, 2006), and we examined the factor loadings from a single-factor EFA. Both analyses suggested that a single dimension reasonably accounted for GPD liability, ω_h = .69, average factor loading = .64 (range = .40 – .85).

We then tested several FMMs, beginning with traditional CFA and LCA models. To explore whether GPD is a unitary, but non-normal, latent dimension, we tested two forms of FMM that enforced strict MI: one that allowed GPD factor means to vary across latent classes while constraining the factor variance to zero (i.e., a non-parametric FA approach), and another that allowed both GPD factor means and variances to vary (i.e., semi-parametric FA). To temper the complexity of this example, we did not test FMMs that allowed for measurement parameters (e.g., factor loadings or item thresholds) to vary across classes.

Unidimensional latent trait model: CFA

The unidimensional CFA model provided a marginal fit to the data, χ²(20) = 75.96, p < .0001, CFI = .95, RMSEA = .10 (90% CI: .074 – .12), AIC_C = 3981.48, BIC = 4066.29. Standardized factor loadings for the eight GPD items ranged from .46 to .84 (M = .68, SD = .11), consistent with the one-factor EFA solution. Examination of the model modification indices suggested that there was considerable residual correlation between the inappropriate anger (borderline PD) and bears grudges (paranoid PD) items, r = .42, perhaps reflecting interpersonal reactivity. Thus, we allowed for a residual covariance between these items and re-estimated the model. A CFA model that included this residual covariance term fit the data reasonably well, χ²(20) = 46.38, p = .0004, CFI = .98, RMSEA = .07 (90% CI: .044 – .094), AIC_C = 3958.48, BIC = 4047.29, and represented a significant improvement in fit over the basic CFA, χ²_D(1) = 21.66, p < .0001. The association between inappropriate anger and bearing grudges could also be incorporated into the LCA/LPA or factor mixture models below to represent their item-level covariation (Qu, Tan, & Kutner, 1996). This would relax the conditional independence assumption, which holds that that for LCA/LPA models, item responses are independent after accounting for class membership; or for FMMs, that items responses are independent after accounting for class membership and factor level. We did not include this item-level covariation below because it would add complexity to the example and because including this association did not alter the substantive conclusions about latent structure.

Latent subtypes model: LCA/LPA

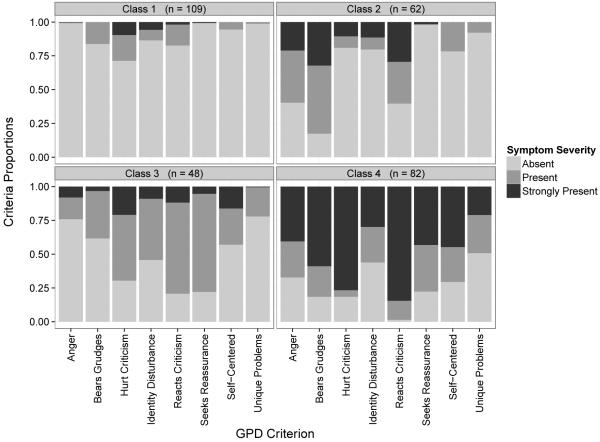
Latent class analyses imposing no measurement model on the items indicated that a 4-class solution provided the best fit to the data, according to the AIC_C and BLRT criteria (Table 2; Figure 4). In order of severity, the first class (n = 109) consisted primarily of individuals who exhibited few, if any, of the GPD symptoms. The second class (n = 62) included persons who tended to show interpersonal reactivity (inappropriate anger, bearing grudges, and reacting to criticism with rage, humiliation, or shame) but few other GPD symptoms. The third class (n = 48) exhibited a broader array of GPD symptoms, particularly reassurance-seeking and reactivity to criticism. Finally, individuals in the fourth class (n = 82) expressed most of GPD symptoms. This solution suggests differences of both a quantitative nature (Class 4 is more severe than Classes 2 and 3, which are more severe than Class 1) and a qualitative nature (Class 2 differs in profile from Class 3).

Table 2.

Model fit statistics for LCA, SP-FA, and NP-FA models

Model	Number of classes	LL	Number of Parameters	AICC	BIC	BLRT p
LCA	1	−2204.594	16	4443.09	4500.608
	2	−1972.815	33	4019.973	4134.184	< .0001
	3	−1933.449	50	3987.136	4152.584	< .0001
	4	−1898.077	67	3968.927	4178.973	< .0001
	5	−1883.275	84	4000.055	4246.504	0.74
SP-FA	1	−1964.58	24	3981.48	4066.29
	2	−1961.99	27	3983.49	4078.26	.13
NP-FA	1	−2204.59	23	4459.15	4540.60
	2	−1985.98	25	4026.65	4114.80	< .0001
	3	−1963.28	27	3986.06	4080.83	< .0001
	4	−1961.91	29	3988.19	4089.51	< .0001
	5	−1961.26	31	3991.84	4099.65	0.17

Figure 4.

Four-class LCA solution for the GPD criteria.

Note. The stacked bars denote the observed proportions of individuals in each class with absent, present, or strongly present levels of each GPD criterion.

Latent means and variances FMM: Semiparametric FA

A two-class FMM allowing latent means and variances to vary across latent classes did not fit the data better than the basic CFA model: the AIC_C and BIC were higher for the two-class FMM and the BLRT was nonsignificant (Table 2). Thus, an FMM modeling the possibility that GPD is best represented by a continuous non-normal dimension was not supported by our data.

Latent means FMM: Nonparametric FA

To explore whether GPD represents a continuous trait, but with discrete levels along the dimension, we next fit an FMM that allowed factor means to vary across classes, but that constrained factor variances to zero in each class. For this nonparametric FA approach, a 4-class model fit best according to the BLRT (Table 2). However, this solution included one class that contained only a single individual, suggesting a spurious class. In addition, the AIC_C was lowest for the 3-class solution. Thus, we chose the 3-class solution as the optimal solution for the nonparametric FA analyses. In order of severity, the first class (n = 108) had few, if any, PD symptoms. The second class (n = 119) had, on average, three of eight GPD symptoms, particularly negative reactions to criticism (Narcissistic PD) and bearing grudges (Paranoid PD). The third class (n = 76) had six or more GPD symptoms, on average, especially negative reactions to criticism, seeking reassurance, and bearing grudges.

As described above, the NP-FA model allows for the GPD factor means to vary across latent classes in order to represent discrete severity levels along the GPD continuum. In the case of the three-class model, the first class had a GPD factor mean of −2.83, the GPD mean in the second class was 0.0, and the GPD mean in the third class was 2.73. In NP-FA, the factor mean in one of the classes must be fixed at zero — this defines a reference group and defines the scale for the latent trait. In the case of the three-class NP-FA, the three classes are spaced approximately equally across the GPD dimension, representing in low, medium, and high variants of GPD. The class sizes suggest that low and moderate GPD were approximately equal in proportion, whereas severe GPD was more rare.

Deciding on the optimal latent structure of GPD

The best models from each of the forms of FMM above were compared to each other on the basis of the AIC_C, as well as scientific interpretability. Because the semiparametric FA model did not improve on the CFA model, it was not among the candidate models considered. As displayed in Table 3, the CFA model allowing for residual item covariation between the anger and grudge-bearing criteria had an AIC_C approximately 10 points lower than the second-best model, the 4-class LCA. Moreover, the Akaike weight for the CFA model was .99, indicating substantially greater evidential support (Burnham & Anderson, 2002). The BIC was also much lower for the CFA than the LCA or NP-FA models, corroborating our decision. We caution researchers against interpreting poor-fitting models, such as the 4-class LCA here, even if the results are intuitively appealing, because the data do not support the parsimony or accuracy of such models. In addition to having poor fit, these models did not contribute incremental scientific insights into the latent structure of GPD liability. In summary, GPD appeared to be best represented by a unidimensional latent trait model in our sample.

Table 3.

Model fit statistics for the best-fitting models from each form of FMM

Candidate model	LL	Number of Parameters	AICC	BIC	Akaike w	Entropy
CFA, anger–grudge covariance	−1952.15	25	3958.99	4047.14	.99	N/A
4-class LCA	−1898.08	67	3968.93	4178.97	.007	.81
Basic CFA	−1964.58	24	3981.48	4066.29	1.30 × 10−5	N/A
3-class NP-FA	−1963.28	27	3986.06	4080.83	1.32 × 10−6	.69

Note. LL = log-likelihood; AIC_C = corrected Akaike’s information criterion (Sugiura, 1978); BIC = Bayesian information criterion (Schwarz, 1978); Akaike w = Akaike weight, the evidence in favor of a model relative to the other models listed here (Burnham & Anderson, 2002); CFA = confirmatory factor analysis; LCA = latent class analysis; NP-FA = non-parametric factor analysis.

Conclusion

The results of our empirical example raise an important point about testing and interpreting FMMs: latent trait models often provide a parsimonious representation of personality and psychopathology, and in some cases, FMMs with many more parameters may not fit the data any better than conventional CFA approaches (see also Eaton et al., this issue). A major motivation for exploring FMMs is to test plausible alternative hypotheses about the latent structure of personality that are not possible using conventional factor analytic or latent class approaches. In this regard, the inclusion of FMMs among a family of models to be tested is consistent with the recommendation to compare several competing models in order to identify the most informative one (Bollen, 1989; Burnham & Anderson, 2002; Meehl & Waller, 2002). Likewise, an important aspect of developing psychometric tests is to identify the form and number of latent factors that underlie responses on a given instrument, which requires the comparison of alternative dimensional models (Nunnally & Bernstein, 1994). Thus, we recommend that researchers consider FMMs when their data and/or theory suggest that the latent traits are not normally distributed or when heterogeneity in observed responses may represent underlying traits and qualitative similarities among subgroups of people.

We hope that the conceptual framework articulated here (which extends Masyn et al., 2010) clarifies how a range of latent structure models can be conceptualized under the umbrella of factor mixture modeling. Moreover, we are optimistic that the wider application of factor mixture models in personality research will expand and enrich our understanding of both person- and variable-oriented heterogeneity, which may inform clinical assessment and psychological theory.