Abstract
The segmentation of infant brain tissue images into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) plays an important role in studying early brain development in health and disease. In the isointense stage (approximately 6–8 months of age), WM and GM exhibit similar levels of intensity in both T1 and T2 MR images, making the tissue segmentation very challenging. Only a small number of existing methods have been designed for tissue segmentation in this isointense stage; however, they only used a single T1 or T2 images, or the combination of T1 and T2 images. In this paper, we propose to use deep convolutional neural networks (CNNs) for segmenting isointense stage brain tissues using multi-modality MR images. CNNs are a type of deep models in which trainable filters and local neighborhood pooling operations are applied alternatingly on the raw input images, resulting in a hierarchy of increasingly complex features. Specifically, we used multimodality information from T1, T2, and fractional anisotropy (FA) images as inputs and then generated the segmentation maps as outputs. The multiple intermediate layers applied convolution, pooling, normalization, and other operations to capture the highly nonlinear mappings between inputs and outputs. We compared the performance of our approach with that of the commonly used segmentation methods on a set of manually segmented isointense stage brain images. Results showed that our proposed model significantly outperformed prior methods on infant brain tissue segmentation. In addition, our results indicated that integration of multi-modality images led to significant performance improvement.
Keywords: Image segmentation, multi-modality data, infant brain image, convolutional neural networks, deep learning
1. Introduction
During the first year of postnatal human brain development, the brain tissues grow quickly, and the cognitive and motor functions undergo a wide range of development (Zilles et al., 1988; Paus et al., 2001; Fan et al., 2011). The segmentation of infant brain tissues into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) is of great importance for studying early brain development in health and disease (Li et al., 2013a,b; Nie et al., 2011). It is widely accepted that the segmentation of infant brains is more difficult than that of the adult brains. This is mainly due to the lower tissue contrast in early-stage brains (Weisenfeld and Warfield, 2009). There are three distinct WM/GM contrast patterns in chronological order, which are infantile (birth), isointense, and adult-like (10 months and onward) (Paus et al., 2001). In this work, we focused on the isointense stage that corresponds to the infant age of approximately 6–8 months. In this stage, WM and GM exhibit almost the same level of intensity in both T1 and T2 MR images. This property makes the tissue segmentation problem very challenging (Shi et al., 2010b).
Currently, most of prior methods for infant brain MR image segmentation have focused on the infantile or adult-like stages (Cardoso et al., 2013; Gui et al., 2012; Shi et al., 2010a; Song et al., 2007; Wang et al., 2011, 2013; Weisenfeld and Warfield, 2009; Xue et al., 2007). They assumed that each tissue class can be modeled by a single Gaussian distribution or the mixture of Gaussian distributions (Xue et al., 2007; Wang et al., 2011; Shi et al., 2010a; Cardoso et al., 2013). This assumption may not be valid for the isointense stage, since the distributions of WM and GM largely overlap due to early maturation and myelination. In addition, many previous methods segmented the tissues using a single T1 or T2 images or the combination of T1 and T2 images (Kim et al., 2013; Leroy et al., 2011; Nishida et al., 2006; Weisenfeld et al., 2006a, b). It has been shown that the fractional anisotropy (FA) images from diffusion tensor imaging provide rich information of major fiber bundles (Liu et al., 2007), especially in the middle of the first year (around 6–8 months of age). The studies in Wang et al. (2014, 2012) demonstrated that the complementary information from multiple image modalities was beneficial to deal with the insufficient tissue contrast.
To overcome the above-mentioned difficulties, we considered the deep convolutional neural networks (CNNs) in this work. CNNs (LeCun et al., 1998; Krizhevsky et al., 2012) are a type of multi-layer, fully trainable models that can capture highly nonlinear mappings between inputs and outputs. These models were originally motivated from computer vision problems and thus are intrinsically suitable for image-related applications. In this work, we proposed to employ CNNs for segmenting infant tissue images in the isointense stage. One appealing property of CNNs is that it can naturally integrate and combine multi-modality brain images in determining the segmentation. Our CNNs took complementary and multimodality information from T1, T2, and FA images as inputs and then generated the segmentation maps as outputs. The multiple intermediate layers applied convolution, pooling, normalization, and other operations to transform the input to the output. The networks contain millions of trainable parameters that were adjusted on a set of manually segmented data. Specifically, the networks took patches centered at a pixel as inputs and produced the tissue class of the center pixel as the output. This enabled the segmentation results of a pixel to be determined by all pixels in the neighborhood. In addition, due to the convolution operations applied at intermediate layers, nearby pixels contribute more to the segmentation results than those that are far away. We compared the performance of our approach with that of the commonly used segmentation methods. Results showed that our proposed model significantly outperformed prior methods on infant brain tissue segmentation. In addition, our results indicated that the integration of multi-modality images led to significant performance improvement. Furthermore, we showed that our CNN-based approach outperformed other methods at increasingly large margin when the size of patch increased. This is consistent with the fact that CNNs weight pixels differently based on their distance to the center pixel.
2. Material and methods
2.1. Data acquisition and image preprocessing
The experiments were performed with the approval of Institutional Review Board (IRB). All the experiments on infants were approved by their parents with written forms. We acquired T1, T2, and diffusion-weighted MR images of 10 healthy infants using a Siemens 3T head-only MR scanner. These infants were asleep, unsedated, fitted with ear protection, and their heads were secured in a vacuum-fixation device during the scan. T1 images having 144 sagittal slices were acquired with TR/TE as 1900/4.38 ms and a flip angle of 7° using a resolution of 1 × 1 × 1 mm3. T2 images having 64 axial slices were acquired with TR/TE as 7380/119 ms and a flip angle of 150° using a resolution of 1.25 ×1.25 ×1.95 mm3. Diffusion-weighted images (DWI) having 60 axial slices were acquired with TR/TE as 7680/82 ms using a resolution of 2 × 2 × 2 mm3 and 42 non-collinear diffusion gradients with a diffusion weight of 1000s/mm2.
T2 images and fractional anisotropy (FA) images, derived from distortion-corrected DWI, were first rigidly aligned with the T1 image and further up-sampled into an isotropic grid with a resolution of 1 × 1 × 1 mm3. A rescanning was executed when the data was accompanied with moderate or severe motion artifacts (Blumenthal et al., 2002). We then applied intensity inhomogeneity correction (Sled et al., 1998) on both T1 and aligned T2 images (but not for FA image since it is not needed). After that, we applied the skull stripping (Shi et al., 2012) and removal of cerebellum and brain stem on the T1 image by using in-house tools. In this way, we obtained a brain mask without the skull, cerebellum and brain stem. With this brain mask, we finally removed the skull, cerebellum and brain stem also from the aligned T2 and FA images.
To generate manual segmentation, an initial segmentation was obtained with publicly available infant brain segmentation software, IBEAT (Dai et al., 2013). Then, manual editing was carefully performed by an experienced rater according to the T1, T2 and FA images for correcting possible segmentation errors. ITK-SNAP (Yushkevich et al., 2006) (www.itksnap.org) was particularly used for interactive manual editing. For each infant brain image, there are generally 100 axial slices; we randomly selected slices from the middle regions (40th – 60th slices) for manual segmentation. This work only used these manually segmented slices. Since we were not able to obtain the FA images of 2 subjects, we only used the remaining 8 subjects in this work. Note that pixels are treated as samples in segmentation tasks. For each subject, we generated more than 10,000 patches centered at each pixel from T1, T2, and FA images. These patches were considered as training and testing samples in our study.
2.2. Deep CNN for multi-modality brain image segmentation
Deep learning models are a class of machines that can learn a hierarchy of features by building high-level features from low-level ones. The convolutional neural networks (CNNs) (LeCun et al., 1998; Krizhevsky et al., 2012) are a type of deep models, in which trainable filters and local neighborhood pooling operations are applied alternatingly on the raw input images, resulting in a hierarchy of increasingly complex features. One property of CNN is its capability to capture highly nonlinear mappings between inputs and outputs (LeCun et al., 1998). When trained with appropriate regularization, CNNs can achieve superior performance on visual object recognition and image classification tasks (LeCun et al., 1998; Krizhevsky et al., 2012). In addition, CNN has also been used in a few other applications. In Jain et al. (2007); Jain and Seung (2009); Turaga et al. (2010); Helmstaedter et al. (2013), CNNs were applied to restore and segment the volumetric electron microscopy images. Ciresan et al. (2013, 2012) applied deep CNNs to detect mitosis in breast histology images by using pixel classifiers based on patches.
In this work, we proposed to use CNN for segmenting the infant brain tissues by combining multi-modality T1, T2, and FA images. Although CNN has been used for similar tasks in prior studies, none of them has focused on integrating and combining multi-modality image data. Our CNN contained multiple input feature maps corresponding to different data modalities, thus providing a natural formalism for combining multi-modality data. Since different modalities might contain complementary information, our experimental results showed that combining multi-modality data with CNN led to improved segmentation performance. Figure 1 showed a CNN architecture we developed for segmenting infant brain images into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF).
Figure 1.

Detailed architecture of the convolutional neural network taking patches of size 13 × 13 as inputs.
2.3. Deep CNN architectures
In this study, we designed four CNN architectures to segment infant brain tissues based on multi-modality MR images. In the following, we provided details on one of the CNN architectures with input patch size of 13 × 13 to explain the techniques used in this work. The detailed architecture was shown in Figure 1. This CNN architecture contained three input feature maps corresponding to T1, T2, and FA image patches of 13 × 13. It then applied three convolutional layers and one fully connected layer. This network also applied local response normalization and softmax layers.
The first convolutional layer contained 64 feature maps. Each of the feature maps was connected to all of the three input feature maps through filters of size 5 × 5. We used a stride size of one pixel. This generated feature maps of size 9 × 9 in this layer. The second convolutional layer took the output of the first convolutional layer as input and contained 256 feature maps. Each of the feature maps was connected to all of the feature maps in the previous layer through filters of size 5 × 5. We again used a stride size of one pixel. The third convolutional layer contained 768 feature maps of size 1 × 1. They were connected to all feature maps in the previous layer through 5 × 5 filters. We also used a stride size of one pixel in this layer. The rectified linear unit (ReLU) function (Nair and Hinton, 2010) was applied after the convolution operation in all of the convolutional layers. It has been shown (Krizhevsky et al., 2012) that the use of ReLU can expedite the training of CNN.
In addition to the convolutional layers, a few other layer types have been used in the CNN. Specifically, the local response normalization scheme was applied after the third convolutional layer to enforce competitions between features at the same spatial location across different feature maps. The fully-connected layer following the normalization layer had 3 outputs that correspond to the three tissue classes. A 3-way softmax layer was used to generate a distribution over the 3 class labels after the output of the fully-connected layer. Our network minimized the cross entropy loss between the predicted label and ground truth label. In addition, we used dropout (Hinton et al., 2012) to learn more robust features and reduce overfitting. This technique set the output of each neuron to zero with probability 0.5. The dropout was applied before the fully-connected layers in the CNN architecture of Figure 1. In total, the number of trainable parameters for this architecture is 5,332,995.
We also considered three other CNN architectures with input patch sizes of 9×9, 17×17, and 22 × 22. These CNN architectures consisted of different numbers of convolutional layers and feature maps. Both local response normalization and softmax layers have been applied on these architectures. We also used max-pooling layer for the architecture with input patch size of 22 × 22 after the first convolutional layer. The pooling size was set to 2 × 2 and a stride size of 2 × 2 was used. The complete details of these architectures were given in Table 1. The numbers of trainable parameters for these architectures are 6,577,155, 5,947,523, and 5,332,995, respectively.
Table 1.
Details of the CNN architectures with different input patch sizes used in this work. “Conv.”, “Norm.”, and “Full conn.” denote convolutional layers, normalization layers, and fully-connected layer, respectively.
| Patch size | Layer 1 | Layer 2 | Layer 3 | Layer 4 | Layer 5 | Layer 6 | Layer 7 | |
|---|---|---|---|---|---|---|---|---|
| 9 | Layer type | Conv. | Conv. | Norm. | Full Conn. | softmax | - | - |
| # of Feat. Maps | 256 | 1024 | 1024 | 3 | 3 | - | - | |
| Filter size | 5 × 5 | 5 × 5 | - | 1 × 1 | - | - | - | |
| Conv. stride | 1 × 1 | 1 × 1 | - | 1 × 1 | - | - | - | |
| Input size | 9 × 9 | 5 × 5 | 1 × 1 | 1 × 1 | 1 × 1 | - | - | |
| 13 | Layer type | Conv. | Conv. | Conv. | Norm. | Full Conn. | softmax | - |
| # of Feat. Maps | 64 | 256 | 768 | 768 | 3 | 3 | - | |
| Filter size | 5 × 5 | 5 × 5 | 5 × 5 | - | 1 × 1 | - | - | |
| Conv. stride | 1 × 1 | 1 × 1 | 1 × 1 | - | 1 × 1 | - | - | |
| Input size | 13 × 13 | 9 × 9 | 5 × 5 | 1 × 1 | 1 × 1 | 1 × 1 | - | |
| 17 | Layer type | Conv. | Conv. | Conv. | Conv. | Norm. | Full Conn. | softmax |
| # of Feat. Maps | 64 | 128 | 256 | 768 | 768 | 3 | 3 | |
| Filter size | 5 × 5 | 5 × 5 | 5 × 5 | 5 × 5 | - | 1 × 1 | - | |
| Conv. stride | 1 × 1 | 1 × 1 | 1 × 1 | 1 × 1 | - | 1 × 1 | - | |
| Input size | 17 × 17 | 13 × 13 | 9 × 9 | 5 × 5 | 1 × 1 | 1 × 1 | 1 × 1 | |
| 22 | Layer type | Conv. | Pooling | Conv. | Conv. | Norm. | Full Conn. | softmax |
| # of Feat. Maps | 64 | 64 | 256 | 768 | 768 | 3 | 3 | |
| Filter size | 5 × 5 | - | 5 × 5 | 5 × 5 | - | 1 × 1 | - | |
| Pooling size | - | 2 × 2 | - | - | - | - | - | |
| Pooling stride | - | 2 × 2 | - | - | - | - | - | |
| Input size | 22 × 22 | 18 × 18 | 9 × 9 | 5 × 5 | 1 × 1 | 1 × 1 | 1 × 1 |
2.4. Model training and calibration
We trained the networks using data consisting of patches extracted from the MR images and the corresponding manual segmentation ground truth images. In this work, we did not consider the segmentation of background as this is clear from the T1 images. Instead, we focused on segmenting the three tissue types (GM, WM, and CSF) from the foreground. For each foreground pixel, we extracted three patches centered at this pixel from T1, T2, and FA images, respectively. The three patches were used as input feature maps of CNNs. The corresponding output was a binary vector of length 3 indicating the tissue class to which the pixel belonged. This procedure generated more than 10, 000 instances, each corresponding to three patches, from each subject. We used leave-one-subject-out cross validation procedure to evaluate the segmentation performance. Specifically, we used seven out of the eight subjects to train the network and used the remaining subject to evaluate the performance. The average performance across folds was reported. All the patches from each training subject are stored in a batch file separately, leading to seven batch files in total. We used patches in these seven batches as the input of CNN consecutively for training. Note that patches in each batch file were presented to the training algorithm in random orders as was commonly used.
The weights in the networks were initialized randomly with Gaussian distribution N(0, 1×10−4) (LeCun et al., 1998). During training, the weights were updated by stochastic gradient descent algorithm with a momentum of 0.9 and a weight decay of 4 × 10−4. The biases in convolutional layers and fully-connected layer were initialized to 1. The number of epochs was tuned on a validation set consisting of patches from one randomly selected subject in the training set. The learning rate was set to 1 × 10−4 initially.
Following Krizhevsky et al. (2012), we first used the validation set to obtain a coarse approximation of the optimal epoch by minimizing the validation error. This epoch number was used to train a model on the training and validation sets consisting of seven subjects. Then the learning rate was reduced by a factor of 10 twice successively, and the model was trained for about 10 epochs each time. By following this procedure, the network with a patch size of 13 × 13 was trained for about 370 epochs. The training took less than one day on a Tesla K20c GPU with 2496 cores. The networks with other patch sizes were trained in a similar way. One advantage of using CNN for image segmentation is that, at test time, the entire image can be used as an input to the network to produce the segmentation map, and patch-level prediction is not needed (Giusti et al., 2013; Ning et al., 2005). This leads to very efficient segmentation at test time. For example, our CNN models took about 50–100 seconds for segmenting an image of size 256×256.
3. Results and discussion
3.1. Experimental setup
In the experiments, we focused on evaluating our CNN architectures for segmenting the three types of infant brain tissues. We formulated the prediction of brain tissue classes as a three-class classification task. For comparison purposes, we also implemented two other commonly used classification methods, namely the support vector machine (SVM) and the random forest (RF) (Breiman, 2001) methods. The linear SVM was used in our experiments, as other kernels yielded lower performance empirically. The performance of SVM was generated by tuning the regularization parameters using cross validation. An RF is a tree-based ensemble model in which a set of randomized trees are built and the final decision is made using majority voting by all trees. This method has been used in image-related applications (Amit and Geman, 1997), including medical image segmentation (Criminisi and Shotton, 2013; Criminisi et al., 2012). In this work, we used RFs containing 100 trees, and each tree was grown fully and unpruned. The number of features at each node randomly selected to compete for the best split was set to the square root of the total number of features. We used the “randomForest” R package (Liaw and Wiener, 2002) in the experiments. We reshaped the raw training patches into vectors whose elements were considered as the input features of SVM and RF. We also compared our methods with two common image segmentation methods, namely the coupled level set (CLS) (Wang et al., 2011) and the majority voting (MV) methods. Note that the method based on local dictionaries of patches proposed in Wang et al. (2014) requires the images of different subjects to be registered, since a local dictionary was constructed by using patches extracted from the corresponding locations on the training images. We thus did not compare our methods with the one in Wang et al. (2014).
To evaluate the segmentation performance, we used the Dice ratio (DR) to quantitatively measure the segmentation accuracy. Specifically, let A and B denote the binary segmentation labels generated manually and computationally, respectively, about one tissue class on pixels for certain subject. The Dice ratio is defined as
where |A| denotes the number of positive elements in the binary segmentation A, and |A∩B| is the number of shared positive elements by A and B. The Dice ratio lies in [0, 1], and a larger value indicates a higher segmentation accuracy. We also used another measure known as the modified Hausdorff distance (MHD). Supposing that C and D are two sets of positive pixels identified manually and computationally, respectively, about one tissue class for a certain subject, the MHD is defined as
where d(C, D) = maxc∈Cd(c, D), and the distance between a point c and a set of points D is defined as d(c, D) = mind∈D||c − d||. A smaller value indicates a higher proximity of two point sets, thus implying a higher segmentation accuracy.
3.2. Comparison of different CNN architectures
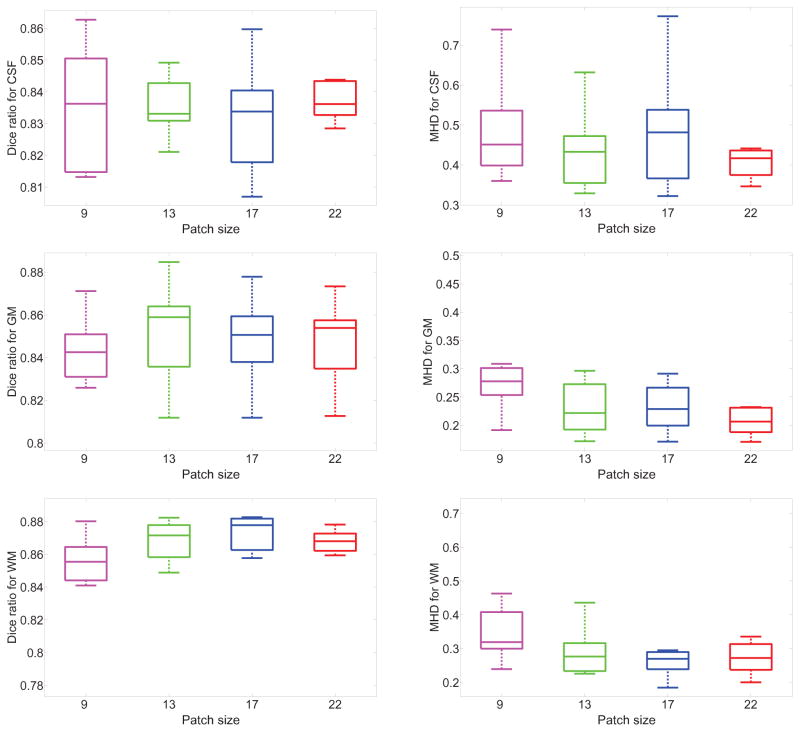
The nonlinear relationship between inputs and outputs of a CNN is represented by its multi-layer architecture using convolution, pooling and normalization. We first studied the impact of different CNN architectures on segmentation accuracy. We devised four different architectures, and the detailed configuration have been described in Table 1. The classification performance of these architectures was reported in Figure 2 using box plots. It can be observed from the results that the predictive performance is generally higher for the architectures with input patch sizes of 13 × 13 and 17 × 17. This result is consistent with the fact that networks with more convolutional layers and feature maps tend to have a deeper hierarchical structure and more trainable parameters. Thus, these networks are capable of capturing the complex relationship between input and output. We can also observe that the architecture with input patch size of 22 × 22 did not generate substantially higher predictive performance, suggesting that the pooling operation might not be suitable for the data we used. In the following, we focused on evaluating the performance of CNN with input patch size of 13 × 13. To examine the patterns captured by the CNN models, we visualized the 64 filters in the first convolutional layer for the model with an input patch size of 13 × 13 in Figure 3. Similar to the observation in Zeiler and Fergus (2014), these filters capture primitive image features such as edges and corners.
Figure 2.
Box plots of the segmentation performance achieved by CNNs over 8 subjects for different patch sizes. Each plot in the first column uses Dice ratio to measure the performance for each of the three tissue types, and four different architectures are trained by using different patch sizes of 9 × 9, 13 × 13, 17 × 17, and 22 × 22, respectively. The performance is evaluated using leave-one-subject-out cross validation and 8 test results are collected for each patch size of each plot. The central mark represents the median, the edges of the box denote the 25th and 75th percentiles. The whiskers extend to the minimum and maximum values not considered outliers, and outliers are plotted individually. The plots in the right column are the results measured by MHD using the same configuration.
Figure 3.

Visualization of the 64 filters in the first convolutional layer for the model with an input patch size of 13 × 13.
3.3. Effectiveness of integrating multi-modality data
To demonstrate the effectiveness of integrating multi-modality data, we considered the performance achieved by each single image modality. Specifically, the T1, T2, and FA images of each subject were separately used as the input of the architecture with a patch size of 13 × 13 in Table 1. The segmentation performance achieved using different modalities was presented in Tables 2 and 3. It can be observed that the combination of different image modalities invariably yielded higher performance than any of the single image modality. We can also see that the T1 images produced the highest performance among the three modalities. This suggests that the T1 images are most informative in discriminating the three tissue types. Another interesting observation is that the FA images are very informative in distinguishing GM and WM, but they achieved low performance on CSF. This might be because the anisotropic diffusion is hardly detectable using FA for liquids such as cerebrospinal fluid (CSF) in brain. In contrast, T2 images are more powerful for capturing CSF instead of GM and WM. These results demonstrated that certain modality is more informative in distinguishing certain tissue types, and combination of all modalities leads to improved segmentation performance.
Table 2.
Comparison of segmentation performance over different image modalities achieved by CNN with input patch size of 13 × 13 on each subject in terms of Dice ratio. The best performance of different tissue segmentation tasks is highlighted.
| Sub.1 | Sub.2 | Sub.3 | Sub.4 | Sub.7 | Sub.8 | Sub.9 | Sub.10 | ||
|---|---|---|---|---|---|---|---|---|---|
| CSF | T1 | 0.7797 | 0.7824 | 0.7928 | 0.8072 | 0.7931 | 0.8076 | 0.7610 | 0.8176 |
| T2 | 0.6906 | 0.7238 | 0.7459 | 0.7614 | 0.7792 | 0.7737 | 0.7328 | 0.7934 | |
| FA | 0.6021 | 0.5838 | 0.6068 | 0.5378 | 0.6076 | 0.6001 | 0.6374 | 0.5408 | |
| All | 0.8323 | 0.8314 | 0.8304 | 0.8373 | 0.8482 | 0.8492 | 0.8211 | 0.8339 | |
| GM | T1 | 0.8123 | 0.8039 | 0.8001 | 0.7529 | 0.7693 | 0.7499 | 0.7273 | 0.8146 |
| T2 | 0.6094 | 0.5884 | 0.6026 | 0.4973 | 0.5897 | 0.6142 | 0.6027 | 0.6266 | |
| FA | 0.7256 | 0.7459 | 0.7282 | 0.6065 | 0.7224 | 0.7126 | 0.6991 | 0.7827 | |
| All | 0.8531 | 0.8572 | 0.8848 | 0.8184 | 0.8119 | 0.8652 | 0.8628 | 0.8607 | |
| WM | T1 | 0.8241 | 0.7476 | 0.8269 | 0.7751 | 0.8006 | 0.8223 | 0.7527 | 0.7996 |
| T2 | 0.6942 | 0.7021 | 0.7181 | 0.6318 | 0.6917 | 0.7001 | 0.6892 | 0.6979 | |
| FA | 0.8082 | 0.6816 | 0.6627 | 0.7238 | 0.7824 | 0.7774 | 0.8131 | 0.8163 | |
| All | 0.8798 | 0.8116 | 0.8824 | 0.8489 | 0.8689 | 0.8677 | 0.8742 | 0.8760 |
Table 3.
Comparison of segmentation performance over different image modalities achieved by CNN with input patch size of 13 × 13 on each subject in terms of modified Hausdorff distance (MHD). The best performance of different tissue segmentation tasks is highlighted.
| Sub.1 | Sub.2 | Sub.3 | Sub.4 | Sub.7 | Sub.8 | Sub.9 | Sub.10 | ||
|---|---|---|---|---|---|---|---|---|---|
| CSF | T1 | 0.7245 | 0.6724 | 0.6428 | 0.6072 | 0.5537 | 0.5027 | 0.6021 | 0.4478 |
| T2 | 0.9048 | 0.8228 | 0.7932 | 0.6978 | 0.6004 | 0.5938 | 0.6989 | 0.5457 | |
| FA | 1.2446 | 1.3895 | 1.3348 | 1.4277 | 1.3271 | 1.4297 | 0.9312 | 1.3389 | |
| All | 0.6320 | 0.3293 | 0.3659 | 0.4395 | 0.4268 | 0.4482 | 0.4970 | 0.3442 | |
| GM | T1 | 0.5069 | 0.4237 | 0.4892 | 0.6528 | 0.6187 | 0.6691 | 0.6843 | 0.3971 |
| T2 | 1.2372 | 1.3728 | 1.2871 | 1.8421 | 1.5980 | 1.2963 | 1.3325 | 1.2241 | |
| FA | 0.6839 | 0.6781 | 0.6538 | 0.9479 | 0.6843 | 0.6945 | 0.7461 | 0.4322 | |
| All | 0.2067 | 0.2490 | 0.2010 | 0.2964 | 0.4398 | 0.2367 | 0.1839 | 0.1719 | |
| WM | T1 | 0.4796 | 0.6526 | 0.4232 | 0.6455 | 0.4726 | 0.4271 | 0.5023 | 0.4047 |
| T2 | 0.9171 | 0.7381 | 0.7974 | 1.0043 | 0.9423 | 0.7169 | 0.8274 | 0.8934 | |
| FA | 0.4162 | 0.8924 | 1.0258 | 0.7523 | 0.6228 | 0.5428 | 0.4238 | 0.5016 | |
| All | 0.2258 | 0.4362 | 0.2401 | 0.3275 | 0.2504 | 0.3050 | 0.3029 | 0.2271 |
3.4. Comparison with other methods
In order to provide a comprehensive and quantitative evaluation of the proposed method, we reported the segmentation performance on all 8 subjects using leave-one-subject-out cross validation. The performance of CNN, RF, SVM, CLS, and MV was reported in Tables 4 and 5 using the Dice ratio and MHD, respectively. We can observe from these two tables that CNN outperformed other methods for segmenting all three types of brain tissues in most cases. Specifically, CNN could achieve Dice ratios as 83.55%±0.94% (CSF), 85.18%±2.45% (GM), and 86.37% ± 2.34% (WM) on average over 8 subjects, yielding an overall value of 85.03% ± 2.27%. In contrast, RF, SVM, CLS, and MV achieved overall Dice ratios of 83.15% ± 2.52%, 76.95% ± 3.55%, 82.62% ± 2.76%, and 77.64% ± 8.28%, respectively. Meanwhile, CNN also outperformed other methods in terms of MHD. Specifically, CNN could achieve MHDs as 0.4354 ±0.0979 (CSF), 0.2482 ±0.0871 (GM), and 0.2894 ±0.0710 (WM), yielding an overall value of 0.3243 ± 0.1161. In contrast, RF, SVM, CLS, and MV achieved overall MHDs of 0.4593 ± 0.2506, 0.6424 ± 0.2665, 0.4839 ± 0.1597, and 0.7076 ± 0.5721, respectively.
Table 4.
Segmentation performance in terms of Dice ratio achieved by the convolutional neural network (CNN), random forest (RF), support vector machine (SVM), coupled level sets (CLS), and majority voting (MV). The highest performance in each case was highlighted, and the statistical significance of the results were given in Table 6.
| Sub.1 | Sub.2 | Sub.3 | Sub.4 | Sub.7 | Sub.8 | Sub.9 | Sub.10 | ||
|---|---|---|---|---|---|---|---|---|---|
| CSF | CNN | 0.8323 | 0.8314 | 0.8304 | 0.8373 | 0.8482 | 0.8492 | 0.8211 | 0.8339 |
| RF | 0.8192 | 0.8135 | 0.8323 | 0.8090 | 0.8306 | 0.8457 | 0.7904 | 0.7955 | |
| SVM | 0.7409 | 0.7677 | 0.7733 | 0.7429 | 0.7006 | 0.7837 | 0.7243 | 0.7333 | |
| CLS | 0.8064 | 0.8152 | 0.732 | 0.8614 | 0.8397 | 0.8238 | 0.8087 | 0.828 | |
| MV | 0.7072 | 0.6926 | 0.6826 | 0.6348 | 0.6313 | 0.6136 | 0.6904 | 0.692 | |
| GM | CNN | 0.8531 | 0.8572 | 0.8848 | 0.8184 | 0.8119 | 0.8652 | 0.8628 | 0.8607 |
| RF | 0.8288 | 0.8482 | 0.8772 | 0.8078 | 0.7976 | 0.8498 | 0.8461 | 0.8353 | |
| SVM | 0.7933 | 0.7991 | 0.8294 | 0.7527 | 0.7416 | 0.7996 | 0.8017 | 0.8038 | |
| CLS | 0.8298 | 0.8389 | 0.8498 | 0.8343 | 0.813 | 0.8719 | 0.8612 | 0.8421 | |
| MV | 0.849 | 0.8442 | 0.8525 | 0.8027 | 0.7831 | 0.797 | 0.8372 | 0.8299 | |
| WM | CNN | 0.8798 | 0.8116 | 0.8824 | 0.8489 | 0.8689 | 0.8677 | 0.8742 | 0.8760 |
| RF | 0.8612 | 0.7816 | 0.8687 | 0.8373 | 0.8479 | 0.8575 | 0.8393 | 0.8353 | |
| SVM | 0.8172 | 0.7404 | 0.7623 | 0.8030 | 0.7997 | 0.7919 | 0.7059 | 0.7585 | |
| CLS | 0.8383 | 0.8054 | 0.7998 | 0.8238 | 0.8437 | 0.8213 | 0.8297 | 0.8107 | |
| MV | 0.8631 | 0.8002 | 0.8504 | 0.8171 | 0.8389 | 0.8373 | 0.8412 | 0.8445 |
Table 5.
Segmentation performance in terms of modified Hausdorff distance (MHD) achieved by the convolutional neural network (CNN), random forest (RF), support vector machine (SVM), coupled level sets (CLS), and majority voting (MV). The best performance in each case was highlighted, and the statistical significance of the results were given in Table 6.
| Sub.1 | Sub.2 | Sub.3 | Sub.4 | Sub.7 | Sub.8 | Sub.9 | Sub.10 | ||
|---|---|---|---|---|---|---|---|---|---|
| CSF | CNN | 0.6320 | 0.3293 | 0.3659 | 0.4395 | 0.4268 | 0.4482 | 0.4970 | 0.3442 |
| RF | 1.0419 | 0.5914 | 0.6802 | 0.9042 | 0.3610 | 0.4935 | 0.9151 | 0.6949 | |
| SVM | 1.1426 | 0.8867 | 0.7571 | 0.9014 | 1.0020 | 0.4743 | 1.1789 | 0.8866 | |
| CLS | 0.6420 | 0.3487 | 0.8151 | 0.4875 | 0.4987 | 0.4939 | 0.4717 | 0.4986 | |
| MV | 1.5287 | 1.3788 | 1.3566 | 1.5178 | 1.4157 | 2.1068 | 1.1156 | 1.2889 | |
| GM | CNN | 0.2067 | 0.2490 | 0.2010 | 0.2964 | 0.4398 | 0.2367 | 0.1839 | 0.1719 |
| RF | 0.2771 | 0.2739 | 0.1524 | 0.3033 | 0.3429 | 0.2315 | 0.2517 | 0.2708 | |
| SVM | 0.5247 | 0.2916 | 0.3566 | 0.4015 | 0.6308 | 0.3809 | 0.4466 | 0.4362 | |
| CLS | 0.3615 | 0.2950 | 0.2683 | 0.3577 | 0.3872 | 0.2536 | 0.2530 | 0.3655 | |
| MV | 0.2834 | 0.2743 | 0.2483 | 0.3395 | 0.4316 | 0.3569 | 0.2687 | 0.3324 | |
| WM | CNN | 0.2258 | 0.4362 | 0.2401 | 0.3275 | 0.2504 | 0.3050 | 0.3029 | 0.2271 |
| RF | 0.3022 | 0.7981 | 0.2648 | 0.3201 | 0.5020 | 0.3321 | 0.3268 | 0.3909 | |
| SVM | 0.3218 | 0.8290 | 0.5276 | 0.5751 | 0.4784 | 0.4445 | 0.9407 | 0.6029 | |
| CLS | 0.6320 | 0.4923 | 0.7207 | 0.5425 | 0.6947 | 0.4485 | 0.5627 | 0.7216 | |
| MV | 0.3063 | 0.5314 | 0.2824 | 0.2907 | 0.2922 | 0.3323 | 0.3271 | 0.3751 |
To assess the statistical significance of the performance differences, we performed one-sided Wilcoxon signed rank tests on both Dice ratio and MHD produced by the 8 subjects, and the p-values were reported in Table 6. When considering the Dice ratio, we chose the left-sided test with the alternative hypothesis that the averaged performance of CNN is higher than that of either RF, SVM, CLS or MV. The right-sided test was considered for MHD. We can see that the proposed CNN method significantly outperformed SVM, RF, CLS and MV in most cases. These results demonstrated that CNN is effective in segmenting the infant brain tissues as compared to other methods.
Table 6.
Statistical test results in comparing CNN with RF, SVM, CLS, and MV, respectively. We calculated the p-values by performing one–sided Wilcoxon signed rank tests using the performance reported in Tables 4 and 5. We performed the left-sided test for the Dice ratio, and the right-sided test for the MHD.
| CSF | GM | WM | ||
|---|---|---|---|---|
| Dice ratio | CNN vs. RF | 3.30E-03 | 1.55E-04 | 4.02E-04 |
| CNN vs. SVM | 2.55E-05 | 2.51E-09 | 1.87E-04 | |
| CNN vs. CLS | 6.59E-02 | 8.88E-02 | 8.37E-04 | |
| CNN vs. MV | 6.22E-06 | 2.50E-03 | 1.71E-05 | |
| MHD | CNN vs. RF | 2.30E-03 | 2.72E-01 | 2.16E-02 |
| CNN vs. SVM | 1.39E-04 | 3.67E-04 | 7.99E-04 | |
| CNN vs. CLS | 5.75E-02 | 1.85E-02 | 5.57E-04 | |
| CNN vs. MV | 1.09E-05 | 4.30E-03 | 1.52E-02 |
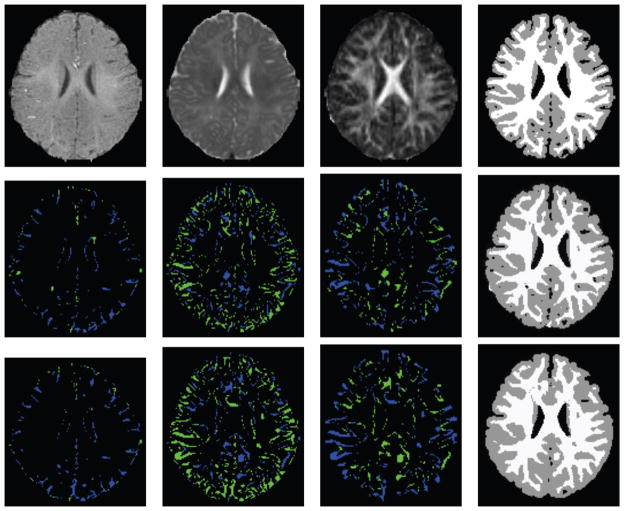
In addition to quantitatively demonstrating the advantage of the proposed CNN method, we visually examined the segmentation results of different tissues for two subjects in Figures 4 and 5. The original T1, T2, and FA images were shown in the first row and the following three rows presented the segmentation results of human experts, CNN, and RF, respectively. It can be seen that, the segmentation patterns of CNN are quite similar to the ground truth data generated by human experts. In contrast, RF generated more defects and fuzzy boundaries for different tissues. These results further showed that the proposed CNN method was more effective than other methods.
Figure 4.
Comparison of the segmentation results with the manually generated segmentation on Subject 1. The first row shows the original multi-modality data (T1, T2 and FA), and the second row shows the manual segmentations (CSF, GM, and WM). The third and fourth rows show the segmentation results by CNN and RF, respectively.
Figure 5.
Comparison of the segmentation results with the manually generated segmentation on Subject 2. The first row shows the original multi-modality data (T1, T2 and FA), and the second row shows the manual segmentations (CSF, GM, and WM). The third and fourth rows show the segmentation results by CNN and RF, respectively.
In order to further compare results by different methods, the label difference maps that compare the ground-truth segmentation with the predicted segmentation were also presented. In Figures 6 and 7, the original T1, T2, FA images and the ground-truth segmentations for two subjects were shown in the first rows. The false positives and false negatives of CNN and RF were given in the second and third rows, respectively. We also showed the segmentation results in these two figures. We can see that the CNN outperformed RF in both the number of false pixels and the performance of tissue boundary detection. For example, RF generated more false positives around the surface of brain, and also more false negatives around hippocampus for white matters on Subject 2. We can also observe that most of the mis-classified pixels are located in the areas having large tissue contrast, such as cortices consisting of gyri and sulci. This might be explained by the fact that our segmentation methods are patch-based, and patches centered at boundary pixels contain pixels of multiple tissue types.
Figure 6.
Label difference maps of the results generated by CNN and RF on Subject 1. The first row shows the original images and manual segmentation (T1, T2, FA, and manual segmentation). The second and third rows show the results by CNN and RF (CSF, GM, WM, segmentation result). In each label difference map, dark blue color indicates false positives and the dark green color indicates false negatives.
Figure 7.
Label difference maps of the results generated by CNN and RF on Subject 2. The first row shows the original images and manual segmentation (T1, T2, FA, and manual segmentation). The second and third rows show the results by CNN and RF (CSF, GM, WM, segmentation result). In each label difference map, dark blue color indicates false positives and the dark green color indicates false negatives.
To compare the performance between CNNs and RF when the patch size varies, we reported the performance differences between CNNs and RF averaged over 8 subjects for different input patch sizes in Figure 8. We can observe that the performance gains of CNNs over RF are generally amplified for an increased input patch size. This difference is even more significant for the results of CSF and WM, which have more restricted distributions than GM. This is because of the fact that RF treated each pixel independently, and therefore, did not leverage the spatial relationships between pixels. In comparison, CNNs weighted pixels differently based on their spatial distance to the center pixel, enabling the retaining of spatial information. The impact of this essential difference between CNNs and RF is expected to be more significant with a larger patch size, since more spatial information is ignored by RF. This difference probably also explains why CNNs could segment the boundary pixels with a higher accuracy, which was shown in Figures 4 and 5.
Figure 8.

Comparison of performance differences between CNNs and RF averaged over 8 subjects for patch sizes of 9 × 9, 13 × 13, 17 × 17, and 22 × 22, respectively. The performance differences were obtained by subtracting the performance of RF from that of CNNs. The left and right figures show the results of Dice ratio and MHD, respectively.
4. Conclusion and future work
In this study, we aimed at segmenting infant brain tissue images in the isointense stage. This was achieved by employing CNNs with multiple intermediate layers to integrate and combine multi-modality brain images. The CNNs used the complementary and multimodality information from T1, T2, and FA images as input feature maps and generated the segmentation labels as output feature maps. We compared the performance of our approach with that of the commonly used segmentation methods. Results showed that our proposed model significantly outperformed prior methods on infant brain tissue segmentation. Overall, our experiments demonstrated that CNNs could produce more quantitative and accurate computational modeling and results on infant tissue image segmentation.
In this work, the tissue segmentation problem was formulated as a patch classification task, where the relationship among patches was ignored. Some prior work has incorporated geometric constraints into segmentation models (Wang et al., 2014). We will improve our CNN models to include similar constraints in the future. In the current experiments, we employed CNNs with a few hidden layers. Recent studies showed that CNNs with many hidden layers yielded very promising performance on visual recognition tasks when appropriate regularization was applied (Krizhevsky et al., 2012). We will explore CNNs with many hidden layers in the future as more data become available. In the current study, we used all the patches extracted from each subject for training the convolutional neural network. The number of patches from each tissue type is not balanced. The imbalanced data might affect the prediction performance. For example, we might use sampling and ensemble learning for combating this imbalance problem, although this will further increase the training time. The current work used 2D CNN for image segmentation, because only selected slices have been manually segmented in the current data set. In principle, CNN could be used to segment 3D images when labeled data are available. In this case, it is more natural to apply 3D CNN (Ji et al., 2013) as such models have been developed for processing 3D video data. The computational costs for training and testing 3D CNNs might be higher than those for training 2D CNNs, as 3D convolutions are involved in these networks. We will explore these high-order models in the future.
Highlights.
We study the segmentation of isointense infant brain images.
We integrate multi-modality images.
We employ deep convolutional neural networks.
Integration of multi-modality images improves performance.
Deep convolutional neural networks outperform other methods.
Acknowledgments
This work was supported by the National Science Foundation grants DBI-1147134 and DBI-1350258, and the National Institutes of Health grants EB006733, EB008374, EB009634, AG041721, MH100217, and AG042599.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amit Y, Geman D. Shape quantization and recognition with randomized trees. Neural computation. 1997;9(7):1545–1588. [Google Scholar]
- Blumenthal JD, Zijdenbos A, Molloy E, Giedd JN. Motion artifact in magnetic resonance imaging: implications for automated analysis. Neuroimage. 2002;16(1):89–92. doi: 10.1006/nimg.2002.1076. [DOI] [PubMed] [Google Scholar]
- Breiman L. Random forests. Machine learning. 2001;45(1):5–32. [Google Scholar]
- Cardoso MJ, Melbourne A, Kendall GS, Modat M, Robertson NJ, Marlow N, Ourselin S. Adapt: An adaptive preterm segmentation algorithm for neonatal brain mri. Neuro Image. 2013;65:97–108. doi: 10.1016/j.neuroimage.2012.08.009. [DOI] [PubMed] [Google Scholar]
- Ciresan D, Giusti A, Gambardella LM, Schmidhuber J. Deep neural networks segment neuronal membranes in electron microscopy images. In: Pereira F, Burges C, Bottou L, Weinberger K, editors. Advances in Neural Information Processing Systems. Vol. 25. Curran Associates, Inc; 2012. pp. 2843–2851. [Google Scholar]
- Ciresan DC, Giusti A, Gambardella LM, Schmidhuber J. Mitosis detection in breast cancer histology images with deep neural networks. Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention; 2013. pp. 411–418. [DOI] [PubMed] [Google Scholar]
- Criminisi A, Shotton J. Decision Forests for Computer Vision and Medical Image Analysis. Springer; 2013. [Google Scholar]
- Criminisi A, Shotton J, Konukoglu E. Decision forests: A unified framework for classification, regression, density estimation, manifold learning and semi-supervised learning. Foundations and Trends in Computer Graphics and Vision. 2012;7(2–3):81–227. [Google Scholar]
- Dai Y, Shi F, Wang L, Wu G, Shen D. ibeat: a toolbox for infant brain magnetic resonance image processing. Neuroinformatics. 2013;11(2):211–225. doi: 10.1007/s12021-012-9164-z. [DOI] [PubMed] [Google Scholar]
- Fan Y, Shi F, Smith JK, Lin W, Gilmore JH, Shen D. Brain anatomical networks in early human brain development. Neuroimage. 2011;54(3):1862–1871. doi: 10.1016/j.neuroimage.2010.07.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giusti A, Cireşan DC, Masci J, Gambardella LM, Schmidhuber J. Fast image scanning with deep max-pooling convolutional neural networks. 2013 IEEE International Conference on Image Processing; 2013. pp. 4034–4038. [Google Scholar]
- Gui L, Lisowski R, Faundez T, Hüppi PS, Lazeyras F, Kocher M. Morphology-driven automatic segmentation of mr images of the neonatal brain. Medical image analysis. 2012;16(8):1565–1579. doi: 10.1016/j.media.2012.07.006. [DOI] [PubMed] [Google Scholar]
- Helmstaedter M, Briggman KL, Turaga SC, Jain V, Seung HS, Denk W. Connectomic reconstruction of the inner plexiform layer in the mouse retina. Nature. 2013;500(7461):168–174. doi: 10.1038/nature12346. [DOI] [PubMed] [Google Scholar]
- Hinton GE, Srivastava N, Krizhevsky A, Sutskever I, Salakhutdinov RR. Improving neural networks by preventing co-adaptation of feature detectors. 2012 arXiv preprint arXiv:1207.0580. [Google Scholar]
- Jain V, Murray JF, Roth F, Turaga S, Zhigulin V, Briggman KL, Helmstaedter MN, Denk W, Seung HS. Supervised learning of image restoration with convolutional networks. Computer Vision, 2007. ICCV 2007; IEEE 11th International Conference on. IEEE; 2007. pp. 1–8. [Google Scholar]
- Jain V, Seung S. Natural image denoising with convolutional networks. In: Koller D, Schuurmans D, Bengio Y, Bottou L, editors. Advances in Neural Information Processing Systems. Vol. 21. 2009. pp. 769–776. [Google Scholar]
- Ji S, Xu W, Yang M, Yu K. 3D convolutional neural networks for human action recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(1):221–231. doi: 10.1109/TPAMI.2012.59. [DOI] [PubMed] [Google Scholar]
- Kim SH, Fonov VS, Dietrich C, Vachet C, Hazlett HC, Smith RG, Graves MM, Piven J, Gilmore JH, Dager SR, et al. Adaptive prior probability and spatial temporal intensity change estimation for segmentation of the one-year-old human brain. Journal of neuroscience methods. 2013;212(1):43–55. doi: 10.1016/j.jneumeth.2012.09.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krizhevsky A, Sutskever I, Hinton G. Imagenet classification with deep convolutional neural networks. In: Bartlett P, Pereira F, Burges C, Bottou L, Weinberger K, editors. Advances in Neural Information Processing Systems. Vol. 25. 2012. pp. 1106–1114. [Google Scholar]
- LeCun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998 Nov;86(11):2278–2324. [Google Scholar]
- LeCun Y, Bottou L, Orr GB, Müller K-R. Neural Networks: Tricks of the Trade. Springer; Berlin Heidelberg: 1998. Efficient backprop; pp. 9–50. [Google Scholar]
- Leroy F, Mangin J-F, Rousseau F, Glasel H, Hertz-Pannier L, Dubois J, Dehaene-Lambertz G. Atlas-free surface reconstruction of the cortical grey-white interface in infants. PloS one. 2011;6(11) doi: 10.1371/journal.pone.0027128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Nie J, Wang L, Shi F, Lin W, Gilmore JH, Shen D. Mapping region-specific longitudinal cortical surface expansion from birth to 2 years of age. Cerebral Cortex. 2013a;23(11):2724–2733. doi: 10.1093/cercor/bhs265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G, Wang L, Shi F, Lin W, Shen D. Multi-atlas based simultaneous labeling of longitudinal dynamic cortical surfaces in infants. Medical Image Computing and Computer-Assisted Intervention–MICCAI; 2013; Springer; 2013b. pp. 58–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw A, Wiener M. Classification and regression by randomforest. R news. 2002;2(3):18–22. [Google Scholar]
- Liu T, Li H, Wong K, Tarokh A, Guo L, Wong ST. Brain tissue segmentation based on dti data. Neuro Image. 2007;38(1):114–123. doi: 10.1016/j.neuroimage.2007.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. Proceedings of the 27th International Conference on Machine Learning (ICML-10); 2010. pp. 807–814. [Google Scholar]
- Nie J, Li G, Wang L, Gilmore JH, Lin W, Shen D. A computational growth model for measuring dynamic cortical development in the first year of life. Cerebral Cortex. 2011 doi: 10.1093/cercor/bhr293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ning F, Delhomme D, LeCun Y, Piano F, Bottou L, Barbano PE. Toward automatic phenotyping of developing embryos from videos. IEEE Transactions on Image Processing. 2005;14(9):1360–1371. doi: 10.1109/tip.2005.852470. [DOI] [PubMed] [Google Scholar]
- Nishida M, Makris N, Kennedy DN, Vangel M, Fischl B, Krishnamoorthy KS, Caviness VS, Grant PE. Detailed semiautomated mri based morphometry of the neonatal brain: preliminary results. Neuroimage. 2006;32(3):1041–1049. doi: 10.1016/j.neuroimage.2006.05.020. [DOI] [PubMed] [Google Scholar]
- Paus T, Collins D, Evans A, Leonard G, Pike B, Zijdenbos A. Maturation of white matter in the human brain: a review of magnetic resonance studies. Brain research bulletin. 2001;54(3):255–266. doi: 10.1016/s0361-9230(00)00434-2. [DOI] [PubMed] [Google Scholar]
- Shi F, Fan Y, Tang S, Gilmore JH, Lin W, Shen D. Neonatal brain image segmentation in longitudinal mri studies. Neuroimage. 2010a;49(1):391–400. doi: 10.1016/j.neuroimage.2009.07.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F, Wang L, Dai Y, Gilmore JH, Lin W, Shen D. Label: Pediatric brain extraction using learning-based meta-algorithm. Neuro Image. 2012;62(3):1975–1986. doi: 10.1016/j.neuroimage.2012.05.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi F, Yap P-T, Gilmore JH, Lin W, Shen D. Medical Imaging and Augmented Reality. Springer; 2010b. Spatial-temporal constraint for segmentation of serial infant brain mr images; pp. 42–50. [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in mri data. Medical Imaging, IEEE Transactions on. 1998;17(1):87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Song Z, Awate SP, Licht DJ, Gee JC. Clinical neonatal brain mri segmentation using adaptive nonparametric data models and intensity-based markov priors. Medical Image Computing and Computer-Assisted Intervention–MICCAI; 2007; Springer; 2007. pp. 883–890. [DOI] [PubMed] [Google Scholar]
- Turaga SC, Murray JF, Jain V, Roth F, Helmstaedter M, Briggman K, Denk W, Seung HS. Convolutional networks can learn to generate affinity graphs for image segmentation. Neural Computation. 2010;22(2):511–538. doi: 10.1162/neco.2009.10-08-881. [DOI] [PubMed] [Google Scholar]
- Wang L, Shi F, Gao Y, Li G, Gilmore JH, Lin W, Shen D. Integration of sparse multi-modality representation and anatomical constraint for isointense infant brain MR image segmentation. Neuro Image. 2014;89:152–164. doi: 10.1016/j.neuroimage.2013.11.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Lin W, Gilmore JH, Shen D. Automatic segmentation of neonatal images using convex optimization and coupled level sets. Neuro Image. 2011;58(3):805–817. doi: 10.1016/j.neuroimage.2011.06.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Yap P-T, Gilmore JH, Lin W, Shen D. 4D multi-modality tissue segmentation of serial infant images. PloS ONE. 2012;7(9) doi: 10.1371/journal.pone.0044596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L, Shi F, Yap PT, Lin W, Gilmore JH, Shen D. Longitudinally guided level sets for consistent tissue segmentation of neonates. Human brain mapping. 2013;34(4):956–972. doi: 10.1002/hbm.21486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weisenfeld NI, Mewes A, Warfield SK. Segmentation of newborn brain mri. Biomedical Imaging: Nano to Macro, 2006; 3rd IEEE International Symposium on. IEEE; 2006a. pp. 766–769. [Google Scholar]
- Weisenfeld NI, Mewes AU, Warfield SK. Highly accurate segmentation of brain tissue and subcortical gray matter from newborn mri. Medical Image Computing and Computer-Assisted Intervention–MICCAI; 2006; Springer; 2006b. pp. 199–206. [DOI] [PubMed] [Google Scholar]
- Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain mri. Neuroimage. 2009;47(2):564–572. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, Rueckert D, Hajnal JV. Automatic segmentation and reconstruction of the cortex from neonatal mri. Neuroimage. 2007;38(3):461–477. doi: 10.1016/j.neuroimage.2007.07.030. [DOI] [PubMed] [Google Scholar]
- Yushkevich PA, Piven J, Hazlett HC, Smith RG, Ho S, Gee JC, Gerig G. User-guided 3d active contour segmentation of anatomical structures: significantly improved efficiency and reliability. Neuroimage. 2006;31(3):1116–1128. doi: 10.1016/j.neuroimage.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Zeiler MD, Fergus R. Visualizing and understanding convolutional networks. Proceedings of the European Conference on Computer Vision; Springer; 2014. pp. 818–833. [Google Scholar]
- Zilles K, Armstrong E, Schleicher A, Kretschmann HJ. The human pattern of gyrification in the cerebral cortex. Anatomy and embryology. 1988;179(2):173–179. doi: 10.1007/BF00304699. [DOI] [PubMed] [Google Scholar]