Identifying Future Research Priorities Using Value of Information Analyses: Left Atrial Appendage Occlusion Devices in Atrial Fibrillation

Abstract

Background

Left atrial appendage occlusion devices are cost effective for stroke prophylaxis in atrial fibrillation when compared with dabigatran or warfarin. We illustrate the use of value‐of‐information analyses to quantify the degree and consequences of decisional uncertainty and to identify future research priorities.

Methods and Results

A microsimulation decision‐analytic model compared left atrial appendage occlusion devices to dabigatran or warfarin in atrial fibrillation. Probabilistic sensitivity analysis quantified the degree of parameter uncertainty. Expected value of perfect information analyses showed the consequences of this uncertainty. Expected value of partial perfect information analyses were done on sets of input parameters (cost, utilities, and probabilities) to identify the source of the greatest uncertainty. One‐way sensitivity analyses identified individual parameters for expected value of partial perfect information analyses. Population expected value of perfect information and expected value of partial perfect information provided an upper bound on the cost of future research. Substantial uncertainty was identified, with left atrial appendage occlusion devices being preferred in only 47% of simulations. The expected value of perfect information was $8542 per patient and $227.3 million at a population level. The expected value of partial perfect information for the set of probability parameters represented the most important source of uncertainty, at $6875. Identified in 1‐way sensitivity analyses, the expected value of partial perfect information for the odds ratio for stroke with left atrial appendage occlusion compared with warfarin was calculated at $7312 per patient or $194.5 million at a population level.

Conclusion

The relative efficacy of stroke reduction with left atrial appendage occlusion devices in relation to warfarin is an important source of uncertainty. Improving estimates of this parameter should be the priority for future research in this area.

Introduction

Atrial fibrillation (AF) is associated with substantial morbidity and mortality, principally from AF‐related strokes.¹ The most common agent for AF stroke prophylaxis is warfarin. Although highly efficacious, the use of warfarin is limited by the need for regular monitoring and an increased risk of bleeding. There has been tremendous interest in novel anticoagulant agents and nonpharmacological devices that overcome these limitations.^2–4 Previously, our group published a decision‐analytic model that evaluated the cost‐effectiveness of left atrial appendage (LAA) occlusion devices compared with dabigatran and warfarin for stroke prevention in AF.⁵ LAA occlusion devices were cost effective compared with warfarin; however, we found that there was substantial uncertainty surrounding this conclusion.⁶

Decision‐analytic modeling provides a framework to explicitly incorporate all available evidence in order to weigh the potential benefits and trade‐offs of alternative treatment options.^7–8 Model parameters are often obtained from the published literature.⁷ Such data are uncertain or imperfect, meaning that they have uncertainty, typically represented by confidence intervals.⁸ The confidence intervals represent the range across which the true certain value is likely to be located, with 95% certainty. If the available research is sparse, the uncertainty around a parameter can be substantial (ie, a wide confidence interval). When an uncertain parameter is entered into a model, this uncertainty is propagated into the model's final output, leading to the potential for the model results to be incorrect.⁶ For a decision maker, it is important to know the likelihood of an incorrect conclusion and the consequences of making an incorrect decision.

Value of information (VOI) analysis is a methodological extension of decision‐analytic modeling that addresses the aforementioned issues.^7–8 VOI quantifies the potential costs of uncertainty by determining the expected consequences of an incorrect decision based on uncertain data.⁸ Uncertainty can be reduced by new research; it is important to know where one should focus this research based on the relative impact of uncertainty in one parameter versus another. The choice of research priority will have important implications for the allocation of further research funds and the design of subsequent studies. In our AF model, comparative data on LAA occlusion devices were very sparse; therefore, the parameter estimates had substantial uncertainty.^3–4 Future research will reduce this uncertainty. However, as with most complex clinical problems, there are multiple potential areas of uncertainty and resulting difficulty in knowing how to focus new research. With LAA occlusion devices, for example, is it of greater importance to generate better data on periprocedural complications or on the efficacy of stroke prophylaxis? An important use of VOI analyses is to shape future research so as to reduce decision uncertainty.^9–12.

Accordingly, our objective was to identify research priorities in stroke prophylaxis for AF using VOI methods. Our target audiences are cardiovascular clinicians and researchers with health services interest and expertise who may not be familiar with this particular method.

Methods

This study was approved by the institutional research ethics board at Sunnybrook Health Sciences Centre in Toronto, Canada.

We designed a Markov decision‐analytic model. In a Markov model, at any 1 point in time, patients may exist in mutually exclusive health states (eg, death or stroke). The time spent in a particular health state is termed the cycle length of the model. Transitions from one health state to another are based on transitional probabilities that are input into the model. Every health state is associated with a particular cost and a utility weight. The utility weight is a factor that adjusts for the quality of life of the time spent in a particular health state; this can range from a lower limit of “0” for death and a ceiling of “1” for perfect health. Our model was a microsimulation in which each patient moved through the model individually. The cumulative effectiveness and cost for an individual patient was estimated by the summation of the quality‐adjusted life gained and costs accumulated in each health state that the individual transitioned through until death. This process was repeated for all of the patients in the microsimulation, and an average was calculated for the model. In the following sections, a more technical description of the model is provided.

Model Details

We will briefly describe the cost–utility decision model from our previously published paper (Figure 1). We developed a microsimulation model with 10 000 individual patient iterations (referred to as inner loops) to assess the costs and outcomes for patients with AF at risk of stroke without contraindications to oral anticoagulation.⁵ Three treatment strategies were evaluated in the original paper: (1) dose‐adjusted warfarin with a target international normalized ratio of 2.0 to 3.0, (2) dabigatran, and (3) an LAA occlusion device.⁵

Figure 1.

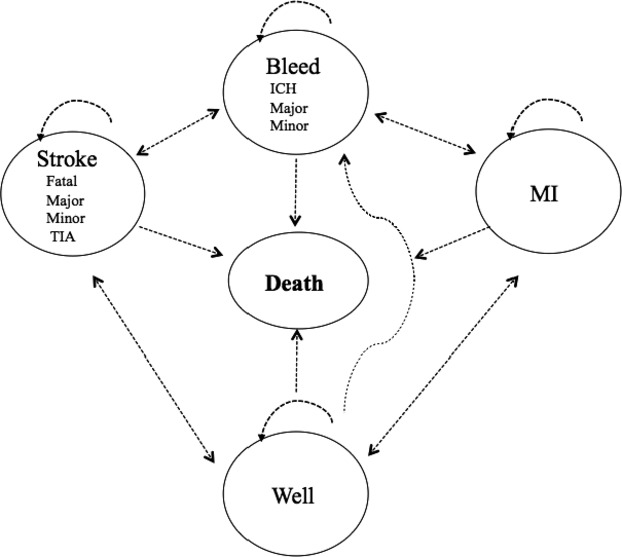
Structure of the decision model. For each of the treatment options patients can be in 1 of 5 health states: well, sustain an MI, have a stroke, bleed, or die. Patients may transition from one health state to another after each cycle (1 month). ICH indicates intracranial hemorrhage; MI, myocardial infarction; TIA, transient ischemic attack.

Outcomes of interest were life expectancy (measured in years), quality‐adjusted life years (QALY), costs (reported in 2012 Canadian dollars), and the incremental cost‐effectiveness ratio. The model was analyzed from the perspective of the Ontario Ministry of Health and Long‐Term Care (MOHLTC), the third‐party payer for government‐insured health services in the province of Ontario, Canada. Cycle length was 1 month, with a lifetime time horizon.⁵ All health outcomes and costs were discounted at 5% per year, as per recommendations from the Canadian Agency for Drug and Technology in Health.¹³ Effectiveness and utility data were obtained from the published literature. Cost data were obtained from the Ontario Drug Benefits Formulary and the Ontario Case Costing Initiative.

We found that warfarin therapy had the lowest discounted QALYs at 4.55, followed by dabigatran at 4.64 and LAA occlusion devices at 4.68. The average discounted lifetime cost was $21 429 for a patient taking warfarin, $25 760 for a patient taking dabigatran, and $27 003 for LAA occlusion devices. Compared with warfarin, the incremental cost‐effectiveness ratio for LAA occlusion devices was $41 565, whereas that for dabigatran was $46 560. Consequently, the LAA occlusion device was the preferred option.⁵ We quantified parameter uncertainty through a probabilistic sensitivity analysis using Monte‐Carlo simulations with 1000 outer loops in addition to the 10 000 inner loops. The outer loops draw possible values from a distribution for each parameter and keep it fixed in each simulation of the inner loop. Distributions were created for each of the 129 parameters and were based on means and standard deviations from source documentation. For each outer loop, the net monetary benefit (NMB) was calculated for LAA occlusion devices, dabigatran, and warfarin.

NMB is the difference between cost and the product of QALY and a willingness to pay (WTP) threshold (NMB=QALY×WTP−cost).⁷ The strategy with the highest NMB in a particular outer loop is the preferred option.⁷ A cost‐effectiveness acceptability curve shows the proportion of the 1000 outer loops with LAA occlusion device being the preferred option (ie, higher NMB) at different WTP thresholds from $0 to $100 000.¹⁴ Our cost‐effectiveness acceptability curve showed a considerable amount of decision uncertainty because the strategy of the LAA occlusion device was cost effective in only 47% of simulations using a WTP threshold of $100 000, whereas dabigatran was the preferred option in ≈20% of simulations at this WTP (Figure 2).

Figure 2.

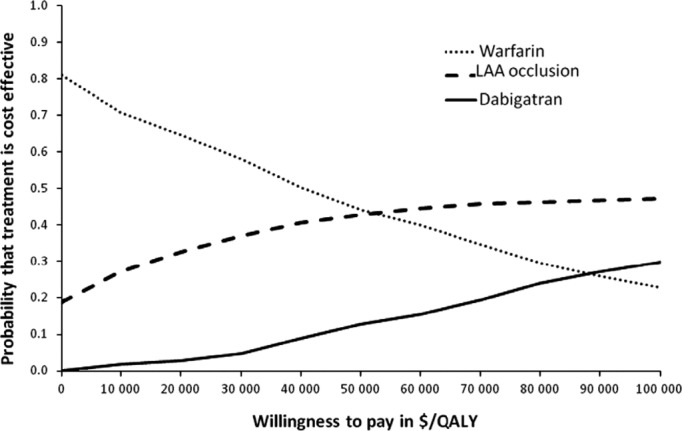
Cost‐effectiveness acceptability curve. A probabilistic sensitivity analysis was performed with 1000 outer loops and 10 000 inner loops. Willingness to pay is shown in 2012 Canadian dollars. LAA indicates left atrial appendage; QALY, quality‐adjusted life year.

Although the cost‐effectiveness acceptability curve indicates decisional uncertainty, the opportunity cost of that uncertainty is not apparent, that is, we do not know the consequences of being incorrect. In the following sections, we will describe VOI methods to quantify and explore the uncertainty in a decision model using the expected value of perfect information (EVPI) and the expected value of partial perfect information (EVPPI).

Value of Information

EVPI

The base‐case NMB results allow clinicians or policy makers to make a decision based on current, imperfect data. The optimal decision is to choose the intervention that generates the maximum expected NMB based on the current parameters in the model. If one theoretically obtains perfect information, there is the possibility that one of the other treatment options (eg, warfarin or dabigatran in our model) would have led to a higher NMB and thus would be the preferred option. In this hypothetical situation, we have incurred a cost in terms of health benefits and resources forgone by making an incorrect decision. This is the expected cost of uncertainty of this decision or the expected opportunity loss; it is a metric that is dependent on both the frequency of making an incorrect decision and the consequences of that incorrect decision. We can calculate this metric using the EVPI, which is the difference between the NMB with perfect and current information.

To find the expected value of a decision made with perfect information, one averages the maximum NMB over the joint distribution of the parameters. This is operationalized in a decision‐analytic model using the results of each outer loop of the probabilistic sensitivity analysis. In Table 1, we show an example of the calculations needed for determining EVPI.

Table 1.

Sample Calculation of Expected Value of Perfect Information Using a Simulated Output of Costs, Effectiveness, and Net‐Monetary Benefit for 10 Iterations

	Treatment Strategy						Optimal Choice	Maximum Net Benefit ($)	Opportunity Loss (EVPI)
	Warfarin			LAA Occlusion Device
	Cost ($)	Effectiveness (QALY)	NMB (WTP=$100 000)	Cost ($)	Effectiveness (QALY)	NMB (WTP=$100 000)
Iteration 1	19 688.00	4.58	438 601.60	32 138.60	4.52	419 543.20	Warfarin	438 601.60	19 058.40
Iteration 2	19 881.70	4.58	437 745.50	20 514.90	4.84	463 363.40	LAA occlusion	463 363.40	0
Iteration 3	20 766.80	4.54	433 453.80	19 104.70	4.86	467 280.00	LAA occlusion	467 280.00	0
Iteration 4	20 168.70	4.55	435 035.00	26 638.20	4.67	440 207.70	LAA occlusion	440 207.70	0
Iteration 5	20 220.20	4.58	437 617.40	24 538.20	4.75	449 992.30	LAA occlusion	449 992.30	0
Iteration 6	20 343.20	4.56	435 430.20	25 111.00	4.71	445 595.70	LAA occlusion	445 595.70	0
Iteration 7	20 780.00	4.55	434 030.50	31 271.00	4.55	424 200.50	Warfarin	434 030.50	9830.0
Iteration 8	20 961.10	4.55	433 893.70	28 563.70	4.64	435 406.70	LAA occlusion	435 406.70	0
Iteration 9	20 019.80	4.55	435 033.60	27 927.60	4.62	434 547.60	Warfarin	435 033.60	486.0
Iteration 10	19 700.80	4.57	437 555.70	21 898.90	4.79	457 368.10	LAA occlusion	457 368.10	0
Overall expectation	20 253.00	4.56	435 839.70	25 770.70	4.70	443 750.50	LAA occlusion**	446 688.00	2937.40

Example of EVPI calculation: Each row of Table 1 represents the costs, effectiveness, and NMB for each treatment strategy for 10 sample outer‐loop iterations. With current information, we would choose the treatment strategy with the highest overall expected net benefit, which in this case is LAA occlusion with an expected net benefit of $443 750.50 (shown with **). With perfect information, we would choose the treatment strategy with the greatest net benefit for each iteration, that is, we would choose warfarin for iteration 1, an LAA occlusion device for iteration 2 to 6, warfarin for iteration 7, and so forth. If the preferred strategy for the iteration is different from the overall optimal strategy (ie, LAA occlusion device), then an opportunity cost is associated with that iteration. The opportunity cost for the iteration is the difference in NMB for the treatment strategies. In iteration 1, for example, warfarin is the preferred option; therefore, an opportunity cost exists for this iteration and is equal to the NMB of warfarin ($438 601.60)—NMB of LAA occlusion ($419 543.20). The average opportunity cost across all of the outer‐loop iterations represents the EVPI, which, in this example of 10 iterations, is $2937.40. The higher the EVPI, the larger the opportunity cost of an incorrect decision. EVPI indicates expected value of perfect information; LAA, left atrial appendage; NMB, net monetary benefit; QALY, quality‐adjusted life year; WTP, willingness to pay.

EVPPI

It is not possible to perform research to obtain perfect information on all parameters in the model. Instead, it is important to examine, through the EVPPI, the particular parameters that are most important in terms of having the greatest value of information. This method logically follows from EVPI because it identifies the key parameters for which more precise estimates will be most valuable and helps plan, prioritize, and fund future clinical research. EVPPI is calculated as the difference between the expected NMB with perfect information about our parameter of interest and the expected value with current information. Similar to calculations of EVPI, the true value of the parameter of interest is unknown, so the expected value of a decision made with perfect information is found by averaging the maximum net benefit over the joint distribution of that parameter. Operationally, it requires a third loop on our simulation, in which the parameter of interest is drawn from its distribution, whereas all other parameters are varied on the outer loop. We determine whether the preferred option for each third loop iteration is different from that for the overall analysis. If there is a difference, it represents an opportunity cost due to imperfect information on that parameter. The average opportunity cost across all of the third‐loop iterations represents the EVPPI.

In our model, we first performed EVPPI analyses to assess sets of parameters. Specifically, we did separate analyses for all probabilities (Table 2), costing parameters (Table 3), and utilities (Table 3). In this manner, we determined the relative impact of uncertainty in each of these sets of parameters. Finally, we did EVPPI analyses on individual parameters that were identified as important based on 1‐way deterministic sensitivity analyses with a WTP of $100 000 per QALY. Our model was sensitive to the odds ratio (OR) for stroke with LAA occlusion devices. This stroke OR had a value of 1.34 with a 95% confidence interval from 0.81 to 2.21. We did a final EVPPI with the OR for stroke with an LAA occlusion device in the third outer loop, as a log‐normal distribution.

Table 2.

Model Variables and Ranges Used in Sensitivity Analyses

	Value	Low	High	Distribution
Age	76	74.47	77.53	Normal
Male sex	0.5	0.484	0.516	Beta
Disease prevalence
Diabetes	0.255	0.241	0.269	Beta
Heart failure	0.314	0.299	0.329	Beta
Hypertension	0.824	0.812	0.836	Beta
Stroke	0.19	0.177	0.203	Beta
MI	0.166	0.154	0.178	Beta
Bleed history	0.085	0.076	0.094	Beta
Abnormal liver function	0.309	0.294	0.324	Beta
Abnormal renal function	0.097	0.088	0.107	Beta
Excessive alcohol consumption	0.027	0.022	0.032	Beta
Labile INR	0.268	0.179	0.357	Beta
Vascular disease	0.0362	0.035	0.038	Beta
Disease incidence (1 year)
Diabetes	0.63	0.42	0.84	Beta
Hypertension	3.21	3.17	3.25	Beta
Heart failure	1.93	1.75	2.11	Beta
2‐year medication discontinuation rates
Warfarin	0.166	0.161	0.171	Beta
Dabigatran 150 mg bid	0.212	0.207	0.217	Beta
Dabigatran 110 mg bid	0.207	0.202	0.212	Beta
HR of death after ICH
0 to 1 months	20.8	13.87	27.73	Log‐normal
1 to 12 months	4.5	3.0	6.0	Log‐normal
12 to 72 months	2.2	1.47	2.93	Log‐normal
HR of death after bleed
0 to 8 months	4.2	3.28	5.12	Log‐normal
HR of death after major stroke
0 to 8 months	8.2	6.39	10.01	Log‐normal
8 to 54 months	2.17	1.45	2.89	Log‐normal
HR of death after minor stroke
0 to 8 months	2.5	1.01	3.99	Log‐normal
HR of death after MI
0 to 60 months	1.7	1.13	2.27	Log‐normal
60 to 120 months	1.2	0.8	1.6	Log‐normal
Stroke OR
Warfarin	0.31	0.21	0.41	Log‐normal
Dabigatran 150 mg	(0.76×warfarin OR)	0.66	0.86	Log‐normal
Dabigatran 110 mg	(1.11×warfarin OR)	1.03	1.19	Log‐normal
LAA occlusion device	(1.34×warfarin OR)	0.32	2.36	Log‐normal
Proportion of patients with
Fatal stroke	0.082	0.055	0.109	Beta
Major stroke	0.402	0.268	0.536	Beta
Minor stroke	0.425	0.283	0.567	Beta
TIA	0.091	0.061	0.121	Beta
Bleeding odds ratio
Warfarin	1	—	—	Log‐normal
Dabigatran 150 mg	0.91	0.88	0.94	Log‐normal
Dabigatran 110 mg	0.78	0.76	0.80	Log‐normal
LAA occlusion
<6 months	0.837	0.56	1.12	Log‐normal
≥6 months	0.62	0.23	1.01	Log‐normal
Dual antiplatelet plus OAC	1.4	0.93	1.87	Log‐normal
Proportion of patients with
ICH	0.021	0.015	0.027	Beta
Fatal ICH	0.308	0.269	0.347	Beta
Major bleed	0.298	0.279	0.317	Beta
Minor bleed	0.68	0.661	0.699	Beta
1‐year probability of MI
Warfarin	0.53	0.0044	0.0062	Beta
Dabigatran 150 mg	0.72	0.0063	0.0085	Beta
Dabigatran 110 mg	0.74	0.0061	0.0083	Beta
OR for reduction in MI risk with use of dual antiplatelet agents	0.77	0.71	0.83	Log‐normal

Abnormal liver function includes chronic hepatic disease, cirrhosis, or biochemical evidence of significant hepatic derangement. Abnormal renal function includes chronic dialysis, renal transplantation, or serum creatinine ≥200 μmol/L. Bleed history includes anemia. Excessive alcohol consumption is defined as ≥8 alcoholic drinks per week. Hypertension is defined as systolic blood pressure >160 mm Hg. Labile INR is time in therapeutic range <60%. Major bleeding is any bleeding requiring hospitalization and/or causing a decrease in hemoglobin level of >2 g/L and/or requiring blood transfusion that was not a hemorrhagic stroke. Stroke is a focal neurologic deficit of sudden onset, diagnosed by a neurologist, and lasting >24 hours. Vascular disease includes peripheral artery disease, prior myocardial infarction, or aortic plaque. Bid indicates twice a day; HR, hazard ratio; ICH, intracranial hemorrhage; INR, international normalized ratio; LAA, left atrial appendage; MI, myocardial infarction; OAC, oral anticoagulants; OR, odds ratio; TIA, transient ischemic attack.

Table 3.

Health Utilities and Costs With Ranges Used in Sensitivity Analyses

	Value	Low	High	Distribution
Health state utilities
Atrial fibrillation	0.998	0.665	1	Beta
ICH	0.189	0.126	0.252	Beta
Major stroke 1st year	0.3	0.2	0.4	Beta
Major stroke 2nd year	0.4	0.27	0.53	Beta
Abnormal renal function	0.58	0.39	0.77	Beta
Heart failure	0.63	0.61	0.65	Beta
Hypertension	0.72	0.71	0.73	Beta
Minor stroke 1 month	0.75	0.5	1	Beta
Vascular disease	0.8	0.53	1	Beta
Diabetes mellitus	0.84	0.56	1	Beta
MI 1st year	0.87	0.67	1	Beta
MI 2nd year	0.94	0.62	1	Beta
MI thereafter	0.95	0.63	1	Beta
Abnormal liver function	0.92	0.61	1	Beta
Utility decrement warfarin	0.013	0	0	Beta
Utility decrement dabigatran	0.006	0	0	Beta
Utility decrement aspirin	0.002	0	0	Beta
Utility decrement major bleed	0.159	0	0	Beta
Utility decrement pericardial effusion	0.159	0	0	Beta
Utility decrement device embolization	0.25	0	0	Beta
Utility decrement procedure‐related stroke	0.25	0	0	Beta
Utility decrement LAA implant	0.06	0	0	Beta
Costs
Medication costs (monthly)
Warfarin	$36	24	48	Gamma
Dabigatran	$99	—	—	—
Aspirin	$0.93	0.62	1.23	Gamma
Aspirin plus clopidogrel	$31	21	42	Gamma
Transitional 1‐time costs
Stroke (major minor, TIA)	$6595	12	13 178	Gamma
ICH	$15 190	10 127	20 253	Gamma
Major bleed	$4890	3260	6520	Gamma
Minor bleed	$77	51	102	Gamma
MI	$8972	122	17 822	Gamma
Ongoing monthly costs
ICH	$6335	4223	8446	Gamma
Major stroke	$6001	4001	8001	Gamma
Minor stroke	$2745	1830	3660	Gamma
MI	$317	211	422	Gamma
LAA occlusion device costs
Unit cost per device	$8500	6800	10 200	Gamma
Anesthesia fee	$500	—	—	—
Nursing fee	$1700	1500	2000	Gamma
Physician fee	$456	—	—	—
1 night hospitalization	$1773	—	—	—
TEE at procedure	$211	—	—	—
6‐week/month TEE	$303	—	—	Gamma
LAA occlusion device complications
Pericardial effusion	$9900	6600	13 200	Gamma
Device embolization	$26 428	17 618	35 237	Gamma
Procedure‐related stroke	$6595	12	13.178	Gamma

ICH indicates intracranial hemorrhage; LAA, left atrial appendage; MI, myocardial infarction; TEE, transesophageal echocardiogram; TIA, transient ischemic attack.

Population EVPI and EVPPI

The framework for both EVPI and EVPPI can be extended beyond the individual patient level to all other current and future patients.⁸ The population EVPPI represents the incremental NMB for the population of patients that may benefit from additional information over the expected lifetime of the technology. The expected lifetime of the technology is the period over which information about the current decision would be useful; this choice of time horizon depends on future changes in technologies, prices, and evidence and, as such, is an approximation. Because our original model was done from the perspective of the Ontario MOHLTC and thus included only costs incurred by this payer, we determined the number of incident AF patients over a 5‐year period from April 1, 2005, to March 31, 2010, through linkage with administrative databases held at the Institute for Clinical Evaluative Sciences. We assumed that this 5‐year period was the period over which the new information would be valuable. We restricted our cohort to patients who had a new emergency room visit for AF in the National Ambulatory Care Reporting Service (NACRS) database, which contains data for hospital‐based ambulatory care, including emergency department visits.^15–18 This source has been previously validated for accuracy in identifying AF patients.^15–18 We excluded patients with AF in the previous 3 years and restricted our cohort to patients with a CHA₂DS₂‐VASc (Congestive Heart Failure, Hypertension, Age ≥75 Years, Diabetes Mellitus, Stroke, Vascular Disease, Age 65 to 74 Years, Sex Category) stroke risk score of ≥2, who would qualify for stroke prophylaxis.¹⁹ We identified 30 727 incident cases over the 5 years, and that group represented the population of interest. We assumed a uniform incidence over the 5 years, calculated as an annual incidence of 6145 cases per year. The population EVPI and EVPPI is calculated as the product of the incident cases and individual EVPI or EVPPI per year, summed over the time horizon of 5 years. Consistent with our original economic model, we discounted the population VOI estimates at a rate of 5% per year.

Statistics

All analyses were conducted using TreeAge Pro Suite 2012 software release 2 (TreeAge Software Inc). In our model, the EVPI was calculated based on 1000 outer loops and 10 000 inner loops, consistent with the cost‐effectiveness acceptability curve. For the EVPPI calculations, given their computational intensity, we performed 250 iterations on each of the inner, second, and third loops. We used a WTP threshold of $100 000 per QALY in all calculations.

Results

Value of Information

EVPI

The EVPI for the comparison of LAA occlusion devices, dabigatran, and warfarin was $8542 per patient at a WTP threshold of $100 000 per QALY (Table 4). The population EVPI based on incident AF cases in Ontario was $227.3 million. These values are the upper bound of the expected opportunity loss from having imperfect information on all of the parameters in our model and represent the maximum amount that the Ontario MOHLTC should spend on research comparing these 3 strategies for stroke prophylaxis in AF.

Table 4.

EVPI and EVPPI Results

	Willingness to Pay Threshold of $100 000
	Per Patient	Population
EVPI	$8542	$227.3 million
EVPPI for utilities	$1181	$31.4 million
EVPPI for cost	$503	$13.3 million
EVPPI for probabilities	$6875	$182.9 million
EVPPI for LAA occlusion device stroke odds ratio	$7312	$194.5 million

EVPI indicates expected value of perfect information; EVPPI, expected value of partial perfect information; LAA, left atrial appendage.

EVPPI

The results of the EVPPI calculations are found in Table 4. The EVPPI for the set of probability parameters represented the most important source of uncertainty, at $6875 per patient at a WTP of $100 000. In contrast, the impact of uncertainty in the utilities and cost parameters was relatively modest at $1881 and $503, respectively, per patient at this threshold. Further refining the parameters chosen for the EVPPI using 1‐way sensitivity analyses results, we calculated the EVPPI on the OR for stroke with LAA occlusion devices. At a WTP threshold of $100 000, the EVPPI for the OR for stroke with an LAA occlusion device was $7312 per patient. This represented 86% of the total EVPI, reinforcing the importance of the uncertainty in this parameter and highlighting that this should be a priority for research. The population EVPPI for the OR for stroke with an LAA occlusion device was $194.5 million, which represents the maximum amount the Ontario MOHLTC should spend on further research to improve this 1 parameter.

Discussion

In this paper, we present VOI analyses to understand the sources of uncertainty when comparing LAA occlusion devices with dabigatran or warfarin for stroke prophylaxis in AF and to identify priorities for further research in this area. We found that although LAA occlusion devices are cost effective based on current data, there was a considerable amount of uncertainty. This uncertainty is particularly focused on data regarding the relative efficacy of LAA occlusion devices in ischemic stroke prevention compared with warfarin. Our study suggests that refining this single parameter through further research will be of particular importance in reducing decisional uncertainty.

Cost‐effectiveness reports are increasingly published in general medical and cardiovascular scientific journals as opposed to specialized technical journals in health economics. We are enthusiastic supporters of the more widespread availability of such scientific manuscripts. In particular, we believe cost‐effectiveness is especially relevant in cardiovascular disease, given that it is the most expensive medical condition to treat. With the current environment of budgetary constraints, health technology assessments and cost‐effectiveness analyses provide important information to policy makers on the efficient use of scarce resources.²⁰ We believe a comprehensive approach to evaluating the uncertainty in such models is key to their best use.

There are numerous types of uncertainty in economic models. Current guidelines highlight the presence of first‐order uncertainty, heterogeneity, structural uncertainty, and parameter uncertainty.⁶ First‐order uncertainty or variability is the random variation that can occur between identical patients.⁶ It is represented in a model through microsimulation. Heterogeneity is the variability between patients that can be attributed to patient characteristics.⁶ Often modelers examine heterogeneity through the use of scenario analyses. Structural uncertainty is due to assumptions inherent in the modeling form.⁶ The impact of this uncertainty can be tested by using different modeling structures with alternative assumptions to determine whether there are qualitative differences in the conclusions. Parameter uncertainty is due to uncertainty in the estimation of the input parameters, in other words, uncertainty due to imperfect data.

Parameter uncertainty can be reduced through the acquisition of more perfect parameters. Typically this requires new research. The VOI methods presented in this paper allow researchers and policy makers to determine whether the effort of acquiring additional data through new research is worthwhile. In addition, these methods provide insight as to how that research should be focused. We believe that both of these areas are important because they will help direct to whom and how research funding is allocated.

It is insightful to use our example to illustrate each step in the examination of model uncertainty. In our model of LAA occlusion devices versus dabigatran or warfarin, we found that based on the best currently available information, LAA occlusion devices were a cost‐effective option; however, there was an almost 50% probability that this conclusion was incorrect, based on the cost‐effectiveness acceptability curve. The impact of this incorrect decision was determined by the EVPI, at almost $8542 per patient. To put this number in context, the EVPI per patient for comparing 3 bronchodilators for chronic obstructive lung disease was ≈€1985,¹² whereas the EVPI for magnetic resonance imaging in knee trauma was estimated to be only €2.1.²¹ Consequently, there is substantial value in allocating research to AF. The EVPPI analyses indicate that we should focus our future research on improving probability parameters, specifically, improving the precision of the OR of LAA occlusion devices in preventing stroke in comparison to warfarin. The population EVPPI of $194.5 million for this parameter is a very conservative estimate because it includes only patients in Ontario, whereas one would expect new knowledge from a new study in this area to affect patients in other jurisdictions. The population EVPI represents the ceiling of funding that a policy maker should allocate to this area. This can then be combined with other information, such as feasibility of evaluation; relevance to contemporary practice; and, importantly, the cost of conducting the actual research to make final allocation decisions.

Expected value of sample information is a methodological extension that allows one to explicitly consider the cost of the actual research in making a decision. Population EVPI and EVPPI provide an upper bound of how much should be spent on all further research to eliminate all uncertainty; however, any 1 future study will not eliminate uncertainty but rather will reduce uncertainty by a factor that will be proportional to its design, in particular, its sample size. For a randomized controlled trial with the exact same protocol, and thus internal validity, a study with a larger sample size would expect to have a greater impact on lowering decisional uncertainty. Balanced against this is the fact that larger trials would require higher levels of funding. Moreover, the design and the study outcomes may have implications for the cost of the study; for example, the cost of conducting research on utilities may be extremely inexpensive compared with research on probabilities. Expected value of sample information allows one to balance the cost of conducting a particular type of study and the value of the data expected from the study.²² The expected value of sample information provides the upper bound of funds that should be spent on any 1 specific future trial.²² These advanced methods require additional software beyond that used to create our current AF model and, as such, are beyond the scope of this manuscript. We advise interested readers to review the work of Briggs et al,⁸ Yokota and Thompson,¹¹ Ades et al,²² and Janssen and Koffijberg.²³

Our study should be interpreted in the context of several limitations that merit discussion. First, although we argue that VOI analyses should be part of the process of planning new research, we are not suggesting that they be the sole consideration. Second, the computational intensity of VOI analyses often precludes very complex models. Consequently, models will necessarily require many simplifying assumptions. This reinforces that suggestion that, despite our presentation of only EVPI and EVPPI analyses, a more comprehensive presentation of all forms of uncertainty, including first‐order, structural, and parameter uncertainty should be part of the presentation of all economic models. In the EVPPI analyses, we restricted our simulations to only 250 iterations because this was the limit of computational feasibility with random sampling, despite the use of 32‐core cloud computing. To overcome the limitation of computational intensity, more efficient sampling techniques have been developed, such as Latin hypercube sampling or orthogonal arrays.^24–25 Finally, in our primary analysis, we have looked only at LAA occlusion devices versus dabigatran or warfarin. Given the newer anticoagulants on the market such as apixaban and rivaroxaban, understanding where the uncertainty lies when all alternatives are included is an important next step to direct further research.

In conclusion, we have presented an example of using VOI analyses to help prioritize research in stroke prophylaxis in AF. We found that improving the estimates of the relative efficacy of LAA occlusion devices compared with warfarin in stroke prevention should be the most important focus for future research in this field.